Muscle Synergies May Improve Optimization Prediction of Knee Contact Forces During Walking

Abstract

The ability to predict patient-specific joint contact and muscle forces accurately could improve the treatment of walking-related disorders. Muscle synergy analysis, which decomposes a large number of muscle electromyographic (EMG) signals into a small number of synergy control signals, could reduce the dimensionality and thus redundancy of the muscle and contact force prediction process. This study investigated whether use of subject-specific synergy controls can improve optimization prediction of knee contact forces during walking. To generate the predictions, we performed mixed dynamic muscle force optimizations (i.e., inverse skeletal dynamics with forward muscle activation and contraction dynamics) using data collected from a subject implanted with a force-measuring knee replacement. Twelve optimization problems (three cases with four subcases each) that minimized the sum of squares of muscle excitations were formulated to investigate how synergy controls affect knee contact force predictions. The three cases were: (1) Calibrate+Match where muscle model parameter values were calibrated and experimental knee contact forces were simultaneously matched, (2) Precalibrate+Predict where experimental knee contact forces were predicted using precalibrated muscle model parameters values from the first case, and (3) Calibrate+Predict where muscle model parameter values were calibrated and experimental knee contact forces were simultaneously predicted, all while matching inverse dynamic loads at the hip, knee, and ankle. The four subcases used either 44 independent controls or five synergy controls with and without EMG shape tracking. For the Calibrate+Match case, all four subcases closely reproduced the measured medial and lateral knee contact forces (R² ≥ 0.94, root-mean-square (RMS) error < 66 N), indicating sufficient model fidelity for contact force prediction. For the Precalibrate+Predict and Calibrate+Predict cases, synergy controls yielded better contact force predictions (0.61 < R² < 0.90, 83 N < RMS error < 161 N) than did independent controls (-0.15 < R² < 0.79, 124 N < RMS error < 343 N) for corresponding subcases. For independent controls, contact force predictions improved when precalibrated model parameter values or EMG shape tracking was used. For synergy controls, contact force predictions were relatively insensitive to how model parameter values were calibrated, while EMG shape tracking made lateral (but not medial) contact force predictions worse. For the subject and optimization cost function analyzed in this study, use of subject-specific synergy controls improved the accuracy of knee contact force predictions, especially for lateral contact force when EMG shape tracking was omitted, and reduced prediction sensitivity to uncertainties in muscle model parameter values.

Introduction

Knowledge of subject-specific joint contact and muscle forces during activities of daily living could improve the treatment of movement-related disorders such as osteoarthritis, stroke, cerebral palsy, and Parkinson's disease [1]. However, it is currently impossible to measure these quantities in vivo, and calculating them with musculoskeletal computer models is hindered by the redundant nature of human neural control (i.e., more muscles than degrees of freedom in the skeleton). Walking is a particularly important activity of daily living to understand since loss of mobility is associated with increased morbidity and decreased quality of life [2].

To address the muscle redundancy problem, numerous studies have used optimization methods to estimate a unique set of muscle (and sometimes joint contact) forces during walking [3–11]. The challenge for optimization methods is that the cost function being minimized by the human body (if it exists) remains unknown. Furthermore, this cost function is likely to be invalid for individuals with movement disorders. Some studies have attempted to address these issues by taking advantage of muscle electromyographic (EMG) signals measured during gait [12–15]. Rather than predicting muscle excitations based on a selected optimization cost function, these studies controlled muscle excitations in their models directly with processed experimental EMG data after calibrating muscle model parameter values via an optimization process. Controlling muscles with processed EMG data reduces redundancy, and no assumptions are required regarding the control strategy being used by the nervous system. However, crosstalk and noise in EMG signals [16,17], along with uncertainties in calibrated muscle model parameter values, pose challenges for this approach. Furthermore, EMG data are difficult or impossible to collect from deep muscles, and specifying excitations for muscles without EMG data remains a challenge.

Other studies have used muscle synergy analysis to explore how the human nervous system reduces control complexity during walking [18–20]. The key concept behind muscle synergy analysis is dimensionality reduction. The analysis assumes that processed muscle EMG signals are not independent from one another but can be factored into a smaller number of independent control signals called neural commands. The processed EMG signals can then be closely reconstructed using a linear combination of the calculated neural commands. For walking, only three to seven neural commands are typically required to account for over 90% of the variability in as many as 32 processed lower extremity EMG signals [18–20]. To date, muscle synergy analysis has been used primarily for analyzing experimental EMG data, with only a few studies using it to inform muscle force optimizations [8,10,21–23]. Use of experimentally determined neural commands to drive simulated muscle excitations may reduce control redundancy by limiting the excitations that can be constructed. Furthermore, it could minimize the effect of any EMG crosstalk that may be present. While these potential benefits are being explored for muscle force predictions, they have yet to be investigated for contact force predictions in the knee during walking.

This study evaluated whether use of experimentally calculated neural commands to control simulated muscle excitations improves knee contact force predictions generated by a subject-specific musculoskeletal model. The study was performed by applying a mixed dynamic optimization technique (i.e., inverse skeletal dynamics with forward muscle activation and contraction dynamics) to walking data collected from a subject implanted with a force-measuring knee replacement. Twelve optimization problems were formulated to investigate how using independent muscle excitations versus interdependent muscle excitations constructed from a small number of neural commands affects knee contact force predictions, with secondary consideration of how calibration of muscle model parameter values and tracking of experimental EMG shapes influence the predictions. In addition to evaluating contact force predictions using the instrumented knee data, we also evaluated muscle excitation predictions for problem formulations that did not track experimental EMG data. Availability of instrumented knee data provided a unique opportunity to evaluate the tradeoffs of the different optimization approaches.

Methods

Experimental Data.

Experimental data from the Third Grand Challenge Competition to Predict in vivo Knee Loads [24] were used for this study. The data were collected from a single subject implanted with a force-measuring knee replacement (female, left knee, age: 69 y, mass: 78 kg, height: 167 cm). Institutional review board approval and subject informed consent were obtained prior to testing. The subject performed overground walking trials at a self-selected speed (1.3 m/s) while marker trajectory, ground reaction force and moment, EMG, and knee implant load data were collected simultaneously (for data collection details, please see Ref. [24]). One representative normal walking cycle was selected for analysis. For knee implant loads, three orthogonal forces and moments were measured at the center of the tibial post and level with the top surface of the tibial tray [25]. EMG data were collected from 13 muscles including the biceps femoris long head (BifemLH), semimembranosus (Semimem), medial gastrocnemius (MedGas), lateral gastrocnemius (LatGas), tensor fascia latae (TFL), vastus lateralis (VasLat), rectus femoris (RF), sartorius (Sart), gracilis (Grac), soleus (Sol), tibialis anterior (TA), peroneus longus (PerLong), and adductor magnus (AddMag). These data were high-pass filtered (zero-lag fourth-order Butterworth at 30 Hz), full-wave rectified, and low-pass filtered (zero-lag fourth-order Butterworth at 6 Hz) to create experimental muscle excitation profiles. Ground reaction and knee contact loads were also filtered with a zero-lag fourth-order Butterworth filter with a cutoff frequency of 6 Hz for consistency with kinematic and EMG data [26].

Muscle synergy analysis was performed on the 13 experimental EMG profiles to calculate neural commands (i.e., a lower-dimensional set of time-varying signals) and synergy vectors (i.e., the sets of weights that specify how each neural command contributes to the excitation of each muscle) using nonnegative matrix factorization (NMF) [27,28]. To achieve equal weighting between muscles for the NMF analysis, we normalized each processed EMG signal to its maximum value over the selected gait cycle, which resulted in the magnitude of all EMG signals ranging from zero to one. The number of synergies was increased until the variance accounted for (VAF) was at least 95% for each muscle [18]. Five muscle synergies were found to be sufficient, and the five resulting neural commands were used to define synergy controls for all muscles (Fig. 1). Further details on our muscle synergy analysis method can be found in the http://dx.doi.org/10.1115/1.4026428 to be linked here April 2014.

Fig. 1.

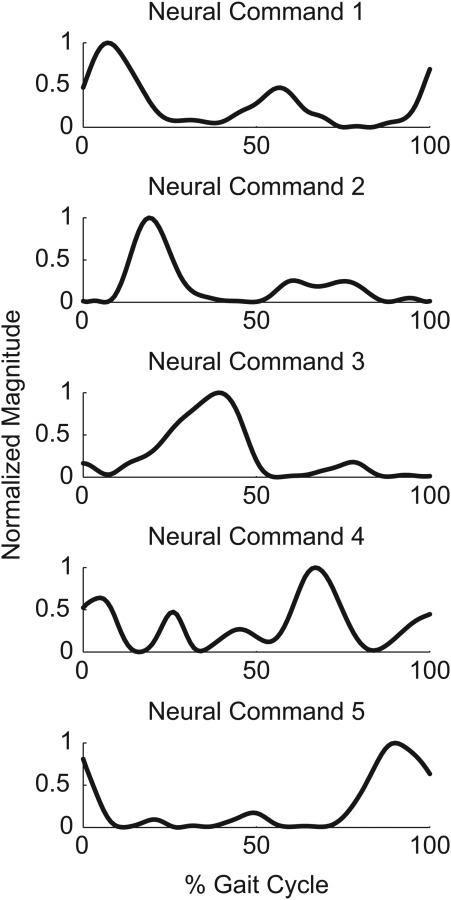
Normalized neural command curves calculated from 13 processed experimental EMG signals. These five neural commands were able to account for 95% of the variability in all experimental EMG curves and were used to construct 44 simulated muscle excitation signals for muscle force optimizations using synergy controls.

Musculoskeletal Model.

We created a subject-specific musculoskeletal model in OpenSim [29] by combining a subject-specific inverse dynamic skeletal model with subject-specific implant-bone geometric models. The subject-specific inverse dynamic model was created from a full-body dynamic walking model developed in Autolev (OnLine Dynamics, Sunnyvale, CA) and the subject's marker trajectory and ground reaction data [30,31]. The full-body model possessed 27 degrees of freedom (DOFs) including six DOFs between the pelvis and ground, three DOFs for the lower back, two DOFs for each shoulder, one DOF for each elbow, three DOFs for each hip, one DOF for each knee, and two DOFs for each ankle. Where possible, we defined locations of joint centers and orientations of joint axes in the implanted left leg to match anatomic measurements (e.g., distance between hip joint centers in the pelvis) made using subject-specific bone geometries. We calibrated the remaining joint parameter values along with segment inertial parameter values to the subject's movement data (i.e., static trial, joint range of motion trials, and the selected walking trial) via a previously published optimization process [30,31]. The cost function minimized marker tracking errors (inverse kinematics) while simultaneously minimizing residual forces and torques acting on the pelvis (dynamic consistency). After joint and inertial parameter values were calibrated in the full-body Autolev model, we constructed an OpenSim inverse dynamic model that replicated the pelvis and left leg of the calibrated Autolev model.

Subject-specific implant-bone geometric models were created from computerized tomography (CT) scans of the subject's pelvis and left leg and from polygonal surface models of the subject's implant components. Cortical bone edges were segmented from pre-surgery CT scan data spanning the knee, while cortical bone and metallic implant edges were segmented from post-surgery CT scan data spanning the pelvis to calcaneus. All segmentation was performed using commercial image processing software (SliceOmatic, Tomovision, Montreal, Canada). Polygonal surface geometry was constructed for each bone (pelvis, femur, patella, tibia, fibula, talus, and calcaneus) from the segmented point clouds using commercial reverse engineering software (Geomagic Studio, Raindrop Geomagic, Research Triangle Park, NC). The presurgery surface models for the femur, tibia, and patella were aligned to the corresponding post-surgery surface models, while surface models of the implant components were aligned to their post-surgery point clouds (femoral component and tibial tray) or bone peg holes (patellar button). After trimming and merging, the final implant-bone models consisted of the post-surgery bone models replaced with the pre-surgery distal femur, proximal tibia, and patella trimmed to accommodate the properly positioned implant components.

The final subject-specific musculoskeletal model was constructed by incorporating the subject-specific implant-bone geometric models into the subject-specific OpenSim inverse dynamic model. Alignment of the implant-bone models with the OpenSim kinematic model structure was achieved using corresponding joint centers and anatomical landmarks. The one DOF knee joint in the OpenSim model was redefined to permit six DOFs between the femoral component and tibial tray and six DOFs between the femoral component and patellar button. For the tibiofemoral joint, the origin was defined as the origin of the tibial tray so that inverse dynamic loads calculated by OpenSim would be consistent with contact loads measured by the instrumented implant. Forty-four lower extremity muscles were added to the model by scaling a generic OpenSim model [32] and transferring the scaled muscle attachment points and wrapping surfaces to the subject-specific bones. Nominal muscle model parameter values (tendon slack lengths, optimal fiber lengths, maximum isometric strengths, and pennation angles) were also obtained from the generic model. Further details on the model construction process can be found in the http://dx.doi.org/10.1115/1.4026428 to be linked here April 2014.

Joint kinematics for the OpenSim musculoskeletal model were calculated via a four-step process using a combination of marker trajectory, instrumented knee implant, and single-plane fluoroscopic knee motion data. Each step determined one or more kinematic trajectories needed for the subsequent steps. The four steps were: (1) initial inverse kinematic analysis to determine knee flexion kinematics, (2) optimization analysis to determine tibiofemoral kinematics, (3) optimization analysis to determine patellofemoral kinematics, and (4) final inverse kinematic analysis to determine pelvis, hip, and ankle kinematics. The first step calculated knee flexion kinematics using marker trajectory data for the selected walking trial. This step performed an initial inverse kinematic analysis in Matlab using the calibrated full-body Autolev model with a one DOF knee joint. The second step calculated more accurate tibiofemoral kinematics using knee flexion kinematics prescribed from the first step, instrumented implant data from the selected walking trial, and fluoroscopic knee motion data from treadmill gait collected from the same subject during a different test session. This step performed an optimization analysis in Matlab using a six DOF elastic foundation contact model of the subject's femoral component and tibial insert. For each time frame, the optimizer adjusted contact-sensitive DOFs (i.e., superior-inferior translation, varus-valgus rotation, and medial-lateral translation [33]) so that calculated contact forces matched measured tibial contact forces, while the remaining DOFs were locked at values from inverse kinematics (flexion angle) and fluoroscopy (anterior-posterior translation and internal-external rotation) [11,34]. The third step estimated patellofemoral kinematics using tibiofemoral kinematics prescribed from the first two steps. This step performed an optimization analysis in Matlab using a six DOF elastic foundation contact model of the subject's femoral component and patellar button with patella. For each time frame, the optimizer adjusted all six DOFs to balance calculated contact forces, patellar ligament forces (modeled as three linear springs), and initial estimates of quadriceps forces acting on the patella [11]. The fourth step calculated pelvis, hip, and ankle kinematics using marker trajectory data and knee kinematics prescribed from the previous three steps. This step performed a final inverse kinematic analysis in OpenSim using the subject-specific pelvis and left leg OpenSim model where the tibiofemoral and patellofemoral joints each possessed 6 DOFs.

Mixed Dynamic Optimization.

Leg muscle and knee contact forces were estimated using a mixed dynamic optimization approach combining inverse skeletal dynamics with forward muscle activation and contraction dynamics. Muscle forces were optimized to balance the inverse dynamic loads at the hip (three moments), knee (one or three loads), and ankle (two moments). Inverse dynamic loads represent the net loads experienced by a joint due to internal muscle, contact, and ligament forces. For the knee flexion moment, if contact and ligament forces are assumed to contribute minimally, this load can be balanced by muscle forces alone. For the knee superior-inferior force and varus-valgus moment, if measured tibiofemoral contact loads are applied to the inverse dynamic model and ligament forces are assumed to contribute minimally, these two additional inverse dynamic loads can also be balanced by muscle forces alone. Thus, access to measured knee contact loads permitted two categories of optimization problems: one that applied the measured contact loads to the subject-specific OpenSim model and balanced three inverse dynamic loads at the knee (used to verify that the model could reproduce the experimental knee contact forces) and another that predicted contact loads and balanced only one inverse dynamic load at the knee. To calculate knee contact forces with the OpenSim model, we used a validated regression equation for the subject's implant components that converted superior-inferior force and varus-valgus moment from inverse dynamics (with muscle forces applied) into medial and lateral contact forces [24].

During each optimization, muscle forces were calculated using models of activation and contraction dynamics where calculated muscle-tendon length and velocity trajectories provided boundary conditions for muscle force generation. Simulated muscle excitation signals were converted into simulated activation signals using excitation scaling, a pure time delay, activation dynamics, and a nonlinear function. Each excitation curve was scaled up or down with an excitation scaling parameter to define excitation magnitude. A pure time delay of 20 ms was added to account for electrical transmission time [35]. A linear first-order ordinary differential equation (ODE) with activation and deactivation time constants was used to model activation dynamics [36,37]. A two-phase nonlinear model was included to reshape the final activation curve based on methods reported for EMG-driven models [38]. Each resulting activation signal was converted into a tendon force using a Hill-type muscle-tendon model with compliant tendon [39]. A nonlinear first-order ODE with force-length and force-velocity properties was used to model contraction dynamics. Activation and contraction dynamics were solved in a computationally efficient manner by discretizing both ODEs using central differences and solving the resulting system of linear or nonlinear equations over all time frames simultaneously.

Muscle excitations were modeled using either 44 independent curves (henceforth called “independent controls”) or five neural command curves (henceforth called “synergy controls”) that were linearly combined to create 44 excitations. Each independent and synergy control curve was parameterized using 25 B-spline nodes treated as design variables. For the synergy controls, simulated neural command curves were restricted to remain close to the experimental neural command curves, and the weights in the associated synergy vectors were also treated as design variables.

Optimization Problem Formulations.

Twelve optimization problems were formulated comprised of three cases with four subcases each (Tables 1 and 2). The three cases (Table 1), which evaluated how calibration of muscle model parameter values influenced knee contact force predictions, were defined as follows: (1) Calibrate muscle model parameter values to match experimental knee contact forces by design (Calibrate+Match), (2) predict experimental knee contact forces using muscle model parameter values precalibrated by the first case (Precalibrate+Predict), and (3) calibrate muscle model parameter values while simultaneously predicting knee contact forces (Calibrate+Predict). The Calibrate+Match case tracked three inverse dynamic knee loads since the experimentally measured knee contact forces were applied to the model. The goal of this case was to verify that the model possessed sufficient fidelity to reproduce all experimental data simultaneously. If the experimental knee contact forces could not be reproduced when they were known, there would be little hope of predicting them accurately when they were not known. The Precalibrate+Predict and Calibrate+Predict cases tracked only one inverse dynamic knee load since the experimental contact forces were not applied to the model. The goal of these cases was to evaluate how well the model could perform true predictions of knee contact forces as a function of how muscle model parameter values were calibrated. The four subcases (Table 2) evaluated whether use of synergy controls in place of independent controls improved prediction of knee contact forces and whether tracking of experimental EMG shapes provided any additional benefit. The four subcases performed for each case were: (1) independent controls with EMG shape tracking (IndEMG), (2) synergy controls with EMG shape tracking (SynEMG), (3) independent controls without EMG shape tracking (Ind), and (4) synergy controls without EMG shape tracking (Syn). All optimization problems were solved using Matlab's unconstrained lsqnonlin nonlinear least squares algorithm.

Table 1.

Summary of three optimization cases (with four subcases each—see Table 2) that varied how muscle model parameter values were calibrated and whether experimental contact forces were tracked. Calibrate indicates that muscle model parameter values were calibrated by the optimization, while Precalibrate indicates that precalibrated muscle model parameter values were taken from the corresponding Calibrate+Match subcase. Match indicates that experimental contact forces were matched by tracking three rather than one inverse dynamic knee load, while Predict indicates that experimental knee contact forces were predicted by tracking only one inverse dynamic knee load. F/E indicates flexion/extension, S/I superior/inferior, and V/V varus/valgus.

Optimization Case Abbreviation	Model Parameter Calibration	Contact Force Tracking	Knee Loads Tracked
Calibrate+Match	Yes	Yes	F/E moment S/I force V/V moment
Precalibrate+Predict	No	No	F/E moment
Calibrate+Predict	Yes	No	F/E moment

Table 2.

Summary of four optimization subcases (performed for each case - see Table 1) that varied how muscle excitations were constructed and whether experimental EMG shapes were tracked. Ind indicates that all 44 muscle excitation controls were constructed independently, while Syn indicates that the 44 muscle excitation controls were constructed from linear combinations of only 5 neural commands obtained from synergy analysis of the 13 processed experimental EMG signals. EMG indicates that the shapes of processed experimental EMG signals were tracked.

Optimization Subcase Abbreviation	Control Method	EMG Tracking
IndEMG	Independent	Yes
SynEMG	Synergy	Yes
Ind	Independent	No
Syn	Synergy	No

Design variables for the 12 optimizations consisted of a combination of muscle excitation, muscle-tendon model, and musculoskeletal model parameter values. For the Calibrate+Match and Calibrate+Predict subcases, design variables were B-spline nodes for independent and synergy control curves, weights in synergy vectors (for synergy controls), excitation scaling parameters, electrical time delays, activation and deactivation time constants, nonlinearization parameters, tendon slack lengths, optimal muscle fiber lengths, tendon stiffness scaling parameters, muscle peak isometric forces, B-spline nodes defining changes in nominal tibiofemoral anterior-posterior translation, and B-spline nodes defining changes in nominal muscle moment arm curves. For the Precalibrate+Predict subcases, only design variables related to independent and synergy control curves, weights in synergy vectors, excitation scaling parameters, and tibiofemoral anterior-posterior translation were included, with all design variables related to muscle-tendon model and musculoskeletal model parameter values taken from the corresponding Calibrate+Match subcase.

The cost function for each optimization minimized muscle excitations and included penalty terms for tracking inverse dynamic loads at the hip, knee, and ankle and bounding changes in model parameter values within physiological ranges. For each type of muscle-tendon model parameter (e.g., peak isometric force), bounding was achieved by minimizing variations in individual parameter values away from corresponding literature values scaled by a single common scale factor. All quantities in the cost function were squared by the optimization algorithm. For optimizations involving EMG shape tracking, terms were added to track the shapes of processed experimental EMG curves. To facilitate optimization convergence, we solved each optimization problem using a modified univariate search method that varied groups of similar design variables separately (e.g., all peak isometric force values, then all tendon slack length values, etc.) before varying groups of different design variables together (e.g., all muscle excitation variables with all optimal fiber length values). To reduce the likelihood of entrapment in a local minimum, we perturbed all design variables by a small amount following each sequence of optimizations and repeated the process until the final cost function value changed by less than 5% between successive sequences.

Evaluation.

The ability of each optimization to track or predict medial and lateral knee contact forces was evaluated using medial, lateral, and total contact force R² (coefficient of determination) values and RMS errors. Tracking of inverse dynamic loads was evaluated using R² values for three hip, one or three knee, and two ankle loads. The similarity of simulated muscle excitation shapes to processed EMG shapes was evaluated using %VAF and R² values for muscles with experimental EMG data.

Results

Inverse Dynamic Loads.

All 12 optimizations tracked the inverse dynamic loads accurately with an average (standard deviation) R² value of 0.97 (0.01), with R² values for individual optimizations ranging between 0.94 and 0.99. Optimizations that used synergy controls (Syn and SynEMG subcases; average R² value = 0.97 (0.01)) tracked inverse dynamics loads as well as optimizations that used independent controls (Ind and IndEMG subcases; average R² value = 0.96 (0.01)).

Contact Forces.

Muscle model calibration method influenced the accuracy of contact force predictions. For the Calibrate +Match subcases, medial, lateral, and total contact force were reproduced closely with average R² values of 0.96 (<0.01), 0.95 (0.01), and 0.99 (<0.01), respectively (Figs. 2 and 3). For the Precalibrate+Predict subcases, medial, lateral, and total contact forces were predicted with lower average R² values of 0.76 (0.08), 0.74 (0.08), and 0.78 (0.06), respectively. For the Calibrate+Predict subcases, average R² values for medial, lateral, and total contact force were the lowest at 0.53 (0.46), 0.60 (0.25), and 0.59 (0.36), respectively. Contact force RMS errors for the three cases followed similar trends to the R² values (Figs. 2 and 3), with the lowest average medial and lateral RMS error being for the Calibrate +Match subcases (61 (5) N) and the highest average medial and lateral RMS errors being for the Calibrate+Predict subcases (180 (78) N). Sensitivity of predicted contact forces (Precalibrate+Predict versus Calibrate+Predict subcases) to how muscle model parameter values were calibrated was minimal for synergy controls (SynEMG and Syn) and more pronounced independent controls (IndEMG and Ind), especially when EMG shape tracking was omitted.

Fig. 2.

Root-mean-square errors and R² values for medial, lateral, and total knee contact force predictions from all optimizations. For the Calibrate+Match cases, muscle model parameter values were calibrated to match experimental knee contact forces. For the Precalibrate+Predict cases, experimental knee contact forces were predicted using precalibrated muscle model parameter values from the first case. For the Calibrate+Predict cases, muscle model parameter values were calibrated while knee contact forces were predicted simultaneously. Subcases that used synergy controls are indicated by the label Syn, while subcases that used independent controls are indicated by the label Ind. Subcases that tracked EMG shapes are indicated by the additional label EMG.

Fig. 3.

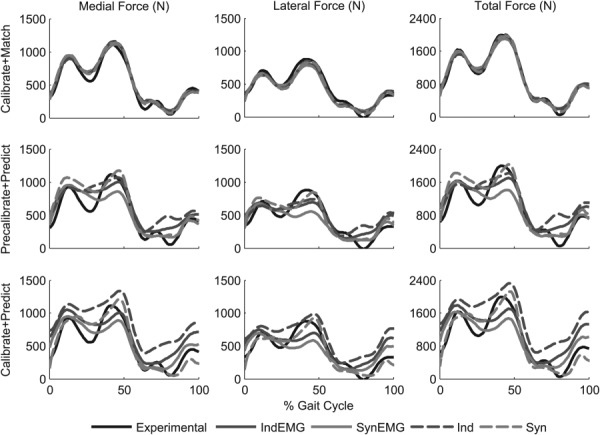
Experimental and predicted medial, lateral, and total knee contact forces for all optimizations. See caption of Fig. 2 for descriptions of cases and subcases.

For optimizations that predicted contact forces (Precalibrate+Predict and Calibrate+Predict cases), synergy controls (Syn and SynEMG subcases) improved contact force predictions (average medial, lateral, and total R² value = 0.79 (0.09)) compared to independent controls (Ind and IndEMG subcases; average R² value = 0.54 (0.31)). For the same cases, average medial and lateral contact force RMS errors were smaller for synergy controls (Syn and SynEMG subcases, 132 (27) N) than for independent controls (Ind and IndEMG subcases, 190 (70) N). Differences in contact force predictions between the two types of controls were most evident in the contact force “trough” near the middle of stance phase and throughout swing phase, where synergy controls followed the experimental trends more closely.

Use of EMG shape tracking for optimizations that predicted contact forces (Precalibrate+Predict and Calibrate+Predict cases) reduced prediction accuracy for synergy controls (lateral contact force only) but improved it for independent controls. Adding EMG shape tracking (SynEMG) to synergy control subcases (Syn) reduced average medial, lateral, and total R² values from 0.84 (0.04) to 0.74 (0.09) and increased average medial and lateral RMS errors from 117 (30) N to 147 (13) N. In contrast, adding EMG shape tracking (IndEMG) to independent control subcases (Ind) increased average medial, lateral, and total R² values from 0.38 (0.36) to 0.71 (0.09) and decreased average medial and lateral RMS errors from of 224 (86) N to 156 (31) N. However, contact force predictions for synergy controls without EMG shape tracking (Syn) were still more accurate than predictions for independent controls with EMG shape tracking (IndEMG).

Muscle Excitations.

In contrast to contact force results, muscle model calibration method did not have a large affect on the agreement between predicted and experimental excitation shapes. For each subcase, R² and %VAF values were roughly consistent across the Calibrate+Match, Precalibrate+Predict, and Calibrate+Predict cases (Fig. 4), with the best agreement between experimental EMG and simulated excitation shapes occurring for optimizations that tracked EMG shapes.

Fig. 4.

Average %VAF and R² values for EMG shape predictions from all optimizations. Each bar represents the average and each whisker the standard deviation for all muscles with experimental EMG data. See caption for Fig. 2 for descriptions of cases and subcases.

For optimizations that predicted contact forces (Precalibrate+Predict and Calibrate+Predict cases), the selected control method influenced EMG prediction accuracy depending on the muscle model calibration method used. Synergy controls achieved higher R ² and %VAF values than did independent controls for the Precalibrate+Predict case, while the opposite trend was observed for the Calibrate+Predict case. For these two cases combined, optimizations that used synergy controls (Syn subcases) resulted in an average R² value of 0.19 (0.47) and an average %VAF value of 69 (16) compared to an average R² value of 0.17 (0.21) and an average %VAF value of 66 (11) for optimizations that used independent controls (Ind subcases).

Use of EMG shape tracking in optimizations that predicted contact forces (Precalibrate+Predict and Calibrate+Predict cases) significantly improved agreement with experimental EMG patterns. For synergy controls (SynEMG) and independent controls (IndEMG), the average R ² value was 0.86 (0.06) and the average %VAF value was 94 (2) between experimental and simulated excitation shapes. When EMG shape tracking was not used (Syn and Ind subcases), the agreement was lower with an average R² value of 0.18 (0.37) and average %VAF value of 68 (14).

Computation Time.

Optimizations for all subcases converged with the cost function changing by less than 5% between successive optimization sequences. For subcases where model parameter values were calibrated (Calibrate+Match and Calibrate +Predict subcases), total optimization time averaged 54 (21) h on a personal computer workstation with two quad-core Intel Xeon 3.2 GHz processors. For subcases where only muscle excitation patterns were adjusted (Precalibrate+Predict subcases), average optimization time was 34 (21) h. Optimization time was comparable when using synergy controls (Syn and SynEMG subcases; 57 (17) h) instead of independent controls (Ind and IndEMG subcases; 51 (25) h).

Discussion

This study investigated the ability of subject-specific muscle synergy controls with and without EMG shape tracking to improve optimization prediction of knee contact forces and muscle excitations during walking. Optimization formulations that tracked the experimental knee contact forces and EMG shapes (Calibrate+Predict cases with IndEMG and SynEMG subcases) reproduced inverse dynamic loads closely (R² ≥ 0.95), medial and lateral contact forces closely (R² ≥ 0.94), and muscle EMG shapes reasonably well (average R² ≥ 0.81), indicating that the musculoskeletal model and optimization methods were theoretically capable of predicting the instrumented knee measurements. Optimization formulations that predicted experimental knee contact forces (Precalibrate+Predict and Calibrate+Predict cases) produced the best predictions when subject-specific muscle synergy controls were used (R ² between 0.61 and 0.90 compared to R ² between −0.15 and 0.81 for independent controls), especially when EMG shape tracking was omitted. Furthermore, use of synergy controls reduced the sensitivity of predicted knee contact forces to uncertainties in muscle model parameter values. However, use of synergy controls instead of independent controls did not improve overall prediction of experimental muscle excitations, which was unexpected. Thus, while synergy controls show promise for improving prediction of knee contact forces, further investigation is required to determine whether they can improve prediction of muscles excitations as well.

While the best contact force estimates with synergy controls occurred when EMG shape tracking was omitted, the best estimates with independent controls occurred when it was included (Figs. 2 and 3). The addition of EMG shape tracking degraded lateral (but not medial) contact force predictions for synergy controls but produced large improvements for independent controls, indicating that EMG shape tracking was critical for independent controls. It is possible that for synergy controls, inclusion of EMG shape tracking overconstrained the achievable simulated excitation patterns, since experimental neural commands (obtained from experimental EMG data) and experimental EMG signals were being tracked simultaneously.

For synergy controls as well as independent controls, EMG shape tracking underpredicted the second peak of knee contact force during late stance phase (Fig. 3). This result was due to reduced force in the four muscles that affected knee contact forces the most (MedGas, LatGas, VasMed, and RF; Fig. 5). Force reduction in these muscles may have been caused by incorrectly calibrated muscle model parameter values, deficiencies in the methods used to process and track EMG data, undetected problems with the EMG data for these muscles, or an inappropriate optimization cost function. Preliminary optimizations revealed that EMG shape tracking and net load tracking were inconsistent with each other, particularly for MedGas and RF, which had the largest muscle contributions to knee contact forces. To achieve good EMG shape tracking without degrading net load tracking, the optimizer tended to make the peak isometric force or muscle excitation scaling parameter small for these two muscles so that EMG shape could be matched without generating large muscle forces that worsened net load tracking. This inconsistency between EMG shape tracking and net load tracking was less pronounced for these two muscles when precalibrated muscle model parameter values were used, suggesting that uncertainties in parameter values were a contributing factor and that better calibration methods (e.g., involving use of dynamometer data) would be beneficial. While EMG shape tracking degraded prediction accuracy for the second peak in contact force, this result may not occur for other subjects, trials, or optimization cost functions, or for optimizations that use a different approach for calibrating muscle model parameter values. Thus, further testing should be performed to evaluate how EMG shape tracking affects the accuracy of knee contact force predictions when different muscle model calibration methods are used.

Fig. 5.

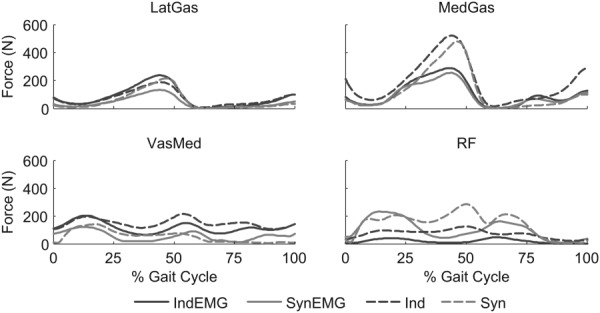
Sample muscle forces for Calibrate+Predict case for muscles (lateral gastrocnemius – LatGas, medial gastrocnemius – MedGas, rectus femoris – RF, and vastus medialis – VasMed) with large contributions to knee contact forces. See caption for Fig. 2 of descriptions of cases and subcases.

Though synergy controls worked better than independent controls for estimating knee contact forces accurately, both types of controls produced contact forces with the correct general amplitude and shape (Fig. 3). This outcome may be related to our use of accurate subject-specific bone geometry constructed from CT scan data, combined with our use of recently reported muscle origin, insertion, and wrapping surface data [32] that were scaled and projected onto our subject-specific bone models. If this hypothesis is correct, development of simple and inexpensive methods that can improve the subject-specificity of the skeletal anatomy should be explored.

The medial and lateral contact force predictions in our study were as good as or better than predictions generated by other recent studies that used the Knee Grand Challenge data sets [40–44]. Our best knee contact force predictions were for the Calibrate+Predict case when synergy controls were used without EMG shape tracking. For that problem formulation, RMS errors were 130 and 83 N for medial and lateral contact force, respectively, with R ² values of 0.84 and 0.90. These results were especially good for lateral contact force, which historically has been the most difficult to predict. For the four Knee Grand Challenge competitions held thus far, the best blinded predictions had RMS errors of 187 and 144 N for medial and lateral contact force, respectively, with corresponding R² values of 0.82 and 0.67. For unblinded predictions, the best results were RMS errors of 130 and 112 N with R ² values of 0.95 and 0.78. Note, however, that these competition results were not produced by the same model on the same gait trial but represent the best results overall from any model and gait trial.

Constructing all simulated muscle excitations from subject-specific neural commands did not consistently improve or worsen prediction of experimental EMG signals compared to using independent controls (Fig. 4). Since the neural commands were calculated from experimental EMG data, we expected that synergy controls would limit the achievable muscle excitation patterns and make them more similar to the experimental EMG patterns. However, this outcome did not occur for all muscles. The fact that the shapes of the medial and lateral contact force curves were predicted better using synergy controls (especially the “trough” near 25% of the gait cycle and throughout swing phase) suggests that synergy controls produced more realistic net muscle loading on the knee. However, individual muscle contributions to the net muscle loads likely remained inaccurate as some EMG patterns were not well predicted. Since optimizations that predicted excitation patterns used muscle model parameter values calibrated without the use of EMG data, it is possible that uncertainties in these parameter values were a significant contributing factor to our poor EMG predictions. Use of muscle model parameter values calibrated with the use of EMG data for optimizations that do not track EMG data could potentially improve prediction of EMG shapes.

Several recent studies have explored how muscle synergies can be used to reduce control complexity in muscle force optimizations [8,10,21–23]. These studies evaluated their models by predicting joint moments and muscle forces, whereas our study focused on predicting knee contact forces and muscle forces. Furthermore, our study constructed simulated excitations for all muscles (including those without EMG data) using linear combinations of all available neural commands, whereas previous studies constructed muscle excitations using only a subset of available neural commands (typically one and at most three), with some muscle excitations defined using block or bimodal patterns. Another important difference is that our study used subject- and task-specific neural commands from a single gait trial while previous studies used synergy information that was averaged across subjects and/or motion cycles.

Our study possessed several limitations that should be considered when assessing our findings. The first limitation was that we simulated only a single subject performing a single gait trial. Due to the large amount of computation time required to perform each optimization, simulation of multiple gait trials was not feasible. Use of instrumented knee data from additional subjects, gait trials, or movement tasks may provide greater distinction between the methods tested. A second limitation was that our optimization predictions are dependent on our selected cost function, which minimized sum of squares of muscle excitations while tracking and bounding various experimental quantities and model parameter values. Future studies should investigate how different cost function formulations affect predicted leg muscle and knee contact forces. A third limitation was the lack of a separate process specifically for calibration of muscle model parameter values. We attempted to predict knee contact forces using the simplest approach possible, which involved calibrating the necessary muscle model parameter values directly from the gait trial being analyzed. For EMG-driven models, it is common to perform an initial calibration using data from dynamometer trials and different types of movements [12], which likely improves calibration accuracy. A fourth limitation was our adjustment of knee kinematics for consistency with experimental knee contact force data. While these kinematic adjustments improved the fidelity of our model, they are not adjustments that can normally be made, since in vivo knee contact force and fluoroscopy data are not usually available. If these in vivo data had not been available, we could have used tibiofemoral kinematics calculated by the Autolev model about its optimal knee flexion-extension axis. How this change would have affected our muscle and contact force predictions is unknown since we chose to make use of the available fluoroscopic and contact force data to evaluate optimization performance under best possible conditions.

In conclusion, our optimization results suggest that subject-specific muscle synergy controls may improve the accuracy of knee contact force predictions while reducing prediction sensitivity to uncertainties in muscle model parameter values. Our results also suggest that tracking experimental EMG data may improve knee contact force predictions when not using synergy controls. Future research that uses experimentally calculated neural commands to construct simulated excitation patterns for all muscles, including those without EMG data, should focus on the use of better methods for calibrating muscle model parameter values.

Nomenclature

AddMag =

adductor magnus

BifemLH =

long head biceps femoris

CT =

computerized tomography

DOF =

degree of freedom

EMG =

electromyographic

Grac =

gracilis

Ind =

independent control of muscle excitations

LatGas =

lateral gastrocnemius

MedGas =

medial gastrocnemius

N =

Newtons

PerLong =

peroneus longus

R² =

coefficient of determination

RF =

rectus femoris

RMS =

root-mean-square

Sart =

sartorius

Semimem =

semimembranosus

Sol =

soleus

Syn =

synergy control of muscle excitations

TA =

tibialis anterior

TFL =

tensor fascia lata

VAF =

variance accounted for; %VAF indicates VAF multiplied by 100

VasLat =

vastus lateralis

VasMed =

vastus medialis