Finite Element Prediction of Transchondral Stress and Strain in the Human Hip

Abstract

Cartilage fissures, surface fibrillation, and delamination represent early signs of hip osteoarthritis (OA). This damage may be caused by elevated first principal (most tensile) strain and maximum shear stress. The objectives of this study were to use a population of validated finite element (FE) models of normal human hips to evaluate the required mesh for converged predictions of cartilage tensile strain and shear stress, to assess the sensitivity to cartilage constitutive assumptions, and to determine the patterns of transchondral stress and strain that occur during activities of daily living. Five specimen-specific FE models were evaluated using three constitutive models for articular cartilage: quasilinear neo-Hookean, nonlinear Veronda Westmann, and tension-compression nonlinear ellipsoidal fiber distribution (EFD). Transchondral predictions of maximum shear stress and first principal strain were determined. Mesh convergence analysis demonstrated that five trilinear elements were adequate through the depth of the cartilage for precise predictions. The EFD model had the stiffest response with increasing strains, predicting the largest peak stresses and smallest peak strains. Conversely, the neo-Hookean model predicted the smallest peak stresses and largest peak strains. Models with neo-Hookean cartilage predicted smaller transchondral gradients of maximum shear stress than those with Veronda Westmann and EFD models. For FE models with EFD cartilage, the anterolateral region of the acetabulum had larger peak maximum shear stress and first principal strain than all other anatomical regions, consistent with observations of cartilage damage in disease. Results demonstrate that tension-compression nonlinearity of a continuous fiber distribution exhibiting strain induced anisotropy incorporates important features that have large effects on predictions of transchondral stress and strain. This population of normal hips provides baseline data for future comparisons to pathomorphologic hips. This approach can be used to evaluate these and other mechanical variables in the human hip and their potential role in the pathogenesis of osteoarthritis (OA).

Introduction

Abnormal cartilage mechanics are thought to initiate and advance osteoarthritis by damaging the cartilage matrix and altering cartilage metabolism [1,2]. Contact stress and maximum shear stress predict cartilage fissuring under impact loads in vitro [3,4], while compressive, tensile, and shear loading alter cartilage metabolism in a dose-dependent manner [2,5–7]. Early signs of OA in vivo include fibrillation and fissuring of the articular surface and cartilage delamination from the bone [3,4,8–13]. Clinical observation, in vivo animal studies, and computational modeling suggest that fibrillation and fissuring are caused by elevated tensile strains near the articular surface, while delamination is caused by elevated shear stress at the osteochondral interface [12–23]. Therefore, understanding the patterns of tensile strain and shear stress at the articular surface, at the osteochondral interface, and transchondrally during activities of daily living would provide insight into the mechanisms responsible for the onset of OA at the tissue level. In this context, “transchondral” indicates the variation in measures through the thickness of the cartilage, between the articular surface, and the osteochondral interface. Evaluation of transchondral stress and strain may provide greater insight than evaluation of stress and strain at the surfaces of the cartilage because transchondral gradients can provide information about the locations of peaks, as well as possible locations and reasons for damage.

In the hip, OA affects 9.5% of men and 11.2% of women [24]. An improved understanding of tissue-level tensile strain and shear stress in both the normal and pathomorphologic hip could provide insight into the pathogenesis of hip OA and, thus, guide the development of strategies to prevent or delay the onset of hip OA. Cartilage tensile strain and shear stress are difficult to directly measure in the hip but can be predicted with finite element (FE) analysis. Previous FE analyses of the human hip have focused on prediction of contact stress and contact area on the articular surfaces [25–34]. In a recent series of directly validated, specimen-specific FE models of the hip, we demonstrated that contact stress and area were relatively insensitive to material nonlinearity and spatial inhomogeneity in the cartilage constitutive model [34]. However, contact stress and area depend primarily on the surface geometry and local cartilage thickness. Further, contact stress and area on the articular surface have only an indirect relationship to the stress- and strain-dependent variables that are relevant to cartilage matrix failure and the initiation and progression of OA. Therefore, it is important to determine whether or not transchondral stresses and strains exhibit a similar insensitivity to the choice of constitutive model for cartilage.

Predictions or measurements of three-dimensional transchondral stress and strain in the cartilage of the hip have never been reported. Modeling strategies for the accurate prediction of these variables and their gradients must be determined before subject-specific simulations can yield reliable predictions for pathomorphologic populations, such as patients with dysplasia or femoroacetabular impingement. Cartilage exhibits rate- and time-dependent behavior, material nonlinearity, tension-compression nonlinearity, and transchondral variation in properties [35–42]. Nearly incompressible elastic behavior is an appropriate assumption for activities wherein the loading occurs quickly [43–45]. However, even with the assumption of nearly incompressible elastic behavior, other aspects of cartilage material behavior, such as tension-compression nonlinearity of the fibrillar collagen and proteoglycan matrix [46–48], are known to significantly influence its response to various loading modalities [49]. Therefore, the objectives of this study were to use a population of validated FE models of normal human hips to evaluate the mesh resolution required for converged predictions of cartilage tensile strain and shear stress, to assess the sensitivity of cartilage tensile strain and shear stress on the choice of cartilage constitutive assumptions, and to assess the most realistic patterns of transchondral stress and strain that occur during activities of daily living.

Methods

Five cadaveric hips from male donors were used for this study (40 ± 14 years old, mass 63 ± 14 kg, height 177 ± 9 cm). Specimen-specific FE models were generated (Fig. 1) and underwent direct validation of contact stress and contact area as part of a previous study [34]. Four activities of daily living were simulated using loading conditions based on instrumented implant and gait data that were matched to previous experimental trials: heel strike during walking (WH), midstance during walking (WM), heel strike during stair descent (DH), and heel strike during stair ascent (AH) [34,50]. All FE models were analyzed in NIKE3D [51] and postprocessed in PostView [52].

Fig. 1.

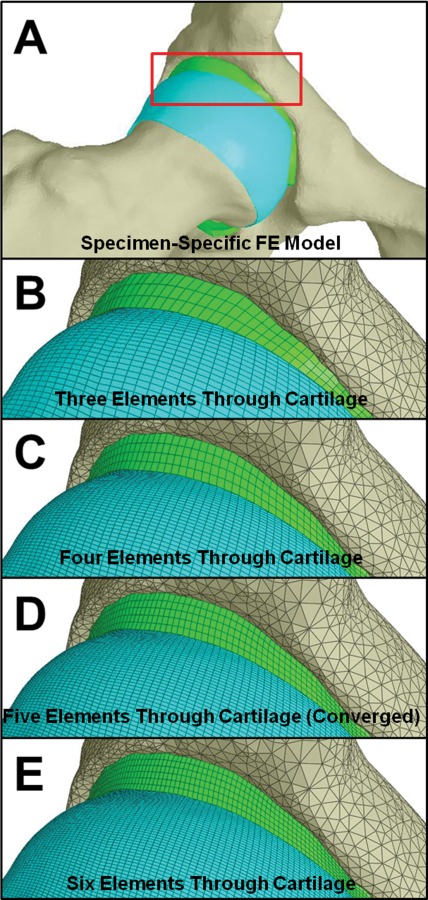
Representative FE model and mesh convergence analysis. (a) View of the whole joint. The red box indicates the region shown in the remaining images. Lines in the remaining images show discretization. (b) FE model with three elements through the cartilage thickness. (c) FE model with four elements through the cartilage thickness. (d) FE model with five elements through the cartilage thickness (this was the converged mesh density). (e) FE model with six elements through the cartilage thickness.

Cartilage mesh convergence was evaluated by analyzing four different mesh densities in one of the five models for all loading scenarios. Meshes for both the femoral and acetabular cartilage were generated with three, four, five, and six hexahedral elements through the cartilage thickness using TrueGrid (XYZ Scientific, Livermore, CA) (Fig. 1). Mesh density was increased while approximately maintaining the same element Jacobian, thus resulting in a simultaneous refinement of the mesh density over the articular surfaces. The resulting models of the cartilage layers consisted of 39,300, 108,972, 185,020, and 303,804 hexahedral elements for meshes with three, four, five, and six transchondral elements, respectively. All models for mesh convergence analysis used a Veronda Westmann constitutive model for cartilage [53]. Convergence was defined by a change less than 10% in first principal strain at the articular surface and maximum shear stress at the osteochondral interface between mesh refinements. As per our previous studies [25,30,34], all models used trilinear hexahedral elements based on a physically stabilized, enhanced strain element formulation [51,54]. This element is often more robust than standard trilinear hexahedral elements for simulations that involve large compressive contact strains.

The nearly incompressible material behavior of human hip cartilage under physiological loading rates was characterized by testing cartilage samples from the contralateral joint of each specimen in unconfined compression as part of a previous study [34]. Three hyperelastic constitutive models were fit to experimental data (Fig. 2). The simplest constitutive model was an uncoupled version of the isotropic, hyperelastic neo-Hookean model [55], with strain energy $W$ given by

Fig. 2.

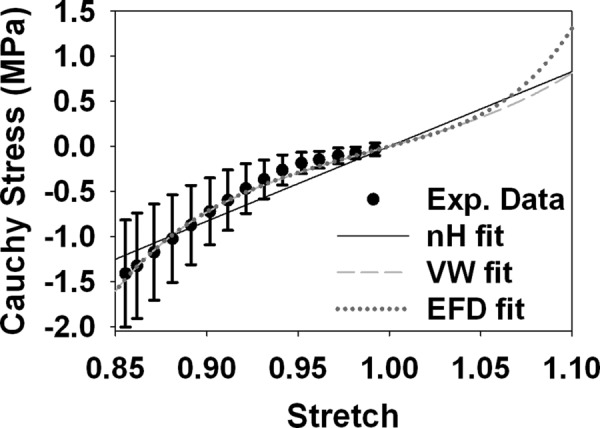
Uniaxial stress response of the three constitutive models. Experimental data are shown. At small strains (stretch values near 1.0), there were minimal differences between the three models. At larger tensile strains, there were drastic differences. The EFD model was the stiffest at higher levels of stretch due to the fiber contribution to the response, likely resulting in both the higher τ_max and lower E₁ at large magnitudes (Fig. 5). In compression (stretch values less than 1), the EFD and VW constitutive models predicted nearly identical responses. Error bars = standard deviation.

$$W=\frac{1}{2}\mu ({\tilde{I}}_1-3)+\frac{1}{2}K{\left(\ln \left(J\right)\right)}^2$$ (1)

In this expression, ${\tilde{I}}_1$ is the first deviatoric invariant of the right Cauchy deformation tensor, J is the Jacobian of the deformation, μ is the shear modulus in the limit of small deformations, and K is the bulk modulus. This model was selected as a baseline constitutive model both because of its simple quasilinear stress-stretch relationship and because it has been used previously in FE models of the human hip joint [25–32]. The second constitutive model was an uncoupled version of the isotropic, hyperelastic Veronda Westmann (VW) model [53,55]:

$$W=C_1(\text{exp}\hspace{0.17em}\left[C_2({\tilde{I}}_1-3)\right]-1)-\frac{C_1{C}_2}{2}({\tilde{I}}_2-3)+\frac{1}{2}K{\left(\ln \left(J\right)\right)}^2$$ (2)

Here, ${\tilde{I}}_2$ is the second deviatoric invariant of the right Cauchy deformation tensor, the coefficient C₁ scales the overall response, the coefficient C₂ controls the exponential response, and K is the bulk modulus. Although the VW model is isotropic, it captures strain-dependent material nonlinearity [53]. The final constitutive model was an uncoupled version of the ellipsoidal fiber distribution (EFD) model, with a neo-Hookean ground matrix [49,55,56]. The fiber strain energy W_f for the EFD model was in the form [49,55,56]

$$W_f={\int }_{A}H({\tilde{I}}_n-1)\xi \left(\mathbf{n}\right){({\tilde{I}}_n-1)}^{\beta \left(\mathbf{n}\right)}\mathit{dA}$$ (3)

Here, ${\tilde{I}}_n$ is the square of the deviatoric fiber stretch and $\mathbf{n}$ is the unit vector along the fiber direction in the reference configuration. The integral is evaluated over the unit sphere $A$ spanned by all directions $\mathbf{n}$; H(·) is the unit step function ensuring that only fibers under tension contribute to the strain energy density. The material coefficient ξ scales the fiber response and β controls the nonlinearity of the fibers. Both ξ and β may vary with $\mathbf{n}$ according to an ellipsoidal distribution with respective semiaxes (ξ ₁, ξ ₂, ξ ₃) and (β ₁, β ₂, β ₃); however, an initially isotropic fiber distribution was assumed in this study. For this case, the fiber material coefficients are equal in all directions, such that ξ ₁ = ξ ₂ = ξ ₃ = ξ($\mathbf{n}$) and β ₁ = β ₂ = β ₃ = β($\mathbf{n}$). The total strain energy was the sum of the fiber strain energy in Eq. (3) and the neo-Hookean strain energy in Eq. (1) that represented the nonfibrillar matrix [55]. This constitutive model captures tension-compression nonlinearity via the nonlinear stress-strain behavior of the fibers since they only resist tensile deformation [49]. Further, the model simulates the strain-induced anisotropy of articular cartilage [56].

Material coefficients for each of the constitutive models were determined by fitting the experimental stress-stretch curves to analytical solutions for the isochoric unconfined compression response, using a constrained nonlinear least squares method (SigmaPlot 11.0, Systat Software Inc., San Jose, CA). To determine average coefficients for all cartilage samples, experimental data from all samples were fit simultaneously to the stress-stretch expressions in Eqs. (4), (5), and (6). This method is slightly different from the method used in our previous study, where experimental data from each sample were fit individually and then material coefficients were averaged [57]. The method used in the present study resulted in better agreement in the compressive response of the EFD and Veronda Westmann constitutive models than the method in the previous study. For an incompressible material subjected to unconfined compression by a stretch ratio of λ, the neo-Hookean Cauchy stress along the loading axis is

$$\sigma =\frac{1}{2}\mu ({\lambda }^2-\frac{1}{\lambda })$$ (4)

For an incompressible material subjected to unconfined compression by a stretch ratio of λ, the VW Cauchy stress along the loading axis is

$$\sigma =C_1{C}_2[(2{\lambda }^2-\frac{2}{\lambda })\text{exp}\hspace{0.17em}\left[C_2({\lambda }^2+\frac{2}{\lambda }-3)\right]-\lambda +\frac{1}{{\lambda }^2}]$$ (5)

For an incompressible material subjected to unconfined compression by a stretch ratio of λ, the EFD Cauchy stress along the loading axis is

$$\begin{array}{c}\multicolumn{1}{c}{\sigma =\frac{1}{2}\mu ({\lambda }^2-\frac{1}{\lambda })\hspace{1em}-\frac{256\pi \xi (8\lambda -15{\lambda }^2+6{\lambda }^3-10{\lambda }^4+24{\lambda }^5-15{\lambda }^6-2{\lambda }^7)}{315{\lambda }^5{(1+\lambda +{\lambda }^2)}^{3/2}}}\end{array}$$ (6)

Equation (6) was calculated in Mathematica (Wolfram Research, Champaign, IL) from Eqs. (1) and (3) using previously described methods [56]. Preliminary data demonstrated that the least squares fit was relatively insensitive to the choice of β for integer values above 2.0. Thus, the value of β was set to 4.0 since this integer value resulted in a closed-form equation that could be used for curve fitting. Although cartilage was only tested in compression, data were fit to the tensile response of the fibers in the EFD model. This was possible because an isochoric response in unconfined compression also produces tensile strains. For the prescribed compressive stretch of λ = 0.85, the maximum tensile stretch experienced during unconfined compression testing was 1.085. For all constitutive models, the uniqueness of the best-fit material coefficients was verified by perturbing the initial guesses.

To evaluate the effects of cartilage constitutive model on FE predictions of transchondral stress and strain, FE models of all specimens and loading scenarios were analyzed with the three cartilage constitutive models. Based on the results of our previous studies [25,58], cortical bone was represented as isotropic linear elastic for all analyses (E = 17 GPa, ν = 0.29) [59]. Average neo-Hookean cartilage coefficients were μ = 5.52 MPa and K = 550 MPa. Average VW cartilage coefficients were C₁ = 0.34 MPa, C₂ = 5.57 MPa, and K = 1178 MPa. Average EFD cartilage coefficients were μ = 1.82 MPa, ξ = 9.19 MPa, β = 4, and K = 1860 MPa. The bulk modulus values were selected for each cartilage constitutive model to ensure near-incompressibility. This was confirmed by examining the Jacobian field in the articular cartilage for each simulation. In all cases, the largest change in volume at all locations in the finite element meshes was less than 4%.

Green–Lagrange first principal strain (E₁) and Cauchy maximum shear stress (τ_max) were evaluated in each FE model. E₁ is the first eigenvalue of the Green–Lagrange strain tensor and represents the largest tensile strain at each point. E₁ was sampled at the articular surfaces and transchondrally at the location of the peak E₁ on the articular surface. τ_max was evaluated at the osteochondral interface and transchondrally at the location of the peak τ_max on the osteochondral interface. The locations for sampling transchondral E₁ and τ_max were selected to provide a systematic approach to evaluating results. Results were analyzed on the femoral head and in six anatomical regions on the acetabulum (Fig. 3(a)).

Fig. 3.

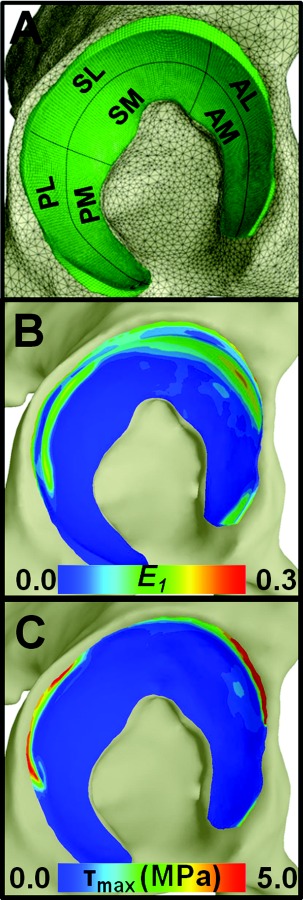
E₁ and τ_max results on the acetabulum in the EFD models of one specimen. (a) Lateral view of the acetabulum with the six anatomic regions used for analysis. (b) E₁ at the articular surface. (c) τ_max at the osteochondral interface.

FE predictions from the three different constitutive models were compared. The acetabular cartilage was divided into six regions for analysis: anterolateral (AL), anteromedial (AM), superolateral (SL), superomedial (SM), posterolateral (PL), and posteromedial (PM) [60–61] (Fig. 3(a)). Results for the acetabular cartilage were compared within region and activity using repeated measures analysis of variance (ANOVAs) on ranks with Tukey post hoc analysis. Results for transchondral mechanics in the femoral cartilage were compared using repeated t tests within activity and location. Patterns of E₁ and τ_max were evaluated within constitutive model using random effects linear regression, accounting for the nonindependence of data clustered within each specimen and loading scenario, with the resulting p values corrected for multiple comparisons via Finner's procedure [57,62]. Significance was set at p ≤ 0.05.

Although we have shown previously that the presence or absence of the labrum has a minimal effect on predictions of contact stress or contact area in a normal hip during simulated physiological loading [30], there was concern that this may not be the case for predictions of transchondral stress and strain. When the labrum is not included in the FE models, the acetabular cartilage has a free lateral edge. To assess the effects of the labrum, an additional model of a normal subject was evaluated. We analyzed normal and dysplastic models of the hip including the labrum previously for predictions of contact stress and contact area [30]. To evaluate the potential effects of the labrum on FE predictions of transchondral E₁ and τ_max, the normal hip modeled in our previous study was remeshed at the higher mesh density used in the present study and evaluated in a neutral loading position. Two FE models were generated: one with the acetabular labrum and one without the acetabular labrum. Models were analyzed using the EFD constitutive model for cartilage and a transversely isotropic constitutive model for labrum [30,63]. Predictions of transchondral stress and strain were compared between the two models.

Results

Mesh convergence analysis demonstrated that meshes with five transchondral elements were converged, predicting results that were less than 10% different than meshes with six transchondral elements. The change in peak E ₁ at the articular surface was ≤16%, ≤3% and <1% between models with three versus four, four versus five, and five versus six transchondral elements, respectively. Therefore, models with four transchondral elements would have been appropriate for predicting E ₁ alone. Convergence in τ_max was evaluated for peak osteochondral values away from the edge of the acetabular cartilage. The change in peak τ_max was ≤37%, ≤13%, and <10% between models with three versus four, four versus five, and five versus six transchondral elements, respectively. Comparisons of transchondral predictions demonstrated that models with three transchondral elements missed features of the depth-wise gradients, which were captured at all other mesh resolutions. There were only minor differences between the transchondral predictions from models with five and six transchondral elements, confirming that meshes with five transchondral elements were adequate for the variables of interest. Therefore, results for models with five transchondral elements are reported for the remainder of the study. Model run times were 1.4 ± 0.3 h, 5.0 ± 1.6 h, 8.3 ± 1.3 h, and 24.3 ± 10.8 h for meshes with three, four, five, and six transchondral elements, respectively.

Differences in the three constitutive models were apparent in the uniaxial stress response at the approximate strain levels predicted in the FE models, with the most dramatic differences in tension (Fig. 2). The EFD constitutive model produced the stiffest tensile stress response due to the upwardly concave material behavior of the tension-only fibers. The material nonlinearity in the VW model predicted the next highest stresses in tension. The tensile response of the neo-Hookean constitutive model was smaller than the other two models at large stretch values. In compression, the response of the VW and EFD constitutive models was nearly identical and reflected the nonlinearity measured during experimental unconfined compression testing. The quasilinear behavior of the neo-Hookean constitutive model resulted in overpredictions of compressive stress magnitudes at stretch values near unity and underpredictions of compressive stress magnitudes at stretch values near 0.85.

The choice of cartilage constitutive model significantly affected predictions of osteochondral τ_max and articular E₁ in the acetabulum (Figs. 3 and 4). Generally, the EFD model predicted larger stresses, while the neo-Hookean model predicted larger strains. Specifically, at locations of high peak values, use of the EFD constitutive model resulted in significantly larger predictions of peak τ_max than the other two constitutive models (Fig. 4(a), AL, SL, and PL regions). In contrast, there were minimal or no differences in peak τ_max at locations with lower magnitudes. VW cartilage predicted significantly smaller average τ_max than neo-Hookean cartilage in all regions (Fig. 4(b)). The VW constitutive model also predicted significantly smaller average τ_max than the EFD model in two regions. Trends in E₁ were approximately opposite those in τ_max (Figs. 4(c) and 4(d)). At large strain values, peak E₁ was significantly larger in neo-Hookean models than in the other two models (Fig. 4(c), AL and SL regions). At low strain values, peak E₁ was significantly larger in neo-Hookean models than in the other two models (Fig. 4(c), AM, SM, and PM regions). Average E₁ at large values was significantly larger in VW models than in the other two models (Fig. 4(d), AL, SL, and SM regions). At low average E₁, results were significantly smaller in the neo-Hookean models than in the other two models (Fig. 4(d), AM, PM, and PL regions).

Fig. 4.

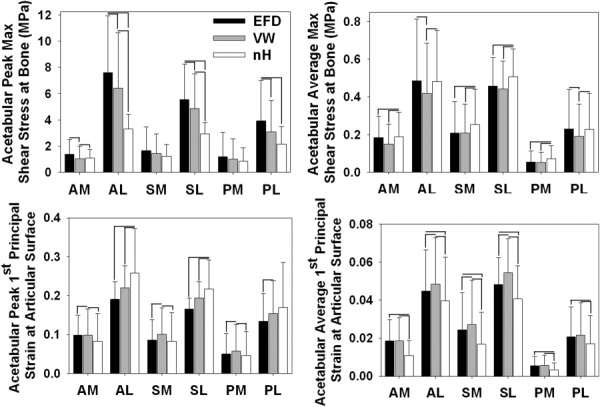
Results in six anatomical regions on the acetabular cartilage. (a) Peak τ_max at the osteochondral interface. (b) Average τ_max at the osteochondral interface. (c) Peak E₁ at the articular surface. (d) Average E₁ at the articular surface. At high stress values, the EFD models predicted the largest stresses. A high strain values, the neo-Hookean models predicted the largest strains. Error bars = standard deviation.

The three constitutive models predicted significantly different transchondral τ_max and E₁ (Fig. 5). Consistent with the acetabular results, peak τ_max at the femoral osteochondral interface was significantly larger in the EFD models than in the other two models (Fig. 4(a)). These differences persisted partway through the cartilage thickness from the osteochondral interface. However, at the articular surface corresponding to the location of peak τ_max at the osteochondral interface, there were trends toward higher τ_max for the neo-Hookean models. This indicated a smaller depthwise gradient in τ_max for the neo-Hookean models than for the other two models. There was a peak in transchondral E₁ just below the articular surface for all constitutive models in the femoral cartilage (Figs. 5(b) and 6). While this was consistent across specimens and loading scenarios in the femoral cartilage, it was not seen in the acetabular cartilage (Fig. 6).

Fig. 5.

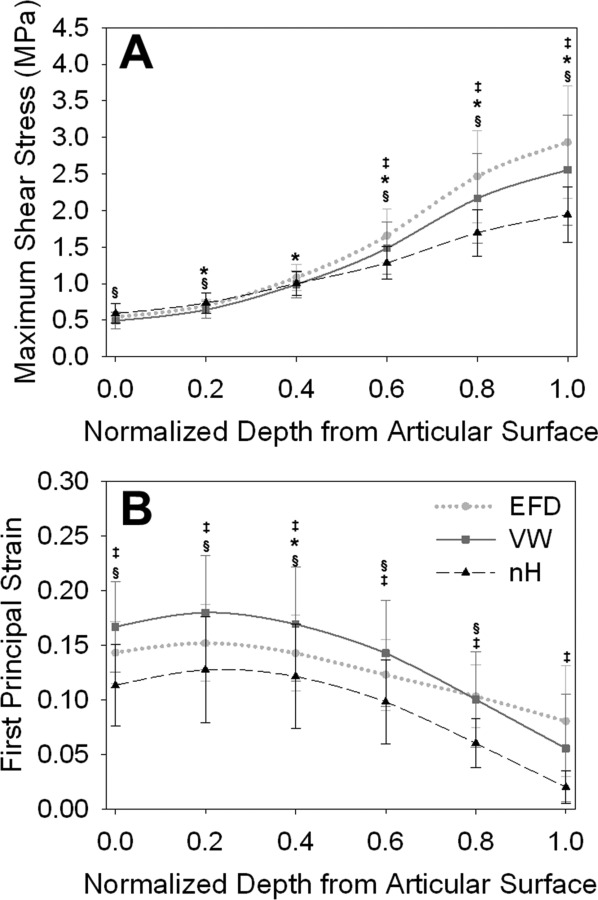
Results through the depth of the femoral cartilage during AH. (a) τ_max at the location of the osteochondral peak. (b) E ₁ at the location of the articular peak. While τ_max near the osteochondral interface was larger in the EFD model, it was larger in the neo-Hookean (nH) models near the articular surface. For all constitutive models, E ₁ peaked just below the articular surface. * indicates differences between EFD and VW, ‡ indicates differences between EFD and nH, and § indicates differences between VW and nH. Error bars = standard deviation.

Fig. 6.

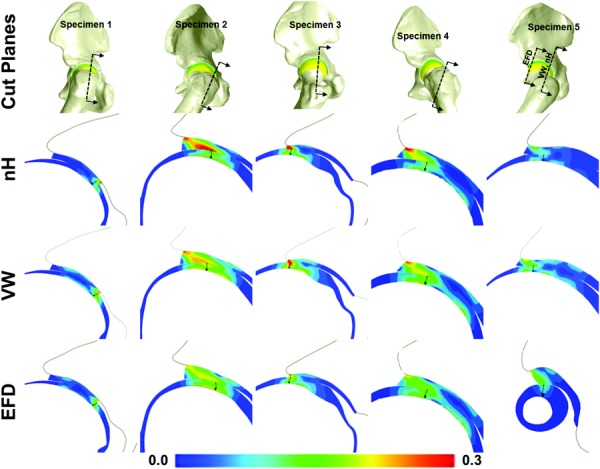
Cut planes for femoral E ₁ as reported in Fig. 6(b). Each column is for one specimen. The top row indicates the location of the cut planes. The next three rows are the nH, VW, and EFD model results, respectively. The arrows in each cut figure indicate the location and direction of sampling.

There were distinct regional variations in E₁ and τ_max (Fig. 7). Based on the results between FE models with different cartilage constitutive models described above, regional differences were evaluated in the EFD models. At the osteochondral interface, the AL region had larger peak τ_max than all other regions (Fig. 7(a)). The next largest magnitude of peak τ_max was the in SL region, followed by the PL region. Of the medial regions, the largest peak τ_max was found in the SM region. Average τ_max followed similar trends to peak τ_max (Fig. 7(b)). Average τ_max was largest in the AL region, but average τ_max in this region was only significantly larger than in the AM, SM, PM, and PL regions. Average τ_max in the PM region was smaller than in all other regions. At the articular surface, the AL region also had larger peak E₁ than all other regions (Fig. 7(c)). Again, this was followed by the SL and PL regions, with the smallest magnitudes in the PM region. Average E₁ was also largest in the AL region but was only significantly larger than the AM, SM, PM, and PL regions (Fig. 7(d)). Average E₁ was the smallest in the PM region.

Fig. 7.

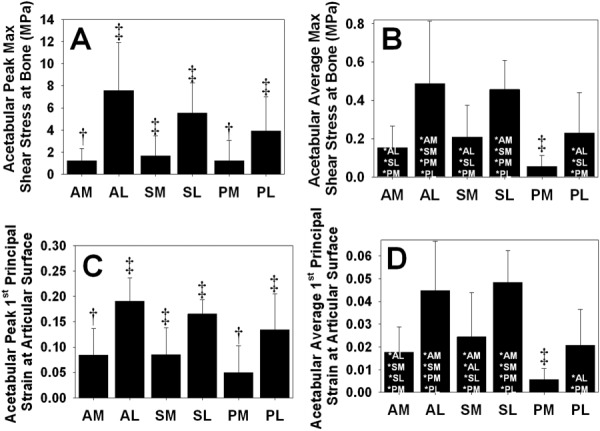
E₁ and τ_max in six anatomical regions on the acetabulum the EFD models. (a) Peak τ_max at the osteochondral interface. (b) Average τ_max at the osteochondral interface. (c) Peak E₁ at the articular surface. (d) Average E₁ at the articular surface. ‡ indicates p ≤ 0.05 against all other regions. † indicates p ≤ 0.05 against all other regions except the one with the same symbol in the same panel. * indicates p ≤ 0.05 against the listed region. Error bars = standard deviation. There were distinct regional differences in E₁ and τ_max, with the largest values occurring the AL region and the smallest values occurring in the PM region.

In the model of the normal hip with and without the labrum, the labrum reduced the magnitudes of E₁ and τ_max predicted by the FE models (Fig. 8). However, the labrum had a minimal effect on articular surface patterns, osteochondral interface patterns, or transchondral trends in either variable on the cartilage (Fig. 8(a)).

Fig. 8.

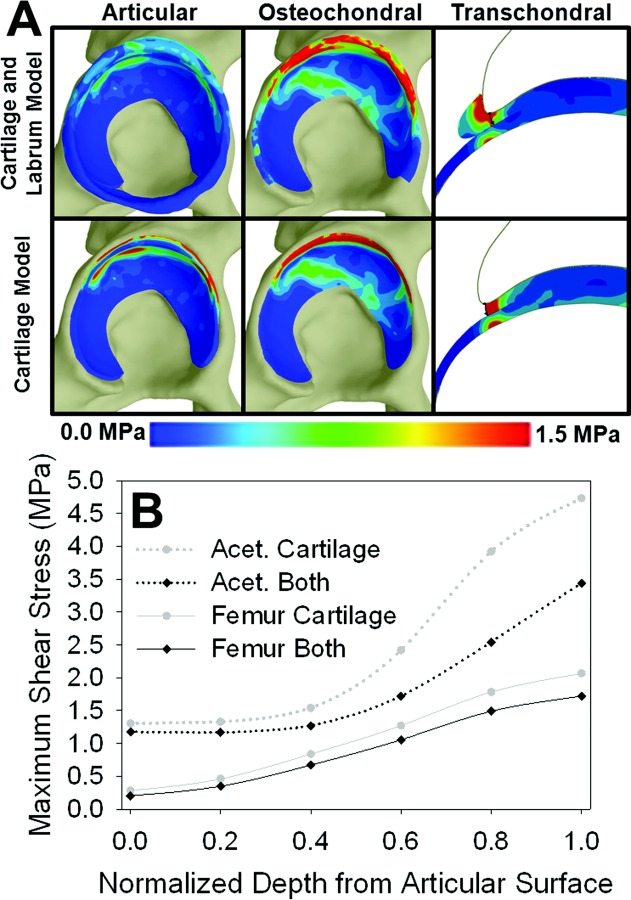
τ_max in the normal subject model without the labrum compared to the normal subject model with the labrum. (a) Acetabular τ_max results at the articular surface, at the osteochondral interface and transchondrally at the location of the osteochondral cartilage peak. Note that the location of the osteochondral peak is identical in the models with and without the labrum. (b) Transchondral τ_max for the both the acetabular and femoral cartilage in the model without the labrum (“cartilage”) and the model with the labrum (“both”). While the acetabular labrum decreased the magnitudes of τ_max, articular, osteochondral, and transchondral τ_max patterns were relatively unaffected. The acetabular labrum had a similar effect on predicted E₁.

Discussion

This study focused on the prediction of two invariants of the three-dimensional stress and strain fields in hip articular cartilage, τ_max and E₁. These variables were selected because they may be important in the pathogenesis of OA, especially in the human hip [12–23,60,64]. Cartilage delamination, which is thought to be caused by high levels of osteochondral τ_max, occurs frequently in the acetabulum of patients with cam femoroacetabular impingement [12–14,17,19–21,23]. In the present study with a normal population of hips, the largest peak τ_max occurred in the AL region, which is where cartilage delamination is often seen in pathomorphologic hips. Although normal hips do not often exhibit delamination, this finding can serve as a baseline for ongoing research using peak τ_max to predict cartilage delamination in pathomorphologic hips. Cartilage fibrillation, which may be caused by elevated articular E₁, occurs early in the OA process in most joints [9–11]. Thus, accurate predictions of E₁ may be able to predict the early stages of hip OA.

In addition to providing insight into regions where cartilage failure may occur, regional variations in E₁ and τ_max can be compared with our previous research evaluating contact stress and contact area [57]. Most of these variables were largest in the AL region and smallest in the PM region of the acetabulum. However, there were more significant differences between other regions in E₁ and τ_max than in contact stress and contact area. For example, the AL, SL, and PL regions had significantly different peak τ_max than all other regions in the present study (Fig. 7(A)), but only the AL region had significantly different peak contact stress than all other regions in our previous study [57]. This finding suggests that E₁ and τ_max may be more sensitive in predicting cartilage failure in comparison to contact stress and contact area. Regional variations in acetabular cartilage E₁ and τ_max (Fig. 7), as well as transchondral gradients in E₁ and τ_max (Figs. 5 and 6) can also serve as baseline values in normal hips for future comparisons against pathomorphologic hips.

The quasilinear, nonlinear, and tension-compression nonlinear constitutive models affected FE predictions of τ_max and E₁ in a manner consistent with the key features of the constitutive models. The quasilinear behavior of the neo-Hookean constitutive model resulted in lower FE predicted τ_max and higher FE predicted E₁, especially at large magnitudes. This can be explained by the fact that the neo-Hookean constitutive model underpredicts the behavior of cartilage away from the limits of small deformation (Fig. 2). Thus, the neo-Hookean constitutive model resulted in an effectively softer tangent modulus than the other two constitutive models at larger magnitudes of stress and strain. Conversely, the EFD constitutive model resulted in the highest values of τ_max and the lowest values of E₁. This was due to the stiffening of the fibers in the EFD model in tension. Prior studies have clearly established the importance of modeling tension-compression nonlinearity of the cartilage matrix in order to accurately capture the distinct response of the tissue to uniaxial tensile [48] and compressive [46] loading. Furthermore, it has been shown that modeling the cartilage matrix with a continuous fiber distribution; in contrast to only three orthogonal fiber bundles [65,66], provides more accurate predictions of a wide range of experimental observations [49]. The presence of significant differences between FE model predictions with the EFD model and those with the other two constitutive models, combined with previous literature demonstrating that the EFD model is the most accurate of the three constitutive models tested in this study, suggests that the EFD model is preferred for predicting transchondral E₁ and τ_max in the human hip.

Differences in the transchondral gradient of τ_max between the constitutive models demonstrate the role of tension-compression nonlinearity in predictions of this variable. Although the influence of the gradient in τ_max on cartilage damage has not been evaluated, experimental measurements of impact damage indicate that stress gradients may be more relevant than stress magnitudes in the pathogenesis of OA. As an example, the gradient of contact stress on the joint surface was a better predictor of failure than the magnitude of contact stress as measured by pressure-sensitive film in a rabbit joint under impact loading [4]. In the present study, the largest gradients in transchondral τ_max were in the EFD models, whereas the neo-Hookean models predicted drastically smaller gradients.

Although the magnitudes of transchondral E₁ were affected by cartilage constitutive model, all models predicted high E₁ close to the articular surfaces, with values decreasing away from the peaks on the articular surfaces. Cadaveric studies have found fibrillation on the femoral head at younger ages than in the acetabulum in both loaded and unloaded portions of the femur [67–70]. Thus, the high values of femoral E₁ predicted near the articular surface of the femoral cartilage may be relevant in the fibrillation of the femoral head that occurs in early degenerative changes in the human hip.

While there has been limited use of advanced constitutive models in FE analysis of articular cartilage mechanics in the human hip, the results of the present study can be compared to FE analyses in the knee. Parametric FE studies have been performed to examine the influence of fiber orientation and transchondral variation in properties on predictions of knee cartilage stress and strain [71–76]. The collagen fiber orientation affected predictions of transchondral mechanics in the knee. Specifically, the highly aligned superficial zone fibers decreased strains at the articular surface [72–75], while an arcadelike transchondral fiber orientation decreased the transchondral von Mises stress and increased the transchondral axial strains when compared to predictions with all fibers aligned parallel to the articular surface [72]. Depth-dependent fiber orientation also decreased the tensile stress and strain at the osteochondral interface in comparison to a homogeneous fiber orientation in the knee [76]. Consistent with the present study, these findings highlight the effects of anisotropy and tension-compression nonlinearity on transchondral predictions of cartilage stress and strain. These findings also indicate that transchondral variation in fiber orientation can influence FE predictions. In the present study, a homogeneous and initially isotropic distribution of fiber orientation was assumed. This provides a reasonable representation of the middle zone, but it is likely less applicable to the fiber topography of the superficial and deep zones of the articular cartilage in the hip. Experimental studies are needed to quantify transchondral fiber orientation in the articular cartilage of the hip, as data are not yet available in the literature. Unlike variation in the fiber orientation, transchondral variation in the matrix elastic modulus had small effects on cartilage stress and strain [72,77]. This provides confidence in the use of depth-averaged matrix properties in the present study.

The results of the present study can be considered in light of previous FE models that provide insight into the effects of constitutive assumptions and model geometry on predictions of τ_max. In a plane strain analysis of biphasic cartilage layers, peak values of τ_max occurred at the osteochondral interface but were not directly under the location of peak contact stress [15,16]. In a plane strain FE model of impact loading, the location of highest τ_max varied with the assumed cartilage constitutive model [78]. Specifically, peak τ_max occurred at the articular surface when cartilage was modeled as transversely isotropic but occurred at the osteochondral interface when the cartilage was modeled as isotropic. However, even this trend in transversely isotropic models could be altered by the curvature of the articular layer, with peak τ_max shifting from the surface to the deep zone with increasing curvature [79]. In an FE study of the human knee, peak τ_max was predicted at the osteochondral interface when the meniscus was modeled, but peak τ_max was predicted at the articular surface without the meniscus modeled [80]. These studies demonstrate that both constitutive model and local geometry affect predictions of τ_max. The results of the present study are consistent with the conclusion that the constitutive model affects predictions of peak τ_max, and add insight regarding the importance of the cartilage constitutive model on transchondral τ_max.

Predictions of τ_max and E₁ were relatively sensitive to the cartilage constitutive model. In contrast, our previous studies demonstrated that predictions of contact stress and contact area are relatively insensitive to variations in the material nonlinearity, spatial inhomogeneity, and material coefficients of the cartilage constitutive model [25,34]. Under fast loading rates, contact stress and area are the result of the total load supported by the cartilage, which is largely supported by the fluid phase [15,44,45,81]. Therefore, it is logical that these variables would be relatively insensitive to cartilage representation. In fact, if cartilage contact stress and area are the only results of interest, discrete element analysis provides accurate predictions in a fraction of the time required for FE analysis [82]. Conversely, predictions of τ_max and E₁ represent the deviatoric response of hydrated tissue under fast loading, and it is, therefore, logical that they are more sensitive to the cartilage constitutive model.

The required mesh density to accurately predict transchondral τ_max was higher than the mesh density in previous FE models of live subjects [29,32]. Thus, subject-specific models for predicting transchondral E₁ and τ_max will require more computational resources and analysis time than previous subject-specific models for predicting contact stress and contact area required. Because transchondral E₁ and τ_max are pertinent to the pathogenesis of hip OA, the mesh density and constitutive model requirements found in this study are directly applicable to the ongoing use of FE analysis for the study of the human hip.

The effect of the acetabular labrum on predictions of E₁ and τ_max provides new insight into the role of the labrum in the normal hip. In a previous study that evaluated contact stress and contact area in models with and without the acetabular labrum, it was found that the contact stress was only minimally affected by the removal of the labrum because of compensation by increased contact area [30]. Thus, the decrease in FE predictions of E₁ and τ_max with the labrum in the present study indicates that the magnitudes of these variables are more sensitive than the magnitude of contact stress to the inclusion of the acetabular labrum. Therefore, if threshold values of E₁ and τ_max are important to the prediction of failure, then the inclusion of the labrum may be necessary to accurately predict the magnitude of these variables for evaluating potential causes of OA in future studies. Conversely, if models are used to predict differences in cartilage E₁ and τ_max between groups, then the actual magnitudes may be less consequential and the labrum may be omitted from the models.

There are several limitations to this study that warrant discussion. While these models have undergone direct validation of contact stress and contact area at the articular surface against experimental measurements on a specimen-specific basis, neither E₁ nor τ_max was directly validated [34]. Confidence in both variables comes primarily from the combination of direct validation of contact stress and contact area with accurate cartilage constitutive models and a mesh convergence study. While the magnitudes of E₁ in the present study are consistent with those measured experimentally in the human patellofemoral joint [83], τ_max cannot be measured experimentally for direct or indirect validation.

Although the cartilage constitutive assumptions in the present study are more complex than in previous hip FE analysis, the models still make use of a number of simplifying assumptions. The material properties of cartilage vary transchondrally, but this variation was not represented in this study. It has been established that the variation between tensile and compressive moduli is larger than transchondral variation in cartilage moduli [35,38,42]. In the context of FE analysis, transchondral variation in elastic modulus had a minimal effect on predictions of 3D knee cartilage stress and strain [72] and a minimal effect on predictions of transchondral stress and strain in an axisymmetric indentation analysis [77]. Therefore, the assumption of homogeneity in material properties in the transchondral direction is reasonable for this study. Cartilage behavior is also biphasic and viscoelastic [37,39,41]. The assumption of rate-independent behavior is justified by the loading rates in this study [34,44,45,57] and by previous biphasic analysis of an idealized hip joint [84]. However, if activities that occur at slower loading rates, such as standing, are considered in future studies, then the rate dependence of cartilage behavior may become important for accurate predictions.

Although the acetabular labrum was not included as part of the specimen-specific FE models, we are confident that the conclusions of the present study would be unaffected if the acetabular labrum were included. The strategy of modeling the normal human hip without the acetabular labrum is based on the results of several studies that suggest limited loading on the labrum in the normal hip [30,85,86], and the approach is consistent with previous FE analyses of the normal hip by our group and others [25,32,34]. Further, the minimal effect on the patterns of cartilage E₁ and τ_max in our evaluation of a normal hip with and without the acetabular labrum provides confidence that the acetabular labrum would not alter the effects of the cartilage constitutive model on FE predicted E₁ and τ_max.

In conclusion, this study demonstrated that tension-compression nonlinearity of a continuous fiber distribution exhibiting strain-induced anisotropy incorporates features that have large effects on predictions of transchondral τ_max and E₁ in the human hip. Further, this study indicates that at least five trilinear elements through the cartilage thickness are required for converged predictions of E₁ and τ_max. The regional and transchondral results can serve as baseline values in normal hips for future comparisons against pathomorphologic hips. While there are other mechanical variables that may be important predictors of the onset and progression of cartilage damage, further experimental studies are needed to determine the variables that are most predictive of cartilage damage at the tissue and joint levels. The approach highlighted in this study can be used to evaluate these additional mechanical variables in the human hip and their potential role in the pathogenesis of OA.