Effects of Intraluminal Thrombus on Patient-Specific Abdominal Aortic Aneurysm Hemodynamics via Stereoscopic Particle Image Velocity and Computational Fluid Dynamics Modeling

Abstract

The pathology of the human abdominal aortic aneurysm (AAA) and its relationship to the later complication of intraluminal thrombus (ILT) formation remains unclear. The hemodynamics in the diseased abdominal aorta are hypothesized to be a key contributor to the formation and growth of ILT. The objective of this investigation is to establish a reliable 3D flow visualization method with corresponding validation tests with high confidence in order to provide insight into the basic hemodynamic features for a better understanding of hemodynamics in AAA pathology and seek potential treatment for AAA diseases. A stereoscopic particle image velocity (PIV) experiment was conducted using transparent patient-specific experimental AAA models (with and without ILT) at three axial planes. Results show that before ILT formation, a 3D vortex was generated in the AAA phantom. This geometry-related vortex was not observed after the formation of ILT, indicating its possible role in the subsequent appearance of ILT in this patient. It may indicate that a longer residence time of recirculated blood flow in the aortic lumen due to this vortex caused sufficient shear-induced platelet activation to develop ILT and maintain uniform flow conditions. Additionally, two computational fluid dynamics (CFD) modeling codes (Fluent and an in-house cardiovascular CFD code) were compared with the two-dimensional, three-component velocity stereoscopic PIV data. Results showed that correlation coefficients of the out-of-plane velocity data between PIV and both CFD methods are greater than 0.85, demonstrating good quantitative agreement. The stereoscopic PIV study can be utilized as test case templates for ongoing efforts in cardiovascular CFD solver development. Likewise, it is envisaged that the patient-specific data may provide a benchmark for further studying hemodynamics of actual AAA, ILT, and their convolution effects under physiological conditions for clinical applications.

1. Introduction

An abdominal aortic aneurysm (AAA) is a permanent focal dilation of an artery to at least 1.5 times its normal diameter [1]. AAAs are characterized by the degradation of the elastinous constituents and the adaptive growth and remolding of the collagen, smooth muscle cell loss with thinning of the medial wall, infiltration of lymphocytes and macrophages, and neovascularization [2–4]. AAA is responsible for at least 15,000 deaths annually in 2000, and it was the 10^th leading cause of death in white males 65 to 74 years of age in the United States [5]. The pathogenesis of AAA formation is not well understood but four factors contributing to AAAs have been identified, including: (1) proteolytic degradation of aortic wall connective tissue, (2) inflammation and immune responses, (3) biomechanical wall stress, and (4) molecular and genetic pathways [6]. Among them, biomechanical wall stresses play an important role that is of importance both in aneurysm development and rupture risk assessment [6].

Hemodynamic flow field, structure, composition, and nutrition of the aortic wall each contribute to AAA formation, growth, and its chief complication: the formation of intraluminal thrombus (ILT). ILT is a 3D fibrin structure comprised of blood cells, platelets, blood proteins, and cellular debris, and is present in approximately 75% of all AAAs [7,8]. However, the mechanical role of ILT on AAA wall mechanics has been controversial [7,9]. One study showed that ILT within the aneurysm does not reduce the mean and pulse pressure near the aneurysmal wall simultaneously and is thus unlikely to reduce the risk of rupture of the aneurysm [10]. In contrast, other studies reported that ILT was beneficial for preventing AAA rupture [7,11]. Hemodynamic analysis offers a promising strategy toward gaining a better understanding of AAA, ILT, and their integrated effects [12]. In addition, the calculated wall shear stress (WSS) may shed light on the initiation of aneurysm formation where low WSS is thought to give rise to continued enlargement of the aneurysm [13] although the growth and remolding factors which influence aneurysm evolution significantly were not implemented in this work [4]. The present emphasis focuses mostly on developing numerical techniques [14,15] to simulate blood flow in AAA models [16–22]. The experimental arm of AAA research has received relatively less attention where a trustworthy experimental method for computational data validation, especially in three dimensions, is needed. An integrated experimental and computational fluid dynamics (CFD) study can contribute to this challenge.

Digital PIV is an optical and nonintrusive whole-field flow visualization method [23] and offers several advantages over image modalities such as laser Doppler and magnetic resonance imaging (MRI) due to its higher spatial resolution (∼10⁻¹μm) and at least a two-velocity component acquisition [24]. Using PIV, particle distributions are recorded at two instants of time and the flow motion is determined from the correlation of particle intensity distribution over time [23]. Extending the conventional two-dimensional (2D) PIV method to a stereoscopic PIV method for investigation of patient-specific hemodynamics is necessary for more accurate wall shear stress evaluation and hemodynamic analysis as well as reducing the artifacts during 3D flow reconstruction with only 2D PIV data. Recently one group details flow structures in a patient-specific AAA model by measuring 14 planes using 2D PIV and reconstructs the acquired 2D flow field data into 3D to have a global view of the entire flow field [25]. However, the reconstruction algorithm applied in this study depends heavily on the interpolation routine and needs to be validated to quantify its 3D resolution. Likewise, another recent study [26] used 3D CFD modeling and 3D PTV to investigate the steady flow in a patient-specific AAA model that showed good agreement between experimental and CFD results. Nevertheless, a reliable stereoscopic PIV technique is necessary since PTV can only track individual particles and thus hampers the accurate estimate of WSS. One study [27] has been reported using 3D CFD modeling and 2D PIV to investigate flow instabilities in patient-specific anatomical total cavopulmonary connection models, and consistent results between experimental and CFD data are reached. More accurate 3D CFD modeling methods can benefit from advances in stereoscopic PIV techniques. Additionally, it is important to use a patient-specific model for both experimental and numerical methods [28] to approach clinical hemodynamic conditions [29], and thus increase the prediction accuracy of AAA evolution. In light of the preceding discussion, a study that can bridge numerical, experimental, and the clinical studies is necessary. Therefore, the objective of this investigation is to develop a reliable stereoscopic PIV protocol to investigate hemodynamic behaviors in patient-specific AAA models in steady flow conditions as a starter for further unsteady flow assessments.

2. Materials and Methods

2.1. Transparent Patient-Specific Anatomical Model Fabrication.

Two patient-specific 3D anatomical models, with and without ILT, i.e., WT and WOT, respectively, were fabricated by a stereolithography method as described in our previous study [30]. The geometry of the models was acquired from a patient-specific computed tomography angiography (CTA) scan at Allegheny General Hospital (Pittsburgh, PA) and post-processed using 3D reconstruction software (Simpleware Ltd., Exeter, UK) and Geomagic (Geomagic Inc., NC) followed by rapid-prototype machining. Examples of the final AAA WT and WOT models are shown in Fig. 1. Walls of these two models were rigid as it has been shown that the wall motion does not practically affect its mechanical loading in a complete fluid–structure interaction analysis [31] and this finding was also recognized by another experimental study [25]. Patient-specific blood flow distribution was acquired at a plane immediately below the renal arteries using non-contrast phase-contrast MRI (PC-MRI) at 40 phases of the cardiac cycle under resting conditions. Note that AAA without ILT model is a discrete anatomical step as the formation of ILT progresses in parallel with the growth of AAA. However, the exclusion of ILT in this case facilitates the identification of the ILT effect on the hemodynamic changes. This complements the information in addition to the AAA with ILT model.

Fig. 1.

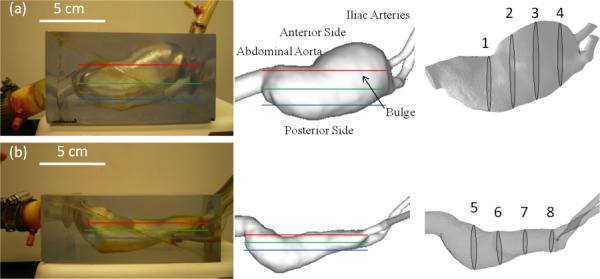
Transparent patient-specific rapid prototype replica, representative measurement planes, and corresponding anatomical views showing the geometry of each lumen. (a) AAA model without ILT and (b) AAA model with ILT. Left column: Transparent models; middle and right column: CFD models. Positions of three stereoscopic PIV measurement planes are outlined in red (top plane), green (middle plane), and blue (bottom plane).

2.2. In Vitro Flow Loop Setup.

The flow loop was constructed using T-slotted aluminum framing (80/20 Inc., IN), tygon tubing, a steady submersible pump (Franklin Electric Co., IN), two flow meters (Dwyer Instruments, Inc., IN) and two AAA phantoms (WOT and WT). The configuration is shown in Fig. 2. To match physiological human blood flow conditions, a blood analog solution was prepared with a mixture of NaI (Sigma-Aldrich, Corp., MO) and water. The role of NaI in the blood analog solution was designed to match the refractive index of the phantom material (n = 1.51). The density of the final mixture solution was 1.88 g/cm³ and the kinematic viscosity of the mixture was 1.72 cS. 15 μm fluorescent particles (Microgenics, Inc., CA) were added to the blood analog solution as tracers. The two AAA models were operated at steady flow conditions corresponding to a peak systolic flow obtained from the PC-MRI data of the patient (110 cm³/s, which corresponds to 39.55 cm/s of peak velocity at inlet). The split ratio of the two outlets (iliac arteries) is 50:50 (each with a flow rate of 3.3 l/min). The Reynolds number (Re) was therefore set to be 2234. To attach tubing and allow fully established flow, the inlet was extended by more than 25 hydraulic diameters using a rigid plastic tube. These extensions employed gradual transition from the tube cross section to the cross sections of patient-specific models. Outlets were extended by 6–8 hydraulic diameters. The flow loop was tested under steady flow conditions using systolic peak parameters and transient flow structures associated with pulsatile conditions may not be able to be captured using the current methodology. However, it is believed that the relative sizes of circulating flow structures will change slightly with pulsatile boundary conditions, resulting in minor variations in mean flow patterns, and the pulsatile flow variations should be considered only when parameters like time average wall shear force or oscillatory shear index (OSI), etc are analyzed. As the main message of this study is to study the effect of the ILT in AAA hemodynamics in 3D using a stereoscopic PIV technique, the peak systolic value was used as a representative point in the cardiac cycle.

Fig. 2.

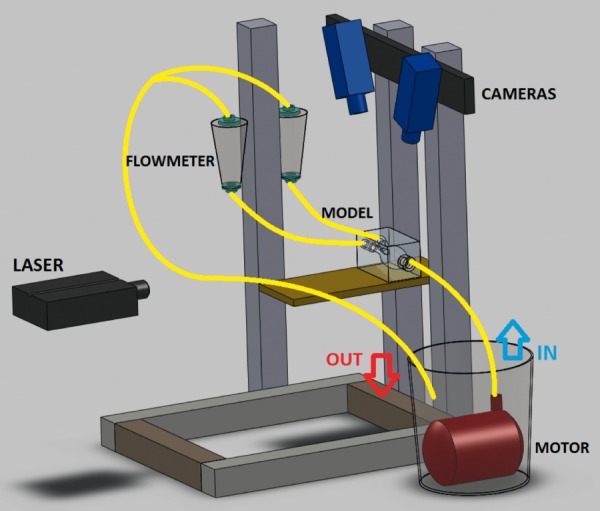
Schematic representation of stereoscopic PIV configuration [45]

2.3. Stereoscopic PIV Setup and Processing.

A double-pulse Nd:YAG laser (Model Twins BSL 50, Quantel, Montana) was used, each with energy of 50 mJ per pulse at 532 nm and operated at a repetition rate of 15 Hz. A laser sheet with a thickness of 2 mm was positioned at three different planes: 2.5, 3.5, and 4.5 cm from the WOT model bottom wall (posterior side) and 1.4, 2.1, and 2.8 cm from the WT model for PIV measurements, respectively. Laser pulse delay time (dt) was determined to be 1500 μs, satisfying the one-quarter rule [32]. To obtain reliable PIV velocity data, increasing total number of frames (2, 10, 50, 100, 200, 300, 400, and 500) were processed to check the calculated velocity error for the entire flow domain. The average velocity variations with respect to the average velocity at the inlet between 199 and 200 frames, 299 and 300 frames, and 399 and 400 frames were 0.004%, 0.002%, and 0.001%, respectively. It was thus considered that a sufficient level of convergence of the running average was achieved with 300 image pairs, and processed to obtain “image-pair independent” PIV velocity data.

Two CCD cameras (model Imager Pro X 2 M, LaVision, Germany) with a 1600 × 1200 pixel resolution were used to record stereo PIV images. The cameras were each fitted with a high-pass filter to block laser light (green, 532 nm) and to transmit emitted fluorescence (red, >590 nm). The angle separation between the two cameras was 45 deg, and each camera was oriented 90 deg from the laser (Fig. 2). Stereoscopic calibration for both cameras was performed using a polygon mapping function with a two-level calibration plate under the camera pinhole model setting, with the root mean square (rms) error as a measure of image reconstruction error. Self-calibration [33] was performed to eliminate disparity errors in the vector calculation due to possible misalignment of the laser plane and the calibration plate plane. The resultant rms of stereo calibration and average deviation of self-calibration were <0.3 and <0.1 pixels, respectively. The raw PIV images were preprocessed by subtracting the sliding minimum over a specified time to eliminate background noise. Furthermore a Gaussian smoothing filter was employed that removed the pixel-to-pixel noise [34]. Particle intensity normalization technique was subsequently applied to reduce high intensity fluctuations of particles in the entire flow domain. Stereo velocity vectors were calculated using PIV multipass stereo cross correlation. Window sizes were 64 × 64 pixel (first pass, 3.84 × 3.84 mm²) and 32 × 32 pixel (second pass) with a 50% overlap.

2.4. Numerical Modeling Methods.

The Gambit 2.4 (Ansys, Inc., PA) grid generation package was used to generate the 3D mesh. For the commercial solver, FLUENT 12.1 (Ansys, Inc., PA) was selected. Assessment of the mesh quality was defined as devoid of high cell skewness, as there is a known relationship between mesh quality, simulation convergence, and convergence time [35]. A mesh density sensitivity analysis followed [36] based on achieving a relative difference of less than 5% variations in pressure at the inlet and the average WSS.

The in-house CFD code implements a multigrid artificial compressibility solver for incompressible, Newtonian flows, and employs a second-order accurate finite-difference numerical discretization scheme. A direct numerical simulation (DNS) flow unsteady flow solution was computed on a immersed boundary Cartesian grid, using steady inflow conditions (Re = 2235). The boundaries of the grid are prepared using a surface mesh of the fluid domain. The in-house cardiovascular flow solver has been validated for jet flow regimes studied using DNS and used extensively for image-based hemodynamic modeling [37,38]. The simulation used a high-density spatial grid with a total of ∼1 M fluid nodes, with a grid spacing of 0.03D, where D represents the inlet diameter of the model, which is 1.88 cm, and a nondimensional simulation time step of 0.01 (∼5 × 10⁻⁴ s in physical time) to achieve the resolution required to reasonably match with the PIV data. Grid sensitivity studies were conducted using grids of increasing size (starting with ∼250,000 nodes, to ∼1 M, in steps of ∼250,000) comparing the running average flow velocity, averaged spatially over a volume in the jet region past the inlet, over time. Spatial resolution was deemed as satisfactory when no appreciable change in the aforementioned mean velocity of temporal convergence was noted on subsequent grid refinement (<5% change) after 10,600 simulation time steps when no appreciable change in the jet-region-averaged velocity was noted, as seen in the running average flow field. In addition, for the PIV data validation, a correlation coefficient value was calculated to show the consistency between PIV and numerical methods using Eq. (1)

$$\mathit{Correl}\hspace{1em}(X,Y)=\frac{\Sigma (x-\overline{x})(y-\overline{y})}{\sqrt{\Sigma (x-\overline{x}){\hspace{0.17em}}^2\Sigma (y-\overline{y}){\hspace{0.17em}}^2}}$$ (1)

where x and y are acquired velocity values from PIV, and CFD methods, respectively.

3. Results and Discussion

3.1. Raw Stereoscopic PIV Image Preprocessing.

To acquire the out-of-plane velocity components, the two PIV cameras were inclined with respect to the laser plane. This arrangement can cause strong light scattering from the patient-specific model boundary especially when the model has tracer particles trapped in its irregular anatomic geometry and cannot be flushed out over reasonable times. A strong peak-locking effect and biased velocity vectors will be obtained if applying the PIV algorithm directly to this type of raw images without using any image preprocessing method. The probability density function (PDF) can be used to assess the degree of significance of the peak-locking effect. The PDF computes a histogram of a vector field where each velocity component is discretized in to certain velocity intervals. If the peak-locking effect is insignificant, peak lock values will be smaller than 0.1 pixel.

Image preprocessing was applied in this study; representative images before and after the image preprocessing step are shown in Fig. 3. Results showed that before applying image preprocessing, peak lock values in three directions (x, y, and z) were larger than 0.5 pixel, which indicates a strong peak-lock effect in the calculated PIV data. In contrast, peak lock values were found to be less than 0.1 pixel after image preprocessing methods were applied. The PIV algorithm was subsequently applied to these preprocessed PIV images where the peak-locking effect is insignificant.

Fig. 3.

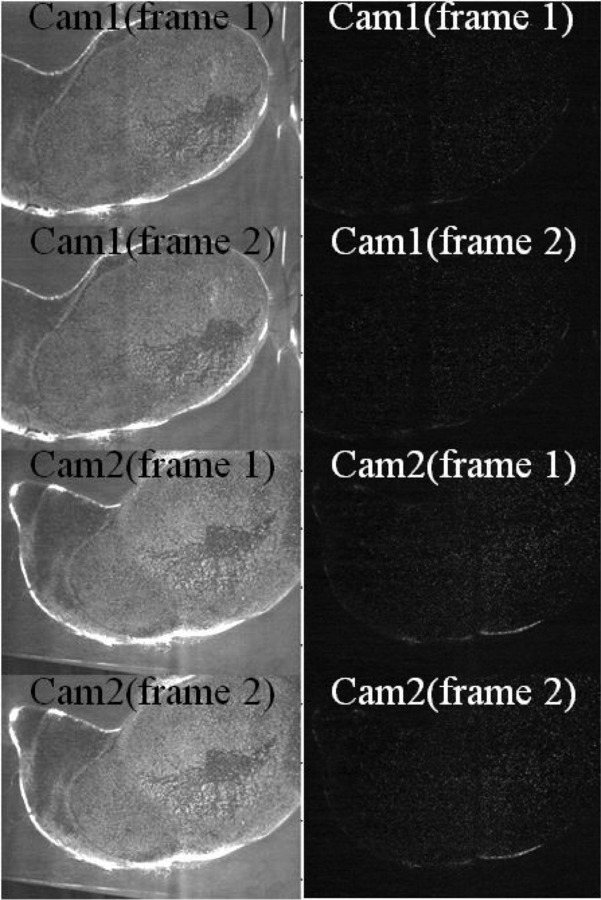
Before and after image preprocessing of stereoscopic PIV data from AAA model without ILT (left column: before; right column: after image preprocessing). Time between frame 1 and frame 2 was set to be 1.5 ms.

3.2. Jet Flows in WOT and WT Models.

Velocity distributions in three directions of the WOT and WT models at three different measurement planes (top, middle, and bottom) are plotted in Figs. 4(a) (WOT) and 4(b) (WT). In Figs. 5(a) and 5(c) (WOT) and 5(b) and 5(d) (WT), the 2D in-plane velocity vectors are overlaid with the raw PIV images together with their 2D streamtraces and the V_z velocity component. Two different jet flow patterns were observed in these two models. At the middle plane of the aneurysm bulge of the WOT model, a major jet flow structure was redirected by sweeping the AAA sac lumen after its first impingement on the wall [at the lateral region as shown in Fig. 4(a)]. Following its second impingement [at the distal region which is near the iliac arteries as shown in the first two rows of Figs. 4(a) and 5(a)], the flow recirculated and a separation flow vortex was formed. In contrast, for the WT model [Figs. 4(b) and 5(b)], the jet flow followed the sac geometry uniformly toward the outlets downstream without any major rotational flow structure. These characteristic jet flow routes were caused by the differences in lumen geometries of the models and primarily due to the absence or presence of ILT, respectively.

Fig. 4.

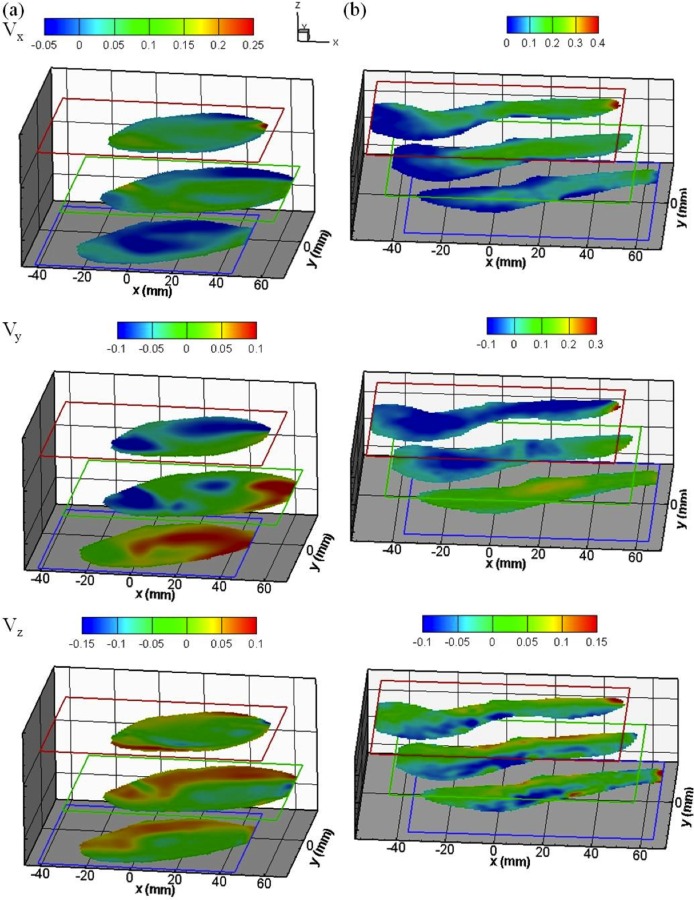
Stereoscopic PIV velocity data of both AAA models (a) without and (b) with ILT. Velocity fields on each measurement plane are shown in x (the first row), y (the second row), and z (the third row) directions. Unit of color bars: m/s.

Fig. 5.

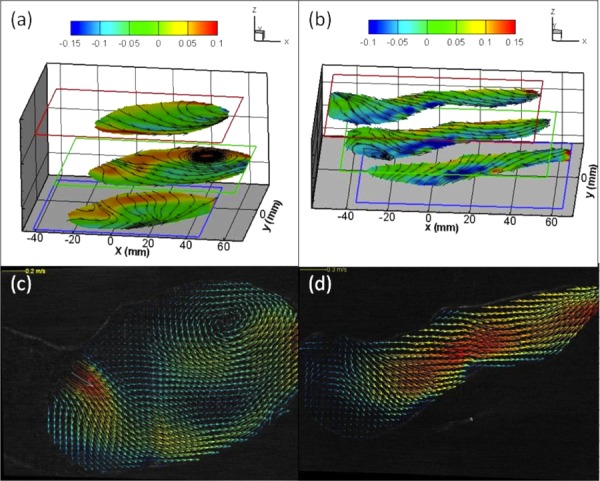
Comparison of flow patterns between AAA models with and without ILT. A vortex was observed in the middle plane near the aneurysm bulge region of the AAA model without ILT as evidenced by (a) V_z contour map overlaid with 2D streamtraces at three measurement planes and (c) 2D velocity vectors overlapped with raw PIV image. No vortex was found in the same region of the AAA model with ILT as evidenced by (b) and (d).

Internal shear layers induced by distinct jet flow fields can generate flow instability as discussed in our earlier work [30,39]. To quantify such flow fluctuations in the AAA bulge, velocity at five selected locations, which are along the shear layer of each jet, was sampled. In the WOT model, velocity fluctuations ranged from 18% to 29% (18.4%, 19.8%, 20.5%, 26.9%, and 28.7%). These values are relatively large in comparison to the velocity fluctuations in the shear layer of the WT model, which ranged from 10% to 12% (10.1%, 10.3%, 10.3%, 11.6%, and 11.8%). The lower velocity fluctuations in the WT model are due to the streamlined pathway that was achieved by the ILT formation, which redirected the flow toward a more preferential direction. In contrast, for the WOT model, the cross section of the aneurysm region is relatively large, allowing the jet flow to recirculate in the aneurysm pouch. The development of the jet flow in this region contributed to the higher velocity fluctuations, and a vortex core was formed due to a part of the jet flow spreading along the geometry of the sac wall, rather than flowing through the outlet.

3.3. Swirl Motion and 3D Vortex in the WOT Model.

As presented in the first row of Fig. 4(a), the distal region of the middle plane (aneurysm bulge region) shows two regions with opposite out-of-plane velocity components. Negative x-component velocities appeared on the upper region (lateral side), whereas positive velocities were located in the center (medial region) of the aneurysm bulge, indicating an axially swirling or helical flow. Further examination of the y-component contour map [the second row of Fig. 4(a)] reveals a transverse swirling flow. PIV measurements indicate that this flow structure should appear in a cross region where two swirls were intersected as shown in Figs. 5(a) and 5(c). In contrast to the WOT model, this flow structure was not found in the WT model as shown in Figs. 4(b), 5(b), and 5(d).

The 3D flow structure of the vortex including vortex core in the WOT model can be further visualized more clearly by overlapping 2D streamtraces with the out-of-plane velocity contour plots as shown in Figs. 5(a) and 5(c). In the middle plane of Fig. 5(a), two opposite out-of-plane flow directions were observed (contour plot), and the boundary between these two flows passed through the 2D vortex core (outlined by streamtraces). Based on this observation, it can be concluded that the vortex has a complex 3D flow topology (with out-of-plane clockwise rotation along the x axis) rather than a simple planar rotational flow structure. To estimate the size of this 3D vortex, velocity results from three different locations of measurement planes were compared. Since the stereoscopic data was acquired at 1 cm intervals (laser sheet is 2 mm in thickness) and the vortex occurred only in the middle plane, it can be concluded that the diameter of the vortex core is approximately 3 cm in diameter and slightly less than 2 cm in thickness. This vortical structure is orientated longitudinally in the direction of the main blood flow in the AAA bulge and rotated counterclockwise (viewed from anterior side or from flow outlets). This rotational flow structure occupies nearly half of the aneurysm bulge region and should have a dominant impact on subsequent ILT formation.

During ILT formation, as the anatomy transformed from WOT to WT, the AAA sac wall experienced a dramatic change in WSS. This change in WSS can promote the formation of ILT with subsequent obstruction of a blood vessel [25]. It is possible that the geometry effect plays a major role in the disappearance of the vortex as evidenced in the WT model where the blood flow domain in the aneurysm sac was squeezed due to the formation of ILT. A simple dimensional comparison of the two AAA models supports this hypothesis. Before the ILT formation, in the WOT model, the width of the aneurysm region was approximately 5 cm and the vortex diameter was approximately 3 cm. The width of the aneurysm region then decreased to 2 cm in the WT model due to the growth of ILT, and the vortex vanished. Since the vortex only existed in the WOT model, the space where the vortex occurred (3 cm in diameter) instead can be occupied by the formation of an ILT as observed in the WT model.

Solid evidences have been shown in this study that indicates a possible correlation between the rotational flow and the subsequent generation of ILT. This result is consistent with a previous published study [40] where a recirculation zone formed inside the aneurysm cavity creates conditions that may promote thrombus formation. Furthermore, slowly recirculating regions were recorded at the very early stages in the aneurysm enlargement [41]. Especially intermitted WSS changes are believed to play an important role in the etiology of the disease by triggering the endoluminar thrombus formation [41]. Further studies support the fact that the impact of vortices on the distal walls of the AAA is one of the important factors contributing to the ruptured aneurysm [42]. The presence of flow recirculation regions also increases the near wall residence time of fluid particles [25]. Still the pathological function of the rotational flow needs to be elucidated with additional patient-specific models.

3.4. 3D Flow Patterns in WOT and WT Models.

The 3D velocity distribution in all of the measurement planes show that the in-plane profile of the bottom planes (posterior side) has a different trend than the top and middle planes (anterior side) in both models. In the second row of Fig. 4(a), positive y-component velocities occupied a larger region of the flow domain at the posterior side. After being in contact with the lateral wall, the flow moved to the opposite wall rather than following the normal pathway dictated by the lumen geometry, as opposed to what have observed at the anterior side. Similar flow patterns were observed in Fig. 4(b) for the y-component velocities at the posterior side of the WT model where positive velocities were also found in the majority of the flow domain. These patterns indicate that flow regimes at the posterior side are significantly different compared to that of at the anterior side. Further investigation of the x-component velocity contour plot in both models [the first row of Figs. 4(a) and 4(b)] reveals similar flow distributions. At the anterior side of both models, the main streamwise direction is dominated by the jet flow (toward the aneurysm bulge region), which followed the lumen geometry after the first impingement. However, the direction of the main stream at the posterior side is toward the lateral side of the aneurysm bulge, opposite of what is observed at the anterior side. As for the third velocity component shown in Figs. 4(a) and 4(b), flow patterns are similar at all three measurement planes. These flow behaviors in both models are not uniform as flows with opposite directions were found on each measurement plane. However, the distributions are similar in all three planes as flow regimes with positive velocity values were found on the upper region of each plane, whereas the negative flow regimes were found on the lower region. The out-of-plane flow kept impinging both the anterior and posterior walls in a circulating fashion as found in both experimental models before and after the formation of ILT. This intermittent flow behavior could be another driving force to further enhance the platelet activation in the aneurysm lumen. In summary, flow regimes in the x and y directions at the posterior side in both models exhibited significant differences from those at the anterior side, but not in the out-of-plane direction. This complex flow phenomenon in both AAA models implies an altered WSS on the sac wall, which may influence the location of ILT over time. The WSS distribution of both AAA models is provided in Fig. 6.

Fig. 6.

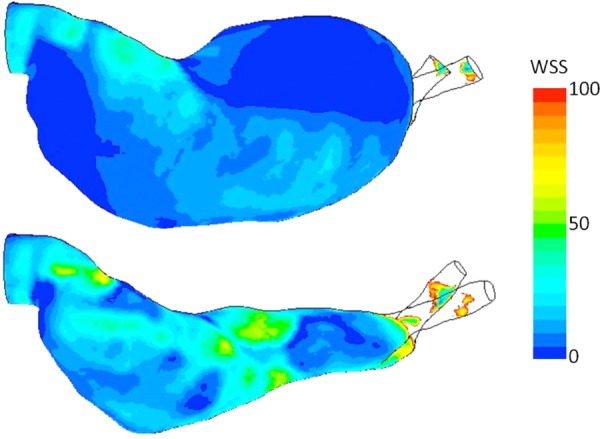
Wall shear stress distribution for both AAA models. Unit of the color bar: Pa.

The steady peak flow and rigid wall assumptions made in this study are approximations to the real pathological cases, but the main purpose of the study is to establish a method that could be used in the future for pulsatile flow and compliant wall conditions. This study was targeted to help establish some basic correlations regarding ILT and flow structures to benefit subsequent AAA studies. In addition, even under steady conditions as presented in this study the rationale for ILT formation was quite apparent by virtue of the large recirculation zones. These effects are believed to be more pronounced under actually physiological conditions.

3.5. Error and Validation Tests for Stereoscopic PIV Out-of-Plane Velocity Measurements.

The out-of-plane velocity measurement capability in patient-specific models was examined and quantified in this study. In this work, the ratio of out-of-plane velocity error to the in-plane velocity error was computed to be 2.4 based on the methodology suggested by [43]. The error ratio for the present stereo experiments are similar to the previously reported ranges [34] in idealized geometries. For subsequent quantitative physical validation, the experimentally measured out-of-plane velocity distribution in the WOT model were compared to the computed data from the two common numerical CFD methods. The experimental and computational WT results displayed excellent agreement and are therefore not included in this paper. For the WT model, better agreement is expected since the flow regime for WT is simpler and constitutes relatively straightforward flow physics for contemporary CFD solvers.

The out-of-plane velocity data at the middle plane of the WOT model obtained using stereoscopic PIV, Fluent, and in-house CFD methods are presented in Fig. 6. The distribution of flow contours was qualitatively similar for the experiment and computations. To investigate the degree of data consistency between experimental and CFD methods, velocity data were extracted along a polyline in the aneurysm bulge region from each contour map. These values are plotted as velocity profiles as also shown in Fig. 7. The statistical correlation coefficient between PIV and Fluent is found to be 0.92, and between PIV and the in-house CFD method it is 0.85. These support that experimental PIV data provide similar velocity distributions for both numerical methods. To confirm the reliability of the two numerical methods, the correlation coefficient between Fluent and the in-house CFD methods was found to be 0.96. Still, differences between Fluent and the in-house CFD results can be identified especially at the entrance region of the aneurysm bulge. The jet flow structure is more pronounced in the in-house CFD results than the Fluent results. This variation might be possibly attributed by much higher grid density applied in the in-house CFD method. In summary, a good agreement was found between the experimental stereoscopic PIV method and the two simulation methods in the aneurysm sac. This further validates the accuracy of numerical results using the presented experimental methodology. To further enhance the degree of accuracy of this experimental methodology, a physical Windkessel model should be incorporated in the AAA flow loop for a better match of physiological conditions as indicated by a recent published in vitro validation of an AAA study [44].

Fig. 7.

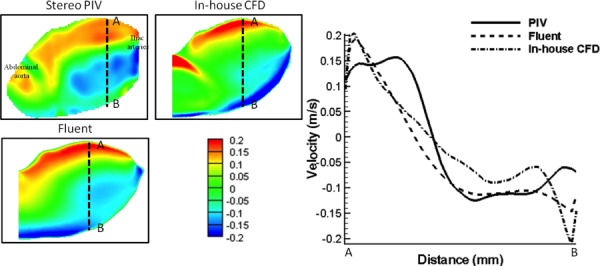
(a) Out-of-plane velocity data comparison of patient-specific AAA model without ILT using stereoscopic PIV, Fluent, and in-house CFD methods. Left panel: Out-of-plane velocity contour maps; right panel: quantitative velocity profile comparison. Data were extracted from each A-B line (50 mm) of contour plots (left panel). Correlation coefficients between stereoscopic PIV and Fluent, stereoscopic PIV and in-house CFD, and Fluent and in-house CFD are 0.92, 0.85, and 0.96, respectively. Unit of the color bar: m/s.

4. Conclusions

In this study, a stereoscopic PIV flow visualization method was applied in combination with a series of image preprocessing methods to acquire and calculate reliable two-dimensional, three-component velocity field data in patient-specific AAA phantoms with and without intraluminal thrombus. Three planes (top, middle, and bottom) were used in each model to provide detailed flow information of the entire AAA phantom. Experimental stereoscopic PIV data was utilized to validate two computational methods with high consistency; thus demonstrating its utility for flow visualization in pathological models of large arteries. The experimental method can be further used to validate new numerical modeling methods on incremental formation of ILT for advanced AAA studies of growth and remodeling. Experimental and computational data showed that a vortex was generated in the AAA model without the thrombus model and then disappeared in the model with thrombus. The existence of this vortex is linked to blood recirculation in the aneurysm sac, which led to thrombus formation. This outcome suggests that proper control of vortex dynamics in the AAA may reduce the formation of thrombus and ultimately influence its rupture risk.