Numerical Evaluation of Myofiber Orientation and Transmural Contractile Strength on Left Ventricular Function

Abstract

The left ventricle (LV) of the heart is composed of a complex organization of cardiac muscle fibers, which contract to generate force and pump blood into the body. It has been shown that both the orientation and contractile strength of these myofibers vary across the ventricular wall. The hypothesis of the current study is that the transmural distributions of myofiber orientation and contractile strength interdependently impact LV pump function. In order to quantify these interactions a finite element (FE) model of the LV was generated, which incorporated transmural variations. The influences of myofiber orientation and contractile strength on the Starling relationship and the end-systolic (ES) apex twist of the LV were assessed. The results suggest that reductions in contractile strength within a specific transmural layer amplified the effects of altered myofiber orientation in the same layer, causing greater changes in stroke volume (SV). Furthermore, when the epicardial myofibers contracted the strongest, the twist of the LV apex was greatest, regardless of myofiber orientation. These results demonstrate the important role of transmural distribution of myocardial contractile strength and its interplay with myofiber orientation. The coupling between these two physiologic parameters could play a critical role in the progression of heart failure.

1. Introduction

Cardiac muscle fibers, also referred to as “myofibers,” are arranged as counter-wound helices surrounding the ventricular cavities. Their orientation depends on the transmural location. Specifically, epicardial myofibers are predominantly left-hand oriented whereas endocardial myofibers are right-hand oriented [1–3]. The alignment of these myofibers smoothly rotates toward the circumferential direction in the midmyocardial region [4]. The counter-wound helical structure of myofibers serves to equalize the myocyte strain and stress, allows the LV to undergo torsional deformation during myocyte shortening, and thereby optimize the volume of blood ejected during systole (i.e., SV), as demonstrated in previous computational studies [4–8]. The myofiber orientation, therefore, is a key determinant of LV pump function.

Another important factor influencing LV function is the contractile property (e.g., contractile strength) of myocardium, which is directly linked to myocyte shortening and force generation. Recently, both computational and ex vivo studies have demonstrated transmural differences in myocyte contractile function at the cellular level [9,10]. In these studies, the peak isometric tension generated by myocytes depended on their transmural location in the LV wall. These studies, however, reported different patterns of transmural variations, suggesting that the transmural distribution of myocyte contractile strength may vary from species to species, and even from individual to individual. Moreover, the transmural distribution of myocyte contractile function also could be changed during the development of heart disease, as demonstrated in ex vivo studies [10]. Although the transmural variations in myocyte contractility have been implicated in cellular level measurements [9–11], their effects on the global function of the LV still remain unclear and the potential interplay between myofiber orientation and transmural myocardial contractility has been neglected in previous studies.

Therefore, the goal of the present study was to introduce transmural variations of myocardial contractility into a computational simulation of global LV function. Our hypothesis is that the transmural distributions of myofiber orientation and myocyte contractile strength interdependently impact LV pump function. For this purpose, two representative transmural distributions of peak isometric tension (i.e., either endocardium > midcardium > epicardium or epicardium > midcardium > endocardium) were used to assess the influence of myofiber orientation on different clinical indicators of cardiac performance. The first is the well-known Starling relationship (SV/end-diastolic pressure (EDP) relationship) and the second is the ES apex twist of the LV, which is emerging as a sensitive clinical parameter. In doing so, the results of the present study shed light on the important role of transmural myocardial contractile strength in regulating myofiber structure-dependent LV pump function.

2. Methods

2.1. FE Model.

A 3D FE model was created based on the geometry of a sheep LV at early diastole [12] (Fig. 1(a)). The geometry of this model was simplified as a truncated ellipsoid with a base-to-apex length of 77.4 mm. Wall thickness in the model ranged from approximately 8 mm near the apex to 13 mm at the base. The FE mesh was produced by filling the volume between endocardial and epicardial surfaces with hexahedral brick elements incorporating a trilinear interpolation scheme (TrueGrid; XYZ Scientific, Inc., Livermore, CA, U.S.A). In order to investigate the effects of transmural variations in myocardial mechanical properties, the entire ventricular wall was evenly divided into three layers, representing epi-, mid-, and endocardium, respectively (Fig. 1(b)).

Fig. 1.

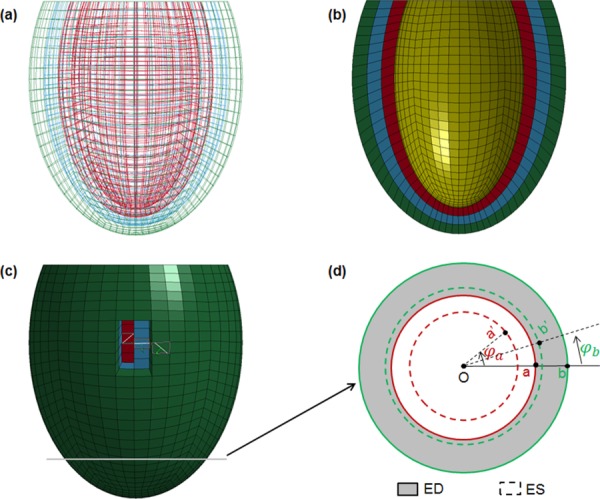
A 3D FE model was created to simulate the function of LV. (a) Wireframe view of the LV, which was represented by an ellipsoidal morphology; (b) view with half of the model removed to show the LV wall with three transmural layers of equal thickness, outermost = epicardium, middle = midwall, and innermost = endocardium; (c) epicardial view of model with transmural variation in myofiber orientation (white lines within elements) and a radial–circumferential plane near the apex where the LV twist was assessed, and (d) example of the rotation angles of two specific nodes on the inner and outer surface of LV wall from end-diastolic to ES states.

The passive material properties of the ventricular wall were considered to be nearly incompressible, hyperelastic, and transversely isotropic with respect to the local fiber direction [13]. The strain energy function was defined as

$$W=\frac{c}{2}(e^Q-1)$$ (1)

$$Q=b_f{E}_{11}^2+b_t(E_{22}^2+E_{33}^2+E_{23}^2+E_{32}^2)+b_{\mathit{fs}}(E_{12}^2+E_{21}^2+E_{13}^2+E_{31}^2)$$ (2)

where c, b_f, b_t, and b_fs are diastolic myocardial material parameters, E ₁₁ is strain in fiber direction, E ₂₂ is cross-fiber in-plane strain, E ₃₃ is radial strain transverse to the fiber direction, and the remaining terms are shear strains. Systolic contraction was modeled as the sum of the passive stress derived from the strain energy function and an active stress component along the fiber direction

$$\mathit{S}=\mathit{pJ}{\mathit{C}}^{-1}+2J^{-\frac{2}{3}}\mathrm{Dev}\left(\frac{\partial \tilde{W}}{\partial \tilde{C}}\right)+{\mathit{T}}_0\{t,{\mathrm{Ca}}_0,l,T_{\max }\}$$ (3)

where S is the second Piola–Kirchhoff stress, C is the right Cauchy–Green tensor, J is the Jacobian, p is the pressure, and Dev() is the deviatoric operator [14]. The active tension T ₀ is defined by a time-varying elastance model and is a function of time t, peak intracellular calcium concentration Ca₀, sarcomere length l, and maximum isometric tension T _max achieved at the longest sarcomere length and maximum peak intracellular calcium concentration [15]. At end-systole (i.e., t = t ₀ in Eqs. (8)–(11) [15]), the active tension is reduced to

$$T_0=T_{\max }\frac{{\text{Ca}}_0^2}{{\text{Ca}}_0^2+\frac{{({\text{Ca}}_0)}_{\max }^2}{\hspace{0.17em}\text{exp}\hspace{0.17em}[B(l_R\sqrt{2E_{11}+1}-l_0)]-1}}$$ (4)

Moreover, a cross-fiber in-plane stress component equivalent to 40% of T ₀ was added based on biaxial stretching experiments [16] and FE analyses [17]. Both the passive and active material laws were implemented through the use of a material subroutine in the FE solver ls-dyna (Livermore Software Technology Corporation, Livermore, CA, U.S.A).

The material constants for both passive and active myocardium were chosen based on previous studies [15,18,19] (Table 1). Some parameters (i.e., c and B) were adjusted to obtain the end-diastolic volume (EDV) and end-systolic volume (ESV) prescribed in previous work [3,20]. In order to introduce transmural changes in active contraction, two distributions of T _max parameters were selected according to previously reported results from either normal or failing hearts [9,10]. The values of T _max for epi-, mid-, and endocardium were, in case (i) 150, 110, and 70 kPa, respectively, and in case (ii) 70, 110, and 150 kPa, respectively.

Table 1.

Numerical values for passive and active myocardium constants

Constants	Values	Description
c	0.28 kPa	Diastolic stiffness parameter
bf	18.48	Transverse isotropy parameter [18]
bt	3.58	Transverse isotropy parameter [18]
bfs	1.627	Transverse isotropy parameter [18]
B	1.4 μm−1	Shape constant of peak isometric tension–sarcomere length relation
l 0	1.58 μm	Sarcomere length at which no active tension develops [15]
Ca0	4.35 μM	Peak intracellular calcium concentration [15]
Camax	4.35 μM	Maximum peak intracellular calcium concentration [15]
t0	0.3 s	Time to peak tension
m	0.1312 s/μm	Slope of linear relaxation duration–sarcomere length relation [19]
b	−0.09434 s	Time-intercept of linear relaxation duration–sarcomere length relation [19]
lR	Epi: 1.91 μm, mid: 1.85 μm, and endo: 1.78 μm	Stress-free sarcomere length at each myocardium layer [18]

2.2. Myofiber Orientation and Boundary Conditions.

For simplification, only transmural variations in myofiber orientation were considered; the helical angle of myofibers was assumed to transition linearly from the outer surface of the epicardium to the inner surface of endocardium (Fig. 1(c)). To assess the influence of epi-myofibers on LV function, the helical angle of myofibers in the epicardium was assigned values ranging from −60 deg to 0 deg, while the myofiber helical angle in the endocardium was fixed at 60 deg. For the assessment of endo-myofibers, the helical angle in the endocardium varied from 10 deg to 90 deg; in these cases, the myofibers in the epicardium were fixed at −30 deg. It should be noted that the myofiber angle range was larger than the typical range seen for a given species in a healthy or disease state to better understand their effects [21–24].

The boundary conditions of the LV were assigned to fully constrain the displacement at the entire surface of the base. In order to simulate the steady ED and ES states, the LV cavity was loaded with prescribed pressures. Specifically, the pressure of the LV cavity was quickly increased to the prescribed value and maintained at the same level until the simulation reached a steady-state solution at ED and ES [25].

2.3. Calculation of SV/EDP (Starling) Relationship.

For each combination of T _max distributions and myofiber angles, the EDV and ESV were determined, respectively, at ranges of EDP (0–18.75 mmHg) and ES pressure (ESP) (0–97.5 mmHg) with steady-state simulations. The linear ESP-ESV relationship was obtained by means of least-square regression analysis, and represented as

$$\mathrm{ESP}={\mathit{E}}_{\mathrm{es}}(\mathrm{ESV}-V_0)$$ (5)

where V ₀ is the volume intercept and E _es is the LV elastance. The arterial elastance E _a was calculated using the equation

$$E_{\mathrm{a}}=\frac{\mathrm{ESP}}{\mathrm{EDV}-\mathrm{ESV}}$$ (6)

where ESP = 97.5 mmHg, EDV = 135 ml, and ESV is the value corresponding to 97.5 mmHg. With the least-square regression analysis, the EDP and EDV values were fit to the following equation:

$$\mathrm{EDP}={\beta }_0+{\beta }_1\mathrm{EDV}+{\beta }_2{\mathrm{EDV}}^2$$ (7)

where β ₀, β ₁, and β ₂ are the stiffness parameters of the LV diastolic compliance. The SV was calculated as

$$\mathrm{SV}=\frac{\mathrm{EDV}-V_0}{1+\frac{E_{\mathrm{a}}}{E_{\mathrm{es}}}}$$ (8)

Finally, the SV and EDP (Starling) relationship was determined from Eqs. (7) and (8).

2.4. Calculation of ES Apex Twist Angle.

The steady ED and ES states were simulated at EDP = 15 mmHg and ESP = 90 mmHg, respectively, for each T _max and myofiber case. To determine the systolic twist of apex about the long axis of the LV, two nodes on a radial–circumferential plane near the apex (Fig. 1(c)) were chosen. One node (node a) was located at the inner edge of endocardium and another (node b) was at the outer edge of epicardium (Fig. 1(d)). The rotation of each node during systole, i.e., φ_a and φ_b (Fig. 1(d)), relative to a fixed point (0,0), was the net difference between angles at ED and ES. The systolic twist angle of apex (φ) was the averaged rotation angles of the two nodes; i.e.,

$$\varphi =\frac{{\varphi }_a+{\varphi }_b}{2}$$ (9)

3. Results

3.1. Effects of Myofiber Orientation and Contractility on the LV Starling Curve.

In general, altering the endo-myofibers (Figs. 2(a) and 2(b)) or epi-myofibers (Figs. 2(c) and 2(d)) toward a more longitudinal orientation caused an increase in SV. This trend occurred independently of the transmural distribution of contractile strength. More specifically, when the helical angles of epi-myofibers were fixed at −30 deg, increasing the helical angles of endo-myofibers from 10 deg to 90 deg caused a progressive increase in SV to a peak level, which was followed by a decrease (Figs. 2(a) and 2(b)). The SV underwent similar biphasic changes when the left-handed helical angles of epi-myofibers varied from 0 deg to −60 deg with endo-myofibers oriented at a fixed right-handed helical angle of 60 deg (Figs. 2(c) and 2(d)).

Fig. 2.

The transmural distribution of myocardium contractile strength altered the effects of myofiber orientation on the Starling relationship of LV. With the helical angle of epi-myofibers fixed at −30 deg, the effects of changes in endo-myofiber helical angle on the Starling curve of LV were assessed when T _max for epi-, mid-, and endocardium was 150, 110, and 70 kPa, respectively, [case (i); (a)], and 70, 110, and 150 kPa, respectively, [case (ii); (b)]. The effects of epi-myofiber helical angle on LV Starling curve were assessed when the endo-myofibers were set at 60 deg for cases i (c) and ii (d), respectively.

When comparing the two transmural distributions of T _max, i.e., case (i) and case (ii), different optimal myofiber orientations that produced the highest SV were observed. For case (i), the maximum SV was achieved with an epi-myofiber angle of −30 deg and an endo-myofiber angle of 70 deg (Fig. 1(a)), but for case (ii), the maximum SV was achieved with an epi-myofiber angle of −50 deg and an endo-myofiber angle of 60 deg (Fig. 1(d)). Additionally, when comparing case Figs. 1(a) and 1(b), it can be seen that case (i) produced the maximum SV within those fiber ranges. When comparing case Figs. 1(c) and 1(d), it can be seen that case (ii) produced the maximum SV within those fiber ranges.

The variation in the Starling curves, i.e., the spread between them as the helical angle of either endo- or epi-myofibers varied, was different in these two cases. Specifically, when the epicardial myofiber angle was fixed at −30 deg and the endocardium contracted weakest (case (i), Fig. 2(a)), the magnitude of changes in SV due to changes in endocardial fiber angle was larger, compared to case (ii) when the endocardium contracted strongest (Fig. 2(b)). However, when the endocardial myofiber angle was fixed at 60 deg and the epicardium contracted weakest (case (ii), Fig. 2(d)), the magnitude of changes in SV due to changes in epicardial fiber angles was larger, compared to case (i) when the epicardium contracted strongest (Fig. 2(c)).

3.2. Effects of Myofiber Orientation and Contractility on the ES Apex Twist Angle.

From ED to ES, the LV apex in our simulations underwent a counterclockwise rotation about the long axis of the ventricle, as viewed from the apex. These rotations were regarded as positive twist angles. When the epi-myofibers were fixed at −30 deg and the helical angle of endo-myofibers increased, it was found that the apex twist angle was progressively reduced, independently of the T _max distribution (Fig. 3(a)). In contrast, there was an overall increase in the apex twist angle when the endo-myofibers were fixed at 60 deg and the helical angle of epi-myofibers varied from 0 deg to −60 deg (Fig. 3(b)). Moreover, for each set of myofiber orientations, the LV apex twist angle was larger in case (i) when the epi-myocardial fibers contracted strongest, compared to case (ii) when the endo-myocardial fibers contracted strongest. At certain myofiber orientations, the apex twist angle was nearly doubled when the epicardial T _max was higher than the endocardial T _max.

Fig. 3.

The transmural variations of myofiber orientation and contractile strength interdependently influenced the systolic twist angles of left ventricular apex. The apex twist angle of the LV from ED to ES was determined at EDP = 15 mmHg and ESP = 90 mmHg. The effects of endo-myofiber (a) and epi-myofiber (b) helical angles on LV apex twist were examined, respectively, for cases (i) and (ii).

4. Discussion

The results of the current study showed that both the transmural distribution of contractile strength and orientation of myofibers can affect LV pump function and torsion. Moreover, there was a strong coupling effect that alters the influence of these parameters.

Previous studies have shown that LV myofibers are organized to maximize the ejection fraction [6]. Consistent with those results, a maximal SV was achieved when either the endo- or epi-myofibers shifted from a circumferential orientation to a longitudinal orientation in the present study. This trend occurred no matter how the myocardial contractile strength was distributed transmurally (Fig. 2). Notably, the observed optimal set of myofiber orientations, which produced the highest LV–SV, was within the physiological range of myofiber helical angles measured for a variety of species [21,22,26,27].

According to previous FE simulations, the optimal myofiber orientation serves to minimize the transmural variance of the sarcomere strain and stress distribution during systole, in order to achieve maximum LV pumping efficiency [6]. Since systolic strain and stress are directly linked to contractile function, the results of that study point to a potential role for the distribution of myocyte contractile strength as a key factor in optimizing myofiber orientation and LV pumping efficiency. In support of this, the current study showed that changes in transmural distribution of myocyte contractile strength altered not only the optimal helical angles of myofibers in both endo- and epicardial regions to achieve a maximal SV but also the magnitude of SV achieved (Fig. 2). Therefore, LV pump function directly depends on the combination of transmural myofiber orientation and the distribution of contractility. Moreover, incorrect representation of transmural contractility may lead to inaccurate computational evaluation of LV pump function. As a demonstration, when the myofibers shifted from −60 deg/60 deg to −30 deg/90 deg (epi/endo) in our FE model, two representative myofiber sets seen in mammals [21,22], the SV at EDP = 20 mmHg increased by 4.2% in case (i) but decreased by 14.5% in case (ii). These differences highlight the importance and necessity of incorporating transmural variations of myocardial contractile strength in the computational evaluation of LV pump function.

The transmural distribution of T _max also dramatically influenced the sensitivity of LV pump function to changes in the helical angles of myofibers, which is represented by the spread of the Starling curves (Fig. 2). The FE results suggest that reductions in contractile strength amplified the effects of altered myofiber orientation in the same myocardial layer. To put a different way, the more strongly a particular myocardial layer can contract, the less the reorientation of its myofibers can impact LV pump function. This may have important implications in the development of heart disease, especially those associated with myofiber reorientation as well as transmural changes in myocardium contractile function [10].

Another principle finding of the present study relates to the torsional deformation of the LV during systole, which plays an important role in maintaining normal LV pump function [28]. In general, the torsional deformation of the LV is driven by the imbalance of torque generated by the two opposite types of oblique (i.e., right- and left-handed) myofibers [29]. A counterclockwise twist, reflected as positive angles (Fig. 3), was favored because of the predominant torque produced by the left-handed oblique myofibers, which occupy the outer myocardial regions and have larger radii (i.e., longer lever arm) compared to the inner right-handed oblique myofibers [29]. Along this line, increases or decreases in the relative amount of left-handed oblique myofibers would increase or decrease the counterclockwise twist of LV apex, respectively. In our model, an increase in the right-handed helical angle of endo-myofibers actually switched myofibers in the midmyocardium to a more right-handed oblique orientation, based on the assumption of linear transmural distribution. This increased the relative proportion of right-handed oblique myofibers and led to smaller counterclockwise twist (Fig. 3(a)). In contrast, changes in the left-handed helical angle of epi-myofibers from 0 deg to −60 deg shifted midmyofibers to a more left-handed oblique orientation, causing the LV to twist more (Fig. 3(b)). In addition to the relative amount, the torque generated by oblique myofibers is also determined by the force generated during contraction. An enhancement in the epicardial forces, therefore, further boosted their predominant contribution, leading to more twist at ES (Fig. 3). These results further confirm the differential effects of different myocardial regions on LV function.

There are several model limitations, which mainly arose from a few simplifying assumptions that were made to the model. First, the LV anatomy was approximated by an axi-symmetrical ellipsoidal shape, without taking into account the effects of the right ventricle and other ventricular structures, such as papillary muscles. Second, only the helical angle of myofibers was considered and assumed to change linearly from epi- to endocardium. Moreover, the variations in the base-to-apex direction were excluded. Third, only two steady states, i.e., ES and ED, were assessed. Despite these limitations, our model generated results consistent with reported measures in terms of the SV at clinically measured pressures, optimal myofiber helical angles [6], and apex twist angles at ES [30]. Moreover, the present study focused on the potential effects of transmural variations of myocardial contractile strength on myofiber structure-dependent LV function. Although the interaction between these two parameters is not thoroughly understood, the differences observed in the present study provide preliminary, but important evidence that transmural distribution of myofiber orientation and myocardial contractile function interdependently influences LV function and should be accounted for in computational modeling of ventricular mechanics.

5. Conclusions

The results of the present study demonstrate, for the first time, the important role of transmural distribution of myocardial contractile strength and its interplay with myofiber orientation in regulating LV pump function. The coupling between these two physiologic parameters could play a critical role in the progression of heart failure. Incorporating the correct transmural distribution of myofibers and contractility can affect the predicted results of simulations. Therefore, a computational model with inaccurate representation of transmural myocardial contractile properties may overestimate or underestimate LV pump function.