Biomechanics and Mechanobiology of Trabecular Bone: A Review

Abstract

Trabecular bone is a highly porous, heterogeneous, and anisotropic material which can be found at the epiphyses of long bones and in the vertebral bodies. Studying the mechanical properties of trabecular bone is important, since trabecular bone is the main load bearing bone in vertebral bodies and also transfers the load from joints to the compact bone of the cortex of long bones. This review article highlights the high dependency of the mechanical properties of trabecular bone on species, age, anatomic site, loading direction, and size of the sample under consideration. In recent years, high resolution micro finite element methods have been extensively used to specifically address the mechanical properties of the trabecular bone and provide unique tools to interpret and model the mechanical testing experiments. The aims of the current work are to first review the mechanobiology of trabecular bone and then present classical and new approaches for modeling and analyzing the trabecular bone microstructure and macrostructure and corresponding mechanical properties such as elastic properties and strength.

Introduction

Trabecular bone tissue is a hierarchical, spongy, and porous material composed of hard and soft tissue components which can be found at the epiphyses and metaphyses of long bones and in the vertebral bodies (Fig. 1). At the macrostructural scale, the hard trabecular bone lattice, composed of trabecular struts and plates, forms a stiff and ductile structure that provides the framework for the soft, highly cellular bone marrow filling the intertrabecular spaces. At a microstructural scale, trabecular architecture is organized to optimize load transfer. Mineral and collagen content and architecture determine the mechanical properties of trabecular bone tissue [1].

Fig. 1.

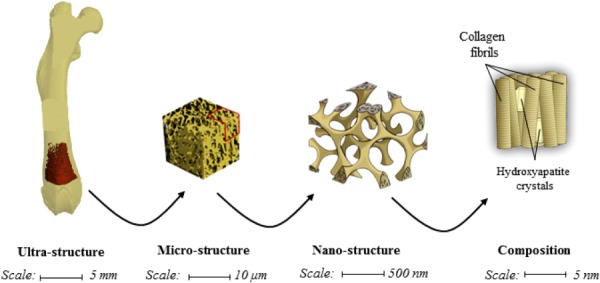
An illustration of the hierarchical nature of trabecular bone

In the appendicular skeleton, trabecular bone transfers mechanical loads from the articular surface to cortical bone, whereas in the vertebral bodies it represents the main load bearing structure. Bone tissue mechanical properties and architecture of trabecular bone are two main factors which determine the mechanical properties of trabecular bone. Fragility fractures that arise in the context of metabolic bone diseases such as osteoporosis usually occur in regions of trabecular bone.

Several numerical tools, such as micro finite element methods, have been used to investigate the mechanical properties of trabecular bone from the compositional to organ levels [2–4]. Several new approaches relate the mechanical properties of trabecular bone to its compositional material properties [5], including decomposition of trabecular bone into its volumetric components (i.e., plates and rods) [4,6–8]. In this review paper, we first focus on the biology of trabecular bone and then on classical and new approaches for modeling and analyzing the trabecular microstructure and macrostructure and their corresponding mechanical properties.

Trabecular Bone Biology

Cell Populations.

The integrity of the skeletal system is maintained by a continuous remodeling process that responds to mechanical forces and that results in the coordinated resorption and formation of skeletal tissue. This process occurs on a microscopically scale within bone tissue by basic multicellular units (BMUs) in which the cellular components are osteoclasts and osteoblasts [9]. Osteoclasts differentiate from hematopoietic progenitor cells of the monocyte/macrophage lineage, and it is hypothesized that they recognize and target skeletal sites of compromised mechanical integrity and initiate the bone remodeling process, although the exact signals and underlying mechanisms that target osteoclasts to specific sites remain unknown [10]. Osteoclastic bone resorption is followed by the recruitment of osteoblasts, which are derived from mesenchymal stem cells [11,12]. Osteoblasts actively synthesize extracellular matrix on bone surfaces, which is subsequently mineralized [13,14].

Osteoblasts entrapped in matrix differentiate into osteocytes and compose 90–95% of the cells embedded in the mineralized matrix of bone [15]. Osteocytes residing in lacunae distributed within the matrix communicate through their interconnecting dendritic processes through a large lacuno-canalicular network which allows osteocyte communication with cells on the bone surface and access to the nutrients in the vasculature (Fig. 2) [16,17]. Osteocytes are ideally distributed to sense external mechanical loads [18–20] and to control the process of adaptive remodeling by regulating osteoblast and osteoclast function [21].

Fig. 2.

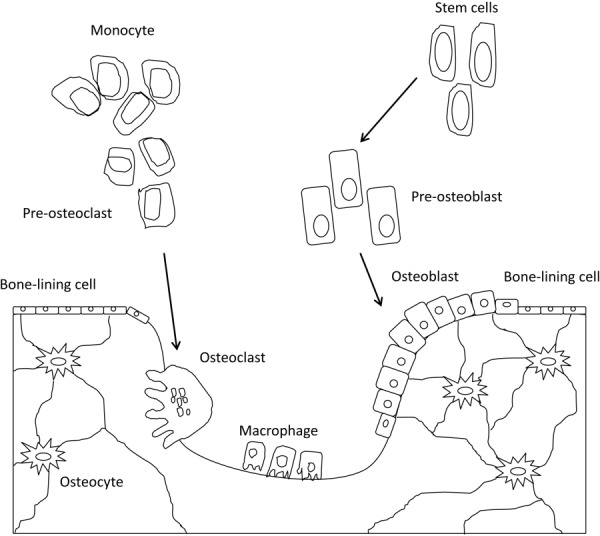
An illustration of bone cell population

Mechanosensation.

A key regulator of osteoblast and osteoclast activity is mechanical strain. Bone has an intrinsic ability to adapt its morphology by adding new bone to withstand increased amounts of loading, and by removing bone in response to unloading or disuse [22,23]. How the osteocytes sense the mechanical loads and coordinate adaptive alterations in bone mass and architecture is not yet completely understood [24]. However, it is accepted that mechanical loads placed on bones generate several stimuli that could be detected by the osteocyte. These include physical deformation of the bone matrix itself [25–27], load-induced flow of canalicular fluid through the lacuno-canalicular network [28,29], and electrical streaming potentials generated from ionic fluid flowing past the charged surfaces of the lacuno-canalicular channels [30–34]. in vivo, it is difficult to separate the three types of stimuli because mechanical loading will result in osteocyte exposure to bone matrix deformation, canalicular fluid flow shear stress, and associated streaming potentials [21]. Weinbaum et al. [29] proposed a fluid flow shear stress hypothesis to explain how bone cells detect mechanical loading and developed a mathematical model for flow through the pericellular matrix surrounding an osteocyte process in its canaliculus. The model predicted that despite the small deformations of whole bone tissue and the small dimensions of the pericellular annulus (typically 0.1 μm), the fluid flow shear stress on the membranes of the osteocyte processes was roughly the same as for the vascular endothelium in capillaries. This is relevant because of the hypothesis that fluid flow shear stress on osteocyte processes in the lacuno-canalicular porosity signaled cellular excitation for many actions such as detecting mechanical loading, activating ATP, cyclic AMP and prostaglandin E ₂ release, inhibition of osteocyte apoptosis, and inhibition of osteoclast formation among others [35].

Several studies demonstrated that bone cells are more responsive to fluid flow than to mechanical strain [28,36,37]. These studies strongly suggested that, in culture, direct mechanical strains appeared to be far less important than fluid flow shear stress in cellular excitation, as no biochemical responses were detected for cellular-level mechanical strains less than 0.5% [28]. This represents a fundamental paradox in bone tissue: cellular-level mechanical strains greater than 0.5% may cause bone tissue damage, yet tissue-level strains caused by locomotion seldom exceed 0.2% [38,39]. This paradox suggests that whole tissue mechanical strains need to be amplified to elicit a cellular biochemical response [35]. A strain-amplification model for the mechanical stimulation of the osteocyte was developed based on the hypothesis that the dendritic process of the osteocyte behaves as a suspended cable by virtue of its attachment to adhesion proteins lining the canalicular wall [40]. The fibers mediating this attachment were proposed to be proteoglycans that spanned the fluid annulus and attached to the membrane of the osteocyte process. Accordingly, when the mineralized tissue is deformed, the fluid passing through the osteocyte pericellular matrix creates a hydrodynamic drag that would put the tethering fibers in tension, thereby producing a radial strain on both the process membrane and its underlying central actin filament bundle (Fig. 3). The predictions of this model demonstrated a cellular level strain amplification of 10 - to 100-fold. According to the strain-amplification model, the activating mechanical signal was not fluid flow shear stress but the flow-induced drag on the tethering fibers.

Fig. 3.

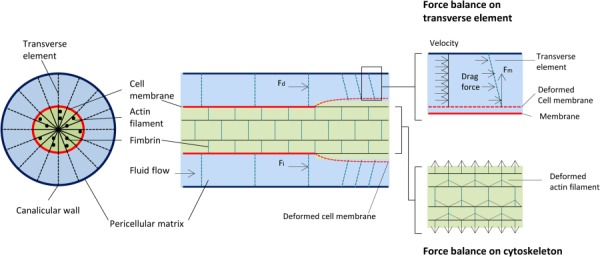
Strain-amplification model illustrating the osteocyte process in cross section and longitudinal section. Actin filaments span the process, which is attached to the canalicular wall via transverse elements. Applied loading results in interstitial fluid flow through the pericellular matrix, producing a drag force on the tethering fibers.

Proteoglycans are not initiators of intracellular signaling, and therefore, it has been suggested that the osteocyte processes might be attached directly to the canalicular wall by β3 integrins at the apex of canalicular projections (Fig. 4) [41]. A theoretical model was developed that predicts that the tensile forces acting on these integrins can be as large as 15 pN, and thus provide stable attachment in the range of physiological loading [42]. The model also predicts that axial strains caused by the sliding of actin microfilaments relative to the fixed attachments are two orders of magnitude greater than whole-tissue strains thereby producing local membrane strains in the cell process that can exceed 5%. In vitro experiments indicated that membrane strains of this order are large enough to open stretch-activated cation channels [28]. It is likely that stretch-activated ion channels play a role in the transduction of mechanical stimuli into a chemical response in osteocytes. However, the involvement of specific ion channels in the mechanoresponse of osteocytes has not been elucidated.

Fig. 4.

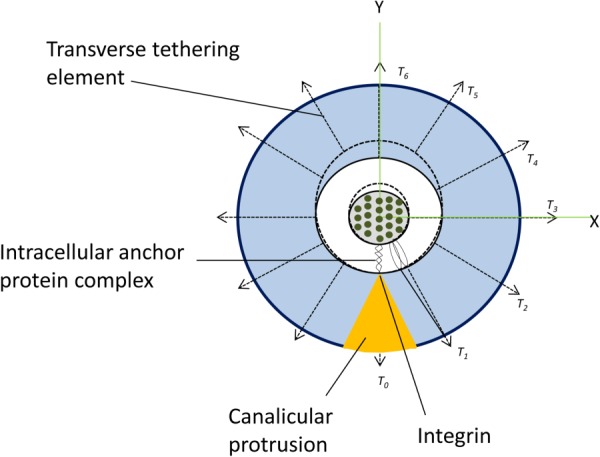
Illustration of an integrin-based strain-amplification model

Thus far, it has not been determined which cellular component of the osteocyte is the most important in sensing mechanical strain [43]. It has been proposed that the osteocyte only senses mechanical loads through its dendritic processes, and that the osteocyte cell body is relatively insensitive to mechanical strain [18,44,45]. Others have proposed that osteocytes sense strain through both the cell body and the dendritic processes [46], or that the primary cilium, a single hairlike projection, is the primary strain-sensing mechanism in the osteocyte [47,48]. There appears to be evidence for all three mechanisms, and it remains unclear whether the cell body, cell processes, and cilia work separately or in conjunction to sense and transmit mechanical stimuli [49].

Mechanotransduction.

An important step leading to adaptation of bone to mechanical loading is the transduction of physical stimuli into biochemical factors that can alter the activity of the osteoblasts and osteoclasts. In osteocytes, fluid flow shear stress induces the increase of intracellular calcium through ion channels and the release of intracellular stores [31,50,51]. The rise in intracellular calcium concentration is necessary for the activation of calcium/calmodulin-dependent proteins such as nitric oxide synthase (NOS). Additionally, the activation of phospholipase A2 results in the stimulation of arachidonic acid production and prostaglandin (PGE2) release mediated by the enzyme cyclooxygenase (COX) [52,53]. In bone, nitric oxide (NO) released from osteocytes and osteoblasts in response to loading inhibits resorption and promotes bone formation [54] and may also prevent osteocyte apoptosis [55,56]. On the other hand, PGE₂ released by mechanical loading acts through the β-catenin pathway to enhance connexin expression and gap junction function [57] and to protect osteocytes from glucocorticoid-induced apoptosis [58].

Another family of molecules that very recently has been identified as mediator of the adaptive response of bone to mechanical loading is the Wnt family of proteins. Osteocytes use the canonical Wnt-β-catenin signaling pathway to transmit signals of mechanical loading to lining cells on the bone surface [59]. Wnt binds to specific receptors, called frizzled, and to low-density lipoprotein receptor-related proteins 5 and 6 (LRP5 and LRP6). These interactions lead to the stabilization of β-catenin, which translocates to the nucleus and regulates gene expression [60]. Inactivating mutations in the LRP5 cause osteoporosis [61], while gain-of function mutations in the LRP5 coreceptor increase Wnt signaling and result in higher bone mass [62,63].

Mechanostransduction involves many different pathways that include fluid flow shear stress inducing the increase of intracellular calcium through ion channels and the activation of several molecules, such as arachidonic acid, prostaglandins, COX and NO, that will inhibit bone resorption and promote bone formation. At the gene expression level, there is the Wnt family of proteins that activate specific signaling pathways and interactions which will result in the translocation of the β-catenin protein to the nucleus and regulates gene expression.

Tissue Properties

Tissue Composition.

Trabecular bone, just like compact cortical bone consists of mainly hydroxyapatite, collagen, and water. However, trabecular bone has lower calcium content [64], tissue density (1.874 g/mm³), and ash fraction (33.9%) [65] compared to cortical bone. Consequently, it has higher water content (27% compared to 23% for cortical bone). These results are consistent with the fact that trabecular bone is more active in remodeling and, as a consequence, less mineralized. In other words, more recently formed bone has lower mineralization than older bone. Trabecular bone has high surface to volume ratio and the considerable bone remodeling compared to cortical bone (26% volume per year turnover rate for trabecular and 3% for cortical bone) [66].

Tissue Elastic Properties.

In this section, unless noted otherwise, tissue properties imply the properties at the trabacular level. Collagen and mineral orientations and organizations are the most important factors to determine bone tissue properties since they are building blocks of bone at nanolevel structure [67]. At the microstructural scale, single trabeculae consist of groups of parallel lamellae bounded by cement lines primarily oriented parallel to trabecular surfaces. The lamellae are composed of mineralized collagen fibrils with ellipsoidal shaped lacunae that house osteocytes distributed among the lamellae. The size and distribution of the lacunae are another important factor in bone microstructure since the elevated stress concentration located at the longitudinal direction of lacuna can cause microdamage in trabecular bone packets [68]. As of any other biological structure, bone tissue composition along with microstructural architecture determines the tissue mechanical properties of trabecular bone [67].

Characterizing the tissue-level mechanical properties of trabecular bone is relatively difficult due to the minuscule dimensions of the trabeculae. Various methods, including buckling analysis [69,70] and nano-indentation [1,71–80], have been used to determine the tissue modulus of trabecular bone at trabecular level. Other methods include uniaxial tensile test [81,82], bending test [83–85], ultrasonic measurements [75,81,86,87], combinations of mechanical testing and finite element modeling [88–90], and microindentation [76,91]. Other new methods have used macroscale relationships between bone density and apparent elastic modulus [92] and digital volume correlation in conjunction with X-ray computed tomography [93].

Studies of buckling analysis implement the Euler buckling formula [94] for elastic beam to find the maximum stress that a single trabeculae can bear. Townsend et al. [70] evaluated the buckling stress as a function of slenderness ratio (ratio of trabecular length to the minimum radius of gyration of the trabecular cross section) and then extrapolated it for an ideal slender ratio of a single trabeculae. They estimated the modulus as 14.13 GPa for dry and 11.38 GPa for wet tissue (Table 1). There are several drawbacks for this buckling test method which include difficulty in measuring the slenderness ratio of intact trabeculae and also the assumption of constant tissue modulus for the bone tissue.

Table 1.

Tissue elastic modulus of trabecular bone

Reference	Testing technique	Bone type	Tissue modulus (Gpa)
[70]	Buckling	Human proximal tibia	11.38 (wet), 14.13 (dry)
[115]	Experiment-FEA	Human proximal tibia	23.6 ± 3.34
		Human greater trochanter	24.4 ± 2.0
Human femoral neck		21.4 ± 2.8
[1]		Human femoral neck	18.0 ± 2.8
[98]		Bovine proximal tibia	18.7 ± 3.4
[88]		Human vertebra	6.6 ± 1.0
[89]		Human vertebra	5.7 ± 1.6
[194]	Human proximal femur	10 ± 2.2
[99]		Bovine proximal tibia	6.54 ± 1.11
[96]	Ultrasonic technique	Human femur	13.0 ± 1.47
[75]		Human femur	17.5 ± 1.12
[96]		Bovine femur	10.9 ± 1.57
[86]		Human tibia	14.8 ± 1.4
[86]		Human vertebra	9.98 ± 1.31
[81]	Human tibia	14.8 ± 1.4
[74]	Nano-indentation	Human femoral neck	11.4 ± 5.6
[75]		Human distal femur	18.1 ± 1.7
[77]		Human vertebra	13.4 ± 2.0
[195]		Human femural head	21.8 ± 2.9
	Human femur trochander	21.3 ± 2.1
[196]		Human distal radius	13.75 ± 1.67
	Human vertebrae	8.02 ± 1.31
[76]		Porcine femur	21.5 ± 2.1
[79]		Human tibia/vertebrae	19.4 ± 2.3
[97]		Sheep proximal femur	20.78 ± 2.4

Ultrasonic technique, which mainly has been used to calculate the apparent elastic moduli of trabecular bone, [95] can also be used for determination of mechanical properties at tissue level. The ultrasonic technique can be applied to either a whole specimen [86,96] or a single trabecula [81]. The reported tissue moduli for trabecular bone are different based on species and anatomical site: 13.0 ± 1.47 GPa [96] and 17.5 ± 1.12 GPa [75] for human femur, 10.9 ± 1.57 GPa for bovine femur [96], 14.8 ± 1.4 GPa for human tibia, 9.98 ± 1.31 GPa for human vertebra [86], and 14.8 ± 1.4 GPa for human tibia [81] (Table 1). In ultrasonic technique, the measurement is usually based on sample length and not ultrasound wave length which limits accuracy of the measurement.

In recent years, nano-indentation has been used to characterize the tissue properties of trabecular bone. Nano-indentation resolution can be as small as 0.05 μN in load and 0.01 nm in displacement [97]. The elastic modulus is calculated based on the unload portion of the displacement curve. Using nano-indentation, the mechanical properties of trabecular bone can be found at material level (Table 1). Zysset et al. [74] reported 11.4 ± 5.6 GPa for average tissue elastic moduli of wet trabecular bone in the human femoral neck. 13.4 ± 2.0 GPa for tissue modulus is also reported using dry samples of vertebral trabeculae [77]. Turner et al. [75] reported 18.1 ± 1.7 GPa for trabecular bone tissue from a distal femoral condyle which is higher compared to previously reported results. Using high resolution nano-indentation, Brennan et al. [97] were able to measure elastic modulus across normal and ovariectomized sheep trabecular specimen. They reported that the modulus decreases as the distance from the trabecular core increases (Fig. 5). As seen in Fig. 5(c), elastic modulus ranges from 17.2 GPa in the superficial region to 23.4 GPa in trabeculae core. These results can be served as an input for finite element modeling of trabecular bone.

Fig. 5.

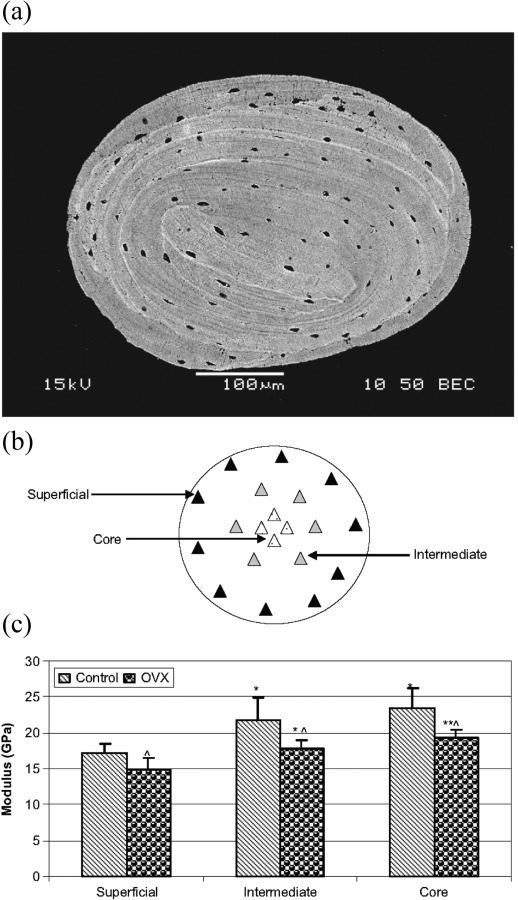
(a) Scanning electronmicroscopy image of atrabeculum. (b) Indent locations across the width of a trabeculum. (c) Tissue Young modulus of trabecular bone using nano-indentation from skeletally mature sheep after undergoing overiectomy (OVX). (From Reference 97 with permission.)

Using finite element analysis in conjunction with experimental testing is another way of estimating tissue modulus of trabecular bone. First, apparent elastic modulus is determined based on a conventional method such as ultrasonic technique or mechanical testing and a 3D model of the sample is generated using micro computed tomography (μCT) or micro Magnetic resonance imaging (μMRI) imaging. By applying the same boundary conditions as in the experiments, the 3D model is solved assuming the tissue modulus as an arbitrary value E_i. Assuming linear elasticity, the real tissue modulus E_t can be found as

$$E_t=\frac{E_{\exp }}{E_{\mathrm{FEM}}}{E}_i$$ (1)

where $E_{\exp }$ and $E_{\mathrm{FEM}}$ are the apparent elastic moduli of the bone based on experiment and finite element method, respectively. Niebur et al. [98] used high resolution finite element models and experiments to calibrate this linear model and reported 18.7 ± 3.4 GPa for bovine trabecular bone tissue modulus, which is in agreement with the results reported by Turner et al. [75] using nano-indentation. Using a similar method, 18.0 ± 2.8 GPa for human femur [1] and 6.54 ± 1.11 GPa for bovine tibia [99] also have been reported (Table 1). The results for tissue elastic modulus show high variability across anatomical sites and species. Bayraktar et al. [1] argue that this discrepancy can be cause of end-artifacts or measuring of transverse modulus. Other factors include spatial sampling and anatomic site-dependence. Verhulp et al. [99] consider this variability as a result of variations in tissue density, sample size, strain rate, and the way the strain is measured. Generally, the results based on the back calculation using finite element modeling show higher variability than other methods which suggest that these methods find an “effective” tissue modulus to correlate the elastic modulus in the apparent level. On the other hand, nano-indentation quantifies tissue modulus locally and can show heterogeneity along the trabecular bone tissue [97].

Elastic Behavior of Trabecular Bone

Studying the elastic behavior of trabecular bone is important as it is the main load bearing bone in vertebral bodies and also transfers the load from the joints to the cortical bone in long bones. Furthermore, it relates to the strength and affects fracture risk of the bone structure [100,101]. The elastic properties of trabecular bone are showcased in its mechanical behavior during normal daily activity, and different experiments have shown it to have a linear behavior [102]. Therefore, linear elasticity can predict the elastic properties of trabecular bone. Based on the generalized Hook’s law, the elastic properties of the structure can be described by a fourth rank tensor $C_{\mathit{ijkl}}$, where it linearly relates stresses and strains in the structure as ${\sigma }_{\mathit{ij}}=C_{\mathit{ijkl}}{\varepsilon }_{\mathit{kl}}$. The elastic tensor in its most general form has 21 independent components. Trabecular bone generally is assumed to behave as an orthotropic structure with three planes of symmetry (nine independent components to fully describe the elastic behavior of the structure). However, it also can be described as a transversely isotropic structure which is rotationally symmetric around its axis of symmetry (five independent components).

Predicting the mechanical properties of trabecular bone is challenging because of the heterogeneous [103–105] and anisotropic nature of bone [100,106–110]. The elastic behavior, and in general, the mechanical properties of the trabecular bone depend on loading direction [111–114], anatomical site [115–117], size of the sample under consideration [109,118,119], and even cartilage damage adjacent to subchondral trabecular bone [120]. Day et al. [120] have shown that volume fraction of subchondral trabecular bone increases to balance the loss of tissue modulus caused by cartilage damage. Nazarian et al. [117] have shown that the mechanical performance of each region in human proximal femur is highly dependent on the corresponding trabecular microstructure (Fig. 6).

Fig. 6.

(a) The layout of the cored specimens (S1–S7) demonstrated on a proximal femur image. Three-dimensional visualization of the average (b) modulus (E) with the upper and lower limits of data at each site; and (c) bone volume fraction (BV/TV) distribution of human proximal femur. In (a), sites S1, S4, S6, and S7 form a loop or belt from the femoral head, through the neck and onto the trochanteric region, where the applied load (in a relatively uniform magnitude) traverses through the proximal femur and disburses into the cortical shaft. It is possible that the loads resultant from normal daily activities are mostly translated though this loop, whereas sites S2 and S3 encounter the higher loads applied to the proximal femur for higher impact activities. (From Reference 117 with permission.)

Many studies have shown that the elastic behavior of trabecular bone in compression and tension are the same [121,122]. There are two different experimental setups to assess the elastic modulus of trabecular bone: mechanical testing [123,124] and ultrasound techniques [95,121,125]. Mechanical testing can be performed in compression and tension [123] to evaluate the axial moduli or in torsion to evaluate the shear moduli [102]. To increase the reproducibility of mechanical testing, samples should first go through a number of conditioning cycles before reaching a steady state [123,124]. Ultrasound technique is another mode to assess elastic modulus which can give nine orthotropic constants of bone specimens.

To generate the relationship between elastic properties and structural parameters of trabecular bone, mechanical and structural specific parameters are gathered from trabecular bone samples. Then, based on statistical analysis, they found the best fit between these parameters [126,127]. Several single- and two-parameter power law or linear functions have been proposed to predict the elastic modulus of trabecular bone (Table 2) [126–129]. Apparent density (${\rho }_{\mathrm{app}}$), which is the product of bone volume fraction and bone tissue density, is the primary component affecting the mechanical properties of trabecular bone [130,131]. The general form of $E=a{\left({\rho }_{\mathrm{app}}\right)}^r$ is proposed for this relationship, and several studies have found “r” to be nearly two with high correlation rate between the mathematical relationship and experimental results [130,132]. However, as shown by Ulrich et al. [133], although 86% of the variation in elastic properties can be explained by bone volume fraction, the difference between elastic moduli can be up to 53% at certain volume fractions. Furthermore, due to the challenges mentioned at the beginning of this section, these functions cannot individually predict the elastic properties of the trabecular bone in different anatomic sites and species (Table 2).

Table 2.

Mathematical relationships of elastic modulus trabecular bone (density in g/cm³ and R ² is the determination coefficient)

Reference	Bone type	Range	Elastic modulus (Gpa)	R 2
[176]	Human vertebra	ρ app: 0.11–0.27	E = 2.1 ρapp − 0.08	0.61
[128]	Human proximal femur	BV/TV: 0.15–0.40	E = 7.541(BV/TV) − 0.637	0.88
[126]	Human	α a : 0.174–0.662 BV/TV b : 0.022–0.843	E = 84.37 (BV/TV)2.58 α 2.74	0.97
[115]	Human vertebrae	ρ app: 0.11–0.35	E = 4.730 (ρ app)1.56	0.73
	Human proximal tibia	ρ app: 0.09–0.41	E = 15.520 (ρ app)1.93	0.84
	Greater trochanter	ρ app: 0.14–0.28	E = 15.010 (ρ app)2.18	0.82
	Human femoral neck	ρ app: 0.26–0.75	E = 6.850 (ρ app)1.49	0.85
Pooled	ρ app: 0.09–0.75	E = 8.920 (ρ app)1.83	0.88
[197]	Human distal femur	ρ ash: 0.102–0.331	E = 10.88 (ρ app)1.61	0.78
[195]	Human Femur	BV/TV: 0.06–0.33	E = 10.89 (BV/TV)2.84	0.95
[105]	Human mandibular condyle	BV/TV: 0.09–0.28	E 1 = 0.02054 × 100.1063 ( B V/TV)	0.69
			E 2 = 0.006001 × 100.1499 ( B V/TV)	0.80
			E 3 = 0.001037 × 100.1753 ( B V/TV)	0.76
			G 12 = 0.004812 × 100.1332 ( B V/TV)	0.81
			G 13 = 0.03215 × 100.1218 ( B V/TV)	0.82
			G 23 = 0.001458 × 100.1486 ( B V/TV)	0.73
[129]	Rat femur	ρ app b : 0.301–1.553	E = 3.711 (ρapp)1.87	0.74

^aAsh fraction.

^bTrabecular and cortical bone.

Several studies have correlated elastic properties of trabecular bone to the fabric tensor, since fabric tensor is a descriptor of the anisotropy of trabecular bone [125,134]. The relation between elastic constants and fabric tensor was first introduced by Cowin [111]. Based on this model, Turner et al. [125] quantified it for trabecular bone using bovine samples. Later, Van Rietbergen and coworkers [134] found a reliable fit between components of fabric tensor and elastic constants in trabecular bone.

Numerical methods (mainly finite element models) based on nondestructive imaging, such as μCT and μMR, have been introduced to determine the elastic moduli of trabecular bone from 3D generated models [135,136]. Two methods have been employed to build the 3D finite element model based on the bone images: one method is to convert each voxel in the computer reconstructed representation of bone structure to a brick element with same size and coordinate [137,138]. Another method is to use marching cubes algorithm [135,139] and divide the bone structure into tetrahedron elements which vary in size and shape based on their coordinates in the structure. Using this method the generated model is smoother; however, the computational effort increases as a result.

Many limitations and errors associated with mechanical testing, due to end-artifacts [108] and off-axis measurements, [114] can be eliminated using micro finite element (μFE) analysis. Finite element models gather displacements and forces throughout the sample and not just the surfaces. Also, different boundary conditions can be applied to evaluate all independent components of the elastic tensor. On the other hand, it is difficult to employ heterogeneity and anisotropy of bone tissue in the FE model, where simplifications are in order [140]. Micro finite element analysis has been applied to large sets of data to find the orthotropic components of trabecular bone [141,142]. Both studies have shown that there are strong correlations between bone volume fraction and elastic and shear moduli, whereas this correlation is weak for Poisson’s ratio and bone volume fraction. For the FE analysis, many studies have shown that anisotropy of trabecular bone at tissue level has little impact on overall anisotropy of the trabecular bone, which means that anisotropy of bone architecture is dominant [88,143]. To find the elastic tensor, many studies verified the use of orthotropic tensors to represent the elastic behavior of trabecular bone [145,145]. Rietbergen et al. [144] found that there is little error between modeling and experiment, assuming elastic tensor as orthotropic by comparing two whale vertebral samples. Odgaard and coworkers [145] observed that the orthotropic principal axes are nearly aligned with fabric tensor directions.

Expansion of computational resources have led to larger finite element models of up to 1 billion degrees of freedom [146]. However, these large finite element models require supercomputers for computation which are not available everywhere. On the other hand, homogenized macro scale models lag in accuracy. Therefore, multiscale finite element analysis of trabecular bone has been introduced [147]. Recently, Podshivalov et al. [147] have proposed a multiscale finite element model to fill the gap between homogenized macroscale and high resolution micro finite element models. Their model has several intermediate levels, in which bone material characteristics are updated based on change of porosity in different material scales (Fig. 7). In their model, effective mechanical properties vary at each intermediate level due to the changes in geometry. Using fourth order polynomial equation, they further improve their model by correlating porosity and effective material properties [148].

Fig. 7.

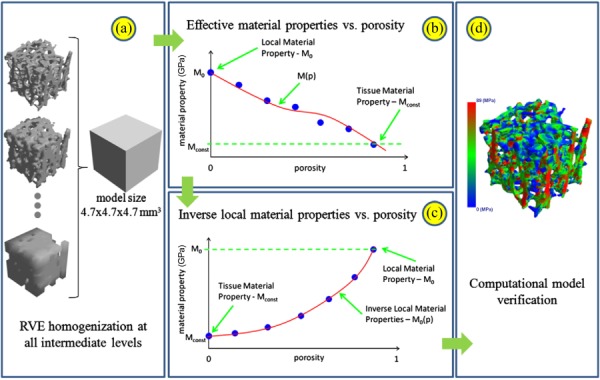
Schematic flowchart of computing multiscale material properties: (a) representative elementary volume (RVE) homogenization for estimation of the effective material properties of the bone model at all intermediate levels; (b) a correlation between the porosity of the geometrical models and their respective effective material properties; (c) inverse local material properties model as a function of porosity; and (d) computational model verification. (From Reference 147 with permission.)

In recent years, individual trabecular segmentation (ITS) of trabecular bone into rods and plates has been developed [4,6–8] and has been used to identify and relate the separate plate–rod configurations to mechanical properties of bone. One of the pioneering publications in this area was the work conducted by Stauber and Müller [7]. They decomposed the trabecular bone into its volumetric elements using skeletonization, optimization, and multicolor dilation algorithms (Fig. 8). The advantage of ITS is that it reduces the computational effort for finite element analysis and also examines the contribution of each component to the mechanical properties of trabecular bone. Wang et al. [149] examined the accuracy of this conversion by constructing idealized plate–rod and rod–rod microstructures at typical μCT resolution. They compared the ITS-based finite element model with a voxel-based finite element model and found that the ITS based FE model significantly reduced the computational effort and yet preserved the accuracy of Young moduli and yield strength predictions.

Fig. 8.

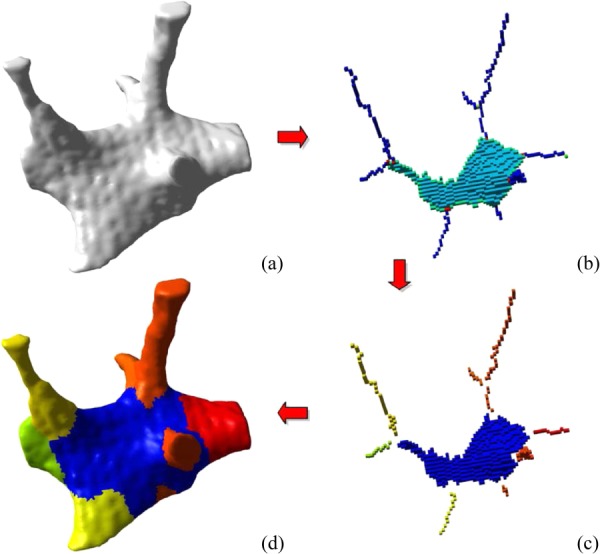
Spatial decomposition of trabecular bone. The initial binary image that served as input for our algorithm is shown in panel (a). A skeletonization and optimization algorithm is applied to get a homotopic shape preserving skeleton as shown in panel (b). This skeleton is then point-classified, thus arc-, surface-, border-, and intersection-points are shown in different colors. (c) This point-classified skeleton is then spatially decomposed by removing the intersection points. (d) A two-way multicolor dilation algorithm was applied to find the volumetric extend of each element, yielding in the final spatially decomposed structure. (From Reference 7 with permission.)

Helgason et al. [150] reviewed the several mathematical relationships between elastic modulus and apparent density and categorized the relationships based on specimen boundary conditions, specimen geometry, and anatomic site. Although they could not draw a definite conclusion from these relationships, they proposed a roadmap to standardize the mechanical testing and also set up indirect validation methodologies to find the most reliable mathematical relationships. As mentioned earlier, trabecular bone is a highly anisotropic and heterogeneous structure, whose mechanical properties are highly dependent upon anatomical site and species. Therefore, the perfect mathematical model should be chosen based on these variables.

Strength of Trabecular Bone

Strength is defined as the ultimate stress which the structure can bear before failure, which is the maximum stress in the stress–strain curve. Studying the strength of trabecular bone is important, since it can be related to bone fracture, damage, which causes the bone remodeling, and failure of bone implants [151–153]. To understand the mechanisms of failure in trabecular bone, several models have been proposed. One of the earliest models is based on the cellular solid theory which uses the power law relationship between strength and bone apparent density [154]. In cellular solid theory, trabecular bone is assumed to be a structure with periodic boundary conditions, and a unit cell for trabecular bone is derived. Solving this unit-cell with basic analytical equations, cellular solid theory quantifies the effect of architecture and bone material properties on apparent mechanical properties.

Another model, considers trabecular bone as a lattice type structure, where the structure is solved using numerical methods such as finite element analysis [155,156]. None of these models creates a realistic representation of trabecular bone. Recent improvements in high-resolution imaging and processing power make it possible to have realistic 3D representations of trabecular bone and then solve the model based on microfinite element analysis [157–159]. The advantage of this method is that the sample under consideration can be tested multiple times with different loading types and boundary conditions for failure analysis. In one of the earlier works in this area, Fyhrie and Hou [157] used large scale nonlinear finite element analysis and found that the results depend on tissue mechanical properties. In another study, Van Rietbergen et al. [158] predicted the failure behavior of five human trabecular bone samples from tissue yield criteria, and found that the predicted strength is in the 15% range of measured strength from the experiments; however, ultimate strain was underestimated by 35%. In a later study, Niebur et al. [98] successfully predicted apparent ultimate compressive and tensile stresses and failure strains for seven bovine tibia samples using asymmetric tissue yield strains in tension (0.6%) and compression (1.01%).

When studying the failure behavior of trabecular bone, multi-axial analysis of trabecular bone has clinical importance, since multi-axial stresses can occur during fall, accidents and also in the bone implant interface [151–153]. For multi-axial strength analysis, bone volume fraction and architectural variation in specimens should be taken into consideration. There are several fracture criteria applied in material science which have been adopted for bone mechanics. Von Mises criterion is one of the first formulas to predict the bone fracture [126,160]. This formula uses principal stresses ${\sigma }_i$ and ultimate stress ${\sigma }_v$ in compression (or tension) and can be written as

$$\sqrt{{({\sigma }_2-{\sigma }_3)}^2+{({\sigma }_3-{\sigma }_1)}^2+{({\sigma }_1-{\sigma }_2)}^2}={\sigma }_v$$ (2)

It has been shown that this criterion may not be a good fracture predictor, since it does not account for asymmetry of strength in compression and tension [161]. The maximum principal stress criterion [162], maximum principal strain criterion [161], and maximum shear stress and strain criterion [162] have also been applied for predicting bone fracture. Mechanistic analysis using cellular solid criteria has also been used, since it accounts for different mechanisms of failure in the analysis [163,164]. This criterion has been applied to bovine tibia bone [161] with the percentage error between failure prediction and experimental failure as low as 7.7% for compression–shear and 5.2% for tension–shear. Among these failure criteria, Tsai–Wu criterion seems to be a very good candidate for trabecular bone failure analysis, since it accounts for anisotropy, loading direction and strength asymmetry of trabecular bone. The Tsai–Wu criterion which considers the existence of a failure surface in the stress space is in the form of

$$f\left({\sigma }_k\right)=F_i{\sigma }_i+F_{\mathit{ij}}{\sigma }_i{\sigma }_j=1\hspace{1em}i,j=1,2\dots 6$$ (3)

here F_i and F_ij are the second and forth order tensors depending on tissue material properties, and σ_i’s are the principal stresses. The constraint $F_{\mathit{ii}}{F}_{\mathit{jj}}-F_{\mathit{ij}}^2\ge 0$ should also be satisfied for accurate analysis. One of the drawbacks of this criterion is the large number of constants which should be determined through experiments. Fenech and Keaveny [161] used this criterion and predicted fracture load for bovine femurs specimens within a 20% error. In another study, Keaveny et al. [165] found material dependent parameters for Tsai–Wu criterion as a function of apparent density using bovine tibial specimens. They found that failure surface depends on apparent density and is aligned with the principal material directions.

Several studies have shown that the axial strength of the bone structure better correlates with axial elastic modulus than structural density [100,101]. In contrast to elastic modulus, which is the same in compression and tension, tensile strength is reported to be less than compressive strength for trabecular bone [100,101]. Similar to elastic modulus, heterogeneity of trabecular bone makes it difficult to establish a general rule for strength. To overcome this issue, use of nondimensional parameters such as strain has been proposed [166]. Nazarian et al. [167] showed that because of the heterogeneity of trabecular bone, subregions with minimal bone volume / total Volume (BV/TV) values are better predictors of trabecular failure than the average specimen BV/TV (Fig. 9). Similar to elastic analysis, studies show that the anisotropy of trabecular tissue material can be ignored, since in most cases trabecular bone elements (i.e., struts and plates) are loaded uniaxially [144]. This assumption forces the apparent principal axes of trabecular bone to coincide with the principal axes of microstructural anisotropy (i.e., principal axes of fabric tensor).

Fig. 9.

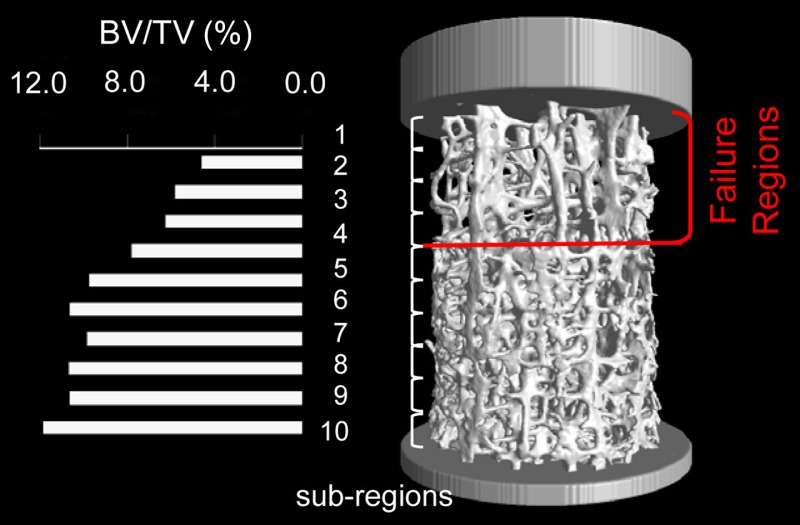
Failure occurs at subregions with the lowest BV/TV values. Subregions number 1, 2, 3, and 4 with the lowest BV/TV values here coincide with the four regions that fail based on the visual data provided by the time-lapsed mechanical testing. (From Reference 167 with permission.)

Animal age, bone organ type, anatomic site, and diseases such as osteoporosis have a significant impact on strength of trabecular bone structure by impacting bone apparent density, architecture and tissue mechanical properties. Regarding anatomic site, failure stresses for human bone can vary between 2 MPa for vertebral trabecular bone and 7 MPa for distal femoral bone [106,168]. With regards to age, studies show that the ultimate strength decreases by almost 7% and 11% for proximal femoral and vertebral bone, respectively, between the ages of 20 and 100, mainly due to volume fraction decrease [106,169]. Other studies have shown that strength variation may not be fully predicted by age. Maximum strength reported for human proximal tibial and vertebral bone occur in the age range of 40–50 yr [170] and 30–40 yr [106], respectively. Loading mode is another factor that impacts trabecular bone strength. Different studies on bovine tibial bone [159,171] show that compression strength is higher than tensile and shear strength and shear strength is the lowest of all [171]. Tested bovine trabecular bone specimens are more plate like structures and so may not be plausible to generalize those findings for human trabecular bone, which its architecture varies by anatomic site. For human trabecular bone, Morgan and Keaveny [116] studied different anatomic sites including vertebra, proximal tibia, femoral greater trochanter, and femoral neck and showed that yield strain is dependent upon anatomic site. They found that yield strain is higher for the femoral neck in compression and higher for vertebrae in tension compared to other sites. They also have shown that for all anatomic sites, yield strain for compression is higher than tension. Considering both anisotropy and heterogeneity of osteoarthritic trabecular bone, Tassani et al. [172] have shown that error in predicting compressive strength can be reduced by 17% in residual error.

The quest for having strength-density relation have led to various power law relationships, which most have reported that square relationship are more accurate [173]. Sanyal et al. [174] reported that compressive and shear strength depend on bone volume fraction with an exponent of 1.7 in human trabecular bone. Based on the shear to compressive strength ratio (0.44 ± 0.16), they concluded that shear strength is much weaker than compressive strength. For human trabecular bone, strength-density relations do not significantly change with anatomic site. However, Morgan and Keavery [116] argue that for yield criteria, the relationships predict more accurate yield strains when accounting anatomic site in the analysis. In addition, predicting the failure of trabecular bone based on apparent density may not be accurate [89], since different microstructure failure mechanisms occur during apparent mechanical testing. However, experiments on human femoral head have shown that variations in ultimate strength correlate well with variations in bone volume fraction; and therefore, local BV/TV is a better strength predictor than overall BV/TV [175].

Regarding tensile and compressive strengths, Keaveny et al. [166] showed that the post yield load bearing capacity of trabecular bone for compression is higher than for tension. A study on bovine bone [166] and human bones [176] showed that differences between compressive and tensile strength increase linearly with elastic modulus. The interpretation of these results leads to the use of strains to describe the failure of trabecular bone, since they are independent of elastic modulus, nearly homogenized, and higher in compression. This interpretation is broadly supported by the experiments showing nearly no dependence of failure strain on apparent density [88,166,176]; however, they can depend on anatomic site [116]. Adopting strain failure criteria have shown to be accurate in finite element analysis of human vertebra bone [177] and rat tibia [178]. In this regard, there is a controversy about the isotropy of yield strength: Turner et al. [179] reported a weak relationship between failure strain and fabric tensor for bovine distal femur, suggesting that failure strains are isotropic; and Mosekilde et al. [106] found that for human vertebral body, the failure strains are anisotropic. In addition, experiments on bovine tibial bone have also shown slight anisotropy for shear strain [171] or no anisotropy at all [165]. It seems that although yield and ultimate strains varies across anatomic sites, since they are generally uniform within the particular site, they are the good predictors of trabecular bone failure.

Damage, Fatigue and Creep

Damage and repair of trabecular bone is a daily physiologic process [180]. Time dependent behavior and damage susceptibility behavior during cycling loading are the two main characteristics of trabecular bone [181]. Damage has a direct effect on fracture risk in musculoskeletal diseases, such as osteoporosis [180,182] and bone remodeling [183], and can occur by implantation of prostheses [182] and bone joint diseases [184].

Experiments on trabecular bone specimens of bovine tibia [185] and human vertebra [182] show that, after the yield point, the structure unloads to a residual strain (1.05% for human vertebra with 3.0% compressive strain) with no stress [182]. This level of strain causes an 85% reduction in modulus and can be used as a quantitative measure of bone damage behavior. Several studies have shown that damage does not depend on bone organ type [186], density or anatomic site [185,187], and that it occurs at the compositional level of collagen and hydroxyapatite [185,188]. Along with that, Haddock et al. [189] showed that fatigue behavior of human vertebral and bovine tibial trabecular bone are similar by quantitative comparison of cycles to failure in cycling loading. They conclude that dominant failure mechanisms are in bone ultrastructural level for cyclic loading, regardless of anatomical site and species. Figure 10 shows the cyclic test data for human vertebral bone which shows the progressive loss of modulus and accumulation of strain similar to tibial bovine trabecular bone tests [190].

Fig. 10.

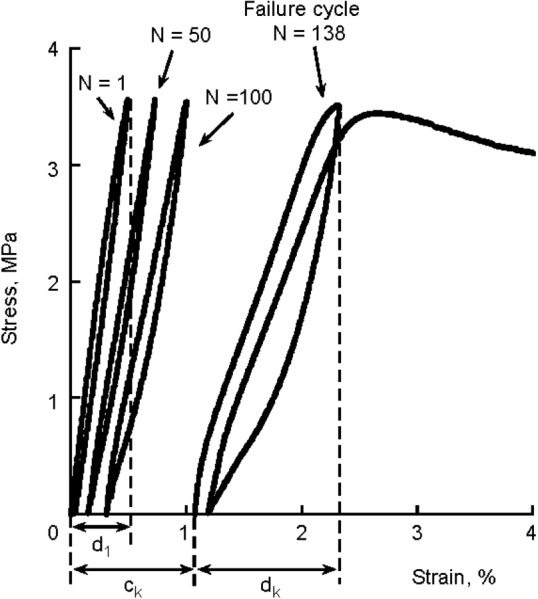
Reductions in secant modulus and accumulation of strain with increasing number of load cycles characterized the cyclic behavior of trabecular bone. Failure was defined as the cycle before which a specimen could no longer sustain the prescribed normalized stress, as indicated by a rapid increase in strain upon the subsequent loading cycle. Creep strain was defined by translation along the X-axis (c_k), and damage strain was defined by the difference of the hysteresis loop strains (d_k + d₁). Total strain was the sum (c_k + d_k). (From Reference 189 with permission.)

Creep is the tendency for bone to permanently deform under applied mechanical loads, and fatigue is the weakening of bone under repetitive or cyclic loading. Trabecular bone shows the classical creep characteristics with three phases: high elastic strain response, steady state response, and necking (which the strain rate exponentially increases) [191]. Creep and cyclic loading tests are implemented to model daily mechanical loadings on trabecular bone. Then, the standard stress-life and strain-time curves are plotted to understand the effects of these types of loadings on trabecular bone structure. Fatigue test results, conducted in-vitro and without considering bone healing, show that cyclic loading reduces stiffness up to 70% after 10⁶ cycles [190]. Therefore, the results can serve as a lower bound for the lifetime of bone. Using specimens from human femur and bovine vertebra, Dendorfer et al. [192] showed that in cyclic loading, strain localizes even at very low load levels, and microcracks are induced just after load cycles. Consistent with this finding, it has been shown that microcracks and microdamage propagation are major failure mechanisms and result in large specimen modulus reduction [193].

Conclusion

Volume fraction, trabecular tissue material properties, and architecture determine the mechanical properties of trabecular bone. These features are of great interest for the study and understanding of biomechanics and mechanobiology of trabecular bone.

Bone cell population comprised osteoblasts, osteoclasts, and osteocytes. Osteoblasts are derived from hematopoietic progenitor cells; recognize and target specific skeletal sites; and begin the bone remodeling process. Osteoblasts differentiate from mesenchymal stem cells; are recruited when remodeling process starts; and actively synthesize extracellular matrix on bone surface and will later differentiate into osteocytes. Osteocytes compose approximately 95% of the cells in the mineralized matrix of bone; sense mechanical loads; and control the process of adaptive remodeling by regulating osteoblast and osteoclast function.

The way by which osteocytes sense mechanical strain has yet to be determined. Many theories have been proposed to explain this. For instance, the osteocyte only senses mechanical loads through its dendritic processes, and that the osteocyte cell body is relatively insensitive to mechanical strain. Alternatively, other authors proposed that osteocytes sense mechanical loads through both, the cell body and dendritic processes, or that the primary cilium is the strain-sensing mechanism. This issue is still undetermined since evidence for all theories have been found.

Mechanotransduction is the mechanism by which these mechanical strains are transmitted to bone cell to maintain bone tissue. Several studies demonstrated that bone cells are more responsive to fluid flow than to mechanical strain. These studies strongly suggested that, in culture, direct mechanical strains appeared to be far less important than fluid flow shear stress in cellular excitation as no biochemical responses were detected for cellular-level mechanical strains less than 0.5%. Different pathways as the induction of the increase of intracellular calcium through ion channels and the activation of several molecules are involved in mechanotransduction. Additionally, the β-catenin protein, at the gene expression level, is theorized to be involved in this process.

The results for tissue elastic modulus show high variability across anatomical sites and species as shown in Table 1. This discrepancy can be caused by several reasons including end-artifacts, measuring of transverse modulus, spatial sampling, anatomic site-dependence, variations in tissue density, sample size, strain rate, and the way the strain is measured [1,99]. As seen in Table 1, tissue modulus calculation using back calculation with finite element modeling shows higher variability than other methods such as nano-indentation, which calculate the tissue modulus locally [97].

With respect to apparent elastic behavior of trabecular bone, Helgason et al. [150] compared different mathematical relationships and have shown high discrepancy among these relationships. They have suggested a road map to standardize the mechanical testing and set up indirect validation methodologies to find the most reliable mathematical relationships. Based on the highly anisotropic and heterogeneous nature of trabecular bone, the perfect mathematical relationship should be chosen considering these variables.

In recent years, microfinite element analysis has provided a substantial tool for researchers to evaluate different aspects of mechanical properties of trabecular with high accuracy. The growth of these computational tools has led to finite element models with almost 1 billion degrees of freedom [146]. In addition, ITS of trabecular bone into its basic structures of rods and plates has been developed to relate the different rod–plate configurations to mechanical properties of trabecular bone [4,6–8].

Regarding strength of trabecular bone, it appears that although yield and ultimate strains are good predictors of trabecular bone failure, and as they vary across anatomic sites, they are generally uniform within the particular site. With respect to damage, several studies have shown that damage behavior of trabecular bone does not depend on bone organ type [186], density, or anatomic site [185,187]; and therefore damage occurs at the compositional levels of collagen and hydroxyapatite [185,188].

As discussed earlier, developing high resolution finite element modeling and sophisticated experimental tools and techniques have greatly improved our understanding of trabecular bone complexity and its behavior under different types of loading. In future, multidisciplinary approaches and multiscale modeling of trabecular bone can address more complex behavior of this biological tissue, reduce the computational time, and maintain model accuracy.