An Engineering Model of Human Balance Control—Part I: Biomechanical Model

Abstract

We developed a balance measurement tool (the balanced reach test (BRT)) to assess standing balance while reaching and pointing to a target moving in three-dimensional space according to a sum-of-sines function. We also developed a three-dimensional, 13-segment biomechanical model to analyze performance in this task. Using kinematic and ground reaction force (GRF) data from the BRT, we performed an inverse dynamics analysis to compute the forces and torques applied at each of the joints during the course of a 90 s test. We also performed spectral analyses of each joint's force activations. We found that the joints act in a different but highly coordinated manner to accomplish the tracking task—with individual joints responding congruently to different portions of the target disk's frequency spectrum. The test and the model also identified clear differences between a young healthy subject (YHS), an older high fall risk (HFR) subject before participating in a balance training intervention; and in the older subject's performance after training (which improved to the point that his performance approached that of the young subject). This is the first phase of an effort to model the balance control system with sufficient physiological detail and complexity to accurately simulate the multisegmental control of balance during functional reach across the spectra of aging, medical, and neurological conditions that affect performance. Such a model would provide insight into the function and interaction of the biomechanical and neurophysiological elements making up this system; and system adaptations to changes in these elements' performance and capabilities.

1. Introduction

Bipedal standing balance is inherently unstable and must be actively controlled to prevent falling. This involves a complex interaction of the sensorimotor system and the multisegment musculoskeletal system that is not yet clearly understood. Young healthy individuals maintain their balance almost without thinking, even when subjected to substantial disturbances. Fall risk increases with age-induced deterioration of sensorimotor and musculoskeletal elements responsible for balance [1,2]. Neurological disorders, disease, and injury can also compromise balance, especially when combined with age, leading to injurious and life-threatening falls. Fall-related injuries constitute two thirds of all unintentional injuries leading to death in older adults; of those over 65 hospitalized as a result of a fall, half do not survive the coming year [3]. Falls often occur in a larger functional or perturbational context than simply maintaining balance. Standing reach, for example, consists of three subtasks: fixing gaze, reaching to acquire an object, and maintaining balance. These subtasks must be coordinated and sensorimotor resources properly allocated between them. An integral part of coordination and resource allocation is the ability to adapt to the aforementioned neural, physiological, and musculoskeletal deficits. Fall risk thus increases with sensorimotor and musculoskeletal deterioration, and a reduced ability to coordinate and allocate resources between movement subtasks, and adapt to deficits.

A variety of clinical diagnostic instruments have been developed to assess balance and fall risk (e.g., Refs. [4–6]), each with inherent limitations. They typically evaluate outward aspects of a specified stance or simple movement, often employing subjective scales. Such instruments do not adequately meet the practice needs of rehabilitation professionals [7–9], while reports regarding reliability in predicting fall risk are inconsistent [10–14]. Quantitative models with sufficient neurophysiological and biomechanical complexity are needed to enable mathematical characterization of multisegmental motor tasks requiring functional balance control. Movement scientists have long employed engineering concepts such as system identification [15] and feedback control [16] to study balance. Although not all (e.g., Refs. [17] and [18]), most have employed simplified balance dynamics to study small perturbations in a single plane for which the standing body can be represented by a linear, two-dimensional, single link inverted pendulum rotating about the ankles, controlled by a generic proportional–integral–derivative (PID) controller. While such models convey overall movement mechanics, they are largely limited to cause-and-effect behavior, and lack the complexity to accurately characterize the integrated multisegmental motor control of functional human balance.

Our long-term objective is to develop a model of functional balance and its control that accurately captures the underlying anatomical and neural determinates of performance; in order to better quantify fall-risk, target therapies, and quantify treatment response. To accomplish this we are proceeding along two parallel tracks. The first is to develop a control system model of balance that reflects its multidimensional, multisegmental nature, as well as its underlying neurophysiology. The model will be used to assess performance in an experimental protocol, the BRT, whose development constitutes the second track. The BRT simulates a complex reaching task in three-dimensional space. Such a task is fundamental to activities of daily living, and represents an important class of balance disturbances: expected disturbances brought about by volitional movements of the body and its parts. We will then develop a group-representative model (track 1) and BRT performance measures (track 2) for a cohort of YHSs for comparison across the aging and disease spectrum, including low- and high-fall risk elderly and individuals with neurological conditions known to increase fall-risk. We hypothesize that such comparisons will enable us to better characterize the multisegmental nature of functional balance in health and disease to enhance diagnostic specificity, better target movement therapy, and quantify treatment response including changes in balance referenced against young healthy controls.

This article is the first in a series addressing the first track. Here we present (a) the neurophysiological basis for balance and a description of the overall model we are developing based on it; (b) the results of the first phase of our model development: a generalized three-dimensional biomechanical model of standing reach with an approximately stationary base of support (BoS); (c) the BRT protocol to assess balance performance in the standing reach task; and (d) the results of an inverse dynamics analysis of the data obtained from two subjects who performed the BRT: a YHS and an older HFR subject before and after participating in a balance training intervention.

2. Methods

2.1. Neurophysiologically Inspired Model of Balance.

A simple but effective way to characterize balance disturbances is as either expected or unexpected (Fig. 1), which the brain responds to in fundamentally different ways [19]. The response to an expected balance disturbance, often referred to as an anticipatory postural adjustment (APA), is initially mediated by supra-brainstem (cortex, cerebellum, and basal ganglia) predictive and motor planning processes (Fig. 1, top) in advance of the disturbance. Subsequent phases of the response are then modulated by lower-level sensory feedback and reflexive processes involving the brainstem and spinal cord [20–24]. Supra-brainstem processes are hypothesized to function according to the internal model (IM) paradigm [25,26]. This postulates that movement and balance are controlled by highly adaptable neural structures [27] that represent the kinematics and dynamics of the body and its parts, and the forces and constraints imposed by the external environment (for a historical perspective, see Ref. [28]). Responses to unexpected balance disturbances are triggered by sensory information indicating that the state of the body is shifting to an out-of-balance (OoB) condition. The initial response is generated by the lower level brain stem and spinal cord processes and subsequently modulated by the higher level supra-brainstem processes [29,30] (Fig. 1, bottom). Lower level processes are comprised of preprogramed muscle synergies (hypothesized to be the means by which the brain solves the motor redundancy problem [31]) “hardwired” [32,33] into the brain stem and spinal cord [34,35] and activated and modulated directly by sensory signals. There is evidence that a relatively small number of synergies can account for the large majority of reflexive balance responses [36–38]. These synergies can be scaled in magnitude and superposed upon one another to achieve the necessary directional response [39,40].

Fig. 1.

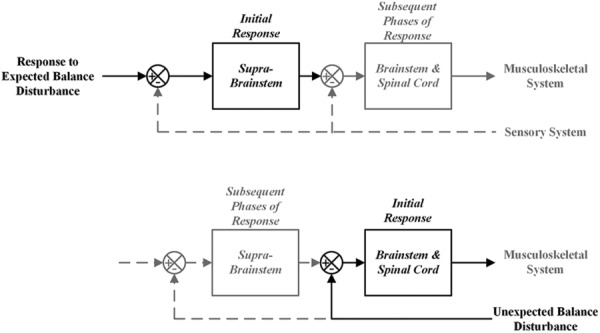
Response to expected and unexpected balance disturbances

Balance control can thus be modeled as having two “controllers” (the supra-brainstem and brainstem/spinal cord processes) which superpose their outputs upon one-another to maintain balance (Fig. 2). An IM structure comprises the supra-brainstem controller. A mathematical implementation of IMs employing stochastic optimal feedback control theory [41] has been proposed [42], consistent with experimental evidence that the brain employs a strategy predicted by optimal feedback control [43–45] when controlling movement tasks. Instead of developing a unique, optimal response to a predicted OoB condition, we hypothesize that the higher level brain centers delegate the response to the lower level centers by “mimicking” the sensory feedback signal that the predicted OoB condition would elicit. Predicted and actual OoB signals are added to one another, providing a single combined input to the lower level centers. We further hypothesize that higher level processes receive information about the responses generated by the lower level processes and incorporate this into their predictions. Four sensory modalities are involved in balance: proprioception, plantar pressure haptics, vision, and vestibular sensation [46]. There is evidence that the signals from these systems are integrated according to Bayesian decision theory (BDT) [47] to arrive at an optimal estimate of the current state of balance. BDT holds that sensory signals are combined as a weighted sum based on their relative uncertainties and that signals with greater uncertainties are assigned less weight than those with lesser uncertainties. Feed-forward motor delays (τ_SBS and τ_BSSC in Fig. 2) and noise (σ_SBS and σ_BSSC) are incorporated in the model, as are sensory delay and noise terms specific to each modality [48,49].

Fig. 2.

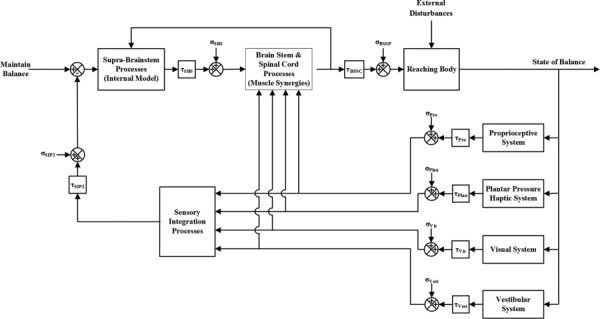
Balance control system block diagram

Stable upright balance requires that the projection of the body's center of mass (CoM) onto the ground plane be maintained within the area of its base of support (BoS) delimited by the feet [50,51]. Pai and Patton [52] extended this by proposing that maintenance of standing balance is a function of both the CoM's projected position and its projected velocity with respect to the boundaries of the BoS, and derived a feasible CoM position–velocity space within which balance can be maintained. The IM represents structures that monitor and predict whole body CoM position and velocity, identify impending OoB conditions according to the Pai/Patton paradigm, and issue signals to lower level processes to counteract them. Lower level processes respond to unpredictable OoB conditions by activating weighted combinations of individual muscle synergies, which can also be thought of as joint synergies, which ensure the CoM remains within the feasible space. The muscular responses are scaled by a factor that is a function of the proximity of the CoM to the boundary of the BoS and the speed with which the CoM is approaching the BoS.

2.2. Generalized Three-Dimensional Biomechanical Model.

Our balanced reach biomechanical model is composed of 13 rigid segments and 12 joints (Fig. 3 and Appendix A; appendices are available under http://dx.doi.org/10.1115/1.4031486 tab for this paper on the ASME Digital Collection website). Sex-specific anthropometric data for this model were obtained from de Leva [53] (http://dx.doi.org/10.1115/1.4031486). A local coordinate system CS_j (x_j, y_j, z_j) was assigned to each body segment j (1 ≤ j ≤ 13) with its origin at the segment’s CoM and oriented in the manner indicated. These local CSs were fixed with respect to their associated segments and moved in the same manner as the segments. A fixed global CS₀ (x₀ y₀ z₀) was located between the two feet approximately in the middle of the BoS. Free body diagrams (FBDs) of each body segment showing all of its associated forces and torques, and the position vectors locating these with respect to the segment’s CoM are shown in http://dx.doi.org/10.1115/1.4031486. Using these CSs and FBDs, a mathematical representation of the model was obtained using Newton–Euler Dynamics (http://dx.doi.org/10.1115/1.4031486). That is, $\sum \mathbf{F}=m\hspace{0.17em}\mathbf{a}$ and $\sum \mathbf{T}=[\mathbf{I}]\hspace{0.17em}\mathbf{\alpha }+\mathbf{\omega }\times [\mathbf{I}]\hspace{0.17em}\cdot \hspace{0.17em}\mathbf{\omega }$, where F refers to force, m to mass, a to acceleration, T to torque, I to moment of inertia, α to angular acceleration, and ω to angular velocity (see Nomenclature). The trajectories (position as a function of time) of each body segment CoM and joint CoR were measured with respect to the fixed global CS₀ by the motion detection system (see Sec. 2.3). Body segment linear velocities and accelerations, angular velocities and accelerations, and angular orientations (i.e., rotation matrices) were derived from these trajectories (http://dx.doi.org/10.1115/1.4031486). The motion detection system was also used to obtain the aforementioned segment lengths and position vectors. In order to solve and manipulate the system of equations described in http://dx.doi.org/10.1115/1.4031486, it is necessary to express the various quantities in different CSs. This task is most conveniently accomplished through the use of homogeneous transformation matrices [54,55] (http://dx.doi.org/10.1115/1.4031486). They also reduce the Newton and Euler Equations for each body segment from two equations to one, taking the form

Fig. 3.

Thirteen-segment biomechanical model of standing balance (frontal view)

$${\mathit{\Phi }}_{0\mathit{j}\mathit{c}}={\mathit{H}}_{0\mathit{j}\mathit{c}}\hspace{0.17em}{\mathit{J}}_{0\mathit{j}\mathit{c}}-{\mathit{J}}_{0\mathit{j}\mathit{c}}\hspace{0.17em}{\mathit{H}}_{0\mathit{j}\mathit{c}}^T\hspace{0.17em}$$ (1)

for 1 ≤ j ≤ 13. Here Φ_0jc is the Action Matrix, containing the resultant forces and torques acting on the CoM of body segment j referenced to the global CS₀; H_0jc is the Acceleration Matrix containing the linear and angular accelerations of segment j’s CoM; and J_0jc is the pseudo-inertial matrix for that segment. It is more convenient to compute the segment inertias with respect to their local CSs and then refer them to CS₀ through the homogeneous transformation matrix M_0j as

$${\mathit{J}}_{0\mathit{j}\mathit{c}}={\mathit{M}}_{0\mathit{j}}\hspace{0.17em}{\mathit{J}}_{\mathit{j} \mathit{j}\mathit{c}}\hspace{0.17em}{\mathit{M}}_{0\mathit{j}}^T\hspace{0.17em}$$ (2)

With this, Eq. (1) becomes

$${\mathit{\Phi }}_{0\mathit{j}\mathit{c}}={\mathit{H}}_{0\mathit{j}\mathit{c}}\hspace{0.17em}\hspace{0.17em}{\mathit{M}}_{0\mathit{j}}\hspace{0.17em}{\mathit{J}}_{\mathit{j}\mathit{j}\mathit{c}}\hspace{0.17em}{\mathit{M}}_{0\mathit{j}}^T-{\mathit{M}}_{0\mathit{j}}\hspace{0.17em}\hspace{0.17em}{\mathit{J}}_{\mathit{j}\mathit{j}\mathit{c}}\hspace{0.17em}{\mathit{M}}_{0\mathit{j}}^T\hspace{0.17em}\hspace{0.17em}{\mathit{H}}_{0\mathit{j}\mathit{c}}^T\hspace{0.17em}$$ (3)

Since all of the quantities on the right hand side of Eq. (3) are known (linear and angular velocities and accelerations of each segment’s CoM, its mass and moments of inertia), the Action Matrices Φ_0jc associated with each body segment can be computed and conform to the following structure:

(4)

where T_0jc is the skew symmetric representation of the resultant torque T_0jc and F_0jc is the resultant force acting on segment j’s CoM. Extracting these resultant forces and torques from Eq. (4), we can then form a single system of equations to obtain the unknown forces F_0jk and torques T_0jk acting at each segment’s proximal and distal joints described in http://dx.doi.org/10.1115/1.4031486.

2.3. The BRT.

During the BRT (Fig. 4), subjects stood on a platform with each foot supported on a separate triaxial force plate (AMTI Optima series). A 6′ × 10′ reverse-projection screen (Da-Lite) was located approximately one arm’s length in front of the subject, and approximately aligned to the subject’s frontal plane. An image of a disk was projected onto the screen from the rear by a high resolution digital projector (BenQ SP 890) connected to a desktop PC. Subjects stood facing the screen and pointed with the dominant hand index finger to the center of the disk as it moved around the screen.

Fig. 4.

In performing the BRT, subjects stood on force platforms, fixed gaze on disk, and pointed to it as it moved around screen. The locations of two landmarks on each foot (see text) were recorded during the test along with other kinematic data, and these were used to compute the perimeter of the BoS at each sampling instant. This computation is robust enough to accurately represent the perimeter should the subject shift their stance or momentarily raise up on the ball of one foot (as shown in the figure).

The horizontal (X) and vertical (Y) positions of the disk at each time instant t were determined by a sum of 14 sine functions, resulting in a motion that appeared random to the subject

$$X\left(t\right)=\sum _{i=1}^{14}\frac{1}{2\pi f_i}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{sin}(2\pi f_i\hspace{0.17em}t),\hspace{0.17em}Y\left(t\right)=\sum _{i=1}^{14}\frac{1}{2\pi f_i}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{sin}(2\pi f_i\hspace{0.17em}t+{\varphi }_i)$$ (5)

Frequencies (f_i, Table 1) were selected to lie within a range (0.05 ≤ f_i ≤ 3.0 Hz) that can be visually tracked by healthy subjects [56]. The amplitudes of the individual sinusoids were scaled by their respective frequencies so that each had the same peak velocity. A randomly selected phase shift (ϕ_i, Table 1) was then applied to each term of the vertical sum-of-sines, Y(t), so that the vertical component of the disk’s motion would not appear to be correlated with the horizontal component. At the beginning of each experiment, we measured the subject’s arm length (AL), as the distance from the tip of their pointing finger to the acromium process, with the arm extended in front of the body. Five multiples of AL were then computed by multiplying this quantity by the multiples at the bottom of Table 1. Once the disk’s overall trajectory was computed, its overall excursion amplitude in the medial-lateral and superior-inferior directions was normalized to unity, and then multiplied by one of these multiples, depending on the particular test condition. If the frequencies are integer multiples of one another (Table 1, Predictable Frequency Set), then the overall motion will be periodic and in theory predictable by the subject [57]. If they are not integer multiples of one another (Table 1, Unpredictable Frequency Set) they should, in theory, not be predictable. We incorporated both frequency sets into our experiment to determine subjects’ ability to predict the disk’s motion. Subjects completed the tracking task for all combinations of frequency set and overall excursion amplitude (ten trials). The duration of each trial was 90 s, so that greater than two complete cycles of the lowest frequency sinusoid were captured.

Table 1.

Disk motion parameters

Unpredictable frequency set			Predictable frequency set
fi (Hz)	Period (s)	ϕi (deg)	fi (Hz)	Period (s)	ϕi (deg)
0.024	41.67	90	0.024	41.67	90
0.056	17.86	284	0.048	20.83	76
0.104	9.62	76	0.096	10.42	192
0.184	5.43	215	0.192	5.21	238
0.296	3.38	122	0.288	3.47	99
0.344	2.91	99	0.336	2.98	145
0.488	2.05	330	0.480	2.08	261
0.584	1.71	145	0.576	1.74	30
0.712	1.40	261	0.720	1.39	168
0.824	1.21	238	0.816	1.23	284
0.904	1.11	168	0.912	1.10	215
1.432	0.70	192	1.416	0.71	307
2.104	0.48	30	2.184	0.46	330
2.936	0.34	53	2.928	0.34	122

Note: Overall excursion amplitudes: 0.5, 0.6563, 0.8125,.09688, 1.25 ALs.

Subjects’ tracking hands were placed in a splint to prevent movement at the wrist and more distal hand joints with respect to the forearm. As they pointed to the disk, moved their bodies and shifted their weight to maintain contact with the disk, the forces and moments applied by each foot were measured by the force plates. Kinematic data (the position and orientation vs. time of each body segment) were recorded by a motion detection system (Northern Digital OpoTrak Certus). Eye motion relative to the head was captured using an eye tracking system (SR Research EyeLink II,). Electromyographs (EMGs) of certain muscles (Table 2) used while pointing to the moving disk and responding to the resulting, self-induced balance perturbations were recorded using a wireless EMG system (Noraxon). Measurement data from the force plates, motion detection, eye tracking, and EMG systems were synchronized and consolidated by a Motion Monitor (Innovative Sports Technologies); which also established the global coordinate system CS₀ (x₀,y₀,z₀) whose origin lay approximately between the subject’s feet (Fig. 3), where +x points to the subject's left, +y in the subject's superior direction, and +z in the subject's anterior direction. Force plate and motion detection data were sampled at 60 Hz, eye tracking data at 250 Hz, and EMG data at 3000 Hz. EMG data were down-sampled to 60 Hz and Eye Tracker data were interpolated to 60 Hz using third-order spline interpolation polynomial, so that combined analyses with force plate and motion detection data could be carried out. All quantities were referred to CS₀.

Table 2.

Measured muscle activations

Right and left soleus

Right and left tibialis anterior

Right and left pectoralis major (claudal head)

Right and left anterior deltoid

Right and left middle deltoid

Right and left sternocleidomastoid

Right and left paraspinal

Subject-specific local CSs for each body segment, as well as segment CoMs and CoRs were obtained before each experiment using the motion detection system (for details see http://dx.doi.org/10.1115/1.4031486). We also obtained the position of the tracking fingertip relative to its respective forearm’s local CS, and the positions of two landmarks on each foot which together delineated the BoS. These points were the fourth metatarsal joint and the outside of the heel. Together, the projection of these four points onto the ground plane comprised the vertices of a quadrilateral that was used to compute the center and boundaries of the BoS at each sampling instant. We sought to minimize changes to the BoS by instructing subjects to move their feet as little as possible during the test, and to always maintain contact with the ground with both feet. Occasionally, however, some subjects would shift the position of their feet slightly, or raise up on the ball of one or the other foot, as shown in Fig. 4. Because the center and boundaries of the BoS were computed at each sampling instant from the aforementioned landmarks, such changes in the BoS were accounted for. (A test was incorporated into the calculation to determine if the front or back of a foot was off the ground. If so, the associated landmark was excluded and the computed perimeter of the BoS became triangular shaped.) We found, however, that shifting stance or raising up on the ball of the foot occurred very infrequently and in the latter case only for very brief periods of time during any given test. For all tests, the positions of the center and the vertices of the BoS remained very nearly constant throughout.

After the projection screen had been positioned in front of the subject, the high-resolution projector was positioned so that the horizontal limits of its projection area were located approximately 1½ ALs from each shoulder joint. Four calibration points were then projected onto the screen at known positions (in projector coordinates, or pixels) and their locations in the global CS recorded using the digitizing stylus. Using these data, a best-fit function was derived to map the disk’s position from projector coordinates to global coordinates (meters), so that the disk’s trajectory during each tracking experiment could be expressed in global coordinates and compared with the positions of subjects’ tracking fingertip and CoM as they performed the tracking task.

2.4. Use of the Model and the BRT to Assess Balance.

All of the data provided by the BRT will ultimately be used to inform the development of the overall control system model of Fig. 2. The biomechanical model described in this article employs the kinematic and force plate data. EMG data will be analyzed to provide information on motor signal timing and transmission delays and on the timing and execution of APAs. EMG and eye tracker data will be used to inform the development of the supra-brainstem/spinal cord controller, the brainstem/spinal cord controller, and the sensory systems component. EMG data will also be used in the quantification of the transmission delays between the various components of the model. A more complete discussion of the use of the EMG and eye tracker data will be provided in the ensuing articles of this series. The experimental data are of course valuable in their own right and separate analyses are being undertaken in the second track of our work (See Sec. 1).

The BRT was designed to challenge balance and to bring subjects to the limits of their balance (without substantially moving their feet), just short of inducing a fall. When the target disk moves to the extremes of its movement range, subjects are at the limits of their balance (CoM at or near the boundaries of the BoS) and would have to step in order to maintain contact with the disk without falling if it moved any farther. (In a subsequent phase of this test not reported here, we do move the disk farther and instruct subjects to step when “absolutely necessary” in order to precisely quantify their “balance limit.”) YHSs are able to perform the task with relative ease, but older and/or disabled subjects are visibly less steady performing the task and more conservative in their reaching movements—when the disk moves to the extremes of its movement range they remain more centered over their BoS, limiting their reach sooner and tracking the disk less accurately than similarly sized YHSs. Even short of a fall, then, the manner in which balance is controlled in these latter populations differs from that of the YHSs whom we take as exemplars of performance.

To demonstrate the descriptive power and sensitivity of the biomechanical model as well as the BRT, we performed an inverse dynamics analysis of data obtained from a YHS and an older HFR subject tracking a disk moving according to the predictable frequency set with an overall excursion amplitude of 0.8125 ALs (Table 1). Both subjects provided informed consent according to the guidelines of the University of Maryland School of Medicine and Baltimore Veterans Administration Institutional Review Boards. Prior to applying the experimental data to the model, we filtered it with a fifth-order low pass Butterworth filter with a cutoff of 5 Hz. For each of the subjects’ joints, we computed the net force applied at the joint (in each dimension) as a function of time. We also computed the one-sided Fourier transforms of the disk and force trajectories, and from these the amplitudes of the individual frequency components (twice the absolute value of the Fourier transform coefficients) to obtain the frequency spectra for each. By comparing the frequency spectra of this system’s input (the trajectory of the target disk) with the spectra of its various outputs (the individual force trajectories), and the output spectra with one another, we gain a different perspective of its performance. We are able to state at which frequencies of the disk’s motion each joint is responding to, and thus estimate the joints’ bandwidths. If a joint’s frequency response contains only frequencies contained in the disk’s motion, we can conclude that the joint responds approximately linearly to this input. If this is the case, we could compute the transfer function for each joint (spectra of the force trajectory divided, componentwise, by the spectra of the disk’s motion) and then estimate the response of that joint to a different disk motion (this will be addressed in a subsequent article). All data analyses were performed using matlab (The MathWorks Inc., Natick, MA).

3. Results

3.1. Young Healthy Adult Performance in BRT.

For each of the YHSs (28-year-old left-handed female, 167.3 cm height, 61.51 kg weight) joints we computed the magnitude of the force applied and took its mean over the duration of the test (90 s). We first compared this to the weight of the body segments (http://dx.doi.org/10.1115/1.4031486) that joint supports (Table 3). The shoulder, for example, supports the weight of the upper arm, forearm, and hand; and the two hips together support the weight of the lower trunk, trunk, arms, and head. Mean computed forces and the corresponding supported segment weights were found to be nearly equal and within physiologic ranges. This simple but important validation along with visual inspection of joint force time series (not shown) showed that the forces applied by each joint fluctuate narrowly about the weight of the segments that the joint supports, indicating that during the course of the tracking task these joints alternatively accelerate and decelerate their supported body segments against and with gravity.

Table 3.

Mean resultant joint forces versus weight of body segments supported

Joint	Mean computed joint force (N)	Supported segment weight (N)
Left and right ankle	588.97	589.82
Left and right knee	530.95	531.57
Left and right hip	353.00	352.59
L5/S1	274.97	277.08
C7/T1	47.11	51.13
Right shoulder	27.26	27.18
Right elbow	11.82	11.75
Left shoulder	27.31	27.19
Left elbow	11.96	11.75

The overall results of the inverse dynamics analysis for this subject are summarized in Fig. 5, which plots the magnitudes of the joint forces, normalized to body weight, in the time (Fig. 5(a)) and frequency (Fig. 5(b)) domains (black solid lines), along with the corresponding motion of the disk (gray dotted lines). We first consider the three lower extremity (LE) joint forces (ankle, knee, hip— Fig. 5, lower three rows). On the time domain plots (Fig. 5(a)), the medial–lateral position of the disk is plotted (right axes), such that the movement of the disk to the subject’s right is plotted as a positive value and movement to the left is plotted as a negative value. The left axis is normalized force. The right-side LE joint forces moved in phase with the disk, indicating that the subject shifted her weight to the right as the disk moved in that direction, and shifted her weight to the left as the disk moved in that direction. Consistent with this, the left side LE joint forces moved out of phase with the disk, such that the subject’s weight was shifted off of her left to her right side as the disk moved right and vice versa. The frequency domain plots (Fig. 5(b)) show that the LE joint forces followed the high amplitude, low-frequency components of the disk’s motion (Table 1). The forces generated by the upper extremity (UE) joints (L5/S1, pointing shoulder and elbow, and C7/T1, Fig. 5—upper four rows) do not resemble those generated by the LE joints. In the time domain (Fig. 5(a)), the magnitude of the disk’s position is plotted (right axes), because the UE segments are involved in tracking the complete motion of the disk, in contrast to the primarily medial–lateral disk motion tracked by the LE segments. L5/S1 and the (left) pointing shoulder and elbow responded primarily to frequencies above approximately 0.5 Hz, while C7/T1 responded throughout the frequency range (Fig. 5(b)—upper four rows). Only a 5 s epoch from 40 to 45 s is shown in these upper plots to demonstrate this more clearly (Fig. 5(a)).

Fig. 5.

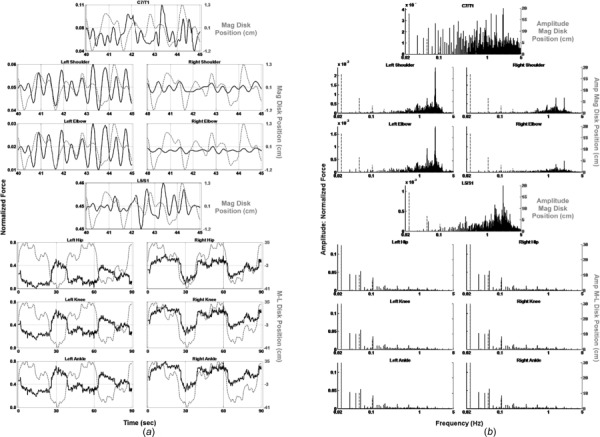
(a) Normalized joint force (black solid lines) and disk position (gray dotted lines) versus time. (b) Frequency spectra of normalized force (black solid lines) and disk position (gray dotted lines). YHS.

3.2. Older HFR Adult Performance in BRT.

We also performed an inverse dynamics analysis of the data obtained from an older HFR subject (76-year-old right-handed male, 190.5 cm height, 99.25 kg weight, who had fallen once in the year prior to testing). The subject performed the BRT before (Fig. 6) and after (Fig. 7) an eight-week, twice per week, 60-min balance training intervention. The pretraining LE time plots (Fig. 6(a)—lower three rows) show that unlike the younger subject, the normalized force was asymmetrically distributed between the two legs throughout the pointing task. In addition, the spectral domain plots (Fig. 6(b)—lower three rows) show that the low frequency normalized amplitude components of this subject’s response are substantially below those of the YHS. The frequency spectra for C7/T1 and L5/S1 (Fig. 6(b)—first and fourth rows) are shifted entirely toward the low end of the spectrum, and the component amplitudes are markedly higher as compared to the YHS. Moreover, C7/T1’s spectrum is remarkably similar to that of L5/S1 (again, in contrast to the YHS), as are the time domain plots. Between the two subjects, only the pointing shoulder and elbow appeared to possess similar time and frequency domain features. Post-training plots (Fig. 7) show substantial changes in the subject’s performance. In particular, the LE joint force activations are more symmetrically distributed between right and left, and their component amplitudes have increased. The spectra for L5/S1 and C7/T1 are both shifted to the higher end of the frequency range and their component amplitudes have decreased. The previously observed similarity between these latter two times and frequency plots has also disappeared.

Fig. 6.

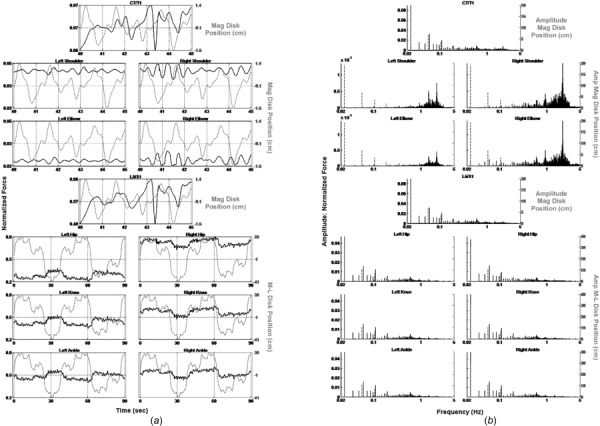
(a) Normalized joint force (black solid lines) and disk position (gray dotted lines) versus time. (b) Frequency spectra of normalized force (black solid lines) and disk position (gray dotted lines). Older HFR subject before balance training.

Fig. 7.

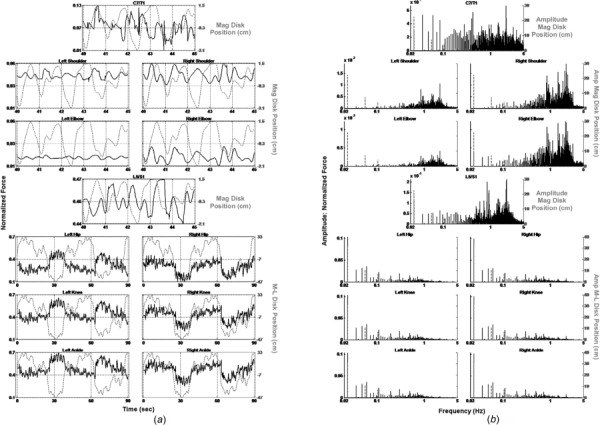
(a) Normalized joint force (black solid lines) and disk position (gray dotted lines) versus time. (b) Frequency spectra of normalized force (black solid lines) and disk position (gray dotted lines). Older HFR subject after balance training.

4. Discussion

Inverse dynamics analysis revealed substantial differences between the YHS and HFR subject in terms of discrete body segment asymmetries and overall performance capacities, and distinct improvements toward symmetry in those same body segments in the HFR subject following balance training. First, the YHS demonstrated a coordinated, frequency- and task-specific role for each body segment, with LE body segments behaving as one integrated lower frequency platform unit, while the UE body segments operated as a second higher frequency reaching unit. LE joints responded to low-frequency components of the disk’s motion (Fig. 5(b)), shifting the body primarily in the medial–lateral directions, with leg joints’ activated in opposite phases to one another, corresponding to the UE tracking of the disk. Congruence between LE joint forces and medial–lateral disk motion shows that LE joints were primarily engaged in weight shifting precisely timed to UE disk tracking. The LE unit thus acted as a platform upon which the UE was stabilized and operated. Within the UE, L5/S1 responded to the middle and high frequency components of disk motion (Fig. 5(b)), bending and turning the trunk to bring the pointing arm and hand into proximity with the disk center. C7/T1, which constitutes a parallel branch of the kinematic chain, responded throughout the frequency range of the disk’s motion, turning the head to follow the disk and bring it into view of the eyes, which provided positional information to guide the rest of the body in the tracking task. Finally, the left (pointing) shoulder and elbow responded to the high-frequency components of the disk’s motion, bringing the pointing finger into contact with the disk’s center as it moved.

In contrast to the YHS, the HFR subject’s baseline LE joint forces (Fig. 6(a)—lower three rows) were asymmetrically distributed throughout the pointing task, indicating more weight bearing on the right and little weight shifting. Clinical correlation revealed bilateral knee osteoarthritis, with replacement surgery planned for the right knee. C7/T1 and L5/S1 forces (Figs. 6(a) and 6(b)—first and fourth rows) also differed from the YHS with frequency spectra shifted to the low end, and quite similar time frequency plots. This revealed that the HFR subject’s trunk and head moved more as a single unit with little relative motion between them. Only the pointing shoulder and elbow behaved similarly to those of the YHS. Notably, the HFR subject’s BRT performance improved substantially after balance training (Fig. 7), including increased medial–lateral weight shifting, moving LE force trajectories markedly closer to those of the YHS. Further, L5/S1 and C7/T1 both shifted to the higher end of the frequency range, and activated independently of one another. Finally, the frequency content of the pointing shoulder and elbow increased dramatically, indicating a more robust response of these joints to the motion of the disk.

The use of this detailed biomechanical model to analyze a complex three-dimensional balance task is unique, defining multisegmental joint activation patterns and movement pathologies that are not revealed by simpler models of balance [15,58,59]. Simple linear single link inverted pendulum models activated only by ankle torques in a single plane lack the complexity to quantify multisegmental movement patterns and asymmetries. Pre-existing models can simulate and analyze responses to quiet sway or small disturbances in the sagittal plane, generating estimates of system level properties such as stiffness, damping, and feedback time delays. Some of these incorporate visual, vestibular, or proprioceptive feedback [60–62], and examine the manner in which these sensory modalities influence balance [15,63,64], but do not access complex whole-body movements in three dimensions as does the more extensive biomechanical model that we have introduced.

The BRT was designed to simulate an everyday circumstance that can lead to falls in older and/or impaired populations. Reaching, bending, and stretching movements that require the body to assume complex three-dimensional, multisegmental, configurations, or “poses” can disturb its state of balance. This contrasts with conventional clinical and laboratory balance tests that employ quiet sway or small perturbations to the BoS [15,58,59], or discrete perturbations, movements, or poses in a single plane [4–6,65]. The disk’s random motion induces balance challenges in continuously varying directions. The task elements (maintain balance, fix gaze on, and point to the randomly moving disk) place more stringent demands on system resources than these simpler tests, and better simulate the real-world conditions in which volitional movements of the body could precipitate a fall. It challenges not only the integrity of sensorimotor and musculoskeletal systems but also the neural control of subtasks and adaptations.

Though we demonstrate the biomechanical model provides detailed assessments of individual joint performance in the BRT, there are limitations from the model’s assumptions, particularly with respect to the representation of the musculoskeletal system. The body is not composed of separate segments whose only connections are through a joint, rather, adjoining segments are connected by muscle, tendons, and tissue, forming a continuum with varying viscoelastic properties, thereby introducing error. The upper trunk and spine are not perfectly rigid, as we assume, but flexible, as are the feet below the ankle. Although subjects are instructed to keep both feet on the force platforms, occasionally they raise up on the ball of one foot. Our model is able to account for such movements of the feet, but it assumes that their shape remains constant. When one raises up on the ball of one foot, the toes are placed in hyperextension and the shape of the foot changes. We do not anticipate that this introduces a serious error, however, because the mass of the toes is substantially less than the rest of the foot, leaving the foot’s inertial properties relatively unaffected. Finally, in vivo, the forearm and hand do not form a single, rigid unit. During testing, we made these segments a single unit to satisfy this assumption. As with all biomechanical models of this kind, averaged anthropometric data obtained from other studies are employed. We used data collected by Zatsiorsky et al. [66] and subsequently modified by de Leva [53] to reference segment endpoints to joint CoRs (http://dx.doi.org/10.1115/1.4031486). The Zatsiorsky data are from young healthy white Russians. To our knowledge, anthropometric data of this kind for older individuals or other races is not available. The Zatsiorsky/de Leva data are, however, “scalable,” in that all anthropometric parameters are a function of subject height and weight. So long as other subjects are of approximately the same build as the subjects employed in Zatsiorksy’s study (which in our study they are), the anthropometric data can be applied to them as well. Zatsiorsky et al. [66] estimated that for young, physically developed individuals with 8–20% body fat, the accuracy of their data was between 3% and 10%, depending on the body segment under consideration.

The work in this paper is the first phase of a larger experimental framework within which we will undertake the study of more complex balance tasks, define those differences attributable to graded sensorimotor deficits, and move toward a multisystem engineering model of neural control. The biomechanical model described in this article is being integrated into the larger control system model of Fig. 2 to permit an analysis of the forward dynamics of balance control. In the second phase, we will develop the sensory integration component based on BDT [47], an important feature of which is the unique delay and noise characteristic associated with each sensory modality [48,49]. In the third phase, we will develop the brain stem and spinal cord component of balance control based upon the muscle synergy literature [32–40]. In the fourth phase, we will develop the supra-brainstem controller, employing a stochastic optimal feedback controller [42] to simulate an IM-based controller [25]. This mathematical construct imparts a biologically inspired structure to the control task, which takes us a step closer to modeling the neurophysiological processes underlying the motor control task. Though IMs have been used extensively to describe and explain the motor control task, to our knowledge none have ever been used to simulate three-dimensional multisegmental control of balance, as we propose here.

Appendices

All appendices are available under the Supplemental Data tab for this paper on the ASME Digital Collection website.

Nomenclature

The following variables are used in this analysis, where vector quantities are indicated in bold face:

a_ijk =

acceleration (m/s²)

CS_j =

coordinate system

f =

sum of sines frequency (Hz)

F_ijk, W_ij =

force, weight (N)

g =

gravitational acceleration (9.80665 m/s²)

H_ijk =

acceleration matrix

[I_ijk] =

mass moment of inertia tensor (kg m² or N · m s²)

J_ijk =

pseudo-inertial matrix

L_i =

length (m)

m_i =

mass (kg or N s²/m)

M_ij =

homogeneous transformation matrix

R =

rotation matrix

r_ijk =

position vector (m)

t =

time (s)

T_ijk =

torque (N · m)

v_ijk =

velocity (m/s)

X(t) =

horizontal trajectory of disk

Y(t) =

vertical trajectory of disk

α_ijk =

angular acceleration (rad/s²)

θ_ijk =

angular displacement (rad)

σ =

variance

τ =

time delay (s)

ϕ =

sum of sines phase shift

Φ_ijk =

action matrix

ω_ijk =

angular velocity (rad/s)

Here, the subscript i refers the coordinate frame the variable is referenced to, j indicates the body segment (equivalently, the local coordinate frame) the variable is associated with, and k is the point [proximal (p) or distal (d) joint, or center of mass (c)] that the force, torque, or position vector acts upon. For example, F_02p designates the force acting on the proximal joint of the right shank, referenced to the global coordinate frame; and r_55d designates the position vector from the left shank’s center of mass to its distal (ankle) joint, referenced to the left shank’s body-fixed coordinate frame.

The following abbreviations are employed:

3D =

three-dimensional

AL =

arm length

APA =

anticipatory postural adjustment

BDT =

Bayesian decision theory

BoS =

base of support

BRT =

balanced reach test

CoM =

center of mass

CoR =

center of rotation

C7/T1 =

intervertebral disk between the seventh cervical and first thoracic vertebrae

EMG =

electromyography

FBD =

free body diagram

GRF =

ground reaction force

HFR =

high fall risk

IM =

internal model

LE =

lower extremity

L5/S1 =

intervertebral disk between the fifth lumbar and first sacral vertebrae

OoB =

out of balance

PID =

proportional-integral-derivative

T =

skew symmetric representation of vector t

UE =

upper extremity

YHS =

young healthy subject