A Method for Predicting Collagen Fiber Realignment in Non-Planar Tissue Surfaces as Applied to Glenohumeral Capsule During Clinically Relevant Deformation

Abstract

Previously developed experimental methods to characterize micro-structural tissue changes under planar mechanical loading may not be applicable for clinically relevant cases. Such limitation stems from the fact that soft tissues, represented by two-dimensional surfaces, generally do not undergo planar deformations in vivo. To address the problem, a method was developed to directly predict changes in the collagen fiber distribution of nonplanar tissue surfaces following 3D deformation. Assuming that the collagen fiber distribution was known in the un-deformed configuration via experimental methods, changes in the fiber distribution were predicted using 3D deformation. As this method was solely based on kinematics and did not require solving the stress balance equations, the computational efforts were much reduced. In other words, with the assumption of affine deformation, the deformed collagen fiber distribution was calculated using only the deformation gradient tensor (obtained via an in-plane convective curvilinear coordinate system) and the associated un-deformed collagen fiber distribution. The new method was then applied to the glenohumeral capsule during simulated clinical exams. To quantify deformation, positional markers were attached to the capsule and their 3D coordinates were recorded in the reference position and three clinically relevant joint positions. Our results showed that at $60\mathrm{deg}$ of external rotation, the glenoid side of the posterior axillary pouch had significant changes in fiber distribution in comparison to the other sub-regions. The larger degree of collagen fiber alignment on the glenoid side suggests that this region is more prone to injury. It also compares well with previous experimental and clinical studies indicating maximum principle strains to be greater on the glenoid compared to the humeral side. An advantage of the new method is that it can also be easily applied to map experimentally measured collagen fiber distribution (obtained via methods that require flattening of tissue) to their in vivo nonplanar configuration. Thus, the new method could be applied to many other nonplanar fibrous tissues such as the ocular shell, heart valves, and blood vessels.

1. Introduction

Biological soft tissues are composed of highly complex underlying micro-structural components. Micro-structural properties of the tissue contribute to its overall mechanical behavior. For instance, the relative organization of the extracellular proteins (e.g., collagen and/or elastin) leads to the tissue-level mechanical anisotropy [1–3]. Consequently, to better understand the in vivo mechanical responses of the soft tissue, detailed knowledge of its micro-structure is essential.

Due to its importance in understanding tissue damage and/or remodeling [4–9], the effect of tissue-level deformation on the micro-scale extracellular matrix (ECM) collagen fiber realignment has been studied extensively. For example, it has been shown via experimental measurements that collagen fiber alignment changes following both uniaxial [10–13] and biaxial [14–16] extension. Although quantification of collagen fiber distribution is possible via numerous optical and image-based techniques [10,12,17–19], currently available methods that involve measurements under mechanical loads (e.g., small angle light scattering [13,14], polarized light imaging [10,20,16], and second harmonic generation microscopy [12,15]) require a planar tissue setup. While such tissues are relatively thin and could be treated as 2D surfaces, their clinically-relevant deformations are generally not planar [13,21]. Therefore, direct measurement of collagen fiber realignment under such deformations are rendered impossible via 2D planar mechanical testing devices.

An alternative method to predict fiber-level changes following macro-scale deformation is using theoretical models [22–25]. Assuming that ECM fibers affinely follow the macro-scale deformation, many investigators have developed finite element models to predict tissue fibers realignment due to mechanical loading [24,25]. Although not all soft tissue deformations are purely affine [13,26,27], the assumption provides a practical method to characterize micro-structural changes analytically.

If the clinically relevant macro-scale deformation is available via in vivo or in vitro measurements, with the assumption of affine deformation, fiber-level changes could be predicted only via kinematics. Since there is no need for solving the stress balance equations, the computational efforts are much reduced. In addition, simplifying the experimentally measured distribution functions into some analytic or parametric form (e.g., in the format of an orientation tensor [2,24]) is not required.

The objective of this work was to develop a method to directly predict changes in the collagen fiber distribution in nonplanar tissue surfaces when their clinically relevant deformation is available via experimental measurement. The new method was applied to the glenohumeral capsule as it deformed in vitro at clinically relevant joint positions. The glenohumeral capsule is a collagenous tissue that stabilizes the glenohumeral joint during extreme abduction and external rotation. Injury to the anteroinferior glenohumeral capsule is a common result of anterior dislocation [28]. Characterization of the micro-structural changes in the capsule during joint movements, could provide a better understanding of the injury mechanism and develop improved diagnostic and surgical procedures.

2. Methodology

The new methodology assumes that tissue strain can be calculated using 3D positional data of strain markers obtained experimentally. The strain values were then used to predict changes in the fiber distribution functions using the assumption of affine deformation on curved surfaces. Calculation of strain and fiber distribution changes and experimental data acquisition for the glenohumeral capsule in clinically relevant positions are then presented.

2.1. Strain Calculation.

Assuming that the experimental deformation of the tissue were measured by recording a set of positional data from fiducial markers, the strain tensor was calculated via a method similar to that described previously by Filas et al. [29]. Briefly, surface triangular meshes were created from the marker positional data using the Delaunay triangulation function in matlab (Mathworks Inc., Natick, MA). From the marker tracking system, the 3D position of each marker was represented by $\stackrel{\wedge }{\mathbf{R}}$ and $\stackrel{\wedge }{\mathbf{r}}$ vectors in a global Cartesian coordinate system for un-deformed and deformed configuration, respectively. At each point on the surface of a triangular element, the position vectors were defined via bi-linear interpolation of the nodal positions

$$\mathbf{R}=\sum _{p=1}^3{\Phi }_p(\xi ,\eta ){\stackrel{\wedge }{\mathbf{R}}}_p$$ (1)

$$\mathbf{r}=\sum _{p=1}^3{\Phi }_p(\xi ,\eta ){\stackrel{\wedge }{\mathbf{r}}}_p$$ (2)

where ${\Phi }_p(\xi ,\eta )$'s were the bi-linear basis functions, $\xi$ and $\eta$ were the computational coordinates ($\xi \in [0,1]$ and $\eta \in [0,1]$), ${\stackrel{\wedge }{\mathbf{R}}}_p$'s were nodal position vectors in un-deformed configuration ${\Omega }_0$, and ${\stackrel{\wedge }{\mathbf{r}}}_p$'s were nodal position vectors in deformed configuration ${\Omega }_1$ (Fig. 1). A local coordinate system $(X^1,X^2,X^3)$ was then defined at each point on the un-deformed surface which was convected to a curvilinear coordinate system $(x^1,x^2,x^3)$ on the deformed surface. With the assumption that $X^3$ was a single value function of $X^1$ and $X^2$ (i.e., $X^3=X^3(X^1,X^2)$), and $x^{\alpha }=x^{\alpha }(X^1,X^2)$, the covariant base vectors in the surface of the element were calculated

Fig. 1.

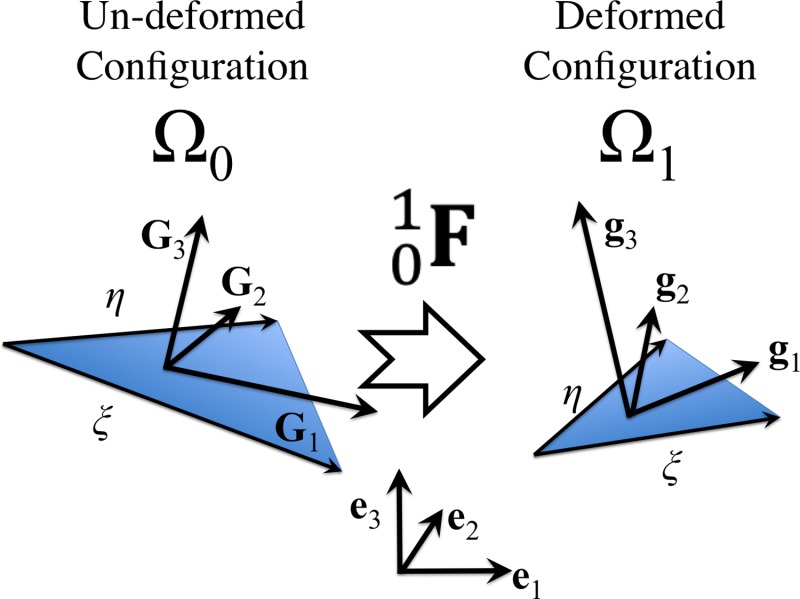
Schematic of a triangular element deformed from un-deformed configuration ${\Omega }_0$ to deformed configuration ${\Omega }_1$ via deformation tensor ${\hspace{0.17em}}_0^{1}F$. The covariant surface base vectors $G_1$ and $G_2$ as well as $g_1$ and $g_2$ are not necessarily orthogonal but they are expressed in terms of their components in an orthogonal coordinate system (i.e., ($e_1,e_2,e_3$)) to take advantage of $3\times 3$ matrix algebra.

$${\mathbf{G}}_{\alpha }={\mathbf{R}}_{,\alpha }={\mathbf{e}}_{\alpha }+X^3(X^1,X^2){\hspace{0.17em}}_{,\alpha }{\mathbf{e}}_3$$ (3)

$${\mathbf{g}}_{\alpha }={\mathbf{r}}_{,\alpha }=x^{\beta }(X^1,X^2){\hspace{0.17em}}_{,\alpha }{\mathbf{e}}_{\beta }+x^3(X^1,X^2){\hspace{0.17em}}_{,\alpha }{\mathbf{e}}_3$$ (4)

with $\alpha$ and $\beta$ being the dummy indices, ${\mathbf{e}}_{\alpha }$ being the orthogonal unit vector, ${\mathbf{G}}_{\alpha }$ being the covariant base vector in the un-deformed configuration and ${\mathbf{g}}_{\alpha }$ being the covariant base vector in the deformed configuration. The detailed methods for obtaining the derivatives of position vectors used in Eqs. (3) and (4) are presented in the Appendix. To take advantage of $3\times 3$ matrix algebra, two out-of-plane unit vectors were defined as the third covariant base vectors ${\mathbf{G}}_3$ and ${\mathbf{g}}_3$ for the un-deformed and deformed configurations, respectively:

$${\mathbf{G}}_3=\frac{{\mathbf{G}}_1\times {\mathbf{G}}_2}{\Vert {\mathbf{G}}_1\times {\mathbf{G}}_2\Vert }$$ (5)

$${\mathbf{g}}_3=\frac{{\mathbf{g}}_1\times {\mathbf{g}}_2}{\Vert {\mathbf{g}}_1\times {\mathbf{g}}_2\Vert }$$ (6)

The contravariant base vectors in un-deformed configuration were calculated as the following:

$${\mathbf{G}}^1=\frac{{\mathbf{G}}_2\times {\mathbf{G}}_3}{\sqrt{G}},\hspace{1em}{\mathbf{G}}^2=\frac{{\mathbf{G}}_3\times {\mathbf{G}}_1}{\sqrt{G}},\hspace{1em}{\mathbf{G}}^3=\frac{{\mathbf{G}}_1\times {\mathbf{G}}_2}{\sqrt{G}}$$ (7)

where the scaling factor $\sqrt{G}$ was defined by

$$\sqrt{G}={\mathbf{G}}_1·({\mathbf{G}}_2\times {\mathbf{G}}_3)$$ (8)

After obtaining the three components of each base vector from Eqs. (4), (6), and (7), the deformation gradient tensor $\mathbf{F}$ and the left Cauchy-Green strain tensor $\mathbf{B}$ were calculated

$$\mathbf{F}={\mathbf{g}}_I\otimes {\mathbf{G}}^I$$ (9)

$$\mathbf{B}={\mathbf{FF}}^T$$ (10)

2.2. Fiber Affine Deformation.

Consistent with its planar definition [30], the 2D collagen fiber distribution (density) function $R_0(\Theta )$ was defined as the angle histogram normalized so that the area under the curve was unity

$$\int R_0(\Theta )\mathrm{d}\Theta =1$$ (11)

The angle $\Theta$ on the surface of each triangular element was measured from the un-deformed covariant base vector ${\mathbf{G}}_1$. The choice of the vector from which $\Theta$ is measured is completely arbitrary. Using ${\mathbf{G}}_1$ is, however, advantageous as the experimental fiber structure is generally available via a 2D planar measurement method [17,18]. In particular, when the planar configuration is considered as the reference frame for strain measurement, $X^1$ and $X^2$ lie in the same plane and $X^3$ would be zero. Therefore, ${\mathbf{G}}_1$ will be same as ${\mathbf{e}}_1$ according to Eq. (3).

The collagen fibers were assumed to deform affinely with the macro-scale deformation. Since the total number of fibers are unchanged following deformation, it was concluded that

$$\int R_0(\Theta )\mathrm{d}\Theta =\int R_1(\theta )\mathrm{d}\theta =1$$ (12)

where $R_0(\Theta )$ was the fiber density function in un-deformed configuration ${\Omega }_0$, $R_1(\theta )$ was the density function in deformed configuration ${\Omega }_1$, and $\theta$ was measured from the convected covariant base vector ${\mathbf{g}}_1$. From Eq. (12), it was concluded that

$$\frac{R_0(\Theta )}{R_1(\theta )}=\frac{\mathrm{d}\theta }{\mathrm{d}\Theta }$$ (13)

As shown in Fig. 2(a), $\mathrm{d}\Theta$ could be calculated from un-deformed differential areal vector $\mathrm{d}\mathbf{A}$ and position vectors $\mathrm{d}\mathbf{R}$ as follows:

Fig. 2.

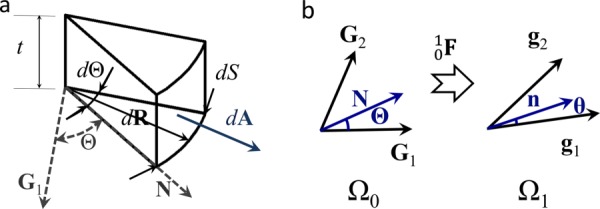
(a) Schematic of the volume differential element used to calculate $d\Theta$, with $t$ being the surface thickness, $G_1$ being the covariant surface base vectors, $N$ being the unit vector at angle $\Theta$, $dR$ being the differential position vector, $dS$ being the differential arc length, and $dA$ being the differential area vector. (b) The angle $\Theta$ in the un-deformed configuration was related to $\theta$ in the deformed configuration using the deformation of a normal vector $N$ to $n$ as described by Eqs. (21) and (22).

$$\mathrm{d}\Theta =\frac{\mathrm{d}S}{\Vert \mathrm{d}\mathbf{R}\Vert },\hspace{1em}\mathrm{d}S=\frac{\Vert \mathrm{d}\mathbf{A}\Vert }{t},\hspace{1em}\Vert \mathrm{d}\mathbf{A}\Vert =\frac{\mathrm{d}\mathbf{A}·\mathrm{d}\mathbf{R}}{\Vert \mathrm{d}\mathbf{R}\Vert }$$ (14)

where $t$ was the surface thickness and $\mathrm{d}S$ was the differential arc length. Equation (14) resulted in

$$\mathrm{d}\Theta =\frac{\mathrm{d}\mathbf{A}·\mathrm{d}\mathbf{R}}{t\Vert \mathrm{d}\mathbf{R}\Vert {\hspace{0.17em}}^2}$$ (15)

Similarly in the deformed configuration

$$\mathrm{d}\theta =\frac{\mathrm{d}\mathbf{a}·\mathrm{d}\mathbf{r}}{t\Vert \mathrm{d}\mathbf{r}\Vert {\hspace{0.17em}}^2}$$ (16)

From Nanson's relation

$$\mathrm{d}\mathbf{a}=J{\mathbf{F}}^{-T}\mathrm{d}\mathbf{A}$$ (17)

where

$$J=det(\mathbf{F})$$ (18)

and by definition, the stretch $\lambda (\theta )$ along the unit vector $\mathbf{n}(\theta )$ in the deformed configuration was

$$\lambda (\theta )=\frac{\Vert \mathrm{d}\mathbf{r}\Vert }{\Vert \mathrm{d}\mathbf{R}\Vert }=\frac{1}{\sqrt{{({\mathbf{B}}^{-1}\mathbf{n}(\theta ))}^T\mathbf{n}(\theta )}}$$ (19)

Combining Eqs. (13), (15), (16), (17), and (19), gave

$$R_1(\theta )=R_0(\Theta )\frac{{({\mathbf{B}}^{-1}\mathbf{n}(\theta ))}^T\mathbf{n}(\theta )}{J}$$ (20)

As shown in Fig. 2(b), $\Theta$ was related to $\theta$ via the deformation of a normal vector $\mathbf{N}$ in the undeformed configuration into $\mathbf{n}$

$$\mathbf{N}(\theta )=\lambda (\theta )({\mathbf{F}}^{-T}\mathbf{n}(\theta ))$$ (21)

After calculating $\mathbf{N}$ from Eq. (21), $\Theta$ was obtained from

$$\text{tan}\hspace{0.17em}(\Theta )=\frac{N^2\Vert {\mathbf{G}}_2\Vert \hspace{0.17em}\text{sin}\hspace{0.17em}\left(\stackrel{\wedge }{{\mathbf{G}}_1,{\mathbf{G}}_2}\right)}{N^1\Vert {\mathbf{G}}_1\Vert +N^2\Vert {\mathbf{G}}_2\Vert \hspace{0.17em}\text{cos}\hspace{0.17em}\left(\stackrel{\wedge }{{\mathbf{G}}_1,{\mathbf{G}}_2}\right)}$$ (22)

where $N^{\alpha }$'s were contravariant components of $\mathbf{N}$ in un-deformed configuration ${\Omega }_0$ and $(\stackrel{\wedge }{{\mathbf{G}}_1,{\mathbf{G}}_2})$ was the angle between the base vectors ${\mathbf{G}}_1$ and ${\mathbf{G}}_2$. To implement Eq. (20), $\theta$ was discretized by one degree. With the assumption that F and B were known from kinematics, for each $\theta$, the corresponding un-deformed angle $\Theta$ was calculated from Eq. (22). Since $R_0(\Theta )$ was a known function, calculation of $R_1(\theta )$ from Eq. (20) was then possible.

$R_0(\Theta )$ has been generally defined by analytical periodic functions [25,15]. In the case of glenohumeral capsule, for simplicity, a periodic version of the normal distribution was employed to specify $R_0(\Theta )$. The method explained above, however, could be implemented for any form of $R_0(\Theta )$.

To better visualize the orientation data, the main fiber direction $\mu$ and an orientation index $\mathit{OI}$ from $R_0(\Theta )$ were defined. With the assumption that $R_0(\Theta )$ was defined by a normal distribution, $\mu$ was simply chosen to be its mean. $\mathit{OI}$ was defined as the angle that contains one half of the total area under $R_0(\Theta )$ [31]

$${\int }_{\mu -(\mathit{OI}/2)}^{\mu +(\mathit{OI}/2)}{R}_0(\Theta )\mathrm{d}\Theta =0.5$$ (23)

To obtain a more intuitive definition for the fiber orientation (as suggested by Joyce et al. [31]), the normalized orientation index $\mathit{NOI}$ was calculated

$$\mathit{NOI}=\left(\frac{(\pi /2)-\mathit{OI}}{(\pi /2)}\right)100\%$$ (24)

The larger values of $\mathit{NOI}$ were associated with more aligned collagen fibers and the smaller values were associated with more scattered collagen fibers.

To validate the mathematical framework of the strain and fiber affine deformation calculations, the methodology was applied to multiple computationally generated sets of data points with known deformations. For example, a random distribution of points on a unit spherical surface subjected to various deformed scenarios were simulated. In addition, the methodology was employed to predict changes in the fiber orientation of a cylindrical shell with $\mathit{NOI}$ of 25% in the un-deformed configuration subjected to the stretch values of 1.25, 1.5, 1.75, 3.5, and 4 in the axial direction.

2.3. In Vitro Deformation of the Glenohumeral Capsule.

Six cadaveric shoulders ($71\hspace{1em}\pm \hspace{1em}8$ yrs.) were dissected down to the glenohumeral capsule (Figs. 3(a) and 3(b)). A $7\times 11$ grid of strain markers was then fixed to the anteroinferior capsule (Fig. 3(b)). The humerus and scapula were fixed in epoxy putty and each joint was mounted to a robotic/universal force-moment sensor (UFS) testing system that was used to apply external loads and torques to the humerus [32]. The 3D positions of the strain markers were recorded in the reference strain configuration, which was determined via inflation, using a three-camera motion tracking system (Spicatek, accuracy: 0.05 mm) [33]. Simulated clinical exams were then performed on each shoulder at $60\mathrm{deg}$ abduction, and $0\mathrm{deg}$, $30\mathrm{deg}$, and $60\mathrm{deg}$ of external rotation by applying a 25 N anterior load to the humerus while maintaining a 22 N compressive load to center the humeral head on the glenoid [13,33–35]. The 3D positions of the strain markers were recorded at these three joint positions with the loading conditions applied. Because the markers on the posterior band side were not detectable during the entire range of motion, they were excluded from the final strain calculation (Fig. 3(b)).

Fig. 3.

Experimental Setup. Anterior (a) and inferior (b) views of a typical shoulder specimen. A 7$\hspace{1em}\times \hspace{1em}$11 grid of strain markers were positioned on the tissue. The anteroinferior capsule was divided into six sub-regions: posterior axillary pouch glenoid side (PPG), posterior axillary pouch humeral side (PPH), anterior axillary pouch glenoid side (APG), anterior axillary pouch humeral side (APH), anterior band glenoid side (ABG), and anterior band humeral side (ABH). Note that the markers on the posterior band side were excluded from the final strain calculation.

Previous work has shown that the average $\mathit{NOI}$ in planar tissue samples from the axillary pouch under a small preload is 40% [13,36]. Therefore, based on this value, the standard deviation of the Gaussian distribution was computed and used to define the un-deformed fiber distribution $R_0(\theta )$. The un-deformed main fiber orientation $\mu$ was assigned randomly for each element using the rand function in matlab (The Mathworks Inc., Natick, MA). The deformed fiber orientations were then calculated using the new methodology.

Because understanding the fiber distribution and fiber realignment could help predict risk factors associated with injury in specific regions of the tissue, it was essential to make comparative analysis between such clinically relevant sub-regions. In particular, the anteroinferior capsule was divided into six sub-regions (Fig. 3(b)): (1) posterior axillary pouch glenoid side, (2) posterior axillary pouch humeral side, (3) anterior axillary pouch glenoid side, (4) anterior axillary pouch humeral side, (5) anterior band glenoid side, and (6) anterior band humeral side. The $\mathit{NOI}$ values for each element, in each deformed configuration, were then averaged in each capsule sub-region for every specimen individually. As the average $\mathit{NOI}$ values were not normally distributed, Friedman tests with Wilcoxon Signed Ranks post hoc tests were used to compare between capsule sub-regions and between joint positions. Significance was set at $\alpha =$ 0.05 for all comparisons.

3. Results

For any specific tissue specimen, changes in the fiber distribution function at each deformation step were obtained within less than 4 min of computer run time when the simulations were conducted using a Macintosh laptop (2.66 GHz Intel Core 2 Duo processor and 4 GB memory). Because the tissue surface was not folded on itself at any of the un-deformed or deformed configurations, the implementation of the method was straightforward and it did not require any major run-time trouble shooting. The triangulation scheme created a few fictitious out-of-plane elements that were deleted manually.

When a randomly distributed set of the data points on a unit sphere (Fig. 4(a)) were used to validate the strain calculation methodology, the model results agreed well with the imposed deformations. Not all of the cases examined are presented here but the calculated strains of a typical case in which $x=2X$, $y=3Y$, and $z=3Z$ are shown in Fig. 4(b). At the north pole of the sphere where the surface was subjected to biaxial stretch (${\lambda }_x=2$ and ${\lambda }_y=3$), the areal stretch was around 6, whereas on the equator depending on the location, the areal stretch values varied between 2 and 3. Similarly, when the affine deformations of fibers on a cylindrical shell were predicted for various cases of axial or radial deformations, the reorientation of the fibers agreed with the direction of major principal strain. The angle between the main fiber direction $\mu$ and a unit vector along the cylinder axis decreased from $40.3\hspace{1em}\pm \hspace{1em}18.5\mathrm{deg}$ (mean $\hspace{1em}\pm \hspace{1em}$ standard deviation) at the un-deformed configuration to $30.6\hspace{1em}\pm \hspace{1em}15.9\mathrm{deg}$, $23.0\hspace{1em}\pm \hspace{1em}10.8\mathrm{deg}$, $17.2\hspace{1em}\pm \hspace{1em}7.0\mathrm{deg}$, $6.5\hspace{1em}\pm \hspace{1em}2.3\mathrm{deg}$, and $5.5\hspace{1em}\pm \hspace{1em}1.9\mathrm{deg}$ for the axial stretch values of 1.25, 1.5 (Fig. 4(d)), 1.75, 3.5, and 4, respectively. The value of $\mathit{NOI}$ changed from 25% to $26.2\hspace{1em}\pm \hspace{1em}3.0$%, $29.9\hspace{1em}\pm \hspace{1em}4.8$%, $34.4\hspace{1em}\pm \hspace{1em}6.2$%, $61.7\hspace{1em}\pm \hspace{1em}7.1$%, and $66.5\hspace{1em}\pm \hspace{1em}6.3$% for axial stretch values of 1.25, 1.5 (Fig. 4(d)), 1.75, 3.5, and 4, respectively.

Fig. 4.

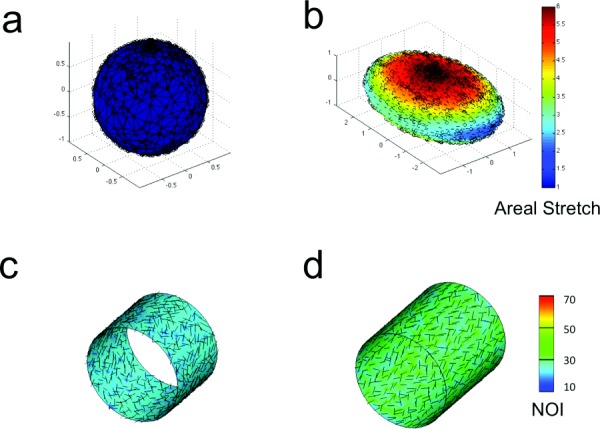
(a) Data points were generated on the surface of a unit sphere using matlab rand function. (b). Areal stretch after extension in x- and y-directions ($x\hspace{1em}=\hspace{1em}2X$, $y\hspace{1em}=\hspace{1em}3Y$, $z\hspace{1em}=\hspace{1em}Z$). Arrows show the direction of the major principal strain. (c) Main fiber direction $\mu$ (arrows) and normalized orientation index $\mathit{NOI}$ (contour plots) in un-deformed configuration. (d) Main fiber direction $\mu$ and normalized orientation index $\mathit{NOI}$ following axial extension (${\lambda }_x\hspace{1em}=\hspace{1em}1.5$).

In the tissue experiments, the position of the strain markers changed significantly between each external rotation position examined (Figs. 5(a)–5(d)). At each joint position, the $\mathit{NOI}$ values were larger on the glenoid compared to the humeral side of the anteroinferior capsule for larger values of the external rotation. For example, most of the triangular elements that shared nodes on the glenoid edge of the typical sample shown in Fig. 5 had $\mathit{NOI}$ values larger than 50% at $60\mathrm{deg}$ of abduction and $60\mathrm{deg}$ of external rotation. The $\mathit{NOI}$ values in each capsule sub-region generally had an increasing trend with higher values of external rotation (Fig. 6). For example, in the glenoid side of the posterior axillary pouch, $\mathit{NOI}$ value increased by 7.5%$\hspace{1em}\pm \hspace{1em}9.4$% ($\mathrm{mean}\hspace{1em}\pm \hspace{1em}\mathrm{SD}$), 11.5% $\hspace{1em}\pm \hspace{1em}9.9$%, and 21.7% $\hspace{1em}\pm \hspace{1em}11.3$% with $0\mathrm{deg}$, $30\mathrm{deg}$, and $60\mathrm{deg}$ of external rotation, respectively. In the humeral side of the posterior axillary pouch, $\mathit{NOI}$ value were 2.7% $\hspace{1em}\pm \hspace{1em}6.7$%, 8.2% $\hspace{1em}\pm \hspace{1em}4.6$%, and 18.6% $\hspace{1em}\pm \hspace{1em}15.2$% higher after $0\mathrm{deg}$, $30\mathrm{deg}$, and $60\mathrm{deg}$ of external rotation, respectively. Friedman tests revealed differences in the $\mathit{NOI}$ values at $0\mathrm{deg}$, $30\mathrm{deg}$ and $60\mathrm{deg}$ of external rotation only on the glenoid side of the posterior axillary pouch ($p=$ 0.01). More specifically, this capsule sub-region exhibited a significantly larger $\mathit{NOI}$ at $60\mathrm{deg}$ of external rotation compared to both $0\mathrm{deg}$ ($p$ = 0.03) and $30\mathrm{deg}$ of external rotation ($p=$ 0.03). It should be noted that the humeral side of the axillary pouch and the anterior band of the inferior glenohumeral ligament experienced very little change with joint position.

Fig. 5.

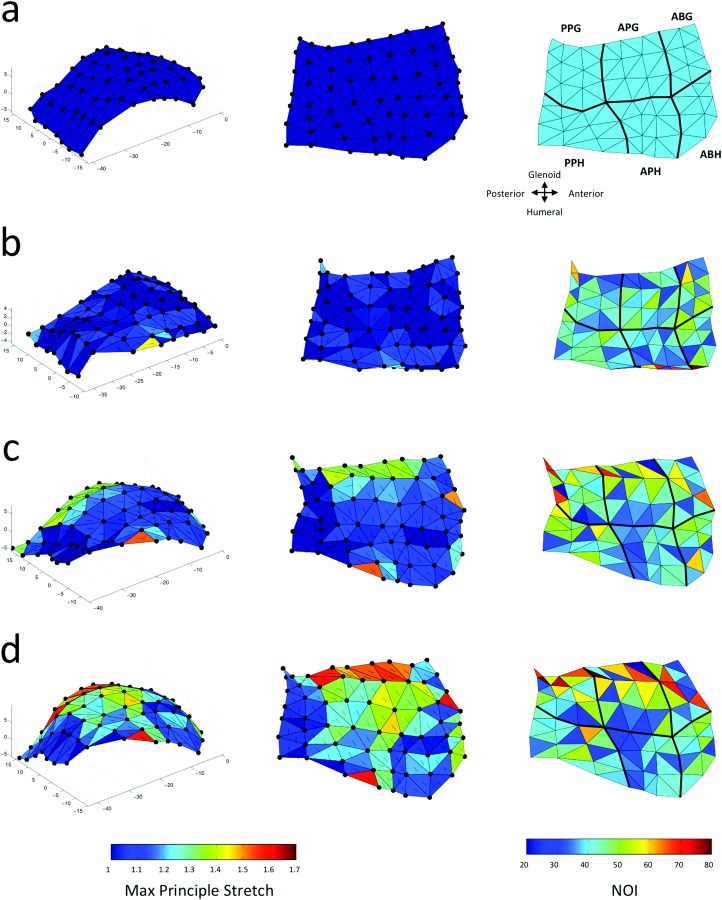
Maximum principle stretch and normalized orientation index $\mathit{NOI}$ in each element for a representative anteroinferior capsule at (a) referential configuration, and (b)–(d) deformed configurations of $60\hspace{1em}\mathrm{deg}$ of abduction accompanied by (b) $0\hspace{1em}\mathrm{deg}$, (c) $30\hspace{1em}\mathrm{deg}$, and (d) $60\hspace{1em}\mathrm{deg}$ of external rotation. The arrows on each element show the direction of the maximum principle stretch. The black lines on the $\mathit{NOI}$ contours separate the capsule sub-regions (b).

Fig. 6.

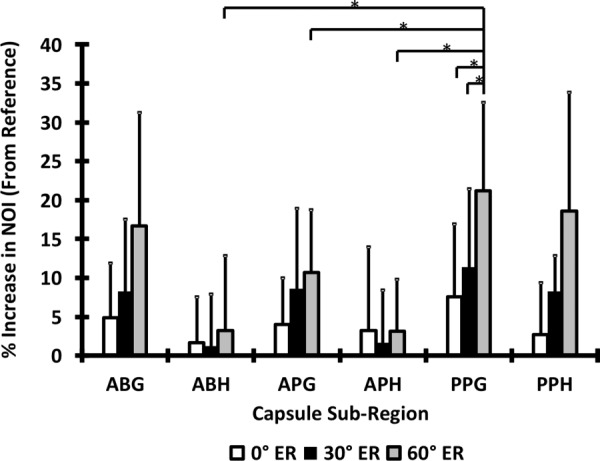
Percent increase in normalized orientation index $\mathit{NOI}$ of different capsule sub-region following $0\hspace{1em}\mathrm{deg}$, $30\hspace{1em}\mathrm{deg}$, and $60\hspace{1em}\mathrm{deg}$ of external rotation. The asterisks show the significant differences calculated from the Wilcoxon signed-ranks post hoc tests. Error bars are standard deviations.

Differences between capsule sub-regions were only significant at $60\mathrm{deg}$ of external rotation ($p=$ 0.02). At this joint position, the glenoid side of the posterior axillary pouch exhibited $\mathit{NOI}$ values of that were significantly larger than those in all other regions except the glenoid side of the anterior band and axillary pouch of the inferior glenohumeral ligament (all shown with asterisks in Fig. 6). With the exception of the posterior axillary pouch, the increase in the $\mathit{NOI}$ was much larger in the glenoid side in comparison to the humeral side at $60\mathrm{deg}$ of external rotation (16.7%$\hspace{1em}\pm \hspace{1em}14.5$% and 10.6% $\hspace{1em}\pm \hspace{1em}8.0$% increase on the glenoid side versus 13.1% $\hspace{1em}\pm \hspace{1em}9.6$% and 3.1% $\hspace{1em}\pm \hspace{1em}6.7$% change on the humeral side for the anterior band and anterior axillary pouch of the inferior glenohumeral ligament, respectively).

4. Discussion

Using the method presented in this study, changes in the collagen fiber distribution of curved tissue surfaces could be predicted whenever the deformation is known experimentally. Therefore, tissues with curved surfaces such as blood vessels [37], heart valves [38], ocular globe [39], fetal membrane [40], and glenohumeral capsule can be analyzed. Because both collagen micro-structure and in vivo (or in vitro) deformations have been quantified in many of these tissues via experimental methods, implementation of the presented method is highly relevant.

Two major advantages of this method are its reduced computational effort and its robustness in using any mathematical format of the fiber distribution function. To minimize computational costs, continuous fiber distribution functions have been generally integrated over spherical volume elements and repressed as a few parameters in an orientation tensor (e.g., Gasser et al. [24]). Because the deformation of the tissue is known via experimental measurements a prior, solving the stress balance equations is not required for the quantification of the deformation tensor. Therefore, the computational efforts are much reduced even though instead of using only a few parameters of the orientation tensor, the full continuous distribution function is employed. Further, although for simplicity a normal distribution was chosen to represent fiber density functions, the presented model is independent of the mathematical form of the distribution function. In particular, in many cases, multiple families of collagen fibers are present in the tissues (e.g., in the human cornea [41] or artery [42,43]). Although mathematical functions such as a generalized form of Von Mises distribution [15] are available to approximate such experimental measurements, the method presented in this study could predict the changes in the fiber distribution following deformation directly from the experimental forms of the undeformed distribution functions. Therefore, the extra step of fitting the data to known mathematical functions are not necessary in the current model. Although this methodology was primary developed for nonplanar surfaces, it is applicable to the planar cases, too. In fact, simplifying the equations for planar cases would lead to expressions similar to those previously used with experimental data [11,14].

The model was utilized to compare the collagen fiber alignment in the anteroinferior glenohumeral capsule at three clinically relevant joint positions with the assumption of affine deformation (i.e., the local fiber kinematics follow global tissue deformation). A similar initial fiber distribution in all regions resulted in significantly more aligned fibers on the glenoid side of the posterior axillary pouch in positions of external rotation. As increased fiber alignment indicates larger amounts of fiber rotation, this sub-region may be more susceptible to injury under larger deformations compared to other capsule sub-regions. As expected, the larger degree of fiber alignment on the glenoid side of the anteroinferior capsule compares well with other experimental and clinical studies which have reported maximum principle strains to be greater on the glenoid compared to the humeral side [33,35,44,45]. As localized areas of increased fiber alignment occurred in all sub-regions, this work further exemplifies that the anatomic description of the glenohumeral capsule as discrete regions does not correspond to its functional role [33].

The current technique of predicting fiber distribution changes in the anteroinferior glenohumeral capsule could further address research questions regarding diagnostic and repair techniques targeted to the specific sub-regions of the capsule. For example, current arthroscopic plication procedures to repair the glenohumeral capsule following dislocation allow for selective tightening of localized capsule regions. Understanding the fiber distribution in the capsule as well as fiber realignment under clinically relevant deformations may help predict specific regions which may be at risk for injury. In addition, knowing how fiber realignment occurs in the healthy capsule could help surgeons properly restore damaged regions of the capsule to a normally functioning state following dislocation.

A major limitation of the presented method is its two-dimensional assumption. While the current model can be used in co-planar fibrous tissues, the 3D fiber distribution functions were not included. Thus, this model is not applicable when complex 3D fiber distribution is present. Another potential limitation of this work was the assumption of affine fiber kinematics. The reliability of affine versus nonaffine assumptions in various soft and fibrous tissues has been studied previously [11,26,27]. For example, Lake et al. [11] have shown that in human supraspinatus tendon factors such as the orientation of the samples and their locations on the tendon were associated with the success of the affine prediction. Therefore, when using the developed model, one should be cautious of whether the assumption of affine fiber kinematics is reasonable within a certain level of confidence. In the anteroinferior capsule, the fiber kinematics may or may not be truly affine [13] but differences in collagen fiber alignment were detected using the affine assumption. Based on additional experimental analyses, a structural model, which makes this assumption, could be implemented in finite element models of the glenohumeral capsule when examining similar loading conditions to those presented here. This work demonstrates a experimental/computational approach to determine fiber distributions in 3D soft tissue structures which can be used in the future to validate fiber distributions generated by purely computational models [25].

Because the experiential fiber structure is generally available via 2D planar measurement methods [17,18], the newly developed model could be used in the mapping of such micro-structural data from the 2D planar configuration to the nonplanar clinically relevant configurations. In particular, the collagen structure of the tissues may be obtained after their in vivo deformations have been quantified. If the fiducial markers, used for in vivo (or in vitro) strain tracking, are detectable on the fiber distribution map obtained from a tissue characterization device (e.g., small angle light scattering [18]), the deformation from the latter planar configuration into the clinically-relevant shape can be quantified. Therefore, the method, presented here, could be used for mapping of the micro-structural information into physiologically-relevant 3D shape of the tissues. Using the same fiducial markers for strain measurement and micro-structural analysis has another convenient outcome: if there exists any residual strains in the tissue of interests, it would be detected by the markers following tissue dissection and isolation. Thus, deformation both due to rigid body motion (caused by flattening of the tissue) and due to residual strains or tissue mounting/manipulation would be incorporated in the mapping of the micro-structure.

Appendix

To calculate the derivative with respect to $X^{\alpha }$ (used in Eqs. (3) and (4)), the components of Eqs. (1) and (2) were employed to interpolate the values from the nodal positional data

$$X_{,\alpha }^3=\sum _{p=1}^3{\Phi }_p{(\xi ,\eta )}_{,\alpha }{\stackrel{\wedge }{X^3}}_p$$ (A1)

$$x_{,\alpha }^{\beta }=\sum _{p=1}^3{\Phi }_p{(\xi ,\eta )}_{,\alpha }{\stackrel{\wedge }{X^{\beta }}}_p$$ (A2)

The derivative of the bi-linear basis functions (${\Phi }_{,\alpha }$) used in equations (A1) and (A2) can be obtained from

$${\Phi }_{,\alpha }=\frac{\partial \Phi }{\partial \xi }{\xi }_{,\alpha }+\frac{\partial \Phi }{\partial \eta }{\eta }_{,\alpha }$$ (A3)

The terms ${\xi }_{,\alpha }$ and ${\eta }_{,\alpha }$ were calculated from the inverse relations

$$X^{\alpha }(\xi ,\eta )=\sum _{p=1}^3{\Phi }_p(\xi ,\eta ){\stackrel{\wedge }{X^{\alpha }}}_p$$ (A4)

and

$$\frac{\partial X^{\alpha }}{\partial \xi }=\sum _{p=1}^3\frac{\partial \Phi }{\partial \xi }{\stackrel{\wedge }{X^{\alpha }}}_p$$ (A5)

$$\frac{\partial X^{\alpha }}{\partial \eta }=\sum _{p=1}^3\frac{\partial \Phi }{\partial \eta }{\stackrel{\wedge }{X^{\alpha }}}_p$$ (A6)

Thus

$$\left[\begin{array}{cc}\multicolumn{1}{c}{{\xi }_{,1}}& \hfill {\xi }_{,2}\hfill \\ \multicolumn{1}{c}{{\eta }_{,1}}& \hfill {\eta }_{,2}\hfill \end{array}\right]=\frac{1}{j}\left[\begin{array}{cc}\multicolumn{1}{c}{\frac{\partial X^2}{\partial \eta }}& \hfill -\frac{\partial X^1}{\partial \eta }\hfill \\ \multicolumn{1}{c}{-\frac{\partial X^2}{\partial \xi }}& \hfill \frac{\partial X^1}{\partial \xi }\hfill \end{array}\right]$$ (A7)

where

$$j=\frac{\partial X^1}{\partial \xi }\frac{\partial X^2}{\partial \eta }-\frac{\partial X^1}{\partial \eta }\frac{\partial X^2}{\partial \xi }$$ (A8)

Nomenclature

$\mathbf{a}$ =

areal vector in deformed configuration $({\mathrm{m}}^2)$

$\mathbf{A}$ =

areal vector in un-deformed (referential) configuration $({\mathrm{m}}^2)$

$\mathbf{B}$ =

left Cauchy-Green strain tensor

${\mathbf{e}}_{\mathbf{\alpha }}$ =

orthogonal unit vectors

$\mathbf{F}$ =

deformation tensor

$G$ =

square value of scaling factor in un-deformed (referential) $\mathrm{configuration}$

${\mathbf{g}}_{\mathbf{\alpha }}$ =

covariant base vectors in deformed $\mathrm{configuration}$

${\mathbf{G}}_{\mathit{\alpha }}$ =

covariant base vectors in un-deformed (referential) $\mathrm{configuration}$

${\mathbf{G}}^{\mathit{\alpha }}$ =

contravariant base vectors in un-deformed (referential) $\mathrm{configuration}$

$j$ =

Jacobean of $\mathrm{transformation}$

$J$ =

volumetric $\mathrm{change}$

$\mathbf{n}$ =

unit vector in deformed configuration

$\mathbf{N}$ =

unit vector in un-deformed (referential) configuration

$N^{\alpha }$ =

contravariant components of $\mathbf{N}$

$\mathit{NOI}$ =

normalized orientation index

$\mathit{OI}$ =

orientation $\mathrm{index}\hspace{1em}(\mathrm{Rad})$

$\mathbf{r}$ =

position vector in deformed configuration $(\mathrm{m})$

$\mathbf{R}$ =

position vector in un-deformed (referential) configuration $(\mathrm{m})$

${\stackrel{\wedge }{\mathbf{r}}}_{\mathit{p}}$ =

position vector of node $p$ in deformed configuration $(\mathrm{m})$

${\stackrel{\wedge }{\mathbf{R}}}_{\mathit{p}}$ =

position vector of node $p$ in un-deformed (referential) configuration $(\mathrm{m})$

$R_0$ =

fiber distribution function in un-deformed (referential) configuration $({\mathrm{Rad}}^{-1})$

$R_1$ =

fiber distribution function in deformed configuration $({\mathrm{Rad}}^{-1})$

$S$ =

arc length in un-deformed (referential) configuration $(\mathrm{m})$

$t$ =

surface thickness $(\mathrm{m})$

$x^{\alpha }$ =

local convective coordinates in deformed configuration $(\mathrm{m})$

$X^{\alpha }$ =

local coordinates in un-deformed (referential) configuration $(\mathrm{m})$

$\alpha$ =

dummy index

$\eta$ =

computational coordinate

$\lambda$ =

$\mathrm{stretch}$

${\Omega }_0$ =

un-deformed (referential) configuration

${\Omega }_1$ =

deformed configuration

$\Phi$ =

bi-linear basis function

$\theta$ =

in-plane angle in deformed coordinate $\mathrm{system}\hspace{1em}(\mathrm{Rad})$

$\Theta$ =

in-plane angle in un-deformed (referential) coordinate $\mathrm{system}\hspace{1em}(\mathrm{Rad})$

$\xi$ =

computational coordinate