The Comprehension of Sentences Involving Quantity Information Affects Responses on the Up–Down Axis

Abstract

We investigated the use of space in the comprehension of the concept of quantity in text. Previous work has suggested that the right–left axis is useful in spatial representations of number and quantity, while linguistic evidence points toward use of the up-down axis. In Experiment 1, participants read sentences containing quantity information and pressed buttons in either (1) an up and a down position or (2) a left and a right position. In Experiment 2, the participants pressed buttons in either (1) up and down positions or (2) left and right positions, but heard the sentences rather than reading them. We found spatial compatibility effects for the up–down axis, but not for the right–left axis. Additionally, the spatial compatibility effect was observed whether or not the participants moved to make their responses. We discussed the results in the context of embodied approaches to the comprehension of quantity information.

How are abstract concepts understood? One influential approach to this question suggests that abstractions are understood by being grounded in concrete domains of experience (e.g., Barsalou, 2008; Lakoff & Johnson, 1980). A large body of evidence has suggested that at least some abstractions are understood through this sort of grounding. In particular, a number of studies have shown that people understand time through spatial representations (e.g., Boroditsky & Ramscar, 2002; Casasanto & Boroditsky, 2008; Lakoff & Johnson, 1980; Sell & Kaschak, 2011). Lakoff and Johnson (1980) proposed that time is mapped onto space such that the future is represented as in front of a person, and the past is represented as behind the person (at least in Western cultures). Boroditsky and Ramscar (2002) showed that priming individuals to think about moving through space primes them to think about time in a particular way. Sell and Kaschak (2011) further showed that comprehension of sentences about the future and past facilitates the preparation of movements away from and toward the body, respectively. Quantity and numerosity are other abstract domains that appear to be grounded in spatial representations. A well-known example of this grounding is the “spatial numerical association of response codes” (SNARC) effect (Dehaene, Bossini, & Giraux, 1993). The canonical SNARC finding is that when evaluating the parity of a number, participants are faster to respond to larger numbers when responding with their right hand, and faster to respond to smaller numbers when responding with their left hand. Additional evidence has suggested that the processing of quantity information affects the execution of motor responses (e.g., Badets, Andres, Di Luca, & Pesenti, 2007).

The claim that time and quantity are understood via spatial representations is supported by evidence from neuroscience. Critchley (1953) noted several cases in which patients with parietal lobe damage displayed simultaneous deficits in understanding and moving in space, understanding quantity and numerosity, and making judgments about time. Subsequent work has demonstrated that cortical regions in and around the intraparietal sulcus play roles in the control of reaching and grasping in space (Rizzolatti & Sinigaglia, 2008) and in the processing of information related to number, quantity, and time (Chiou et al., 2009; Walsh, 2003). Walsh proposed that number, quantity, and time are all understood via the representational system that allows for the coordination of action in space. According to Walsh (2003), coordinating action requires knowing “how far, how fast, how much, how long, and how many” (p. 486).

Whereas evidence suggests that the understanding of time and quantity is grounded in spatial/motoric representations, it appears that there is flexibility in how space is used to understand these concepts. Tasks that employ categorical judgments (such as the parity judgment used in many SNARC studies) seem to allow for different spatial schemas to be used to understand abstract concepts. The SNARC effect has been shown on both the right–left and up–down axes, and it can be flipped (i.e., faster responses to small numbers on the right and to large numbers on the left) by having participants imagine the number line in reverse (Ristic, Wright, & Kingstone, 2006). Representational flexibility is taken to be a hallmark of top-down organizational factors influencing the use of spatial schemas during a task (e.g., Hubbard, Piazza, Pinel, & Dehaene, 2005; Ristic et al., 2006). Santiago, Lupiáñez, Pérez, and Funes (2007) showed similar flexibility in tasks involving judgments about time, which can be mapped onto the front–back axis (as in the linguistic metaphors) or onto the right–left axis (Santiago et al., 2007; Torralbo, Santiago, & Lupiáñez, 2006). Interestingly, representational flexibility is not observed in tasks in which participants process temporal concepts while reading sentences or stories. Sell and Kaschak (2011) showed that motor responses moving away from the body on the front–back axis are facilitated by reading sentences about future events, and that responses moving toward the body are facilitated by reading sentences about past events. Thus, processing language about shifts in time produces motor compatibility effects, as suggested by the “future is in front, past is behind” metaphor. Ulrich and Maienborn (2010) failed to find a motor compatibility effect on the right–left axis when participants processed sentences about past and future events. The only time that sentence reading produced a right–left compatibility effect was when participants responded to the sentences by making explicit judgments about whether the sentences described past or future events. This suggests a general principle: Judgment tasks allow for flexibility in the use of space to understand abstract concepts, but linguistic-processing tasks that lack a judgment component involve the use of only metaphor-driven mappings of abstractions onto space.

The idea that the flexibility with which space is used to represent abstract concepts depends on the tasks that are being performed has been documented in the domain of time (Santiago et al., 2007), and evidence has suggested that quantity-related information can be represented flexibly in judgment tasks (e.g., Dehaene et al., 1993). What is lacking in the literature is an assessment of whether flexibility in spatial representations of quantity can be observed within the context of a language comprehension task. Lakoff and Johnson (1980) suggested that quantity is understood through use of the up–down axis (i.e., more is up). If our proposal is correct, it should be possible to observe activation of this axis during the comprehension of language about increases or decreases in quantity. Langston (2002) demonstrated that sentences violating the more is up metaphor are harder to understand than sentences that fit the metaphor (e.g., Coke was placed above Sprite because it has less caffeine vs. Coke was placed below Sprite because it has less caffeine). This observation supports the claim that spatial representations are active during the comprehension of language about quantity, but the lack of a spatial response during the experiment renders the result inconclusive as regards the nature of the representation activated during comprehension.

We conducted two experiments in which participants were presented with four short stories sentence by sentence. These sentences were read off the computer screen in Experiment 1 and presented auditorily in Experiment 2. Each story included six sentences that contained quantity information (e.g., More/Less runs were being scored this game). In both studies, participants used response keys aligned on either the up–down or the right–left axis to perform the reading task. In Experiment 1, we manipulated whether participants needed to produce an arm movement in order to move from sentence to sentence in the story. In the movement condition, the participants held down one button to read the sentence (e.g., the top button on the up–down axis) and had to move to press the other button (e.g., the bottom button) in order to indicate that they had finished reading the sentence. In the no-movement condition, the participants positioned one hand over the button that was used to display the sentence (e.g., the top button on the up–down axis) and positioned the other hand over the button that needed to be pressed to indicate that they had finished the sentence (e.g., the bottom button on the up–down axis). We manipulated whether the participants moved during the task to determine whether the comprehension of sentences involving quantity would produce spatial compatibility effects (e.g., SNARC), motor compatibility effects (e.g., the action–sentence compatibility effect; Glenberg & Kaschak, 2002), or both.

We expected spatial compatibility effects to arise on the up–down axis, where the manual response was arrayed along the dimension that linguistic metaphors use when coding quantity in terms of space, but not on the right–left axis. Although there is evidence to suggest that quantity can be represented on the up–down and right–left axes, the effects on the right–left axis appear to be driven by the demands of the binary judgment tasks that are employed in the experiments (as discussed above). As such, and as there is no linguistic metaphor relating quantity to the right– left axis, we do not expect this axis to be activated during a reading task that lacks judgments about quantity.

EXPERIMENT 1

Method

Participants

A group of 104 undergraduate psychology students participated in Experiment 1. All were right-handed (self-reported). The up–down axis and the right–left axis conditions had 52 participants each.

Materials

Four stories were adapted from Speer and Zacks (2005). Nineteen of the sentences in each story were filler items and did not contain any quantity information. The remaining six sentences were critical items (More/Less runs were being scored this game). Each sentence had a more and a less version. We created two counterbalanced lists of stimuli, in which an item appeared in one version (more) on the first list and in the opposite version (less) on the second list. We counterbalanced story order, so that stories appeared as the first, second, third, or fourth story equally often across participants. In order to avoid overlap between the metaphors more is up and good is up, we asked a separate group of 28 participants to rate each target sentence on a scale of −5 to 5 in terms of whether it described a “good thing” or a “bad thing” in relation to the rest of the story. More and less items were seen as slightly positive events; however, less items were viewed more positively than more items (p < .01), thereby eliminating concerns of metaphor overlap.

Apparatus

We created a response device from a standard QWERTY keyboard. We covered the entire keyboard in folder paper and then attached plastic blocks to the “A” key and the “6” key (on the number pad) to raise them above the folder paper and to make for easier button-pressing.

Procedure

Stories were presented to participants sentence by sentence. The participants pressed either the “A” or the “6” key (depending on the counterbalance condition) when they saw a central fixation symbol. They were instructed to hold down the button until they finished reading the sentence. When they finished, they were instructed to release the designated button and to press the other button. Halfway through, a message appeared on the screen indicating that they would be switching response modes. Participants then responded in the opposite direction from which they had started. For the movement condition, participants pressed both keys with their right hand. For the no-movement condition, participants responded by holding their left hand on the appropriate button to read the sentence, while their right hand was positioned over the other response button. Four yes/no comprehension questions followed each story. To avoid alerting the participant to the quantity items, the questions were based on the filler items and never mentioned quantity. Participants were told that they could rest after each set of comprehension questions, though most participants did not require much rest.

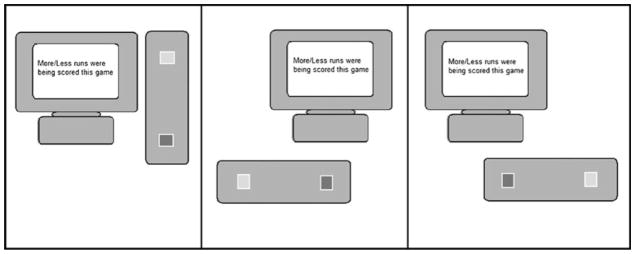
Keyboard orientation

In the up–down condition, the keyboard was attached to a stand next to the monitor so that it was positioned up, end to end, on the desk (see Fig. 1); in this condition, the keyboard was not moved during the experiment. In the right–left condition, the orientation of the keyboard apparatus in was on the right–left axis. The “A” key was aligned with a midline mark on the desk, so that that key was also at the midline of the participant (see Fig. 1). Half of the participants started with the “6” key to the right of the “A” key, and the other half started with the “6” key to the left of the “A” key. Halfway through the experiment, the experimenter flipped the keyboard 180 deg, so that the “6” key was on the opposite side of the “A” key from the beginning of the experiment.

Fig. 1.

Keyboard orientations for Experiments 1 and 2.

Design and analysis

The dependent variable in this experiment was reading time, or the duration that participants held down the first key before releasing it so that the second key could be pressed. The data were analyzed as follows. First, to eliminate preemptive responses (i.e., the participants lifted off the key too early) and obvious outliers, response times <500 or >5,000 ms were eliminated. We then eliminated response times that were more than two standard deviations from each participants’ mean in each cell of the design. The remaining data were analyzed using mixed-model regression. Participants and Items were crossed random factors in the model, and intercepts were allowed to vary for both participants and items. The data were coded as either match or mismatch. Responses to more sentences at the right or the up location were coded as matches, as were responses to less sentences at the left or down location. Responses to more at the left or down location, as well as responses to less at the up or right location, were coded as mismatches. The following variables were included in the model: sentence length (in characters), axis (up–down or right–left), matching (match or mismatch), movement (moving or not moving), and the Axis × Match interaction. To avoid issues with collinearity, all numerical, nonbinary variables were grand-mean centered. Mixed-model analyses were conducted using the HLM statistical software.

Results and discussion

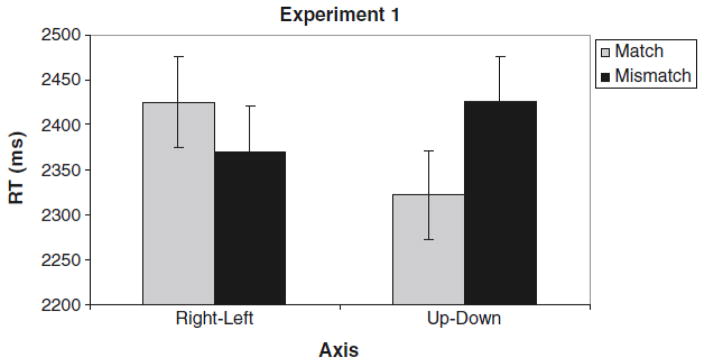
The regression analysis results are presented in Table 1. The Axis × Match interaction was significant [t(2252) 0 2.55, p 0.01], suggesting that the compatibility effect on the up–down axis was statistically different from the compatibility effect on the right–left axis. Follow-up analyses showed that matching responses were faster for the up– down axis [t(1156) = −3.166, p = .002] but not for the right–left axis [t(1096) = 0.676, p = .499] (see Fig. 2). Movement was not significant [t < 1], showing that the overall pattern of responding was not affected by whether the participant moved to respond.

Table 1.

Results of Experiment 1: Mixed-effect model results

Predictor	Coefficient	SE	t Value	df	p Value
Intercept	2,429	67.65	35.91	2252	<.001
Sentence length in characters	38.67	3.76	10.28	2252	<.001
Axis	−62.69	83.03	−0.76	2252	AS
Matching	−104.22	34.82	−2.99	2252	<.001
Axis by matching	155.88	61.2	2.55	2252	0.01
Movement	−48.22	68.19	−0.71	2252	0.48

Fig. 2.

Estimated means from the regression analysis of Experiment 1.

Our data demonstrated a spatial compatibility effect on the up–down axis (responses to more sentences being faster to the up location, and responses to less sentences being faster to the down location), but not on the right– left axis. This result is consistent with our expectation that a reading task would elicit compatibility effects based on linguistic metaphors (more is up) and would not show compatibility effects on the non-metaphor-based right–left axis.

EXPERIMENT 2

Experiment 1 showed that the right–left axis is not automatically used to represent quantity information during language comprehension. It could be that use of the right–left axis was impeded by the right–left eye movements made while reading. The left-to-right movement associated with reading a passage induces a strong spatial bias (e.g., Chatterjee, Southwood, & Basilico, 1999; Dobel, Diesendruck, & Bölte, 2007; Maass & Russo, 2003; Spalek & Hammad, 2005) and could have interfered with use of the right–left axis during representation. In order to remove this problem, in the second experiment we presented sentences auditorily.

Method

A group of 128 undergraduates participated. The experiment was identical to Experiment 1, except for the auditory presentation of the sentences. Additionally, since the movement manipulation in Experiment 1 did not affect performance, only the nonmovement condition was run in Experiment 2. The participants pressed one of the buttons with their left hand to hear the sentence, and then pressed the other button with their right hand when they had finished listening. Halfway through the experiment, they switched their direction of responding. The order of directions was counterbalanced across participants. Sixty of the participants responded on the up–down axis, and the other 68 responded on the right–left axis.

Results and discussion

The data from Experiment 2 were prepared for analysis as in Experiment 1, with one exception; the data were trimmed using the difference between sentence length (in milliseconds) and the latency, instead of just the latencies. We again analyzed the response times with a mixed-model regression that included the variables sentence length (in milliseconds), axis (up–down or right–left), matching (match or mismatch), and the Axis × Match interaction.

The results of the mixed-effects model are presented in Table 2. The Axis × Match interaction showed a pattern similar to that of Experiment 1 [t(2524) = −1.80, p = .072]. Follow-up analyses showed that matching responses were faster for the up–down axis [t(1209) = −1.989, p = .047] but not for the right–left axis [t(1291) = 0.621, p = .531] (see Fig. 3). Additionally, we found a main effect of direction in which down responses were faster than up responses on the up–down axis [t(1209) = 2.48, p = .013]. No other effects were significant.

Table 2.

Results of Experiment 2: Mixed-effect model results

Predictor	Coefficient	SE	t Value	df	p Value
Intercept	2608.81	45.85	58.47	2524	<.001
Sentence length in characters	0.92	0.03	26.39	2524	<.001
Axis	−71.23	64.51	−1.10	2524	.27
Matching	9.22	16.25	0.57	2524	.57
Axis by matching	−42.11	23.37	−1.80	2524	.07

Fig. 3.

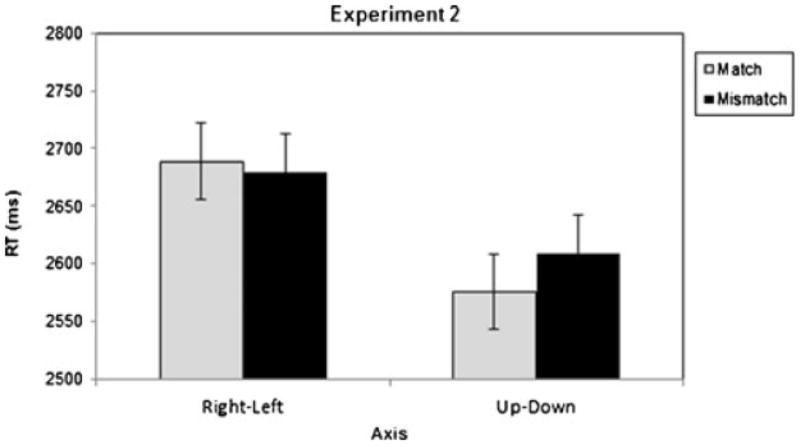
Estimated means from the regression analysis of Experiment 2.

These results suggest that the compatibility effects found in Experiment 1 are replicable when participants are hearing sentences containing quantity information (but perhaps not as strong as when they are reading sentences containing quantity information). The results further show that the lack of a right–left compatibility effect in Experiment 1 was not due to the demands of reading from left to right.

GENERAL DISCUSSION

We conducted these experiments to assess whether motor/spatial compatibility effects would be observed when reading sentences about quantity information, and if so, whether the compatibility effects would be observed on multiple axes. Our data suggest that spatial and motor compatibility effects are observed when reading sentences about quantity information, and that these effects are observed only on the up–down axis.

The presence of compatibility effects on the up–down axis is consistent with previous reports on the use of space to represent quantity information. Behavioral evidence (e.g., Dehaene et al. 1993; Fischer, Castel, Dodd, & Pratt, 2003) and data from neuroscience (e.g., Walsh, 2003) have suggested that spatial representations are important in understanding numerosity, and thus it is not surprising that reading sentences about quantity should affect the execution of responses to different spatial locations. The fact that the compatibility effect was observed both when participants moved to make their responses and when they did not suggests that it is the spatial location or axis that is activated when comprehending quantity-related sentences, rather than a particular action code for responding. Our results are consistent with the structure of the more is up metaphor discussed by Lakoff and Johnson (1980), as the locations (up and down) are what matter for expressions based on this metaphor, rather than movement toward those locations.

The spatial compatibility effect from Experiment 1 is consistent with reports of compatibility effects in other tasks involving numerosity (e.g., Dehaene et al., 1993; Fischer et al., 2003), but they are distinct from the previous findings in that our compatibility effect was isolated to the up–down axis. Unlike other studies that have investigated magnitude information in the context of categorical judgments or attention to spatial location (e.g., Fischer et al., 2003; Pecher & Boot, 2011), we saw no evidence for a motor/spatial compatibility effect on the right–left axis, even after removing the spatial demands introduced by reading direction. It appears that whereas spatial representations play a key role in understanding quantity, the axis that is used to do so may depend on the context in which the quantity information is being considered. In cases in which participants are asked to make numerical and categorical judgments (e.g., parity judgments on numbers), the right–left or up–down axes can be activated. It may be that categorical judgments, in conjunction with the use of both hands to make responses, helps to activate a mental number line across the body on the right–left axis or the up–down axis. This makes any axis useful for organizing and comparing numerical representations. Several studies have shown the SNARC effect to be flexible and dependant on a frame of reference defined by the experiment (Gevers, Lammertyn, Notebaert, Verguts, & Fias, 2006; Ristic et al., 2006). In cases of the vertical SNARC, participants are usually given a specific spatial schema (e.g., a clock face) to prime them into using the up–down axis to organize their responses (e.g., Ristic et al., 2006). Our task did not involve explicit numerical judgments or explicit attention to spatial location or numerical information, and thus the participants may have activated the up–down axis to represent quantity because this axis is commonly encountered in the context of language use (as evidenced by the prevalence of the more is up metaphor; Lakoff & Johnson, 1980). While both processes rely on spatial representation, the understanding of number, and the use of a number line when making categorical numerical judgments, may be distinct from the comprehension of quantity in a general, semantic sense.

The present findings demonstrate that the right–left axis is not necessarily privileged with respect to the representation of quantity: Spatial representations underlie the understanding of quantity, but the spatial axis that is used to do so depends on the circumstances under which the quantity information is encountered. The seeming inflexibility of the spatial axis used to represent quantity during language processing is perhaps a good thing, as the consistency of the metaphor aids in the successful communication of information about quantity. On a broader level, the finding that spatial compatibility effects are observed when participants comprehend sentences about quantity is consistent with embodied approaches to language comprehension, which hold that systems of perception and action planning ground our ability to understand language (e.g., Bub, Masson, & Cree, 2008; Glenberg & Kaschak, 2002; Kaschak et al., 2005; Zwaan & Taylor, 2006). By noting that compatibility effects can differ according to the demands of the task at hand, it may be possible to begin to generate more detailed hypotheses about the ways that the space around the body is used to ground the understanding of abstract concepts.