Abstract
In this work, we explore the seasonal relationships (i.e., the phenology) between sea ice retreat, sea surface temperature (SST), and atmospheric heat fluxes in the Pacific Sector of the Arctic Ocean, using satellite and reanalysis data. We find that where ice retreats early in most years, maximum summertime SSTs are usually warmer, relative to areas with later retreat. For any particular year, we find that anomalously early ice retreat generally leads to anomalously warm SSTs. However, this relationship is weak in the Chukchi Sea, where ocean advection plays a large role. It is also weak where retreat in a particular year happens earlier than usual, but still relatively late in the season, primarily because atmospheric heat fluxes are weak at that time. This result helps to explain the very different ocean warming responses found in two recent years with extreme ice retreat, 2007 and 2012. We also find that the timing of ice retreat impacts the date of maximum SST, owing to a change in the ocean surface buoyancy and momentum forcing that occurs in early August that we term the Late Summer Transition (LST). After the LST, enhanced mixing of the upper ocean leads to cooling of the ocean surface even while atmospheric heat fluxes are still weakly downward. Our results indicate that in the near‐term, earlier ice retreat is likely to cause enhanced ocean surface warming in much of the Arctic Ocean, although not where ice retreat still occurs late in the season.
Keywords: Arctic Ocean, surface warming, phenology, sea ice retreat, atmospheric forcing
Key Points
How warm the upper Arctic Ocean gets each summer strongly depends on the relationship between sea ice retreat and atmospheric heat input
2007 was warmer than 2012 owing to earlier sea ice loss over a wide area near the peak of atmospheric heat flux
Sea surface temperature peaks in areas of early retreat before the net surface flux turns from downward to upward owing to vertical mixing
1. Introduction
Seasonal sea ice retreat in the Arctic Ocean has intensified in recent years [e.g., Comiso and Hall, 2014], with (as of early summer, 2016) an historic ice extent minimum in 2012 and a next‐lowest value in 2007 [Comiso et al., 2008; Parkinson and Comiso, 2013]. The resulting increase in summer open water area has allowed the upper ocean to warm to unprecedented levels [Steele et al., 2008; Timmermans and Proshutinsky, 2015]. Model simulations indicate that in most areas, the main driver of seasonal ocean surface warming is downward atmospheric heat fluxes, although inflow areas like the Chukchi and southwestern Beaufort Sea also warm via ocean advection [Steele et al., 2010]. A warmer ocean surface encourages more sea ice melt via “ice‐albedo feedback” [Perovich et al., 2011], affects planktonic ecosystems [Arrigo et al., 2008], and in the fall acts to warm the lower atmosphere [Serreze et al., 2009], retard ice advance [Stroeve et al., 2014], and form subsurface warm ocean layers that may persist through the winter [Jackson et al., 2010; Steele et al., 2011].
Recent summer sea surface temperature (SST) anomalies are shown in Figure 1, for the area of the Arctic Ocean termed the “Pacific Sector” by Steele et al. [2010]. Every year from 2007 through 2014 has an areal‐mean SST anomaly warmer than the 1982–2006 mean. Interestingly, the anomaly in 2007 is nearly three times warmer than that in 2012, even though 2012 had more open water by the end of summer. Why is this? Here we seek an answer to this question by examining ocean warming and its forcings. The study of seasonal relationships between biological ecosystem components and climate forcing is commonly referred to as “phenology.” Here we borrow this term to refer only to the relationships between Arctic Ocean surface climate system components, specifically between the timing of seasonal sea ice retreat, ocean warming, and atmospheric heat fluxes. We consider the following questions: Does early ice retreat always lead to warmer SSTs? Does early ice retreat lead to an earlier date of peak SST? What role does the seasonal cycle of atmospheric heat fluxes play in these relationships? And finally, how are these relationships changing over the past few decades? Section 2 discusses the data we use, while section 3 presents our methodology. In section 4, we focus on the relationship between seasonal ice retreat and ocean warming, while in section 5 we also include the timing of atmospheric heat fluxes. Section 6 consists of a summary and discussion.
Figure 1.
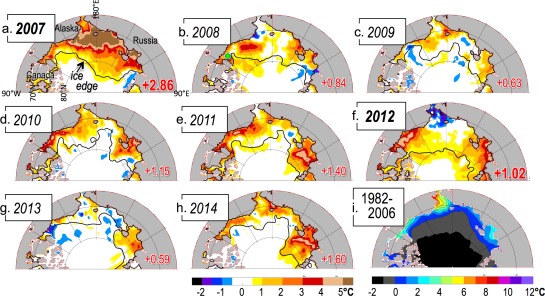
(a–h) August–September sea surface temperature (SST) anomalies for the years 2007–2014 from OISST (see section 2) in the “Pacific Sector” of the Arctic Ocean, (i) relative to the August–September 1982–2006 mean. The September mean ice edge (from 25 km passive microwave data) is also shown (black contour). In each plot, the areal mean anomaly is shown in red, where the area is defined as north of Bering Strait and the coastlines up to the ice edge. The 2 years 2007 and 2012 with strongest historical ice retreat are highlighted in bold font. For the year 2008, a green dot in the eastern Beaufort Sea indicates the position of the time series presented in Figure 2.
2. Data
Our focus in this study is on globally gridded products for SST, ice concentration (IC), and atmospheric net surface heat flux (Qnet). For SST, we mainly use NOAA's OISST data set, a global, daily mean product with 0.25° spatial resolution [Banzon et al., 2016; Reynolds et al., 2007]. We use the version derived from a blend of in situ observations and AVHRR infrared sensors, which provides a consistent multiyear time series over the years 1982–2014. For a previous 1° resolution version of this data set [Reynolds et al., 2002], SSTs were found to be biased relative to in situ observations by ∼0.5°C, with RMS errors up to 1.5°C [Steele et al., 2008]. A more recent comparison with ship CTD observations found a bias of only −0.02°C, but an RMS error of 1.77°C [Stroh et al., 2015]. We also make some comparison of OISST with two other gridded data sets. The first is the UK Meteorological Office's Operational Sea Surface Temperature and Sea Ice Analysis (OSTIA), a global, daily mean product with 0.05° spatial resolution [Donlon et al., 2012; Roberts‐Jones et al., 2012]. This analysis blends in situ observations with both infrared and passive microwave satellite sensor data, with a quoted global accuracy of 0.57°C compared to in situ observations, and Arctic Ocean bias/RMSE of −0.26°C/1.2°C [Stroh et al., 2015]. The second is the Canadian Meteorological Center's (CMC) global, daily mean SST product with 0.2° spatial resolution [Brasnett, 2008]. This analysis blends in situ and satellite data, with a stated global/arctic RMSE of 0.4/0.55°C [Canada Meteorological Center (CMC), 2012]. All SST data are interpolated for analysis onto a 25 km resolution EASE grid (http://nsidc.org/data/ease).
In situ SST observations under the sea ice pack are relatively sparse, while satellite data are completely unavailable. To handle this deficiency, gridded global SST data sets generally include an “ice mask” where SST is fixed or damped to a freezing temperature or to a climatology. For years through 2004, the OISST product uses IC from 25 km resolution passive microwave satellite sensors, processed with the NT1 = NASA “team” algorithm [Cavalieri et al., 1999]. For more recent years, OISST uses an operational product from NOAA [Grumbine, 1996]. In this study, we separately downloaded the NASA IC data from the National Snow and Ice Data Center [Cavalieri et al., 1996] and used these data for the entire time series, in order to preserve temporal consistency of ice‐related variables. In the OISST algorithm, no modification of the initial SST field is made for IC < 0.5, but for IC ≥ 0.5, “proxy” SSTs are created and used in the optimal interpolation algorithm, assuming a linear, monthly varying climatological relationship between IC and SST that varies with longitude, with SST at −1.8°C for IC = 1.0. OSTIA uses the same satellite brightness temperatures as OISST for IC, processed using an alternate algorithm by the Ocean and Sea Ice Satellite Application Facility (OSI‐SAF) [Eastwood et al., 2015]. For 0 < IC < 0.5, the initial SST field derived from in situ and satellite observations is relaxed to a spatially varying weekly climatology over a 30 day time scale. For IC ≥ 0.5, the initial SST field is relaxed to −1.8°C over a time scale that varies linearly from 17.5 to 5 days over concentrations from 0.5 to 1.0. For OSTIA, we used the IC data provided as part of the SST data set. Finally, CMC uses OSI‐SAF data (but also including scatterometer observations) to estimate IC on a 10 km global grid [Buehner et al., 2016]. For IC < 0.6, no modification of the initial guess SST field is made. For 0.6 ≤ IC ≤ 1.0 in winter, a proxy SST “observation” at every grid point of −1.8°C is created, with a large observation error. In summer (i.e., when surface air temperature from a climate model warms above 0°C), the value of the proxy observation is changed to 0°C for 0.6 ≤ IC ≤ 0.9. For CMC, we used the IC data provided as part of the SST data set.
In order to examine the atmospheric heat fluxes that force upper ocean warming, we use output from NASA's Modern‐Era Retrospective Analysis for Research and Applications (MERRA) [Rienecker et al., 2011]. This reanalysis provides realistic surface fluxes in the Arctic Ocean relative to independent observations, and outperforms other reanalyses in producing a realistic sea ice thickness when used as forcing to a coupled sea ice‐ocean model [Lindsay et al., 2014]. Our focus here is on the total surface atmospheric heat input Qnet, which describes the net surface heat flux at the bottom of the atmosphere, i.e., air‐sea flux in open water conditions, air‐ice flux where IC = 1.0, and a linear combination of the two in partial ice cover. All turbulent and radiative terms contribute to the net flux, although in summer (roughly, June–August) the net shortwave flux dominates [Lindsay, 1998] and has a small (relative to other reanalysis products) negative bias of 12 W m−2 [Cullather and Bosilovich, 2012; Lindsay et al., 2014]. Hourly MERRA output is averaged into daily means, and is interpolated onto the same EASE grid for analysis as used for SST and IC.
3. Methods
Our focus here is on the seasonal timing of, and relationships between, key events during the arctic sea ice retreat season (Figure 2). An example is provided in Steele et al. [2015], who define two key dates during seasonal sea ice loss: the Date of Opening (DOO) when IC at a given location drops below 80%, and the Date of Retreat (DOR) when IC drops below 15%. Both are defined by finding the final date before the summer concentration minimum that these drops occur, given the not uncommon circumstance of multiple drops [e.g., Steele et al., 2015, Figure 2]. DOO captures the start of the seasonal ice loss period, while DOR is the traditional value used to determine the ice edge, i.e., it captures the end of the ice loss period. The lag between the two can be many weeks, as illustrated in Figure 2a. We here refer to this lag as the Seasonal Loss of Ice Period, or SLIP.
Figure 2.
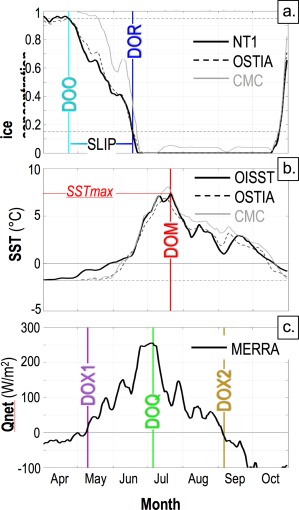
Time series of ice concentration (IC), sea surface temperature (SST), and net atmospheric surface heat flux (Qnet) at 71.5°N, 128°W during 2008 (green dot in Figure 1b). (a) IC from NT1 and that used by the OSTIA and CMC data sets (see section 2). Also shown are the Date of Opening (DOO; final date before the IC minimum when IC drops below 95%), the Date of Retreat (DOR; same as DOO, but for IC = 15%), and the Seasonal Loss of Ice Period, or SLIP = DOR – DOO, where these three quantities are defined using the NT1 data. IC = 95% and 15% are marked by dashed lines. (b) SST time series from OISST, OSTIA, and CMC, showing the Date of Maximum SST (DOM) when the SSTmax is achieved (defined using OISST data). Also marked are 0°C (solid horizontal line) and −1.8°C (dashed horizontal line). (c) Net atmospheric surface heat flux Qnet from MERRA, showing the Date of maximum Qnet (DOQ) when Qnetmax is achieved, as well as the zero crossing dates DOX1 and DOX2 (Qnet = 0 marked with a solid horizontal line). All time series are smoothed with a running 15 day boxcar filter.
In this study, we have modified the DOO and DOR algorithm relative to Steele et al. [2015] in two ways. First, we apply a 15 day running mean boxcar smoother to the daily IC time series, in keeping with our procedure for SST and atmospheric heat flux time series to be discussed below. Second, we here shift the DOO criterion to IC = 95%, in order to better capture the start of the ocean warming period.
Ice loss during the SLIP is generally similar in the NT1 and OSTIA data sets, as illustrated in Figure 2a (and in a variety of other locations in our domain, not shown). The time series frequently show episodes wherein ice retreat stalls for several days or even reverses, likely a result of synoptic wind‐forced advection of the ice pack [Steele et al., 2015; Steele and Ermold, 2015]. At this particular location, the DOO and DOR are both relatively early and the SLIP is relatively long; areal‐mean, climatological‐mean versions of these plots are discussed in section 5. The CMC ice concentrations frequently produce a later DOO relative to the other two data sets, but a similar DOR, i.e., the SLIP is shorter. This might result from CMC's use of scatterometer data, which has higher resolution and less error in wet ice conditions relative to passive microwave data [Ivanova et al., 2015].
Summer warming of the ocean surface is illustrated in Figure 2b. As discussed in section 2, warming during the SLIP is built into these data sets to account for observed ocean surface warming even in the presence of sea ice. Warming above the winter freezing point starts earliest in the OISST data, in response to the assumed linear relationship between SST and IC for concentrations between 1 and 0.5. The other two data sets show an initially slower warming response as IC declines, but then a rapid rise in SST so that all three SST products produce quite significant warming during the SLIP, in this case reaching values of ∼ 0°C at the DOR. After the DOR, SSTs generally agree between the data sets in open water. During this open water period, SST warms to its maximum value SSTmax at the Date of Maximum SST (i.e., DOM), and then cools through the late summer and into fall.
The atmospheric net surface heat flux Qnet that is largely responsible for ocean surface warming is shown in Figure 2c. This flux turns from upward (i.e., surface cooling) to downward (i.e., surface warming) in spring, at the first Date of fluX crossing DOX1. It then rises to a maximum heating rate in summer at the Date of maximum Qnet (DOQ) and subsequently declines, crossing the zero line at the second Date of fluX crossing DOX2 in late summer/early fall.
Recent seasonal ice retreat has been quite dramatic, but perennial ice still persists at the end of summer even in extreme years. One consequence is that in northern parts of our domain, DOR is rarely or never achieved, i.e., IC rarely or never drops below 15%. This is illustrated in Figure 3, which also shows that in southern areas, most or all years experience a DOR. As noted above, large‐scale SST data sets disagree on the course of warming before the DOR, but tend to agree afterward. A study of warming during the SLIP is worthwhile but is beyond the scope of this study. Thus, we here filter our time series of key variables (i.e., those noted in Figure 2) by only considering years when a DOR is achieved at each location. This means that the number of years used to compute statistics like the mean, variance, and trend is relatively large in southern areas, and relatively small in northern areas. In order to provide reliable statistics, when computing variance, trend, and correlation at any particular location, we require a minimum of 10 years with a DOR. Further, for SST variables SSTmax and DOM, we require that the DOM occur after the DOR. This means that we do not consider time series when the maximum SST happens within the SLIP, since SLIP warming is highly parameterized in these data sets (section 2). This eliminated ∼ 10% of the DOM events. If future work on verifying SST behavior during the SLIP in these data sets provides more confidence in the values before the DOR, these steps will likely become unnecessary.
Figure 3.
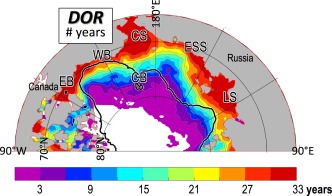
Number of years (out of a possible total of 33 from 1982 to 2014) when the ice concentration dropped below 15% (i.e., a DOR was achieved) over our study domain, plotted on a 25 km EASE grid. A 3x3 two‐dimensional boxcar smoother has been applied to this and all following contour maps. The white area in the north denotes where no DOR was achieved in any year. Geographic locations are marked as follows: EB = Eastern Beaufort Sea, WB = Western Beaufort Sea, CS = Chukchi Sea, CB = Chukchi Borderland, ESS = East Siberian Sea, LS = Laptev Sea. Black contour line marks the 500 m isobath [Jakobsson et al., 2012].
4. Ice Retreat and Ocean Warming
In this section, we explore how the seasonal timing of ice retreat (i.e., the DOR) affects two variables: (i) the amplitude of maximum ocean surface warming (i.e., the SSTmax), and (ii) the date at which SSTmax is achieved (i.e., the DOM). We do this via examination of long‐term means and linear trends, interannual variance, and detrended correlations. How these variables are affected by the seasonality of atmospheric heat fluxes Qnet will be discussed in section 5.
4.1. Ice Retreat and the Amplitude of Ocean Warming
Our first question is, does early seasonal ice loss lead to warmer ocean surface waters? The parameters we use to answer this question are presented in Figure 4. Seasonal ice loss is not a simple function of latitude, but rather responds to regional forcing such as local wind [Steele et al., 2015]. The result is that some areas such as the Chukchi Sea, the eastern Beaufort Sea, and the Laptev Sea have early ice opening and ice retreat, relative to other areas (Figures 4a and 4b). The heavy black contour in Figure 4b marks the 1 August DOR, which we use to define early versus late DOR. This contour also roughly delimits early versus late DOO (Figure 4a). The SLIP is ∼ 40–70 days in much of the Beaufort and Laptev Seas (Figure 4c), while it is much shorter (∼20–40 days) in the Chukchi Sea, owing to a much earlier DOR. The rest of the domain shows SLIPs of ∼50–80 days. A Marginal Ice Zone (MIZ) of 150 km width [Strong and Rigor, 2013] retreating northward at a constant rate of 5–10 km/d [Steele and Ermold, 2015] corresponds to a SLIP of 15–30 days. This rough calculation indicates that in many areas, the SLIP likely represents a combination of simple, monotonic MIZ retreat plus the effects of ice edge loitering and multiple retreat/advance events [Steele and Ermold, 2015].
Figure 4.
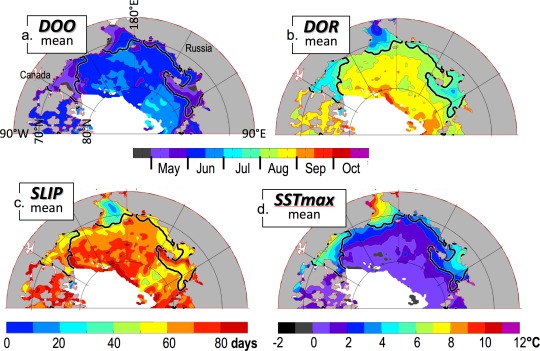
1982–2014 mean (a) DOO, (b) DOR, (c) SLIP, and (d) SSTmax. At each location, the mean for each parameter is calculated only for those years when ice concentration fell below 15%, i.e., when there was a DOR (see section 3). White denotes the area in the north with no DOR in any year. The black contour is the same in all panels, delimiting early DOR areas (before 1 August) from late DOR areas (after this date). This contour is used in other maps to follow.
The key result here is that in the mean, early DOR areas correspond to warmer SSTmax areas (Figure 4d). The earliest DOR in our domain occurs in the Chukchi Sea, likely a result of two processes: (i) earlier Qnet heating at these lower latitudes, and (ii) warm water advection from the south [e.g., Gong and Pickart, 2015]. The warmest SSTmax values are also seen in this area. Relatively warm SSTmax values are also found in the eastern Beaufort Sea and (with a smaller amplitude) in the Laptev Sea, areas with relatively early DOR. Areas to the north of the DOR = 1 August contour are generally much cooler than those to the south. Thus it seems that in the mean, the answer to our question is yes: ocean surface warming has an inverse relationship with the date of ice retreat.
To explore this relationship in further detail, we consider the long‐term trends and the detrended interannual variance in DOR and SSTmax (Figure 5). Trends in DOR (Figure 5a) are negative at −0.5 to −2.5 d/yr in the western Beaufort Sea and the northern Chukchi Sea into the Chukchi Borderland region, in keeping with recent results [Frey et al., 2015; Stammerjohn et al., 2012; Steele et al., 2015], and are also negative in the Laptev Sea. Perhaps equally interesting is that many areas show no trend (the deep basins and the eastern Beaufort and East Siberian Seas), or only a weak negative trend (the southern and central Chukchi Sea). Thus while total arctic sea ice extent in every season has statistically significant negative trends [Cavalieri and Parkinson, 2012], trends in the timing of how this ice loss begins are highly spatially variable.
Figure 5.
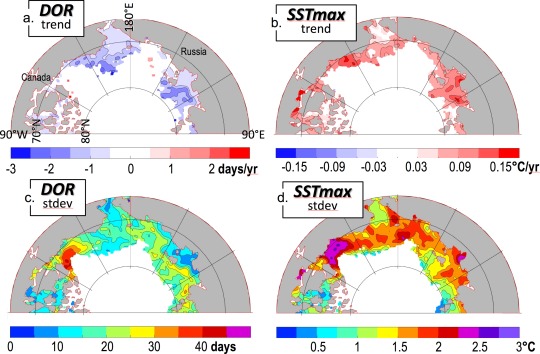
The long‐term trend over the years 1982–2014 in (a) DOR and (b) SSTmax. Only trends that are statistically significantly different from zero at 95% confidence are plotted. The detrended interannual standard deviation of (c) DOR and (d) SSTmax.
The spatial pattern of SSTmax trends is very similar to that for DOR (Figure 5b), i.e., where ice is retreating earlier each year, the maximum seasonal SST is rising. In these areas, a typical DOR trend is about −1 d yr−1 and SST trend is ∼ 0.1°C yr−1, i.e., for every day of earlier DOR, the maximum SST rises by 0.1°C. This means that over the ∼ 30 years of our study period, SSTmax has warmed in the areas with negative DOR trends by 30 years × 0.1°C yr−1 = 3°C.
Much of our domain lacks significant long‐term linear DOR or SSTmax trends. Nonetheless, there have been dramatic recent changes in some areas (e.g., unprecedented warming in the north, Figure 1) that have not yet persisted long enough to meet a linear significance test. Further, the Chukchi Borderland area shows a significant DOR trend but no significant SSTmax trend. We return to this apparent contradiction below.
With regard to variance, the highest values for DOR are generally found within ∼ 500 km of the coast in the Beaufort, north Chukchi, East Siberian, and Laptev Seas, with the strongest signal in the eastern Beaufort Sea (Figure 5c). This variance may have several sources, although a major contributor is likely wind forcing [Steele et al., 2015]. The spatial pattern of SSTmax variance is very similar to that for DOR (Figure 5d), indicating that areas with interannually variable DOR are also areas with interannually variable SSTmax.
Does a DOR anomaly in any particular year predict a SSTmax anomaly in that year? The answer is yes: the correlation of the detrended variables (Figure 6a) is significant and relatively high (r = −0.5 to −0.9) for roughly the same area where variance is high (Figures 5c and 5d). The domain mean correlation (Figure 6b) r = −0.79, with a linear slope of −0.08°C d−1, i.e., for every day of earlier DOR, the maximum summer ocean surface warming SSTmax increases by 0.08°C. However, this slope varies through the year, which is evident from the nonlinear (i.e., concave upward) shape of the data scatter in Figure 6b.
Figure 6.
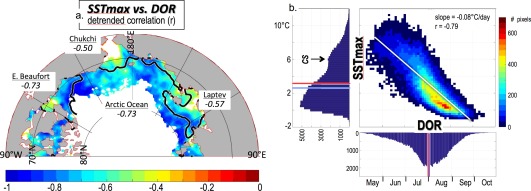
(a) Detrended correlation of the SSTmax and the DOR (95% significant trends only) over the years 1982–2014. Regional mean correlations are also shown, as well as the mean DOR = 1 August black contour (Figure 4). (b) Scatter plot of detrended SSTmax versus detrended DOR, with the overall linear best fit shown as a thin white line. Also shown are the histograms for each axis with pixel counts. The early, warm peak in Chukchi Sea (CS) SSTmax is noted. The mean (red line) and median (blue line) for each axes' histogram are also shown.
Specifically, the slope of SSTmax versus DOR (Figure 6b) shows three phases through the summer. In the early summer when the ice edge is retreating through the Chukchi Sea, the scatter in Figure 6b is wide and the slope is not significant. This is likely a result of northward warm ocean currents that, in this highly advective area, have a stronger influence on SSTmax than the timing of sea ice retreat. The slope becomes significant after this period, with a steeper value in mid‐summer relative to late summer. This indicates that the relationship between DOR and SSTmax is strongest in mid‐summer, but relatively weak in late summer, for reasons to be discussed in section 5.1.
So why were ocean surface temperatures warmer in 2007 relative to those in 2012 (Figure 1), even though 2012 had more total ice loss by the end of summer? In 2007 (Figure 7a), a broad area of anomalously early DOR (∼ 1 month or more) is evident stretching westward from the western Beaufort Sea across the northern Chukchi Sea and Chukchi Borderland and into the eastern East Siberian Sea, with another area in the Laptev Sea. Comparing to Figure 4b, this shifted the DOR for that year to ∼ early July. The corresponding SSTmax anomaly (Figure 7c) has a spatial pattern similar to that for the DOR anomaly. On the other hand, the 2012 DOR anomaly (Figure 7b) shows a strong signal in the eastern Beaufort Sea, but then a much weaker and more diffuse early anomaly spreading westward at higher latitude than that seen for 2007. At these higher latitudes, this shifted the DOR for that year to ∼ early August. The corresponding 2012 SSTmax anomalies (Figure 7d) are very warm in the eastern Beaufort Sea and the southern Laptev, but are otherwise quite weak. Thus we see that a key difference between 2007 and 2012 was in the timing of ice retreat: in 2007, DOR was shifted to early July and allowed much more ocean surface warming, relative to the DOR shift to early August in 2012 which had a much smaller effect on SST.
Figure 7.
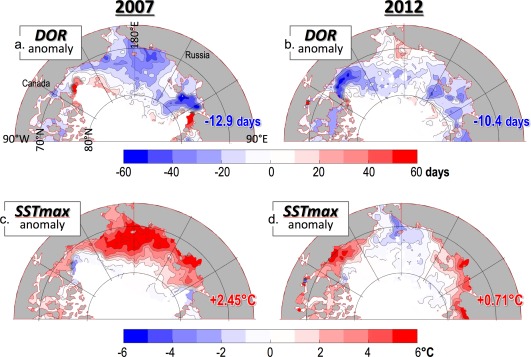
The (a) 2007 and (b) 2012 DOR anomaly relative to the long‐term mean (Figure 4b). Also shown are the (c) 2007 and (d) 2012 SSTmax anomalies relative to the long‐term mean (Figure 4d). The areal‐mean values are shown in the bottom right corner of each plot.
In summary, we have found that early DOR generally leads to a warmer SSTmax in most of our domain. However, this relationship breaks down in late summer (i.e., by ∼ August). What causes this breakdown in the DOR versus SSTmax relationship? As we will discuss in section 5, a key factor is the timing of DOR anomalies relative to the atmospheric heat flux signal, in addition to changes in the buoyancy and kinetic energy inputs at the ocean surface.
4.2. Ice Retreat and the Timing of Ocean Warming
Our second question from the Introduction was, does the date of ice retreat (DOR) influence the date of maximum seasonal SST (i.e., the DOM)? Figure 8a indicates that there is indeed some relationship, in that the areas of early mean DOR in the Chukchi, Eastern Beaufort, and Laptev Seas are areas where the mean DOM is in early/mid‐August, i.e., about 2 weeks earlier than in the rest of the domain where DOM occurs in late August/early September. This means that the DOM occurs 30–60 days after the DOR in the Chukchi Sea, 20–40 days after the DOR in the Eastern Beaufort and Laptev Seas, and within a month of the DOR in the rest of the domain (Figure 8b).
Figure 8.
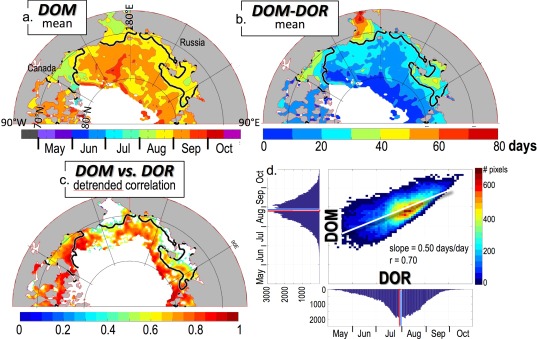
The 1982–2014 mean (a) DOM and (b) DOM‐DOR. (c) Detrended correlation of the DOM and the DOR (95% significant trends only) over the years 1982–2014. The mean DOR = 1 August black contour is also shown in Figures 8a–8c. (d) Scatter plot of detrended DOM versus detrended DOR, with the overall linear best fit shown as a thin white line, similar to the scatter plot in Figure 6b.
We can also ask (as in Figure 6), does an early DOR in any particular year lead to an early DOM in that year? The answer is yes, with the largest effect generally found within ∼ 500 kilometers of the coast (Figure 8c). In the Chukchi Sea where warm ocean advection likely dominates, the relationship is not evident. The domain‐mean correlation between DOM and DOR is 0.70, with a slope of 0.50 days/day (Figure 8d). This means that for every day of earlier DOR, DOM is earlier by ½ a day. In summary, the timing of ice retreat (i.e., the DOR) does influence the timing of when SST reaches its maximum value (i.e., the DOM). However, this relationship (like that for DOR and SSTmax) has some regional variation.
5. The Phenology of Ice Retreat, Ocean Warming, and Atmospheric Heat Fluxes
We have shown in section 4 that the DOR impacts both the amplitude and the timing of seasonal ocean surface warming, and that this impact is strongly dependent on the time of year as the ice edge sweeps northward during the retreat season. A key forcing that has strong seasonal variation is the net atmospheric heat flux Qnet, which is dominated by the net shortwave flux but also has contributions from the net longwave flux and (to a lesser extent) turbulent fluxes [Lindsay, 1998]. In this section, we discuss the impact of seasonally varying Qnet on ocean surface warming in the presence of seasonally varying ice retreat. We first present the “big picture” of how ice extent, SST, and Qnet vary seasonally, i.e., the phenology of these variables. In the following subsections, we will then seek explanations for the SST and DOR relationships found in section 4.
The key dates introduced in Figure 2 are presented as 1982–2014 mean arctic maps in Figure 9, and as regional mean time series in Figure 10. In Figure 10, we have combined the Eastern Beaufort and Laptev Seas into one region, since both experience moderately early ice retreat and moderate SST warming. In most areas, the seasonal progression of key dates during the retreat season can be summarized as DOX1 ≤ DOO ≤ DOQ ≤ DOR ≤ DOM ≤ DOX2. In words, ice opening happens about the same time or later than when Qnet starts warming the surface. Then, in most areas, the date of maximum warming rate occurs, followed by the date when ice fully retreats, and then by the date of maximum SST. The final step in the ice retreat season is when Qnet starts cooling the ocean. Statistically significant long‐term trends are negligible for all variables except the DOR (shown in Figure 5a) and the DOO (not shown, but with a similar pattern to the DOR). The SSTmax also has significant trends, as shown in Figure 5b.
Figure 9.
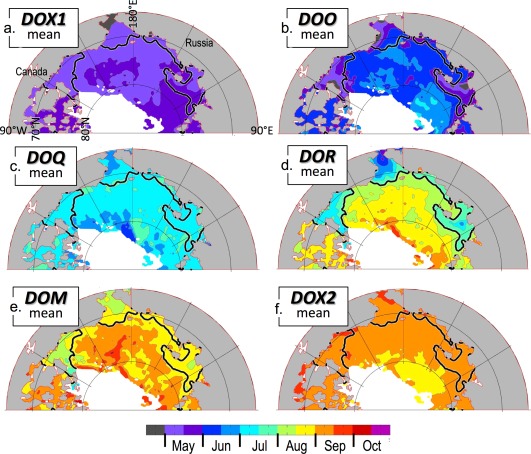
Key dates of seasonal change (defined in Figure 2) in the “Pacific Sector” of the Arctic Ocean, averaged over 1982–2014. Also shown is the mean DOR = 1 August black contour. White areas never experience a DOR in any year.
Figure 10.
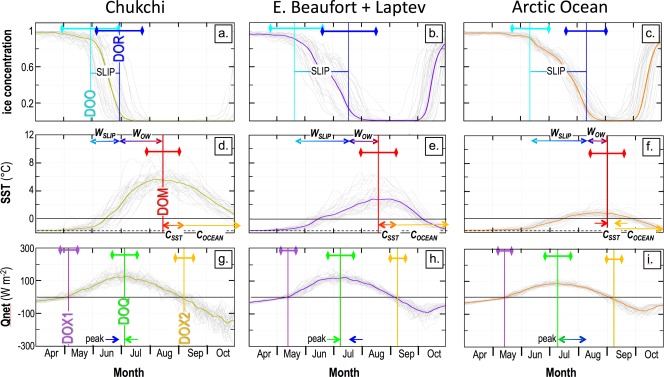
Seasonal time series over the years 1982–2014, averaged over three regions: the Chukchi Sea (left column), the Eastern Beaufort and Laptev Seas (middle column), and the rest of the domain, termed “Arctic Ocean” (right column). The Chukchi and Eastern Beaufort Sea areas are defined using the coastlines and the mean DOR = 1 August contour; the Laptev Sea is similar but has longitude limits 116°E to 155°E. Gray lines are regional median time series for each year; the thicker colored line in each panel provides the multiyear median. Also shown are the key dates defined in Figure 2 (vertical lines), ± one standard deviation of interannual variability in these dates (horizontal bars with diamond symbol end‐points), the two warming phases WSLIP and WOW, the two cooling phases CSST and COCEAN, and the time difference between the DOQ and the DOR, termed “peak” here.
In general, there are two phases of warming (as discussed in section 3), i.e., (i) warming during the SLIP “WSLIP” and (ii) warming in open water after DOR “WOW.” These are marked in Figure 10. Since the SLIP lasts longer in areas with later DOR (Figure 4c), WSLIP becomes a greater fraction of the total warming time in these later DOR areas (i.e., compare Figures 10d–10f). However, as noted in section 3, “SLIP warming” is poorly constrained by observations and so a discussion of the relative amplitudes and periods of these two warming phases will not be a focus of this study. There are also two phases of cooling. The first, denoted “CSST” in Figure 10, occurs between DOM and DOX2, and has a relatively small negative SST slope. The second cooling phase, denoted “COCEAN” in Figure 10, has a steeper SST decline just after DOX2, which eventually abates in late October. These two cooling periods will be discussed in further detail in section 5.2. Figure 10 also marks the period between the DOQ and the DOR, denoted “peak.” This period is key to understanding the strength of SST response to DOR, and so will be discussed in further detail in section 5.1.
5.1. Why Does Not Early DOR Always Lead to Warmer SSTmax?
Over most of our domain, ice retreat happens on or after the date when Qnet is maximum (Figures 9 and 10). Thus the open ocean is fully exposed only when atmospheric heat fluxes are already on the decline. In the Chukchi Sea, this mean relationship is slightly reversed, i.e., the DOR happens ∼ 1 week before the DOQ, likely owing to the strong ocean advection in this area. In the Eastern Beaufort and Laptev Seas, the DOR happens ∼ 1–2 weeks after the DOQ, while in the rest of the domain, the DOR lags the DOQ by an average of ∼ 1 month (see “peak” in Figure 10).
A map of the long‐term trend in DOR‐DOQ (Figure 11a) indicates that the DOR is becoming closer to the DOQ in the western Beaufort, Chukchi Borderland, and Laptev Seas. This is mostly because the DOR is trending earlier in those regions (compare Figures 5a and 11a). A comparison of DOR‐DOQ in the 1980s versus the 2010s is presented in Figures 11b and 11c. In the Chukchi Sea, the DOR was ∼ coincident with the DOQ (±20 days) in the early period, while in the most recent period it is more uniformly before the DOQ. In the Beaufort and Laptev Seas, the DOR shift has been much larger, from up to ∼ 1 month later then the DOQ to 1–4 weeks earlier. Finally, in the rest of the domain, southern areas have transitioned from a DOR that was much later than the DOQ to a date that is 0–4 weeks later, while northern areas are retreating for the first time and are still 1.5 months or more later than the DOQ.
Figure 11.
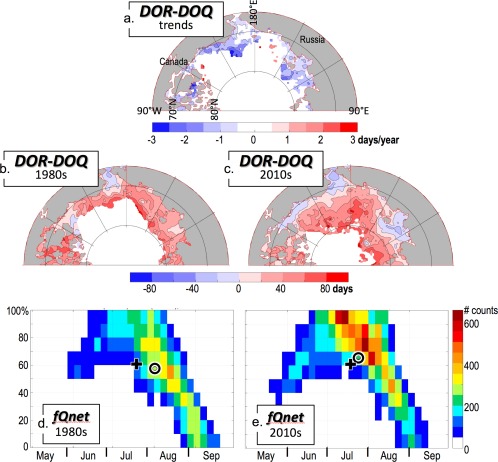
(a) Long‐term linear trends (95% or greater significance only) over 1982–2014 of the time difference DOR‐DOQ. Also shown are the mean DOR‐DOQ values averaged over (b) 1980–1989, and (c) 2010–2014. (d, e) The fraction fQnet (expressed as a percent) of Qnet at the time of ice retreat, relative to that at the Qnet maximum, for all points in the domain, i.e., fQnet = Qnet(DOR)/Qnet(DOQ) for the 1980s and the 2010s. The circle represents the centroid of all pixels, while the plus symbol provides a reference at a fixed location in both plots, i.e., (20 July, 60%).
The main point here is that if ice retreat happens before or near the DOQ, then Qnet has the ability to substantially warm the ocean surface. In the past, this only happened in the Chukchi Sea, but in recent years, the Eastern Beaufort Sea, Laptev Sea, and some other more southern parts of our domain are also experiencing ice retreat near or even before the date of maximum atmospheric heat flux. This allows substantial warming, resulting in the SSTmax trends presented in Figure 5b. On the other hand, areas with later mean ice retreat are, even in recent years, still exposing the ocean surface to atmospheric warming only quite late in the Qnet cycle. This timing is less conducive to ocean warming.
Another way to look at this problem is to consider the variable “fQnet,” defined as the amplitude of Qnet at the time of the DOR, or Qnet(DOR), as a fraction of the maximum seasonal Qnet, or Qnet(DOQ), i.e., fQnet = Qnet(DOR)/Qnet(DOQ). This is presented as two‐dimensional histograms in Figures 11d and 11e for the 1980s versus the 2010s over our entire domain. The overall envelope of values has shifted to earlier DOR in recent years, while the domain‐mean fQnet has increased from 55% to 63%. This is evident as a shift toward values closer to 1.0, i.e., ice retreat is happening closer to the time of peak atmospheric heat flux. Nonetheless, there is still substantial late‐season ice retreat, when fQnet is small and thus warming is weak.
So now we can explain the weak link between the DOR and the SSTmax in areas of late retreat (section 4.1). In these areas, the ice edge sweeps northward and exposes the ocean to atmospheric warming many weeks after the Qnet maximum (compare Figures 9c and 9d), when Qnet is still downward but small. This provides only a weak heat flux to warm the ocean surface. The result is that in these areas, ice retreat generally leaves cold water in its wake [e.g., Steele and Ermold, 2015, Figure 16b]). If the DOR in these areas becomes earlier by only a few weeks over a number of years, it will still be much later than the DOQ, and thus will have little impact on SST.
5.2. Why Does Early DOR Sometimes Lead to Early DOM?
In a well‐mixed open water environment with no advection, the ocean surface should start warming when the atmospheric net surface heat flux Qnet turns from upward to downward, i.e. at the DOX1. It should reach a maximum warming rate at the date of peak downward heat flux, i.e., the DOQ, and then continue to warm (albeit at a slower rate) until Qnet turns from downward to upward, i.e., at the DOX2. A simple approximation of this relationship assumes that Qnet and SST both vary as sine waves over the season, with SST lagged relative to Qnet by 90° [e.g., Turner and Kraus, 1967, Figure 1]. Now consider the arctic situation, in which ice suppresses ocean warming for some time during the summer, thus affecting the magnitude of the maximum warming SSTmax (section 4.1). However, once the ice finally retreats, we might expect that SST always warms until the DOX2, so that DOM = DOX2, with no influence of the DOR.
In fact, we do find that DOM ∼ DOX2 in northern, late‐retreating areas of our domain, where the open water period between the DOR and the DOX2 is short (Figure 12). Interestingly, some places show a DOM occurring after the DOX2, possibly a result of heat advection by ocean currents in late summer [Steele et al., 2010]. However, we find a very different situation in areas of early mean DOR (i.e., the Chukchi, Eastern Beaufort, and Laptev Seas), where the DOM leads the DOX2 by ∼ 10–40 days. To a lesser extent this also holds for southern parts of our “late DOR” domain, i.e., in the Western Beaufort and East Siberian Sea, where the DOM leads the DOX2 by ∼ 20 days. In these areas (i.e., where the DOM leads the DOX2), by the time the atmosphere starts cooling the ocean surface (i.e., at the DOX2), SSTs have already been declining for 10–40 days. Clearly, another process is in play before the DOX2 that varies with the time of year during the retreat season.
Figure 12.
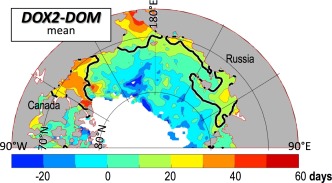
The quantity DOX2‐DOM, i.e., the time period between the date of maximum seasonal SST (i.e., the DOM) and the date when Qnet turns from downward heating to upward cooling (i.e., DOX2). Also shown is the mean DOR = 1 August black contour.
Early in the Arctic Ocean retreat season, i.e., in June and July, Qnet is near its peak. At the same time, freshwater fluxes from sea ice melt and from river discharge are also near their peak seasonal values [Markus et al., 2009; Rawlins et al., 2009; Steele and Flato, 2000; Steele et al., 2010; Whitefield et al., 2015], while surface wind speed is near its seasonal minimum (Figure 3b) [Martin et al., 2014]. On the other hand, by late August and early September Qnet has substantially declined in amplitude (although it is still downward), while surface winds have increased in magnitude. Freshwater fluxes are nil in the areas that have already opened, although near the retreating ice edge they are still substantial, but declining.
Thus a change in forcing occurs in early August that we term the “late summer transition” (LST). Some areas experience ice retreat before the LST, i.e., the Chukchi, Eastern Beaufort, and Laptev Seas, and (a bit later) the Western Beaufort and East Siberian Seas (Figure 9d). In these areas, the open ocean initially warms in a thin, highly stratified surface layer. After the LST, these areas experience enhanced winds and declining freshwater flux, so that the mixed layer deepens [Peralta‐Ferriz and Woodgate, 2015], redistributing the surface heat downward even as the ocean is still weakly gaining heat from the net downward Qnet. The result is a slow SST cooling, i.e., the period CSST as denoted in Figure 10 [e.g., Turner and Kraus, 1967, Figure 2], and a DOM that occurs before the DOX2. This continues until Qnet finally turns upward at the DOX2, at which point the atmospheric heat source is lost and in the presence of strong wind mixing, SSTs cool rapidly (i.e., COCEAN in Figure 10).
On the other hand, more northerly parts of our domain experience ice retreat only at or after the LST. Here mixed layers are climatologically a bit deeper [Peralta‐Ferriz and Woodgate, 2015], and conditions after the LST induce a more strongly mixed environment. In this situation, SST evolution follows the theoretical warming scenario described at the start of this subsection, i.e., the upper ocean warms in response to the (weak) downward Qnet flux up until the DOX2, when cooling commences. In this case, DOM ∼ DOX2.
In summary, the timing of the seasonal maximum SST (i.e., the DOM) depends on ice retreat (i.e., the DOR) because of the changing buoyancy and momentum fluxes that occur through the retreat season (i.e., the LST). Early retreat areas are able to build up a warm and thin surface layer in open water, which then cools as this heat is mixed downward in late summer. Late retreat areas only experience the more strongly mixed open water condition, and so weakly warm up until the date when atmospheric fluxes start to cool the surface. To better confirm these ideas, in situ observations would be useful but are unfortunately rare, given the severe seasonal bias of staffed expeditions and the ice‐deployed bias of most autonomous arctic observing platforms.
6. Summary and Discussion
We have found that early ice retreat leads to warmer SSTs in the “Pacific Sector” of the Arctic Ocean. This generally applies to the 1982–2014 long‐term mean (Figure 4), as well as to trends and interannual variance (Figure 5). Further, an ice retreat anomaly in any given year is strongly correlated with a SST anomaly in that year (Figure 6). However, these relationships between the Date of Retreat (i.e., the DOR) and the maximum seasonal SST (i.e., the SSTmax) are relatively weak in the Chukchi Sea, where ocean advection plays a strong role in SST. They are also weak in areas where the ice edge resides late in the season. The reason is that late in the summer, the net atmospheric downward heat flux Qnet is only weakly positive, so that a small change in ice retreat date hardly affects the amount of heating that the ocean experiences. A much stronger ocean response occurs when the DOR changes near the Date of maximum Qnet (i.e., the DOQ), which induces a strong DOR versus SSTmax relationship (Figure 6).
We also find that early DOR leads to an early Date of Maximum SST, or DOM (Figure 8). It is not immediately obvious why this should be, if we use only a simple idealized one‐dimensional air‐sea flux model. The reason this happens is because there is often a transition in the buoyancy and momentum forcing to the upper ocean that in the mean occurs in early August, a change that we term here the Late Summer Transition, or LST. When ice retreats before the LST, it experiences strong Qnet, strong freshwater fluxes, and weak wind forcing, which together promote the formation of shallow, warm mixed layers. In these early retreat areas, post‐LST conditions include weak Qnet, weak freshwater fluxes and stronger wind forcing, which together result in mixing down of the warm surface layer. This cools the SST up to a month before Qnet turns to a net cooling flux in September (i.e., the second Date of fluX crossing, or DOX2). On the other hand, in northern parts of our domain, ice retreats after the LST and so the open ocean never builds a shallow warm layer. In these areas, weak warming proceeds up until the DOX2 (Figure 12).
These ideas explain the very different ocean response to extreme sea ice loss in the years 2007 versus 2012 (Figure 7). In 2007, ice retreat was anomalously early before the LST, which allowed strong ocean surface warming on the continental shelves and into the southern basins. In 2012, on the other hand, ice retreat was quite unusual, with lingering regions of low ice concentration over a large area that only disappeared after a strong early August storm event [Simmonds and Rudeva, 2012; Zhang et al., 2013]. This created anomalous ice retreat at northern latitudes late in the season, i.e., near or after the LST, so that the SST response was weak.
It is perhaps worth noting that the date of minimum arctic ice extent, which typically happens in mid‐September every year, is not necessarily the date of maximum SST everywhere in the Arctic Ocean. In most southern areas the ocean surface is already cooling by this time, in response to a vertical redistribution of ocean heat forced by changing wind and freshwater fluxes. And in some northern areas, the ocean continues to warm a week or so after the ice minimum, owing to lateral redistribution of heat via ocean currents [Steele et al., 2010]. Of course, we are here discussing the long‐term mean situation: in any given year and in any particular location, fluxes and conditions can vary from the mean in substantial ways, leading to freezing conditions during summer and melting conditions during the “freeze‐up” period.
Thus we see that the relationship between sea ice retreat and the seasonal cycle of atmospheric surface heating is key to understanding how the Arctic Ocean surface seasonally warms. How do we expect this phenology to change in the future? In the near term, years like 2007 might become more common as ice thickness declines and ice retreats early within a few hundred kilometers of the coast. This will induce warming in these areas. On the other hand, we expect more northern latitudes of the Arctic Ocean will, in the near term, either remain ice‐bound throughout the summer, or retreat only late in the season, when the ocean warming response is weak. However, over a longer time horizon (to be determined e.g., by coupled modeling), more northerly areas may experience ice retreat early enough in the season to induce substantial warming.
Acknowledgments
This work was funded by NASA grant NNX13AE29G, ONR grant N00014‐12‐0224, and NSF grants OCE‐1233255 and ARC‐1203506. We thank the two anonymous reviewers for very valuable suggestions, and the following for discussions that helped clarify our thoughts: C. Gentemann, R. Lindsay, and A. Schweiger. Sea surface temperature (SST) data from OISST were downloaded at http://www.ncdc.noaa.gov/oisst on 6 April 2015, from OSTIA at ftp.nodc.noaa.gov on 14 March 2016, and from CMC at http://podaac.jpl.nasa.gov on 17 December 2015. Sea ice concentration (IC) data from NASA Team 1 were downloaded at https://nsidc.org/data/nsidc-0051 on 10 May 2015, and from OSTIA and CMC at the same sites as for sea surface temperature. Net atmospheric surface heat flux Qnet data were downloaded from http://disc.sci.gsfc.nasa.gov/mdisc on 14 June 2015.
Steele, M. , and Dickinson S. (2016), The phenology of Arctic Ocean surface warming, J. Geophys. Res. Oceans, 121, 6847–6861, doi:10.1002/2016JC012089.
References
- Arrigo, K. R. , van Dijken G., and Pabi S. (2008), Impact of a shrinking Arctic ice cover on marine primary production, Geophys. Res. Lett., 35, L19603, doi:10.1029/2008GL035028. [Google Scholar]
- Banzon, V. , Smith T. M., Chin T. M., Liu C., and Hankins W. (2016), A long term record of blended satellite and in situ sea surface temperature for climate monitoring, modeling and environmental studies, Earth Syst. Sci. Data, 8, 165–176. [Google Scholar]
- Brasnett, B. (2008), The impact of satellite retrievals in a global sea‐surface‐temperature analysis, Q. J. R. Meteorol. Soc., 134(636), 1745–1760, doi:10.1002/qj.319. [Google Scholar]
- Buehner, M. , Caya A., Carrieres T., and Pogson L. (2016), Assimilation of SSMIS and ASCAT data and the replacement of highly uncertain estimates in the Environment Canda Regional Ice Prediction System, Q. J. R. Meteorol. Soc., 142, 562 ‐ 573, doi:10.1002/qj.2408. [Google Scholar]
- Canada Meteorological Center (CMC) (2012), GHRSST Level 4 CMC 0.2deg Global Foundation Sea Surface Temperature Analysis (GDS version 2). Ver. 2.0. PO.DAAC, CA, USA, Meteorological Service of Canada, Dorval, Quebec, Canada, doi:10.5067/GHCMC-4FM02.
- Cavalieri, D. J. , and Parkinson C. L. (2012), Arctic sea ice variability and trends, 1979‐2010, Cryosphere, 6(4), 881–889, doi:10.5194/tc-6-881-2012. [Google Scholar]
- Cavalieri, D. J. , Parkinson C. L., Gloersen P., Comiso J. C., and Zwally H. J. (1999), Deriving long‐term time series of sea ice cover from satellite passive‐microwave multisensor data sets, J. Geophys. Res., 104(C7), 15803–15814, doi:10.1029/1999JC900081. [Google Scholar]
- Cavalieri, D. J. , Parkinson C. L., Gloersen P., and Zwally H. J. (1996), Sea Ice Concentrations from Nimbus‐7 SMMR and DMSP SSM/I‐SSMIS Passive Microwave Data, Version 1. NASA Natl. Snow and Ice Data Cent. Distrib. Active Arch. Cent., Boulder, Colo. [Available at http://dx.doi.org/10.5067/8GQ8LZQVL0VL.]
- Comiso, J. C. , and Hall D. K. (2014), Climate trends in the Arctic as observed from space, Wires Clim. Change, 5(3), 389–409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Comiso, J. C. , Parkinson C. L., Gersten R., and Stock L. (2008), Accelerated decline in the Arctic Sea ice cover, Geophys. Res. Lett., 35, L01703, doi:10.1029/2007GL031972. [Google Scholar]
- Cullather, R. I. , and Bosilovich M. G. (2012), The Energy Budget of the Polar Atmosphere in MERRA, J. Clim., 25(1), 5–24, doi:10.1175/2011JCLI4138.1. [Google Scholar]
- Donlon, C. J. , Martin M., Stark J., Roberts‐Jones J., Fiedler E., and Wimmer W. (2012), The Operational Sea Surface Temperature and Sea Ice Analysis (OSTIA) system, Remote Sens. Environ., 116, 140–158, doi:10.1016/j.rse.2010.10.017. [Google Scholar]
- Eastwood, S. , Jenssen M., Lavergne T., Sorensen A. M., and Tonboe R. (2015), Global sea ice concentration reprocessing product user manual, version 2.2, EUMETSAT Ocean and Sea Ice SAF, Prod. OSI‐409, pp. 1–29, Norwegian Meteorological Institute, Oslo, Norway. [Google Scholar]
- Frey, K. E. , Moore G. W. K., Cooper L. W., and Grebmeier J. M. (2015), Divergent patterns of recent sea ice cover across the Bering, Chukchi, and Beaufort seas of the Pacific Arctic Region, Prog. Oceanogr., 136, 32–49, doi:10.1016/j.pocean.2015.05.009. [Google Scholar]
- Gong, D. L. , and Pickart R. S. (2015), Summertime circulation in the eastern Chukchi Sea, Deep Sea Res. Part II, 118, 18–31, doi:10.1016/j.dsr2.2015.02.006. [Google Scholar]
- Grumbine, R. W. (1996), Automated passive microwave sea ice concentration analysis at NCEP, NOAA Tech. Note, 120, 13 pp., National Center for Environmental Prediction, National Weather Service, National Oceanic and Atmospheric Administration (NCEP/NWS/NOAA), Camp Springs, Md. [Google Scholar]
- Ivanova, N. , et al. (2015), Inter‐comparison and evaluation of sea ice algorithms: Towards further identification of challenges and optimal approach using passive microwave observations, Cryosphere, 9(5), 1797–1817, doi:10.5194/tc-9-1797-2015. [Google Scholar]
- Jackson, J. M. , Carmack E. C., McLaughlin F. A., Allen S. E., and Ingram R. G. (2010), Identification, characterization, and change of the near‐surface temperature maximum in the Canada Basin, 1993‐2008, J. Geophys. Res., 115, C05021, doi:10.1029/2009JC005265. [Google Scholar]
- Jakobsson, M. , et al. (2012), The International Bathymetric Chart of the Arctic Ocean (IBCAO) Version 3.0, Geophys. Res. Lett., 39, L12609, doi:10.1029/2012gl052219. [Google Scholar]
- Lindsay, R. (1998), Temporal variability of the energy balance of thick Arctic pack ice, J. Clim., 11(3), 313–333. [Google Scholar]
- Lindsay, R. , Wensnahan M., Schweiger A., and Zhang J. (2014), Evaluation of seven different atmospheric reanalysis products in the Arctic, J. Clim., 27(7), 2588–2606, doi:10.1175/JCLI-D-13-00014.1. [Google Scholar]
- Markus, T. , Stroeve J. C., and Miller J. (2009), Recent changes in Arctic sea ice melt onset, freezeup, and melt season length, J. Geophys. Res., 114, C12024, doi:10.1029/2009JC005436. [Google Scholar]
- Martin, T. , Steele M., and Zhang J. L. (2014), Seasonality and long‐term trend of Arctic Ocean surface stress in a model, J. Geophys. Res. Oceans, 119, 1723–1738, doi:10.1002/2013JC009425. [Google Scholar]
- Parkinson, C. L. , and Comiso J. C. (2013), On the 2012 record low Arctic sea ice cover: Combined impact of preconditioning and an August storm, Geophys. Res. Lett., 40, 1356–1361, doi:10.1002/grl.50349. [Google Scholar]
- Peralta‐Ferriz, C. , and Woodgate R. A. (2015), Seasonal and interannual variability of pan‐Arctic surface mixed layer properties from 1979 to 2012 from hydrographic data, and the dominance of stratification for multiyear mixed layer depth shoaling, Prog. Oceanogr., 134, 19–53, doi:10.1016/j.pocean.2014.12.005. [Google Scholar]
- Perovich, D. K. , Richter‐Menge J. A., Jones K. F., Light B., Elder B. C., Polashenski C., Laroche D., Markus T., and Lindsay R. (2011), Arctic sea‐ice melt in 2008 and the role of solar heating, Ann. Glaciol., 52(57), 355–359. [Google Scholar]
- Rawlins, M. A. , Steele M., Serreze M. C., Vorosmarty C. J., Ermold W., Lammers R. B., McDonald K. C., Pavelsky T. M., Shiklomanov A., and Zhang J. L. (2009), Tracing freshwater anomalies through the air‐land‐ocean system: A case study from the Mackenzie River Basin and the Beaufort Gyre, Atmos. Ocean, 47(1), 79–97, doi:10.3137/OC301.2009. [Google Scholar]
- Reynolds, R. W. , Rayner N. A., Smith T. M., Stokes D. C., and Wang W. Q. (2002), An improved in situ and satellite SST analysis for climate, J. Clim., 15(13), 1609–1625. [Google Scholar]
- Reynolds, R. W. , Smith T. M., Liu C., Chelton D. B., Casey K. S., and Schlax M. G. (2007), Daily high‐resolution‐blended analyses for sea surface temperature, J. Clim., 20(22), 5473–5496. [Google Scholar]
- Rienecker, M. M. , et al. (2011), MERRA: NASA's Modern‐Era Retrospective Analysis for Research and Applications, J. Clim., 24(14), 3624–3648, doi:10.1175/JCLI-D-11-00015.1. [Google Scholar]
- Roberts‐Jones, J. , Fiedler E. K., and Martin M. J. (2012), Daily, global, high‐resolution SST and sea ice reanalysis for 1985‐2007 using the OSTIA system, J. Clim., 25(18), 6215–6232, doi:10.1175/JCLI-D-11-00648.1. [Google Scholar]
- Serreze, M. C. , Barrett A. P., Stroeve J. C., Kindig D. N., and Holland M. M. (2009), The emergence of surface‐based Arctic amplification, Cryosphere, 3(1), 11–19. [Google Scholar]
- Simmonds, I. , and Rudeva I. (2012), The great Arctic cyclone of August 2012, Geophys. Res. Lett., 39, L23709, doi:10.1029/2012GL054259. [Google Scholar]
- Stammerjohn, S. , Massom R., Rind D., and Martinson D. (2012), Regions of rapid sea ice change: An inter‐hemispheric seasonal comparison, Geophys. Res. Lett., 39, L06501, doi:10.1029/2012GL050874. [Google Scholar]
- Steele, M. , and Ermold W. (2015), Loitering of the retreating sea ice edge in the Arctic Seas, J. Geophys. Res. Oceans, 120, 7699–7721, doi:10.1002/2015JC011182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steele, M. , and Flato G. (2000), Sea ice growth, melt, and modeling: A survey, in The Freshwater Budget of the Arctic Ocean, edited by E. L. Lewis, pp. 549–587, Kluwer, Dordrecht, Netherlands. [Google Scholar]
- Steele, M. , Ermold W., and Zhang J. L. (2008), Arctic Ocean surface warming trends over the past 100 years, Geophys. Res. Lett., 35, L02614, doi:10.1029/2007GL031651. [Google Scholar]
- Steele, M. , Zhang J., and Ermold W. (2010), Mechanisms of summertime upper Arctic Ocean warming and the effect on sea ice melt, J. Geophys. Res., 115, C11004, doi:10.1029/2009JC005849. [Google Scholar]
- Steele, M. , Ermold W., and Zhang J. L. (2011), Modeling the formation and fate of the near‐surface temperature maximum in the Canadian Basin of the Arctic Ocean, J. Geophys. Res., 116, C11015, doi:10.1029/2010JC006803. [Google Scholar]
- Steele, M. , Dickinson S., Zhang J. L., and W. Lindsay R. (2015), Seasonal ice loss in the Beaufort Sea: Toward synchrony and prediction, J. Geophys. Res. Oceans, 120, 1118–1132, doi:10.1002/2014JC010247. [Google Scholar]
- Stroeve, J. C. , Markus T., Boisvert L., Miller J., and Barrett A. (2014), Changes in Arctic melt season and implications for sea ice loss, Geophys. Res. Lett., 41, 1216–1225, doi:10.1002/2013GL058951. [Google Scholar]
- Stroh, J. N. , Panteleev G., Kirillov S., Makhotin M., and Shakhova N. (2015), Sea‐surface temperature and salinity product comparison against external in situ data in the Arctic Ocean, J. Geophys. Res. Oceans, 120, 7223–7236, doi:10.1002/2015JC011005. [Google Scholar]
- Strong, C. , and Rigor I. G. (2013), Arctic marginal ice zone trending wider in summer and narrower in winter, Geophys. Res. Lett., 40, 4864–4868, doi:10.1002/grl.50928. [Google Scholar]
- Timmermans, M.‐L. , and Proshutinsky A. (2015), The Arctic, j. Sea surface temperature [in “State of the Climate 2014”], Bull. Am. Meteorol. Soc., 96(7), S147–148. [Google Scholar]
- Turner, J. S. , and Kraus E. B. (1967), A one‐dimensional model of seasonal thermocline I. A laboratory experiment and its interpretation, Tellus, 19(1), 88 pp. [Google Scholar]
- Whitefield, J. , Winsor P., McClelland J., and Menemenlis D. (2015), A new river discharge and river temperature climatology data set for the pan‐Arctic region, Ocean Modell., 88, 1–15, doi:10.1016/j.ocemod.2014.12.012. [Google Scholar]
- Zhang, J. L. , Lindsay R., Schweiger A., and Steele M. (2013), The impact of an intense summer cyclone on 2012 Arctic sea ice retreat, Geophys. Res. Lett., 40, 720–726, doi:10.1002/grl.50190. [Google Scholar]


