Abstract
Moving beyond the widely used kinematic models for the deformation sources, we present a new dynamic model to describe the process of injecting magma into an existing magma reservoir. To validate this model, we derive an analytical solution and compare its results to those calculated using the Finite Element Method. A Newtonian fluid characterized by its viscosity, density, and overpressure (relative to the lithostatic value) flows through a vertical conduit, intruding into a reservoir embedded in an elastic domain, leading to an increase in reservoir pressure and time‐dependent surface deformation. We apply our injection model to Interferometric Synthetic Aperture Radar (InSAR) data from the ongoing unrest episode at Laguna del Maule (Chile) volcanic field that started in 2007. Using a grid search optimization, we minimize the misfit to the InSAR displacement data and vary the three parameters governing the analytical solution: the characteristic timescale τ P for magma propagation, the maximum injection pressure, and the inflection time when the acceleration switches from positive to negative. For a spheroid with semimajor axis a = 6200 m, semiminor axis c = 100 m, located at a depth of 4.5 km in a purely elastic half‐space, the best fit to the InSAR displacement data occurs for τ P=9.5 years and an injection pressure rising up to 11.5 MPa for 2 years. The volume flow rate increased to 1.2 m3/s for 2 years and then decreased to 0.7 m3/s in 2014. In 7.3 years, at least 187 × 106 m3 of magma was injected.
Keywords: magma injection, unrest, volcano, ground deformation, model, InSAR
Key Points
Our analytical and numerical model describes viscous magma propagation into a reservoir
Increasing conduit inlet pressure and volumetric flow rate accounts for the accelerating uplift
At least 187 million cubic meters of magma with viscosity 100 MPa s was injected between 2007 and 2014
1. Introduction
The injection of basaltic melt into a more evolved magma reservoir is a mechanism that has been proposed to explain an array of geochemical, petrological, and geophysical phenomena, including mafic inclusions, magma mixing, magma residence times, and triggering of explosive eruptions [e.g., Snyder, 2000; Annen and Sparks, 2002; Sparks and Marshall, 1986]. This process plays an important role in the long‐term evolution of silicic magma chambers by repeatedly feeding mantle‐derived basalts from the lower crust into reservoirs in the upper crust [e.g., Wiebe, 1993, 1996; Annen and Sparks, 2002; Annen et al., 2006]. While the growth and incremental assembly of these large silicic magma bodies occur on timescales of the order of 105 to 106 years [Bachmann and Bergantz, 2008; Jellinek and DePaolo, 2003], each mafic injection could be emplaced over a much shorter timescale of weeks to decades [e.g., Snyder, 2000; Druitt et al., 2012].
The arrival of new magma into a reservoir is also a common explanation for inflation observed at volcanic systems measured by geodesy [e.g., Newman et al., 2012; Parks et al., 2012; Chang et al., 2010; Dzurisin et al., 2009]. The addition of new material to the magma chamber is accommodated by deformation of the surrounding crust. In most of these examples, the characteristics of the magma reservoir at depth have been inferred from geodetic data by assuming kinematic, rather than dynamic, models. Although these kinematic models help to constrain the geometry and volume change of an idealized source embedded in a half‐space with uniform elastic properties, the underlying assumptions are too simple in many cases [e.g., Mogi, 1958; Fialko et al., 2001; Battaglia et al., 2003; Dzurisin, 2007; Masterlark, 2007]. Using the Finite Element Method (FEM), several modeling studies have demonstrated the importance of considering additional complexities, including (i) heterogeneities in the rheological properties of the crust [e.g., Trasatti et al., 2003; Currenti et al., 2007; Long and Grosfils, 2009; Gregg et al., 2012, 2013; Masterlark et al., 2012], (ii) inelastic deformation [e.g., Del Negro et al., 2009; Currenti et al., 2010; Hickey et al., 2013], and (iii) a gravitationally loaded crust [e.g., Grosfils, 2007; Currenti et al., 2007; Gerbault et al., 2012; Got et al., 2013; Gregg et al., 2015]. Other models have focused on the thermal aspect of intrusions and their effect on melt generation over timescales of thousands of years [e.g., Wiebe, 1993, 1996; Annen and Sparks, 2002; Annen et al., 2006; Annen, 2009]. All of these models neglect the dynamics of the magmatic fluid during the intrusion to the magma reservoir. Instead, they apply an instantaneous pressure or volume change to an empty reservoir.
Several studies have introduced physics‐based modeling to account for dynamic processes. A model in which a deep, constant‐pressure magma source is hydraulically connected to a shallow reservoir by a magma‐filled conduit has been proposed and applied successfully to interpret the observations of time‐dependent deformation at several active volcanoes [e.g., Mériaux and Jaupart, 1995; Lu et al., 2003; Lengliné et al., 2008; Mastin et al., 2008; Lu et al., 2010; Pinel et al., 2010]. Magma flowing from a deep to a shallow reservoir is also considered in the two‐magma‐chamber model of Reverso et al. [2014] to explain posteruptive inflation at Grímsvötn volcano. The models of Anderson and Segall [2011] include additional processes occurring in the magma chamber and volcanic conduit to explain geochemical and geophysical data sets measured during effusive silicic volcanic eruptions. The model of Macedonio et al. [2014], based on the dynamic model for laccolith formation of Bunger and Cruden [2011a, 2011b] and Michaut [2011], considers the horizontal propagation of a sill to account for a shallow intrusion into sedimentary layers.
In this paper, we focus on modeling the geodetic signature produced by viscous magma flowing into an existing, fluid‐filled reservoir from a deeper source. In our conceptual model, the fluid dynamics of the magma drives the time‐dependent displacement observed at the surface. This model leads to uplift rates that increase with time and can thus explain the acceleration observed in geodetic time series of relative position at several volcanic systems.
One such system is the Laguna del Maule (LdM) volcanic field in the Southern Volcanic Zone of Chile that has been experiencing an unrest episode characterized by high uplift rates (up to 200 mm/yr) starting in 2007 [Feigl et al., 2014; Le Mével et al., 2015]. While its eruptive history spans 1.5 Myr, the last 20 ka show a spatial concentration of rhyolitic material unique in the Southern Andes, all of which erupted in a relatively short period of time [Hildreth et al., 2010]. The combination of magnetotelluric, gravity, geological, and geochemical data suggests that the volcanic field is underlain by a relatively large sill‐like magma reservoir that includes melt of rhyolitic composition [Singer et al., 2014]. Since the deformation episode has been recorded by Interferometric Synthetic Aperture Radar (InSAR) and the Global Positioning System (GPS), LdM constitutes an excellent test case for models of magma injection into a long‐lived silicic magma reservoir. We test the hypothesis that the increase in uplift rate is caused by the injection of material into the existing reservoir. To do so, we develop a dynamic model and apply it to geodetic data.
First, we introduce the conceptual model, the assumptions made in the analytical and numerical approaches, as well as the choice of parameters (section 2). Then, we derive the analytical solutions that govern the magma flow in the chamber for various pressure histories (section 3). These solutions are validated against the numerical models in section 4. Finally, we apply the model to the ongoing volcanic unrest of LdM and present the results of the analytical and numerical models (section 5).
2. Conceptual Model, Assumptions, and Parameters
Figure 1a shows the widely used model of a pressurized cavity, known as the “Mogi model” (after the analytical formulation of Mogi [1958]). Our conceptual model differs from the Mogi model because it accounts for the dynamics of a fluid flowing into an existing, fluid‐filled reservoir. Magma is injected at the base of a conduit and flows into a magma chamber, exerting stress on the surrounding crustal rocks (Figure 1b). Figure 1c represents the FEM configuration used to model the case study of LdM. Below, we describe in detail the four different entities in our model and discuss the relevant parameters (Table 1).
Figure 1.
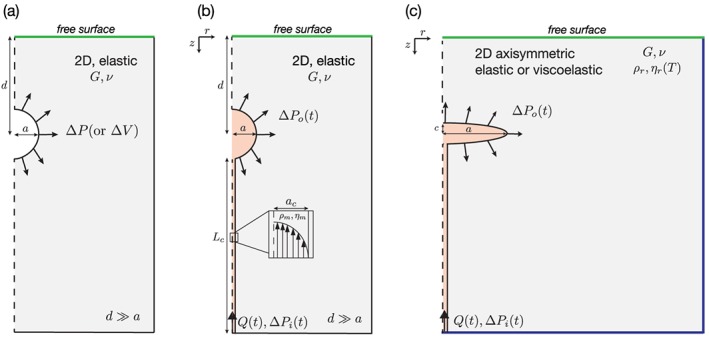
Sketches of conceptual models, including (a) the traditional pressurized spherical cavity model (e.g., Mogi model), (b) the model of laminar flow into a magma‐filled reservoir (analytic solution), and (c) FEM configuration for the model of magma propagation into an ellipsoidal reservoir embedded in a viscoelastic domain. Parameter names and units are listed in Table 1. In Figures 1b and 1c, ΔP i(t) is the time‐dependent magma injection pressure imposed as a boundary condition at the base of the conduit. Dashed line is the symmetry axis in the 2‐D axisymmetric configuration. Green lines denote the free surface at the interface between air and rock. Blue lines in Figure 1c show the fixed boundary conditions in the FEM configuration.
Table 1.
List of Parameters Used in This Study
| Parameter | Definition | Unit |
|---|---|---|
| Geometry | ||
| a | Radius of spherical or semimajor axis of ellipsoidal magma reservoir | m |
| c | Semiminor axis of ellipsoidal magma reservoir | m |
| d | Depth of magma reservoir center | m |
| a c | Radius of conduit | m |
| L c | Length of conduit | m |
| Rheological Properties | ||
| η m | Viscosity of magma | Pa s |
| η r | Viscosity of crustal rocks | Pa s |
| ρ m | Density of magma | kg/m3 |
| ρ r | Density of crustal rocks | kg/m3 |
| G | Shear (or rigidity) modulus | Pa |
| ν | Poisson's ratio | ‐ |
| Parameters for FEM Viscoelastic Models | ||
| k | Thermal conductivity | W/(m.K) |
| C p | Specific heat capacity | J/(kg.K) |
| A D | Dorn parameter | Pa s |
| E A | Activation energy | J/mol |
| R t | Boltzmann constant | J/(mol.K) |
| T 0 | Surface temperature | K |
| T w | Magma chamber wall temperature | K |
| τ M | Characteristic Maxwell time of crustal viscoelastic relaxation | s |
| Analytical Model Parameters | ||
| ΔP i(t) | Injection pressure at inlet | Pa |
| τ P | Characteristic time of the magma propagation | s |
| t 0 | Onset time of uplift episode | s |
| t ∗ | Time when uplift rates start to decrease | s |
| β m | Compressibility of magma | Pa−1 |
| β w | Compressibility of wall rocks | Pa−1 |
| Derived Quantities | ||
| ΔP o(t) | Reservoir pressure at the conduit outlet | Pa |
| Q(t) | Volumetric flow rate | m3/s |
| q | Volumetric flux | m3/(m2.s) or m/s |
| v | Flow velocity | m/s |
| u z(t) | Vertical displacement (uplift) rate | m/s |
2.1. The Magma
We consider a reservoir and a conduit filled with magma. Our model describes it as a single‐phase incompressible Newtonian fluid with dynamic viscosity η m and density ρ m. Magma being a mixture of gas, crystals and melt, the properties defined here represent average, bulk properties of these three phases. Since magma at large depth is relatively free of crystals and gas bubbles, it can be considered as a Newtonian viscous fluid such that shear rate is proportional to shear stress [e.g., Rubin, 1995]. The magma viscosity depends on the amount of dissolved volatiles (e.g., water), temperature, and composition. We consider a constant, uniform value for bulk magma viscosity between 106 Pa s (mafic end‐member) and 1012 Pa s (felsic end‐member).
First, we consider the magma as incompressible and then we consider the effect of the magma compressibility on the deformation field. The magma compressibility depends on the depth of the reservoir, its gas content, crystal content, and temperature [e.g., Johnson, 1992; Huppert and Woods, 2002]. We explore values for magma compressibility ranging from β m∼10−11 Pa−1, as inferred for deep crystal‐poor magmas, to β m∼10−9−10−8 Pa−1 for shallow (saturated) volatile‐rich magmas [Huppert and Woods, 2002]. To account fully for a compressible magma would also require considering temporal variations in density, a calculation that would extend beyond the scope of this paper.
2.2. The Conduit
Studies on ascending melt suggest the existence of long‐lived conduits that channel large volumes of magma through the continental crust [e.g., Pollard, 1976; Spera, 1980; Lister and Kerr, 1991; Brown, 2007]. As sketched in Figure 1b, we assume that the conduit or pipe feeding the chamber has a cylindrical geometry with a constant radius a c and length L c. We choose the length L c to be 25.4 km such that the conduit reaches the base of the continental crust. Since few observations exist to constrain the size of such conduits, we consider possible values for the conduit radius ranging from a c=10 m to a c=100 m. At the inlet (bottom) of the conduit, we impose a time‐varying pressure condition to simulate mass recharge from below (section 3).
2.3. The Magma Reservoir
As described by Bachmann and Bergantz [2008], a magma chamber is a region in the crust where eruptible magma accumulates (with a crystal fraction less than 50%). As suggested by Hildreth [1981], one paradigm describes the reservoir as a multiphase crystal “mush” with variable density in several layers at crustal depths. In our simplified model, we consider the reservoir to be filled with a magmatic fluid of constant average bulk density ρ m and viscosity η m. We neglect the time dependence of these properties due to magmatic processes such as differentiation or partial melting taking place in the chamber over longer timescales. We consider a spherical reservoir for simplicity in the analytical derivations and then consider an ellipsoidal configuration. Indeed, sill‐like magma reservoirs are well approximated by ellipsoids [e.g., Grosfils, 2007; Amoruso and Crescentini, 2009], especially for silicic systems in an extensional regime [e.g., Hughes and Mahood, 2011; Jellinek and DePaolo, 2003] as is the case for the LdM volcanic field.
2.4. The Wall Rocks and the Surface
The crust surrounding the magmatic plumbing is first modeled as a purely elastic half‐space with rigidity (shear modulus) G, Poisson's ratio ν, and density ρ r. Those parameters depend on temperature, pressure, rock type, and the presence of fluids in the crust. For our suite of models, we first consider published ranges of rheological properties for a continental crust. We then consider a linear Maxwell viscoelastic rheology for the crust. We choose to implement a thermomechanical model [e.g., Del Negro et al., 2009; Gregg et al., 2012] to account for the low‐viscosity values expected around a large, long‐lived magma reservoir. The method to obtain the temperature and viscosity fields is described in section 4.
The surface at the interface between air and rock is free to deform. Many studies demonstrate that volcano topography can affect the surface deformation pattern [e.g., Cayol and Cornet, 1998; Williams and Wadge, 1998; Trasatti et al., 2003; Hurwitz et al., 2009] for axisymmetrical stratovolcanoes with significant slope (e.g., Mount Etna). At LdM, the topographic relief is of the order of ∼1 km, considerably less than the ∼5 km depth of the magma chamber inferred from kinematic models of geodetic data [e.g., Le Mével et al., 2015]. Most importantly, the topography is distributed over a large area with no single symmetric, high‐relief volcanic edifice and the major part of the deformation signal lies in a lake basin. Consequently, we assume that the topographic relief of the area has a negligible effect on the magma chamber and the resulting deformation at the surface over geodetic timescales.
To summarize, this conceptual model allows us to investigate the sensitivity of the deformation field to several parameters, including: the magma viscosity and compressibility, the conduit radius, the reservoir dimensions, the inlet magma flux, as well as the rigidity and viscosity of the surrounding crustal rocks.
3. Analytical Formulation for Magma Propagation Into a Reservoir
3.1. Laminar Pipe Flow
Assuming values of magma density ρ m<2700 kg/m3, viscosity η m>106 Pa s, conduit radius a c>10 m, conduit length L c<25.5 km, and volumetric flow rate Q < 10 m3/s, we find the maximum Reynolds number to be , three orders of magnitude smaller than the critical value of R e crit∼2000 that bounds laminar flow [e.g., Turcotte and Schubert, 2014]. Thus, the magma from the lower crust flows in the laminar regime: the viscous forces dominate and we neglect the inertial forces.
The laminar flow develops with velocity v following the difference in pressure P between the base of the conduit (inlet) and the entrance of the reservoir (conduit outlet). The equation governing the conservation of momentum is
| (1) |
where g is the gravitational acceleration and z the vertical coordinate, reckoned positive upward. The first term represents the pressure gradient driving the flow, the second term is the weight of the magma, and the third term is the viscous resistance to flow [e.g., Jaupart and Tait, 1990; Anderson and Segall, 2011].
Integrating equation (1) over the conduit's circular cross‐sectional area A yields the Hagen‐Poiseuille law for the volumetric flow rate:
| (2) |
The pressure P i at the conduit inlet is the sum of the lithostatic pressure at that depth and a time‐dependent overpressure term:
| (3) |
Similarly, the pressure P o at the conduit outlet (i.e., the entrance to the reservoir) is
| (4) |
Assuming a constant‐pressure gradient, we rewrite equation (2) as follows:
| (5) |
The relationship between a pressure change ΔP and volume change ΔV of a cavity of initial volume V 0 at depth, assuming that all the magma remains in the chamber, depends mainly on two quantities: the compressibility β m of the magma, and the compressibility β w of the wall rock (inversely proportional to its shear modulus G) [e.g., Blake, 1981; Anderson and Segall, 2011]:
| (6) |
We first assume a spherical cavity with radius a much smaller than its depth d, filled with incompressible magma (β m=0) and embedded in a half‐space with uniform elastic properties G and ν. A pressure increment ΔP on the boundary of the cavity will increase its volume ΔV as
| (7) |
where β w≃3/(4G) [Dzurisin, 2007]. From equations (5) and (7) and noting that Q(t) = d/dt[ΔV(t)], we find a differential equation for the evolution of the reservoir pressure following the laminar flow into a spherical chamber filled with incompressible magma:
| (8) |
3.2. Case 1: Constant Inlet Pressure
First, we consider the case of a constant injection pressure at the inlet of the conduit such that ΔP i(t) = ΔP i. We set the initial condition at the outlet ΔP o(t = 0) = 0. Solving equation (8) for ΔP o(t) consists in solving a first‐order linear differential equation with constant coefficients [e.g., Lengliné et al., 2008; Carrier et al., 2015]. Its solution is
| (9) |
where
| (10) |
and the characteristic timescale is
| (11) |
For the particular case of a spherical magma chamber and an incompressible magma,
| (12) |
Therefore, applying a constant pressure at the base of the conduit increases the reservoir pressure ΔP o (at exponentially decreasing rates) from its initial value to the value of the applied inlet pressure ΔP i (Figure 2).
Figure 2.
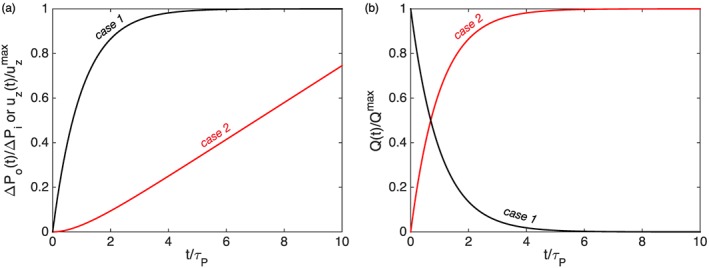
Temporal evolution of (a) the pressure ΔP o(t) at the outlet of the conduit and the maximum vertical surface displacement u z(t), and (b) the volumetric flow rate Q(t) following the application of a constant inlet source pressure ΔP i (black line, case 1), and a linearly increasing inlet source pressure ΔP i(t) (red line, case 2). These dimensionless plots show time t scaled by the characteristic timescale τ P. The reservoir overpressure ΔP o(t) is scaled by the maximum inlet pressure ΔP i. The uplift u z(t) and volumetric flow rate Q(t) are scaled by their respective maximum values, and Q (max).
The resulting temporal evolution of the surface displacement corresponds to the time‐dependent Mogi solution [e.g., Dzurisin, 2007; Segall, 2010] for an observation point located at horizontal distance r from a spherical source at depth d:
| (13) |
At the observation point located at r = 0, directly above the top of the magma reservoir, the maximum upward vertical displacement is
| (14) |
The evolution of uplift with time mirrors the evolution of the reservoir pressure: the rate of uplift decreases exponentially with time (Figure 2) following the Poiseuille timescale τ P of magma propagation in the conduit. In the case of a constant injection pressure ΔP i at the inlet, the volumetric flow rate Q(t) is proportional to −ΔP o(t) and decreases with time, as shown in equation (5) and Figure 2.
3.3. Case 2: Linearly Increasing Inlet Pressure
Next, we set the injection pressure at the inlet ΔP i to be a linearly increasing function of time:
| (15) |
Equation (8) becomes a first‐order linear differential equation with variable coefficients. Its solution is:
| (16) |
where
| (17) |
and Δρ is the density contrast between the crustal rocks and magma defined as ρ r−ρ m. Figure 2 shows the resulting temporal evolution of the reservoir pressure and volumetric flow rate for a source overpressure increasing at a rate of s = 5 MPa/yr. Contrary to case 1, the reservoir pressure or uplift rate increases exponentially with time following a linear increase in inlet pressure (Figure 2a). The volumetric flow rate Q(t) also increases with time but with decreasing rate (Figure 2b).
3.4. Acceleration of Surface Displacement
To evaluate the time dependence of the surface uplift for each case, we calculate the acceleration (i.e., the second derivative with respect to time) of the reservoir overpressure ΔP o(t) (equations (9) and (16)). In this study, we assume that the magma and crust are initially in equilibrium at all depths and thus set the initial condition ρ r=ρ m. The additional buoyancy force created by a density contrast between the new, incoming magma and the surrounding rocks will thus increase the transient pressure at the inlet ΔP i.
For case 1, the acceleration is
| (18) |
where P 1=ΔP i. By definition, we have exp(−t/τ P) > 0 and τ P>0. Thus, the acceleration is always negative.
For case 2, the acceleration is
| (19) |
In the case of neutral buoyancy (ρ r=ρ m), P 2=s τ P and the acceleration is always positive. If ρ r>ρ m, then P 2 is positive only if s τ P−Δρ g L c>0. To characterize the flow, we introduce the dimensionless number F:
| (20) |
representing the ratio of the buoyancy force to the source rate of overpressure multiplied by the timescale of viscous propagation. Henceforth, we only consider the case where 0≤F < 1, leading to a positive acceleration of the reservoir pressure and surface displacement (Figure 2).
3.5. Case 3: Ramping Inlet Pressure
In order to reproduce the transition from acceleration to deceleration of the uplift observed at LdM, we introduce a third case where the inlet pressure first increases to ΔP i and then remains constant (Figure 3). From t = t 0 until t = t ∗, the solution derived in section 3.3 (equation (16)) applies. For t > t ∗, case 1 applies but we solve equation (8) with a new initial condition corresponding to the maximum pressure value ΔP i, which is reached at t = t ∗. Evaluating equation (16) at the transition time t = t ∗, we have
| (21) |
Figure 3.
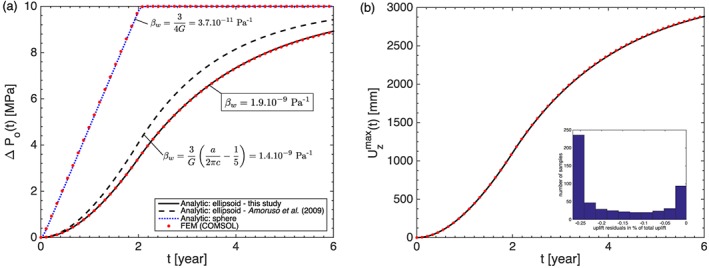
Validation of the analytical solution derived for case 3, as described by equation (22). (a) Evolution of the reservoir pressure following a ramping inlet pressure history, for a spheroidal reservoir with semimajor axes a = b = 6200 m, semiminor axis c = 100 m, and located at depth d = 4.5 km (solid black line) and for a sphere of equivalent volume (dotted blue line). The compressibility of the magma chamber walls β w was chosen to fit the numerical solution as calculated using COMSOL for this geometric configuration (red dots). Agreement is within 0.01 MPa, that is about 0.15% of the total imposed pressure of 5 MPa/yr during 2 years. The analytical solution derived by Amoruso and Crescentini [2009] for a deep oblate spheroid is shown for comparison (dashed black line). (b) Resulting surface vertical displacement at a site located 1 km east of the maximum uplift, as calculated using the horizontal circular crack approximation of Fialko et al. [2001]. (inset) Histogram of the residuals, indicating that the analytical solution agrees with the numerical solution within 8 mm or 0.25% of the maximum uplift signal.
The solution for the reservoir pressure following a ramping inlet pressure is then
| (22) |
3.6. Ellipsoidal Reservoir Geometry
Amoruso and Crescentini [2009] show that for an oblate spheroidal reservoir with semimajor axis a and semiminor axis c, equation (7) becomes
| (23) |
Assuming Poisson's ratio ν = 1/4,
| (24) |
and the wall rock compressibility is then
| (25) |
The previously derived solutions for the reservoir pressure (equation (22)) remain the same but the characteristic time constant τ P becomes
| (26) |
For a horizontally elongated spheroid with small aspect ratio (c/a ≪ 1), the wall rock compressibility B w is much larger than that for a spherical reservoir. Therefore, the characteristic timescale of magma propagation for an oblate spheroid τ P is larger than that for a sphere of equivalent volume V 0 (Figure 3). However, the relationship derived by Amoruso and Crescentini [2009] does not apply to such an elongated reservoir if its depth is shallow [e.g., Anderson and Segall, 2011]. Consequently, we will use a numerical model to estimate the compressibility of the wall rock β w for the geometry of our case study at LdM.
4. Validation Using Numerical Model
In this section, we validate the analytical solution of section 3.5 (equation (22)) using a numerical model of magma flow in a fluid‐filled cavity. The numerical approach also allows us to consider a viscoelastic rheology for the crustal domain.
4.1. Numerical Model Configuration
The governing Navier‐Stokes equations for fluid flow and the elastostatic equations are solved using the time‐dependent solver (PARDISO) of the FEM COMSOL Multiphysics sofware. The two‐way coupling between the flow in the fluid and the deformation in the solid at their interface is implemented using the Fluid‐Structure Interaction (FSI) module of COMSOL v5.1 [e.g., Gregg et al., 2015]. The model configuration consists of a two‐dimensional (2‐D) axisymmetric domain that is 80 km wide and 30 km deep. This large configuration reduces edge effects. It also honors the geodetic observations showing that the rate of deformation is negligible at distances beyond ∼20 km from the center of the lake at LdM. The mesh includes about 30,000 triangular elements and is refined at important boundaries: around the reservoir and in the upper crust forming the roof of the magma chamber, as well as in the boundary layers along the conduit walls where the velocity gradients are high. The geometry and boundary conditions are shown in Figure 1c.
To account for the viscoelastic behavior of the crust, the model applies a generalized Maxwell rheology with one branch (corresponding to a Standard Linear Solid). Following an instantaneous elastic deformation, the stresses relax in the viscoelastic crust. The COMSOL configuration to implement crustal viscoelasticity has been validated against analytical solutions by Hickey and Gottsmann [2014] and Del Negro et al. [2009].
To account for the temperature dependence of the viscosity in the crust surrounding a hot magma reservoir, we also consider a heterogeneous distribution of viscosity η r(r,z). To do so, we first obtain the steady‐state temperature distribution by solving the diffusive heat conduction equation with a magma chamber wall temperature T w=850°C, a surface temperature T 0=0°C, a geothermal gradient of −30°C/km, specific heat capacity C p=1.25 × 103 J/(kg K), and thermal conductivity k = 3 W/(m K). The temperature distribution is then converted to a viscosity distribution using the Arhenius formula, as in Gregg et al. [2012], and assuming the Dorn parameter A D=109 Pa s, an activation energy E A=1.2 × 105 J/mol, and the Boltzmann constant R t=8.3114 J/(mol.K).
4.2. Validation of Time‐Dependent Reservoir Pressure and Surface Displacement
First, we validate equation (22) in the case of a spherical reservoir using a small spherical reservoir of radius a = 1500 m located at a depth of d = 4.5 km, thus satisfying the condition a ≪ d necessary to use the approximation leading to equation (7). The agreement between the analytical and numerical solution for ΔP o is within 0.05 MPa (Figure 3a).
Since the magma chamber wall rock compressibility (β w) depends mainly on the geometry [e.g., Anderson and Segall, 2011], we estimate the correct value of β w for our best spheroid configuration (a = 6200 m, c = 100 m, d = 4.5 km) by minimizing the fit between the analytic solution and the one obtained using the numerical model (section 4.1) consisting of a ramping pressure applied at the base of a conduit connected to a spheroid chamber at depth (Figure 3). Using this estimated value of β w=1.86 × 10−9 Pa−1, the agreement between analytical and numerical solution for the reservoir pressure is better than 0.01 MPa or 0.15% of the total signal (Figure 3a). Consequently, our configuration requires a higher compressibility value β w than the solution derived by Amoruso and Crescentini [2009] for a deep spheroid reservoir. The surface uplift corresponding to our numerical solution is calculated using the expressions derived by Fialko et al.[2001] for a pressurized horizontal circular crack in an elastic half‐space and implemented in Matlab using functions from the dMODELS software package [Battaglia et al., 2013]. The analytical solution agrees with the numerical solution within 8 mm or 0.25% of the total signal (Figure 3b), which is less than the typical uncertainty of our InSAR measurements. The histogram of residuals reveals a nonzero mean, indicating a slight underestimation of the vertical displacement by using the “point crack” approximation [Fialko et al., 2001] for a very elongated ellipsoid of aspect ratio c/a = 0.016.
5. Application to the Volcanic Unrest Episode at LdM
5.1. InSAR Data Set and Modeling Procedure
The InSAR data set consists of 37 interferograms from four satellite missions (ENVISAT, ALOS, TerraSAR‐X/TanDEM‐X, and COSMO‐Skymed) and one airborne mission (UAVSAR) spanning 2003 to 2014, as analyzed by Le Mével et al. [2015]. More details on the data analysis can be found in the supporting information of Le Mével et al. [2015]. The onset time t 0 of the uplift episode could be as early as March 2004 or as late as February 2007, because we could find no well‐correlated interferometric pair spanning this time interval. In the following analysis, we assume that the deformation began in February 2007, at the first SAR epoch of the first InSAR pair that shows deformation. Thus, the estimated value of the total accumulated displacement is a lower bound. The InSAR time series of vertical displacement has been calculated for the pixel corresponding to the location of a continuous GPS station ∼1 km west of the maximum inflation (Figure 4, asterisk), as described by Le Mével et al. [2015].
Figure 4.
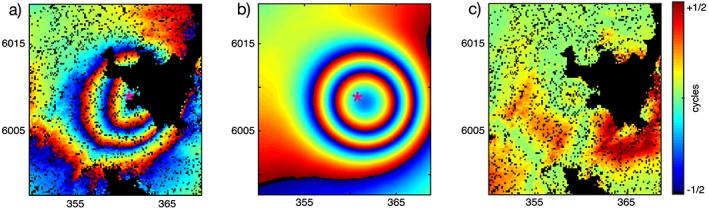
ALOS interferogram for LdM, spanning the 368 day time interval from 17 February 2009 to 20 February 2010. One cycle of phase denotes 118.1 mm of range change. The ALOS orbit numbers are 16338 and 21706. The incidence angle is 41° from vertical and the unit vector from target to sensor is [E,N,U] = [−0.6242,−0.1851,0.7590]. Coordinates are easting and northing in kilometers using the Universal Transverse Mercator projection (zone 19). (a) Observed phase values; (b) modeled phase values calculated from the numerical model of magma injection into a spheroid chamber with semimajor axis a = 6200 m, semiminor axis c = 100 m, located at a depth d = 4.5 km; (c) angular deviations in phase for the best estimate.
The objective of this study is to explain the particular temporal signature observed during the volcanic unrest at LdM using a single mechanism. This physical model should reproduce both the spatial characteristics of the observed deformation pattern (e.g., Figure 4a) and the temporal evolution of the vertical displacement (Figure 5). At LdM, the presence of melt was detected at about 4 to 6 km below the surface, based on magnetotelluric and gravimetric data [Singer et al., 2014]. We choose a 1 year interferogram (from ALOS) to adjust the parameters influencing the spatial features of the deformation pattern, such as the number of fringes and their spacing (Figure 4). The source is modeled as a spheroid and its depth, semimajor, and semiminor axes are adjusted in a forward modeling approach, based on the phase residuals and their circular mean deviation, as calculated by GiPhT [Feigl and Thurber, 2009]. The overall misfit for this interferogram is 0.1209 cycles (about 14 mm) for an axially symmetric spheroid with semimajor axis a = 6200 m, semiminor axis c = 100 m, located at a depth d = 4.5 km. Most of the spatial pattern is retrieved by the 2‐D axisymmetric configuration (Figure 4). The small residuals to the south could be reduced by considering a 3‐D configuration to reproduce the NE‐SW elongated fringe pattern; however, such a 3‐D model is more computationally expensive and is not required to test the hypothesis of magma injection proposed in this study.
Figure 5.
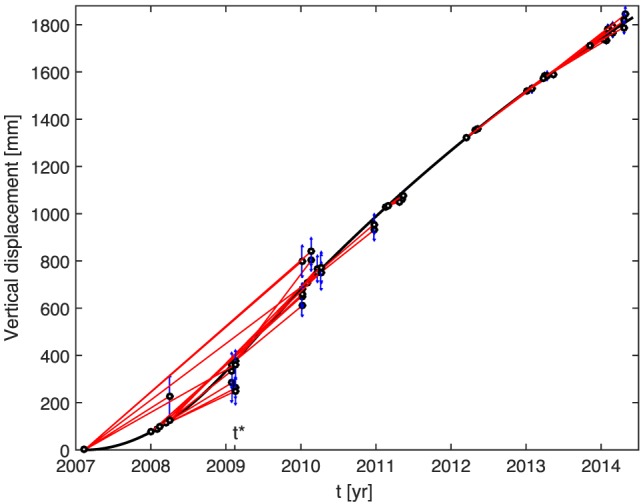
Modeled time series (black curve) of cumulative vertical displacement for a point located at GPS station MAU2 (magenta asterisk on Figure 4) from 2007 to 2014, as derived from InSAR data and assuming a model of magma injection starting in 2007 in an elastic domain. InSAR displacement data set same as presented in Le Mével et al. [2015]. Each red line represents an individual InSAR pair connecting two SAR epochs (black circles). In each InSAR pair, the value of displacement is plotted to fall on the model curve and the value of relative displacement at the second epoch is plotted with its 68% confidence interval (vertical blue bars). The corresponding pressure and volumetric flow rate history are shown in Figure 10.
In addition, the model must also reproduce the essential aspects of the time series of uplift at LdM (Figure 5). At first, the uplift accelerates (i.e., the rate of uplift increases) until t = t ∗. This epoch was previously estimated to be of the order of 3 years after the beginning of the unrest [Le Mével et al., 2015]. Then, for t > t ∗, the vertical displacement rate decreases slowly. To simulate this behavior, we apply the pressure history derived in case 3 and validated in section 4 of an increasing inlet pressure and volumetric flux for t 0≤t≤t ∗, followed by a constant pressure and decreasing volumetric flux for t > t ∗ (Figure 3). We vary each of the three model parameters in equation (22): τ P, t ∗, and ΔP i, in a three‐dimensional grid search over the model space (Figure 6). For each set of parameter values, we calculate the misfit to the InSAR time series of displacement for the chosen pixel as a reduced χ 2 statistic:
| (27) |
where n = 37 is the number of interferometric pairs, u obs is the InSAR‐derived relative vertical displacement with uncertainty σ obs, and u mod is the modeled displacement calculated from the analytical solution for each time interval.
Figure 6.
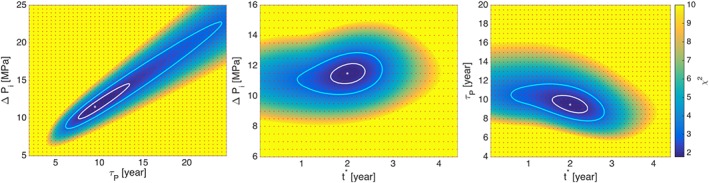
Misfit to the InSAR displacement data for each pair of variables in equation (22), as evaluated by the reduced χ 2 statistic. Blue and white contour lines of equal χ 2 correspond to the regions of 95% and 68% confidence, respectively, as determined by an F test. White star indicates the global minimal χ 2 value found in the 3‐D grid search. Each red dot corresponds to one run of the forward model and evaluation of the misfit.
5.2. Results Using the Analytical Model of Magma Injection
Exploring the model space allows us to narrow the range of possible parameter values. Figure 6 shows the projection of the misfit as a function of each pair of the three parameters varied in the grid search. Performing a statistical F test on the resulting variance allows us to delimit the zone of equally good misfit with 68% (white line) and 95% (blue line) confidence (Figure 6). Finally, the lowest value of χ 2 (Figure 6, white asterisk), χ 2=1.78, is obtained for a characteristic timescale τ P of 9.5 years, a maximum injection pressure ΔP i of 11.5 MPa, and inflection occurring t ∗−t 0=2 years after the start of the injection. These values constitute our preferred estimate of the model parameters for LdM under case 3 in an elastic domain. The corresponding time series of modeled uplift is shown on Figure 5 (black line), along with the displacements derived from InSAR.
Next, we examine the sensitivity of the characteristic Poiseuille timescale τ P to four parameters, including the following: the magma viscosity η m, the crustal shear modulus G, the conduit radius a c, and the magma compressibility β m. For each pair of parameters, we identify a range of plausible values to reach the best τ P. Figures 7a–7c show the trade‐offs between the parameters η m, G, and ΔP i. On the other hand, the compressibility β m depends only very weakly on the model parameters, as shown in Figures 7d–7f. Since this value is 1 or 2 orders of magnitude smaller than the chamber compressibility β w, it has the least influence in equation (11) for τ P.
Figure 7.
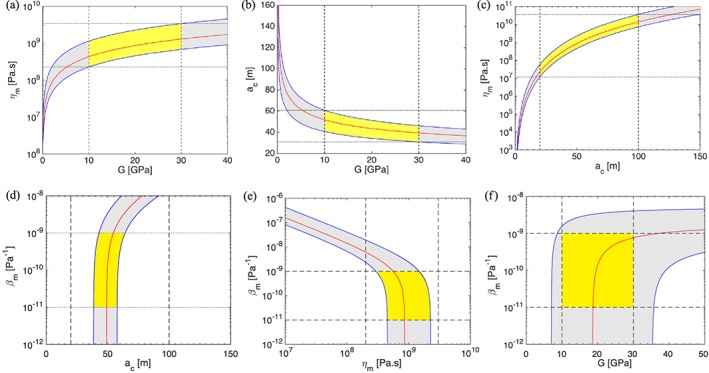
Sensitivity of characteristic timescale τ P to other model parameters. Center red line is the optimal τ P as estimated from the 3‐D grid search (Figure 6). Blue lines delimit the τ P values corresponding to the 95% confidence interval. Yellow region shows the possible ranges of parameter values to obtain an equally good fit. Dashed lines show the ranges of a given parameter estimated from the literature. Dotted lines delimit the resulting ranges of a given parameter. (a–c) For an incompressible magma (β m=0). (d–f) These panels consider a large range of magma compressibility values; little or no trade‐off occurs with the other parameters, as indicated by the nearly vertical curve within each yellow region.
Using this analysis, we can determine the optimal values for the parameters that characterize the magma injection at LdM, assuming an ellipsoid of radius a = 6200 m, thickness c = 100 m, depth d = 4.5 km, and a conduit of length L c=25.4 km, embedded in a uniform Poisson half‐space. Using values from the literature, we can place approximate bounds on each of the model parameters. For example, the shear modulus G of crustal rocks is most likely between 10 and 30 GPa [e.g., Brocher, 2005]. Reading the 68% confidence limits for the characteristic timescale in Figure 7a, we infer that the magma viscosity η m falls between 2 × 108 Pa s and 3 × 109 Pa s. Similarly, the conduit radius a c is likely between 30 m and 60 m (Figure 7b). Increasing the length of the conduit by 10 km to account for the possibility of a thicker crust (∼40 km) does not yield significantly different ranges for the magma viscosity and conduit radius.
6. Discussion
6.1. On the Role of Viscoelastic Relaxation
To evaluate the influence of crustal viscoelasticity on the results, we consider both a homogeneous viscosity distribution with different values of crustal viscosity η r varying between 1017 Pa s and 1019 Pa s, and a stationary heterogeneous viscosity distribution where η r depends on the steady‐state temperature field (Figure 8).
Figure 8.
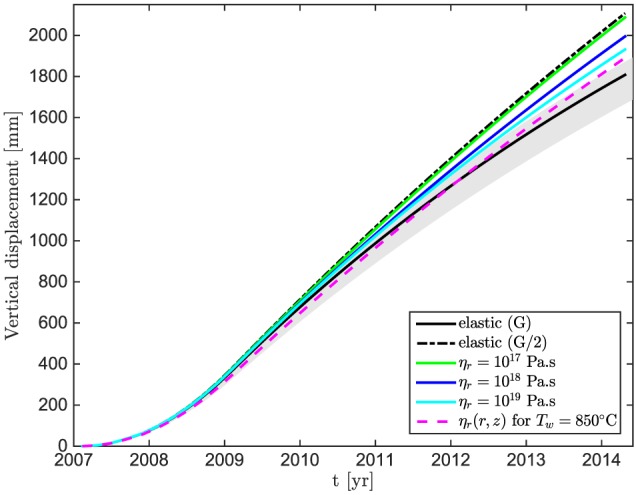
Modeled time series (black curve) of cumulative vertical displacement for a point located at GPS station MAU2 (magenta star on Figure 4) from 2007 to 2014, as derived from InSAR data (Figure 5) and assuming a model of magma injection starting in 2007 in an elastic domain. Several realizations of our model of magma injection in a viscoelastic domain are shown as colored lines.
The viscoelastic relaxation of the crust only plays a role in the temporal evolution of the uplift after t ∼ 4 years. After 7.3 years, all the viscoelastic configurations yield more vertical displacement than the elastic configuration calculated using the total shear modulus G (black line on Figure 8). This result is consistent with previous modeling studies showing that a viscoelastic rheology leads to larger displacements than the elastic one and therefore requires a lower applied pressure to fit a specific data set [e.g., Del Negro et al., 2009; Hickey et al., 2013; Newman et al., 2001; Bonafede and Ferrari, 2009]. However, the results from the most realistic model using the temperature‐dependent crustal viscosity distribution are not meaningfully different from those of the elastic model. The total accumulated vertical displacement after 7.3 years is ∼80 mm higher (4%) for the heterogeneous viscoelastic model, which is within the uncertainty of the elastic model. The elastic model calculated with the total shear modulus G corresponds to the case of infinite crustal viscosity (Figure 8). At large times, all the viscoelastic solutions will converge toward the elastic solution with the fractional shear modulus G 0=G/2 of the viscoelastic branch (black dashed line on Figure 8) when the viscoelastic relaxation is finished.
While it is likely that the crust surrounding the magma chamber behaves in a viscoelastic manner, we emphasize that in our conceptual model for injecting viscous magma into a reservoir, viscoelastic relaxation of the crust is not required to reproduce the exponentially increasing and decreasing uplift rates observed at LdM.
For other volcanic systems, we expect the predominant mechanism in the time series to depend on the relative importance between the characteristic viscoelastic (Maxwell) timescale τ M and the magma flow (Poiseuille) timescale τ P. The magma flow to the reservoir, governed by the characteristic timescale τ P, would be negligible on the geodetic (decadal) timescale in the cases when it is either smaller than weeks or larger than hundreds of years. The former case could occur, for example, in the case of a very fluid magma with very low viscosity η m, yielding an almost instantaneous response following the application of a pressure at the base of the conduit. The latter case of very large τ P could occur in several instances including a very elongated and/or shallow magma reservoir (yielding a large chamber wall compressibility β w) and/or a very viscous magma (large η m). The Maxwell timescale governing the viscoelastic relaxation of the crust is proportional to the crustal rocks viscosity and inversely proportional to their shear modulus G. The crustal viscosity is rarely known. The commonly used value of crustal viscosity η r=1018 Pa s yields a Maxwell time in the order of years, compatible with the timescale of volcanic unrest. However, if the Maxwell time is in the order of decades, the viscoelastic effects would be secondary on the geodetic time series of volcanic unrest.
6.2. Interpretation of Estimated Parameters
Until now, we have considered the magma to be an incompressible fluid (β m=0) and assumed that the accommodation of new magma only occurs through the volume change of the reservoir such that ΔV inj=ΔV ch. Now, we consider that some of the change in volume is accomodated by compression of the magma already residing in the chamber, such that ΔV inj=ΔV ch+ΔV comp [e.g., Johnson et al., 2000] as shown in equation (6). The compressibility of magma has been invoked to explain some apparent discrepancies between the estimated volume of a dike injection and the corresponding change in the chamber volume [Rivalta and Segall, 2008], or the relation between the erupted volume and the volume of magma injected [e.g., Johnson, 1992; Johnson et al., 2000]. Next we calculate the volume change for our preferred model with several values of magma compressibility. Assuming water is the dominant volatile species, we use the relations of Huppert and Woods [2002] with a magma water content between 4 and 6 wt % and a magma crystal fraction between 0.2 and 0.4, to find a value for the magma compressibility β m for the configuration at LdM between 1.4 × 10−10 Pa−1 and 2.1 × 10−9 Pa−1. Accounting for a compressible magma yields markedly higher estimates for the volume of magma injected (Figure 9). The volume of injected magma could be as high as 366 × 106 m3, roughly twice as large as the volume estimate of 187 × 106 m3 estimated for an incompressible fluid (Figure 9). While we do not find any trade‐offs between the magma compressibility and the other model parameters in the τ P value (Figures 7d–7f), more compressible magma could accumulate in the chamber to produce the same amount of deformation at the surface.
Figure 9.
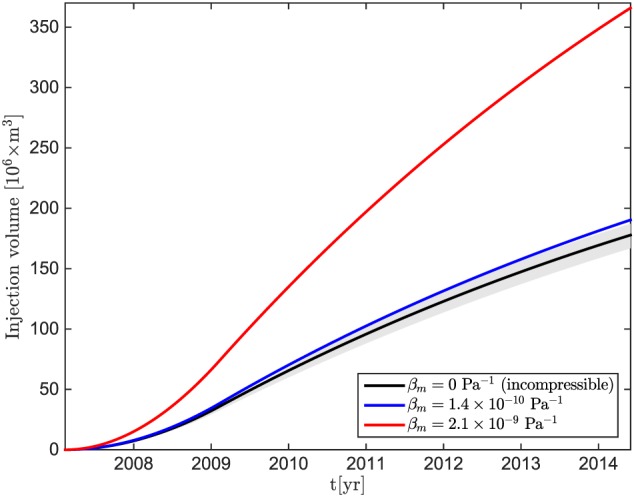
Cumulative volume of magma injected into the reservoir between 2007 and 2014 at LdM, calculated from the pressure history shown in Figure 10 for an incompressible magma (β m=0) (black line), and two extreme values of magma compressibility (blue and red lines). The gray area delimits the volume estimates for the two end‐member models with the maximum and minimum cumulative reservoir pressure (Figure 10) based on the grid search results. The volume estimate after 7.3 years ranges between 187 × 106 m3 (0.19 km3) and 366 × 106 m3 (0.37 km3) of magma.
The modeling results indicate a conduit radius between 30 and 60 m (Figure 7). There are few constraints on the size of conduits that channel melt at large depth. However, the values of tens of meters are consistent with the thickness of the larger dikes intruding the upper crust that have been modeled and observed in the field at different volcanoes [e.g., Rubin, 1995; Fialko and Rubin, 1999; Gudmundsson, 2002].
The modeling results also indicate a magma viscosity between ∼2 × 108 Pa s and ∼3 × 109 Pa s (Figure 7). In our single‐phase flow model, the magma viscosity estimates represent bulk viscosities that include the viscosity of the rock matrix, the crystals, and the melt. The bulk (effective) viscosity depends strongly on the crystal fraction and interstitial melt composition [e.g., Marsh, 1989; Gottsmann et al., 2009]. Following the conceptual model of Hildreth [2004] and Hildreth and Wilson [2007] for Long Valley caldera, we infer that the volcanic system at LdM is underlain by a large crystal‐rich mush [Singer et al., 2014]. In this framework, the estimated range of magma viscosity values may reflect the arrival of mafic magma through a highly viscous mush [e.g., Burgisser and Bergantz, 2011].
6.3. Magma Injection History at LdM and Plausible Mechanisms
The magma injection model allows us to interpret the surface uplift in terms of magma dynamics: when the acceleration is positive, the injection pressure ΔP i(t) at the inlet increases with time and so does the volumetric flow rate Q(t) (Figure 10). An inlet pressure on the order of ∼12 MPa explains the uplift at LdM such that the volumetric flow rate reaches 1.2 m3/s after 2 years (Figure 10). This value of injection pressure falls within the accepted ranges of overpressure that can be sustained in a magma reservoir. For example, Rubin [1995] estimates a critical pressure of ∼10–40 MPa for dikes to propagate to the surface for typical rhyolite viscosities. These values are also well below the critical stress required to initiate faulting in the crust overlying the magma chamber, as indicated by the Mohr‐Coulomb failure criterion [e.g., Gregg et al., 2012] to be of the order of ∼68 MPa. During the entire time interval, new magma flows upward through the conduit and into the reservoir.
Figure 10.
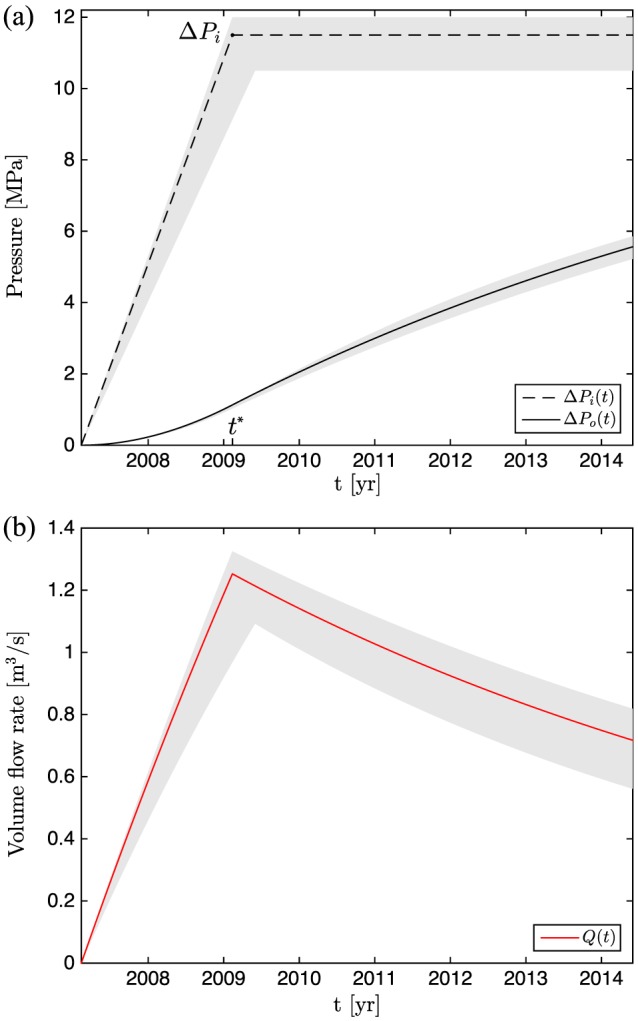
Temporal evolution of (a) inlet pressure ΔP i(t) and reservoir pressure ΔP o(t), and (b) volumetric flow rate Q(t) that best explain the uplift time series at LdM (Figure 5). Light gray envelope delimits the uncertainty on the maximum reservoir pressure estimated from the uncertainty on parameters τ P, ΔP i, and t ∗, as calculated by an F test on the misfit presented on Figure 6.
This study demonstrates that the arrival of magma can be detected by geodesy. The observation of episodic ground motion suggests a pulsating magma supply at the source, as modeled in this study. An increase in magma flux reaching the upper crustal reservoir could be explained by the complex magma ascent paths through the crust, leading to some obstruction in the deeper part of the system followed by magma release and fluid pressure increase. An alternative hypothesis would be an increase in the available source melt from the mantle or a MASH (melting, accumulation, storage, homogenization) zone in the lower crust [e.g., Hildreth and Moorbath, 1988]. The maximum volumetric flow rate reached during magma injection at LdM estimated from this study is in the order of 1.2 m3/s or 0.03 km3/yr. This estimate is higher than the long‐term, average magma production rates inferred at subduction zones [Jellinek and DePaolo, 2003]. However, our estimate is well within the range of volumetric filling rates estimated by Petford et al. [2000] for the emplacement of tabular granitic magma plutons. Similarly, intrusion rates as high as 0.06 km3/yr have been estimated to explain the plutonic volumes of the Altiplano‐Puna Volcanic Complex in the Andes [de Silva and Gosnold, 2007]. The thermodynamic and mechanical models of Caricchi et al.[2014] and Gelman et al. [2013] also consider high instantaneous injection rates between 10−3 m3/s and 1 m3/s. As noted by Jellinek and DePaolo [2003], episodic intrusions in the crust require episodic replenishment with higher magma flux, because the long‐term values of magma supply rates would not generate a dike that propagates into the upper crust. Consequently, the flux estimate from our model of magma injection at LdM is consistent with previous studies and supports the existence of rapid pulses of magma reaching upper crustal magma reservoirs.
7. Conclusion
To simulate the process of magma injection into long‐lived reservoirs, we have developed a model that accounts for magma flow into a fluid‐filled reservoir. By coupling the fluid dynamics in the conduit to the mechanics of the surrounding crustal rocks, this model explains the essential features of the spatial pattern and temporal evolution of the surface deformation observed by InSAR during the ongoing deformation episode at LdM. The acceleration of uplift rates starting in 2007 for about 2 years corresponds to a flow rate as high as Q = 1.2 m3/s (0.03 km3/yr) for the magma feeding the reservoir. Since mid‐2009, the volume flow rate has decreased to Q = 0.7 m3/s (0.02 km3/yr), but the reservoir pressure is still increasing, creating the slowly decreasing uplift rates observed late in the time series. According to this model, the injection will stop when the pressure at the inlet equals that at the outlet.
We have explored the model parameter space using a grid search method to optimize the three governing parameters: the characteristic time constant for magma propagation τ P, the injection pressure ΔP i(t), and the inflection time t ∗ when the acceleration switches from positive to negative. For a spheroid with semi‐major axis a = 6200 m, semiminor axis c = 100 m, located at a depth of 4.5 km in a purely elastic half‐space, the best fit to the InSAR displacement data occurs for a Poiseuille timescale τ P=9.5 years and an injection pressure rising to ΔP i=11.5 MPa at t ∗=2009.3 years. The grid search results and sensitivity analysis have allowed us to constrain the range of possible magma bulk viscosity between 2 × 108 and 3 × 109 Pa s, and the conduit radius a c between 30 m and 60 m for a shear modulus G between 10 GPa and 30 GPa. Our results indicate that the viscoelastic relaxation of the crust has a secondary effect and is not needed to explain the slow decay in uplift rates. The most realistic viscoelastic model for the crust at LdM with a heterogeneous viscosity distribution (calculated assuming an average reservoir temperature of 850°C) yields a larger (∼4%) vertical displacement but falls within the 68% confidence interval estimate for the elastic model. Finally, the total volume of accumulated magma since the onset of the unrest episode at LdM is 187 × 106 m3, assuming an incompressible magma, and could be as high as 366 × 106 m3 if the magma compressibility were 2.1 × 10−9 Pa−1.
Acknowledgments
We thank Nathan Andersen, Tabrez Ali, and Eric Grosfils for helpful discussions. This research was partially supported by grants from NASA (NNX12AO37G, Feigl and Le Mével; 13ESI130034, Gregg), and the U.S. National Science Foundation (EAR1411779, Feigl and Le Mével; EAR0815101, Gregg), as well as the Weeks family and the G.P. Woollard fund. We acknowledge SAR data from the following space agencies: ASI (COSMO‐Skymed), DLR (TerraSAR‐X), JAXA (ALOS), ESA (ERS & ENVISAT), and NASA (UAVSAR). The COMSOL file to generate Figure 3 is available upon request to the first author. The authors thank Virginie Pinel and Eric Grosfils for their assistance in critically and constructively evaluating this paper.
Le Mével, H. , Gregg P. M., and Feigl K. L.(2016), Magma injection into a long‐lived reservoir to explain geodetically measured uplift: Application to the 2007–2014 unrest episode at Laguna del Maule volcanic field, Chile, J. Geophys. Res. Solid Earth, 121, 6092–6108, doi:10.1002/2016JB013066.
References
- Amoruso, A. , and Crescentini L. (2009), Shape and volume change of pressurized ellipsoidal cavities from deformation and seismic data, J. Geophys. Res., 114, B02210, doi:10.1029/2008JB005946. [Google Scholar]
- Anderson, K. , and Segall P. (2011), Physics‐based models of ground deformation and extrusion rate at effusively erupting volcanoes, J. Geophys. Res., 116, B07204, doi:10.1029/2010JB007939. [Google Scholar]
- Annen, C. (2009), From plutons to magma chambers: Thermal constraints on the accumulation of eruptible silicic magma in the upper crust, Earth Planet. Sci. Lett., 284(3–4), 409–416, doi:10.1016/j.epsl.2009.05.006. [Google Scholar]
- Annen, C. , and Sparks R. (2002), Effects of repetitive emplacement of basaltic intrusions on thermal evolution and melt generation in the crust, Earth Planet. Sci. Lett., 203(3–4), 937–955, doi:10.1016/S0012‐821X(02)00929‐9. [Google Scholar]
- Annen, C. , Blundy J. D., and Sparks R. S. J. (2006), The genesis of intermediate and silicic magmas in deep crustal hot zones, J. Petrol., 47(3), 505–539, doi:10.1093/petrology/egi084. [Google Scholar]
- Bachmann, O. , and Bergantz G. (2008), The magma reservoirs that feed supereruptions, Elements, 4(1), 17–21, doi:10.2113/GSELEMENTS.4.1.17. [Google Scholar]
- Battaglia, M. , Segall P., Murray J., Cervelli P., and Langbein J. (2003), The mechanics of unrest at Long Valley caldera, California: 1. Modeling the geometry of the source using GPS, leveling and two‐color EDM data, J. Volcanol. Geotherm. Res., 127(3–4), 195–217, doi:10.1016/S0377‐0273(03)00170‐7. [Google Scholar]
- Battaglia, M. , Cervelli P. F., and Murray J. R. (2013), dMODELS: A MATLAB software package for modeling crustal deformation near active faults and volcanic centers, J. Volcanol. Geotherm. Res., 254, 1–4, doi:10.1016/j.jvolgeores.2012.12.018. [Google Scholar]
- Blake, S. (1981), Volcanism and the dynamics of open magma chambers, Nature, 289, 783–785, doi:10.1038/289783a0. [Google Scholar]
- Bonafede, M. , and Ferrari C. (2009), Analytical models of deformation and residual gravity changes due to a Mogi source in a viscoelastic medium, Tectonophysics, 471(1–2), 4–13, doi:10.1016/j.tecto.2008.10.006. [Google Scholar]
- Brocher, T. M. (2005), Empirical relations between elastic wavespeeds and density in the Earth's crust, Bull. Seismol. Soc. Am., 95(6), 2081–2092, doi:10.1785/0120050077. [Google Scholar]
- Brown, M. (2007), Crustal melting and melt extraction, ascent and emplacement in orogens: Mechanisms and consequences, J. Geol. Soc., 164(4), 709–730, doi:10.1144/0016‐76492006‐171. [Google Scholar]
- Bunger, A. P. , and Cruden A. R. (2011a), Modeling the growth of laccoliths and large mafic sills: Role of magma body forces, J. Geophys. Res., 116, B02203, doi:10.1029/2010JB007648. [Google Scholar]
- Bunger, A. P. , and Cruden A. R. (2011b), Correction to “Modeling the growth of laccoliths and large mafic sills: Role of magma body forces”, J. Geophys. Res., 116, B08211, doi:10.1029/2011JB008618. [Google Scholar]
- Burgisser, A. , and Bergantz G. W. (2011), A rapid mechanism to remobilize and homogenize highly crystalline magma bodies, Nature, 471(7337), 212–215, doi:10.1038/nature09799. [DOI] [PubMed] [Google Scholar]
- Caricchi, L. , Annen C., Blundy J., Simpson G., and Pinel V. (2014), Frequency and magnitude of volcanic eruptions controlled by magma injection and buoyancy, Nat. Geosci., 7(2), 126–130, doi:10.1038/ngeo2041. [Google Scholar]
- Carrier, A. , Got J.‐L., Peltier A., Ferrazzini V., Staudacher T., Kowalski P., and Boissier P.(2015), A damage model for volcanic edifices: Implications for edifice strength, magma pressure, and eruptive processes, J. Geophys. Res. Solid Earth, 120(1), 567–583, doi:10.1002/2014JB011485. [Google Scholar]
- Cayol, V. , and Cornet F. H. (1998), Effects of topography on the interpretation of the deformation field of prominent volcanoes—Application to Etna, Geophys. Res. Lett., 25(11), 1979–1982, doi:10.1029/98GL51512. [Google Scholar]
- Chang, W.‐L. , Smith R. B., Farrell J., and Puskas C. M. (2010), An extraordinary episode of Yellowstone caldera uplift, 2004–2010, from GPS and InSAR observations, Geophys. Res. Lett., 37, L23302, doi:10.1029/2010GL045451. [Google Scholar]
- Currenti, G. , Del Negro C., and Ganci G. (2007), Modelling of ground deformation and gravity fields using finite element method: An application to Etna volcano, Geophys. J. Int., 169(2), 775–786, doi:10.1111/j.1365‐246X.2007.03380.x. [Google Scholar]
- Currenti, G. , Bonaccorso A., Negro C. D., Scandura D., and Boschi E. (2010), Elasto‐plastic modeling of volcano ground deformation, Earth Planet. Sci. Lett., 296(3–4), 311–318, doi:10.1016/j.epsl.2010.05.013. [Google Scholar]
- de Silva, S. L. , and Gosnold W. D. (2007), Episodic construction of batholiths: Insights from the spatiotemporal development of an ignimbrite flare‐up, J. Volcanol. Geotherm. Res., 167(1–4), 320–335, doi:10.1016/j.jvolgeores.2007.07.015. [Google Scholar]
- Del Negro, C. , Currenti G., and Scandura D. (2009), Temperature‐dependent viscoelastic modeling of ground deformation: Application to Etna volcano during the 1993–1997 inflation period, Phys. Earth Planet. Inter., 172(3–4), 299–309, doi:10.1016/j.pepi.2008.10.019. [Google Scholar]
- Druitt, T. , Costa F., Deloule E., Dungan M., and Scaillet B. (2012), Decadal to monthly timescales of magma transfer and reservoir growth at a caldera volcano, Nature, 482(7383), 77–80, doi:10.1038/nature10706. [DOI] [PubMed] [Google Scholar]
- Dzurisin, D. (2007), Volcano deformation: New geodetic monitoring techniques.
- Dzurisin, D. , Lisowski M., and Wicks C. W. (2009), Continuing inflation at Three Sisters volcanic center, central Oregon Cascade Range, USA, from GPS, leveling, and InSAR observations, Bull. Volcanol., 71(10), 1091–1110, doi:10.1007/s00445‐009‐0296‐4. [Google Scholar]
- Feigl, K. L. , and Thurber C. H. (2009), A method for modelling radar interferograms without phase unwrapping: Application to the M 5 Fawnskin, California earthquake of 1992 December 4, Geophys. J. Int., 176(2), 491–504, doi:10.1111/j.1365‐246X.2008.03881.x. [Google Scholar]
- Feigl, K. L. , Le Mével H., Ali S. T., Córdova L., Andersen N. L., DeMets C., and Singer B. S. (2014), Rapid uplift in Laguna del Maule volcanic field of the Andean Southern Volcanic zone (Chile) 2007–2012, Geophys. J. Int., 196(2), 885–901, doi:10.1093/gji/ggt438. [Google Scholar]
- Fialko, Y. , Khazan Y., and Simons M. (2001), Deformation due to a pressurized horizontal circular crack in an elastic half‐space, with applications to volcano geodesy, Geophys. J. Int., 146(1), 181–190, doi:10.1046/j.1365‐246X.2001.00452.x. [Google Scholar]
- Fialko, Y. A. , and Rubin A. M. (1999), Thermal and mechanical aspects of magma emplacement in giant dike swarms, J. Geophys. Res., 104(B10), 23,033–23,049, doi:10.1029/1999JB900213. [Google Scholar]
- Gelman, S. E. , Gutiérrez F. J., and Bachmann O. (2013), On the longevity of large upper crustal silicic magma reservoirs, Geology, 41(7), 759–762, doi:10.1130/G34241.1. [Google Scholar]
- Gerbault, M. , Cappa F., and Hassani R. (2012), Elasto‐plastic and hydromechanical models of failure around an infinitely long magma chamber, Geochem. Geophys. Geosyst., 13(3), Q03009, doi:10.1029/2011GC003917. [Google Scholar]
- Got, J.‐L. , Peltier A., Staudacher T., Kowalski P., and Boissier P. (2013), Edifice strength and magma transfer modulation at Piton de la Fournaise volcano, J. Geophys. Res. Solid Earth, 118(9), 5040–5057, doi:10.1002/jgrb.50350. [Google Scholar]
- Gottsmann, J. , Lavalle Y., Martí J., and Aguirre‐Daz G. (2009), Magma‐tectonic interaction and the eruption of silicic batholiths, Earth Planet. Sci. Lett., 284(3–4), 426–434, doi:10.1016/j.epsl.2009.05.008. [Google Scholar]
- Gregg, P. , de Silva S., Grosfils E., and Parmigiani J. (2012), Catastrophic caldera‐forming eruptions: Thermomechanics and implications for eruption triggering and maximum caldera dimensions on Earth, J. Volcanol. Geotherm. Res., 241–242, 1–12, doi:10.1016/j.jvolgeores.2012.06.009. [Google Scholar]
- Gregg, P. , de Silva S., and Grosfils E. (2013), Thermomechanics of shallow magma chamber pressurization: Implications for the assessment of ground deformation data at active volcanoes, Earth Planet. Sci. Lett., 384, 100–108, doi:10.1016/j.epsl.2013.09.040. [Google Scholar]
- Gregg, P. M. , Grosfils E. B., and de Silva S. L. (2015), Catastrophic caldera‐forming eruptions II: The subordinate role of magma buoyancy as an eruption trigger, J. Volcanol. Geotherm. Res., 305, 100–113, doi:10.1016/j.jvolgeores.2015.09.022. [Google Scholar]
- Grosfils, E. B. (2007), Magma reservoir failure on the terrestrial planets: Assessing the importance of gravitational loading in simple elastic models, J. Volcanol. Geotherm. Res., 166(2), 47–75, doi:10.1016/j.jvolgeores.2007.06.007. [Google Scholar]
- Gudmundsson, A. (2002), Emplacement and arrest of sheets and dykes in central volcanoes, J. Volcanol. Geotherm. Res., 116(3–4), 279–298, doi:10.1016/S0377‐0273(02)00226‐3. [Google Scholar]
- Hickey, J. , and Gottsmann J. (2014), Benchmarking and developing numerical Finite Element models of volcanic deformation, J. Volcanol. Geotherm. Res., 280, 126–130, doi:10.1016/j.jvolgeores.2014.05.011. [Google Scholar]
- Hickey, J. , Gottsmann J., and del Potro R. (2013), The large‐scale surface uplift in the Altiplano‐Puna region of Bolivia: A parametric study of source characteristics and crustal rheology using finite element analysis, Geochem. Geophys. Geosyst., 14(3), 540–555, doi:10.1002/ggge.20057. [Google Scholar]
- Hildreth, W. (1981), Gradients in silicic magma chambers: Implications for lithospheric magmatism, J. Geophys. Res., 86(B11), 10,153–10,192, doi:10.1029/JB086iB11p10153. [Google Scholar]
- Hildreth, W. (2004), Volcanological perspectives on Long Valley, Mammoth mountain, and Mono craters: Several contiguous but discrete systems, J. Volcanol. Geotherm. Res., 136(3–4), 169–198, doi:10.1016/j.jvolgeores.2004.05.019. [Google Scholar]
- Hildreth, W. , and Moorbath S. (1988), Crustal contributions to arc magmatism in the Andes of central Chile, Contrib. Mineral. Petrol., 98(4), 455–489, doi:10.1007/BF00372365. [Google Scholar]
- Hildreth, W. , and Wilson C. J. N. (2007), Compositional zoning of the Bishop Tuff, J. Petrol., 48(5), 951–999, doi:10.1093/petrology/egm007. [Google Scholar]
- Hildreth, W. , Godoy E., Fierstein J., and Singer B. (2010), Laguna del Maule volcanic field: Eruptive history of a Quaternary basalt‐to‐rhyolite distributed volcanic field on the Andean range crest in central Chile, Servicio Nacional de Geología y Minería–Chile Boletin, 63, 142. [Google Scholar]
- Hughes, G. R. , and Mahood G. A. (2011), Silicic calderas in arc settings: Characteristics, distribution, and tectonic controls, Geol. Soc. Am. Bull., 123(7–8), 1577–1595, doi:10.1130/B30232.1. [Google Scholar]
- Huppert, H. E. , and Woods A. W. (2002), The role of volatiles in magma chamber dynamics, Nature, 420(6915), 493–495, doi:10.1038/nature01211. [DOI] [PubMed] [Google Scholar]
- Hurwitz, D. M. , Long S. M., and Grosfils E. B. (2009), The characteristics of magma reservoir failure beneath a volcanic edifice, J. Volcanol. Geotherm. Res., 188(4), 379–394, doi:10.1016/j.jvolgeores.2009.10.004. [Google Scholar]
- Jaupart, C. , and Tait S. (1990), Dynamics of eruptive phenomena, Rev. Mineral. Geochem., 24(1), 213–238. [Google Scholar]
- Jellinek, A. M. , and DePaolo D. J. (2003), A model for the origin of large silicic magma chambers: Precursors of caldera‐forming eruptions, Bull. Volcanol., 65(5), 363–381, doi:10.1007/s00445‐003‐0277‐y. [Google Scholar]
- Johnson, D. J. (1992), Dynamics of magma storage in the summit reservoir of Kilauea volcano, Hawaii, J. Geophys. Res., 97(B2), 1807–1820. [Google Scholar]
- Johnson, D. J. , Sigmundsson F., and Delaney P. T. (2000), Comment on “Volume of magma accumulation or withdrawal estimated from surface uplift or subsidence, with application to the 1960 collapse of Kilauea volcano” by P. T. Delaney and D. F. McTigue, Bull. Volcanol., 61(7), 491–493, doi:10.1007/s004450050006. [Google Scholar]
- Le Mével, H. , Feigl K. L., Córdova L., DeMets C., and Lundgren P. (2015), Evolution of unrest at Laguna del Maule volcanic field (Chile) from InSAR and GPS measurements, 2003 to 2014, Geophys. Res. Lett., 42(16), 6590–6598, doi:10.1002/2015GL064665. [Google Scholar]
- Lengliné, O. , Marsan D., Got J.‐L., Pinel V., Ferrazzini V., and Okubo P. G. (2008), Seismicity and deformation induced by magma accumulation at three basaltic volcanoes, J. Geophys. Res., 113, B12305, doi:10.1029/2008JB005937. [Google Scholar]
- Lister, J. R. , and Kerr R. C. (1991), Fluid‐mechanical models of crack propagation and their application to magma transport in Dykes, J. Geophys. Res., 96(B6), 10,049–10,077, doi:10.1029/91JB00600. [Google Scholar]
- Long, S. M. , and Grosfils E. B. (2009), Modeling the effect of layered volcanic material on magma reservoir failure and associated deformation, with application to Long Valley caldera, California, J. Volcanol. Geotherm. Res., 186(3–4), 349–360, doi:10.1016/j.jvolgeores.2009.05.021. [Google Scholar]
- Lu, Z. , Masterlark T., Dzurisin D., Rykhus R., and Wicks C. (2003), Magma supply dynamics at Westdahl volcano, Alaska, modeled from satellite radar interferometry, J. Geophys. Res., 108, 2354, doi:10.1029/2002JB002311. [Google Scholar]
- Lu, Z. , Dzurisin D., Biggs J., Wicks C., and McNutt S. (2010), Ground surface deformation patterns, magma supply, and magma storage at Okmok volcano, Alaska, from InSAR analysis: 1. Intereruption deformation, 1997–2008, J. Geophys. Res., 115, B00B02, doi:10.1029/2009JB006969. [Google Scholar]
- Macedonio, G. , Giudicepietro F., D'Auria L., and Martini M. (2014), Sill intrusion as a source mechanism of unrest at volcanic calderas, J. Geophys. Res. Solid Earth, 119(5), 3986–4000, doi:10.1002/2013JB010868. [Google Scholar]
- Marsh, B. D. (1989), Magma chambers, Annu. Rev. Earth Planet. Sci., 17(1), 439–472, doi:10.1146/annurev.ea.17.050189.002255. [Google Scholar]
- Masterlark, T. (2007), Magma intrusion and deformation predictions: Sensitivities to the Mogi assumptions, J. Geophys. Res., 112(B6), B06419, doi:10.1029/2006JB004860. [Google Scholar]
- Masterlark, T. , Feigl K. L., Haney M., Stone J., Thurber C., and Ronchin E. (2012), Nonlinear estimation of geometric parameters in FEMs of volcano deformation: Integrating tomography models and geodetic data for Okmok volcano, Alaska, J. Geophys. Res., 117, B02407, doi:10.1029/2011JB008811. [Google Scholar]
- Mastin, L. G. , Roeloffs E., Beeler N. M., and Quick J. E. (2008), Constraints on the size, overpressure, and volatile content of the Mount St. Helens magma system from geodetic and dome‐growth measurements during the 2004–2006 eruption, U.S. Geol. Surv. Prof. Pap., 1750, 461–488. [Google Scholar]
- Mériaux, C. , and Jaupart C. (1995), Simple fluid dynamic models of volcanic rift zones, Earth Planet. Sci. Lett., 136(3), 223–240, doi:10.1016/0012‐821X(95)00170‐H. [Google Scholar]
- Michaut, C. (2011), Dynamics of magmatic intrusions in the upper crust: Theory and applications to laccoliths on Earth and the Moon, J. Geophys. Res., 116, B05205, doi:10.1029/2010JB008108. [Google Scholar]
- Mogi, K. (1958), Relations between the eruptions of various volcanoes and the deformations of the ground surfaces around them, Bull. Earthquake Res. Inst., 36, 99–134. [Google Scholar]
- Newman, A. , Dixon T. H., Ofoegbu G., and Dixon J. (2001), Geodetic and seismic constraints on recent activity at Long Valley caldera, California: Evidence for viscoelastic rheology, J. Volcanol. Geotherm. Res., 105(3), 183–206, doi:10.1016/S0377‐0273(00)00255‐9. [Google Scholar]
- Newman, A. V. et al. (2012), Recent geodetic unrest at Santorini caldera, Greece, Geophys. Res. Lett., 39(6), doi:10.1029/2012GL051286. [Google Scholar]
- Parks, M. M. et al. (2012), Evolution of Santorini volcano dominated by episodic and rapid fluxes of melt from depth, Nat. Geosci., 5(10), 749–754. [Google Scholar]
- Petford, N. , Cruden A., McCaffrey K., and Vigneresse J.‐L. (2000), Granite magma formation, transport and emplacement in the Earth's crust, Nature, 408(6813), 669–673, doi:10.1038/35047000. [DOI] [PubMed] [Google Scholar]
- Pinel, V. , Jaupart C., and Albino F. (2010), On the relationship between cycles of eruptive activity and growth of a volcanic edifice, J. Volcanol. Geotherm. Res., 194(4), 150–164, doi:10.1016/j.jvolgeores.2010.05.006. [Google Scholar]
- Pollard, D. D. (1976), On the form and stability of open hydraulic fractures in the Earth's crust, Geophys. Res. Lett., 3(9), 513–516, doi:10.1029/GL003i009p00513. [Google Scholar]
- Reverso, T. , Vandemeulebrouck J., Jouanne F., Pinel V., Villemin T., Sturkell E., and Bascou P.(2014), A two‐magma chamber model as a source of deformation at Grímsvötn volcano, Iceland, J. Geophys. Res. Solid Earth, 119(6), 4666–4683, doi:10.1002/2013JB010569. [Google Scholar]
- Rivalta, E. , and Segall P. (2008), Magma compressibility and the missing source for some dike intrusions, Geophys. Res. Lett., 35, L04306, doi:10.1029/2007GL032521. [Google Scholar]
- Rubin, A. M. (1995), Propagation of magma‐filled cracks, Annu. Rev. Earth Planet. Sci., 23, 287–336, doi:10.1146/annurev.ea.23.050195.001443. [Google Scholar]
- Segall, P. (2010), Earthquake and Volcano Deformation, Princeton Univ. Press, Princeton, N. J. [Google Scholar]
- Singer, B. et al. (2014), Dynamics of a large, restless, rhyolitic magma system at Laguna del Maule, Southern Andes, Chile, GSA Today, 4–10(12), doi:10.1130/GSATG216A.1. [Google Scholar]
- Snyder, D. (2000), Thermal effects of the intrusion of basaltic magma into a more silicic magma chamber and implications for eruption triggering, Earth Planet. Sci. Lett., 175(3–4), 257–273, doi:10.1016/S0012‐821X(99)00301‐5. [Google Scholar]
- Sparks, R. , and Marshall L. (1986), Thermal and mechanical constraints on mixing between mafic and silicic magmas, J. Volcanol. Geotherm. Res., 29(1), 99–124, doi:10.1016/0377‐0273(86)90041‐7. [Google Scholar]
- Spera, F. J. (1980), Aspects of magma transport, Phys. Magmatic Processes, 7, 265–323. [Google Scholar]
- Trasatti, E. , Giunchi C., and Bonafede M. (2003), Effects of topography and rheological layering on ground deformation in volcanic regions, J. Volcanol. Geotherm. Res., 122(1–2), 89–110, doi:10.1016/S0377‐0273(02)00473‐0. [Google Scholar]
- Turcotte, D. L. , and Schubert G. (2014), Geodynamics, Cambridge Univ. Press, Cambridge, U. K. [Google Scholar]
- Wiebe, R. A. (1993), The Pleasant Bay layered gabbro‐diorite, coastal Maine: Ponding and crystallization of basaltic injections into a silicic magma chamber, J. Petrol., 34(3), 461–489, doi:10.1093/petrology/34.3.461. [Google Scholar]
- Wiebe, R. A. (1996), Mafic‐silicic layered intrusions: The role of basaltic injections on magmatic processes and the evolution of silicic magma chambers, Trans. R. Soc. Edinburgh: Earth Sci., 87, 233–242, doi:10.1017/S0263593300006647. [Google Scholar]
- Williams, C. A. , and Wadge G. (1998), The effects of topography on magma chamber deformation models: Application to Mt. Etna and radar interferometry, Geophys. Res. Lett., 25(10), 1549–1552, doi:10.1029/98GL01136. [Google Scholar]


