Mathematical modeling and synthetic biology

Abstract

Synthetic biology is an engineering discipline that builds on our mechanistic understanding of molecular biology to program microbes to carry out new functions. Such predictable manipulation of a cell requires modeling and experimental techniques to work together. The modeling component of synthetic biology allows one to design biological circuits and analyze its expected behavior. The experimental component merges models with real systems by providing quantitative data and sets of available biological ‘parts’ that can be used to construct circuits. Sufficient progress has been made in the combined use of modeling and experimental methods, which reinforces the idea of being able to use engineered microbes as a technological platform.

Introduction

Through detailed understanding of cellular mechanisms and improved experimental techniques for manipulating a cell’s genotype, it has become possible to engineer a cell so that it exhibits new programmed behavior. Synthetic biology combines classical genetic engineering techniques with engineering concepts such as standardized parts, functional modules and computer-aided design [1]. In this new field, a large variety of functional genetic components such as promoters, ribosome binding sites and protein sequences are characterized to generate a pool of biological ‘parts’. These parts can be assembled to construct biological circuits, which can then be reused in different ways to form larger circuits, much like how complex electronic circuits are constructed from smaller modules. The ability to construct complex biological circuit makes it possible to resolve health, environmental and energy issues by using engineered microbes. In this review, we discuss how mathematical modeling is valuable in synthetic biology as a means of understanding and engineering networks.

Modeling

Modeling can provide mechanistic understanding of a given system. Models that are able to correctly predict the behavior of a system allow engineers to program new cellular behavior without having to perform large numbers of trial-and-error experiments. One can consider graphical models, such as cartoons of biochemical pathways, as simple examples of qualitative models. Qualitative models have inherent limitations because they rely on interpretations which are not amenable to analysis by mathematics and computer algorithms [2]. For this reason, quantitative models will be the subject of interest in this article.

In synthetic biology, modeling serves as a tool for an engineer to predict how a network will behave when it is modified in certain ways. Because simpler models are generally easier to analyze and require fewer known parameters, they are preferred over complex models as long as the ability to reproduce the observed behavior of the system is not compromised [3]. For this reason, many models use a variety of assumptions to simplify the model. When building models of metabolic networks, signaling pathways or gene regulatory networks, one of the most common assumptions is that the molecular species are uniformly distributed inside the cell. This assumption allows one to eliminate diffusion rates from the model altogether because there are no concentration gradients. It should be noted, however, that this assumption may become invalid in some situations [4]. Models that involve enzyme kinetics or transcriptional regulation often make additional assumptions that some of the chemical reactions are at equilibrium or steady state, and these assumptions can further simplify the model without significantly affecting its ability to reproduce observed behavior. When models fail to reproduce observed behaviors, some of the assumptions must be revisited.

One of the most common ways to model a biological system is to describe it as a dynamic system composed of molecular species and reactions. Each reaction is characterized by the species that are consumed and produced and a reaction rate, which is a function of the species concentrations. Once all the reaction rates are defined, the dynamics of the chemical reaction model can be observed through deterministic or stochastic simulations.

A classical example of a chemical reaction model is an enzyme-catalyzed reaction (Fig. 1). Suppose the system of interest has four species: the substrate (S), the enzyme (E), the product (P) and the enzyme–substrate complex (ES). There are three reactions, or events, in this system: E + S → ES, ES → E + S and ES → E + P. Each of the three reactions has a corresponding rate equation. For example, the reaction rate for the reaction, E + S → ES, is k × E × S, where E and S are the concentrations of species E and S, respectively, and k is the rate constant.

Figure 1.

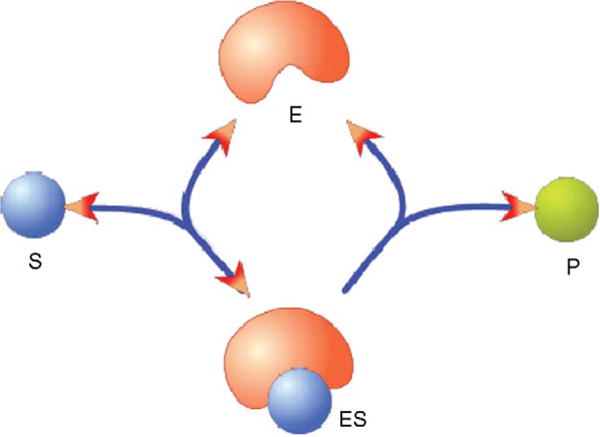
Enzyme-catalyzed reaction. The enzyme, E, converts the substrate, S, to the product, P. The enzyme and substrate form an intermediate complex, ES, which can dissociate back to E and S or form P and free the enzyme, E. This model treats the production of P from the ES complex as an irreversible reaction because the reversible reaction rate may be negligible.

Deterministic chemical reaction models

A mathematical model can be constructed once all the reactions and species that comprise a network are identified. Deterministic mathematical models do not include any random fluctuations, whereas stochastic models do. Differential equation models are one of the most common types of deterministic models.

Differential equation models

Once the rate equations are formulated for each of the reactions, then a deterministic model can be constructed by defining the rate of change for each of the species in the following way:

$$\frac{\mathit{dX}}{\mathit{dt}}=\text{production rate}-\text{consumption rate}$$

In the above formula, X represents a particular species in the system; the term ‘production rate’ represents the sum of the rates for all the reactions where X is produced; the term ‘consumption rate’ is sum of the rates for all the reactions where X is degraded or consumed as a substrate. For example, the differential equation for the species S in Fig. 1 would be as follows:

$$\frac{dS}{dt}=\left(k_1\times ES\right)-\left(k_2\times E\times S\right)$$

The expressions, k₁ × ES and k₂ × E × S, represent the rates for the respective reactions: ES → E + S and E + S → ES (k₁ and k₂ are constants). The complete differential equation model would consist of four such differential equations, one for each of the four species.

Analyses of differential equation models

Being able to represent a system as a set of differential equations allows for analysis by existing numerical methods from the established field of nonlinear dynamics. Numerical integration, or simulation, is used to generate time series trajectories of the species concentrations. Often, a researcher is interested in how the steady state values are affected due to changes in a variable, in which case steady state analysis is used. Steady state analysis can often identify sensitive points where the system changes abruptly [5,6]. Some systems have interesting qualitative behaviors, such as multiple stable states or oscillations, in which case bifurcation analysis can be a valuable tool [7]. Bifurcation analysis has been used to examine the range of parameters in which a biological system can exhibit particular behaviors such as oscillations [8]. Being able to model a biological circuit as a system of differential equations provides an engineer with various techniques such as the ones mentioned above. These techniques give insight on which features and parameters of the system should be adjusted to achieve a particular behavior.

Stochastic chemical reaction models

A natural system consisting of molecular interactions will have inherent noise due to random events. The amount of noise is a property of the system itself, and it may or may not cause significant deviation from the deterministic model. Stochastic models take into account the randomness that exists in natural systems and can be used to investigate whether or not the noise has significant consequences.

One method that is commonly used in this category is the stochastic simulation algorithm (SSA) [9]. In the SSA, the system is perceived as a collection of randomly moving molecular species that interact with one another. Owing to the random motion, the number of interactions that occur within a given time frame will follow a Poisson distribution. Thus, each reaction can be modeled as a Poisson process with the rate parameter, λ, being proportional to the reaction rate. Because it is a Poisson process, SSA deals with discrete values. The model is defined in terms of species and probabilities for the occurrences of each reaction, which are related to the reaction rate. Because SSA uses probabilities, repeated simulations of the same system will produce slightly different results. The average of many repeated stochastic simulations can agree with a deterministic simulation when the variance is not significant or is averaged out [10]. However, there are cases when stochastic and deterministic simulations may provide qualitatively different behaviors of the system. For example, in a system with multiple possible steady states, a deterministic simulation may reach one steady state and remain there indefinitely. By contrast, stochastic simulation may leave one steady state due to random fluctuations and move to another [11]. Therefore, simulating a system stochastically can be used to confirm whether stochastic variation in a system affects its expected behavior significantly.

Matrix representation

Systems that are described by molecular species and reaction rates can be represented using a stoichiometry matrix and corresponding reaction rate equations. The stoichiometry matrix, N, contains rows equal to the number of species in the system and columns equal to the number of reactions in the system. The matrix stores values indicating how much each species has consumed or produced in each reaction. The stoichiometry matrix is such that the matrix product, Nv, will yield a vector with the rates of change for all the species, where v is the vector containing the reaction rates. This matrix representation permits analytical methods from linear algebra to be used to analyze biological networks. One such popular method is flux balance analysis [12].

Flux balance analysis

For many well-studied organisms, such as E. coli, the metabolic reactions in the organism may be known, but the rates, or flux, of the reactions are difficult to measure. Flux balance analysis makes the assumption that the species concentration in a system, such as a bacterial cell, is at steady state. This assumption allows one to conclude that Nv = 0, where N and v include the reactions within the system as well as reactions where species are imported and exported from the system. Solving for v provides one with the flux values at steady state [13]. Owing to multiple solutions to this linear equation, an optimization step is required to find the optimal v. Flux balance analysis optimizes v for a particular objective, such as maximizing protein or ATP production, under the constraint that Nv = 0, thus providing the steady state flux values for all the reactions in that system. As a latter example will briefly illustrate, flux balance analysis can be used in metabolic engineering to examine the change in flux levels because of a change in the reaction network.

Modeling gene regulatory networks

A vast majority of the current synthetic biology designs are strictly gene regulatory networks (GRN) (Fig. 2). GRN models make use of the fact that transcription factor binding and unbinding are much faster than transcription and translation of genes [14]. Owing to this difference in speed, one can assume that the transcription factor binding and unbinding reactions are always at equilibrium. Thus, the rate of production of a protein becomes a function of the equilibrium concentrations of bound and unbound transcription factors.

Figure 2.

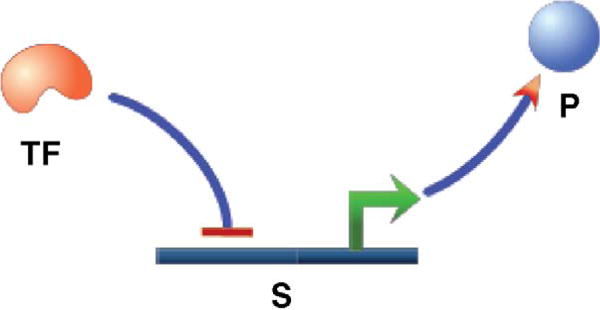
Gene regulation. The transcription factor, TF, binds to the operator sequence and controls the production of the gene product, P. This model is similar to the one shown in Fig. 1; TF takes the place of E, the promoter takes the place of S, and the product, P, remains the same.

As an example, consider a situation where a single gene is regulated by a transcription factor (Fig. 2). The following formula captures the fraction of transcription factors that are bound: θ= TF/(K_d + TF), where TF is the monomeric transcription factor and K_d is the dissociation constant. If TF is an activator that increases the production of the protein, P, then the rate of production of P will be proportional to θ. If TF is a repressor, then the rate will be proportional to (1 − θ). When there is cooperativity or multimerization of the transcription factor, an additional parameter called the Hill coefficient, h, is included in the equation [15]: θ = TF^h/K_d + TF^h. Using this formula, one can model the dynamics of a gene regulatory network by formulating the rate of production and rate of degradation or dilution for each protein in the network. A typical equation for the rate of change of a protein, P, is as follows: dp/dt = (k₁(TF^h/(K_d + TF^h))) − (δ_p × P), where TF is the transcription factor that positively regulates the production of protein P and δ_p is the degradation rate for P. The equation becomes more complex when multiple transcription factors are involved in the regulation of the same gene [11]. One needs to consider all the possible states and formulate an equation for θ as the ratio of active states and all states, where the active states refer to the states where the gene is transcribed [16].

Rate expressions such as the ones described above involve multiple reactions. For example, a single rate expression may represent the binding of transcription factors, the binding of RNA polymerase, transcription, and translation. This simplification may have significant influence on a model’s behavior. One issue is that there is a time delay from the start of transcription to the protein production, which is not captured in the equations above. In some cases, this delay can alter the behavior of the model [17,18]. Another issue is that stochastic fluctuations of the intermediate steps are ignored when using a simplified rate expression, which can affect stochastic simulation results [19]. Nonetheless, in several cases, models with equilibrium assumption have been successful in capturing observed behaviors and predicting new behaviors of GRNs [20–24].

Boolean models of gene regulatory networks

Boolean networks [25] are a frequent alternative to using reactions and species to describe GRNs. In the Boolean framework, each gene can have two states: ‘on’ or ‘off’. Boolean logic is used to determine the state of each gene. For example, the activity of gene X might be defined as Y AND NOT Z, which means that the gene Y activates X but only when the repressor Z is not expressed. Such models provide a higher level view of the gene regulatory network without considering the smaller details. Variants of Boolean models sometimes replace the Boolean functions with sigmoid functions or probabilistic functions [26].

Details versus simplicity in modeling

Protein production is a complex process involving transcription initiation, elongation and translation. One can argue that the modeling technique discussed in the earlier section is too simple to describe the entire process. However, a model should not be penalized for being simple, or parsimonious, provided that it is able to correctly predict experimental data. The type of experimental data therefore determines the level of detail that is demanded from the model. For example, Boolean models may be sufficient to predict microarray data, where the data show whether or not a gene is upregulated as a result of some stimulus, but they may not be enough to show the continuous change in the concentration of some protein. Differential equation models using the equilibrium assumption about transcription factor binding have been shown to predict experimental data generated at steady state [27]. However, when the time course behavior is of interest the equilibrium assumption can be an oversimplification. In addition time course dynamics may also require additional features such as explicitly modeling mRNA production and degradation [18]. As measuring techniques improve, models will necessarily need to become more complex to match the experimental results [28].

Experimental methods to complement modeling techniques

Experiments with quantitative results provide parameter values and validation data to support models. Further, to build a circuit that has been analyzed through mathematical models, an engineer requires circuit building components, or biological ‘parts’, that fit the requirements of the model. Experimental techniques in synthetic biology try to characterize and standardize biological parts so that they can be reliably used to construct a design. Therefore, a discussion on modeling is incomplete without a discussion on experimental techniques in synthetic biology.

Owing to the improvement in engineering techniques in recent years, there are now many examples of synthetic systems that match the qualitative behavior predicted by computational models after some iterations of construction and testing. These include the repressilator [20], a genetic toggle switch [21], a pulse pattern forming device [22]; gene regulation function at a single-cell level [23], a biological concentration detector [24] and a transcriptional AND gate [29]. In general, it is possible to design a genetic system based on simple design principles, but then experimental trial and error is needed to get the system to work properly. For example, promoter and ribosome binding site (RBS) sequences often have to be mutated to select for the desired activity through directed evolution [30]. However, construction of genetic systems from parts that behave as a model predicts has proven difficult for many reasons such as mismatched expression levels between system parts, unknown interactions between the system and host strain, and toxicity from expression of the system. Ideally the synthetic biology community would like to have well-characterized parts with well-defined parameters so that they can be reliably used in models to design systems with confidence.

Toward this goal, many synthetic biologists assemble systems together using standard biological parts. A standard biological part is a genetically encoded object that performs a biological function and that has been engineered to meet specified design or performance requirements [31]. The first working standard was the BioBrick assembly method for the physical composition of biological parts [32], which allowed synthetic biologists to easily assemble multiple parts on a DNA strand (Fig. 3). Biological parts that use the BioBrick standard have become common in the synthetic biology community. The MIT Registry of Standard Biological Parts [33] maintains over 3200 standard biological parts encoded on plasmids that are available to researchers and used by various groups.

Figure 3.

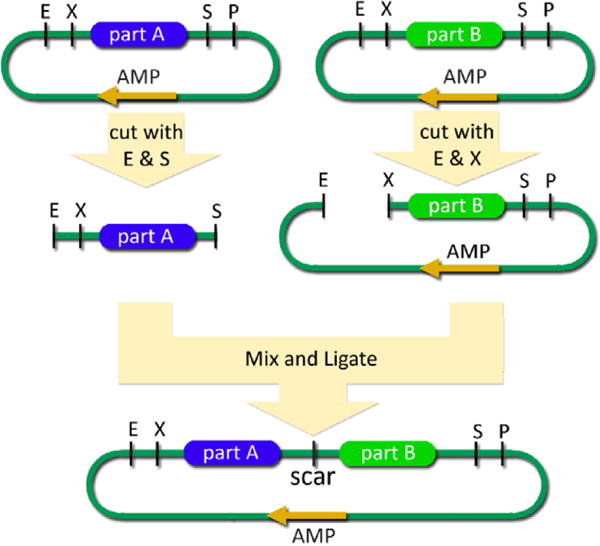
Standard BioBrick Assembly. Parts A and B are ligated together through a standard assembly protocol. The first plasmid is digested with EcoRI (E) and SpeI (S), while the second plasmid is digested with EcoRI (E) and XbaI (X). After ligation, a new plasmid is formed with both parts in tandem with a ‘scar’ which does not contain a restriction enzyme recognition site. The PstI site (P) is left unused in this scheme, but could be used if the parts were assembled in reverse order. (Figure adapted with permission from the MIT Registry of Standard Biological Parts.)

While the standard assembly allows faster construction of circuits, quantitative characterization of parts is still needed for mathematical models. One recent example of such an effort is the development of standard measurement kits for characterizing BioBrick promoters and ribosome binding sites [34]. Because experimental measurements vary greatly between laboratories, these measurement kits allow for the measurement of a promoter or RBS of interest relative to a reference standard. The activity of a given promoter or RBS can be reported in standard units. There are some limitations to measurement kits that include context-dependence of parts within a particular system, host strain and media. However, the overall benefit for having well-characterized parts is that a researcher can model the activity of a particular part and decide whether or not to use it in their designed system.

Modeling software for synthetic biology

Because synthetic biology encompasses different disciplines, software can help bridge the gap between experts in different areas, particularly computational and experimental. While systems biology software [35–37] provide an array of computational analysis features as well as visual interfaces, synthetic biology requires tools that utilize the notion of biological parts, support parts database(s) and include data that characterize the kinetic behavior of parts. The first application that addressed these goals was BioJade developed by Goler [38]. BioJade is a software tool that allows users to visually build and simulate synthetic biology networks. The networks resemble electrical engineering diagrams, BioJade uses the MIT Registry of Parts [1] to obtain the list of biological parts. Parts in BioJade have specific functions which are loaded from the database; although such well-defined parts do not exist in the database at this time, it is the hope that such a detailed database will become available in the near future. A recent application, Athena (http://www.codeplex.com/athena), has been created with the same expectation. Athena introduced an interface for constructing modules, or biological circuits that can connect to one another to form larger networks. Athena has been succeeded by TinkerCell (http://www.tinkercell.com), which also makes use of modules. The visual representations of the quantitative models in TinkerCell are similar to the cartoon diagrams of biological networks (Fig. 4). TinkerCell models contain details about each part, such as promoter or RBS strengths. It is anticipated that such parameters will be obtained directly from database(s) in the future.

Figure 4.

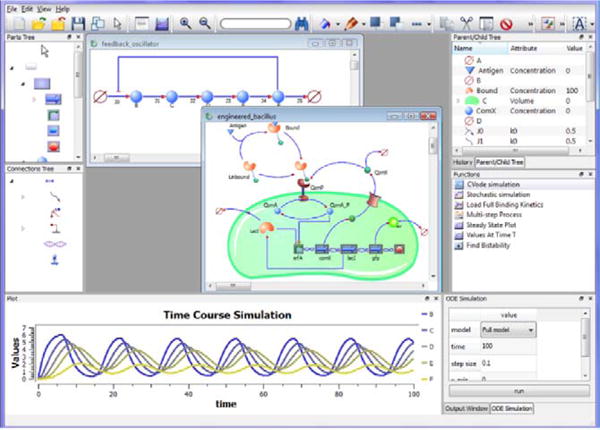
Screenshot of TinkerCell. The screenshot shows two models that are open. One (top left) is a feedback oscillator, and its simulated output is plotted below. The other window (bottom right) is a model consisting of a cell, membrane proteins, and gene regulation. See http://www.tinkercell.com/ for more information.

Case studies

The next few sections will discuss selected synthetic biology examples that will elucidate many of the concepts discussed in the earlier sections, particularly the use of modeling to design biological circuits.

Oscillators

The earliest example of using mathematical modeling to design and build a synthetic system was the repressilator, three transcriptional repressor systems engineered together to make an oscillating system [20]. The repressilator consists of three repressor genes connected in a feedback loop, such that each gene represses the next gene in the loop, and is repressed by the previous gene (Fig. 5). Green fluorescent protein (GFP) is periodically activated as a readout of the oscillating state in individual cells. The design of the repressilator started with a simple mathematical model of transcriptional regulation in this oscillating system. Because not enough was known about the molecular interactions inside the cell to make a precise description of this system, the authors instead identified possible classes of dynamic behavior and determined which experimental parameters should be adjusted to obtain sustained oscillations. To do this, the values of several parameters were determined, including the transcription and translation rate, degradation rates of messenger RNA and protein and the number of proteins necessary to half-maximally repress a promoter. The authors found that stable oscillations were favored by strong promoters coupled to efficient ribosome-binding sites, tight transcriptional repression, cooperative repression characteristics and roughly equivalent mRNA and protein degradation rates. Several control experiments of this system showed that oscillations occurred only when certain parameters values were used, illustrating the importance of modeling complex synthetic systems before their engineering and subsequent characterization.

Figure 5.

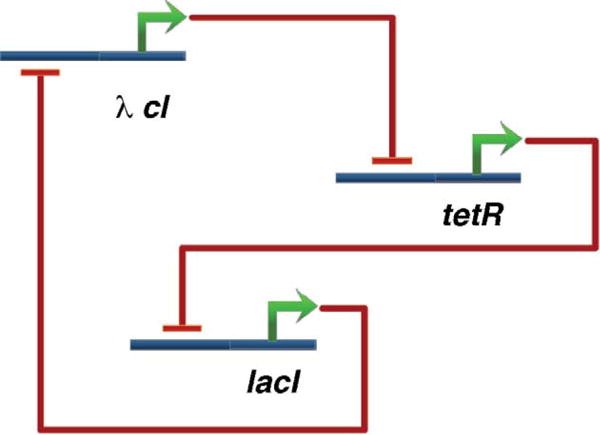
The repressilator constructed by Elowitz and Leibler [20]. Three genes produce repressor proteins. The cycle of repression causes the network to oscillate.

A second example of engineering a new biological function is the robust genetic oscillator using a combination of positive and negative feedback loops (Fig. 6) in E. coli [18]. Having previously engineered oscillatory behavior in bacterial cells [20], the work primarily focused on the design principles that would ultimately lead to robust and tunable oscillations. From computational simulations, it was discovered that a full-scale model that accounted for intermediate steps such as translation and proteins binding to DNA were necessary for the model to accurately predict oscillatory behavior. This revelation also highlighted the importance of a time delay in the negative feedback loop of the circuit to achieve sustainable oscillation, a well-known phenomenon in control engineering. To confirm this phenomenon, an oscillatory circuit was created using a single negative feedback, where the delay was provided by the transcription, translation and protein folding. While negative feedback with a delay was sufficient for producing oscillations, the cycles were irregular, and the circuit was sensitive to parameter changes. Modeling the system revealed that adding positive feedback loops to the design allowed the oscillations to be more robust to changes in parameters. In this design consisting of positive and negative feedback, the strengths of the feedbacks controlled the period of the oscillations. Construction and experimental observation of the proposed circuit confirmed these predictions. It was shown that altering levels of each of the two inducers resulted in different oscillatory periods, thus demonstrating the effect of the feedback loops on tunability.

Figure 6.

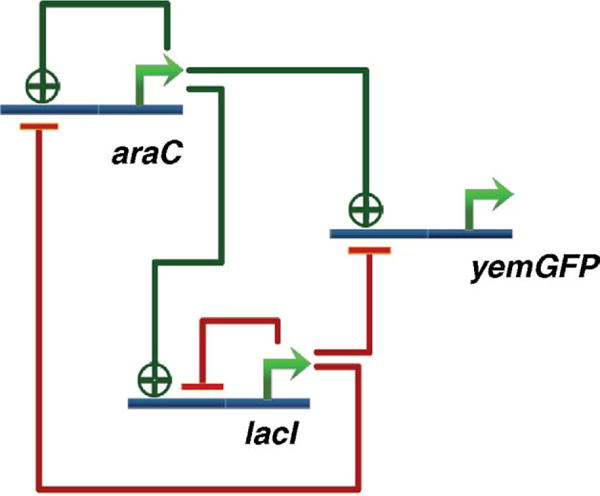
The robust oscillator constructed by Stricker et al. [18]. The combination of the negative and positive feedback causes the network to be robust to parameter changes. The strength of the repression (by lac inhibitor) can be controlled by the lactose analog, IPTG.

Incoherent feed-forward network

Feed-forward networks are small three member networks that are found in abundance in natural genetic networks [39]. Different types of feed-forward networks have different properties when analyzed through differential equation models using Hill equations [40]. An incoherent feed-forward network (I-FFN) is the one where an inducer can directly activate or indirectly repress the expression of a downstream protein. Basu et al. [22] had demonstrated that the I-FFN using five genes can behave as a biological concentration sensor, where gene expression is minimal at very high and very low concentrations of an inducing molecule. In a later work, mathematical models of GRNs were used to predict that an I-FFN with three-gene network can achieve the same behavior. The synthetic construct used T7 RNA polymerase (RNAP), metJ and GFP (Fig. 7) [24]. The steady state values of the gene products in this synthetic network [24] are summarized by the following equations:

$$\mathit{met}j\propto \frac{T7\mathit{RNA}{P}^{h_1}}{K_d+T7\mathit{RNA}{P}^{h_1}};\mathit{GFP}\propto \frac{T7\mathit{RNA}{P}^{h_1}}{K_d+T7\mathit{RNA}{P}^{h_1}+\mathit{met}{j}^{h_2}}$$

The above mathematical model of the incoherent feed-forward network illustrates that it can behave as a concentration sensor because GFP is upregulated only for an intermediate concentration of T7 RNAP; too low or too high levels of T7 RNAP result in the downregulation of GFP. Additionally, these models showed that peak location and peak height of gene expression, with respect to inducer concentration, could be tuned by varying the affinity at the inhibitory binding site. By introducing mutations to promoter sites in an attempt to alter inhibitory strength, the ability to tune the peak location and peak height were verified. Subsequent assembly and transformation of three feed-forward loop variants, each comprising unique biological components, in E. coli allowed for further experimental validation of the predicted behavior of the network [24].

Figure 7.

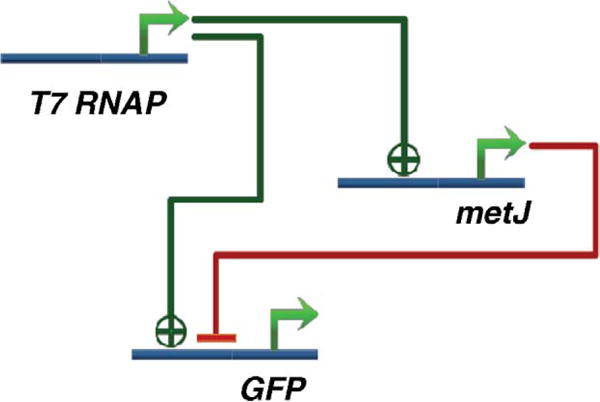
The incoherent feed-forward network constructed by Entus et al. [24]. The T7 RNA polymerase (RNAP) activates metJ and GFP, but metJ represses GFP. Thus, T7 RNAP directly activates GFP but indirectly repressed GFP, causing T7 RNAP to act as an activator or a repressor depending on its concentration.

Antimalaria drug

While bacteria have been transformed with foreign genes to use them as a factory for the production of a protein or metabolite, the ambition of synthetic biology is to be able to do the same for entire pathways. This ambition is exemplified by the genetically engineered Artemisinic acid producing yeast [2]. Artemisinic acid is the precursor to Artemisinin, an effective medicine against malaria that is produced by the plant Artemisia annua L. Extracting sufficient amount of Artemisinin from the plant requires large farms and a large amount of plant matter to extract sufficient amounts of this chemical. The ideal alternative was to engineer a microbe to produce the compound more effectively. The primary task in this process was identifying the various enzymes that are required in the production of Artemisinin. E. coli was originally engineered to produce part artemisinic acid from acetyl-CoA [41]. However, one of the necessary enzymes was found to be of the cytochrome P450 family, a Eukaryotic protein for which yeast was a more suitable host. The engineered yeast is capable of producing 500-fold more artemisinic acid than the plant from which it was derived [42]. The precursor to artemisinic acid, amorphadiene, was still obtained from E. coli. Flux balance analysis of the E. coli central metabolism allowed reengineering the pathway to increase the production of amorphadiene [43]. This was achieved by building a large model composed of 238 reactions and 184 metabolites. Sufficient amounts of data must be obtained to define the parameters of such large models; for this work, the data came from mass spectrometry performed on 13 amino acids from cells that were grown in ¹³C glucose solution. Using nonlinear optimization, different flux values were obtained that can maximize the production of amorphadiene. Removal of two reactions from the set of solutions increased amorphadiene production by 24% and 9% [43].

Modular antitumor bacteria

A successful demonstration of a modular synthetic system is the engineered E. coli that is capable of invading tumor cells [44]. The work is based on the observation that various bacteria localize in areas around tumor growth for various reasons such as nutrients, lower immune system activity and anaerobic environment. In addition, these bacteria have the innate ability to detect their own cell density through a quorum sensing system. Hence, the quorum sensing system provides a means for detecting the areas of tumor growth because those regions will have high cell density. The quorum sensing system was used as an input to an antitumor module. The antitumor module was composed of the invasin gene that allowed the bacteria to invade various mammalian cells.

Future directions

The field of synthetic biology is heading in a direction that will allow faster and more precise construction of biological circtuits.

Standardized parts and computer-aided design

Efforts to quantitatively characterizing parts, such as measuring promoter strengths, and building databases of parts that conform to a standard are the first steps toward building database(s) of standardized and well-characterized biological parts. The characterization of these parts will allow the construction of computational models that would correctly represent the real system, and the standardization of the parts, in addition to aiding the models, also allow the parts to be assembled more efficiently. With computer-aided design and analytical tools, models can be built and analyzed to test whether they exhibit the desired behaviors. Standards also play an important role in the representation of computational models. Standard formats for storing computational models will allow efficient translation of information from database(s) to mathematical models. Although standards such as the Cell Markup Language [45] and Systems Biology Markup Language [46] exist to describe the dynamics of the model, it is not yet clear whether these file formats will suffice for synthetic biology. An ideal file that describes a synthetic biology model should store the dynamical description of the model as well as information required for the construction of the model. There are on-going efforts to establish a standard language for describing the physical makeup of a synthetic part [47] as well as standard visual representations [48]. Including dynamical properties of parts along with standards that describe physical makeup may be a more difficult task. Questions such as what parameters are required to sufficiently model a promoter or what aspects of a part is changed when it is used in different species have yet to be answered [49]. Progress in fundamental science and engineering techniques will affect the characterization of biological parts.

DNA synthesis

One of the hopes of the synthetic biology community is to shift from reliance on laborious classical genetic engineering techniques to DNA synthesis [1]. With DNA synthesis, the process involving design and modeling can be easily extended to construction because the software that generates the models can also output the complete sequence encoding the models (third step in Fig. 8). The sequence can be directly synthesized and placed inside a candidate host cell, thus greatly reducing the time and labor required for the construction of the actual biological circuit. Such rapid construction procedure will allow engineers to build and test variants of the same model and test which variant works best. Further, numerous variants of a part, such as a promoter or RBS, can be synthesized to test which mutant is most suitable for a particular circuit; constructing such a large number of mutants would be extremely time consuming without DNA synthesis technology. The cost of DNA synthesis is the major obstacle at present, although progress is being made to make synthesis more affordable [50].

Figure 8.

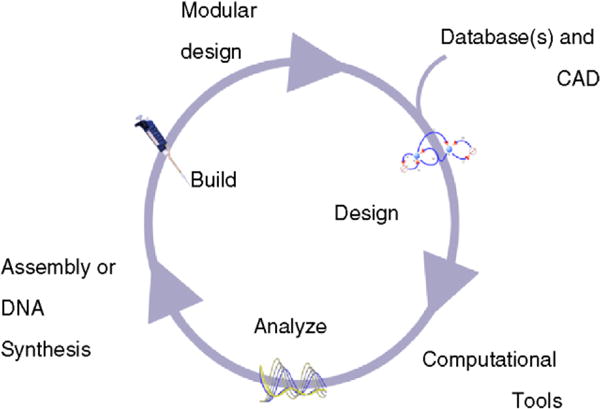
A simplified design process for synthetic biology that would be possible in the future. Using computer-aided design (CAD) and database(s) of parts, a synthetic biologist can create multiple models that satisfy his or her idea. Using computational tools, the models can be analyzed in detail and modified as needed. Using efficient assembly procedures or DNA synthesis technology, the models can be built. If the design is modular, then the working product can be reused in another model.

Modularity

Modularity is an integral concept in synthetic biology, as it is in any engineering discipline. While a precise definition of a ‘module’ with respect to biology is still unclear, from the engineering perspective, a module is something that retains its function independent of where it is used [51,52]. A simple example would be the incoherent feed-forward network discussed earlier in this article. The feed-forward network functions as a concentration detector. If this network is modular, then it can be used as an input to another system that needs a concentration-dependent response; the additional connections with the other system should not affect the function of the feed-forward network. The advantage of such modularity is that it allows complex networks to be built by connecting existing networks with one another (last step in Fig. 8). It is possible that the network will retain its function as long as the demand, or impedance, by the system that it is connected to is not substantial. Further experimentation is needed to identify the requirements for a synthetic biological network to be considered a ‘module’.

Synthetic protein networks

Although the vast majority of synthetic networks are gene regulatory networks, that is not a limitation of synthetic biology. Gene regulatory networks are common because of the ease by which one gene can be placed under the control of another by simply changing the cis-regulatory elements. Building synthetic protein networks involves modifying protein–protein interactions. One elegant way to achieve this is by using synthetic protein scaffolds that bind to the proteins of interest. The scaffold will bring the proteins in the vicinity of one another, increasing the rate at which they interact. This concept has been demonstrated by modifying the MAPK pathway in yeast [53].

Faster and more diverse reporters

Just as an electric engineer makes use of measuring devices such as multimeters or visual outputs from light emitting diodes, measuring devices are integral to synthetic biology. Current measurement methods rely on fluorescent proteins as reporters. Fluorescent proteins capable of producing different colors [54] allow a synthetic biologist to monitor activities inside a cell. There are two inherent problems with these reporters. One is that they can consume a significant amount of the cell’s resources, which can disrupt the cell’s behavior. The other is that there is a significant delay between the start of transcription and visible fluorescence owing to the time required for transcription, translation and maturation of the fluorescent protein. This lag time is in the order of minutes [55], which may be too slow to measure many of the activities inside a cell. As an alternative, molecular events can be reported using methods such fluorescence resonance energy transfer [56] or RNA aptamers [57], which can be faster and may not drain as many resources as protein synthesis. Future methods for reporting molecular events or even quantifying biological parts may depend on such methods rather than expression of fluorescent proteins.

Networks robust to parameters

One of the issues when moving from a computation model to the actual constructed network is that the parts used in the network may have slightly different behavior depending on environmental conditions. Further, there may be intrinsic noise in the system, which may also be dependent on other variables. Taking every possible parameter into account will generally be impractical; the more elegant solution is to design the model such that it produces the desired behavior for a wide range of parameter values and different noise levels. It is possible to design such models; an example of such a design is the oscillator utilizing positive and negative feedback [18] that was discussed earlier in this article.

Role of evolution in synthetic biology

Natural selection can be a beneficial or detrimental force in the construction of synthetic biological circuits. Synthetic circuits burden the engineered cells with additional load that usually reduces their growth rate. Therefore, mutants that do not have a functional circuit may have a growth advantage and outcompete the functional cells. Therefore, natural selection works against the synthetic biologist. A situation where natural selection can work in favor of the engineer is when the engineer is using it as a method for optimizing a circuit [30]. The two situations are described below.

One problem with engineered circuits or systems in synthetic microbes is their evolutionary stability in the absence of a selective environment due to mutation and natural selection. A recent simulation study predicted that the time it takes a nonfunctional mutant of a synthetic microbe to become the majority of the population is a function of the growth rate difference between the mutant and wild-type, circuit size, circuit architecture and mutation rate [49]. It is clear we need to have better design principles for engineering evolutionary robust circuits and selective regimes for maintaining synthetic circuits over evolutionary time. It may be possible to measure the evolutionary stability of different biological parts and use this evolutionary robustness parameter in a computer model so that a synthetic system can be designed to maximize its evolutionary robustness.

By contrast, directed evolution can be used to optimize genetic circuits and engineer proteins through mutation and natural selection. Directed evolution has been common in areas such as protein engineering, where novel proteins are engineered by screening for the desired function from a library of millions of random proteins [58]. The same concept has been used to evolve a nonfunctional genetic circuit containing improperly matched components into a functional one [30]. Because synthetic circuits are made of parts optimized in their natural context, the combination of mathematical modeling and directed evolution offers an approach to identify mutational targets and selection for properly functioning circuits [59].

Conclusion

Although in its infancy, the field of synthetic biology has great potential. With the conjunction of well-characterized biological parts, computer-aided design tools, mathematical modeling and efficient methods for assembling or synthesizing the sequence of parts, synthetic biology brings the capability for using cells as devices, much in the same manner in which electronic or mechanical devices are used. This capability can bring novel ways of resolving problems ranging from health issues to environmental issues; cells can be engineered to combat cancer, produce drugs, detect pollutants, catalyze reactions such as carbon fixation or detoxification, or produce environmentally safer fuel.