Contextual processing in unpredictable auditory environments: the limited resource model of auditory refractoriness in the rhesus

Refractoriness may reflect the gradual decay of an auditory perceptual short-term memory trace that mirrors expenditure and gradual recovery of a limited physiological resource. Our findings suggest that items are cleared from the trace not only by recovering expended resource but also by partially overwriting traces of previous tones when little resource remains. This nonlinearity and the ensuing shift toward a single-item memory trace provide new perspectives on refractoriness and performance on short-term memory tasks.

Abstract

Auditory refractoriness refers to the finding of smaller electroencephalographic (EEG) responses to tones preceded by shorter periods of silence. To date, its physiological mechanisms remain unclear, limiting the insights gained from findings of abnormal refractoriness in individuals with schizophrenia. To resolve this roadblock, we studied auditory refractoriness in the rhesus, one of the most important animal models of auditory function, using grids of up to 32 chronically implanted cranial EEG electrodes. Four macaques passively listened to sounds whose identity and timing was random, thus preventing animals from forming valid predictions about upcoming sounds. Stimulus onset asynchrony ranged between 0.2 and 12.8 s, thus encompassing the clinically relevant timescale of refractoriness. Our results show refractoriness in all 8 previously identified middle- and long-latency components that peaked between 14 and 170 ms after tone onset. Refractoriness may reflect the formation and gradual decay of a basic sensory memory trace that may be mirrored by the expenditure and gradual recovery of a limited physiological resource that determines generator excitability. For all 8 components, results were consistent with the assumption that processing of each tone expends ∼65% of the available resource. Differences between components are caused by how quickly the resource recovers. Recovery time constants of different components ranged between 0.5 and 2 s. This work provides a solid conceptual, methodological, and computational foundation to dissect the physiological mechanisms of auditory refractoriness in the rhesus. Such knowledge may, in turn, help develop novel pharmacological, mechanism-targeted interventions.

NEW & NOTEWORTHY

Refractoriness may reflect the gradual decay of an auditory perceptual short-term memory trace that mirrors expenditure and gradual recovery of a limited physiological resource. Our findings suggest that items are cleared from the trace not only by recovering expended resource but also by partially overwriting traces of previous tones when little resource remains. This nonlinearity and the ensuing shift toward a single-item memory trace provide new perspectives on refractoriness and performance on short-term memory tasks.

patients with schizophrenia (SZ) suffer from sensory and perceptual deficits (Leitman et al. 2010) that can be described as an impairment to adjust processing of local stimulus features to the stimuli's immediate sensory context (Dakin et al. 2005; Green et al. 2009; Javitt 2015; Must et al. 2004; Roth et al. 1980; Shelley et al. 1999; Yang et al. 2013). In the auditory domain, contextual deficits can manifest as an impairment in using past auditory information to optimize processing of upcoming sounds. For example, individuals with SZ show reduced auditory prepulse inhibition and adaptation (Braff et al. 1992) and suffer from decreased perceptual accuracy in delayed pitch discrimination (Strous et al. 1995) and speech-sound categorization tasks (Cienfuegos et al. 1999). Such low-level deficits may be passed on to later processing stages and have been hypothesized to affect a range of diverse cognitive skills, such as speech comprehension or the extraction of emotional context from prosody (Hoekert et al. 2007; Javitt 2009; Kantrowitz et al. 2013).

An important electrophysiological finding that speaks to abnormal integration of past auditory information is altered auditory refractoriness in SZ (Rosburg et al. 2008; Shelley et al. 1999). Auditory refractoriness refers to the phenomenon that the amplitudes of certain electroencephalography (EEG) components are smaller for sounds that are preceded by shorter periods of silence. The term auditory refractoriness is typically only used to refer to EEG components or their generators, i.e., postsynaptic potentials. It is usually considered to be distinct from stimulus-specific adaptation (Ulanovsky et al. 2003) or forward suppression (Brosch and Schreiner 1997; Wehr and Zador 2005) that describes related effects for spiking activity. It is further important to note that although the term auditory refractoriness was inspired by the concept of the refractory period between action potentials, the two phenomena are not related.

Refractoriness may reflect the formation and gradual decay of a basic perceptual short-term memory trace (Lu et al. 1992a; Näätänen and Picton 1987; Shelley et al. 1999). In healthy individuals, for example, the amplitude of the N1, a frontocentral EEG component that peaks between 80 and 120 ms after stimulus onset (Näätänen and Picton 1987), increases as a function of time from the onset of the last auditory stimulus (stimulus-onset asynchrony; SOA) (Davis et al. 1966; Lu et al. 1992b; Pereira et al. 2014) up to about 8–12 s. Although the mechanisms causing refractoriness and its functional role are still a matter of debate, it is an easily quantifiable marker of how sounds are processed differently depending on the time and identity of previous sounds (Briley and Krumbholz 2013). Individuals with SZ have approximately normal-sized N1 for short SOAs but show a blunted increase with longer SOAs (Shelley et al. 1999). As a result, EEG responses of individuals with SZ do not discriminate between different sensory contexts as well as EEG responses of healthy individuals.

In a groundbreaking study, Javitt et al. (2000) described auditory refractoriness of the presumed P1 and N1 homologs in the nonhuman primate and established this species (i.e., rhesus macaque) as one of the most important model systems of auditory refractoriness and of deficits in auditory refractoriness in SZ. Building on their findings, the current study addresses three main points about the refractoriness of auditory evoked potentials (AEP) in the rhesus: 1) provide a detailed quantification of refractoriness of eight recently identified middle- and long-latency components (Teichert 2016) and 2) use a paradigm that assesses refractoriness in isolation of other confounding factors such as predictive coding. This approach ultimately led us to 3) develop a more flexible and mechanistic model of auditory refractoriness.

Current models of auditory refractoriness provide mostly descriptive fits to response amplitude as a function of either SOA (Briley and Krumbholz 2013; Lu et al. 1992b) or repetition number (Fruhstorfer et al. 1970; Fruhstorfer 1971; Ritter et al. 1968; see materials and methods, Limited resource model of auditory refractoriness), thus making measurements either while the system is approaching a steady state or after the steady state has been reached. However, the paradigm used in this study was actively designed to prevent convergence into a steady state. Hence, it was necessary to develop a more detailed theoretical and computational framework capable of making predictions about response amplitude for any random history of previously presented sounds. To that aim, we developed a simple mechanistic model, the limited resource model of auditory refractoriness, aimed at quantifying the biological processes that underlie auditory refractoriness.

It is currently assumed that refractoriness of EEG responses arises from the recovery cycle or refractory period of its neural generators (Budd et al. 1998; Ritter et al. 1968). The current approach expands this framework by introducing ideas from models of short-term presynaptic depletion that view the number of readily releasable vesicles in a presynaptic terminal as a limited resource, only part of which is released each time an action potential arrives (Regehr 2012; Zucker and Regehr 2002). On the basis of analogy to this process, the crucial novelty of the limited resource model is the possibility that not all of the limited resource, in this case an unspecified physiological variable that determines “generator excitability,” is expended each time a tone is processed. Instead, the model explicitly allows for the possibility that each tone reduces generator excitability only by a certain fraction (Fig. 1).

Fig. 1.

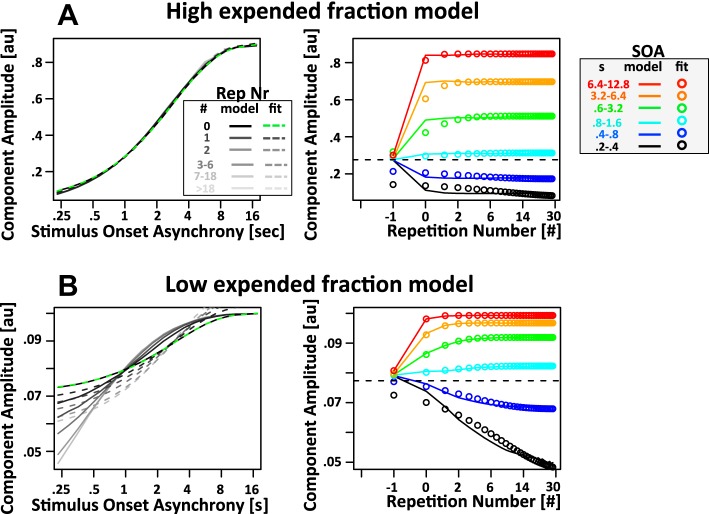
Limited resource model. Depicted are 2 instantiations of the limited resource model of auditory refractoriness. Each tone (blue dot) expends a certain fraction U of a hypothetical limited resource that determines “generator excitability.” The measured EEG amplitude is believed to be proportional to the total amount of resource expended (red). After each tone, the resource is recovered with the time constant τ (identical in both variants of the model). The black line corresponds to the fraction of the resource currently available. A: if the expended fraction U is high, predicted response amplitude reaches a steady state almost instantaneously at the first use of a specific SOA. B: if U is small, EEG response amplitude gradually approaches an asymptotic value over the course of many repetitions of the same SOA. au, Arbitrary units.

If each tone expends close to 100% of the resource, response amplitude will adjust to the new SOA almost instantaneously, i.e., after the first use of a specific SOA (Fig. 1A, left). If, in contrast, only a small amount of the resource is expended, response amplitude will adjust gradually over the course of many repeated presentations of the same SOA (Fig. 1B, left). As outlined in more detail in results, Properties of the limited resource model of auditory refractoriness, and Fig. 2, this limited resource model can account for a rather broad range of behaviors. Also, in addition to enabling the quantification of time constants of auditory refractoriness in a random auditory environment, it will answer the interesting mechanistic question of whether each tone depletes generator excitability completely or only by a certain fraction. This last point will be important to determine if two distinct types of response reduction, as a function of SOA (Fig. 2, A and B, left) and repetition number (Fig. 2, A and B, right), can be explained simultaneously within the framework of the limited resource model.

Fig. 2.

Properties of limited resource model. Shown are simulated responses from the limited resource model with a recovery time constant τ of 2 s. A and B, left: simulated component amplitude as a function of SOA split by repetition number (Rep Nr; black and shaded lines). Right, response amplitude as a function of repetition number split by SOA (black and colored lines). Note that a repetition number of 0 corresponds to the tone following the first time a specific SOA is presented in a series of identical SOAs. Furthermore, a repetition number of −1 corresponds to all tones that preceded tones with a repetition number of 0. Because of the design of the experiment, these trials have a random SOA. Hence, the component amplitude for a repetition number of −1 is approximately identical to the mean over all trials (dashed line). An exponential decay function with time constants of 2 s (same as recovery time constant τ) was fit to the simulated data. In left panels, the fits with λ_SOA = 2 s are indicated by dashed lines; in right panels, the fits with λ_Rep# = 2 s are indicated by colored circles. Note the logarithmic x-axis in both cases. As a result, the exponential recovery functions have a somewhat unusual sigmoidal shape. A: in the high expended fraction model, the effect of SOA is largely independent of the number of repetitions of a particular SOA. The dependence of component amplitude on SOA is captured well by the fits with λ_SOA = 2 s. In contrast, component amplitude as a function of repetition number reaches an asymptote almost instantaneously with the very first use of a particular SOA (repetition number = 0). Hence, the fits with λ_Rep# = 2 s do not capture the simulated data (see circles for deviation of fit from simulated data). B: the low expended fraction model reveals a somewhat complementary pattern of results: the dependence of amplitude on repetition number is captured reasonably well by fits with λ_Rep# = 2 s, especially for tones with SOA above 0.4 s (blue, cyan, green, orange, and red color). Fits become even better because expended fraction is further reduced toward 0 (data not shown). In contrast, the dependence of amplitude on SOA is not captured by fits with λ_SOA = 2 s (note the stark misfit of the dashed lines). The only exception is the data for the first presentation of a particular SOA (repetition number = 0). In this case, the dependence of amplitude on SOA is captured perfectly by a time constant λ_SOA = 2 s (green dashed line).

In summary, this study provides a detailed phenomenological description and mathematical framework of auditory refractoriness using cranial EEG in the rhesus. The overarching goal was to develop a translational platform that allows recording of largely homolog auditory evoked EEG responses in combination with simultaneous intracranial recordings and local pharmacological interventions to further dissect the physiological mechanisms. The striking feature of the data is that the effects of past tones cannot be reduced to a simple linear superposition of responses to past sounds.

MATERIALS AND METHODS

The analyses reported were performed on data that were used in a previous article (Teichert 2016). There is no overlap between the analyses performed in the two articles. Experimental methods are described in more detail in that same previous article (Teichert 2016).

Subjects.

Experiments were performed on four adult male macaque monkeys (Macaca mulatta; monkeys R, W, J, and S). The treatment of the monkeys was in accordance with the guidelines set by the U.S. Department of Health and Human Services (National Institutes of Health) for the care and use of laboratory animals. All methods were approved by the Institutional Animal Care and Use Committee at the University of Pittsburgh. One animal (monkey R, 10.5 kg, 12 yr) had previously performed simple cognitive tasks in a different laboratory. Preliminary data collected from monkey R helped optimize the setup and auditory paradigms used in this study. The other three animals were between 5 and 6 yr old and weighed between 8 and 9 kg at the time of the experiments. Up until the first day of recording for the current experiments, these animals were not exposed to any of the auditory paradigms.

Cranial EEG recordings.

The rhesus EEG recording system was designed to be as similar as possible to that for human scalp recordings while reducing the setup times and facilitating the possibility of stable and reproducible long-term recordings over the period of many months. Building on an approach spearheaded in the laboratory of Jeff Schall (Woodman et al. 2007; Purcell et al. 2013), EEG electrodes manufactured in-house from either medical grade titanium (monkeys R and S) or medical grade stainless steel (monkeys J and W) were implanted in 1-mm-deep nonpenetrating holes in the cranium. All electrodes were connected to a 32-channel Omnetics connector embedded in acrylic at the back of the skull. The different animals had between 21 and 33 electrodes implanted that formed regularly spaced grids covering roughly the same anatomy covered by the international 10-20 system (Teichert 2016).

Experimental setup.

All experiments were performed in two small (4 ft. wide by 4 ft. deep by 8 ft. high) sound-attenuating and electrically insulated recording booths (Eckel Noise Control Technology). Animals were positioned and head-fixed in custom-made primate chairs (Scientific Design). Cranial EEG potentials were recorded with a 32-channel digital amplifier system (RHD2000; Intan Technologies).

Experimental control was handled by a Windows personal computer running an in-house modified version of the MATLAB software package MonkeyLogic. Sound files were generated before the experiments and presented by a subroutine of the MATLAB package Psychtoolbox. The sound files were presented using the right audio channel of a high-definition stereo PCI sound card (M-192; M-Audiophile) operating at a sampling rate of 192 kHz and 24-bit resolution. The analog audio signal was then amplified by a 300-W amplifier (GX3; QSC Audio Products). The amplified electric signals were converted to sound waves using either two insert earphones with foam plugs (ER2; Etymotic; monkeys J and R) or a single-element 4-in. full-range driver (Tang Band W4-1879; TB Speaker) located 8 in. in front of the animal (monkeys W and S).

To determine sound onset with high accuracy, a trigger signal was routed through the unused left audio channel of the sound card directly to one of the analog inputs of the recording system. The trigger pulse was stored in the same stereo sound file and was presented using the same function call. Hence, any delay in the presentation of the tone would also lead to an identical delay in the presentation of the trigger. Thus sound onset could be determined at a level of accuracy that was limited only by the sampling frequency of the recording device (5 kHz, corresponding to 0.2 ms).

Auditory paradigm.

The study used 55-ms pure tones with 5-ms linear rise/fall times. Pure tones rather than clicks or pink noise were used to maximize similarity to clinical studies in humans that often use pure tones (Shelley et al. 1999). The tones had different frequencies ranging between 500 and 4,000 Hz and were presented at 80 dB. During each experimental session, we presented 11 different frequencies spaced linearly in log₂ space. The lowest tone was randomly selected from the interval between 500 and 800 Hz; the highest tone was drawn randomly from the interval of 3,000 to 4,000 Hz (Fig. 3A). Time between individual tone onsets (stimulus-onset interval, SOA) ranged between 0.2 and 12.8 s. Tone presentations were structured into blocks between 9 and 12 min in duration (Fig. 3B). A block was terminated after the randomly determined time criterion or after 600 tone presentations, whichever happened first. The SOAs within each block were randomly drawn from one of two truncated exponential distributions. Each block used two exponential distributions, one with a shorter time constant (300–600 ms) and one with a longer time constant (1,000–2,000 ms). The time constants of the two exponential distributions were drawn randomly at the beginning of each block. At the same time, the program also generated two sequences of random numbers that determined SOA and tone identity (a number between 1 and 11 that corresponded to 1 of the 11 previously generated sound files). A sequence of binary values determined whether the specific combination of tonal frequency and SOA that determined the last tone would be repeated for the next tone, or whether the next tone would be determined by the next pair of SOA and tone identity. In the so-called “random environment,” the likelihood of repeating a tone identity-SOA combination was 10%. In the “regular environment,” the likelihood of repetition was 90%, and the time as well as identity of the upcoming tone could be predicted with high accuracy. Blocks of random and regular environment were presented in an alternating order. As outlined in the Introduction, the current study focused exclusively on the responses in the random condition. The paradigm is referred to as “response suppression kernel,” or RS kernel paradigm.

Fig. 3.

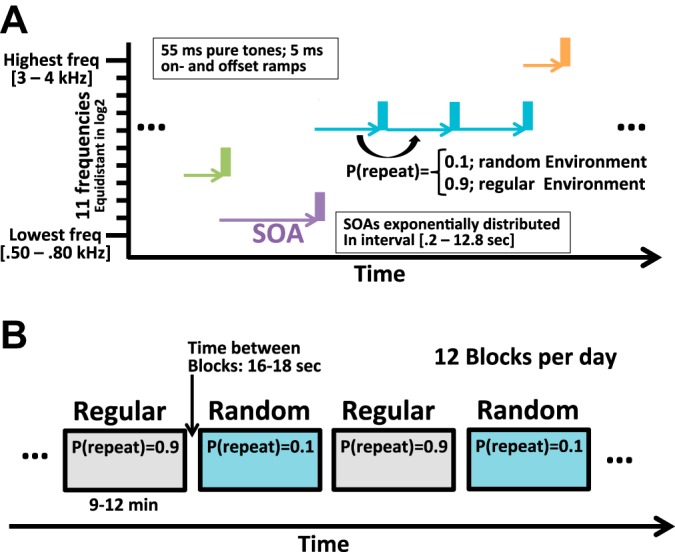
Auditory paradigm. A: subjects passively listened to tones of random auditory frequency presented at random times. During each recording session a new set of 11 tones was generated. The lowest (highest) tone had an audiofrequency randomly picked between 500 and 750 Hz (3,000 and 4,000 Hz). The other tones were spaced equidistantly in log₂ space. Stimulus onset asynchronies were drawn from a mix of 2 exponentially truncated distributions with time constants between 300–600 and 1,000 to 2,000 ms, respectively. A minimum of 200 ms was added to all SOAs, and values above 12.8 s were set to 12.8 s. An auditory event was determined by tone identity (i.e., auditory frequency) and the preceding SOA. B: in alternating blocks of 9–12 min in duration, tones were presented in either a regular or a random environment. In the regular environment, an SOA-tone pair had a 90% chance of being repeated. In the random environment, the probability of a repeated pair was 10%.

Preprocessing.

Onset of the tones was identified from the analog input channel that carried the trigger signal from the left audio channel. The 32-channel time-continuous raw data were downsampled from 5,000 to 500 Hz. The downsampled data were then filtered using a 256-point noncausal digital low-pass finite input response (FIR) filter (firws function from EEGLAB toolbox, Blackman window, high-frequency cutoff 70 Hz, transition bandwidth 21 Hz). The filtered data were then cut into short epochs around the onset of each sound (−150 to 750 ms at 500-Hz sampling rate) and saved in a data format that was compatible with the statistics software R (R Development Core Team 2009).

Because the tone presentations evoked responses whose duration exceeded the shortest SOAs, they may have affected evoked responses to subsequent tones. In three animals there was little evidence of such superposition. However, responses in monkey W were consistent with such an effect. Note that the superposition effect is problematic mostly for sequences of identical tones in the regular environment, because most SOAs are preceded by the same SOA, thus preventing the averaging out that reduces the superposition effect in the random condition.

A subtraction method was used to reduce ERP superposition for tones with short SOA. The method was used in all four animals, regardless of whether or not the uncorrected data contained hints of superposition. The method we used was adapted from Briley and Krumbholz (2013). The aim of the subtraction method was to estimate the response amplitude that would have been observed for the previous tone, shift it in time, and subtract it from the response to the current tone. The challenge was to provide a reasonable estimate of the response to the previous tone, given that the expected response to the previous tone itself is expected to depend on its own SOA as well as the superposition from the preceding tone. Although in principle a deconvolution approach as used in the functional MRI literature would be possible, it was estimated to require a model with at least 2,100 variables (350 time points × 6 for each octave of SOA). Instead, we opted for the simpler subtraction approach. The maximum response duration was estimated to be less than 700 ms. Hence, a correction was deemed necessary only for SOAs below 700 ms. The subtraction method divided the data into two domains. The first domain dealt with instances where the tone was the first to be preceded by the SOA in question. The second domain dealt with instances where the tone in question was preceded by additional instances of the same SOA in question. This was necessary, because the EEG components that lead to overlap also are affected by their own SOA and need to be corrected accordingly.

The correction in the first domain was computed as the average evoked potential to all tones in the random condition that were the first in a sequence to use a particular SOA. For each tone presentation with an SOA below 700 ms, this average response was shifted back in time according to the current SOA and subtracted from the response in the current trial for all channels separately. The correction in the second domain depended on whether the SOA in question was above or below 400 ms. If the SOA was below 400 ms, the correction was computed as the average of all response in the random condition with an SOA below 400 ms, again excluding tones that were repeating the SOA of the previous tone presentation. If the SOA was between 400 and 700 ms, the correction was computed along the same lines, this time only including trials with an SOA between 400 and 700 ms.

This correction routine was deemed adequate for the current purposes. In the future, it may be refined by making the correction in the first domain contingent on the second-to-last SOA or by using a full deconvolution approach. However, a general criticism that remains is the assumption of a linear time-invariant system, i.e., that processing of the first tone proceeds identically after a second tone is presented before processing of the first tone is complete. Previous studies of auditory refractoriness have mostly used series of repeating SOAs without overlap correction. The current approach constitutes an important step forward because it uses an overlap correction as well as blocks of random SOAs that are less prone to overlap artifacts in the first place.

Extraction of trial-based component amplitude.

A previous analysis of this data identified eight distinct middle- and long-latency components (Teichert 2016). Each component was associated with a time window and a list of channels. The components were named according to the average latency of the time windows in all animals (P14, P21, P31, N43, P55, N85, P135, and N170). Component amplitudes on a trial in question were estimated as the averaging activity across the corresponding channels and time bins. Most components could readily be identified in all animals despite clear interindividual differences in timing and topography (Teichert 2016).

Auditory evoked potentials.

Averaged auditory evoked potentials were computed using an in-house toolbox written in the statistics software R (R Development Core Team 2009). For each recording session, all valid trials (see below) were sorted according to the SOA, averaged, and saved for future analysis. Trials during which the animal moved were accompanied by large low-frequent deviations of EEG activity. To reduce such motion artifacts, trials with peak-to-peak amplitude above 450 μV were excluded. A second source of artifacts arose from the clenching of jaw muscles and could be detected mainly in the higher frequency band in electrodes located toward the edge of the implant. Trials with jaw muscle artifacts could reliably be identified by bandpass filtering the data (Blackman window, 30–500 Hz, 54-Hz transition bandwidth) and computing total signal power across a predefined set of susceptible channels.

Limited resource model of auditory refractoriness.

The time constant of auditory refractoriness is typically defined on basis of the dependence of EEG amplitude as a function of SOA. The underlying assumption is that amplitude recovers back to baseline given enough time between tones. Insufficient time to recover will lead to reduced amplitude. The dependence of amplitude X in a long series of identical SOAs is typically described as an exponential recovery to baseline (Briley and Krumbholz 2013; Lu et al. 1992b), as modeled for example in the following equation:

$$X(SOA)=a-b{\cdot 2}^{\frac{-SOA}{{\lambda }_{SOA}}}$$

In this framework, a refers to the asymptotic value that will be reached when SOA is infinitely long. The factor b determines the maximal reduction of amplitude for short SOAs. Of main interest is the value of the time constant λ_SOA, which determines how quickly amplitude recovers back to baseline for long SOAs. The value λ_SOA describes the time (in seconds) it takes until amplitude has recovered 50% of the value it lost.

The more or less explicit assumption underlying auditory refractoriness is that processing of a sound expends a certain limited resource, and response amplitude recovers as the resource is replenished. For the sake of the analysis presented in is article, this assumption was made explicit and quantified. The resulting “limited resource model of auditory refractoriness” includes two parameters that quantify the fraction U of the available resource Q that is expended for the processing of a single tone and the recovery time constant τ with which the resource is replenished back to baseline levels. The EEG component amplitude is believed to be proportional to the amount of resource expended R, i.e., the product of U and Q:

$$R=U\cdot Q\mathrm{.}$$

At the time of each tone presentation, the amount of available resource is reduced by the factor U:

$$Q_{post}=Q_{pre}-(Q_{pre}\cdot U)\mathrm{.}$$

Between tones separated by an SOA of y seconds, the available resource Q recovers exponentially back to baseline with the recovery time constant τ (Fig. 1, A and B, left):

$$Q_{new}=1-{2^{\frac{y}{\tau }}(1-{\mathrm{Q}}_{old})\mathrm{.}}^{}$$

The limited resource model of auditory refractoriness was motivated by the most basic instantiation of models of short-term presynaptic plasticity. However, in contrast to models of presynaptic plasticity where the limited resource corresponds to the pool of readily releasable vesicles, it is currently not clear what resource mediates auditory refractoriness or whether the resource in question is indeed limited in any meaningful way. The simple computational model proposed in this article will most likely be refined as we gain a better understanding of the underlying biology.

The model can be extended intuitively to include different generators tuned for different frequencies. The current version of the model does not include such an extension for two reasons. First, the effect of changes in frequency (delta frequency) between successive tones was an order of magnitude smaller than the effect of SOA (data not shown). Second, the effect of delta frequency is orthogonal to the main effect of interest, i.e., SOA. The effect of delta frequency as well as other stimulus-specific aspects of refractoriness will be discussed in detail elsewhere.

Model fitting.

A gradient descent method was used to fit the two parameters, U and τ, of the limited resource model to the data. The limited resource model predicts component amplitude on a trial-by-trial basis. On the basis of these predictions, a linear model was fit to the single-trial component amplitudes. The fit was performed for each of the eight components separately. The gradient descent aimed at detecting the parameters that minimized the sum of squares of the residuals. The linear model is described by the following equation:

$$X(n)=a_{freq(n)}+b_{freq(n)}\cdot R(n)+c_{day(n)},$$

where X(n) corresponds to the amplitude of the component in question as measured on trial n, and R(n) corresponds to the component amplitude predicted by the model for trial n. The variable c modeled differences in overall component amplitude on different days as indexed by the function day(n) that was set to 1 for all trials collected on the first day, to 2 for all trials collected on the second day, and so on. The parameter a determined the offset, and the parameter b determined the gain of the modulation by the predictor R. Both variables a and b were allowed to vary between tones of different frequency as indicated by the function freq(n). This function was set to 1 for tones in the lowest half-octave of auditory frequencies (500 to 707 Hz), to 2 for tones in the second-lowest half-octave (707 to 1,000 Hz), and so on. The fit was performed within bins of auditory frequency because a previous study had revealed substantial differences in component amplitude for tones of different frequency (Teichert 2016). Note that freq(n) does not account for differences in frequency between successive tones. As outlined above in Limited resource model of auditory refractoriness, stimulus-specificity of refractoriness will be addressed in the future.

In addition to fitting the model for data combined across all sessions of a particular animal, the fit was also performed for each session separately (see individual subject results in Tables 1 and 2). To account for the overall lower number of trials, the data were split not by bins of half-octave but by full-octave frequency bins. Overall, the medians of the parameters of the fits of the individual sessions were similar to the parameters of the fits that combined data across all sessions. The similarity between the two approaches highlights the quality of the data that allowed us to extract meaningful fits even from individual 2-h-long sessions. However, overall, the fits to the combined data sets were deemed to be more reliable than fits to individual sessions. Hence, for the group analyses, we used the parameters from the combined data sets rather than the medians of the parameters across individual data sets.

Table 1.

Time constants of limited resource model fit

Components	Monkey R	Monkey J	Monkey W	Monnkey S	Group
P14	0.57 ± 0.25	0.74 ± 0.63	0.95 ± 0.78	0.51 ± 1.10	1.30 ± 0.43
P21	0.83 ± 0.65	0.82 ± 0.56	0.70 ± 0.51	1.10 ± 0.13	0.93 ± 0.07
P31	1.00 ± 0.79	1.30 ± 0.09	1.10 ± 0.74	1.30 ± 0.16	1.20 ± 0.12
N43	1.50 ± 0.71	0.63 ± 0.09	0.71 ± 0.81	0.61 ± 0.16	0.60 ± 0.25
P55	2.40 ± 1.00	1.80 ± 0.61	0.89 ± 0.44	2.00 ± 1.10	2.50 ± 0.69
N85	2.10 ± 0.44	1.70 ± 0.63	1.40 ± 0.76	2.10 ± 0.43	1.80 ± 0.10
P135	0.84 ± 0.78	3.30 ± 0.93	2.50 ± 0.76	1.80 ± 0.84	1.50 ± 0.24
N170	0.26 ± 0.62	0.70 ± 0.63	0.31 ± 0.66	0.91 ± 0.26	0.43 ± 0.19

Values are time constant τ (in s) given as median ± SE across sessions for individual animals and mean ± SE across the group. To increase power, single subject values entering group analysis were based on simultaneous fit across all sessions for the animal in question, not the median of fits to individual sessions. Variance between animals was high for components P14 and P55 (bold). This reduces confidence in the group estimate for these two components.

Table 2.

Expended fraction U of limited resource model fit

Components	Monkey R	Monkey J	Monkey W	Monnkey S	Group
P14	0.01 ± 0.09	0.88 ± 0.12	0.40 ± 0.08	0.38 ± 0.13	0.39 ± 0.12
P21	0.53 ± 0.09	0.52 ± 0.08	0.57 ± 0.09	0.66 ± 0.07	0.60 ± 0.04
P31	0.77 ± 0.07	0.64 ± 0.04	0.57 ± 0.07	0.66 ± 0.07	0.66 ± 0.02
N43	0.56 ± 0.11	1.00 ± 0.06	0.01 ± 0.10	0.64 ± 0.11	0.87 ± 0.07
P55	0.69 ± 0.09	0.50 ± 0.06	0.53 ± 0.07	0.58 ± 0.10	0.63 ± 0.04
N85	0.71 ± 0.03	0.83 ± 0.04	0.57 ± 0.09	0.89 ± 0.06	0.70 ± 0.05
P135	0.65 ± 0.09	0.97 ± 0.10	0.70 ± 0.08	0.39 ± 0.09	0.67 ± 0.09
N170	1.00 ± 0.12	1.00 ± 0.08	0.18 ± 0.11	0.56 ± 0.07	0.66 ± 0.23

Values are expended fraction U given as median ± SE across sessions for individual animals and mean ± SE across the group. Variance between animals was high for component N170 (bold). This reduces confidence in the group estimate for this component.

RESULTS

Properties of the limited resource model of auditory refractoriness.

So-called “recovery cycle studies” (Callaway 1973; Loveless 1983) in humans have quantified time constants of auditory refractoriness by fitting a descriptive model to component amplitude as a function of stimulus onset asynchrony (SOA). In particular, the dependence was modeled by an exponential recovery function with a time constant λ_SOA (materials and methods, Limited resource model of auditory refractoriness). However, auditory refractoriness is believed to arise from a mechanistic physiological process such as the gradual recovery of generator excitability that is reduced each time a tone is processed. In the current article, we have used a simple instantiation of such a mechanistic model that we termed the “limited resource model” of auditory refractoriness (Fig. 1). The limited resource model is determined by two variables: the fraction U of the limited resource, i.e., generator excitability or an unspecified physiological process that determines generator excitability, that is expended each time a tone is processed, and the recovery time constant τ that determines how quickly the resource is replenished to baseline levels (materials and methods, Limited resource model of auditory refractoriness).

The simulations of this model depicted in Fig. 2, A and B, left, show that there is no straightforward relationship between the recovery time constant τ of the mechanistic model and the time constant λ_SOA of the descriptive model. The descriptive time constant λ_SOA is a good estimator for underlying the recovery time constant τ only if the expended fraction U of the limited resource model is close to 1, i.e., if each tone uses up almost all of the available resource (Fig. 2A, left). For expended fractions U less than 1, λ_SOA is not a good estimator of τ. Intuitively, this is true because the amplitude is affected by more than just the last SOA, and overlap effects from past tones are stronger if they are closer in time. Hence, there is a disproportionately strong reduction of responses for short SOAs. On the basis of this intuition, there is only one exception: λ_SOA is a good estimator for τ if SOA changes after each tone or if tones that repeat the previous SOA are excluded from the analysis. Note that in long sequences of identical SOAs, component amplitude as a function of SOA saturates earlier than would be expected from the recovery time constant τ (Fig. 2B, compare solid and dashed lines). Hence, if the standard descriptive model were to be fit to such data, λ_SOA would underestimate the true recovery time constant τ of the limited resource model.

So-called “short-term habituation studies” (Callaway 1973; Loveless 1983; reviewed in Budd et al. 1998) measure response amplitude as a function of repetition number in short sequences of identical stimuli. In some cases, these studies estimate time constants using descriptive models that fit an exponential function to the dependence of component amplitude as a function of repetition number, λ_Rep#, in series of tones with identical SOA (Fig. 2, A and B, right; Fruhstorfer 1971; Fruhstorfer et al. 1970; Ritter et al. 1968; Wastell and Kleinman 1980). By using the approach of stimulus repetition, our simulations show that the descriptive model fits will approximate the true underlying recovery time constant τ only if expended fraction U is close to 0 (Fig. 2B, right). The intuition in this case is that to estimate the correct time constants from λ_Rep#, it is essential that successive tones are allowed to superpose approximately linearly. If they do not, as is the case for high expended fractions, then the curves will saturate prematurely. And indeed, for higher expended fractions, the fits of the descriptive exponential recovery model breaks down for all but the longest SOAs (Fig. 2A, right). Note that in this case, i.e., if expended fraction is high, the descriptive time constant λ_Rep# would also underestimate the true underlying recovery time constant τ.

In summary, the simulations show that for both approaches to estimating time constants with the use of descriptive model fits, λ_SOA as well as λ_Rep# will converge on the recovery time constant τ of the limited resource model only under specific restrictions for expended fraction U. In other cases, both λ_SOA and λ_Rep# will underestimate the true underlying recovery time constant τ. Interestingly, whereas the time constant λ_SOA will provide the correct answer if U is equal to 1, λ_Rep# will provide the correct answer if U approaches 0.

Model-free description of auditory refractoriness.

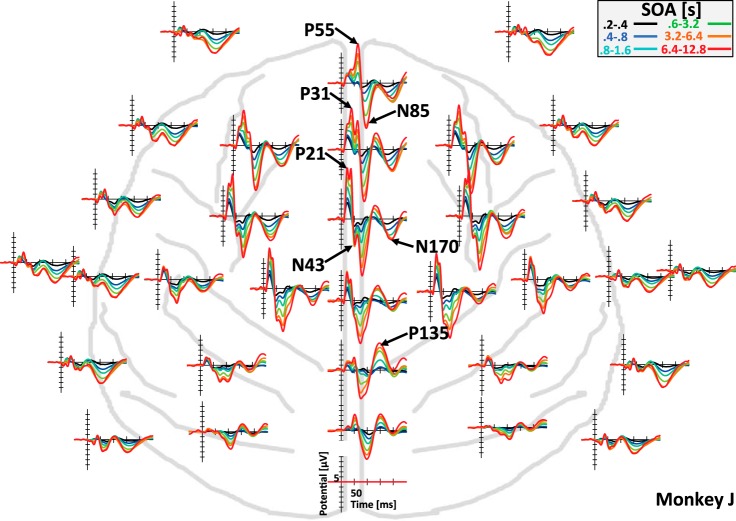
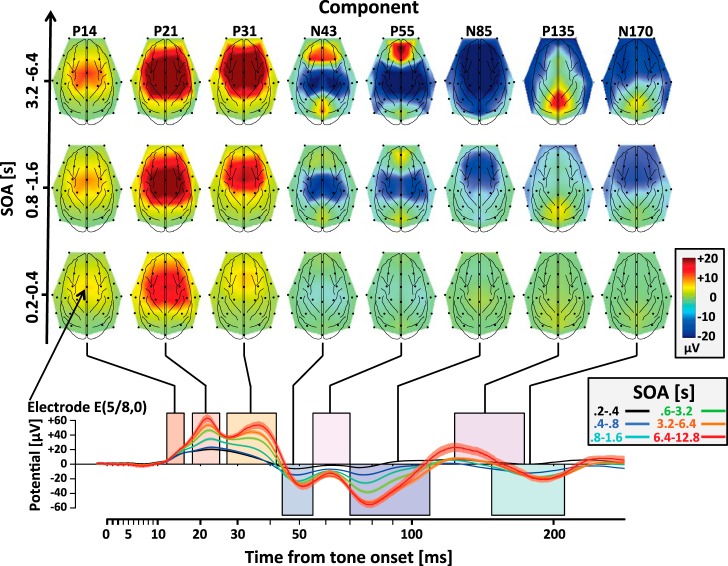
It is well-established that the amplitude of the presumed rhesus P1 and N1 homologs measured with a single frontocentral epidural electrode are modulated by SOA in long predictable sequences of clicks with identical SOA (Javitt et al. 2000). Figure 4 qualitatively extends this finding to a random, nonpredictable environment where SOA and auditory frequency changes after 9 of 10 tones. Furthermore, Fig. 4 shows that increases of response amplitude with SOA can be observed at all electrodes and for all seven middle- and long-latency component peaks that can be identified in this animal. Finally, as expected, the findings show that auditory refractoriness can be elicited by using 50-ms-long sinusoidal tones that are often used in clinical studies rather than clicks. Figure 5 provides an alternative way of looking at the same data while focusing on the topography of the distinct EEG components. It highlights the fact that longer SOAs do not change the topography of a component, but rather scale amplitude at all electrodes. The logarithmic time axis in Fig. 5, bottom, for the evoked potentials recorded at electrode E(5/8,0) also highlights the early emergence of the SOA effect around 12 ms after tone onset.

Fig. 4.

Evoked potentials in example subject. A multiplot of tone-evoked responses in the random environment is shown. In each plot, time is presented on the x-axis relative to tone onset. The y-axis shows average electric potential relative to the reference channel. Different colors represent responses to tones in different ranges of SOA. Note that response amplitude scaled with SOA at all channels. Consistent with this, the peaks of all of the 7 components that were identified in this animal increased with SOA.

Fig. 5.

Topography and component amplitude as a function of SOA. Bottom, responses of electrode E(5/8,0) as a function of time from tone onset. Different colored traces correspond to tones in different ranges of SOA. The colored rectangles indicate the time windows that were previously assigned to the 8 different middle- and long-latency components. Note that in this animal there was no specific peak associated with the P14 component. Top: highlighted topography for the different components as a function of SOA for 3 example bins of SOA.

Our analyses further indicated stronger refractoriness following tones of more similar frequencies (data not shown). This effect was small (∼2 μV) compared with the effect of SOA (>20 μV). Strong refractoriness was observed even for tones of very different frequencies. Hence, the following analyses that focus on the temporal properties of refractoriness as captured by time constant and expended fraction ignored the differences in frequency between successive tones.

Recovery time constant τ differs between EEG components.

The first goal of the current study was to estimate the recovery time constant τ of all eight previously identified auditory EEG components in the rhesus. Because a priori, expended fraction U is not known, neither of the descriptive time constants λ_SOA or λ_Rep# will provide a reliable estimate of τ (see Properties of the limited resource model of auditory refractoriness). Hence, component amplitude was fit with the limited resource model to simultaneously extract the recovery time constant τ as well as expended fraction U. To avoid potential contamination from effects related to the detection of (or deviation from) regularity in the auditory environment, the fits included only trials collected in the random environment. Of all 32 instances (8 components × 4 animals), most showed a significantly improved fit after the SOA-dependent predictor derived from the model was included. With the use of a Bonferroni-corrected P value of 0.01/32 = 0.0003125, 30 of the 32 components showed a significant effect of SOA (nested multiple regression analysis with ANOVA and type II sums of squares). Components that failed to show a significant improvement were component P14 for animal S and component N43 for animal W. Of the remaining 30 fits, 28 were highly significant with P values <10⁻¹⁰.

Figure 6, A and B, shows the result of the fitting process for two example components in one animal. Figure 6C shows the recovery time constants as a function of all eight EEG components in all animals (see also Table 1). Table 1 includes fits to the data from each session separately, as well as fits that combine data from all sessions of a particular animal. With only 7 exceptions, the recovery time constants ranged between 0.5 and 2 s. As hypothesized, the recovery time constants seemed to vary systematically between different EEG components. A repeated-measures ANOVA rejected the null hypothesis that the recovery time constants τ were identical for all eight components at a criterion α = 0.05 [degrees of freedom (DF) numerator = 7, DF denominator = 15, P < 0.006, Huynh-Feldt ε = 0.4240, P_H-Fcorrected < 0.05]. Closer inspection of Fig. 6C revealed large between-subject variability for two of the eight EEG components (P14 and P55). The ANOVA was rerun, excluding these two components and confirmed the results (repeated-measures ANOVA: DF numerator = 5, DF denominator = 15, P < 0.0008, Huynh-Feldt ε = 0.4810, P_H-Fcorrected < 0.02).

Fig. 6.

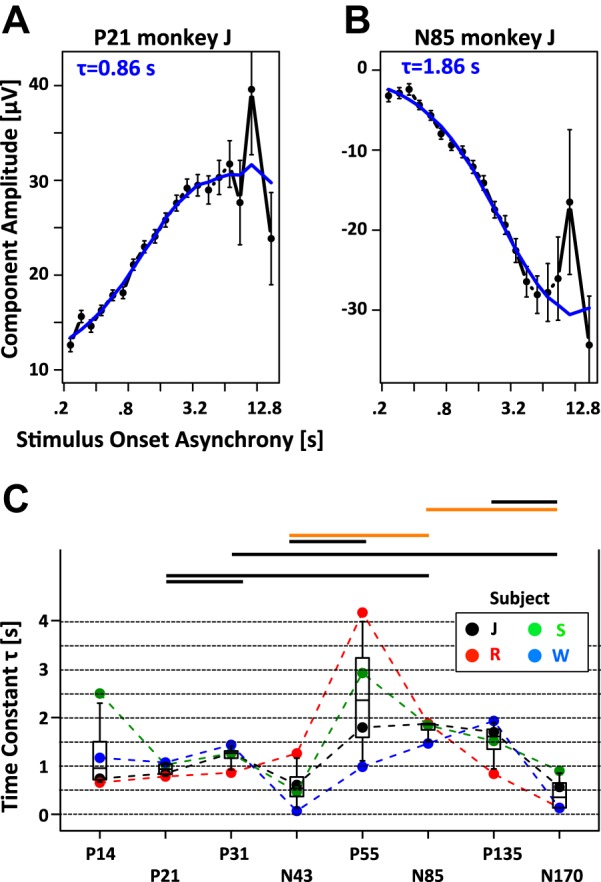
Recovery time constant τ of limited resource model. A and B: component amplitude as a function of SOA for 2 example components (P21 and N85) of monkey J. The blue line corresponds to the fit of the data with the limited resource model. The blue insets depict the value of the recovery time constant τ for the best-fitting models. Note that the recovery time constant is shorter for the P21 compared with the N85 component. C: recovery time constants plotted as a function of EEG component. The different colors represent the 4 different animals (monkeys J, R, S, and W). Note the narrow distributions of time constants for all components except P14 and P55. The results of all pairwise comparisons are indicated by horizontal bars (black: P < 0.05; orange: P < 0.01; red: P < 0.001).

Post hoc t-tests were performed between all pairs of components to determine which components drive the main effect (Fig. 6C). The post hoc tests identified seven significant pairwise differences. The N85 component was involved in three of these pairs and emerged as the main driver. However, the P21, N43, and N170 components also played an important role, contributing two significant post hoc tests each.

Quantification of expended fraction U supports the idea of limited resource.

Figure 7 shows the expended fraction U as a function of EEG component (see also Table 2). Table 2 includes fits to the data from each session separately, as well as fits that combine data from all sessions of a particular animal. With few exceptions, the expended fraction U ranged between 0.5 and 0.75. Within the confines of the model, this clearly suggests that not all of the resource is expended each time a tone is played. However, the data also show that expended fraction is large enough to consider the resource to be “limited” in a meaningful way.

Fig. 7.

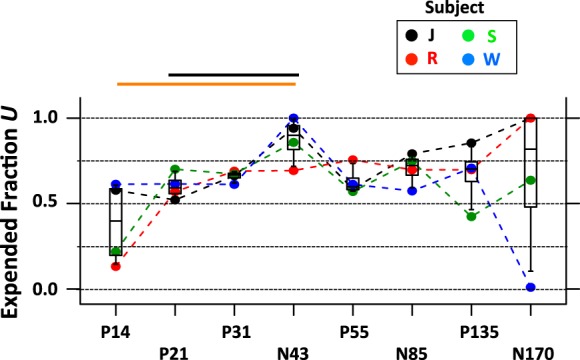
Expended fraction U of limited resource model. Graph visualizes expended fraction U as a function of EEG componen t. Conventions are the same as in Fig. 6C. Most components are best fit by models with an expended fraction between 0.5 and 0.75. The main effect of component was not significant. Hence, the pairwise comparisons should not be given too much weight.

We then tested whether the components also differ with respect to expended fraction U. Results of a repeated-measures ANOVA showed no significant differences of expended fraction for the different components (DF numerator = 7, DF denominator = 15, P < 0.2, Huynh-Feldt ε = 0.4591, P_H-Fcorrected < 0.3). Closer inspection of Fig. 7 revealed large between-subject variability for one of the eight EEG components (N170). Excluding N170 revealed a significant difference in expended fraction between components (repeated-measures ANOVA: DF numerator = 6, DF denominator = 15, P < 0.01, Huynh-Feldt ε = 1.007, P_H-Fcorrected < 0.01). Paired post hoc tests revealed differences between P14 and N43 as well as P21 and N43. Given that the main ANOVA that included all components did not reach significance, these post hoc tests should be interpreted with care.

The finding of expended fraction U between 0.5 and 0.75 indicates a nonlinear interaction of previous tones. For example, a particular tone has less of an effect on the EEG responses elicited by a subsequent tone if a third tone is played in between the two. We further tested if this nonlinearity can be attributed to tones with short SOA that may have led to an overlap of responses to the previous tone. Although our subtraction routine was designed to account for a linear superposition of responses to adjacent tones, it could not account for nonlinear interactions. Hence, we reran the model fits, excluding responses to tones with an SOA below either 500 or 700 ms. Both cases confirmed the main finding of expended fraction U between 0.5 and 0.75 for most components (data not shown). The mean expended fractions across all components and animals remained rather stable after the shortest SOAs were excluded (all SOAs: U = 0.67; SOA > 500 ms: U = 0.62; SOA > 700 ms: U = 0.61).

DISCUSSION

Auditory refractoriness refers to the effect of weaker EEG responses to tones preceded by shorter periods of silence. Refractoriness may reflect the formation and gradual decay of a basic perceptual short-term memory trace (Lu et al. 1992a; Näätänen and Picton 1987; Shelley et al. 1999) that may be mirrored by the gradual recovery of generator excitability (Budd et al. 1998). However, despite findings that identify altered auditory refractoriness as an important marker of altered neural function in SZ (Rosburg et al. 2008; Shelley et al. 1999), it has received only limited study in invasive animal models (Itoh et al. 2015; Javitt 2015; Javitt et al. 2000), and to date its physiological mechanisms remain largely unclear. This incomplete understanding of auditory refractoriness limits the insights gained from clinical studies that point to abnormal refractoriness in SZ. To begin resolving this roadblock, our study provides a solid experimental platform to further dissect the neural mechanisms of auditory refractoriness in the rhesus, one of the most important animal models of auditory dysfunction in SZ (Javitt et al. 1992, 1994, 1995, 1996, 2000).

As expected, the duration of silence before a tone had a substantial and significant effect on the amplitudes of all eight examined middle- and long-latency EEG components in the rhesus (Figs. 4–6). An immediately preceding tone reduced EEG component amplitude to the following tone by up to 80% of the value observed when the preceding tone happened more than 10 s ago (e.g., Fig. 6B). These findings confirm that immediate sensory context is one of the strongest modulators of EEG responses in the rhesus and highlight the importance of understanding the underlying physiology as well as the type of information encoded in this memory trace. Our findings extend earlier studies (Javitt et al. 2000) and provide a solid methodological, computational, and conceptual basis to further dissect auditory refractoriness in the rhesus.

Relation to previous rhesus monkey studies.

Javitt et al. (2000) measured dependence of the P1 and N1 component on SOA in the macaque by using brief 0.1-ms-long clicks and an epidural electrode at Cz. Although there is no one-to-one relation between their P1 component and any of our components, their P1 is most likely an average of responses that contribute to our P21 and P31 components. Similar to our findings, Javitt and colleagues report a slower return to baseline for the N1 component, suggestive of a longer time constant. Despite the overall similarities between studies regarding the N1 component, there are certain differences, mostly with regard to P1. Javitt et al. report two distinct timescales for the P1 component: a fast recovery of amplitude between 150 and 450 ms and a more gradual increase that seemed to continue all the way to 10 s. In contrast, we found a gradual increase of amplitude for all components, including the potential analogs of the P1 component, i.e., P21 and P31, all the way from 200 to 12,800 ms that can be modeled with a single time constant. Furthermore, the time constants of the P21 and P31 components in our study are substantially longer than the short time constant suggested for the P1 component in the Javitt et al. study (saturation after ∼450 ms).

There are several differences in experimental design and analysis that may account for the quantitative differences between the two studies. 1) Whereas Javitt et al. (2000) used short 0.1-ms, 70-dB loud clicks, we used 55-ms-long, 80-dB loud sinusoidal tones. The different types of sounds may have activated different sets of neurons/neural generators; the longer durations and higher sound pressure levels may have driven the responses closer to maximum capacity of the system in our study. 2) The study by Javitt et al. used long sequences of tones with identical SOA, whereas our study used the random environment of the RS kernel paradigm. Hence, the effects in the Javitt et al. study may be driven in part by higher level processes that take advantage of regularity in the auditory environment. 3) We used a two-stage subtraction routine to reduce event-related potential (ERP) overlap from previous tones. Although this procedure had only a minor impact on the overall results in three of the four animals, the procedure did mostly affect components with short latencies such as the P21, P31, and N85 components. Furthermore, the overall effect size of the correction may vary between individuals, as indicated by one of our animals whose results were affected more strongly by the correction routine. 4) The shortest SOA in our study was 200 ms, compared with 150 ms in the study by Javitt et al. By performing our study this way, we might have missed a particularly steep drop of P1 amplitude for SOAs below 200 ms. Alternatively, the use of particularly short SOAs may have led to stronger overlap artifacts in the data of Javitt et al.

Isolation of auditory refractoriness using a random environment.

The key methodological innovation of the current study was the use of a random auditory environment (RS kernel paradigm) that prevented subjects from forming valid predictions about the time or identity of the upcoming tone. Hence, the observed reductions of component amplitude with SOA cannot be attributed to predictive coding (Friston 2005; Rentzsch et al. 2015), predictive suppression (Lakatos et al. 2009, 2013), reduced temporal attention (Lange 2012; Lange and Roeder 2010), or any other explanation that is based on regularity or predictability of the auditory environment. This allowed us to study low-level effects such as refractoriness independently of more cognitive explanations that may account for similar effects in regular and predictable environments. Ruling out more high-level accounts strengthens the case for the involvement of a simple physiological mechanism. The RS kernel paradigm is closely related to a poison-stimulation paradigm used to study synaptic depression in response to complex and realistic patterns of action potentials (Markram and Tsodyks 1996; Tsodyks and Markram 1997; Varela et al. 1997).

Although not the focus of the current study, an intended side-effect of the RS kernel paradigm was that it is possible to predict responses in the regular environment on the basis of data from the random environment. Deviations from these predictions will then be attributable either to properties of the predictable environment (e.g., the presence of longer time constants that fail to be adequately captured by models of the random data) or to the subjects' response to the regularity in the environment.

Between-component differences are explained by different time constants.

Studies in human subjects show that different EEG components have different time constants of refractoriness, indicating that it takes them different amounts of time to recover to baseline amplitude (Budd et al. 1998; Lu et al. 1992b). In the rhesus, time constants of refractoriness have not yet been formally quantified. The quantification of time constants of different components is particularly interesting, because different EEG components have been linked to specific cortical generators on the basis of their topography (Teichert 2016) as well as epidural, transcortical, and laminar recordings (Arezzo et al. 1975). Such knowledge would potentially enable the linking of different time constants to structural and/or molecular differences between brain regions and/or cortical laminae. For example, whereas the P14 and P21 are believed to be generated mainly in the posteromedial part of the superior temporal plane in cytoarchitectonically defined auditory koniocortex, the later N85 is most likely generated more anteriorly in cytoarchitectonically defined parakoniocortex (Arezzo et al. 1975). Similarly, although the rhesus P1 homolog was suggested to be generated in supragranular layers, the rhesus N1 homolog may have its origin in infragranular layers (Javitt 2015).

Recovery time constants for all components were estimated using the limited resource model of auditory refractoriness. In most cases, the time constants ranged between 0.5 and 2 s, indicating that it took component excitability between 0.5 and 2 s to recover half of the value that was lost after a single tone presentation. If we define a “return to baseline” as the time needed to recover 95% of the excitability lost after a single tone presentation, components returned to baseline between 2.16 and 8.64 s after a tone.

One main finding was that recovery time constants differed significantly between components. To a first approximation, we suggest that the components can be grouped into three categories based on the pattern of significant post hoc t-tests and the median recovery time constants: 1) components with short time constants around 0.5 s: N43 and N170; 2) components with medium time constants around 1 s: P14, P21, and P31; and 3) components with long time-constants around 2 s: P55, N85, and P135. Assigning P14 into the medium time-constant group was justified because the one outlier with a substantially longer recovery time constant corresponded to one of the two instances that did not show a significant effect of SOA in the model fit. More detailed studies may reveal a more graded view of the time constants into more than three groups.

On the basis of findings from the human literature, we had hypothesized that 1) recovery time constants would differ for components generated in different brain regions as indicated by component topography (Budd et al. 1998; Lu et al. 1992b) and that 2) there might be a gradual increase of time constants with component latency (Giraud et al. 2000; Harms and Melcher 2002). Indeed, there is some support for both of these hypotheses. According to the first hypothesis, we expect components with dissimilar generators, and hence dissimilar topography, to have dissimilar time constants. The strongest support for this assumption comes from the two components with the shortest time constants. Both N43 and N170 have topographies that differ substantially from the frontocentral topography, consistent with generators in the superior temporal plane that were found for most other components (P14, P21, P31, P55, and N85). Indeed, it is these two components whose distinct topography points to a generator outside of the superior temporal plane that exhibited the shortest time constants. Note that the short time constants cannot simply be explained by overall component latency, because N43 is bordered by P31 and P55, both of which have longer time constants.

According to the second hypothesis, one would predict a gradual increase of time constants with component latency. Indeed, broadly speaking, time constants increase from ∼1 s for the earliest components (P14, P21, and P31) to ∼2 s for later components (P55, N85, and P135). In addition, the data also suggest that time constants decline for components with even longer latency (N170). Overall, this may suggest an inverted U-shape for the relationship of time constant with component latency.

The inverted U-shape of recovery time constants as a function of component latency suggests that refractoriness of later components such as N85 is unlikely to be inherited from the earlier group of components with medium time constants. Similarly, the findings suggest that the long time constants of the P55, N85, or P135 components are not passed on to later components such as N170. These differences in time constants provide an interesting dissociation between components and support the idea that refractoriness may be the result of computations and/or physiological processes that are local in time and neural generator space rather than automatically being passed along the entire processing hierarchy. Furthermore, it suggests that the information that is being passed from earlier to later components is conveyed in a way that does not impose a specific scaling with SOA that may be present in the earlier component.

Overall, the range of time constants identified in our study is similar to the ones reported in humans. For example, Lu et al. (1992a) quantified the time course of the magnetic counterpart of the human N1, the N100m. They found time constants between 1 and 4 s with a median around 1.5 s. Because their time constant was based on an exponential recovery to the base of e, rather than 2 as in our case, these values had to be adjusted by a factor of 1/log(2) for comparison. After this adjustment, their values ranged between 1.44 and 5.77 with a median at 2.16 s. This value is remarkably similar to the time constants of the N85 component, the presumed N1 homolog in our study. This interspecies similarity of time constants matches previous findings (Javitt 2015; Javitt et al. 2000).

Limited resource explains functional properties of auditory refractoriness.

Conceptually, the key difference of the current approach is the use of a simple yet powerful mechanistic model. The core innovation of the limited resource model is the idea that only a fraction U of generator excitability is lost each time a tone is processed. In combination with the second variable of the model, the recovery time constant τ that determines how quickly generator excitability is recovered, the model can explain a wide range of behaviors.

In particular, our simulations show that adjusting expended fraction U can change behavior of the model from a state in which component amplitude is a function of the duration of the very last SOA (Fig. 1A) to a state in which component amplitude is a function of the leaky integration of all past sounds with a leak term defined by the recovery time constant τ (Fig. 1B). Tsodyks and Markram have outlined how the corresponding parameter, i.e., release probability U_SE, in a related model of synaptic depression can change the type of information transmitted between pre- and postsynaptic neurons (Markram and Tsodyks 1996; Tsodyks and Markram 1997).

Fitting the model to the actual data clearly showed that expended fraction U is neither equal to 1 (as implicitly assumed when fitting λ_SOA) nor close to 0 (as implicitly assumed when fitting λ_Rep#). Instead, for most components in all animals, expended fraction U varied between 0.5 and 0.75. Although further studies with higher power may reveal more subtle differences between components, our results are consistent with the assumption that expended fraction is a constant value that is common to all of the eight examined components.

Overall, our findings support a model of auditory refractoriness in which ∼65% of an unspecified limited resource that determines generator excitability is lost each time a tone is processed. Although this is certainly not definite proof for the existence of a physiological analog of the hypothetical limited resource posed by the model, it is certainly suggestive thereof. Knowing functional properties of this hypothetical resource, such as its recovery time constant or its expended fraction, will ultimately prove helpful in narrowing down the range of potential physiological candidates.

Potential physiological correlates of auditory refractoriness.

Several bodies of work have studied response reduction as a function of stimulus repetition or exposure duration. In rat auditory cortex, reduced responses to the second in a series of tones has been suggested to reflect long-lasting synaptic inhibition (Tan et al. 2004). Work in cat and ferret visual cortex has attributed long-lasting decreases in neuronal responsiveness to the activation of a Na⁺-activated K⁺ current (Sanchez-Vives et al. 2000a, 2000b). Work in rat barrel and auditory cortex has implicated synaptic depression of thalamic inputs in response suppression to repeated tones and whisker stimulation (Chung et al. 2002; Wehr and Zador 2005). Given the formulation of the limited resource model, it is particularly appealing to consider synaptic depression as the driving force behind auditory refractoriness. In rat visual cortex, synaptic plasticity was found to comprise one facilitating and two depressing components of different time constant and release fraction. The fast component had a time constant of 0.5 s (corresponding to 0.72 s when a base of 2 is used, as was the case for the time constants in the current analysis) and a release fraction of ∼15%. The slow component had a time constant of 5 s (corresponding to 7.2 s when a base of 2 is used) and a release fraction of ∼2% (Varela et al. 1997). It is interesting to note that the time constant of the fast component is rather close to the 1-s time constant reported presently for the early components believed to be generated in auditory cortex core regions. Furthermore, a release fraction of 15% per action potential would correspond to 65% release fraction if each tone elicits between six and seven spikes. This value of six to seven spikes per tone is reasonably close to spike counts observed in primary auditory cortex of the awake rhesus (Micheyl et al. 2005) as well as anesthetized rat (Tan et al. 2004). Further studies are needed to confirm this tentative link between synaptic plasticity and auditory refractoriness, especially for components with longer time constants around 2 s, such as the N85.

Delineating refractoriness-based contextual effects.

Auditory refractoriness is one of the most basic contextual effects in the auditory domain and may reflect a rudimentary form of perceptual short-term memory. However, the functional properties of refractoriness, and hence the content of the memory trace it encodes, remain poorly understood. Compared with contextual effects in the visual system, it has been surprisingly difficult to quantitatively delineate the extent of refractoriness-based contextual effects in the auditory domain. While the spatial extent of visual nonclassical receptive fields has been delineated in great detail (Angelucci and Bullier 2003; Cavanaugh et al. 2002; Levitt and Lund 1997; Maffei and Fiorentini 1976; Teichert et al. 2007), it is not even immediately clear what metric to use to delineate the type of auditory contextual effects studied here. Typically, one of two distinct metrics are used that quantify either 1) how far back in time the effect reaches (measured in seconds) or 2) how far back in stimulus history the effect reaches (measured as an ordinal number, i.e., last tone, second-to-last tone, and so on). A third metric that quantifies distance in tonotopic space was not considered at this point in time.

Our results suggest that the extent of stimulus context cannot be specified simply in terms of either elapsed time or number of intervening stimuli, but rather as a complex nonlinear interaction of both factors. Within the confines of the model, the only instance in which context can be delineated purely in terms of elapsed time is when expended fraction is so low that it will never come close to being depleted (U close to 0). In this case, the contextual effect of any tone gradually decays back to 0 as the resource that was used to process this tone is replenished. Because the resource is never reduced by a meaningful amount below 100%, the effects of all past tones sum approximately linearly. Behavior on the other end of the spectrum is observed when expended fraction U is equal to 1. In this case, only the time of occurrence of the most recent tone has an effect on the processing of the current tone. The effects of all other tones, no matter how close in time, are wiped out, because all available resource is expended each time a tone is processed.

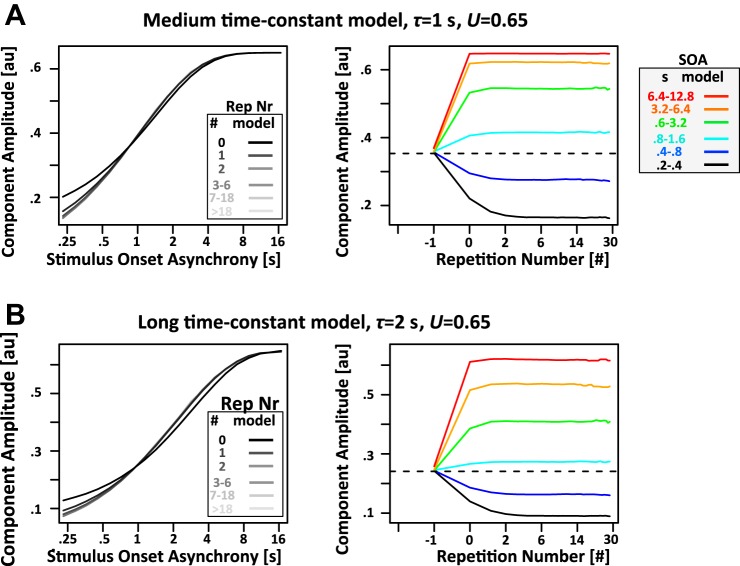
Given that in the actual data, expended fraction was around 0.65, i.e., below 1, it is clear that not only the last tone has an effect (Fig. 8). However, given that expended fraction was also higher than 0, it is clear that the effect of all tones other than the very last tone was lower relative to what would be expected on the basis of elapsed time only, i.e., in the absence of intervening tones. Hence, it is necessary to use a combination of both metrics to accurately delineate the contextual effects measured via auditory refractoriness of EEG components. We suggest that the two parameters of the model, i.e., expended fraction U and recovery time constant τ, are actually the best ways to define and delineate the immediate sensory context that is relevant for auditory refractoriness.

Fig. 8.

Limited resource model with recovered parameters. Shown are simulated responses from the limited resource model with expended fraction U set to average expended fraction from the model fits. A and B: 2 models were simulated, one with a medium time constant of 1 s to approximate properties of the P14, P21, and P31 components, as well as one with a long time constant of 2 s to approximate properties of the N85 and P135 components. In both models, maximum amplitude is equal to the value of the expended fraction U, i.e., 0.65. Minimum amplitude is lower for the long timescale model, indicating a somewhat larger dynamic range given the auditory environment used in the study. The main difference between the models is the earlier saturation of responses as a function of SOA for the medium timescale model (left panels). Dependence of component amplitude as a function of repetition number (right panels) is rather similar between the 2 models. This is due to the fact that as expended fraction U approaches 1, amplitude as a function of repetition number is determined more strongly by U rather than recovery time constant τ.

Link to auditory refractoriness in the human.

To our knowledge, the limited resource model or equivalent models have not been fit to human data. Hence, we cannot directly compare expended fraction between the two species. However, on the basis of our simulations and the available human data, it is possible to venture an educated guess. In particular, studies in humans show that component amplitude reaches a steady state either immediately after the first presentation of a particular SOA or within the first couple of repetitions of the same SOA, thus suggesting fast time constants λ_Rep# (Barry et al. 1992; Budd et al. 1998; Fruhstorfer 1971; Fruhstorfer et al. 1970; Ritter et al. 1968). Other studies in humans suggest rather long time constants, λ_SOA, to explain component amplitude as a function of SOA (Pereira et al. 2014). Our simulations argue that the fast time constant λ_Rep# can be consolidated with the much slower time constant λ_SOA if we assume an intermediate expended fraction U that is closer to 1 than to 0 (Figs. 2A and 8). Hence, we predict that the expended fraction U of the human is in a similar range to that of the rhesus as would be expected from functionally homolog systems. However, additional studies in humans using the RS kernel paradigm in combination with the limited resource model of auditory refractoriness are needed to confirm the homology between species.

On the basis of existing work, however, it is not immediately clear if the limited resource model will fit to the human data as well as it fits the monkey: Fruhstorfer et al. (1970) found that amplitude of the N1b component reached baseline after the second tone for sequences with an SOA of 1 s, whereas it took up to four tone presentations to reach baseline for the sequences with an SOA of 3 s. This finding suggests that either time constant τ or expended fraction U, or both, change as a function of SOA. In our data set both of these parameters are constant, independent of presentation rate of the tones. There are several explanations that may account for these differences. Most importantly, the human subjects in the study of Fruhstorfer and colleagues were exposed to a regular and predictable environment. Hence, it is possible that some of the responses reflect responses to this regularity. Furthermore, it is possible that a closer analysis of the monkey data might reveal more subtle effects such as a gradual change in time constant or expended fraction as a function of average tone presentation rate.

Stimulus-specificity of auditory refractoriness.

The limited resource model as presented in this article does not take changes of auditory frequency between sequential tones into account. As a result, the model implicitly assumes that there is only one pool of neurons/one component generator that processes the different tones regardless of frequency. This simplifying assumption is at odds with the functional organization of the auditory system into frequency-specific channels and renders the memory trace encoded via refractoriness nonspecific. However, as expected from the known organization of the auditory system, our data show small but significant effects of frequency differences between tones (data not shown). If the last tone had a similar frequency, the response to the next tone was attenuated more strongly compared with when the last tone had a dissimilar frequency. The size of the frequency-specific effect (∼2 μV) was an order of magnitude smaller than the effect of SOA. The tuning of this frequency-specific refractoriness was broad and did not reach saturation over the three-octave range used in this study. Despite its broad tuning and small size relative to the effect of SOA, it might still encode a stimulus-specific memory trace similar to that in humans (Briley and Krumbholz 2013).

One potential explanation for the small effect size and the broad tuning is the use of 80-dB stimuli in combination with the commonly assumed V-shaped frequency-amplitude tuning curves in auditory cortex (Recanzone et al. 2000). Hence, softer stimuli might be expected to yield stronger and more narrowly tuned stimulus-specific refractoriness. A second explanation might derive from differences between spiking activity on the one hand and postsynaptic potentials that are believed to underlie the EEG signal on the other. In particular, not all postsynaptic potentials lead to spiking, and thus it is feasible that frequency tuning of the postsynaptic potentials is broader than that of spiking activity (Tan et al. 2004). Ongoing work in the laboratory is measuring single- and multiunit activity, local field potentials (LFP), and current source density in the same task in core and belt regions of auditory cortex. Ultimately, this line of work aims to develop a computationally consistent account that consolidates adaptation effects at different levels of observation, i.e., narrowly tuned unit responses with moderately tuned LFP and weakly tuned EEG.

Limitations and future directions.

The current analysis used one particular mechanistic model of auditory refractoriness and shows that the additional variable it introduces, expended fraction U, is necessary to capture core properties of the data. However, other mechanistic models may provide similar fits to the data. Hence, we make no claims that the proposed model is the only model that can provide a good fit to the data. We anticipate refining the model, especially once we begin to gain a better understanding of the underlying physiology. Potential extensions may include an activity-dependent change in expended fraction or the introduction of a second depressing process with distinct time constant and expended fraction.

A previous analysis of this data set (Teichert 2016) had revealed significant differences in component amplitude as a function of auditory frequency. The current analysis of the data took this effect into account by allowing the model to be scaled differently for tones of different auditory frequency (see Model fitting). However, the current analysis did not allow the model to take on different time constants or expended fractions for different frequencies. Future studies will explicitly test whether populations selective for different frequencies indeed have the same recovery time constants and expended fractions.

GRANTS

This work was supported by National Institute of Mental Health Grants R01 MH094328 (to D. Salisbury) and R01 MH071533 (to R.A. Sweet).

DISCLAIMERS

The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institute of Mental Health, the National Institutes of Health, the Department of Veterans Affairs, or the United States Government.

DISCLOSURES

R.A. Sweet has been a consultant for ABBVIE Inc.

AUTHOR CONTRIBUTIONS

T.T. conception and design of research; T.T. and K.G. performed experiments; T.T. analyzed data; T.T. and R.A.S. interpreted results of experiments; T.T. prepared figures; T.T. drafted manuscript; T.T., D.S., and R.A.S. edited and revised manuscript; T.T. approved final version of manuscript.