Super-Resolution Reconstruction of Diffusion-Weighted Images using 4D Low-Rank and Total Variation

Abstract

Diffusion-weighted imaging (DWI) provides invaluable information in white matter microstructure and is widely applied in neurological applications. However, DWI is largely limited by its relatively low spatial resolution. In this paper, we propose an image post-processing method, referred to as super-resolution reconstruction, to estimate a high spatial resolution DWI from the input low-resolution DWI, e.g., at a factor of 2. Instead of requiring specially designed DWI acquisition of multiple shifted or orthogonal scans, our method needs only a single DWI scan. To do that, we propose to model both the blurring and downsampling effects in the image degradation process where the low-resolution image is observed from the latent high-resolution image, and recover the latent high-resolution image with the help of two regularizations. The first regularization is 4-dimensional (4D) low-rank, proposed to gather self-similarity information from both the spatial domain and the diffusion domain of 4D DWI. The second regularization is total variation, proposed to depress noise and preserve local structures such as edges in the image recovery process. Extensive experiments were performed on 20 subjects, and results show that the proposed method is able to recover the fine details of white matter structures, and outperform other approaches such as interpolation methods, non-local means based upsampling, and total variation based upsampling.

1 Introduction

Diffusion-weighted magnetic resonance imaging (DWI) is a key imaging modality for non-invasive and in vivo characterization of brain white matter microstructure. DWI has been used in early detection of stroke and characterization of neurological disorders, such as multiple sclerosis and epilepsy, where abnormal diffusion changes on specific white matter regions could be useful clues for disease diagnosis [1–5]. However, DWI is largely limited by its relatively low spatial resolution. For example, the resolution of current typical DWI data is 2×2×2 mm³, which means its voxel is 8 times larger than that in the standard T1-weighted structural data (1×1×1 mm³). It has been reported that the scan needs to be repeated 64 times for averaging in order to increase the DWI resolution from 2×2×2 mm³ to 1×1×1 mm³ while keeping the similar signal-to-noise ratio [6].

Besides improving MRI scanner hardware to higher magnetic fields or using stronger gradients, image post-processing methods are considered as a promising alternative for resolution enhancement. Interpolation methods (e.g., with nearest neighbor or spline) are widely used to increase the resolution, but their results often show blurry edges and blocking artifacts. Recently, super-resolution reconstruction (SRR) methods attract increasing research attention, aiming to estimate a high-resolution image from one or more low-resolution inputs [7]. The term super-resolution refers to the consideration of image degradation process where the underlying high-resolution image is translated, blurred, and downsampled to be observed as the low-resolution image. For example, Yuan et al. proposed to minimize total variation (TV) to regularize the recovery of natural images [8]. Manjón et al. used non-local means (NLM) to recover the high-frequency information in SRR of structural MR images on a patch-by-patch basis [9]. Basically, NLM recovers a voxel using a weighted mean of all other similar voxels, with the weights calculated according to the similarity of patches around voxels.

There are only a handful of studies on SRR methods for DWI. In these methods, multiple shifted or orthogonal DWI scans were acquired and then fused into a high-resolution output [10, 11]. However, their methods are hampered for general applications due to two reasons. First, a specially designed image acquisition scheme is needed in these methods to acquire multiple image scans, with longer scanning time. Second, subject motion and eddy current effects in different scans could largely affect the final result. Some other methods attempted to learn the mapping from low resolution to high resolution through training sets using random forests [12] or sparse representation [13]. Here, we focus on the SRR problem for single input image with no training sets. Currently, existing single image SRR methods are generally proposed for 3D structural MR images, while not developed and evaluated in DWI [8, 9, 14, 15]. Note that diffusion-weighted images are in 4-dimensional (4D) space, and more sensitive to noise, especially for the images with large diffusion factor b-value. Directly applying them to DWI may fail or compromise the performance.

In this paper, we proposed a novel SRR algorithm for DWI from single scan. We aim to increase the resolution of input low-resolution DWI to a high-resolution DWI, e.g., at the factor of 2. Our contributions are three-fold: 1) we model both the blurring and downsampling effects in the image degradation process to recover the latent high-resolution image; 2) we propose a novel 4D low-rank regularization to gather self-similarity information from both the spatial domain and the diffusion domain of 4D DWI; 3) we employ total variation to further preserve local structures such as edges from noise. Extensive experiments were performed on 20 real subjects, by comparing the proposed method with the interpolation methods, NLM-based up-sampling, and also TV-based up-sampling method.

2 Method

We introduce below the proposed method for super-resolution reconstruction of diffusion-weighted images. First, an observation model is provided to formulate the reconstruction as a minimization problem for the input low-resolution image and to-be-recovered high-resolution image. Second, we propose a novel low-rank approximation in 4D space on DWI, for helping retrieve the remote self-similarity information. Third, total variation is adopted to further preserve local structures. Finally, we summarize the total cost function and also provide an efficient optimization scheme.

2.1 Observation Model

DWI requires the acquisition of a number of diffusion-sensitized images to probe the diffusion of water molecules in various directions and scales. Denote the latent 4D high-resolution DWI as X, which is composed of N 3D diffusion volumes {X_n|n = 1,2,… N}. Similarly, we denote the observed low-resolution 4D image T containing 3D diffusion volumes {T_n}. Note that T is acquired from a single scan. In image acquisition, a degradation process is involved in to obtain a degraded low-resolution image from the latent high-resolution image:

$$T_n=\mathit{DS}{X}_n+z$$ (1)

where D is a 3D downsampling operator, S is a 3D blurring operator, and z represents the observation noise. In the spirit of super-resolution reconstruction, we estimate the latent high-resolution 4D image X by minimizing the following cost function:

$$\underset{X}{\text{min}}{\sum }_{n=1}^N{\Vert \mathit{DS}{X}_n-T_n\Vert }^2+\lambda \Re \left(X\right)$$ (2)

where the first term is a data fidelity term used for penalizing the difference between the degraded high-resolution image X and the observed low-resolution image T. The second term is a regularization term introducing prior information to help solve the ill-posed problem. Weight λ balances the contributions of the fidelity term and regularization term. Next we introduce two regularization terms, 4D low-rank and total variation, respectively.

2.2 4D Low-Rank Regularization

Rank is a measure of matrix complexity, corresponding to the number of linearly independent rows or columns of the matrix, or the number of nonzero singular values [16]. In natural and medical images, self-similarity is widely observed, where many rows or columns in the matrix could be linearly represented by other rows or columns, showing redundant information. This gives us the idea that diffusion weighted images could also be closely approximated by their low-rank components.

Here we use low rank as a regularization term to help retrieve useful information from all image regions. To compute the rank for a 4D image X, we first unfold it into a 2D matrix along each dimension [16]. Specifically, suppose the size of X is V₁×V₂×V₃×N, we unfold it into four 2D matrices {X_(i), i = 1,2,3,4} with size of V₁× (V₂×V₃×N), V₂× (V₁×V₃×N), V₃× (V₁×V₂×N), and N× (V₁×V₂×V₃), where X_(i) means unfold X along dimension i. Then we compute the sum of the singular values in each matrix for their trace norms ${\Vert X_{\left(i\right)}\Vert }_{tr}$. Finally, the rank of X is approximated as the combination of trace norms of all unfolded matrices:

$${\Re }_{\mathit{rank}}(X)={\sum }_{i=1}^4{\alpha }_i{\Vert X_{\left(i\right)}\Vert }_{\mathit{tr}}$$ (3)

where {α_i} are parameters satisfying α_i ≥ 0 and ${\sum }_{i=1}^4{\alpha }_i=1$. By minimizing this term, we could obtain a low-rank approximation of X. Note that the low rank is applied in 4D image, which means we could retrieve useful information for the reconstruction task from both spatial domain and diffusion domain.

2.3 Total Variation Regularization

Total variation is defined as integrals of absolute gradient of the signal [14]. For a 4D diffusion-weighted image X:

$${\Re }_{t\nu }\left(X\right)={\sum }_{n=1}^N\int \left|\nabla X_n\right|\mathit{dxdydz}$$ (4)

where the gradient operator is performed in 3D spatial space. Here we use TV in 3D space instead of 4D space based on the notion that there is no explicit neighborhood consistency across different diffusion volumes and thus TV in diffusion domain may not be effective. In images, the latent signals without excessive and possibly spurious details generally have low total variation. Accordingly, minimizing the total variation of the signal could generate a close match to the original signal, and removes unwanted noise whilst preserving important details such as edges. In this work, minimizing total variation will reinforce local spatial consistency and preserve edges in the recovered high-resolution image.

2.4 Cost Function and Optimization

The proposed super-resolution reconstruction is thus formulated as below:

$$\underset{X}{\text{min}}{\sum }_{n=1}^N{\Vert \mathit{DS}{X}_n-T_n\Vert }^2+{\lambda }_{\mathit{rank}}{\Re }_{\mathit{rank}}\left(X\right)+{\lambda }_{t\nu }{\sum }_{n=1}^N{\Re }_{t\nu }\left(X_k\right)$$ (5)

We employ the alternating direction method of multipliers (ADMM) algorithm to minimize the cost function in Eq. (5). ADMM has been proven efficient for solving optimization problems with multiple non-smooth terms [17]. Briefly, we first introduce redundant variables ${\left\{M_i\right\}}_{i=1}^4$ with equality constraints X_(i) = M_i(i), and then use Lagrangian dual variables ${\left\{U_i\right\}}_{i=1}^4$ to integrate the equality constraints into the cost function:

$${\text{min}}_{X,{\left\{M_i\right\}}_{i=1}^4,{\left\{U_i\right\}}_{i=1}^4}{\sum }_{n=1}^N{\Vert DS{X}_n-T_n\Vert }^2+{\lambda }_{\mathit{rank}}{\sum }_{i=1}^4{\alpha }_i{\Vert M_{i\left(i\right)}\Vert }_{tr}+{\sum }_{i=1}^4\frac{\rho }{2}\left({\Vert X-M_i+U_i\Vert }^2-{\Vert U_i\Vert }^2\right)+{\lambda }_{t\nu }{\sum }_{n=1}^N\int \left|\nabla X_n\right|\mathit{dxdydz}$$ (6)

We break the cost function into subproblems for X, M, and U, and iteratively update them. The optimization scheme is summarized in Algorithm 1 as below:

Algorithm 1.

Super-Resolution Reconstruction of Diffusion Weighted Images

Input: Low-resolution 4D diffusion-weighted image T;

Initialize the desired high-resolution image X(0) by upsampling T with nearest neighbor interpolation. Set redundant variables $\begin{array}{ccc}{M}_i^{\left(0\right)}=0,& U_i^{\left(0\right)}=0& i=1,2,3,4\end{array}$;

For each iteration k,

Update Xk by using gradient descent:

$\text{arg}\underset{X}{min}{\sum }_{n=1}^N{\Vert DS{X}_n^{\left(k-1\right)}-T_n\Vert }^2+{\sum }_{i=1}^4\frac{\rho }{2}{\Vert X^{\left(k-1\right)}-M_i^{\left(k-1\right)}+U_i^{\left(k-1\right)}\Vert }^2+{\lambda }_{t\nu }{\sum }_{n=1}^N\int |\nabla X_n^{\left(k-1\right)}|\mathit{dxdydz}$ (7)

Update $M_i^{\left(k\right)}$ by using Singular Value Thresholding (SVT) [18]:

$\begin{array}{c}{M}_i^{\left(k\right)}=\mathit{fol}{d}_i\left[SV{T}_{{\lambda }_{\mathit{rank}}{\alpha }_i/\rho }\left(X_{\left(i\right)}^{\left(k\right)}+U_{i\left(i\right)}^{\left(k-1\right)}\right)\right]\\ \text{with}\mathit{fol}{d}_i\left(M_{i\left(i\right)}\right)=M_i\end{array}$ (8)

$\text{Update}{U}_i^{\left(k\right)}\text{by:}{U}_i^{\left(k\right)}=U_i^{\left(k-1\right)}+\left(X^{\left(k\right)}-M_i^{\left(k\right)}\right)$ (9)

Until difference between iterations ||Xk − Xk−1||/||T|| ≤ ε;

End

Output: Reconstructed high-resolution 4D diffusion-weighted image X.

3 Experiments

3.1 Data

The resolution of routine DWI images is of 2 to 3 mm. The goal of experiments is to evaluate the resolution enhancement performance of the proposed method on this resolution level. To make the evaluation in a controlled manner, as a general approach in super-resolution studies [2–4,6], we simulate a group of data with such resolution. In this way, the ground truth data could be used to compare with the recovered results for quantitative performance evaluation.

We used a public dataset from WU-Minn Human Connectome Project (HCP) consortium [19, 20], where high-resolution images were acquired by using novel gradient hardware on a 3T Siemens Connectome scanner. We randomly selected 20 subjects (9 males and 11 females) with the age ranges from 22 to 30 years. Diffusion-weighted image were obtained for 145 axial slices with resolution of 1.25×1.25×1.25 mm³. A total of 288 diffusion volumes were acquired, in which 18 without diffusion gradient (b=0), 90 at b=1,000 s/mm², 90 at b=2,000 s/mm², and 90 at b=3,000 s/mm².

To evaluate the resolution recovery performance, we use HCP data to simulate a group of routine-resolution DWI. To do that, we apply blurring and downsampling operators to the original high-resolution images. Specifically, a Gaussian kernel with standard deviation of 1 voxel was performed to simulate blurring effect. Downsampling was carried out by averaging every 8 voxels in an image to reduce the resolution at a factor of 2. Finally, we obtain DWI with resolution of 2.5×2.5×2.5 mm³, which is at the similar level with current typical DWI resolution.

3.2 Experimental Setting

Parameters were defined experimentally. We set α₁ = α₂ = α₃ = α₄ = 1/4, λ_rank = 0.01, λ_TV = 0.01. The program stopped when the difference in iterations was less than ε = 1e − 5.

To evaluate the image recovery performance, we employ two metrics to compare the recovered high-resolution image to the original image, namely the peak signal-to-noise ratio (PSNR) and the structural similarity (SSIM) [21]. PSNR is measured in decibels (dB), and ranges from 0 to infinity. Higher PSNR generally means better reconstruction performance. SSIM ranges from 0 to 1, and 1 means perfect recovery.

3.3 Results

Experiments were performed on all 20 HCP subjects. We quantitatively measured the performance of the proposed method by comparing the reconstruction results with the original high-resolution images. The performance was further compared with other four methods, including nearest neighbor interpolation (NN), spline interpolation (Spline), non-local means upsampling (NLM), and total variation based upsampling (TV). Due to the availability of NLM implementation on 3D images [9], we run it on each diffusion volume to form the 4D output. TV was implemented through the proposed method by setting λ_rank = 0.

Fig. 1 demonstrates representative reconstruction results of a subject, where coronal views of DWI with different gradients are shown for b=0, 1000, 2000, and 3000, respectively. It can be observed that the results of NN, Spline, and NLM show severe blurring artifacts. TV shows deblurred results while the results of the proposed method show best signal contrast and preserve most fine structural details.

Fig. 1.

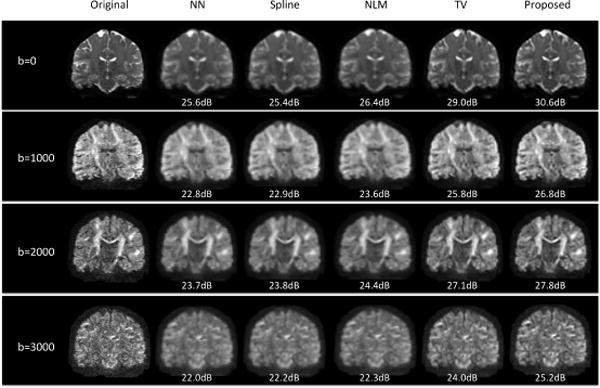
Reconstructed DWI of a typical subject using five different methods. PSNR values were provided, where higher PSNR indicating better reconstruction results.

We then estimated diffusion parameters using diffusion tensor model from the reconstructed multi-shell data (i.e., multiple b-values). Fractional anisotropy (FA) maps are shown in the top row of Fig.2. Close-up views of three selected regions are also color-coded and presented for better visualization. As pointed by yellow arrows, the top row shows bilateral cingulum appearing as the symmetric red dots on the top of genu of the corpus callosum. The middle row shows the fine folding of hippocampus layers, and the bottom row shows small white matter structures. The proposed method outperforms other comparison methods with best reconstruction results in preserving both FA magnitude and white matter shapes.

Fig. 2.

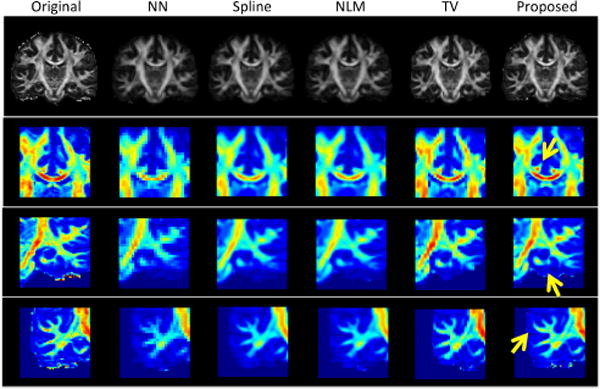
Illustration of FA maps of a typical subject, as well as close-up views of color-coded FA maps in three brain regions. Red indicates high FA value, and blue indicates low FA value.

Quantitative results of DWI reconstructions and parameter maps on 20 HCP subjects are shown in Fig. 3. Both PSNR and SSIM values are provided for showing reconstruction performances on DWI with different gradients (left panel) and diffusion measures (right panel) such as FA, mean diffusivity (MD), axial diffusivity (AD) and radial diffusivity (RD). Similar to the observations from Figs. 1–2, the proposed method achieved significant higher PSNR than the comparison methods in most of measures.

Fig. 3.

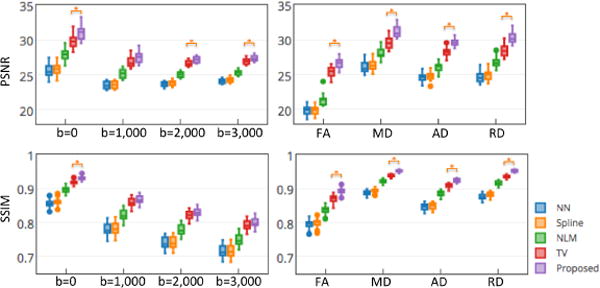
Grouped boxplots of PSNR (top) and SSIM (bottom) results in recovering 20 HCP subjects using five different methods. * indicates the proposed method significantly outperforms the comparison methods (p<0.01 in two-sample t-tests).

We further performed a streamline fiber tractography on the estimated diffusion tensor parameters of these five reconstruction results using inhouse software, with minimal seed-point FA of 0.3, minimal allowed FA of 0.25, maximal turning angle of 45°, minimal fiber length of 20 mm, and maximal fiber length of 300 mm. Here one fiber orientation was estimated for each voxel. Genu and corticospinal tract (CST) were used as regions of interest (ROIs), respectively. Results in Fig. 4 show that the proposed method best preserves the fiber tracts that are the closest to those from the original image. Less or excessive fiber tracts could be observed on results from other methods.

Fig. 4.

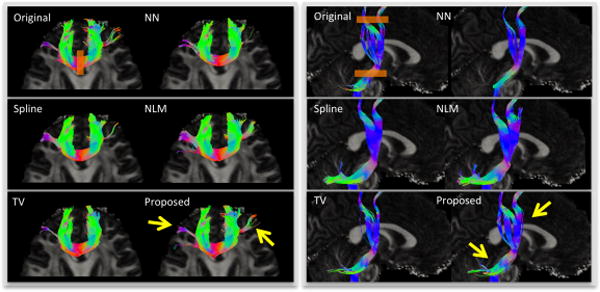
Illustration of fiber tracking results from original image and five reconstruction methods. Gene (left panel) and CST (right panel) were used as ROIs, shown as orange rectangles in the results of original images. Only the fibers pass through ROIs are shown. Yellow arrows indicate the fiber tracts best preserved by the proposed method.

4 Conclusion

We have presented a novel SRR method for 4D DWI from single scan. We sufficiently utilized the self-similarity of DWI in both spatial and diffusion domains, in terms of 4D low-rank and total variation regularizations in the model based resolution recovery. Comprehensive experiments were performed on 20 HCP subjects. NN, Spline, and NLM show inferior performance, which may be because the image degradation is not explicitly modeled in these methods. The proposed method has better performance in recovering both white mater properties and fiber tracts than that of TV, which confirms the usefulness of the inclusion of 4D low-rank in image reconstruction. In future work, we intend to acquire paired low- and high-resolution images from same subjects to further evaluate the proposed method, and further improve the performance by considering more factors such as the influence of diffusion gradient orientations.