Dynamic contrast optical coherence tomography images transit time and quantifies microvascular plasma volume and flow in the retina and choriocapillaris

Abstract

Despite the prevalence of optical imaging techniques to measure hemodynamics in large retinal vessels, quantitative measurements of retinal capillary and choroidal hemodynamics have traditionally been challenging. Here, a new imaging technique called dynamic contrast optical coherence tomography (DyC-OCT) is applied in the rat eye to study microvascular blood flow in individual retinal and choroidal layers in vivo. DyC-OCT is based on imaging the transit of an intravascular tracer dynamically as it passes through the field-of-view. Hemodynamic parameters can be determined through quantitative analysis of tracer kinetics. In addition to enabling depth-resolved transit time, volume, and flow measurements, the injected tracer also enhances OCT angiograms and enables clear visualization of the choriocapillaris, particularly when combined with a post-processing method for vessel enhancement. DyC-OCT complements conventional OCT angiography through quantification of tracer dynamics, similar to fluorescence angiography, but with the important added benefit of laminar resolution.

1. Introduction

Blood is supplied to retinal tissue by two distinct microcirculatory beds. The inner retinal circulation, arising from the central retinal (and/or cilioretinal) artery and draining through the central retinal vein, has a three-layered (“trilaminar”) architecture that primarily feeds the ganglion cell and plexiform layers of the inner retina [1,2]. The retinal circulation is thought to be regulated by central nervous system mechanisms that operate in the brain, including neurovascular coupling, blood gases, and autoregulation [3]. The choroidal circulation, which supplies the metabolically active photoreceptors and outer retina, arises from the posterior ciliary arteries and drains through the vortex veins [4]. The choroid is a high flow vascular bed that is also thought to be weakly regulated [5]. Though sometimes assumed to be “overperfused” based on its high flow and low oxygen extraction [6,7], knowledge of the choroidal circulation is limited, in part, by the lack of appropriate high resolution methodologies to study it in vivo.

Fluorescence angiography, based on the transit of a fluorescent tracer (fluorescein or indocyanine green, ICG) through the vasculature, is routinely used qualitatively to assess arteriovenous transit times or vascular permeability in clinical examination. However, because fluorescence angiography images are essentially photographs of the fundus [8], no depth resolution is achieved. ICG angiography, with a longer excitation and emission wavelength than fluorescein, enables improved assessment of choroidal circulation. Though occasionally fluorescence angiography is used quantitatively [9–11], measuring transit times at the capillary level, as well as the resolution of flow in small vessels in different layers (i.e., retina vs. choroid), remains challenging.

Since ocular clarity and optical quality are needed for good vision, the inner retinal vasculature, situated proximal to the photoreceptors, is usually accessible to high-resolution optical imaging methods. The adaptive optics scanning laser ophthalmoscope [12] enables visualization of individual blood cells in capillaries, including leukocytes [13] and erythrocytes [14], based on intrinsic optical properties. Blood cell velocity can be quantified from a time series of images [15]. However, such high-resolution, small field-of-view methods are inherently low throughput, require expensive adaptive optics technology, and cannot yet be performed in the choriocapillaris or choroid due to difficulties in focusing through the retinal pigment epithelium (RPE).

Recently, optical coherence tomography (OCT)-based methods of blood flow and angiography have emerged. Doppler OCT [16–18] can quantify total retinal blood flow by explicitly determining vessel angle [19] or by using angle-independent methods [20,21]. While Doppler OCT methods provide robust flow estimates in large vessels, they cannot quantify flow in microvasculature where red blood cell flux is intermittent and single-file. OCT angiography techniques [22–25], based on enhancing contrast arising from moving and scattering cells in the blood, are useful for selective imaging of only the “functional” microvasculature perfused with moving blood cells [26–30]. In its most widely-used implementation, angiography is used for visualization of microvasculature; however, recent efforts have pushed towards quantitative angiography using decorrelation rate [31]. Though decorrelation rate may be related to blood speed given a resolution voxel of known size [32,33], issues related to the red blood cell orientation [34], multiple and cooperative scattering in large vessels [35], and possible degradation of the focus in deeper tissues may confound quantification using decorrelation-based methods.

By comparison with the proximal retinal vasculature, the more distal choroidal vasculature is relatively more challenging to probe with light due to the highly scattering and absorbing overlying RPE. Blood-oxygen-level-dependent [36] and arterial spin labelling [37] functional magnetic resonance imaging (MRI) can assess the retina and choroid, but do not resolve the finer layers. Doppler Ultrasound can assess velocity and pulsatility indices in the posterior ciliary, central retinal, and ophthalmic arteries [38], but microvascular imaging remains challenging. For laser Doppler flowmetry [27] and laser speckle [28] imaging, proximal retinal vasculature can confound efforts to isolate choroidal flow, though foveolar choroidal blood flow below the avascular zone can be assessed independently [27]. Fundus pulsations measured using laser interferometry have also been used to indirectly assess regional pulsatile flow [39] and intraocular pressure can be used to estimate pulsatile flow [40]. While OCT angiography has succeeded in producing high-quality choroidal images [41], particularly at longer wavelengths [42], attempts at quantification through Doppler-based methods have had mixed success [43,44], possibly due to difficulties arising from multiple scattering of light transmitted through the RPE.

In this work, we show that dynamic OCT imaging and angiography during the passage of an intravascular scattering contrast agent through the field-of-view reveals laminar ocular blood flow patterns. Relative to a previous investigation of DyC-OCT in the brain [45], in addition to presenting a novel application in the retina and choroid, we also introduce a method for tracer signal calibration as well as a framework for quantification. Blood plasma transit times (based solely on tracer kinetics) are measured in retinal and choroidal vessels, while flow and volume are quantified for each of the microvascular layers.

2. Methods

We performed DyC-OCT by injecting a bolus of Intralipid 20% while imaging the rat eye with OCT angiography at 1300 nm, as shown in Fig. 1. After describing the imaging system, animal preparation, bolus injection protocol, and angiography algorithm, we describe and validate the modeling assumptions used to achieve quantitative measurements of plasma transit time, flow, and volume in individual retinal and choroidal layers.

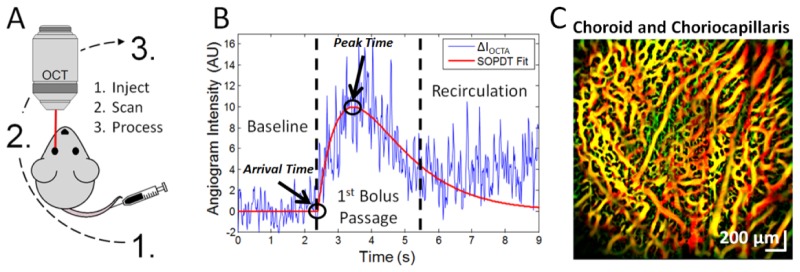
Fig. 1.

Dynamic Contrast Optical Coherence Tomography (DyC-OCT) protocol, DyC-OCT signal, and contrast-enhanced angiogram. A) In DyC-OCT, a blood plasma tracer is injected, continuous OCT imaging of the region-of-interest tracks tracer passage, and finally, data processing extracts hemodynamic information. B) The DyC-OCT signal from a single voxel consists of three phases: a “Baseline” phase before the tracer arrives, a “1st Bolus Passage” phase with a transient increase in signal followed by a decay as the tracer passes through the field-of-view, and a “Recirculation” phase during which the signal eventually settles at a “steady state” value above baseline. The model-based fit to the raw data (red line) excludes the recirculation phase. Transit-time metrics such as arrival time and peak time can be extracted from this model. C) The steady state signal from the tracer enhances OCT angiography after recirculation. A color-coded angiogram of the choroid and choriocapillaris is shown following tracer injection and computational Hessian-based “vesselness” enhancement, with proximal vessels in green, distal vessels in red, and overlapping regions in yellow.

2.1 Imaging system

A 1300 nm spectral / Fourier domain OCT microscope (Thorlabs, USA) was used to image the rat retina and choroid. This system used a bandwidth over 100 nm to provide an axial (depth) resolution of 7 μm in air (5.2 μm in tissue) and a system sensitivity of 91 dB after computational spectral reshaping, at a 91 kHz A-scan rate. A 1024 pixel InGaAs line scan camera was used in the spectrometer. A 5x objective lens with a measured transverse resolution of 8.3 μm FWHM was used to focus the beam onto the rat retina through a contact lens.

2.2 Animal preparation

The animal procedures were approved by the Institutional Animal Care and Use Committee at UC Davis. Male Sprague Dawley rats (n = 4; 250-400 grams) were used in this study. The rats were initially anesthetized in a chamber ventilated with 2% v/v isoflurane in a gas mixture of 80% air and 20% oxygen. After successful induction of anesthesia, the rats were removed from the chamber and placed on a heating blanket (Harvard Apparatus, USA) regulated by a rectal thermometer to maintain a core temperature of 37 degrees Celsius. The rat’s nose was placed in a ventilation cone which continued to deliver anesthesia between 1.25-1.75% isoflurane, adjusted as necessary to minimize discomfort while maintaining healthy breathing. Following a toe pinch to evaluate depth of anesthesia, the head was affixed to a custom frame to reduce motion caused by breathing. A peribulbar nerve block was also performed by injecting 0.1 mL of Lidocaine to prevent movement of the eye during imaging. A drop of 1% Tropicamide was placed on the rat eye to dilate the pupil and Goniovisc was used to facilitate contact between the eye and a fundus laser lens (Ocular Instruments, USA), used to eliminate corneal refraction and keep the eyelids open. Artificial tears were applied to the eye that was not imaged to prevent corneal dehydration. The rats were oriented so that the imaging field-of-view included at least one large vitreal artery-vein pair emanating from the optic nerve head.

2.3 Bolus injection protocol

Intralipid 20%, an FDA approved nutritional supplement for intravascular use in humans, which has been shown to enhance both the OCT Doppler [46] and intensity [45] signals within vasculature, was used as an OCT tracer. A bolus of this tracer was rapidly injected over the course of ~0.5-1 seconds via the tail vein using a 25 gauge syringe. The volume of this bolus was restricted to between 1.5-3 mL/kg weight (~2.4-4.7% of the rat blood volume) to minimize the bolus’s effect on systemic physiology. Previous experiments showed no observable change in blood flow in the mouse neocortex following injection of a similarly proportioned bolus [45].

2.4 OCT imaging protocols

Several imaging protocols were performed on each rat. First a baseline 3-D angiogram of the posterior pole was acquired. Next, DyC-OCT imaging was performed during the bolus injection. Finally, another 3-D angiogram was acquired at steady state, in which the recirculated tracer from the DyC-OCT injection enhanced the intravascular scattering signal.

2.4.1 3-D angiography

The 3-D angiography scanning protocol consisted of a series of repeated B-scans of the rat retina and choroid. Each 3-D angiography scan sampled 500 Y positions over 2 mm where 10 B-scans were repeated at each Y position, for a total of 5000 B-scans. Each B-scan contained 500 A-lines over 2 mm. The 3-D angiography data was acquired in a sequence of 5 blocks (2 × 0.4 mm) with 100 Y positions each over the total field-of-view of 2 × 2 mm.

2.4.2 DyC-OCT

DyC-OCT imaging was performed by acquiring 1000 repeated B-scans at a fixed Y position after the injection of the Intralipid tracer (Fig. 1) to measure the Intralipid signal during its passage through vasculature in the field-of-view. Each B-scan contained 1024 A-lines across 2 mm. B-scans were acquired at ~80 Hz continuously for 13 seconds.

2.5 DyC-OCT theory

In this section, we introduce a mathematical framework for the DyC-OCT signal, with the ultimate aim of quantifying hemodynamics. Unless specified with a subscript “ss,” for “steady state,” all time-dependent quantities are defined to be single-pass, and do not account for recirculation.

2.5.1 Assumptions and caveats

The DyC-OCT analysis, based on indicator-dilution theory, requires several assumptions [47–49]. First, the Intralipid tracer and blood must be well-mixed by the time the tracer particles reach the imaged field-of-view. Second, the Intralipid is assumed to act as a blood plasma tracer, given the small size of the Intralipid particles [50] relative to red blood cells (RBCs), which are >2 orders of magnitude larger in volume. Third, within any given voxel at any point in time, the change in OCT signal relative to baseline is assumed proportional to the number of Intralipid particles in that voxel. Fourth, all hemodynamic parameters must be constant during the experiment, and not perturbed in any way by the injection.

2.5.2 DyC-OCT signal

The baseline backscattering DyC-OCT signal is assumed to arise from endogenous blood cells, predominantly RBCs, and tracer, with backscattering coefficients of ${\mu }_{b,RBC}(z,x)$ and ${\mu }_{b,i}(z,x,t)$, respectively. Assuming that backscattering coefficients add, the OCT angiogram signal is described as the product of a position-dependent sensitivity factor $h(z,x)$and the total backscattering coefficient:

$$I_{OCTA}(z,x,t)=h(z,x)[{\mu }_{b,RBC}(z,x)+{\mu }_{b,i}(z,x,t)].$$ (1)

The factor $h(z,x)$in Eq. (1) defines the space-variant signal change measured by the OCT instrument in response to a local increase in backscattering. It can account for a variety of effects, including spectrometer roll-off, focusing, vignetting, and attenuation due to scattering and/or absorption, all of which are spatially-dependent and subject-dependent. Specifically,

$$h(z,x)=h_{spec}(z)h_{focus}(z)h_{vign}(x)h_{atten}(z,x).$$ (2)

While the tracer itself may cause additional attenuation, $h_{atten}(z,x)$was approximated as time-invariant. The OCT reflectance signal in the avascular outer nuclear layer (ONL) did increase ~10% during the bolus peak. However, this change is small compared to the reflectance increase in the vasculature (~86%) when averaged over the same time window.

The backscattering coefficient of the tracer is assumed to equal the time-dependent tracer concentration times the backscattering cross-section of the tracer:

$${\mu }_{b,i}(z,x,t)=c_i(z,x,t){\sigma }_{b,i}.$$ (3)

Similarly, the backscattering coefficient of endogenous blood is assumed to equal the mean RBC concentration times the backscattering cross-section of RBCs:

$${\mu }_{b,RBC}(z,x)=c_{RBC}(z,x){\sigma }_{b,RBC}.$$ (4)

Note that the mean RBC concentration is equivalent to the local hematocrit in a voxel if the voxel samples only blood. If a voxel samples blood and tissue, causing a partial volume effect, the RBC concentration is lower than the local hematocrit. Also, the mean RBC concentration at a given point, and therefore, RBC backscattering (Eq. (4)), is assumed to be constant throughout the experiment. The change in RBC concentration caused by the volume of injected tracer is neglected. The proportionate scaling of RBC backscattering coefficient with concentration (Eq. (4)) and the superposition of backscattering from RBCs and tracer (Eq. (1)) are both assumptions that may not fully hold in practice due to dependent scattering and shadowing effects in blood [35].

There is initially no tracer present in the field-of-view, so$c_i(z,x,0)=0$, and therefore,${\mu }_{b,i}(z,x,0)=0$. It follows that$I_{OCTA}(z,x,0)=h(z,x){\mu }_{b,RBC}(z,x)$. However, as shown in Fig. 1(B), noise is caused by stochastic fluctuations in instantaneous RBC concentration and speckle. The change in single-pass DyC-OCT signal over time, shown in Fig. 1(B), can thus be written as:

$$\Delta I_{OCTA}(z,x,t)=I_{OCTA}(z,x,t)-I_{OCTA}(z,x,0)=h(z,x){\mu }_{b,i}(z,x,t)=K(z,x)c_i(z,x,t).$$ (5)

In the above expression, $K(z,x)=h(z,x){\sigma }_{b,i}$ represents an unknown calibration factor relating the measured DyC-OCT signal to plasma tracer concentration, the quantity of interest.

2.5.3 DyC-OCT signal calibration

Calibration of the DyC-OCT signal refers to recovering tracer concentration$c_i(z,x,t)$, from $\Delta I_{OCTA}(z,x,t)$. Referring back to Eq. (5) with this goal in mind, local tracer concentration is related to the change in OCT signal through an unknown factor$K(z,x)$, which can differ between eyes, as well as between regions within an eye (e.g. retina versus choroid) due to light attenuation. While the backscattering cross-section (${\sigma }_{b,i}$) for a single batch of tracer and fixed detection geometry can be assumed to be reasonably constant, $h(z,x)$is system, position, and subject variant. Hence, ab initio calibration of the DyC-OCT signal is extremely challenging. Rather than attempting to account individually for all of the effects in Eq. (2), we use the fact that large retinal vessels have a known hematocrit close to the systemic hematocrit. Hence, the fractional plasma volume of voxels in any of these large vessels is relatively constant and known. Thus, DyC-OCT signal changes, if they are normalized or otherwise referenced (as in a deconvolution) to a large vessel with known hematocrit, can be made quantitative.

2.5.4 Quantifying plasma volume from the steady state signal

There are two methods by which quantitative plasma volume can be extracted from the DyC-OCT signal. In the first method, the steady state DyC-OCT signal, after repeated recirculation of the tracer, is compared to baseline and calibrated to yield quantitative plasma volume. Steady-state variables are denoted by the subscript “ss” and are assumed to be time-invariant over the imaging timescale.

$${\mu }_{b,i,ss}(z,x)=c_{i,ss}(z,x){\sigma }_{b,i}$$ (6)

Note that ${\mu }_{b,i}(z,x,t\to \infty )=0\ne {\mu }_{b,i,ss}(z,x)$ and$c_i(z,x,t\to \infty )=0\ne c_{i,ss}(z,x)$, since single-pass quantities decay to zero, while steady state quantities are reached after repeated recirculation. The plasma tracer assumption can be expressed as $c_{i,ss}(z,x)=\alpha c_p(z,x)$, where $c_p(z,x)$ is the fractional plasma volume. Moreover, the coefficient $\alpha$, relating tracer concentration $c_{i,ss}$ to plasma concentration $c_p$, depends on the total plasma volume (related to the total blood volume and hematocrit) of the subject and the amount of tracer injected. Thus,

$$\Delta I_{OCTA,ss}(z,x)=I_{OCTA,ss}(z,x)-I_{OCTA}(z,x,0)=h(z,x){\mu }_{b,i,ss}(z,x)=K_{ss}(z,x)c_p(z,x).$$ (7)

In the above expression, $K_{ss}(z,x)=h(z,x){\sigma }_{b,i}\alpha$represents an unknown constant relating the measured DyC-OCT signal to plasma volume, the quantity of interest.

To calibrate the DyC-OCT signal, we average the DyC-OCT signal over a reference vessel region of interest (ROI) with known area $A_{ROI,ref}$ and hematocrit (being careful to avoid vessel edges with partial volume effects).

$$\Delta I_{OCTA,ss,ref}=\frac{1}{A_{ROI,ref}}{\displaystyle {\iint }_{ROI,ref}\Delta I_{OCTA,ss}(z,x)}dzdx$$ (8)

Ideally, each location in the field-of-view would be calibrated using a reference in its immediate vicinity; however in practice only a few reference vessels are available across the field-of-view. Based on assumed hematocrits in a reference vessel, it is possible to estimate the calibration factor. For instance, macro-vessels (vitreal arteries and veins) in the retina are known to have hematocrits ($H$) close to the systemic hematocrit. Hence the fractional plasma may be estimated as $c_p=1-H$. For instance, if $H=0.45$, then $c_{p,ref}=0.55$.

$$K_{ss}(z,x)\cong K_{ss,ref}=\frac{\Delta I_{OCTA,ss,ref}}{c_{p,ref}}$$ (9)

The plasma volume for individual vessels near a given calibration factor, $K_{ss,ref}$, can then be expressed using the following integral where $P{V}_{V,ss}$ has units of plasma volume per unit length:

$$P{V}_{V,ss}={\displaystyle {\iint }_{ROI,vessel}{c}_p(z,x)dzdx}\cong {\displaystyle {\iint }_{ROI,vessel}\frac{\Delta I_{OCTA,ss}(z,x)}{K_{ss,ref}}dzdx}.$$ (10)

Similarly, plasma volume for different layers of the retinal vasculature can be expressed using the following integral where $P{V}_{L,ss}$ has units of plasma volume per unit en face area and $X_{layer}$is the width of the field-of-view:

$$P{V}_{L,ss}=\frac{1}{X_{layer}}{\displaystyle {\iint }_{ROI,layer}{c}_p(z,x)dzdx}\cong \frac{1}{X_{layer}}{\displaystyle {\iint }_{ROI,layer}\frac{\Delta I_{OCTA,ss}(z,x)}{K_{ss,ref}}dzdx}.$$ (11)

Since reference macro-vessels with known hematocrits are not uniformly available throughout the imaged field-of-view, it is not possible to calibrate each voxel in the image. In this work, we use both a large vitreal artery and a choroidal artery at the center of the field-of-view to perform the calibration for the inner retinal and choroidal vascular networks respectively. Plasma volume measurements are expected to be most quantitatively accurate in the immediate vicinity of the vessel that was used for calibration. While plasma volume measurements can also be mapped on a voxel-by-voxel basis using this method, speckle noise is reduced when integrating the signal over a vessel or layer.

2.5.5 Quantifying plasma flow and volume from signal kinetics

The challenge in using the tracer kinetic signal for quantification is to derive metrics that are independent of arterial inputs. Here we assume that the vascular bed is characterized by a transport function $h_{av}(t)$, or the intrinsic distribution of arteriovenous transit times given an impulsive arterial input at $t=0$(Fig. 2(C)). Thus, $h_{av}(t)=0$, for $t<0$, by causality. Since $h_{av}(t)$ is a distribution, ${\displaystyle {\int }_{-\infty }^{\infty }{h}_{av}(t)dt}=1$. The transport function is characterized by a mean transit time ($MTT$), defined as $MTT={\displaystyle {\int }_{-\infty }^{\infty }t{h}_{av}(t)dt}$. To calculate layer-resolved flow and volume, we define a tissue concentration integrated over a layer, as shown below.

$$C_t(t)=\frac{1}{X_{layer}}{\displaystyle {\iint }_{ROI,layer}{c}_i(z,x,t)dzdx}$$ (12)

$C_t(t)$has units of indicator per unit en face tissue area. Likewise, an arterial input is defined as:

$$c_a(t)=\frac{1}{(1-H)A_{artery}}{\displaystyle {\iint }_{ROI,artery}{c}_i(z,x,t)dzdx}.$$ (13)

If we are careful to avoid edges when selecting the arterial ROI, $c_a(t)$has units of concentration (indicator per unit plasma volume). Based on indicator-dilution theory [47–49],

$$C_t(t)=c_a(t)\ast [PF\times R(t)].$$ (14)

The residue $R(t)=1-{\displaystyle {\int }_{-\infty }^t{h}_{av}(\tau )d\tau }$ is the fraction of tracer remaining in the vascular bed after an impulsive arterial input at $t=0$. As such it is a unitless function that is 0 for $t<0$and decreases monotonically from 1 (at $t=0$) to 0 (as $t\to \infty$). Given these units, and noting that convolution is with respect to time, plasma flow ($PF$) is obtained in units of plasma volume per unit en face tissue area per unit time. The solution of this equation for $PF$requires a deconvolution if $R(t)$is not known a priori. Deconvolution techniques can be divided into model-based and model-independent approaches [51].

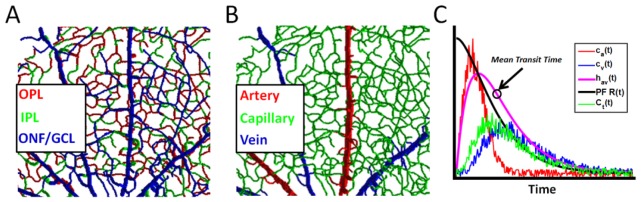
Fig. 2.

DyC-OCT quantifies hemodynamics in the retinal vasculature based on measuring tracer content in different compartments. A) Rendering of trilaminar vasculature of the inner retina, showing the optic nerve fiber / ganglion cell layer (ONF/GCL), inner plexiform layer (IPL), and outer plexiform layer (OPL). B) The capillary compartment makes up the bulk of the vascular network with alternating supplying arteries and draining veins radiating from the optic nerve head. C) One approach (Section 2.5.5) to assess microvasculature uses an arterial input (c_a) and the total tracer signal within microvasculature (C_t) to determine the product of plasma flow (PF) and a residue function (R) that describes the fraction of tracer left in microvasculature after an impulsive arterial input. An alternative, but related, approach (Section 2.5.6) uses an arterial input (c_a) and venous output (c_v) to determine the arteriovenous transport function between them (h_av). The mean transit time, defined as the centroid of h_av(t), is marked.

Moreover, by making use of the fact that areas add under convolution and taking into account the central volume principle (CVP), $PV=PF\times MTT$, with $MTT={\displaystyle {\int }_{-\infty }^{\infty }R(t)dt}$, the following relationship is obtained:

$$PV=\frac{{\displaystyle {\int }_{-\infty }^{\infty }{C}_t(t)dt}}{{\displaystyle {\int }_{-\infty }^{\infty }{c}_a(t)dt}}.$$ (15)

The units of $PV$are plasma volume per unit en face area. If $K(z,x)\cong K_{ref}$is similar for both the arterial ROI and layer ROI, $\Delta I_{OCTA}(z,x,t)$can replace $c_i(z,x,t)$ in Eq. (12) and Eq. (13), and the unknown calibration factor cancels out in both the deconvolution (Eq. (14)) or the normalization (Eq. (15)). Thus, if arterial inputs can be found, both plasma flow and plasma volume can be determined quantitatively in absolute units. Blood flow and blood volume may then be readily determined by assuming a hematocrit for the capillary bed.

2.5.6 Direct arteriovenous transit time measurements

Noting that $h_{av}(t)$ can be measured by deconvolving an arterial input and a venous output, DyC-OCT affords an alternative approach for measuring$MTT$. In particular, since$c_v(t)=c_a(t)\ast h_{av}(t)$, $MTT$can be determined as

$$MTT={\displaystyle {\int }_{-\infty }^{\infty }t{h}_{av}(t)dt}=\frac{{\displaystyle {\int }_{-\infty }^{\infty }t{c}_a(t)dt}}{{\displaystyle {\int }_{-\infty }^{\infty }{c}_a(t)dt}}-\frac{{\displaystyle {\int }_{-\infty }^{\infty }t{c}_v(t)dt}}{{\displaystyle {\int }_{-\infty }^{\infty }{c}_v(t)dt}},$$ (16)

where $c_v(t)$ is measured at a venous output.

If $PV$is determined from Eq. (15) and $MTT$from Eq. (16), $PF=PV/MTT$can be determined from the central volume principle; however, $PF$ will be underestimated if the total plasma volume connecting the artery and vein is not accounted for.

2.5.7 Blood flow index

In addition to the quantitative blood flow metrics proposed in Sections 2.5.5 and 2.5.6, a more qualitative blood flow index can be derived from the DyC-OCT signal. The qualitative blood flow index (BFI) has been used in similar indicator dilution studies [52]. BFI is given by the slope of the rising edge of the DyC-OCT signal and can be calculated as the magnitude of the DyC-OCT signal divided by the difference between arrival and peak times (shown in Fig. 1(B)) and can be additionally normalized to the BFI of the arterial input for better comparisons across animals.

2.5.8 Hematocrit index

The baseline DyC-OCT signal arises from endogenous blood scattering, predominantly from RBCs, while the steady state signal change arises from tracer scattering (Eq. (7)). The ratio of baseline to steady state signal therefore yields a qualitative indicator of hematocrit:

$$H_{index}(z,x)=\frac{I_{OCTA}(z,x,0)}{I_{OCTA}(z,x,0)+\Delta I_{OCTA,ss}(z,x)}=\frac{{\sigma }_{b,RBC}{c}_{RBC}(z,x)}{{\sigma }_{b,RBC}{c}_{RBC}(z,x)+{\sigma }_{b,i}{c}_{i,ss}(z,x)}.$$ (17)

When defined in this way, the problematic system-dependent calibration factor $h(z,x)$is eliminated, and information about the relative concentrations of RBCs and tracer (the latter related to fractional plasma volume) is obtained. A major caveat of this metric is that RBC backscattering ${\sigma }_{b,RBC}$ is highly orientation-dependent; thus, the hematocrit index is expected to be especially unreliable in larger vessels, where RBC orientation varies across the vessel cross-section [34].

2.6 Data processing

Here we describe the steps used to perform angiography on both DyC-OCT time series and 3-D volumes.

2.6.1 Angiography algorithm

Dynamic scattering was isolated by removing the static scattering component of the OCT signal by high-pass filtering consecutive B-scans along the slow axis [53]. This left only the dynamic component of the OCT signal, $I_{OCTA}$(Eq. (1)), which corresponds to moving particles such as blood cells or Intralipid within the vasculature. Here, the high-pass filtering algorithm entailed complex subtraction of consecutive frames, after sub-pixel axial motion correction and bulk phase correction. If the interframe time is sufficiently larger than the intrinsic decorrelation time, the angiogram, derived in this manner, accurately represents intravascular scattering and is relatively insensitive to flow speed. The same angiography algorithm (complex subtraction) was used to generate both DyC-OCT time series and 3-D angiograms. For 3-D angiograms, the dynamic scattering signals were averaged at each Y location, prior to application of Hessian-based vesselness enhancement [54].

2.6.2 Time course fitting

DyC-OCT time courses were determined and fit on a voxel, vessel, or layer basis. The angiography time series showing tracer passage was averaged by convolving it with a 3×3×3 $(z,x,t)$kernel. The baseline value of each voxel was then subtracted, to obtain $\Delta I_{OCTA}(z,x,t)$(Eq. (5)). Next $\Delta I_{OCTA}(z,x,t)$was fit using a second-order plus dead time model (SOPDT) as described in previous literature [45,55] and shown in Fig. 1(B). Based on the fit of the model to the time course, parameters describing the local transit of the injected bolus were determined. DyC-OCT signal was also summed over selected vessels or layers and SOPDT fits and subsequent analysis were applied to the summed signal. Interrogating individual vessels and layers rather than voxels reduced motion artifacts and noise and improved goodness-of-fits.

2.6.3 Vessel segmentation

A binary mask was generated based on the R² (goodness-of-fit) of the model at each individual voxel in the DyC-OCT data set. Voxels with low R² values and non-physiological fits were rejected from the mask before using automated segmentation algorithms to generate a mask for each individual vessel.

2.6.4 Layer segmentation

For the DyC-OCT data, vascular layers of the retina and choroid were segmented manually using the angiograms and structural OCT images to identify key features. The 3-D angiogram data sets were segmented by automatically detecting the sharp increase in OCT signal at the RPE. The signal was integrated across the vessel mask of each layer to reduce noise outside the vasculature.

2.6.5 Tracer kinetics

Measurements of tracer kinetics were extracted directly from the model’s fit to the DyC-OCT time course. Arrival time, peak time, and time to peak were all obtained from parameters of the fit. Arrival time is the earliest appearance of the tracer, peak time is where the tracer signal is at its maximum, and time to peak is the difference between peak and arrival times. Mean transit times were also obtained using Eq. (16) where $c_v(t)$ was replaced by the concentration-time curves in individual microvessels. Inter-animal comparisons were made for arrival and peak time by first referencing them to the earliest arrival times in a retinal or choroidal artery, as appropriate. Time to peak and mean transit time measurements, on the other hand, are inherently comparable across animals, and do not require another time reference.

2.6.6 Plasma volume

As shown in Table 1, there are two approaches to quantify plasma volume. The first, based on Eq. (10) and Eq. (11), uses the steady state tracer signal. The second, based on Eq. (15), uses the integral under the tissue concentration-time curve. Both volume measurements were calibrated (Eq. (9)) using a large vitreal artery, assuming a hematocrit of 45%. An alternative calibration was also performed for the choriocapillaris using a choroidal artery, assuming a hematocrit of 45%.

Table 1. Reference locations for the theory of DyC-OCT metrics.

Metric	Theory	Units	Sections	Equations
Individual Vessel Plasma Volume	Steady-State DyC-OCT Signal	Volume per unit length [pL/mm to nL/mm]	2.5.4	6-9, 10
Total Layer Plasma Volume	Steady-State DyC-OCT Signal	Volume per unit en face area [nL/mm2]	2.5.4	6-9, 11
	Integrated DyC-OCT Signal	Volume per unit en face area [nL/mm2]	2.5.5	12, 13, 15
Total Layer Plasma Flow	Central Volume Principle	Flow per unit en face area [μL/min/mm2]	2.5.5	Inline
	Model-Based Residue Deconvolution	Flow per unit en face area [μL/min/mm2]	2.5.5, 2.6.7	12, 13, 14
	Singular Value Decomposition Residue Deconvolution	Flow per unit en face area [μL/min/mm2]	2.5.5, 2.6.7	12, 13, 14
	Blood Flow Index	Arbitrary Units	2.5.7	N.A.
Hematocrit Index	Ratio Between Plasma Tracer and Baseline Angiogram Signals	Arbitrary Units	2.5.8	17
Mean Transit Time	Arteriovenous Transport Function Centroid	Time [s]	2.5.5	13, 16
	Model-Based Residue Deconvolution	Time [s]	2.5.5, 2.6.7	12-14, Inline
	Singular Value Decomposition Residue Deconvolution	Time [s]	2.5.5, 2.6.7	12-14, Inline
Other Transit Times	Arrival Time, Peak Time, Mean Transit Time, and Time to Peak from Fitted DyC-OCT Curve	Time [s]	2.6.2, 2.6.5	N.A.

2.6.7 Plasma flow

Four plasma flow metrics were implemented based on the total DyC-OCT signal in each vascular layer (Table 1). The first two approaches performed the deconvolution in Eq. (14) to determine $PF\times R(t)$. This was achieved using either a model-independent, truncated singular value decomposition (SVD) approach to invert the arterial input matrix and solve for $PF\times R(t)$ directly, or a model-based approach which assumed a functional form for $R(t)$. Compared to a traditional SVD approach, the truncated SVD removes singular values below a given threshold, determined individually for each arterial input matrix, to reduce the effects of noise when estimating the inverted arterial input matrix. For the model-based approach, by treating the microvasculature as a well-mixed single compartment, we obtained $R(t)=e^{-t/MTT}u(t)$, where $u(t)$ is the unit step function. Plasma flow ($PF$) and the mean transit time ($MTT$) were determined simultaneously by least squares fitting of Eq. (14).

The third approach (Section 2.5.6) determined plasma flow based on the central volume principle (CVP) by dividing the quantitative plasma volume from each layer by the arteriovenous $MTT$. Separate $MTT$values were obtained using artery-vein pairs in the inner retina and the choroid. A single $MTT$was determined for each network (i.e. inner retina and choroid) and used to estimate flow through the CVP for each of the corresponding subnetworks (i.e. ONF/GCL, IPL, OPL, and CC).

Finally, in the fourth approach, BFI was measured (Section 2.5.7) and normalized to the BFI in the same reference artery used for residue deconvolution.

2.6.8 Statistical testing

For statistical testing of significant differences in DyC-OCT metrics across different vascular networks of the eye, a Kruskal-Wallis test was used. This was then followed by Tukey’s honestly significant differences test to account for multiple comparisons.

3. Results

After investigating how the angiogram signal increases after the Intralipid tracer injection, metrics describing tracer kinetics, plasma volume, and plasma flow are shown for different layers.

3.1 DyC-OCT signal and artifacts

Figure 3(A)-3(C) compares a conventional OCT angiogram with the DyC-OCT angiogram, or the angiogram determined from DyC-OCT signal change averaged over the first bolus passage. In addition to providing higher contrast, particularly for the microvasculature, DyC-OCT mitigates some traditional OCT angiogram artifacts. The center of a large choroidal vessel (asterisk) has low angiogram signal (Fig. 3(A)) due to multiple scattering which creates a large false angiogram signal below (i.e. at a larger path length than) the vessel as marked by the arrow. The DyC-OCT signal change angiogram accurately localizes signal to the vasculature and reduces multiple scattering artifacts, as shown in Fig. 3(B). In Fig. 3(C), a color overlay of RBC-based OCT angiography (red) and tracer-based DyC-OCT angiography (green) highlights regions of agreement (yellow). Notable departures include multiple RBC scattering tails (red) under major retinal and choroidal vessels, higher DyC-OCT enhancement (green) in major choroidal vessels and at the edges of some major retinal vessels, and an “hourglass” artifact that transitions from red (vertical axis) to yellow or green (horizontal axis) in some major retinal vessels.

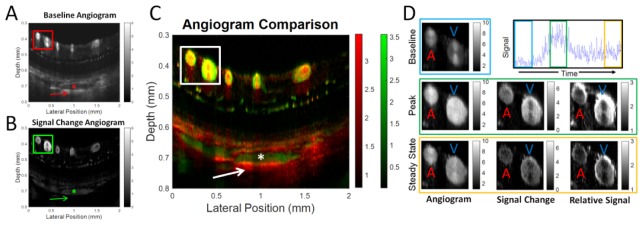
Fig. 3.

Comparison of conventional OCT angiogram and DyC-OCT angiogram cross-sections is shown. A) Conventional OCT angiogram (A) reveals vasculature without the use of a contrast agent; however, the centers of large vessels in the choroid appear dark (*) with bright multiple scattering tails beneath them (arrow). The DyC-OCT angiogram also shows the vasculature (B) based on the mean signal change induced by the contrast agent during the first bolus passage. Choroidal vessels appear bright in DyC-OCT without multiple scattering artifacts. C) Both the conventional OCT angiogram (red) and the DyC-OCT angiogram (green) overlap well (yellow) in the large proximal vessels with some artifacts, while lumens of choroidal vessels are significantly enhanced by the contrast agent. D) Detailed contrast kinetics for the boxed region in A-C are shown. The angiogram (I_OCTA(z,x,t), first column), signal change (ΔI_OCTA(z,x,t), middle column), and relative signal (I_OCTA(z,x,t)/I_OCTA(z,x,0), last column), are shown at baseline (first row), at peak (middle row), and at steady-state (last row) after tracer recirculation. The large retinal artery (labeled “A”) shows a more uniform signal enhancement (middle column) than the large retinal vein (labeled “V”).

Figure 3(D) shows changes in the angiogram signal as the tracer passes through the cross-section of a large artery (labeled “A”) and vein (labeled “V”). Arteries and veins were identified as large vessels with early and late arrival times, respectively. The baseline angiogram demonstrates a well-known hourglass shaped artifact in both vessels, which is caused by shear-induced orientation of red blood cells and their orientation-dependent backscattering [34]. The peak angiogram shows that the tracer increases the angiogram signal and fills the vessel, particularly in the boundary layer, which is typically devoid of RBCs due to the Fåhræus–Lindqvist effect [56]. Interestingly, the signal change, corresponding to $\Delta I_{OCTA}(z,x,t)$given by Eq. (5), also shows an apparent hourglass artifact (Fig. 3(B)). If tracer concentration were uniform across the vessel cross-section and DyC-OCT signal change were proportional to concentration, as assumed in Eq. (5), the signal change would also have been uniform. The fact that an hourglass artifact, albeit inverted, appears in the signal change images (middle column), in spite of a presumably uniform tracer concentration across the vessel cross-section, suggests the presence of orientation-dependent shadowing effects. For reasons that are not entirely clear, the inverted hourglass artifact appears in the venous DyC-OCT signal change, but not the arterial signal as shown in the middle column of Fig. 3(D). This may be related to the smaller diameter, higher pulsatility, or blunted flow profile of the artery. For these reasons, when calibrating quantitative metrics, arteries are preferred over veins, and the sides of vessels are preferred over the top or bottom of vessels.

3.2 Angiogram enhancement

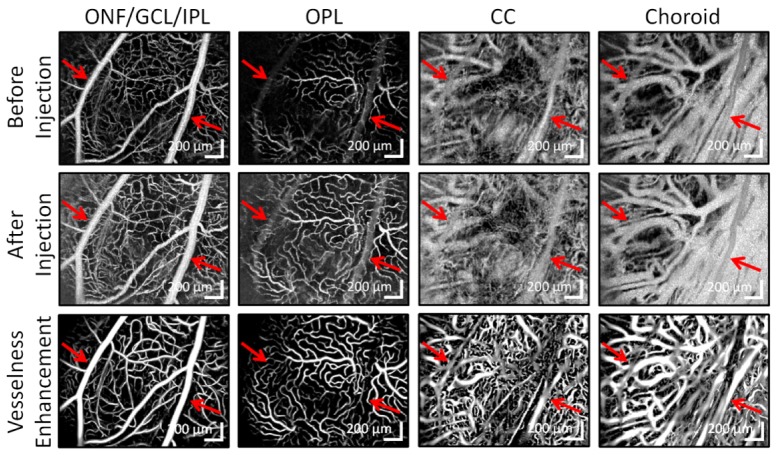
As shown in Fig. 3, injection of the contrast agent increases the signal in the angiogram throughout both the inner and outer retina in cross-section. Figure 4 investigates this signal enhancement using en face projections. Before contrast agent, large retinal vessels create shadows in deeper layers (red arrows). Following Intralipid injection, the false positive angiogram signal created by multiple scattering from these vessels decreases, particularly in the CC and choroid. The contrast agent fills the edges of large vessels and reveals microvasculature. In addition, the last row of Fig. 4 demonstrates how computational “vesselness” enhancement can help to clarify the structure in the extremely dense choriocapillaris and choroid. The fine structure enhanced by the algorithm is not likely caused by noise as angiograms acquired later revealed similar structure.

Fig. 4.

Maximum intensity projection angiograms across 4 vascular layers before contrast injection, after contrast injection (contrast-enhanced), and after applying the vesselness enhancement algorithm to the contrast-enhanced angiogram. Each pair of before and after angiograms in the same column have the same color scale. Red arrows point to large retinal vessels and the shadows that they cast in subsequent layers.

3.3 Vessel-based metrics

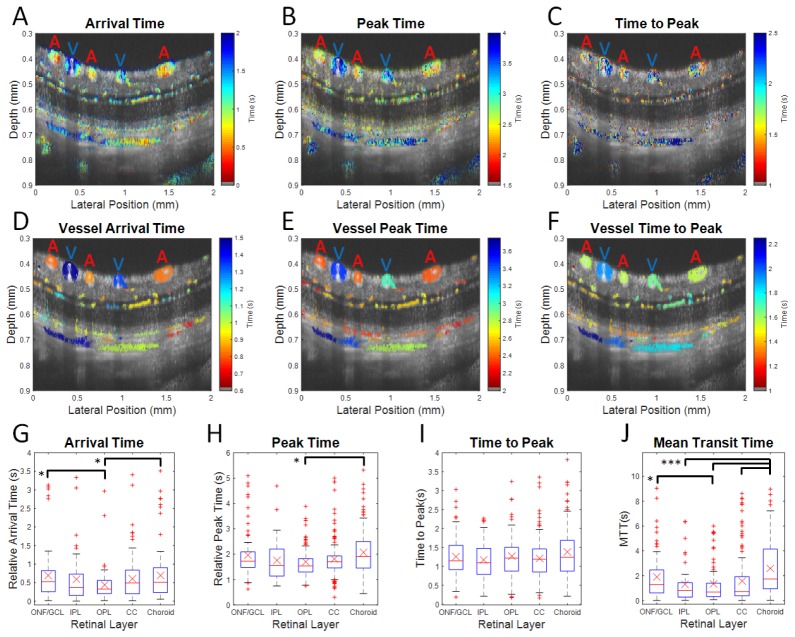
By examining the DyC-OCT signal within individual vessels, both tracer kinetics and plasma volume measurements were extracted. Maps of tracer kinetics for a single animal as well as statistics across the different vascular layers of all animals are shown in Fig. 5.

Fig. 5.

DyC-OCT measures laminar transit time kinetics. False color transit time maps are overlaid on grayscale structural OCT images with large arteries and veins marked (A and V respectively) at both the voxel level (A-C) and the vessel level (D-F). Statistics from vessels across 4 rats are shown (G-J). Metrics are arrival time (A,D, and G), peak time (B,E, and H), time to peak (C,F, and I), and mean transit time (J). The arrival and peak times shown in the first two rows are relative to the imaging start time. In the third row, the ONF/GCL, IPL, and OPL arrival and peak times are referenced, for each rat, to the earliest inner retinal arterial arrival time, while the CC and choroid arrival and peak times are similarly referenced to the earliest choroidal arterial arrival time. Medians (red lines) and means (red X’s) for each layer, with equal weighting for each vessel, are shown. The upper and lower quartile ranges are bounded by the blue box. Outliers (red points) fall outside of 2.5 times the upper or lower quartile range. The maximum and minimum points (dashed black lines), excluding outliers, are shown. Black bars show statistically significant pairwise comparisons (* p < 0.05 and *** p < 0.0005). ONF/GCL – Optic Nerve Fiber/Ganglion Cell Layer, IPL – Inner Plexiform Layer, OPL – Outer Plexiform Layer, and CC – Choriocapillaris.

Figure 5 demonstrates that DyC-OCT measures temporal tracer dynamics both in the retina and choroid, and in some cases, in the scleral vasculature as well. The top row of Fig. 5 shows transit times for each individual voxel, demonstrating heterogeneity within individual vessels. The time to peak measurements in Fig. 5(C) appear to be more sensitive to noise. The middle row shows transit times for each individual vessel, determined by summing the DyC-OCT signal within a vessel before fitting the model. The expected alternating artery/vein structure of the large retinal vessels is now clear from the arrival and peak time maps. The bottom row of Fig. 5 summarizes metrics for individual vessels within each layer. In these charts, arrival and peak times are given in reference to retinal arteries for the ONF/GCL, IPL, and OPL or choroidal arteries for the choroid and choriocapillaris. As each vessel is counted equally and capillaries are most numerous, trends in the bottom row reflect capillaries; however the large vessels tend to contribute extreme outliers to the distributions. Statistically significant differences in arrival time are shown between the macrovascular ONF/GCL and choroid and the microvascular OPL. The arrival time heterogeneity (as shown by the upper and lower quartiles in Fig. 5(G)) is smallest in the OPL compared to all other layers, probably due to the preponderance of capillaries, rather than arterioles and venules, in this layer [54]. Statistically significant differences in peak time are observed between the choroid and the OPL, and the peak time heterogeneity appears to be smallest in the microvascular layers with the highest expected branch orders (OPL and CC). There are no significant differences in time to peak values across layers. Mean transit times ($MTT$) in individual vessels, measured as described in Section 2.6.5, are longest in the choroid. $MTT$values in microvascular layers are shorter than those in the macrovascular layers, at a statistically significant level. In general, based on mean transit time, the tracer appears to circulate from the macrovasculature to the microvasculature and back faster in the inner retina compared to the choroid. However, differences in the other temporal metrics across layers are minimal.

Figure 6(A)-6(B) shows qualitative red blood cell (RBC) content, based on baseline angiogram signal, and quantitative plasma volume measurements, based on tracer signal, from individual vessels in log scale. Using this information, a hematocrit index was mapped for each vessel (Fig. 6(C)). Due to high RBC backscattering signal from orientation effects in large vessels (Fig. 3(D)), the hematocrit index is underestimated, particularly in veins (labelled “V”). After eliminating large vessels, Fig. 6(D) shows the hematocrit index for the total signal in each microvascular layer across 4 animals. In the inner retina, hematocrit index drops in microvascular networks with higher branching orders [54]. In the choriocapillaris, hematocrit index increases, possibly due to the unusually large diameters of capillaries in the choriocapillaris bed [57].

Fig. 6.

RBC signal and plasma volume measurements are used to determine a hematocrit index. False color volume and hematocrit maps are overlaid on grayscale structural OCT images, with large arteries and veins marked A and V, respectively. A) Log scale red blood cell (RBC) content as measured by the qualitative baseline OCT angiogram. B) A quantitative map of plasma volume per vessel shown in log scale. C) Qualitative hematocrit index for individual vessels. D) Mean hematocrit index (red line) and individual hematocrit index measurements (blue lines) across the microvascular layers of four rats. IR – Total Inner Retina, ONF/GCL – Optic Nerve Fiber/Ganglion Cell Layer, IPL – Inner Plexiform Layer, OPL – Outer Plexiform Layer, and CC – Choriocapillaris.

3.4 Layer-based metrics

Quantitative layer-based metrics of key hemodynamic parameters (transit time distribution, plasma volume, and plasma flow) can be assessed using DyC-OCT. Accurate quantification of flow and transit time requires accounting for bolus dispersion using an appropriate arterial input and, for volume or flow, calibration of tracer signal using a vessel of known hematocrit. The following figures will show a retina-based calibration (unfilled symbols) for the retinal layers and both a retina- and a choroid-based calibration (filled symbols) for the choriocapillaris. Unlike the plots in Fig. 5, which weight individual vessels evenly, here the total signal within each layer is used, which inherently weights larger vessels more strongly than smaller vessels; however, the large supplying arteries and draining veins are not included for the layer-based metrics. Large vessels are excluded from layer-based analysis to satisfy assumptions of indicator-dilution theory. Moreover, capillary perfusion is more directly related to nutritive supply in a given retinal area than perfusion in large vessels, which are more densely located near the optic nerve head and sparser at the periphery.

Figure 7 shows transit time measurements across different vascular layers. Arrival times were shortest in the layers closest to the arterial input and increased in more distal vasculature. While the choriocapillaris shows the earliest arrival times using a retinal artery time reference, it is more similar to the inner plexiform layer when using a choroidal artery time reference (Fig. 7(A)). Aside from one high value in the choriocapillaris, the peak times and times to peak were relatively flat across all layers. $MTT$ values determined from an artery-vein pair and from the model-based and SVD methods of deconvolving the residue function are flat across most layers, but increase in the choriocapillaris. Whereas the deconvolution methods produce an $MTT$ for each vascular layer, the CVP method only identifies a single $MTT$ each for the inner retinal and choroidal vascular networks (Fig. 7(D)).

Fig. 7.

Quantitative transit time metrics for individual microvascular layers show similar trends across animals. Kinetic measurements include arrival time (A), peak time (B), time to peak (C), and mean transit time (MTT), where MTT can be calculated from the arteriovenous transport function between artery-vein pairs in the inner retina and choroid (D), from a model-based residue deconvolution approach (E), or from a singular value decomposition (SVD) residue deconvolution solution (F). Measurements from individual animals are shown as blue lines with differently oriented triangles for each animal. Mean values are shown as red squares. Unfilled symbols represent measurements based on a retinal artery time reference (A-C, Section 2.6.5) or calibration (D-F, Section 2.5.3) while filled symbols used a choroidal artery time reference or calibration. IR – Total Inner Retina, ONF/GCL – Optic Nerve Fiber/Ganglion Cell Layer, IPL – Inner Plexiform Layer, OPL – Outer Plexiform Layer, and CC – Choriocapillaris.

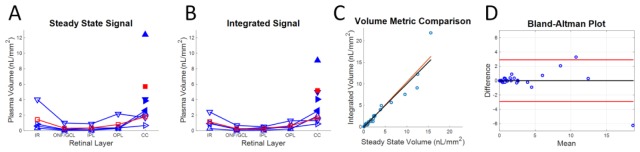
Quantitative plasma volume metrics, based on steady state signal (Fig. 8(A)) and integrated DyC-OCT signal (Fig. 8(B)), are highly correlated (Fig. 8(C)) and agree (Fig. 8(D)). Despite the increased attenuation of the OCT signal, causing underestimation of volume in deeper layers, most animals showed increasing plasma volumes from the inner retinal layers to the choriocapillaris, even when a retinal artery was used for calibration (open symbols). Proper calibration with a choroidal artery demonstrates the extent of the underestimation caused by signal attenuation, increasing choriocapillaris volumes by ~3 times (filled symbols).

Fig. 8.

Quantitative plasma volume metrics for individual microvascular layers show similar trends across animals. Two separate methods of quantifying plasma volume based on the DyC-OCT signal are compared: steady state signal (A) and integrated DyC-OCT signal (B). Measurements from individual animals are shown as blue lines with differently oriented triangles for each animal. Mean values are shown as red squares. Unfilled symbols represent measurements based on a retinal calibration (Section 2.5.3) while filled symbols are from a choroidal calibration. C) Both methods are correlated based on linear regression (red line), with all points near the line of equality (black). D) A Bland-Altman plot demonstrates agreement between the two methods. The black line shows the average difference, centered near zero, and the red lines show two standard deviations from this mean. IR – Total Inner Retina, ONF/GCL – Optic Nerve Fiber/Ganglion Cell Layer, IPL – Inner Plexiform Layer, OPL – Outer Plexiform Layer, and CC – Choriocapillaris.

One qualitative and three quantitative plasma flow metrics all demonstrate similar patterns among different vascular layers, as shown in Fig. 9. As with plasma volume above, increased attenuation of the OCT signal caused underestimation of flow in deeper vascular layers, yet most animals show increasing plasma flow from the inner retinal layers to the choriocapillaris, even when a retinal artery was used for calibration. Proper calibration with a choroidal artery rectifies this underestimation, yielding flow values ~2-3 times higher than with retinal calibration.

Fig. 9.

Plasma flow metrics for individual microvascular layers show similar trends across animals: blood flow index (BFI) (A), central volume principle (CVP)-derived flow using arteriovenous mean transit times from Fig. 7(D) and plasma volumes from Fig. 8(A) (B), a model-based residue deconvolution method (C), and a model-free singular value decomposition (SVD) residue deconvolution method (D). Insets in C and D show respective plots of plasma flow (PF) times the residue (R(t)) for the choriocapillaris, determined by deconvolution. Measurements from individual animals are shown as blue lines with differently oriented triangles for each animal. Mean values are shown as red squares. Unfilled symbols represent measurements based on a retinal calibration (Section 2.5.3) while filled symbols are from a choroidal calibration. IR – Total Inner Retina, ONF/GCL – Optic Nerve Fiber/Ganglion Cell Layer, IPL – Inner Plexiform Layer, OPL – Outer Plexiform Layer, and CC – Choriocapillaris.

4. Discussion

DyC-OCT, or dynamic OCT imaging during the passage of a contrast agent, was performed in the retina and choroid to probe microvascular hemodynamics. Based on features of the dynamic contrast curves, ad hoc metrics such as arrival time and blood flow index (BFI) were demonstrated. A framework for hemodynamic quantification was also introduced. By accounting for dispersion in the arterial input, the intrinsic transit time distribution through the microvasculature was quantified. Finally, by calibrating the DyC-OCT signal, both flow and volume were quantified as well.

4.1 Angiogram enhancement

The Intralipid contrast agent enhances OCT angiogram signal throughout the vasculature. Moreover, it also provides signal in the RBC-free boundary layer and helps compensate orientation-dependent “hourglass” scattering artifacts found in conventional intensity-based OCT angiograms (Fig. 3). These features may enable more accurate quantification of lumen parameters such as diameter or area.

The DyC-OCT angiograms depict more localized intravascular signal in large choroidal vessels (Fig. 3). In conventional OCT angiograms, the scattering signal is usually displaced beneath the vessel due to multiple RBC scattering. Since the signal enhancement is axially displaced from the baseline signal, gains appear modest in en face maximum intensity projection angiograms of the choroid (Fig. 4). However, cross-sectional DyC-OCT images reveal that false positive signals are greatly reduced (Fig. 3(B)-3(C)). The more isotropically scattering Intralipid particles provide additional intravascular backscattering signal and may help to reduce multiple scattering artifacts in the choroid. Both of these effects mitigate false positive angiogram signal beneath large vessels, though artifacts remain, as shown in the first two rows of Fig. 4. The additional vesselness enhancement step performed in post-processing improves maximum intensity projections of the choroid and choriocapillaris (third row of Fig. 4), which are easier to visualize and interpret than their unfiltered counterparts. Due to the small size of the majority of Intralipid particles (<λ) relative to red blood cells (>λ), Intralipid scattering is expected to increase proportionately more than RBC scattering as wavelength is reduced. Hence, Intralipid signal enhancement is expected to be more prominent at the ~800 nm wavelength range used in standard ophthalmic systems than at the ~1300 nm wavelength range used here.

4.2 Kinetic measurements

DyC-OCT time courses contain information about microvascular topology and flow pathways, which are encapsulated in the transit time distribution. Kinetic measurements are inherently more robust than flow or volume, and require only that the transit times are appropriately ascribed to the vessels being measured [45]. Given the high choriocapillaris flow relative to the inner retina (Fig. 9 and Table 2), it is somewhat surprising that transit times, including the MTT, are similar (Fig. 5(G)-5(J) and Fig. 7). However, the CVP dictates that given the high volume of the choriocapillaris relative to the inner retinal capillaries (Fig. 8), a much larger flow is required to achieve a comparable MTT. Beyond the MTT, the full transit time distribution will enable more comprehensive analysis of vessel networks using DyC-OCT. For example, the variance of the transit time distribution is related to efficacy of oxygen extraction, with less transit time heterogeneity enabling a higher maximal oxygen extraction fraction [58]. In particular, DyC-OCT metrics describing changes in flow topology may prove useful as biomarkers for retinal and choroidal diseases. Further investigation is warranted to link the observed transit characteristics to flow topology of each layer.

Table 2. Blood flow estimates of the inner retina and choroid using different DyC-OCT metrics.

	Inner Retina Blood Flow		Choriocapillaris Blood Flow
Technique	Mean	Std Dev	Mean	Std Dev	Ratio
BFI (AU)	2.3	0.8	14.1	19.1	6.1
CVP (µL/min)	7.5	5.9	41.7	17.7	6.5
Model-Based (µL/min)	22.7	6.3	70.9	8.2	3.7
SVD (µL/min)	9.1	4.3	40.0	18.3	5.2

Means, standard deviations, and the ratio between choroidal and inner retinal flow are shown. Blood flow index (BFI), central volume principle (CVP), and singular value decomposition (SVD).

4.3 Plasma volume and flow

Quantitative flow (Fig. 9(B)-9(D)) and volume (Fig. 8) are achieved in DyC-OCT based on Eq. (14) and Eq. (15), respectively. Deconvolution of Eq. (14) ensures that the arterial input function dispersion is accounted for and tracer signal is calibrated. The residue-based analysis in Eq. (14) is valid if signals are integrated across an entire vascular bed comprising all compartments. For these reasons, flow metrics based on tracer dynamics are only used to characterize layers and not individual vessels. Our analysis implicitly assumes that cross-sections chosen for DyC-OCT are representative samples of the entire network. In the future, 3-D DyC-OCT imaging will more comprehensively sample the vascular bed and better satisfy assumptions of residue analysis. Finally, it is important to emphasize that residue analysis is applicable to entire networks (e.g. inner retina and choriocapillaris), and significant flow connectivity between retinal layers [54] would invalidate residue analysis for individual inner retinal layers. Thus, while the flow rates measured for individual microvascular layers may be affected by interconnectivity, the total flow measured for the inner retina is more strictly accurate based on indicator-dilution theory.

While the strong correlation between the two independent methods of quantifying plasma volume (Fig. 8) supports the claim of accurate and quantitative plasma volume measurements, a cross-comparison using an alternative modality was not performed. It should be noted, however, that we previously demonstrated a strong similarity between the in vivo transit profiles of Intralipid 20% and Fluorescein Isothiocyanate-Dextran (FITC-Dextran), which is a fluorescent plasma tracer [45,59]. This supports the claim that Intralipid 20% is also a plasma tracer and can also be used to quantify plasma volume; however, further validation of the DyC-OCT volume measurements and theory is warranted.

As layer-based measurements have units of volume or flow per unit en face area (Table 1), total retinal plasma volume and flow can be estimated if the total en face area is known. Using an estimated en face area of 80 mm² based on previous literature for similar rats [60], a microvascular hematocrit of 15%, and the total plasma flow rates of the retina and choriocapillaris, as measured above, blood flow rates from each of the quantitative flow methods are shown (Table 2). It should be noted that hematocrit within the microvasculature is highly variable from moment to moment, but on average is approximately one-third of the systemic hematocrit [61]. Additionally, local retinal blood flow has been shown to decrease in the periphery relative to the central retina [62], so our flow values, determined by imaging near the central retina, may be overestimated. In spite of the limitations, flow and volume metrics were found to be physiologically plausible [63,64].

It is also important to note that quantifying flow in the eye, and particularly in the choroid and choriocapillaris, has been a historically challenging methodological problem. As such, there is no consensus on blood flow rates in the rat retina and choroid [62–70]. Additional factors that may influence blood flow include but are not limited to the species of the rat, pigmentation of the eye, age, weight, type and level of anesthesia, and presence of visual stimulation. While there is no consensus in the literature on quantitative flow values, choroidal flow values are typically 3-10 times higher than retinal flow values in the rat eye. For the same strain of rats and anesthesia used in this study, previous literature [64] demonstrated a ratio of 5.7, in agreement with our results.

One qualitative flow index metric and three quantitative flow metrics were investigated, each with unique advantages and limitations. Plasma flow ($PF$) derived from the CVP ($PF=PV/MTT$) uses a microvascular plasma volume ($PV$) as well as the mean transit time ($MTT$) between an artery and a vein. The use of the CVP implicitly assumes that the microvascular mean transit time is accurately represented by the chosen artery and vein. The other two quantitative flow methods are based on solving a deconvolution problem (Eq. (14)) to find $PF$ times the residue function, $R(t)$. Residue-based methods do not need to make explicit assumptions of connectivity. Like the CVP method, they require arterial input functions; however, they do not require venous outputs. Though model-based and SVD methods aim to solve Eq. (14), they yield different results. The high flow rates recovered by model-based deconvolution may result from selection of a model that does not fit physiological flow patterns. Specifically, the residue derived from SVD deconvolution (Fig. 9(D) inset) for the choriocapillaris decays more slowly than the exponential form (Fig. 9(C) inset) assumed for model-based deconvolution, suggesting overestimation of flow by model-based deconvolution. SVD-derived flow appears to be more in line with the CVP flow, but requires optimization of an SVD threshold for each experiment.

4.4 Translational feasibility

As Intralipid 20% is widely used for parenteral nutrition, it is appropriate to discuss the potential of DyC-OCT for human use. Current guidelines for Intralipid 20% as a nutritional supplement in humans recommend a low infusion rate (1 mL/min for a first-time recipient) compared to what was used here (1.5-3 mL/kg over ~1 s). However, there has been recent interest in using Intralipid and other lipid emulsions to treat cardiac toxicity following an intravenous overdose of local anesthetic. In case studies using this rescue injection, a lipid bolus ranging from 1.2-3 mL/kg is rapidly injected followed by a slower infusion to aid in the clearance of lipophilic local anesthetic from the cardiac tissue [71,72]. The American Society of Regional Anesthesia and Pain Medicine (ASRA) and Association of Anaesthetists of Great Britain and Ireland (AAGBI) guidelines recommend a bolus of 1.5 mL/kg over 1 minute followed by an infusion of 15 mL/kg/hr, with additional boluses and infusions to be given should resuscitation fail [73]. While further research on ideal injection rates and volumes and patient safety are necessary, this 1.5 mL/kg/min initial bolus may be sufficient for performing DyC-OCT in humans.

Additionally, we project that improvements in the DyC-OCT methodology will enable higher signal with the same injection volume, or the same signal with reduced injection volumes. Intralipid 30% is also commercially available and should provide more signal than Intralipid 20%. Further tracer purification to concentrate only the most highly scattering (i.e. larger) lipid particles would also reduce the injection volume. Other tracers, including those that are not lipid-based, should be investigated for DyC-OCT. Furthermore, the injection site in the tail vein used here likely represents the worst-case scenario for tracer dispersion and time delay due to its remoteness from the heart. Selection of a more proximal injection point such as a vein around the elbow or upper arm would ensure a more condensed bolus, which would again reduce the required injection volume. Finally, higher speed OCT systems, a more optimal wavelength for lipid scattering, and detection geometries that enhance the tracer signal relative to RBC scattering will be investigated.

When scaling DyC-OCT up to humans, the transit time of the tracer will also increase due to the relative size of the human cardiovascular network. This means that the imaging time frame will increase and likely include motion of the eye such as blinking or saccades. Fluorescence angiography is currently performed over a comparable time frame and suffers from these effects. Development of a 4D OCT system for human DyC-OCT imaging will enable out-of-plane motion correction based on volumetric information. Further development of DyC-OCT technology and a thorough investigation into the safety standards of lipid injections will be required to translate these methods for clinical use.

4.5 Future directions

The measurements presented here were all obtained from healthy animals, but DyC-OCT may also monitor layer-specific changes over time due to stimulation or disease. In particular, DyC-OCT may be a valuable tool for the study and early detection of age-related macular degeneration (AMD). Recent evidence suggests that dysfunction of the choriocapillaris may precede damage to the RPE [74]. If DyC-OCT is used to track the progression of AMD, the quantitative measurements of tracer kinetics, flow, and volume in the choriocapillaris may provide new insight into the time frame and mechanism of the disease. Other applications of the method, including the potential visualization of extravasation or leakage, also merit further investigation.

5. Conclusions

Quantification of hemodynamics using intrinsic contrast alone has proved to be challenging due to the complexity of RBC scattering. Here we demonstrate the value of exogenous contrast enhancement for Dynamic Contrast OCT (DyC-OCT) of retinal and choroidal microvasculature. The use of an exogenous plasma tracer removes many obstacles to quantification. Dynamic imaging of contrast agent passage yields depth-resolved hemodynamics. Quantitative measurements of tracer kinetics and layer-resolved plasma volume and flow were demonstrated in vivo in the retina and choroid, yielding flow values that are in line with literature. In the future, DyC-OCT can be used to study outer retinal diseases such as early age-related macular degeneration and retinitis pigmentosa, in experimental models, and potentially also in human subjects.