Changes of collagen ultrastructure in breast cancer tissue determined by second-harmonic generation double Stokes-Mueller polarimetric microscopy

Abstract

Second-harmonic generation (SHG) double Stokes-Mueller polarimetric microscopy is applied to study the alteration of collagen ultrastructure in a tissue microarray containing three pathological human breast cancer types with differently overexpressed estrogen receptor (ER), progesterone receptor (PgR), and human epidermal growth factor receptor 2 (HER2). Kleinman symmetry is experimentally validated in breast tissue for 1028 nm laser wavelength and it has been shown that measurements with only linearly polarized incoming and outgoing states can determine molecular nonlinear susceptibility tensor component ratio, average in-plane orientation of collagen fibers and degree of linear polarization of SHG. Increase in the susceptibility ratio for ER, PgR, HER2 positive cases, reveals ultrastructural changes in the collagen fibers while the susceptibility ratio increase and decrease in degree of linear polarization for ER and PgR positive cases indicate alteration of the ultrastructure and increased disorder of the collagen fibers within each focal volume. The study demonstrates a potential use of polarimetric SHG microscopy for collagen characterization and cancer diagnostics.

1. Introduction

Breast cancer is the most common non-skin malignancy in women worldwide and is second only to lung carcinoma as a cause of female cancer deaths [1]. Complex genetic and epigenetic changes that drive carcinogenesis lead to more than 20 distinct histopathological subtypes of breast cancer [2]. Clinically, breast cancer can be classified based on tumor grade and tumor stage, as well as estrogen receptor (ER) and progesterone receptor (PgR) status and overexpression of human epidermal growth factor receptor 2 (HER2). Presence of ER and PgR receptors can be determined by immunohistochemistry (IHC), and overexpression of HER2 can be assessed by IHC and fluorescence in situ hybridization [3]. Early diagnosis is a vital step in cancer treatment. According to Cancer Research UK, more than 90% of women diagnosed with breast carcinoma at the earliest stage survive for at least 5 years compared to about 15% of women diagnosed with the most advanced stage of cancer [4]. The gold standard of cancer diagnosis is based on microscopy of histopathology slides that are stained with hematoxylin and eosin (H&E) dyes. H&E staining provides high contrast in bright-field microscopy images that can be used to reveal qualitative information on morphological changes due to tumor initiation and progression [5]. The same slides can be conveniently used for multicontrast nonlinear imaging with multiphoton excitation fluorescence, second-harmonic generation (SHG), and third-harmonic generation (THG) microscopy providing complementary information about the tissue structure [6].

Experimental evidence has demonstrated that the structure and composition of the extracellular matrix (ECM) of tumor-affected breast tissue undergoes alteration [7], especially its collagenous component [8, 9]. Regarding the composition of collagen in the ECM, biochemical studies of collagen extracted from breast tissue with infiltrating ductal carcinoma (IDC) indicated an increase of type V collagen up to 10% as compared to the presence of less than 1% in normal breast tissue [10], which might be linked to a derangement of the type I collagen fibers [11]. Furthermore, it has been reported that type I collagen fibers can be degraded by matrix metalloproteinases (MMPs) that are frequently overexpressed in malignant tumors [12]. These factors influence the collagen fibril and the fiber organization.

Collagen is the major constituent of the ECM, and due to a noncentrosymmetric structure, it is capable of generating a strong SHG signal without the need for staining. SHG is a coherent process for which the intensity and polarization of outgoing radiation are sensitive to the structural arrangement of the material. Hence, collagen fiber structure and spatial distribution can be readily visualized and probed using SHG microscopy [13,14]. Several SHG studies have investigated morphological modifications in collagen deposition and arrangement in breast cancer tissue. Intensity of forward-detected to backward-detected SHG was used to show alterations of collagen microstructure in ductal and lobular carcinomas [7]. Using SHG imaging in conjunction with additional correlative microscopy techniques, structural properties of collagen were characterized in order to detect differences in local collagen density near normal glands and mammary tumors, and identify distinct collagen fiber organization around tumors. The result was used to introduce tumor-associated collagen signatures (TACS) related to the progression of breast carcinogenesis in mouse models [8]. Also polarization-resolved SHG microscopy was used to estimate the aligned versus randomly oriented collagen fibers and further employed to differentiate between malignant breast pathologies and normal tissues [15].

Recently, the theory of double Stokes-Mueller polarimetry (DSMP) has been developed for complete polarimetric characterization of the second-order susceptibility tensor in scattering samples [16, 17], where the sample is represented by a 4 × 9 double Mueller matrix, ℳ⁽²⁾. It defines a relation between the polarization states of incoming laser beam and outgoing SHG signals from the sample. The double Mueller matrix contains information about the sample structure, and shows if the susceptibility tensor components are real or complex. The DSMP measurements have been conducted to extract the absolute values of six measurable laboratory-frame susceptibility tensor components, ${\chi }_{XXX}^{(2)}$, ${\chi }_{XZZ}^{(2)}$, ${\chi }_{XXZ}^{(2)}$, ${\chi }_{ZXX}^{(2)}$, ${\chi }_{ZZZ}^{(2)}$, ${\chi }_{ZXZ}^{(2)}$ [18], where XZ is the image plane and the principal light propagation direction is along the Y-axis of the Cartesian laboratory coordinate system. The ${\chi }_{XXZ}^{(2)}/{\chi }_{ZXX}^{(2)}$ value as well as ${\chi }_{XZZ}^{(2)}/{\chi }_{ZXZ}^{(2)}$ value can be used to determine if Kleinman symmetry is valid. Kleinman symmetry can be applied to reduce the number of independent susceptibility tensor components. Previous studies assumed Kleinman symmetry [19–21], however in the current paper, the Kleinman symmetry in collagen structures is experimentally validated to our knowledge for the first time.

If the susceptibility tensor components are real and there is no birefringence in the sample the polarization of the SHG signal will not have a circular component [16]. In the absence of a circularly polarized contribution in the outgoing SHG a reduced polarimetric measurement with only linearly polarized incoming and outgoing states, termed PIPO (for polarization-in, polarization-out), can be performed [16, 17, 22]. In PIPO measurements, a smaller number of states are measured, which are sufficient to extract the molecular second-order susceptibility tensor components ratio, ( $R={\chi }_{zzz}^{(2)}/{\chi }_{zxx}^{(2)}$). The lower case, xyz designated reference frame is associated with the cylindrical structure of collagen within the focal volume. The z-axis is aligned with the projection of the cylindrical axis onto the XZ image plane. The average in-plane fiber orientation, (δ), from the laboratory Z-axis and the degree of linear polarization (DLP) can be also extracted for each pixel of the image using the PIPO measurements [16]. Previously, R was successfully used to differentiate normal and tumor tissue in lung and thyroid histology sections [23,24].

In this paper, we employed polarimetric microscopy measurements to investigate the changes of tumor-affected collagen ultrastructure for three pathologic types of breast cancer in a tissue microarray: ER+, PgR+, HER2+ (triple positive or +/ + /+), ER+, PgR+, HER2− (double positive or +/ + /−), and ER−, PgR−, HER2− (triple negative or −/ − /−), where the positive/negative sign after each abbreviation respectively indicates overexpression/absence of the specific receptor. It is demonstrated that polarimetric SHG microscopy can detect significant differences in collagen organization between normal and malignant breast tissue by measuring R and DLP. Therefore, the R and DLP can be utilized as novel cancer detection parameters and can serve as complimentary measures for H&E histopathology.

2. Materials and methods

DSMP theoretical background

In double Stokes-Mueller polarimetry, a 4×9 double Mueller matrix, ℳ⁽²⁾, relates the polarization states of the incoming laser radiation and the outgoing SHG from the sample as follows:

$$s^{\prime }(2\omega )={ℳ}^{(2)}S(\omega )$$ (1)

where s′(2ω) is a 4×1 Stokes vector representing the outgoing SHG radiation and S(ω) is a 9×1 double Stokes vector representing the polarization state of the incoming laser beam [16]. The double Stokes vector components are a function of the four linear Stokes components of the incoming laser beam [25]. To perform DSMP, a set of nine incoming polarization states is required. The nine incoming polarization states are defined as follows: horizontally (0°) and vertically (90°) linearly polarized (HLP and VLP, respectively), diagonally linearly polarized (± 45°), right- and left-handed circularly polarized (RCP and LCP, respectively), linearly polarized at (−22.5°) and right- and left-handed elliptically polarized (REP and LEP, respectively). They can be presented in Poincaré sphere coordinates as follows [26]:

$$\begin{array}{cccccccccc}Q& 1& 2& 3& 4& 5& 6& 7& 8& 9\\ & \mathit{HLP}& \mathit{VLP}& +45& -45& \mathit{RCP}& \mathit{LCP}& -22.5& \mathit{REP}& \mathit{LEP}\\ \begin{array}{c}\mathrm{\Gamma }\\ \Omega \end{array}& \left(\begin{array}{c}0\\ 0\end{array}\right)& \left(\begin{array}{c}\pi /2\\ 0\end{array}\right)& \left(\begin{array}{c}\pi /4\\ 0\end{array}\right)& \left(\begin{array}{c}-\pi /4\\ 0\end{array}\right)& \left(\begin{array}{c}0\\ \pi /4\end{array}\right)& \left(\begin{array}{c}0\\ -\pi /4\end{array}\right)& \left(\begin{array}{c}-\pi /8\\ 0\end{array}\right)& \left(\begin{array}{c}\pi /2\\ \pi /8\end{array}\right)& \left(\begin{array}{c}\pi /4\\ -\pi /8\end{array}\right)\end{array}$$ (2)

where Q ranges from 1 to 9 representing the index of the incoming polarization state, S_Q. 2Γ is the azimuth angle and 2Ω is the elevation angle in the Poincaré sphere. In a DSMP measurement four Stokes vector components, s̃_γ with γ = 0, 1, 2, 3 of the outgoing SHG signal are measured for each of the nine incoming polarization states, which produces a 4×9 Stokes matrix, s̃_γ,Q. For calculating the double Mueller matrix, the Stokes matrix was filtered from the depolarized contribution to represent only pure polarization states. The filtering is performed by replacing the measured s̃₀ values with calculated $s_0^{\prime }=\sqrt{{\tilde{s}}_1^2+{\tilde{s}}_2^2+{\tilde{s}}_3^2}$ values, and keeping ${\tilde{s}}_{\gamma }=s_{\gamma }^{\prime }$ for γ = 1, 2, 3 [18]. Then the double Mueller matrix of the sample can be obtained from the 4×9 SHG Stokes matrix, $s_{\gamma ,Q}^{\prime }$ and matrix S using the following expression [18]:

$${ℳ}_{\gamma ,i}^{(2)}=s_{\gamma ,Q}^{\prime }{S}_{Q,i}^{-1}$$ (3)

where S⁻¹ is the inverse matrix of S, which is composed of all nine double Stokes vectors arranged as columns [16].

Double Mueller matrix elements are functions of the second-order susceptibility tensor components of the sample. The absolute value of six second-order susceptibility tensor components in the laboratory-frame of reference can be extracted from the top left 2×3 double Mueller matrix components. Furthermore, the degree of polarization (DP), degree of linear polarization (DLP) and degree of circular polarization (DCP) of the outgoing SHG signal can be retrieved from the measured Stokes components [27]:

$$\mathit{DP}=\frac{\sqrt{{\tilde{s}}_1^2+{\tilde{s}}_2^2+{\tilde{s}}_3^2}}{{\tilde{s}}_0}\mathit{DLP}=\frac{\sqrt{{\tilde{s}}_1^2+{\tilde{s}}_2^2}}{{\tilde{s}}_0}\mathit{DCP}=\frac{\sqrt{{\tilde{s}}_3^2}}{{\tilde{s}}_0}$$ (4)

where s̃₀ = I₀ + I₉₀, s̃₁ = I₀ − I₉₀, s̃₂ = I₄₅ − I₋₄₅, s̃₃ = I_RCP − I_LCP.

In summary, for nine incoming polarization states, six outgoing polarization states are measured and a 4×9 Stokes matrix is being formed. From the Stokes matrix, DP, DLP, and DCP are calculated. In addition a 4×9 double Mueller matrix is calculated from the Stokes matrix. Subsequently, six laboratory-frame of reference susceptibility values are extracted from the Mueller matrix. The laboratory-frame susceptibility values are used to test the Kleinman symmetry. The laboratory-frame susceptibility values can also be used for further extraction of the molecular reference frame susceptibility values. However, if susceptibility values are real, and absorption and birefringence are negligible, the molecular susceptibility values can be obtained using only linearly polarized incoming and outgoing polarization states as presented in the following sections.

Reduced DSMP (with linear PIPO) theoretical background

The second-order susceptibility tensors generally have complex components. However, when the absorption in the sample is negligible and birefringence is absent, these components are real. This can be tested with DSMP measurement. When the susceptibility tensor component values are real, the s̃₃ component in the Stokes matrix for all linear incoming polarization states should be zero. Hence, measurements with linear incoming and outgoing polarization states are sufficient to characterize the ultrastructure of the sample. As such, a reduced DSMP measurement with linear polarization-in, polarization-out (PIPO) microscopy can be conducted to investigate the organization of the sample where only the first six columns and three rows of the double Mueller matrix are used and they are enough to extract the molecular-frame second-order susceptibility tensor components ratio, ( $R={\chi }_{zzz}^{(2)}/{\chi }_{zxx}^{(2)}$), the average in-plane fiber orientation from the laboratory Z-axis, (δ), and the degree of linear polarization (DLP) [16,17,22].

If birefringence in the sample is negligible and the Kleinman symmetry is valid (which can be tested using DSMP measurement), then the measured SHG intensity can be formulated for different linear polarization orientation angles of the polarization state generator (PSG), θ, and linear polarization orientation angles of the polarization state analyzer (PSA), ϕ, as follows [14]:

$$I_{\mathit{SHG}}\propto {\left|\text{sin}(\varphi -\delta )\text{sin}(2\theta -2\delta )+\text{cos}(\varphi -\delta ){\text{sin}}^2(\theta -\delta )+\frac{{\chi }_{zzz}^{(2)}}{{\chi }_{zxx}^{(2)}}\text{cos}(\varphi -\delta ){\text{cos}}^2(\theta -\delta )\right|}^2$$ (5)

A trust region reflective (TRR) fitting algorithm [29] in MATLAB was used to fit the intensity variation of every pixel of the image as a function of θ and ϕ with Eq. (5). To improve the fit, the PSG was set to 9 incoming linear polarization orientation angles, and for each incoming polarization state, PSA was set to measure 9 polarization states of the outgoing SHG intensity, resulting in 81 combinations of θ and ϕ. The R and δ for each pixel of the image were extracted using the fitting routine. The R values are presented as color-coded images and values of δ are presented as vector maps. From PIPO microscopy data, the DLP of the outgoing SHG signal can be obtained using Eq. (4). The average collagen fiber orientation angle, δ, at each pixel of the image was used to select the closest incoming polarization angle, θ_c, such that |θ_c − δ| ≤ 11.25° where 11.25° is half of an incremental step of PSG. At each pixel of the image, two sets of data for outgoing SHG signal were used to calculate DLP: DLP₁ was measured using intensity values with ϕ = 0°, 45°, 90°, 135°, and DLP₂ was measured at ϕ = 22.5°, 67.5°, 112.5°, 157.5°. The average DLP was deduced for each pixel of the image as the average of DLP₁ and DLP₂. Similar to the R, the DLP map is presented as color-coded images.

DSMP microscope setup

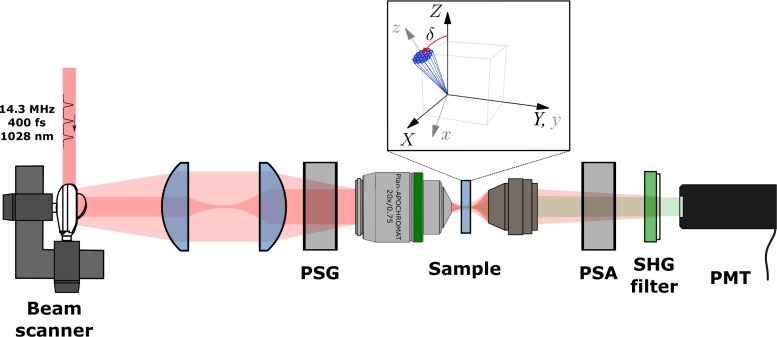
The polarmetric SHG microscope was described earlier [18] and depicted in Fig. 1.

Fig. 1.

DSMP microscope setup. PSG and PSA are polarization state generator and analyzer respectively. collagen fibers are shown in the laboratory coordinate system (XYZ) and molecular coordinate system (xyz) where angle δ is defined as the angle between average fiber axis, z and Z-axis of the laboratory-frame of reference.

Briefly, a home-built diode-pumped ytterbium-ion-doped potassium gadolinium tungstate (Yb:KGW) crystal-based laser oscillator operating at 1028 nm wavelength and generating ∼400 fs pulses at 14.3 MHz repetition rate [28] was coupled to a home-built SHG microscope, which contains a polarization state generator (PSG) and a polarization state analyzer (PSA) to control the incoming and measure the outgoing polarization states, respectively. The PSG contained a fixed linear polarizer (Thorlabs Inc.), a half-wave plate and a quarter-wave plate. The PSA contained a half-wave plate, a quarter-wave plate (all wave plates are from Eksma Optics) and a linear polarizer (Thorlabs Inc.). The laser beam is focused onto the sample using a 20×/0.75 numerical aperture (NA) air objective (Carl Zeiss) and the emitted SHG from the sample is collected in the forward direction with a custom 0.85 NA objective. A single-photon counting photomultiplier tube (Hamamatsu H7422P-40) was used for the SHG detection. To separate the SHG from the laser radiation, a BG 39 filter and a 510–520 nm band-pass interference filter (Edmund Optics) were used. The PSG can be set to produce nine different incoming polarization states (HLP, VLP, +45, −45, RCP, LCP, −22.5, REP, LEP) (see Eq. (2)) where for each of them six outgoing polarization intensities (0, 90, +45, −45, RCP, LCP) were measured using the PSA. Hence, four Stokes vector components of outgoing SHG were measured for each of nine incoming polarization states.

For the reduced DSMP imaging with the linear PIPO measurement [22] the PSG contained a linear polarizer and a half-wave plate, while the PSA contained only a rotating linear polarizer. The PSG half-wave plate was rotated to nine different angles with equal increments from 0° to 180°, while the polarizer of PSA was rotated to nine different evenly spaced angles for each PSG state to perform the PIPO imaging. The samples were rescanned at the initial PSG and PSA settings periodically after measurements with each set of the PSA states to monitor for sample bleaching.

Histology sample preparation

The tissue samples were obtained according to an institutionally-approved protocol (University Health Network, Toronto, Canada). A tissue microarray slide, which was composed of invasive carcinoma and normal breast tissue of 12 patients, was used for this study. The slide contained 4 cores (2 normal and 2 malignant) for each patient. 3 out of 12 patients normal samples were fat tissue which could not be used in our analysis. The tissue cores were 0.6 mm in diameter composed of formalin-fixed tissue specimens sectioned into 5-μm thick slices and mounted on a glass slide. The sections were stained with hematoxylin and eosin (H&E) dyes, and imaged with a bright-field microscope scanner (Aperio Whole Slide Scanner, Leica Biosystems) for reference. Assessment of the tissue architecture and identification of normal and malignant regions of interest were performed by an expert pathologist (S.J.D.). The information on receptor status was taken from the original clinical pathology reports.

Data analysis

Six statistical parameters were extracted from the R, δ and DLP distributions to investigate possible differences between collagen in normal and malignant breast tissue. These statistical parameters are: mean, median, standard deviation (std. dev.), median absolute deviation (MAD), skewness and kurtosis. Mean and median are both a measure of central tendency of the measured parameter, where the median is less sensitive to the presence of outliers. MAD is defined as the median of the absolute deviations from the data’s median [30] and is a measure of statistical dispersion. Skewness and kurtosis are descriptors of the shape of the distribution. Skewness is a measure of asymmetry of a distribution about its mean. Kurtosis on the other hand, is a measure of how flat or peaked the distribution is about its mean [31]. After all statistical features were extracted the Jarque-Bera test was performed to examine the normality of the data distribution. To test for differences between sample groups when the condition of normality and equal variance were met, analysis of variance (ANOVA) followed by Tukey post hoc test was performed. In the case of unequal variances, Welsh followed by Tamhane post hoc tests for multiple comparisons were performed. For cases in which the normality assumption could not be held, a Kruskal-Willis H-test followed by Dunn-Bonferroni post hoc test was used [32]. All tests were performed using built-in functions in MATLAB. Differences with p-value<0.05 were considered as significantly different. All values are reported as mean±standard error, unless otherwise mentioned. To measure possible linear correlation between data sets a Pearson product-moment correlation coefficient was calculated.

3. Results and discussion

DSMP properties of breast tissue

DSMP microscopy was conducted on two areas of double positive malignant breast tissue and two areas of its control normal tissue from the tissue microarray. The DSMP measurements provide information on the birefringence of the sample, reality or complexity of the susceptibility values and validity of Kleinman symmetry. The DSMP provided evidence that linear incoming and outgoing polarization states are sufficient for structural study of collagen in breast tissue.

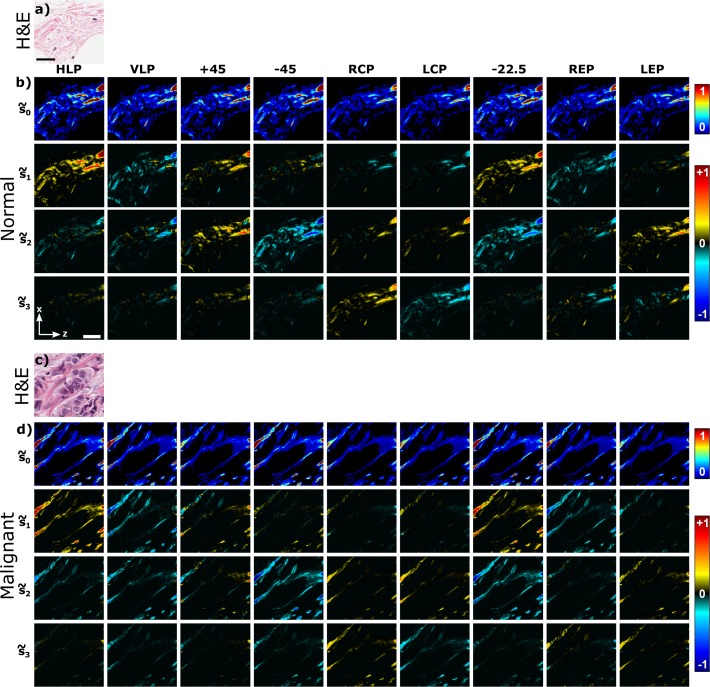
Figure 2 shows the bright-field microscopy images of scanned area (Fig. 2(a, c)) and measured SHG Stokes vector images at each of the nine incoming polarization states (Fig. 2(b, d)). The s̃₀ components have positive values ranging from 0 to 1 with assigned color values from blue to red (see the upper color bar in Fig. 2). The s̃₁, s̃₂, s̃₃ Stokes components vary from −1 to 1, for which the color-mapping is selected in such a way, that blue indicates negative values, red shows positive value and black represents zero. The Stokes matrix images show that the signal depends on the orientation of the collagen fibers in the image plane as well as the selected incoming and outgoing polarization states. It can be seen that s̃₃ elements for both normal and malignant breast tissue are close to zero compared to s̃₁ and s̃₂, when the incoming laser beam is linearly polarized (HLP, VLP, +45, −45, −22.5). On the other hand, when the incoming laser beam is circularly or elliptically polarized (RCP, LCP, REP, LEP), the values of the s̃₃ element are higher, indicating the presence of a circular component in the outgoing SHG signal polarization. Since the circular polarization component of SHG radiation, s̃₃, is small for incoming linear polarization states (7% and 13% of s̃₀ for normal and malignant breast samples, respectively, Fig. 2(b, d) row 4), a reduced DSMP polarimetry can be conducted using only the linearly polarized incoming and outgoing polarization states (the linear PIPO method [16]). Note, however, that measurements with incoming circular and elliptical polarization states also provide useful information about the possible chiral component contribution [16]. In addition, low values of s̃₃ element for the incoming linear polarization states indicate that the birefringence of the sample is small.

Fig. 2.

Measured SHG Stokes matrix elements of normal and malignant breast tissue samples. Bright-field microscopy images of scanned area are presented for the H&E stained a) normal and c) malignant (double positive) breast tissues. Scale bar shown in panel (a) is 25 μm. Measured SHG Stokes matrix elements of b) normal and d) malignant breast tissue are shown. Each row represents SHG Stokes vector components s̃_γ with γ = 0, 1, 2, 3 for each of the nine incoming polarization states indicated on the top of the matrix. Laboratory axes and a 20-μm scale bar are shown in panel (b).

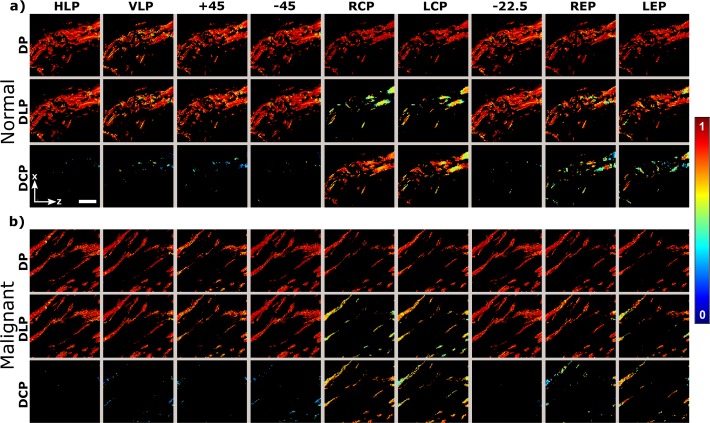
By measuring the DP, DLP, and DCP we can determine the depolarized fraction of total, linear and circular SHG intensity from the sample, respectively. Stokes vector components can be used to obtain DP, DLP, DCP for each incoming polarization state, and the results are shown in Fig. 3. It can be seen that the DLP has the largest contribution to DP, while the DCP is only significant when circular and elliptical incoming polarization states are employed. The degree of polarization measurements also reiterate, that for linear incoming polarization states only linear outgoing polarizations have significant signal, enabling the reduced DSMP using the linear PIPO method [16].

Fig. 3.

Degree of total (DP), linear (DLP), and circular (DCP) polarization of outgoing SHG from breast tissue for the nine different incoming polarization states. The a) normal and b) malignant (double positive) breast tissue were studied. The images are calculated from the data shown in Fig. 2. Only pixels with signal-to-noise>4 are shown. Laboratory axes and a 20-μm scale bar are shown in panel (a).

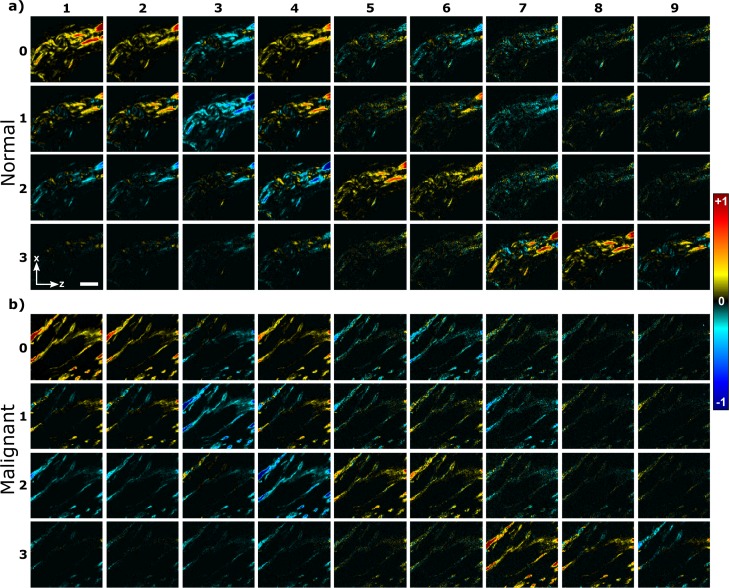
The double Mueller matrix is shown in Fig. 4. It is calculated after filtering the Stokes matrix by setting $s_0^{\prime }=\sqrt{{\tilde{s}}_1^2+{\tilde{s}}_2^2+{\tilde{s}}_3^2}$ and it represents contribution of pure polarization states. Some features of the double Mueller matrix can be visually inspected: when the 3×3 upper right elements as well as the first six elements of the last row of the Mueller matrix are zero, the susceptibility values of the material are real values [16]. Figure 4 shows that most of the Mueller matrix elements containing imaginary components are small compared to elements containing the real susceptibilities ( ${ℳ}_{1,7}^{(2)}$ is 26% of the ${ℳ}_{0,0}^{(2)}$ value for normal tissue and ${ℳ}_{1,7}^{(2)}$ is 29% of ${ℳ}_{0,0}^{(2)}$ value for malignant breast tissue). The noise in the low-level SHG signal contributes to the nonzero values of the Mueller matrix components, but some contribution from the imaginary parts of susceptibility values could also occur.

Fig. 4.

Double Mueller matrix elements of a) normal and b) malignant (double positive) breast tissue. Laboratory axes and a 20-μm scale bar are shown in panel (a).

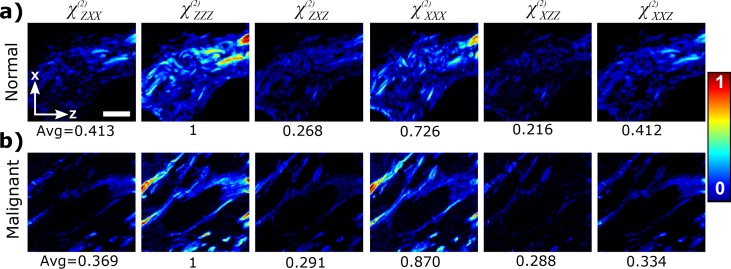
Six laboratory-frame second-order susceptibility tensor elements can be calculated from the 2×3 upper left elements of the double Mueller matrix containing the squared values of the susceptibility components [16]. Figure 5 shows the values of the susceptibility tensor components for each pixel of the image in normal and malignant breast tissue. It can be seen that ${\chi }_{ZXX}^{(2)}$ component is similar to ${\chi }_{XXZ}^{(2)}$ component and ${\chi }_{ZXZ}^{(2)}$ is similar to ${\chi }_{XZZ}^{(2)}$ component in both normal and malignant breast samples. The ${\chi }_{ZXX}^{(2)}/{\chi }_{XXZ}^{(2)}=1.25\pm 0.69\hspace{0.17em}(\mathrm{S}.\mathrm{D}.)$ and ${\chi }_{XZZ}^{(2)}/{\chi }_{ZXZ}^{(2)}=1.27\pm 0.76\hspace{0.17em}(\mathrm{S}.\mathrm{D}.)$, which are close to unity, and therefore provide an experimental evidence that Kleinman symmetry can be assumed to a good approximation for collagen in breast tissue samples with the imaging condition of 1028 nm laser wavelength.

Fig. 5.

Laboratory-frame second-order susceptibility values of breast tissue for a) normal and b) malignant (double positive) breast tissue. The number below each image shows the normalized (to ${\chi }_{ZZZ}^{(2)}$) average value of the non-zero pixels. Laboratory axes and a 20-μm scale bar are shown in panel (a).

In summary, using DSMP measurements we verified that Kleinman symmetry holds to a good approximation for 1028 nm laser wavelength, and the measurements only with linear incoming and outgoing polarization states can be used to characterize the ultrastructure of collagen. Hence, the linear PIPO measurements can be applied to obtain a high-precision R due to larger number of measurements per state. In addition DLP can be obtained which can characterize the ultrastructure of the material. Furthermore, using DSMP we show that the birefringence is negligible in the sample. Therefore, Eq. 5 can be used to fit the data from linear PIPO measurements.

Reduced DSMP investigations of breast cancer tissues

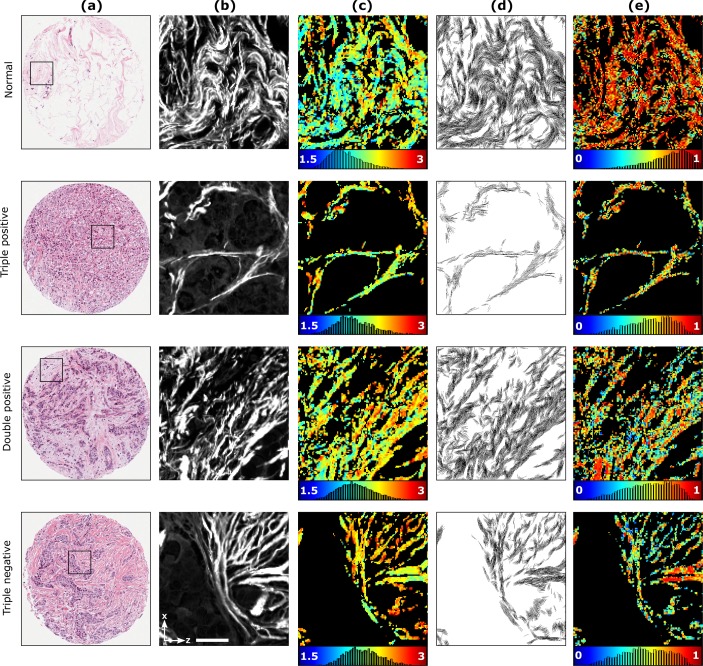
The reduced DSMP measurements with linear PIPO SHG microscopy were conducted to investigate the possible ultrastructural alteration of collagen fibers in normal and malignant breast tissue. A human breast tissue microarray containing different subtypes of invasive carcinoma was studied. Three different types of human breast cancer were investigated based on overexpression of ER, PgR and HER2: (i) 17 areas in three patients with ER+, PgR+, HER2+ (triple positive, or +/ + /+), (ii) 40 areas in six patients with ER+, PgR+, HER2− (double positive, or +/ + /−), and (iii) 15 areas in three patients with ER−, PgR−, HER2− (triple negative, or −/ − /−) malignant breast tissues. Also 32 areas in nine cases of normal tissue were studied as the control samples. The results are presented in Fig. 6. The bright-field images of H&E stained tissue are shown in Fig. 6(a) with a black square indicating the PIPO scan area with the size of 110 μm×110 μm. The SHG images of the scanned area are shown in Fig. 6(b). By fitting the polarization-dependent SHG intensity data with Eq. 5,R of the collagen fiber is extracted for each pixel of the image and displayed as color-coded maps in Fig. 6(c). The R varies from 1.5 to 3 and is represented by a range of colors from blue to red. The colorbar together with the histogram of R occurrence is given below the R map. As it can be seen from the Fig. 6(c), the R maps for malignant breast tissue have more yellow and orange pixels compared to the R map for the normal tissue which are dominated by blue and green pixels, demonstrating that the R of collagen in normal breast tissue has lower values than the collagen in malignant breast tissue. In addition to the R, δ is extracted for each pixel of the image. Figure 6(d) shows the fiber orientation maps where each line represents the cylindrical axis orientation of collagen fibers in every pixel of the image. The DLP for each pixel of the images is also calculated using Eq. 4 and presented as color-coded maps in Fig. 6(e). The values are represented from blue to red corresponding to DLP values from 0 to 1. The colorbar together with the DLP occurrence histogram is given below the DLP map. Six statistical parameters characterizing the occurrence distributions of the corresponding values of the images are extracted (see materials and methods section), and the results are summarized in Table 1. No statistically significant differences observed between patients in control samples. Consequently all the control samples were pooled into one group.

Fig. 6.

PIPO SHG analysis of normal and malignant breast tissue samples. Column (a) shows bright-field microscopy images of the H&E stained tissues with square indicating the scanned area of 110 μm×110 μm used for the SHG data analysis shown in columns (b) to (e). Column (b) visualizes the normalized SHG intensity images (summation of all the polarization states) of the corresponding regions outlined by a black box in H&E images. Column (c) displays the R map where the blue represents an R value of 1.5 and the red represents a R value of 3. The colorbar also contains the R occurrence pixel histogram of the corresponding images. Column (d) shows the orientation map of the cylindrical axis, δ, for each fitted image pixel. Column (e) displays the DLP map where the color bar ranges from 0 to 1 and also contains corresponding DLP occurrence pixel histograms. Laboratory axes and a 25-μm scale bar are shown in the last panel of column (b).

Table 1.

Statistical analysis for the R, δ and DLP values for all patients.^a,^b

		Mean	Median	St. Dev.	MAD	Skewness	Kurtosis	Correlationc
R-ratio	Normal	2.10±0.03	2.06±0.03	0.24±0.01	0.15±0.01	1.02±0.08	5.39±0.27	−0.04±0.02
	+/ + /+	2.21±0.01	2.18±0.01	0.25±0.01	0.16±0.01	0.84±0.04	4.72±0.09	−0.08±0.01
	+/ + /−	2.16±0.01	2.13±0.01	0.24±0.01	0.14±0.01	0.95±0.04	5.16±0.17	−0.06±0.01
	−/ − /−	2.14±0.03	2.12±0.03	0.23±0.01	0.13±0.01	0.79±0.04	4.69±0.16	−0.01±0.04
Orientation	Normal	–	–	49.14±1.72	32.17±3.05	0.30±0.18	2.52±0.26	–
	+/ + /+	–	–	46.65±1.45	20.45±2.90	−0.99 ± 0.40	1.93±0.74	–
	+/ + /−	–	–	43.38±1.41	18.34±0.68	0.07±0.16	4.21±0.11	–
	−/ − /−	–	–	42.16±1.79	26.79±2.35	0.17±0.22	4.28±0.35	–
DLP	Normal	0.80±0.01	0.83±0.01	0.16±0.01	0.09±0.01	−0.86±0.03	4.14±0.18	0.14±0.02
	+/ + /+	0.71±0.04	0.73±0.04	0.17±0.01	0.11±0.01	−0.47±0.09	3.25±0.23	0.22±0.02
	+/ + /−	0.69±0.01	0.73±0.02	0.17±0.01	0.11±0.01	−0.59±0.04	3.21±0.08	0.27±0.01
	−/ − /−	0.65±0.05	0.67±0.06	0.17±0.01	0.12±0.01	−0.36±0.16	3.27±0.45	0.29±0.03

^aValues that are statistically significantly different compared to normal are in bold.

^bThree patients with triple positive, six patients with double positive and three patients with triple negative malignant breast tissue and nine patients as control were studied.

^cThe average correlation coefficient from all images of a particular tissue type is calculated by deducing Pearson’s correlation coefficient respectively between the R and SHG intensity, as well as DLP and SHG intensity. Only well fitted pixels with R and DLP values were taken into account.

The mean and median of the R are found to be higher in malignant breast tissue compared to the normal tissue. The difference in the mean and median of the R values are significant between the normal and malignant tissue in triple positive breast cancer (p-value<0.005) and double positive breast cancer (p-value<0.05). Although the mean and median of R for triple negative breast cancer is slightly higher than in normal tissue, it is not statistically significantly different due to a large variation of the R values for different patients. Therefore, each case for the triple negative sample has to be characterized individually. The spread of the R (see Table 1, St. Dev. and MAD) which indicates a distribution of ratio in the scanned regions due to a natural biological variation of collagen organization in the tissue shows no statistically significant difference between normal and malignant breast tissue. Skewness and kurtosis, which identify the shape of R distribution, either didn’t show any significant differences between normal and malignant breast tissue. In addition, Pearson correlation test showed that there is no correlation between intensity of each pixel and its R value in normal or malignant breast tissue (Table 1). Therefore, the changes in R originate from the structural alterations in collagen that do not influence the SHG intensity in a correlated way. As it has been previously described [23], the R can be influenced by molecular changes of the collagen triple helices, a difference in the triple helices arrangement into fibrils, and alteration in the organization of the fibers in the focal volume.

The average orientation angle of collagen fibers for each pixel in the imaged area was also extracted. Mean and median of the angle over the whole image are not reported since they depend on the orientation of the sample. The values of standard deviation and MAD are smaller in malignant breast tissue compared to normal tissue, which suggest that collagen fibers are getting arranged around a specific orientation angle in the malignant tissue. In other words, the collagen fibers become straighter, or better aligned on a macroscopic level of tissue texture in cancer samples. Standard deviation in the normal and triple negative breast cancer tissues show a statistically significant difference (p-value<0.05), while MAD is different for triple positive and double positive (p-value<0.05) samples. This is in agreement with previous studies, where SHG microscopy was used to differentiate the collagen fiber pattern between tumor-induced breast stromal tissue and normal stroma, and between high-grade and low-grade breast cancer stroma [33]. However, it is not known by what mechanism the collagen fiber realignment occurs [34]. No significant differences are observed in skewness and kurtosis of the distribution of the average orientation angle of collagen fibers.

The order of the fibers and fibrils within individual focal volumes is reflected by the DLP, which is a measure of the average degree of linear polarization of outgoing SHG signal from the sample. The DLP is lower in all malignant cases as it can be seen by the presence of some blue and green pixels in the color-coded images, compared to the dominant red pixels in the normal tissue. Mean and median of DLP in triple positive malignant breast tissue is smaller than normal breast tissue, but the differences are not statistically significant (Table 1). The difference between normal and triple positive malignant breast tissue was significant in skewness and kurtosis (p-value<0.05) showing that DLP value distribution changes in triple positive sample. All statistical parameters of DLP for double positive malignant breast tissue are statistically significantly different from normal breast tissue (p-value<0.05), but only mean, median, skewness and kurtosis show large differences. On the other hand, for triple negative breast cancer tissue, the mean, median, skewness and kurtosis of DLP in two patients (out of three) are significantly different compared to the normal tissue. For example in one patient the mean of DLP was 0.82±0.01 (not significantly different from normal tissue, while for the other two was 0.53±0.02 and 0.61±0.07 which are statistically significantly different from normal tissue with p-value< 0.005). However, there is a high variation of the DLP distribution parameters between the patients. Therefore, each area for the triple negative case has to be studied individually. While the DLP mean and median represent the central tendency of DLP values, Std. Dev., MAD, skewness, and kurtosis show the width and the shape of DLP distribution, respectively. The distribution width of DLP values increases due to the increase in presence of pixels with lower DLP. Since the s̃₃ component of the Stokes matrix for SHG was observed to be small for incoming linear polarization states (as verified by DSMP measurements, see Fig. 2), the lower DLP value is attributed mainly to the increased depolarization due to higher structural disorder of collagen fibers in the focal volume or small collagen fiber segments within the focal volume where SHG is emitted from uncorrelated domains and scattering becomes significant compared to coherent SHG radiation. DLP values and the SHG intensity did not have significant correlation at each pixel of the image in normal breast tissue (Table 1). The correlation of DLP and SHG intensity for malignant breast tissue was also small, however, the correlation value was higher compared to normal tissue. That can be due to increased disorder of collagen in malignant breast tissue that results in lower DLP and SHG intensity.

4. Conclusion

We used SHG DSMP microscopy to verify that Kleinman symmetry can be applied to a good approximation for studying collagen in breast tissue at 1028 nm laser wavelength. The small measured s̃₃ values of the Stokes vector for linear incoming polarization states provided evidence that birefringence in the sample is negligible and also linear PIPO SHG microscopy with 1028 nm fundamental radiation wavelength can be used to investigate the ultrastructural alteration of collagen in different types of breast cancer. Three parameters: R, δ and DLP were extracted for each pixel of the images to differentiate between collagen in normal and malignant breast tissue. Three different pathological conditions of malignant breast tissue were investigated based on overexpressing estrogen receptor (ER), progesterone receptor (PgR), and human epidermal growth factor receptor 2 (HER2). The triple positive malignant breast tissue has strong effect on collagen ultrastructure manifesting itself in increased R, while having only a slight effect on the distribution of DLP values. These results show that most significant change in the triple positive cancer tissue occurs within the triple helix and/or fibril organization affecting primarily the coherent part of the SHG radiation parameters. For the double positive malignant breast tissue, the R and the DLP parameters are significantly different from normal tissue indicating that both changes within triple helix and/or fibril organization as well as increase in disorder of the fibers within focal volume takes place. Triple negative breast cancer is found to have high variability between the patients requiring individual study of each sample, and could reflect different subtypes within triple negative breast cancer. The common significant difference between the normal and all types of malignant tissue is the increased alignment of collagen fibers within the tissue. In addition for all cases, the R and DLP values do not correlate significantly with the SHG intensity. The SHG intensity in the tissue depends on the collagen concentration and the organization of collagen fibers in the focal volume. Therefore, large scan areas are required to correlate SHG intensity with morphological changes of collagen in the tissue. In contrast, R and DLP are directly related to the organization of collagen in a focal volume. Hence SHG polarimetry in addition to SHG intensity measurements are required to discern difference in the ultrastructure of collagen in the cancer tissue. Hence, polarimetric SHG imaging provides quantitative information about the ultrastructural changes of collagen within tissue and can be used with other histopathology techniques for cancer diagnostics.

Funding

Natural Sciences and Engineering Research Council of Canada and the Canadian Institutes of Health Research through a CHRP grant (CPG-134752 and CHRPJ 462842-14).