Optimal wavelengths for optoacoustic measurements of blood oxygen saturation in biological tissues

Abstract

The non-invasive measurement of blood oxygen saturation in blood vessels is a promising clinical application of optoacoustic imaging. Nevertheless, precise optoacoustic measurements of blood oxygen saturation are limited because of the complexities of calculating the spatial distribution of the optical fluence. In the paper error in the determination of blood oxygen saturation, associated with the use of approximate methods of optical fluence evaluation within the blood vessel, was investigated for optoacoustic measurements at two wavelengths. The method takes into account both acoustic pressure noise and the error in determined values of the optical scattering and absorption coefficients used for the calculation of the fluence. It is shown that, in conditions of an unknown (or partially known) spatial distribution of fluence at depths of 2 to 8 mm, minimal error in the determination of blood oxygen saturation is achieved at wavelengths of 658 ± 40 nm and 1069 ± 40 nm.

1. Introduction

The problem of the determination of blood oxygen saturation (the ratio between the concentrations of oxy- and deoxyhemoglobin) is important for a number of medical and biological investigations, for example, for the analysis of the brain hemodynamics of small laboratory animals [1], assessment of the impact of tumor chemotherapy and radiotherapy [2, 3] and the monitoring of wound healing [4]. Since the spectrum of the optical absorption coefficient depends on the ratio of the concentrations of light-absorbing chromophores in the biological tissue, it is possible to estimate the concentration of these chromophores based on their known partial spectra and multispectral measurements of the absorption coefficient. The traditional method of measuring blood oxygen saturation is by diffuse optical spectroscopy (DOS) [5]. Due to the low spatial resolution of the DOS method, the results of such diffuse measurements are oxygenation values, averaged over the volume of the biological tissue. However, for a number of biomedical tasks it is necessary to determine the oxygenation in localized areas of a biological tissue, and this can be achieved by applying a variety of hybrid diagnostic methods, for example, a combination of optical, with one of a number of other research techniques (magnetic resonance [6], ultrasound, X-ray). Optoacoustic (OA) imaging is one such method used to determine the blood oxygen saturation in individual blood vessels.

OA imaging is based on the detection of ultrasonic waves generated in the biological tissue being investigated as optical inhomogeneities absorb optical laser pulses [7]. The laser pulses cause heating and thermal expansion of the light-absorbing parts of the biological tissue, resulting in the generation of acoustic pulses that can be recorded by an ultrasound transducer on the surface of the biological tissue. OA imaging of tissues combines the advantages of the ultrasonic [8] and optical [9–11] methods, respectively, and provides images of tissues with high contrast [12–14] and submicron spatial resolutions at depths of a few millimeters to several centimeters.

Blood, being rich in oxy- and deoxyhemoglobin, is the strongest absorber in the 650 –– 900 nm wavelength range, relative to the other components of biological tissues, so this allows the use of OA methods for the visualization of blood vessels [14,15]. Assuming that blood absorption is determined only by the presence of oxy- and deoxyhemoglobin, two-wavelength OA measurements make it possible to estimate the blood oxygen saturation [16–21].

The amplitude of an OA pulse generated at any given point in the biological tissue is determined by the values of three physical quantities at this point: the optical fluence, the optical absorption coefficient and the Grüneisen parameter [22]. The local value of the optical absorption coefficient is determined by the local concentration of chromophores, the partial absorption spectra of which are well-known. The relationship between chromophore concentration and optical fluence is complicated, because the fluence at any given point within the tissue is determined by the spatial distribution of the chromophores and scatterers belonging to the whole region exposed to the optical radiation.

The unknown spatial distribution of the optical fluence greatly complicates the task of determining the blood oxygen saturation by two-wave OA methods. The assumption that optical fluence has a negligible impact on the assessment of chromophore concentration [23, 24] is generally not justified, because the optical fluence at any given point in the investigated biological tissue depends on the distribution of the optical characteristics of the tissue – its absorption and scattering coefficients at the laser wavelengths used. Thus, the problem of the determination of blood oxygen saturation level is complicated due to the fact that the localized pressure increases in the biological tissues are proportional to the optical fluence, which depends on the wavelength of the laser illumination.

For laser wavelengths corresponding to the transparency window (650 – 1300 nm), the scattering considerably exceeds the absorption, and the extent of fluence varies slowly in the tissues, however, the absorption by blood at these wavelengths is low, which leads to errors in determining the blood oxygen saturation due to the low signal-to-noise ratio. This means that there is an optimal wavelength of laser illumination that allows the determination of blood oxygen saturation with minimal error. It should be noted that in various OA applications (OA microscopy [18, 25, 26] and OA tomography [27, 28]) the optimal wavelengths required for different investigation depths may be in different spectral bands.

The problem of selecting the optimal wavelength for two-wavelength OA measurements of blood oxygen saturation has been raised in a number of studies [29–33]. In [29] the use of the condition number of the absorption spectra matrix as an indicator of the stability for linear least squares spectral unmixing was proposed. In [30] the approach of searching for the optimal wavelengths based on the analysis of the smallest singular value of the absorption matrix was suggested. In [31] an algorithm for optimal wavelength selection, based on the Cramer-Rao lower bound, uses a biological environment model as input data together with initial assumptions about the tissue composition. In most studies [30, 31, 33, 34] the fluence distribution is considered to be known and is calculated from the biological tissue scattering and absorption parameters, which are accepted as being homogeneous in the investigated biological tissue. The optical fluence is calculated either by the Monte Carlo simulation [33], or is given by an exponential decay function depending on depth [31, 34], with the optical parameters taken from [35, 36]. However, biological tissues are not uniformly absorbing and scattering objects, and the large variations of the absorption and scattering parameters of the biological tissue do not allow modeling the fluence with sufficient accuracy, thus resulting in errors in the determination of blood oxygen saturation.

It should also be noted that the absorption of light by blood vessels is usually higher than in the surrounding tissues, and this leads to a large change in fluence inside the vessels at different probing wavelengths. The method proposed in [31] allows the selection of optimal wavelengths for determining the level of blood oxygenation in a vessel located at a particular depth in a biological tissue. However, the proposed model ignores the effect of the size of the blood vessels on the fluence distribution and, consequently, the occurrence of additional errors in determining the level of blood oxygen saturation associated with the finite sizes of blood vessels.

In this paper, we have proposed a method of searching for optimal wavelengths in which the error in the determination of blood oxygen saturation is minimized by taking into account the acoustic pressure noise and the errors in the optical scattering and absorption coefficients when they are used for the calculation of optical fluence. We have also analyzed the influence of optical fluence attenuation in blood vessels of different diameters on the pair of optimal wavelengths.

2. Materials and methods

2.1. Determination of blood oxygen saturation at the surface of a blood vessel

The local increment of OA pressure generated as a result of the illumination of a plane-layered medium by a wide aperture laser pulse, is given by:

$$p_0\left(z,\lambda \right)=\Gamma {\mu }_a\left(\lambda \right)\Phi \left(z,\lambda ,{\mu }_a,{\mu }_s^{\text{'}}\right)$$ (1)

where μ_a [cm⁻¹] is the optical absorption coefficient of the biological tissue at a given depth z, μ_s' is the reduced scattering coefficient of the biological tissue at given depth z, Φ [mJ/cm²] is the optical fluence at the given depth z, and Γ is a Grüneisen dimensionless parameter characterizing the efficiency of OA conversion of the absorbed light into sound. Assuming that the absorption by the blood is defined only by the presence of oxy- and deoxyhemoglobin, μ_a can be represented as the linear combination of the absorption coefficients of both chromophores:

$${\mu }_a^{blood}\left(\lambda \right)=C_{Hb}·{\mu }_a^{Hb}\left(\lambda \right)+C_{{HbO}_2}·{\mu }_a^{{HbO}_2}\left(\lambda \right)$$ (2)

where μ_a^{Hb, HbO2} are the optical absorption coefficients of oxy- and deoxyhemoglobin [cm⁻¹] and C_{Hb, HbO2} are the relative concentrations of oxy- and deoxyhemoglobin at this point. Two-wave OA measurements make it possible to determine C_Hb and C_HbO2 by inverting Eq. (1) and calculating the blood oxygen saturation applying the expression

$${StO}_2=\frac{C_{{HbO}_2}}{C_{Hb}+C_{{HbO}_2}}$$ (3)

OA measurements performed at two wavelengths allow the determination of C_Hb and C_HbO2 from the system of equations:

$$\{\begin{array}{l}{p}_1=\mathrm{K}·\Gamma ·{\Phi }_1·\left[C_{Hb}·{\mu }_a^{Hb}\left({\lambda }_1\right)+C_{{HbO}_2}·{\mu }_a^{{HbO}_2}\left({\lambda }_1\right)\right]\\ p_2=\mathrm{K}·\Gamma ·{\Phi }_2·\left[C_{Hb}·{\mu }_a^{Hb}\left({\lambda }_2\right)+C_{{HbO}_2}·{\mu }_a^{{HbO}_2}\left({\lambda }_2\right)\right]\end{array}$$ (4)

where p_1,2 is the acoustic pressure at wavelength λ_1,2 at different depths, recorded by the acoustic antenna; Φ_1,2 is the optical fluence at the wavelength λ_1,2 at different depths; Κ is a coefficient of instrumentation gain. Thus, from Eq. (3)-(4), the formula for determining the blood oxygen saturation can be obtained:

$${StO}_2=\frac{\frac{p_1}{p_2}·\frac{{\Phi }_2}{{\Phi }_1}·{\mu }_2-{\mu }_1}{\frac{p_1}{p_2}·\frac{{\Phi }_2}{{\Phi }_1}·{\delta \mu }_2-{\delta \mu }_1}$$ (5)

where μ_1,2 is the optical absorption coefficient of Hb at the wavelength λ_1,2 and δμ_1,2 = μ_a^Hb(λ_1,2)-μ_a^HbO2(λ_1,2) is the difference between the optical absorption coefficients of Hb and HbO₂ at the wavelength λ_1,2.

2.2. Uncertainty of measurement of blood oxygen saturation at the surface of a blood vessel

The error δStO₂ in determining blood oxygen saturation by two-wave OA measurements at different depths z can be obtained using Eq. (5) and is given by:

$${\delta StO}_2=\left|\frac{\partial {StO}_2}{\partial \left(\frac{{\Phi }_2}{{\Phi }_1}\right)}\right|·\Delta \left(\frac{{\Phi }_2}{{\Phi }_1}\right)+\left|\frac{\partial {StO}_2}{\partial p_1}\right|·\Delta p_1+\left|\frac{\partial {StO}_2}{\partial p_2}\right|·\Delta p_2$$ (6)

where the first term is associated with the error in the determination of the ratio of fluences at different wavelengths, and the two other terms define the error connected with pressure measurement noise. Since the noise variances in the pressure measurements at different wavelengths are identical, Δp₁ = Δp₂ = Δp, we obtain from Eq. (6) with Eq. (5):

$${\delta StO}_2=\frac{\left|{\delta \mu }_2·{\mu }_1-{\delta \mu }_1·{\mu }_2\right|}{{\left(\frac{p_1}{p_2}·\frac{{\Phi }_2}{{\Phi }_1}·{\delta \mu }_2-{\delta \mu }_1\right)}^2}·\left(\left(\frac{{\Phi }_2}{{\Phi }_1}·\frac{1}{p_2}+\frac{p_1}{p_2}·\frac{{\Phi }_2}{{\Phi }_1}·\frac{1}{p_2}\right)·\Delta p+\frac{p_1}{p_2}·\Delta \left(\frac{{\Phi }_2}{{\Phi }_1}\right)\right)$$ (7)

The values μ_1,2 in Eq. (7) are well known from [7, 37] (Fig. 1). The determination of the values Δp, Φ₂/Φ₁ and Δ(Φ₂/Φ₁) is described in the following subsections.

Fig. 1.

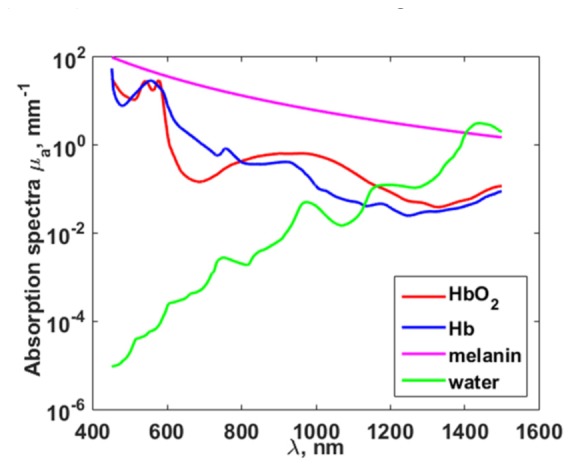
Optical absorption coefficients of oxy- (HbO_2) (red line) and deoxyhemoglobin (Hb) (blue line) [37], melanin (pink line) [7] and water (green line) [37] in the wavelength range of 450 — 1500 nm.

2.2.1 Error of saturation measurement related to acoustic signal-to-noise ratio

The acoustic pressure measurement error Δp is determined by the acoustic signal-to-noise ratio SNR_a = p/(Δp). A typical value of SNR_a was measured for the OA microscope described in [38], which is intended for OA bioimaging. Measurements were carried out at a laser wavelength of 531 nm (corresponding to the isosbestic point of the intersection of the absorption curves of HbO₂ and Hb) and yielded a SNR_a = 30 dB at a depth of 3 mm [39]. Knowing the SNR_a for a fixed depth and wavelength makes it possible to evaluate the terms Δp/(p(λ)) in Eq. (7) according to the formula:

$$\frac{\Delta p}{p\left(\lambda \right)}=\frac{\Phi \left(531\text{nm}\right)·\left[C_{Hb}·{\mu }_a^{Hb}\left(531\text{nm}\right)+C_{{HbO}_2}·{\mu }_a^{{HbO}_2}\left(531\text{nm}\right)\right]}{{SNR}_a\left(531\text{nm}, \text{3mm}\right)·\Phi \left(\lambda \right)·\left[C_{Hb}·{\mu }_a^{Hb}\left(\lambda \right)+C_{{HbO}_2}·{\mu }_a^{{HbO}_2}\left(\lambda \right)\right]}$$ (8)

which allows calculation of the error associated with the noise in the pressure measurements.

2.2.2 In vivo measurements of optical fluence and determination error in the ratio of fluence at two wavelengths

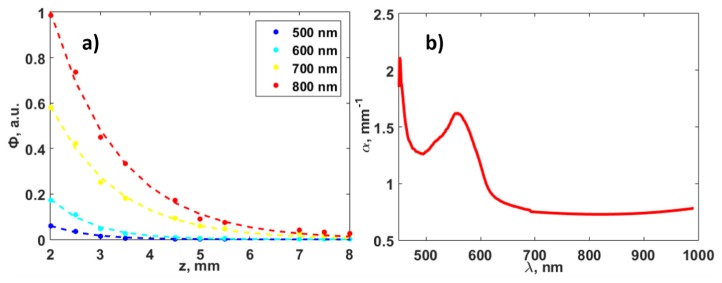
In vivo experiments with transillumination optical spectroscopy on one of the researchers’ hands were conducted in order to determine typical values of the quantities Φ₂/Φ₁ in Eq. (7), depending on the investigation depth z and wavelengths λ_1,2. A xenon lamp with fiber output was used as the source of light. The light spot on the object of investigation was 400 μm, which is equal to the diameter of optic fiber because the source of light was in the contact with the hand. A QE65000 (Ocean Optics, USA) spectrometer with fiber input was used as the detector. The detection 400 μm fiber was also in contact with the hand. Figure 2(a) demonstrates the fluence spectrum Φ_λ(z) obtained in the wavelength range 450-1000 nm at depths from 2 to 8 mm. The measurements were performed at the same region of the researcher’s hand and depth variation was provided with bringing together the source and detector fiber outputs by gentle compression of the human hand.

Fig. 2.

(a) Experimental (in vivo) dependence of the fluence Φ with depth when using different wavelengths: points —experimental data, dotted lines — exponential decay approximations. (b) The dependence of the increment α(λ) of fluence attenuation on the illumination wavelength.

Assuming that the scattering and absorption by the biological tissue are uniform, and taking into account that illumination of the object is close to the plane wave, the experimental data (Fig. 2(a) points) was approximated by an exponential decay model described in [40] (Fig. 2(a) dashed line):

$${\Phi }_{\lambda }\left(z\right)={\Phi }_0·k\left(\lambda \right)·\exp \left(-\alpha \left(\lambda \right)·z\right)$$ (9)

where Φ₀ is the fluence at the object surface; k is the backscattering coefficient; α is the coefficient of fluence attenuation. According to [40], the rate of increase in attenuation can be expressed in terms of the optical parameters of the biological tissue according to the expression

$$\alpha \left(\lambda \right)=\sqrt{3·{\mu }_a\left(\lambda \right)·\left({\mu }_a\left(\lambda \right)+{\mu }_s^{\text{'}}\left(\lambda \right)\right)}$$ (10)

the backscattering coefficient k in Eq. (9) is expressed as follows:

$$k=3+5.4·R_d-2·\exp \left(-R_d\right)$$ (11)

where R_d is the total diffuse reflectance, which is determined by the absorption and scattering coefficients:

$$R_d=\exp \left(-\frac{8}{\sqrt{3·\left(1+{\mu }_s^{\text{'}}/{\mu }_a\right)}}\right)$$ (12)

Figure 2(b) demonstrates the spectral dependency of the increment α(λ) of fluence attenuation in the biological tissue [41] obtained according to the experimental data.

The dependence of the rate of growth of attenuation α and the backscattering coefficient k on μ_a and μ_s' allows expression of the value Δ(Φ₂/Φ₁) from Eq. (7) from error in the determination of the biological tissue’s optical properties. According to Eq. (9):

$$\frac{{\Phi }_2}{{\Phi }_1}=\frac{k_2}{k_1}·\exp \left(-\left({\alpha }_2-{\alpha }_1\right)·z\right)$$ (13)

where α_1,2 = α(λ_1,2) are the increments of fluence attenuation in the biological tissue at wavelengths λ_1,2. Thus, the error in the changes Φ₂/Φ₁:

$$\Delta \left(\frac{{\Phi }_2}{{\Phi }_1}\right)=\frac{{\Phi }_2}{{\Phi }_1}·\left(\frac{\Delta k_1}{k_1}+\frac{\Delta k_2}{k_2}+z·\left(\Delta {\alpha }_1+{\Delta \alpha }_2\right)\right)$$ (14)

where Δα_1,2 are the errors in the determination of the rate of growth of attenuation α at wavelengths λ_1,2, and Δk_1,2 are the errors in the determination of the backscattering coefficient at wavelengths λ_1,2, associated with the error in the determination of the optical parameters of the biological tissue. Taking into account Eq. (10) as well as the dependence of k on the optical parameters of the biological tissue, it is possible to write expressions for the measurement errors of the coefficients μ_s'and μ_a:

$$\Delta \alpha =\frac{1}{2\sqrt{3{\mu }_a·\left({\mu }_a+{\mu }_s^{\text{'}}\right)}}·\left[\left({6\mu }_a+3{\mu }_s^{\text{'}}\right)·{\mu }_a·\delta {\mu }_a+3{\mu }_a·{\mu }_s^{\text{'}}·\delta {\mu }_s^{\text{'}}\right]$$ (15)

$$\Delta k=\frac{12R_d·\left(5.4·R_d+34\exp (-R_d)\right)}{{\left(3\left(1+{\mu }_s^{\text{'}}/{\mu }_a\right)\right)}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}·\frac{{\mu }_s^{\text{'}}}{{\mu }_a}\left[\delta {\mu }_a+\delta {\mu }_s^{\text{'}}\right]$$ (16)

where δμ_a is the relative error of the measurement of μ_a and δμ_s' is the relative error of the measurement of μ_s'.

Taking into account Eq. (14), we obtained the expression for the calculation of the error in the determination of blood oxygen saturation through the errors in determining the scattering and absorption parameters of the biological tissue and the signal-to-noise ratio:

$${\delta StO}_2=\frac{\left|{\delta \mu }_2·{\mu }_1-{\delta \mu }_1·{\mu }_2\right|}{{\left(\frac{p_1}{p_2}·\frac{{\Phi }_2}{{\Phi }_1}·{\delta \mu }_2-{\delta \mu }_1\right)}^2}·\left(\left(\frac{{\Phi }_2}{{\Phi }_1}·\frac{1}{p_2}+\frac{p_1}{p_2}·\frac{{\Phi }_2}{{\Phi }_1}·\frac{1}{p_2}\right)·\Delta p+\frac{p_1}{p_2}·\frac{{\Phi }_2}{{\Phi }_1}·\left(\frac{\Delta k_1}{k_1}+\frac{\Delta k_2}{k_2}+z·\left(\Delta {\alpha }_1+{\Delta \alpha }_2\right)\right)\right)$$ (17)

where the variables Δα_1,2, Δk_1,2 are determined by Eq. (15)-(16), and Δp/(p(λ)) is determined by Eq. (8).

2.3. Accounting for changes in optical fluence inside blood vessels

In section 2.2 the expression for the error in the determination of the ratio of fluences corresponding to different wavelengths at any given depth z was written assuming that the scattering and absorption by the biological tissue is uniform. It is important to consider that, during the assessment of the level of blood oxygenation, the rate of fluence depth-dependent attenuation in a vessel is considerably higher than that in the surrounding tissues, which leads to strong fluence decay in the blood vessel and, as a result, to additional error in the determination of the StO₂ due to the difference in the optical fluences at the two wavelengths.

In the presence of blood vessel with thickness d_v at depth z, the approximation of the stratified medium fluence attenuation is determined by the expression:

$${\Phi }_{\lambda }\left(z\right)={\Phi }_0·k\left(\lambda \right)·\exp \left(-\alpha \left(\lambda \right)·z\right)·\exp \left(-\left({\mu }_a^{blood}(\lambda )-\alpha \left(\lambda \right)\right)·d_v\right)$$ (18)

where μ_a^blood(λ) is the absorption coefficient of blood, defined by Eq. (2) and d_v is the thickness of the blood vessel. Figure 3 shows the dependence of the fluence on depth for wavelengths of 578 nm and 596 nm, in the presence of a blood vessel with a diameter of 150 μm in the light path.

Fig. 3.

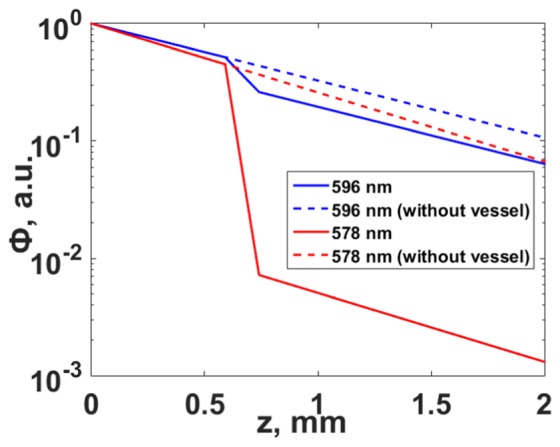
The dependence of fluence Φ on depth corresponding to two wavelengths, considering the attenuation in a blood vessel (solid line), and without attenuation by the vessel (dotted line).

Thus, the change in fluence can be estimated not only for the case of the uniform distribution of scattering and absorption by the biological tissue (as discussed above), but also for the damping in a blood vessel. After we merge Eq. (9) and Eq. (18), the error associated with the changes in fluence will be expressed by the following expression:

$$\Delta \left(\frac{{\Phi }_2}{{\Phi }_1}\right)=\frac{{\Phi }_2}{{\Phi }_1}·\left(\frac{\Delta k_1}{k_1}+\frac{\Delta k_2}{k_2}+(z-d_v)·\left(\Delta {\alpha }_1+{\Delta \alpha }_2\right)-d_v·\left({\mu }_a^{blood}({\lambda }_2)-{\mu }_a^{blood}({\lambda }_1)-{\alpha }_2+{\alpha }_1\right)\right)$$ (19)

Thus, the error in the determination of StO₂ takes the form:

$${\delta StO}_2^{withves}={\delta StO}_2+{\delta StO}_2^{ves}$$ (20)

where δStO₂^ves is an additional term to the saturation error, that occurs due to the fluence attenuation in the blood vessel, and is given by:

$${\delta StO}_2^{ves}=\frac{\left|{\delta \mu }_2·{\mu }_1-{\delta \mu }_1·{\mu }_2\right|}{{\left(\frac{p_1}{p_2}·\frac{{\Phi }_2}{{\Phi }_1}·{\delta \mu }_2-{\delta \mu }_1\right)}^2}·\left(\frac{p_1}{p_2}·\frac{{\Phi }_2}{{\Phi }_1}·\left(d_v·\left(\Delta {\alpha }_1+{\Delta \alpha }_2\right)-d_v·\left({\mu }_a^{blood}({\lambda }_2)-{\mu }_a^{blood}({\lambda }_1)-{\alpha }_2+{\alpha }_1\right)\right)\right)$$ (21)

The influence of this additional term on the optimal wavelengths will be discussed in Section 3.5.

2.4. Calculation of the optimal wavelengths

Equation (17) makes it possible to investigate the influence of pressure noise and the error in the determination of the ratios between fluences corresponding to different wavelengths on the error in calculating the blood oxygen saturation as a result of varying several parameters: the signal-to-noise ratio at a given depth and wavelength, and the error in the determination of the optical parameters of the biological tissue.

In this paper, we present analyses of the error in the determination of blood oxygen saturation in two cases: without taking into account Eq. (17), and taking into account Eq. (21) and the fluence attenuation in the blood vessel. The optimal wavelengths for OA measurements can be found by minimizing the calculated saturation error δStO₂:

$${\lambda }_{1,2}^{opt}=\arg \left(\underset{{\lambda }_{1,2}}{\min }{\delta StO}_2\right)$$ (22)

The procedure is described in sections 3.2-3.4. In section 3.5 the influence of fluence attenuation in a blood vessel on those pairs of optimal wavelengths that correspond to the minimum of Eq. (21) will be analyzed:

$${\lambda }_{1,2}^{opt}=\arg \left(\underset{{\lambda }_{1,2}}{\min }{\delta StO}_2^{ves}\right)$$ (23)

3. Results

3.1. Modeling of optical fluence

Optical fluence was measured using transillumination configuration and different thicknesses of one of the researchers’ hand in the range from 450 to 1000 nm, as described in Section 2.2.2. In order to find the optimal wavelengths in an extended spectral range (450-1500 nm), a modeling of the optical fluence was conducted. In order to prolong the range of wavelengths 1000-1500 nm, the concentrations of the individual components of the biological tissue were determined by approximating the spectrum of α according to Eq. (10) in the wavelength range from 450 nm to 1000 nm, based on experimental data of fluence measurements (Fig. 2(b)).

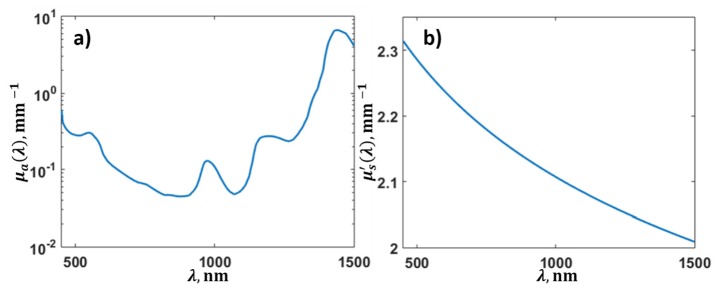
The reduced scattering coefficient was modeled (Fig. 4(b)) by applying the expression ${\mu }_s^{\text{'}}=a·{\left(\frac{\lambda }{450}\right)}^{-b}$. The average values of the constants a and b were taken from [42] corresponding to skin, muscle and mammalian tissue, and were equal to a = 2.3 mm⁻¹, b = 0.1 mm⁻¹.

Fig. 4.

Optical parameters of the biological tissue, obtained from experimental data: (a) optical absorption coefficient of the biological tissue and (b) reduced scattering coefficient of the biological tissue.

We assumed that water, melanin and blood contribute to the absorption spectrum μ_a. The partial absorption spectra of these chromophores (Fig. 1) were taken from [7, 37]. The absorption spectrum of blood was expressed by a linear combination of absorption spectra of oxy- and deoxy- hemoglobin with unknown blood oxygen saturation level. In this case we approximated experimental data with analytical one represented by Eq. (10) with 4 unknown coefficients: relative concentrations of melanin, water, blood and blood oxygen saturation. The obtained relative concentrations of melanin, water and blood were 0.003, 2.1, 0.005, respectively, and the obtained blood oxygen saturation was equal to 0.3. The optical absorption coefficient was calculated as a linear combination of partial absorptions of melanin, water and blood in obtained concentrations and presented in Fig. 4(a).

Figure 5 shows the experimentally obtained dependence of the decay increment α and the result of approximation with the extrapolation to the wavelength range from 1000 nm to 1500 nm.

Fig. 5.

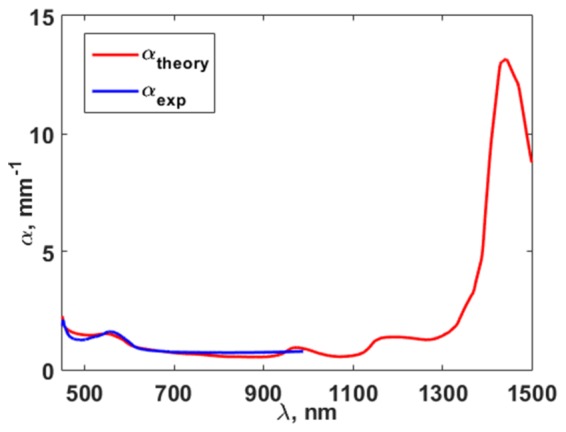
Experimental dependence of rate of increase of fluence attenuation on wavelength (blue line) and the result of its approximation (red line).

The obtained values of μ_a and μ_s´ were used to calculate R_d and k by applying Eq. (12) and Eq. (11), respectively. The approximation allowed extrapolation of the optical fluence measurements into the range from 1000 to 1500 nm and determination of the optimal wavelengths for minimizing the error in the determination of StO₂ in the range from 450 to 1500 nm.

3.2. Optimal wavelengths for determining the blood oxygen saturation with known optical parameters of the biological tissue

Calculations of δStO₂ based on Eq. (17) were carried out for each pair of wavelengths λ₁ and λ₂ in the range of 450-1500 nm with steps of 1 nm (totally 552301 pairs). Calculations applying Eq. (22) in order to find the optimal wavelengths λ₁ and λ₂, corresponding to the minimum δStO₂, were conducted by a brute-force approach (minimum of δStO₂ is defined as the minimum among those values calculated for all abovementioned pairs of wavelengths).

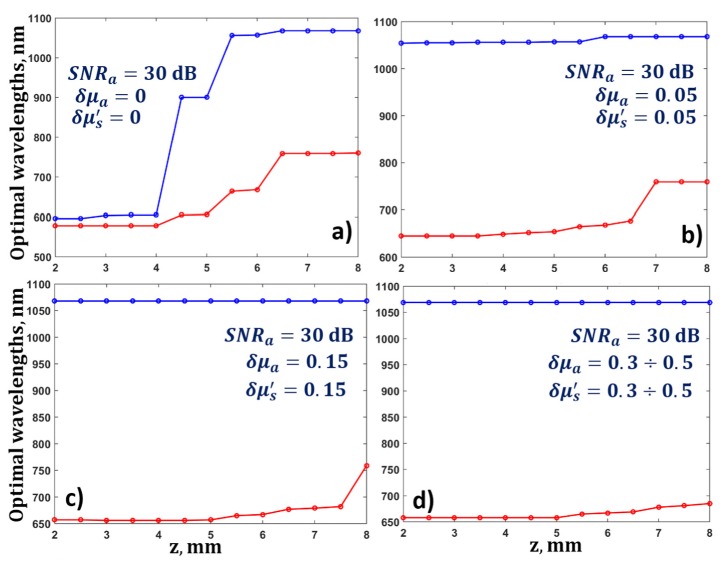
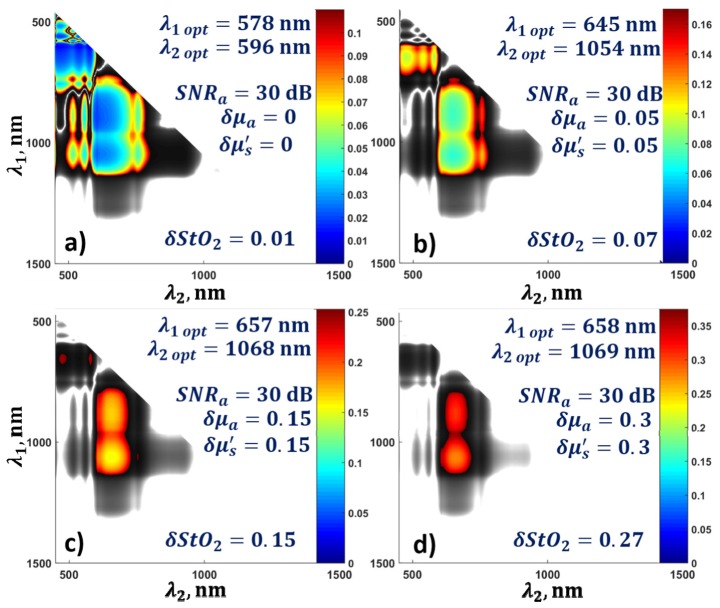
The value of blood oxygen saturation was assumed to be 0.8, and the value of SNR_a was fixed at 30 dB. Firstly, the optical parameters of the biological tissue were assumed to be known, i.e. δμ_a = δμ_s' = 0. The results showed that λ₁ = 578 nm and λ₂ = 596 nm provide the most accurate determination of blood oxygen saturation at depths up to 4 mm, with known fluence distribution (Fig. 6(a)). For depths greater than 4 mm, the optimal wavelengths shifted toward longer wavelengths, so, at depths of 5 to 8 mm the optimal value for λ₁ shifted from 596 to 760 nm, and the optimal value for λ₂ shifted from 900 to 1068 nm (Fig. 6(a)).

Fig. 6.

(a) Dependence of optimal wavelengths for the determination of blood oxygen saturation on depth for a fixed value of SNR_a = 30 dB, and known parameters of the biological tissue δμ_a = 0, δμ_s' = 0, and (b-d) for different values of relative error in the measurements of the optical parameters δμ_a and δμ_s' from 0.05 to 0.5.

3.3. Influence of errors in the determination of the optical parameters of the biological tissue on the optimal wavelengths

The influence of errors in the determination of the ratio of optical fluences corresponding to different wavelengths on the values of the optimal wavelengths was analyzed. For this purpose, the optimal wavelengths were found by applying Eq. (22) for a fixed SNR_a of 30 dB and different values of the relative errors in the determination of the optical parameters of the biological tissue δμ_a and δμ_s' from 0 to 0.5. As one can see from Fig. 6, small values of δμ_a and δμ_s' lead to the conclusion that, even for small depths (of about 2 mm), the OA measurements of blood oxygen saturation should be carried out at wavelengths λ₁ = 645 nm and λ₂ = 1054 nm (Fig. 6(b)). The optimal wavelengths at depths of 7 – 8 mm with δμ_a = 0.05 and δμ_s' = 0.05 are λ₁ = 759 nm and λ₂ = 1068 nm. A gradual increase in the relative error in the determination of the optical parameters to 0.5 leads to a shift of the optimum value λ₂ from 759 to 685 nm (Fig. 6(d)) for diagnostics involving greater depths. Increases in relative errors δμ_a and δμ_s' lead to an increase in the error in the determination of the blood oxygen saturation.

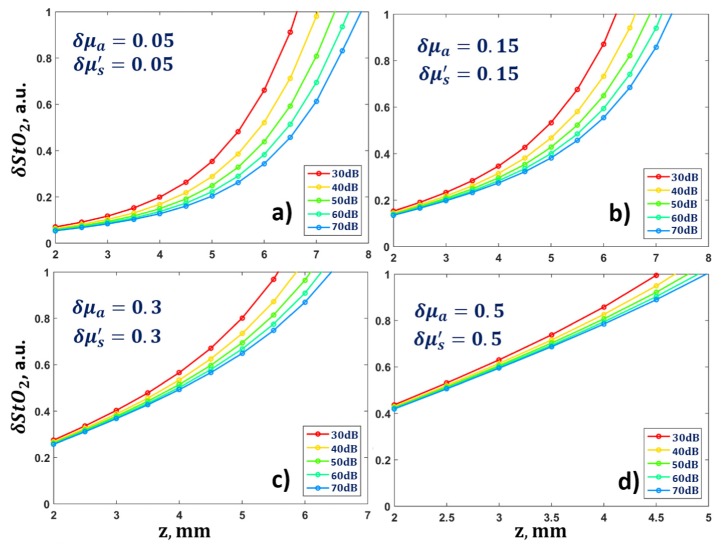
The dependence of the relative error in the determination of blood oxygen saturation on the diagnostics depth when applying optimal wavelengths is shown in Fig. 7. For δμ_a = 0.15 and δμ_s' = 0.15 the blood oxygen saturation can be determined with an accuracy of only 30% for depths up to 3.5 mm. Further increase in the relative errors δμ_a and δμ_s' leads to greater uncertainty in the measurements of blood oxygen saturation, even at a depth of 2 mm.

Fig. 7.

Dependence of the accuracy of the determination of blood oxygen saturation on depth for different values of the relative errors of the optical parameters during diagnostics applying optimal wavelengths and a fixed value of SNR_a = 30 dB.

3.4. Influence of acoustic pressure noise on optimal wavelengths

An investigation of the influence of acoustic pressure measurement noise on the values of δStO₂ and on the optimal wavelengths was conducted. The value of SNR_a was varied from 30 to 70 dB. Figure 8 demonstrates that the values of the optimal wavelengths do not change with an increase of signal-to-noise ratio, however, the value of δStO₂ decreases with increasing SNR_a from 30 dB to 70 dB. When the relative error in the determination of the optical parameters of the biological tissue is small, an SNR_a increase leads to a δStO₂ decrease by 20% (Fig. 8). The errors in the determination of the optical parameters of the biological tissue lead to large errors in the determination of blood oxygen saturation. Thus, for an unknown distribution of optical fluence (δμ_a = 0.5, δμ_s' = 0.5) the saturation error immediately reaches 40%.

Fig. 8.

Dependence of the error in the determination of blood oxygen saturation on depth for different values of the relative error of the optical parameters and for variations in SNR_a from 30 to 70 dB during diagnostics applying the optimal wavelengths obtained in Section 3.3 and shown in Fig. 6.

The question of a possible discrepancy between the optimal wavelength and one, chosen for OA measurement that does not lead to a reduction in the accuracy of the calculation of blood oxygen saturation is also important. Figures 9(a)-9(d) show the error for a depth of 2 mm with a fixed value of the signal-to-noise ratio and for different values of relative error in the determination of the optical parameters of the biological tissue from 0 to 0.3. The confidence intervals for the wavelengths are highlighted. Color shows the deviation of error from the minimum value. With known fluence distribution within the biological tissue, blood oxygen saturation measurements can be performed with an accuracy of 10% by using wavelengths of about 600 nm as well as wavelengths of 700 and 1060 nm. However, even a small error (δμ_a = 0.15, δμ_s' = 0.15) in the determination of the optical properties of the biological tissues reduces the range of optimal wavelengths of laser exposure to only 658 ± 30 nm and 1069 ± 40 nm.

Fig. 9.

Confidence intervals of wavelengths for the determination of blood oxygen saturation error at a depth of 2 mm for a fixed SNR_a = 30 dB and different values of the relative errors of optical parameters from 0 to 0.3.

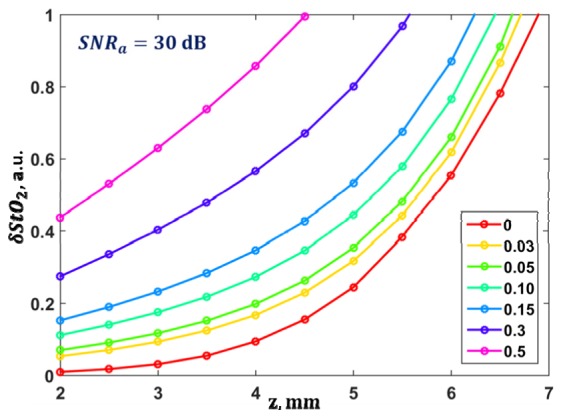
3.5. Accounting for the changes in optical fluence inside a blood vessel

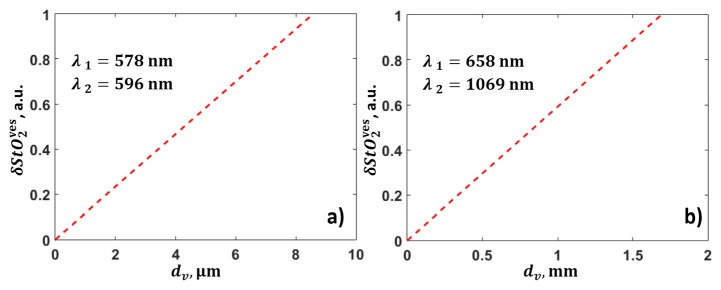
The abovementioned results indicated that, for known optical parameters of the biological tissue, wavelengths of λ₁ = 578 nm and λ₂ = 596 nm are optimal for the most accurate determination of blood oxygen saturation at depths of up to 4 mm. However, blood absorption at these wavelengths is sufficiently large as to lead to a large change in fluence within any blood vessel located in the light propagation path, as was shown in Section 2.3, and, consequently, this leads to additional error in the determination of the blood oxygen saturation.

In order to investigate the effect of the attenuation of optical fluence in blood vessels, the term in Eq. (21), associated with the finite thickness of the blood vessel, was analyzed for two pairs of optimal wavelengths in two different cases. As follows from Fig. 10, two-wave measurements at wavelengths λ₁ = 578 nm and λ₂ = 596 nm lead to excessive uncertainty in the calculation of blood oxygen saturation even for a capillary with a diameter of 3 μm. At the same time, diagnostics at wavelengths λ₁ = 658 nm and λ₂ = 1069 nm makes it possible to determine the blood oxygen saturation with high accuracy (Fig. 10(b)), even if there is a vessel with a thickness of 1 mm in the light propagation path from the surface to depth z.

Fig. 10.

Dependence of errors in the determination of blood oxygen saturation, corresponding to blood vessel diameter for optimal wavelengths (a) λ₁ = 578 nm and λ₂ = 596 nm, and (b) λ₁ = 658 nm and λ₂ = 1069 nm.

4. Discussions

In this paper a method to obtain values for the optimal wavelengths needed for OA measurements of blood oxygen saturation was proposed. It provides minimum error in the determination of blood oxygen saturation at various depths, by taking into account errors in the determination of the optical parameters of the biological tissue, the signal-to-noise ratio of the acoustic pressure measurements and the thickness of the blood vessel chosen for the blood oxygen saturation measurements. It was shown that the error in the determination of blood oxygen saturation increases with increasing depth, this being caused by a decrease in the signal-to-noise ratio and an increase in the difference in the optical fluence in the biological tissue corresponding to different wavelengths.

With a known fluence spectrum, the optimal illumination wavelengths that allow the determination of blood oxygen saturation at depths of up to 4 mm are 578 nm and 596 nm. The resulting pair of wavelengths with a specific distribution of fluence in the biological tissue is confirmed by the results of other authors [31]. However, the model proposed in [31] does not account for the dependence of the fluence distribution on the size of the blood vessels. Our proposed method gives 578 nm and 596 nm as the optimal wavelengths to use at small depths, because the coefficients of absorption of the blood are large at these wavelengths, and therefore, the maximum response of the biological tissue provides a large signal-to-noise ratio in the received acoustic signal. The optimal wavelengths obtained are close, because the difference between the extinction coefficients at these wavelengths is small.

A large difference between the fluence values arises at wavelengths of 578 and 596 nm due to attenuation within the blood vessels. This leads to unacceptably large errors in the determination of blood oxygen saturation, even in the smallest capillaries with diameters of only 3 µm. The results indicate that the use of wavelengths less than 600 nm for measurements, even at small depths, is inappropriate.

A pair of wavelengths from the ranges of 658 ± 30 nm and 1069 ± 40 nm provides an acceptable contrast in optical absorption. At an optimal wavelength of 658 nm, the absorption coefficient of deoxyhemoglobin is bigger than of oxyhemoglobin and vice versa at a wavelength of 1069 nm. This makes it possible to distinguish between oxy- and deoxyhemoglobin. At the same time, the difference in fluence is small at these wavelengths, and, therefore, the term associated with errors in the determination of the scattering and absorption parameters of the biological tissue makes a small contribution to the error in the determination of blood oxygen saturation.

The accuracy of the determination of blood oxygen saturation can be increased by a higher signal-to-noise ratio. An increase in SNRa from 30 to 70 dB extends the depth limits of accurate blood oxygen saturation measurements by 1 mm, without any change in the optimal wavelengths.

The accuracy of the determination of blood oxygen saturation may also be increased by decreasing the error in the determination of the ratio of fluences corresponding to different wavelengths. It should be possible to calculate, precisely, the scattering and absorption coefficients of the biological tissue for different wavelengths and laser illumination geometries. However, in the case of complex illumination geometries such as ring-shaped ones, the plane wave illumination model considered in this paper should be replaced by the Monte Carlo model of light transport applicable for arbitrary geometries. The absorption and scattering parameters of the biological tissues have a very large spread. It is possible to reduce the error in the determination of these parameters only with the use of additional measurements.

For independent measurements of the optical fluence in biological tissue, some authors [43, 44] propose combining OA spectroscopy with diffuse optical tomography (DOT), which allows evaluation of the absorption and scattering coefficients that determine the optical field inside the biological tissue. However, this approach requires additional measurements, and this both complicates construction of the device and increases the dimensions of the scanning unit. A solution has been presented in [45], where the backscattered light from the biological tissue is detected by an acoustic antenna used to receive ultrasonic pulses. However, it is necessary to solve the inverse problem of the three-dimensional reconstruction of the DOT to calculate the optical field when using this information.

The limitations of the proposed method correspond to the model, considered in the paper, which involves the OA sensing of a plane-layered medium with an isolated layer filled with blood. The described method of the determining the error in blood oxygen saturation measurements requires appropriate adjustments for additional chromophores contributing to the received acoustic signal. Certainly, the real biological tissue has a more complex structure than has been used in the article, and the presence of differently oriented blood vessels makes the calculating of the optical fluence within the tissue unrealizable, especially since the internal structure of the tissue in practically unavailable. However, the formula of saturation error includes the ratio of fluences at two wavelengths. In this case the results are not influenced by the absolute value of fluence. Even for complex 3D structures of the biological tissue, this ratio of the fluences will be determined by the variations in parameters of scattering and absorption at two wavelengths, rather than spatial variations of these parameters. Thereby, obtained optimal wavelengths have to work for a real tissue. This assumption can be confirmed only by conducting the additional in vivo studies, and it is a goal of further studies. Moreover, it has been shown that one cannot neglect the presence of separately located blood vessels taking OA measurements at wavelengths in visible spectral range, because of the strong absorption of blood within the blood vessel in comparison to the surrounding tissues. In other words, in visible spectral range the tissue cannot be regarded as a uniform scattering and absorbing medium. The presented calculations showed the inability to reconstruct saturation with sufficient error in the visible spectral range. As for the transparency window, the blood absorption rate is much smaller, and, consequently, the variations of absorption coefficients are relatively small. Therefore, the nature of the decay of optical fluence is close to an exponential, despite the complicated 3D vascular system in biological tissue.

Obviously, measurements at several (more than two) wavelengths can also enhance the accuracy of the calculation of blood oxygen saturation. Furthermore, these measurements allow account to be taken of the contribution to the formation of the OA signal of other tissue chromophores in the investigated volume of the biological tissue, but this issue will be the subject of further studies.

5. Conclusions

This paper has proposed a method for obtaining values for the optimal wavelengths to be used in OA diagnostics, which provide minimum error in the determination of blood oxygen saturation. The method takes into account the acoustic pressure noise and the errors in determining the optical scattering and absorption coefficients used for the calculation of the fluence. The error in the determination of blood oxygen saturation associated with the use of approximate methods of fluence evaluation within the vessel was investigated for OA measurements at two wavelengths. It was shown that minimal error in the determination of blood oxygen saturation can be achieved at wavelengths of 658 ± 30 nm and 1069 ± 40 nm under conditions of unknown (or partially known) spatial fluence distribution, and at depths from 2 to 8 mm.

Funding

Russian Foundation for Basic Research (14-02-00836, 16-32-60093).