Feasibility of spatial frequency domain imaging (SFDI) for optically characterizing a preclinical oncology model

Abstract

Determination of chemotherapy efficacy early during treatment would provide more opportunities for physicians to alter and adapt treatment plans. Diffuse optical technologies may be ideally suited to track early biological events following chemotherapy administration due to low cost and high information content. We evaluated the use of spatial frequency domain imaging (SFDI) to characterize a small animal tumor model in order to move towards the goal of endogenous optical monitoring of cancer therapy in a controlled preclinical setting. The effects of key measurement parameters including the choice of imaging spatial frequency and the repeatability of measurements were evaluated. The precision of SFDI optical property extractions over repeat mouse measurements was determined to be within 3.52% for move and replace experiments. Baseline optical properties and chromophore values as well as intratumor heterogeneity were evaluated over 25 tumors. Additionally, tumor growth and chemotherapy response were monitored over a 45 day longitudinal study in a small number of mice to demonstrate the ability of SFDI to track treatment effects. Optical scattering and oxygen saturation increased as much as 70% and 25% respectively in treated tumors, suggesting SFDI may be useful for preclinical tracking of cancer therapies.

1. Introduction

Despite considerable progress in diagnosis and treatment strategies, cancer remains among the leading causes of morbidity and mortality worldwide [1]. In the United States, the American Cancer Society estimates that cancer will cause nearly 1 of every 4 deaths in 2016, surpassed only by heart disease [2]. Cytotoxic chemotherapy continues to be the primary weapon for combating the death toll, and is used against local and advanced cancers from almost all organ sites [3–5]. Cytotoxic systemic therapies are often combined with other available therapies including hormonal agents, targeted therapies, antiangiogenics, radiation, and surgery in order to improve patient response and prevent future relapse. However, therapeutic efficacy is often impeded by factors such as host toxicity, poor drug delivery, drug resistance, and tumor heterogeneity, all of which may contribute to substantial treatment side effects while offering little or no help for non-responders [5–8]. In vivo surveillance of the tumor state during treatment would allow physicians to make informed “adaptive” changes to treatments in order to enhance efficacy, avoid unwarranted side effects and reduce treatment cost and burden.

Clinical Diffuse Optical Imaging (DOI) techniques including Diffuse Optical Tomography (DOT) and Diffuse Optical Spectroscopy (DOS) are receiving significant interest as emerging non-invasive functional imaging tools, and may be ideally suited to the purpose of longitudinal monitoring of therapy efficacy as they have favorable safety profiles, are relatively inexpensive, and provide important metabolic and hemodynamic information related to the in vivo tumor state [9, 10]. A growing number of reports over the last decade demonstrate the utility of DOI methodologies for tracking changes in tumor functional and metabolic properties during chemotherapy in breast cancer patients [11–13]. Several reports have shown that decreases in hemoglobin content, decreases in water, and/or increases in lipids correlate with pathologic complete response (pCR) in breast cancer patients receiving presurgical, neoadjuvant chemotherapy (NAC) [14–17]. In 2011, it was reported that a rapid gain in tumor oxyhemoglobin (HbO₂) concentration within the first day of therapy is predictive of NAC outcome, suggesting frequent tumor monitoring may reveal important early markers of response [18].

While these findings underline the tremendous potential of DOI for clinical therapy monitoring, there has been relatively little work to date in trying to better understand the cellular, molecular, and physiological origins of these clinical observations, although a small number of recent studies have correlated DOI related metrics to immunohistochemical markers of blood vessel density and metabolism measured from clinical biopsies or surgical specimens [19, 20]. By further exploring the underpinnings of response, it may be possible to not only track treatments more effectively, but also better schedule multi-agent regimens, or detect early signs of therapy resistance based on DOI feedback. This will require careful control over treatments and imaging, with regular access to tumor tissue for correlative measurements. The preclinical setting is ideal for testing these ideas, but it is necessary to track the same DOI-derived parameters in order to translate potential findings to the clinic.

Here we investigate Spatial Frequency Domain Imaging (SFDI) as a new tool to monitor the in vivo tumor state in small animal oncology models. SFDI provides equivalent information to many clinical DOI modalities at a relatively shallower tissue depth, is noncontact, and provides wide-field spatial mapping of tumor optical parameters. SFDI utilizes spatially modulated light patterns of visible and near-infrared (NIR) light (~400 – 1000 nm) to extract optical properties (absorption μ_a, reduced scattering μ_s`) of diffusive media. Absorption values, measured at multiple wavelengths, provide access to tissue hemodynamic status and metabolic properties [9]. Scattering measurements relate to tissue structural properties and provide information about cell and organelle density as well as the extracellular matrix [10]. To date, SFDI has been explored for a number of preclinical and clinical applications including vascular occlusions, reconstructive tissue status, monitoring burn wounds, tracking the progression of Alzheimer’s disease and imaging drug delivery to the brain [21–29]. However, there are only a small number of reports in which SFDI has been used for applications in oncology. These include studies for diagnosing human skin carcinomas, mapping breast lumpectomy specimens, developing tomographic reconstruction of brain tumors in small animals, and PDT dosing monitoring [30–34].

Here we explore the feasibility of using SFDI for frequent longitudinal monitoring of cancer chemotherapy efficacy in a small animal oncology model. A mouse tumor xenograft model based on the human prostate tumor cell line PC3/2G7 was used which produces highly vascularized tumors [5], and responds strongly to the antiangiogenic DC101 and the cytotoxic agent cyclophosphamide (CPA). In order to validate SFDI as an appropriate modality for label-free in vivo longitudinal studies, first a range of spatial frequencies was tested for their ability to accurately extract optical properties (OPs) using a two frequency look-up-table (LUT) over the expected range of tumor μ_a and μ_s` values. OPs were extracted over tumor region of interest (ROI) and fit to extract oxyhemoglobin and deoxyhemoglobin levels. Intratumor heterogeneity and average OP and chromophore values were assessed on individual tumors prior to treatment. Repeatability of mouse tumor measurements was evaluated under three varying procedural conditions that mimic user induced variations in mouse positioning from measurement-to-measurement. Finally, a proof-of-concept preclinical study was performed with frequent and long-term therapy monitoring on a small number of mice. Substantial changes in optical scattering and oxygen saturation were observed during this treatment and tumor growth rebound, as we will show here. In total, these results demonstrate that SFDI holds potential as a cancer therapy monitoring tool in the preclinical setting.

2. Materials and methods

2.1 Spatial frequency domain imaging (SFDI): data acquisition, processing and analysis

Detailed descriptions of SFDI instrumentation and data analysis are provided elsewhere [35, 36]. Briefly, SFDI utilizes projections of spatially modulated visible and/or NIR light to extract intrinsic tissue optical properties (μ_a and μ_s`) over a wide-field area. A digital micromirror device (DMD) or other spatial light modulator is used to project sinusoidal or more exotic patterns onto an object of interest (e.g. tissue, calibration phantom) and the reflected light is imaged with a camera [37]. Projections are typically made at multiple wavelengths and spatial frequencies (f_x) between 0 mm⁻¹ (DC) and 0.5 mm⁻¹. AC projections are captured at three offset phases (0°, 120°, and 240°) and demodulated to obtain a single AC image using established algorithms [36]. In this work, the DC and AC demodulated images were corrected for height and angle of the object surface respectively using a previously developed height-correction algorithm and a modified Lambertian Correction (MLC) angle correction algorithm [38, 39]. The instrument response is then removed from the demodulated images (M_ac) through the use of a calibration phantom with known OPs. A Monte-Carlo (MC) based or analytical forward model is used to extract the diffuse reflectance (R_d) of the calibration phantom from known OPs at each measurement wavelength [36]. This allows sample R_d maps to be extracted using Eq. (1), where subscripts sample and phantom refer to the tissue and calibration phantom, respectively.

$$R_{d\_sample}(f_x)=\frac{M_{ac\_sample}(f_x)}{M_{ac\_phantom}(f_x)}{R}_{d\_phantom}(f_x)$$ (1)

Tissue R_d maps are generated at each f_x and wavelength and represent the turbid media optical Modulation Transfer Function (MTF). The tissue MTF is used as input to an inverse model to extract OPs on a pixel-by-pixel basis. For this study, a two-f_x-look-up table (LUT) based inverse model was used to extract maps of μ_a and μ_s` for each of the acquisition wavelengths. The LUT was generated using a single white MC simulation [40].

The μ_a values extracted at each measurement wavelength were used to determine tissue chromophore concentrations using the Beer-Lambert Law, as shown in Eq. (2). This equation utilizes the measured μ_a values as well as known chromophore extinction coefficients, ε(λ), for oxyhemoglobin (HbO₂) and deoxyhemoglobin (Hb) [41], and is generated for each measured wavelength and solved as a linear system of equations to yield tissue-level chromophore concentrations of HbO₂ and Hb. From these, total hemoglobin content (THb: HbO₂ + Hb) and oxygen saturation (StO₂: HbO₂ /THb × 100) are also determined [9]. Wavelength dependent μ_s` data was fit to a power law using a least squares fitting approach to extract scattering amplitude (a) and scattering slope (b) for each spatial location within the FOV, as shown in Eq. (3). A reference wavelength, λ_o, of 800 nm was used for the power law fitting.

$${\mu }_a(\lambda )={\epsilon }_{Hb{O}_2}(\lambda )C_{Hb{O}_2}+{\epsilon }_{Hb}(\lambda )C_{Hb}$$ (2)

$${\mu }_s`(\lambda )=a{(\raisebox{1ex}{$\lambda $}\!\left/ \!\raisebox{-1ex}{${\lambda }_o$}\right.)}^{-b}.$$ (3)

For this study, the OxImager RS SFDI system (Modulated Imaging Inc., Irvine, CA) was used for all measurements, and is shown in Fig. 1 (left). For this system, light patterns were projected onto a 15 cm × 20 cm FOV, which typically accommodated up to 3 mice at a time. Mice were imaged on a diffuse silicone background phantom. Five spatial frequencies (f_x = 0, 0.05, 0.1, 0.15 and 0.2 mm⁻¹), and four wavelengths (659, 691, 731 and 851 nm) were collected sequentially. Each SFDI measurement was repeated thrice and averaged to minimize breathing artifacts. Typical acquisition times were less than 1.25 minutes for this setup. Raw imaging data was processed using a custom Matlab code that performed demodulation, height and angle corrections, calibration, optical property extractions, and chromophore extractions. Data processing took approximately two minutes for each measurement.

Fig. 1.

SFDI setup for mouse imaging (left), schematic (middle) and setup (right) of tilt measurements.

2.2 Selection of spatial frequencies

The choice of SFDI spatial frequencies is important for accurate separation of absorption and scattering. Generally, DC and lower spatial frequencies are sensitive to both absorption and scattering, while higher spatial frequencies are preferentially sensitive to scattering. Additionally, the effective photon penetration depth δ`_eff, is a function of spatial frequency, and higher spatial frequencies probe more shallow tissue depths [36]. Loosely speaking, if both very low and very high spatial frequencies are used to extract optical properties, partial volume effects may cause errors in OP and chromophore extractions if the measured tissue is not homogeneous in depth. The methods outlined here were designed to determine a two frequency pair that balances accurate OP extractions while minimizing the difference between the two frequencies, and subsequently the difference in probing depth.

A range of spatial frequencies was tested for their ability to accurately extract OPs using a two-f_x-LUT. For all tests, DC (f_x = 0 mm⁻¹) was paired with a second, higher AC spatial frequency (f_x = 0.025, 0.05, 0.1, 0.15, 0.2, 0.3, or 0.5 mm⁻¹). Each combination of DC and AC spatial frequency was compared over a physiologically relevant range of OPs. First, a μ_a and μ_s` pair was chosen. Then, the forward LUT model was used to determine R_d values at the DC and AC spatial frequencies. Next, Gaussian noise was added to these R_d values to simulate experimental measurement noise. Then the two-f_x-LUT was used to back calculate the OP pair. Error was calculated between the original and the estimated OP pair. This process was iterated 1000 times for each OP pair (4 total) and each spatial frequency pair (7 total). The average OP error was calculated and compared for all of the f_x pairs tested and over the range of OPs.

The magnitude of the added Gaussian noise at each spatial frequency was determined by taking 10 repeat measurements on 3 different tumors from 3 different mice, and calculating the average standard deviation in R_d over the 4 measurement wavelengths. The noise levels from DC and four AC spatial frequencies (0.05, 0.1, 0.15, and 0.2 mm⁻¹) were fit to an exponential curve, and fit and extrapolated noise values were then used as estimates of noise for all eight spatial frequencies. OPs were chosen from 10 evenly distributed μ_a values (0.003 - 0.055 mm⁻¹) and 10 μ_s` values (0.5 - 3 mm⁻¹); this range in OPs was based on tumor OP measurements from 3 mice measured with SFDI at 47 longitudinal time points over 45 days.

2.3 Spectral chromophore fitting

The agreement in broadband spectral fits to the four extracted μ_a values was calculated for a set of pixels in several tumor measurements to confirm the ability to accurately fit HbO₂ and Hb. First, HbO₂ and Hb tissue concentrations were determined using the Beer-Lambert Law and the four μ_a values, as described in section 2.1. Then, these HbO₂ and Hb tissue concentrations were multiplied by their corresponding extinction spectra; this was done for every nm increment from 600 to 1000 nm. Tissue μ_a values at each of these wavelengths was determined by summing the μ_a contribution from both HbO₂ and Hb, providing a broadband tissue μ_a spectrum. This μ_a spectrum was plotted with the original four μ_a values, and the % difference between these values at the 4 wavelengths was determined. This same procedure was repeated for scattering, using the a and b scattering parameters to generate the broadband μ_s` spectrum (see Eq. (3)). This procedure is useful for confirming chromophore fitting and for finding outliers in OP extractions.

2.4 Average tumor values and intratumor heterogeneity

For analysis of all mouse tumor data, an ROI was manually chosen over the tumor. This ROI was chosen from the extracted μ_a map; pixels at the extreme edge of the tumor were excluded. A software mask was used to keep only pixels at or below a 70° angle relative to the to the camera axis. This angle mask typically rejected less than 10% of pixels within a tumor ROI. The 70° threshold was chosen based on the working range of the angle correction algorithm [39]. Additionally, pixels with very low μ_a values (μ_a < 0.0001 mm⁻¹) were also masked. The average and standard deviation of all remaining pixels within a tumor ROI were calculated for all SFDI parameters, namely μ_a, HbO_2, Hb, THb, StO₂, μ_s`, a, and b.

Average tumor values and intratumor heterogeneity in SFDI parameters were assessed using 25 tumor data from 13 different mice measured at baseline (prior to any treatment). For average values, first the mean parameter value over each tumor ROI was calculated. Then the average and standard deviation of these values was calculated over the 25 tumors to get typical values and ranges for this xenograft tumor model. For intratumor heterogeneity, first, the % standard deviation was determined for each tumor ROI. Then, the mean tumor heterogeneity was calculated over the 25 tumors. The average tumor values are useful for comparisons to other literature values, and the heterogeneity quantifies the variation in SFDI parameters within single tumors and provides a context for which longitudinal changes can be analyzed.

2.5 Repeatability

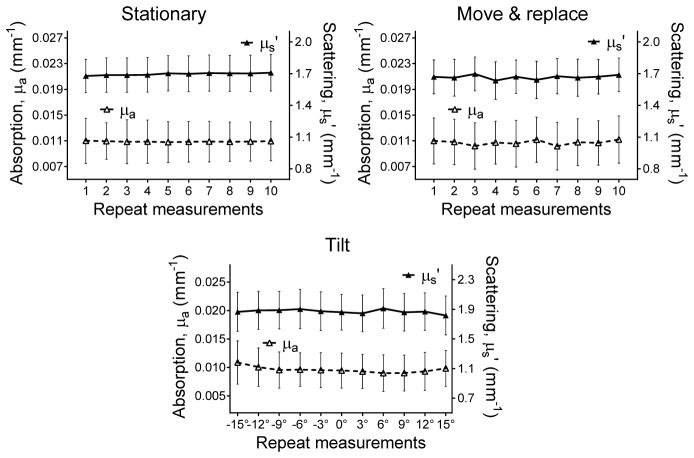
High measurement repeatability is essential for high quality longitudinal chemotherapy monitoring studies. Repeat measurements were taken on individual mouse tumors under a variety of conditions to assess device and user procedure repeatability. To evaluate device repeatability, 10 repeat measurements were taken on individual tumors without making any changes in the instrument or experimental setup between measurements. This condition will be referred to as stationary. User repeatability was assessed in two ways. First, 10 repeat measurements were taken with the mouse removed from the imaging FOV and replaced in similar manner after each measurement. This condition will be referred to as move & replace. Secondly, to assess the effects of angular changes in mouse position between measurements, similar to those which might unintentionally occur during the course of a longitudinal study, a custom made tilting platform was used to collect 11 repeat measurements on individual tumors tilted at 11 different angles (0°, ± 3°, ± 6°, ± 9°, ± 12°, ± 15°) with respect to horizontal, as shown in Fig. 1 (middle and right). The tumor was carefully placed at center of rotation of the tilting platform. Then, the platform was gradually tilted to higher angles, one side at a time. This condition will be referred to as tilt.

In the case of stationary measurements, the tumor ROIs and all data analysis procedures were kept identical for all repeat measurements. For move & replace and tilt measurements, each repeat measurement was treated as a separate and unique measurement, and a separate ROI was manually chosen each time. The ROI area between repeat measurements were kept within approximately ± 150 total pixels of each other to ensure that variations over measurements were not dominated by different ROI selection sizes.

For each of the repeat measurement conditions, the variation in OPs was determined by evaluating the % standard deviation of the mean ROI values. This was done for n = 12 tumors for stationary, n = 12 tumors for move & replace and n = 10 tumors for tilt. The average % standard deviation was calculated over the four wavelengths for all tumors. For tilt measurements, average variations were determined over all tilt angles (up to ± 15°), over the first 7 angles (up to ± 9°), and over the first 5 angles (up to ± 6°).

2.6 Mouse tumor xenograft

The PC3/2G7 prostate tumor xenograft model was used for all tumor experiments [5]. PC3/2G7 cells were grown and expanded at 37°C in a humidified 5% CO₂ atmosphere in RPMI-1640 culture medium containing 7% fetal bovine serum, 100 Units/ml penicillin and 100 μg/ml streptomycin cells were split in 1:3 or 1:4 when cells reached 70-80% confluence to maintain holoclone-forming ability (approximately one passage every 3 days). Severe combined immunodeficient (SCID) hairless outbred mice (SHO MouseCrl:SHO-PrkdcscidHrhr), age 5 to 6 weeks old (21-23 gram), were purchased from Charles River Laboratories, and housed in the Boston University Laboratory Animal Care Facility in accordance with an institutionally approved protocol and federal guidelines. Autoclaved cages containing food and water were changed once a week. Mouse body weight was measured every 3 to 4 days.

On the day of tumor cell inoculation, 4 × 10⁶ PC3/2G7 cells were injected on one or two posterior flanks subcutaneously in 0.2 ml serum-free RPMI using a U-100 insulin syringe with a 28.5 gauge needle. Tumor length (L) and width (W) was measured daily starting from 5 days before treatment, every 3 days during treatment, and twice weekly after treatment using digital calipers (VWR International). Tumor volume was calculated as Vol = (π/6) × (L × W)^3/2. When average tumor volume reached ~500 mm³, mice were treated with either the cytotoxic anticancer drug CPA or the antiangiogenic agent DC101, both given i.p. CPA interferes with DNA replication by forming DNA crosslinks, whereas DC101 is an antagonist monoclonal antibody to mouse VEGF receptor 2 (VEGFR-2). Mice were given CPA on a metronomic schedule at a dose of 140.3 mg/kg every 6 days for 3 cycles. DC101 was administered at a dose of 28.6 mg/kg every 3 days for 6 cycles. CPA was purchased from Sigma Chemical Co. (St. Louis, MO), and DC101 was a gift from Eli Lilly and Company, Indianapolis, Indiana. During SFDI measurements, mice were anesthetized using isoflurane by inhalation (5% induction); except for tilt measurements when mice were anesthetized using ketamine at 50-100 mg/kg + xylazine at 10-15 mg/kg. Mice were euthanized as they approached the tumor size limit according to the approved protocol.

2.7 Longitudinal monitoring of tumor xenografts

SFDI was used to measure tumors in two mice, one treated with CPA and one with DC101. Mice were treated longitudinally for a total of 57 days, including 5 timepoints during the 17 days of tumor growth. SFDI measurements were taken everyday during the 18 days of treatment, and every 2 days during the 22 days after treatment (tumor growth rebound period). In addition to general data processing steps as described in subsection 2.1, a fine tuning algorithm was applied to tissue R_d maps prior to OP extraction. This fine tuning algorithm was developed to correct for changes in system response during warm-up, which we found cause as much as a 5% change in OPs measured at 659 nm in the first 40 minutes the system was powered on. This algorithm relies on the fact that same background imaging phantom was used for all mouse measurements. The R_d of this phantom at all relevant wavelengths and spatial frequencies was determined by an SFDI measurement taken after the system stabilized over a 2-hour timeframe. These R_d values were then used as a gold standard to fine-tune R_d extractions with each imaging field for all mouse measurements. For each new measurement during a longitudinal study, the extracted R_d values at each wavelength and spatial frequency were compared to the gold standard R_d values, and small variations were corrected using Eq. (4).

$$R_{d\_fine\_tuned}(x,y,wv,f_x)=R_d(x,y,wv,f_x)\frac{R_{d\_gold\_s\tan dard}(wv,f_x)}{R_d{(wv,f_x)}_{ROI}}.$$ (4)

Here, R_{d_gold_standard} (wv, f_x) are the average R_d values of the background phantom measured after 2 hours of instrument warmup over a 100 × 150 pixel ROI. R_d (wv, f_x)_ROI is the current measurement R_d, extracted from the average values over the same 100 × 150 pixel ROI on the background phantom. R_d (x, y, wv, f_x) is the uncorrected R_d values at each pixel in the FOV, and R_{d_fine tuned} (x, y, wv, f_x) are the corrected, or fine tuned, R_d values at each pixel in the FOV. The fine tuning algorithm was evaluated by taking 25 repeat phantom measurements over a 41 day period. Optical property precision values were calculated with and without fine tuning.

3. Results

3.1 Selection of spatial frequencies

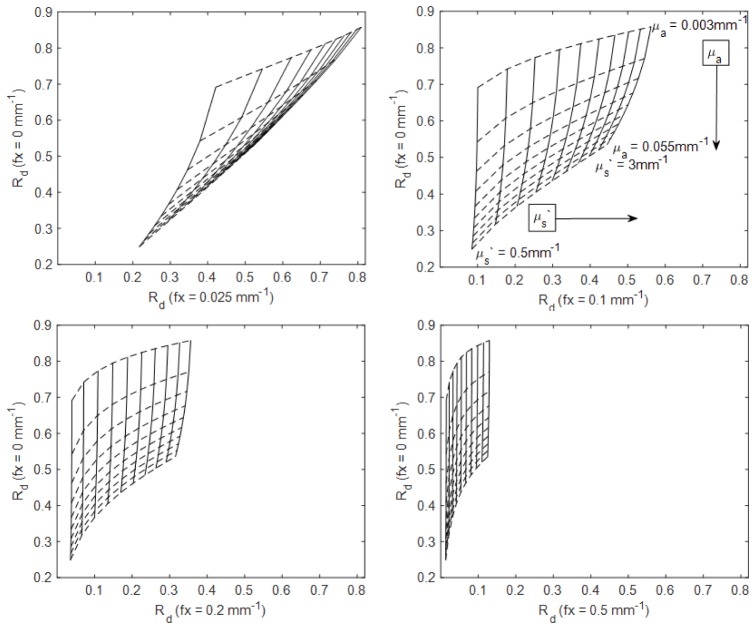
In order to visualize how different choices of SFDI spatial frequencies affect the accuracy of optical property extractions, a range of spatial frequencies was tested using simulated data. Figure 2 shows visualizations of four different two-f_x-LUT’s. For each, the horizontal axis represents R_d at DC (f_x = 0 mm⁻¹) and the vertical axis represents R_d at an AC frequency (f_x = 0.025, 0.1, 0.2, or 0.5 mm⁻¹). R_d values are plotted for 10 evenly distributed μ_a values (0.003 – 0.055 mm⁻¹) and 10 evenly distributed μ_s` values (0.5 - 3 mm<sup>−1</sup>). Differences in the orthogonality of the LUT’s are visually apparent, and in some cases there is significant coupling between μ<sub>a</sub> and μ<sub>s</sub>` (e.g. Fig. 2. top left). In cases where OP isolines collapse on each other the sensitivity to small errors in R_d measurements is likely to manifest as a large error in OP extractions.

Fig. 2.

Two-fx-LUT’s using 10 evenly distributed μ_a values (0.003 – 0.055 mm⁻¹) and 10 evenly distributed μ_s` values (0.5 - 3 mm⁻¹) for DC and 0.025 mm⁻¹ (top left), DC and 0.1 mm⁻¹ (top right), DC and 0.2 mm⁻¹ (bottom left), DC and 0.5 mm⁻¹ (bottom right) f_x pairs.

Figure 3 shows OP extraction errors induced by noise added to R_d values in simulation for seven different choices of SFDI spatial frequency pairs. Errors are shown for four different OP pairs representing the four quadrants of the LUT in Fig. 2. In all cases, relatively high OP extraction errors occurred when DC was paired with a low AC f_x (e.g. 0.025 mm⁻¹, 0.05 mm⁻¹). For this study, DC and 0.1 mm⁻¹ were chosen for all subsequent OP extractions. OP extractions errors were low for this pair (< 2.4% for the range of OPs tested), and this pair minimized depth probe differences better than combinations that included a higher AC f_x.

Fig. 3.

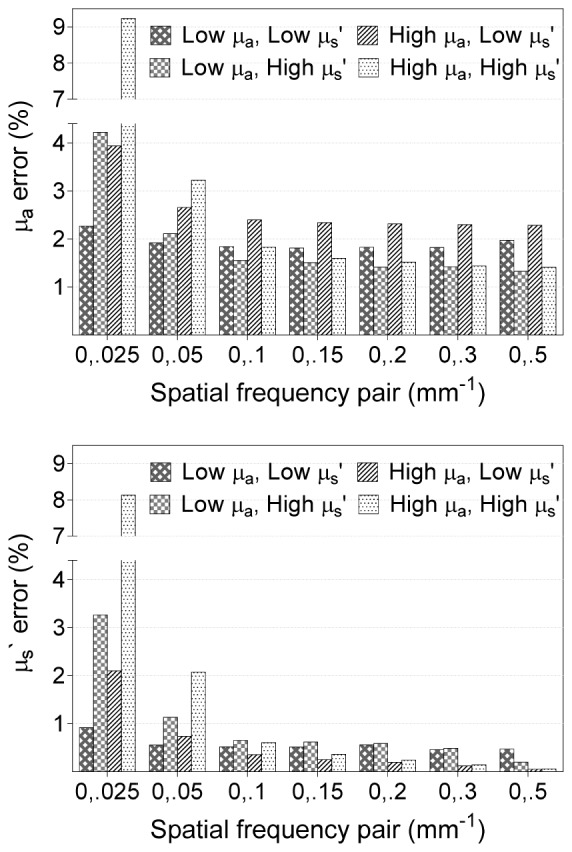
Extraction error of μ_a (top) and μ_s` (bottom), where low μ<sub>a</sub> = 0.005 mm<sup>−1</sup>, low μ<sub>s</sub>` = 0.73 mm⁻¹, high μ_a = 0.035 mm⁻¹, and high μ_s` = 1.89 mm⁻¹.

3.2 Spectral fitting

Figure 4 (top right and bottom right) shows μ_a and μ_s` values extracted at the four SFDI acquisition wavelengths as well as the broadband μ<sub>a</sub> and μ<sub>s</sub>` spectra after chromophore fitting and power law fitting, respectively. Data is shown for a single pixel located on the tumor of a mouse treated with the antiangiogenic agent DC101. Figure 4 (top left and bottom left) displays the pixel location, on the same tumor, at a pretreatment (baseline) and a posttreatment timepoints (day 32 after initial DC101 injection, 17 days after the final DC101 injection). In general, there was good agreement between the extracted μ_a and μ_s` values and the broadband fits. Fitting errors were less than 5% for μ<sub>s</sub>` in all tumors measured. Fitting errors for μ_a ranged between 5% up to 20%, with larger errors often observed at 731 nm. Overall absorption throughout the measured spectral range decreased by posttreatment compared to baseline, whereas scattering amplitude increased. This was a common trend for most measured tumors. It should be noted that lipids and water were not included as chromophores in this study, and therefore μ_a values are likely underreported in the 900-1000 nm range in Fig. 4.

Fig. 4.

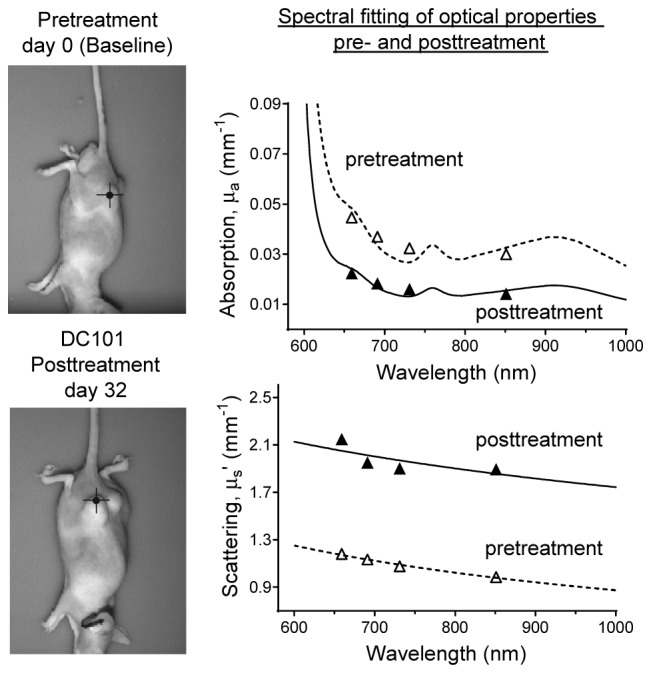
Locations of pixels on a DC101-treated tumor at pretreatment (top left) and posttreatment (bottom left) timepoints. Broadband fitting of absorption (top right) and scattering (bottom right) for pre- and posttreatment timepoints.

3.3 Average tumor values and intratumor heterogeneity

Table 1 shows the average tumor values measured over 25 tumors from 13 mice. All measurements were taken prior to any drug treatment. The average tumor volume for the 25 tumors was 801 mm³ ± 785 mm³.

Table 1. Average SFDI parameters for tumors.

SFDI acquired parameters	Tumor Average ± std
a	0.9 ± 0.1 mm−1
b	0.7 ± 0.1
HbO2	69.8 ± 18.7 µM
Hb	45.1 ± 5.3 µM
THb	114.9 ± 22.3 µM
StO2	59. 9 ± 5.1%

Table 2 shows the percent intratumor heterogeneity in SFDI parameters measured over 25 tumors from 13 mice. Tumor heterogeneity was approximately 9-10% for OPs at all wavelengths. Heterogeneity was higher (15.1%) in the b parameter, and substantially lower (3.7%) in StO₂. In order to explore what effect tumor size has on heterogeneity, the largest five and smallest five tumors were analyzed separately. The largest five tumors had an average volume of 2023 mm³ ± 722 mm³ and the smallest five had an average volume of 181 mm³ ± 76 mm³. Heterogeneity in optical properties in the largest tumors was 11.0% on average compared to 8.4% for the smaller tumors. StO₂ heterogeneity was 4.3% in the largest tumors compared to 2.6% in the smallest tumors. These average and heterogeneity values can help provide context to any observed longitudinal changes in future studies.

Table 2. Intratumor heterogeneity.

SFDI acquired parameters			Average Tumor Heterogeneity
μa	wavelength	659 nm	9.0 ± 2.7%
		691 nm	9.3 ± 3.0%
		731 nm	9.6 ± 3.3%
		851 nm	9.7 ± 3.6%
μs`	wavelength	659 nm	9.2 ± 2.9%
		691 nm	9.3 ± 3.0%
		731 nm	9.3 ± 3.0%
		851 nm	9.8 ± 3.2%
a			9.5 ± 3.1%
b			15.1 ± 4.6%
HbO2			11.6 ± 4.6%
Hb			9.3 ± 2.7%
THb			9.6 ± 3.6%
StO2			3.7 ± 1.9%

3.4 Repeatability

Figure 5 shows example μ_a and μ_s` extractions at 851 nm for a representative tumor for 10 stationary, 10 move & replace, and 11 tilt repeat measurements. Small changes in OPs were observed during stationary repeat measurements; this example had a precision of 0.57% and 0.61% for μ<sub>a</sub> and μ<sub>s</sub>`, respectively. There was slightly larger variability for the move & replace measurements, with precisions of 3.30% and 1.13%. For tilt measurements, the precision was 5.51% and 1.42%, but improved when only the first 7 tilt angles (0 to ± 9°), were analyzed (precision = 2.75% and 1.30%), or first 5 tilt angles (0 to ± 6°) were analyzed (precision = 2.61% and 1.49%).

Fig. 5.

Absorption (left axis) and scattering (right axis) at 851 nm for a representative tumor over 10 stationary (top left), 10 move & replace (top right), and 11 tilt (bottom) repeat measurements.

Table 3 shows average precision (repeatability) values from 8 mice for stationary (n = 12 tumors), move & replace (n = 12 tumors), and tilt conditions (n = 10 tumors). In general, high repeatability (precision ≤ 5.2%) was achieved for most repeat measurements except for those conducted at tilt angles larger than 9°. High repeatability for stationary measurements helps to confirm instrument stability. High precision for move & replace measurements helps to confirm the repeatability of the user to position and image the mouse in a similar manner. High precision in the tilt measurements helps to confirm that even with small changes in the placement of the mouse, repeatable longitudinal measurements are possible. Taken together, these results suggest OP changes larger than a few percent observed over the course of a longitudinal study are likely to be from intrinsic changes in the tumor rather than from small changes in instrument or user procedures. The tilt results suggest that care should be taken to position the animal/tumor as consistently as possible during each imaging session.

Table 3. Repeatability (Precision).

Optical Properties	Average repeatability
	Stationary n = 12	Move & replace n = 12	Tilt n = 10
			0 to ± 15°	0 to ± 9°	0 to ± 6°
µa	1.88%	3.52%	10.14%	5.22%	4.44%
µs`	0.98%	2.30%	3.70%	2.43%	2.13%

3.5 Longitudinal monitoring of tumor xenografts

The fine tuning algorithm improved measurement precision by as much as 17-fold. The measurement precision at 659 nm improved from 3.1% to 0.3% for μ_a, and from 1.7% to 0.1% for µ_s` with the use of the fine tuning algorithm over 25 repeat phantom measurements. Fine tuning was used for all longitudinal mouse measurements.

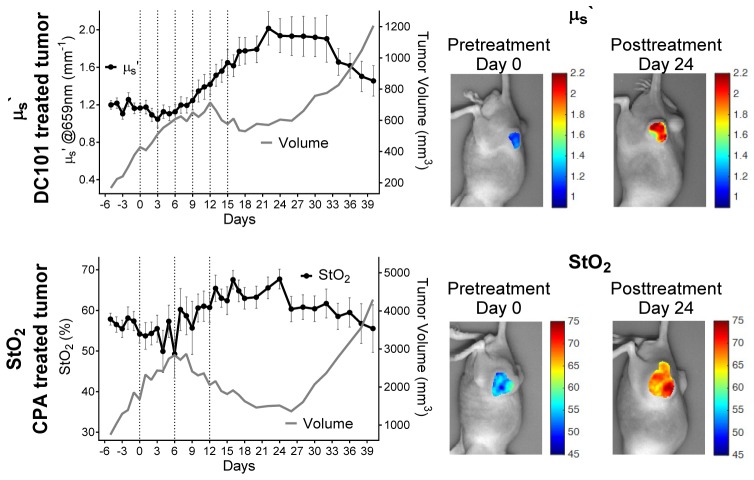
Two mice were tracked longitudinally during the course of chemotherapy as a proof-of-principle demonstration of SFDI for treatment monitoring. Figure 6 (top left) shows changes in tumor μ_s` at 659 nm from a single tumor over the course of 45 days. This mouse received the antiangiogenic DC101 (6 total injections; injections were given every 3 days, injection dates are indicated by the vertical dashed lines). The mean and standard deviation of μ<sub>s</sub>` values extracted over a manually chosen ROI are shown. Tumor volume measurements are shown for reference. During treatment, the average tumor μ_s` increased by approximately 50%. This upward trend continued until treatment ~day 22, with a maximum increase of approximately 70% from baseline, followed by a substantial decrease. These trends do not appear to be related only to tumor volume changes, as μ<sub>s</sub>` both increases and decreases during periods of tumor growth. It is plausible that the change from decreasing to increasing μ_s` at day 3 is predictive of treatment response, but this must be confirmed with additional studies. Figure 6 (top right) shows tumor μ<sub>s</sub>` colormaps overlaid on a planar mouse image at day 0 and day 24. Substantial changes in μ_s` values are apparent throughout the tumor region at these timepoints.

Fig. 6.

μ_s` (left axis) and tumor volume (right axis) over days of DC101 treated tumor (top left), μ<sub>s</sub>` colormaps overlaid on the DC101 treated planar mouse image at day 0 and day 24 (top right), StO₂ (left axis) and tumor volume (right axis) over days for CPA treated tumor (bottom left), StO₂ colormaps overlaid on the CPA treated planar mouse image at day 0 and day 24 (bottom right).

Figure 6 (bottom left) shows tumor StO₂ changes during the course of treatment. This mouse was treated with CPA (3 total injections; injections were given every 6 days), followed by a rebound period. In this tumor, StO₂ initially appears to decrease during rapid tumor growth, but then increases by approximately 25% compared to baseline as CPA treatment takes effect. StO₂ decreases again during the treatment rebound stage correlating with rapid tumor growth. Figure 6 (bottom right) shows the substantial increase in StO₂ from day 0 to day 24. Again, these changes are apparent throughout the tumor area.

In the future, larger animal studies will be conducted and trends in SFDI derived parameters will be analyzed for their ability to indicate response, rebound, and resistance prior to tumor volume changes, with the long term goal of using this technique to guide single and multi-agent cancer treatment regiments.

4. Discussion and conclusion

Diffuse Optical Imaging is a promising in vivo technique for clinical tumor therapy monitoring in cancer patients [14, 18]. The development of complementary preclinical imaging modalities that can track the same optical markers may allow for the exploration of more advanced treatment regimens, multi-agent therapy scheduling, and a better understanding of the biological underpinnings of treatment effects. Towards this aim, the current study demonstrated the feasibility of using SFDI to measure mouse tumor xenografts with high repeatability and to longitudinally monitor therapy efficacy. High in vivo measurement precision was demonstrated using a two-frequency LUT inverse model. Average OP and chromophore values, as well as intratumor heterogeneity were reported for a highly vascularized subcutaneous xenograft prostate tumor model. A proof-of-concept longitudinal study demonstrated that SFDI was able to track changes during treatment and rebound with both the cytotoxic drug CPA and the antiangiogenic agent DC101. In general, tumor OP values showed contrast between pre- and posttreatment days, and the changes in optical parameters tracked were substantially larger than the variation expected from instrument precision, measurement-to-measurement differences in mouse positioning, and intratumor heterogeneity.

Several important SFDI acquisition parameters and measurement procedures were tested in this study, including the choice of spatial frequencies for OP extractions, and the effects of instrument and repositioning errors for repeat measurements. For spatial frequency comparisons, various f_x pairs were tested for accuracy in OP extractions. While all f_x pairs tested provided <10% OP extractions errors, it was found that combinations of DC plus low (0.025 mm⁻¹ and 0.05 mm⁻¹) AC f_x choices produced larger relative extraction errors. For this study, the DC plus 0.1 mm⁻¹ pair was chosen for all data analysis based on small extraction errors (~2.4%) and the avoidance of partial volume probing effects likely to occur from the use of more disparate f_x pairs. While higher dimension LUTs could accommodate more spatial frequencies in the inversion process, the use of only a pair minimizes data acquisition time, which may reduce breathing motion artifacts, reduce the time mice are under anesthesia, and reduce user burden, which can be substantial for studies incorporating multiple treatment groups over long timescales (i.e. months).

Instrument and user placement repeatability were generally high (precision ≤5.2%) for all tested cases except for measurement at large tilt angles ( ± 15°) where μ_a precision was as high as 10%. This is likely due to the capture of a different tumor field-of-view at large tilt angles. Tumor heterogeneity is a well-known phenomenon [42, 43] and intratumor heterogeneity was shown to be as high as 10% for optical properties extractions in this study. Measurement of a different region of the same tumor is likely to yield different results, suggesting that care must be employed when positioning mice for repeat measurements.

Broadband μ_s` power-law fitting errors were typically small (<5%) and broadband chromophore μ_a fits were also generally small, except at 731 nm, where μ_a fitting errors typically ranged from 15% to 20%. These errors may occur in part due to spectral bandwidth of the LED source (~20 nm), which spans the dip in the Hb extinction coefficient near 731 nm [41]. Although the choice of acquisition wavelengths was not tested here, it was previously shown that 670 nm and 850 nm is an optimal two-wavelength choice for oxy- and deoxyhemoglobin extraction using SFDI [44]. These wavelengths closely match two of the four wavelengths used in this study (i.e. 659, 691, 731, and 851 nm).

Despite expected variation in metabolism, vascular density, and tissue architecture between different murine tumor models, baseline optical property and chromophore values reported here are in agreement with several other small animal tumor values reported in the literature. For example, the average baseline μ_s` value at 630 nm was found to be 1.064 mm<sup>−1</sup> (this value was calculated using the average of the a and b values from Table 1 and Eq. (2)). This agrees well with the reported μ<sub>s</sub>` value of 1.048 mm⁻¹ at 630 nm in a radiation-induced fibrosarcoma tumor model in C3H mice measured with a fiber-optic probe-based continuous-wave Diffuse Reflectance Spectroscopy (DRS) system prior to any treatment [45]. Average tumor StO₂ values reported here (59.9 ± 5.1%) were somewhat higher than StO₂ values (40% – 55%) reported in K1735 malignant mouse melanoma subcutaneous tumors measured before treatment by DRS [46]. The increasing trend in both μ_s` and StO₂ during treatment mimics those reported by Karthik et. al. who used a DRS point probe to monitor 4T1 flank tumors (n = 25) treated with a single maximum tolerated dose of doxorubicin over a 13 day treatment period [47]. We hypothesize that changes in SFDI parameters during treatment may be related to a reduction in tumor vasculature and tissue remodeling, but this must be confirmed with future studies. Parameters such as tumor heterogeneity and average optical parameters are specific to the PC3/2G7 xenograft model tested here, and other tumor models are likely to have different properties.

While the results from this study are promising, there are several challenges and limitations to the use of SFDI for small animal imaging. Correction for height and surface angle were essential for accurate optical property extractions due to the small mouse feature size and the large relative surface angles of the tumors; substantial edge artifacts occurred prior to the applications of appropriate corrections [38, 39]. Depth penetration and partial volume effects are also important considerations. In this study, attempts were made to reduce differences in penetration depth by choosing a pair of spatial frequencies that accurately separated absorption and scattering effects while minimizing the difference in spatial frequency and thus depth penetration, but additional modeling studies are needed to better determine the implications of these effects. Tomographic reconstructions using SFDI have previously been demonstrated and would assist in providing depth resolved information for this application in the future [48]. An additional limitation was that only oxy- and deoxyhemoglobin were extracted in this study and there may be prognostically relevant information content in other chromophores including lipids and water. Finally, a better understanding of the biological origins of treatment-induced changes observed in SFDI is necessary to take full advantage of this technique.

In conclusion, SFDI is a promising technique for high precision, longitudinal non-contact and label free metabolic imaging of small animal tumor models. In comparison with intravital techniques including confocal and multiphoton microscopy, SFDI does not require invasive procedures such as skin-flap removal or window chamber implantation, and does not require exogenous agents, parameters which limit their suitability for long term therapy monitoring [49]. SFDI complements other non-invasive diffuse optical techniques such as DRS and Diffuse Correlation Spectroscopy (DCS), which are also under investigation for monitoring hemodynamic response in a variety of preclinical models [46, 47, 50, 51]. In the future, changes in SFDI derived parameters will be analyzed for their ability to predict response, rebound, and resistance prior to anatomic changes in tumor models and the biological origins of these changes will be investigated with ex vivo tissue analysis. In the long term, the use of SFDI to develop adaptive therapies in small animals may support new opportunities for clinical DOI implementation, and help establish these techniques as important feedback methods during cancer treatment.

Funding

The authors gratefully acknowledge funding from the American Cancer Society (Grant RSG-14-014-01-CCE) and Cross-disciplinary Training in Nanotechnology for Cancer (XTNC) 2014-2015.