Toward Polarizable AMOEBA Thermodynamics at Fixed Charge Efficiency Using a Dual Force Field Approach: Application to Organic Crystals

Abstract

First principles prediction of the structure, thermodynamics and solubility of organic molecular crystals, which play a central role in chemical, material, pharmaceutical and engineering sciences, challenges both potential energy functions and sampling methodologies. Here we calculate absolute crystal deposition thermodynamics using a novel dual force field approach whose goal is to maintain the accuracy of advanced multipole force fields (e.g. the polarizable AMOEBA model) while performing more than 95% of the sampling in an inexpensive fixed charge (FC) force field (e.g. OPLS-AA). Absolute crystal sublimation/deposition phase transition free energies were determined using an alchemical path that grows the crystalline state from a vapor reference state based on sampling with the OPLS-AA force field, followed by dual force field thermodynamic corrections to change between FC and AMOEBA resolutions at both end states (we denote the three step path as AMOEBA/FC). Importantly, whereas the phase transition requires on the order of 200 nsec of sampling per compound, only 5 nsec of sampling was needed for the dual force field thermodynamic corrections to reach a mean statistical uncertainty of 0.05 kcal/mol. For five organic compounds, the mean unsigned error between direct use of AMOEBA and the AMOEBA/FC dual force field path was only 0.2 kcal/mol and not statistically significant. Compared to experimental deposition thermodynamics, the mean unsigned error for AMOEBA/FC (1.4 kcal/mol) was more than a factor of two smaller than uncorrected OPLS-AA (3.2 kcal/mol). Overall, the dual force field thermodynamic corrections reduced condensed phase sampling in the expensive force field by a factor of 40, and may prove useful for protein stability or binding thermodynamics in the future.

Graphical Abstract

Introduction

Organic molecular crystals play a central role in chemical, material, pharmaceutical and engineering sciences.^1–4 First principles prediction of their structure^5–9, thermodynamics^{10, 11} and solubility^{12, 13} is a challenge for both potential energy functions and sampling methodologies.^{14, 15} For example, it has been shown that classical force fields based on fixed atomic partial charges (FC), such as Amber¹⁶, CHARMM¹⁷ and OPLS-AA¹⁸, lack the accuracy needed to correctly rank the relative stability of alternative polymorphs.^{19, 20} To achieve sufficient accuracy for crystal structure prediction, atomic multipole expansions can be used to systematically reproduce the electrostatic potential outside the van der Waals surface of a rigid molecule, as defined by electronic structure calculations.^{21, 22} However, molecular charge distributions are sensitive to both conformation and the electric field across the molecule, due in part to electronic polarization.²³ Thus, to apply the configurational sampling algorithms needed to quantify thermodynamics, multipolar force fields must address transferability of their multipole moments as a function of molecular conformation, while also consistently treating both intra- and intermolecular polarization.^{23, 24} A few examples of multipolar energy functions include AMOEBA (Atomic Multipole Optimized Energetics for Biomolecular Applications)^24–26, GMM (Gaussian Multipolar Model)^{27, 28}, SIBFA (Sum of Interactions Between Fragments Ab Initio Computed)^{29, 30} and NEMO (Non-empirical Molecular Orbital)³¹, which are described in recent reviews^32–34. The accuracy and transferability improvements of AMOEBA relative to FC force fields have been demonstrated in the context of water^{25, 35}, ion solvation³⁶, the properties of small organic molecules^{24, 26, 36–38} and for protein energetics.^{34, 39}

The increased domain of applicability of advanced multipolar force fields, however, comes at a price of greater computational expense relative to FC force fields by a factor of 5–10 or more for energy and force evaluations. To ameliorate the expense of sampling advanced potential energy functions, previous work to reweight from molecular mechanics (MM) sampling has been explored in the context of determining thermodynamics for quantum mechanical (QM) or QM/MM potential energy surfaces.^40–49 Recent work includes the dual-topology alchemical Hamiltonian replica exchange method (DTA-HREM)^50–52, non-Boltzmann Bennett (NBB) reweighting^53–55, and the multistate Bennett acceptance ratio (MBAR)^{56, 57} approaches. The emergence of increasingly sophisticated polarizable atomic multipole force fields for organic molecules and proteins further motivates approaches that either reweight FC trajectories or define a path that smoothly connects FC states to those defined by a more advanced multipolar force field.

Perhaps the simplest approach to computing the free energy difference between FC and more advanced force fields, such as AMOEBA, is direct reweighting via the Zwanzig relationship

$$\mathrm{\Delta }{G}_{\text{FC}\to \text{AMOEBA}}=-k_{B}T·ln{\langle e^{-\frac{E_{\text{AMOEBA}}-E_{\text{FC}}}{k_{\mathrm{B}}T}}\rangle }_{\text{FC}}$$ Equation 1

where k_B is Boltzmann’s constant, T is temperature in degrees Kelvin and the angle brackets denote an ensemble average.⁵⁸ This approach evaluates the potential energy of the expensive model only at intermediate samples. The reverse perturbation offers no efficiency improvement due to requiring direct sampling of the more expensive ensemble

$$\mathrm{\Delta }{G}_{\text{AMOEBA}\to \text{FC}}=-{\mathrm{k}}_{\mathrm{B}}T·ln{\langle e^{-\frac{E_{\text{FC}}-E_{\text{AMOEBA}}}{k_{\mathrm{B}}T}}\rangle }_{\text{AMOEBA}}$$ Equation 2

However, convergence of reweighting as shown in Eqs. 1 or 2 may fail due to lack of phase space overlap between force fields, which arises due to differences in bonded terms (i.e. equilibrium bond distances or bond angles) and/or intermolecular contact distances (i.e. due to the balance of van der Waals and Coulombic interactions)^{59, 60}. Phase space overlap between resolutions can be improved by coordinating their design and parameterization^60–62.

Here we explore an approach that performs more than 95% of the sampling using an inexpensive fixed charge force field, followed by the addition of two rigorous corrections to recover thermodynamics consistent with the more advanced force field. The method mitigates nontrivial differences between force fields by defining a dual force field (DFF) potential that enables explicit sampling of the transition between resolutions

$$U_{\text{DFF}}(\lambda ,\mathbf{X})=\lambda ·U_{\text{AMOEBA}}(\mathbf{X})+(1-\lambda )·U_{\text{FC}}(\mathbf{X})$$ Equation 3

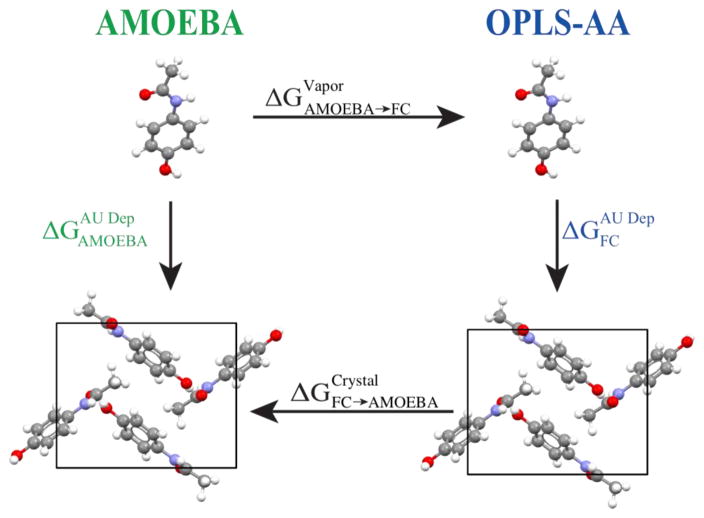
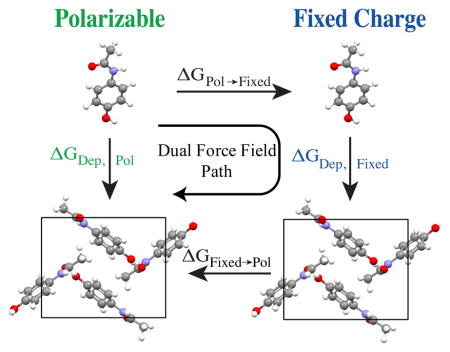
where U_DFF defines a smooth transition between the fixed charge energy function at λ =0 and the polarizable AMOEBA energy function at λ =1. Calculation of free energy differences due to force field resolution changes at both vapor and crystalline end states permits the computationally demanding sublimation/deposition phase transition to be sampled with the inexpensive force field (Figure 1). The approach has similarities to “dual topology” style potential energy functions, which smoothly interpolate between chemical functional groups⁶³.

Figure 1.

This diagram summarizes the thermodynamic cycle for computing absolute deposition free energy at the accuracy of the polarizable AMOEBA force field, but with an efficiency approaching the fixed atomic partial charge OPLS-AA force field. The vertical sublimation/deposition phase transition steps each require ~200 nsec of sampling while the horizontal steps to change resolution converge in only 5 nsec. This equates to a factor of 40 reduction in the amount of condensed phase AMOEBA sampling required.

Using five organic compounds, we show that the DFF approach defines a thermodynamic path that is more efficient than direct simulation in AMOEBA, but maintains its agreement with experiment in the context of calculating absolute sublimation/deposition phase transitions. OPLS-AA^{18, 64} and AMOEBA^24–26 were used as the fixed charge (i.e. cheap) and polarizable multipole (i.e. expensive) force fields, respectively, as implemented in the open source Force Field X (FFX) software package (http://ffx.biochem.uiowa.edu)^65–67 version 1.0.0-beta. Overall, the DFF interpolation between resolutions exhibits rapid convergence relative to the phase transition and allows decreased condensed phase sampling in the expensive potential by a factor of 40 for a thermodynamic path characterized by Growth of the Asymmetric Unit into a Crystal via alCHemy (GAUCHE) and described previously^{14, 15}. Thus, polarizable atomic multipole AMOEBA thermodynamics are reproduced with an expense approaching that of fixed charge models.

Methods

Lattice Potential Energies

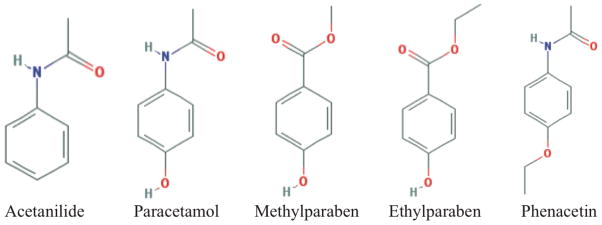
We analyzed five molecules from a prior study on deposition thermodynamics.¹⁵ These compounds are shown in Figure 2 and include acetanilide,⁶⁸ paracetamol (polymorph I),⁶⁹ methyl paraben (polymorph II),⁷⁰ ethyl paraben,⁷¹ and phenacetin.⁷² Experimental lattice parameters and the space group for each compound are given in Table 1, along with asymmetric unit composition and unit cell volume in Table 2. The deposition free energy values from the prior study, computed using AMOEBA directly, will be compared to the three step DFF thermodynamic path that combines FC phase transitions and DFF corrections. Analogous to previous work¹⁵, the five molecules were optimized in the crystalline and vapor states using both the AMOEBA and OPLS-AA force fields within the FFX program. Space group and lattice parameters were constrained to their experimental values (Table 1) for both AMOEBA and OPLS-AA optimizations. AMOEBA parameters were obtained from Poltype³⁸, while OPLS-AA 2005 parameters were obtained from Schrödinger⁷³. To calculate lattice energies, the minimized vapor energy was subtracted from the minimized crystal energy on a per molecule basis.

Figure 2.

The structure of each organic compound.

Table 1.

Compounds studied and their associated CSD reference codes, space groups and unit cell parameters. Roman numerals following paracetamol and methyl paraben correspond to polymorph.

Compound	CSD Code	Space Group	a	b	c	α	β	γ
Acetanilide	ACANIL	Pbca	19.64	9.48	7.98	90	90.0	90
Paracetamol I	HXACAN01	P21/c	11.72	9.40	12.93	90	147.0	90
Methyl Paraben II	CEBGOF03	P21/c	4.82	14.63	10.24	90	99.8	90
Ethyl Paraben	FEGLEI	P21/c	13.76	13.18	11.58	90	125.5	90
Phenacetin	PYRAZB10	P21/c	13.25	9.65	7.81	90	104.9	90

Table 2.

Molecular weight, number of molecules per asymmetric unit (AU), unit cell (UC) volume, number of unit cell molecules, volume per molecule and experimental temperature for each crystal studied.

Compound	Mol. Weight (g/mol)	AU Molecules	UC Vol. (Å3)	Z	Vol./Z (Å3)	Temp. (K)
Acetanilide	135.16	1	1486.1	8	185.8	297
Paracetamol I	151.16	1	776.3	4	194.1	297
Methyl Paraben II	152.15	1	711.3	4	177.8	100
Ethly Paraben	166.17	2	1710.2	8	213.8	297
Phenacetin	179.22	1	965.0	4	241.3	297

$$U_{\text{lattice}}=U_{\text{cryst}}-U_{\text{vac}}$$ Equation 4

A van der Waals cutoff of 12.0 Å was used, with a multiplicative switch tapering the interaction energy to zero starting at 10.8 Å, which is consistent with parameterization of the AMOEBA model for water, organic molecules and proteins^{24, 25, 39}. Polarizable electrostatic evaluations were conducted using a smooth⁷⁴ particle-mesh Ewald⁷⁵ (PME) algorithm for multipoles⁷⁶ which maintained the self-consistent field with a convergence criterion of 10⁻⁵ RMS Debye and supported space group symmetry.⁶⁵ For this work, PME parameters included a real-space cutoff of 9 Å, a mesh density of 2.0 grid points per Å, eighth order B-splines, and an Ewald Parameter of 0.42. The molecules were minimized to a tight RMS gradient convergence criterion of 10⁻⁴ kcal/mol/Å.

Deposition Free Energy and Dual Force Field Corrections

The DFF method, as employed in this work, adds a free energy correction composed of two terms to the deposition free energy calculated using the inexpensive OPLS-AA force field to recover direct AMOEBA thermodynamics, at approximately OPLS-AA efficiency. Consistent with our earlier work on these systems¹⁵, the NVT ensemble was sampled at 298 degrees Kelvin using stochastic dynamics. For each of the three simulation legs, five independent trajectories were collected beginning from different random velocity vectors. The first simulation leg calculates the free energy to change from AMOEBA resolution into OPLS-AA resolution in vapor $\mathrm{\Delta }{G}_{\text{AMOEBA}\to \text{FC}}^{\text{Vapor}}$. Next, the inexpensive potential U_FC(X) is sampled to determine the FC deposition/sublimation phase transition free energy $\mathrm{\Delta }{G}_{\text{FC}}^{\text{Dep}}$. Finally, the last simulation leg calculates the free energy to convert back from OPLS-AA resolution to AMOEBA resolution in the crystal state $\mathrm{\Delta }{G}_{\text{FC}\to \text{AMOEBA}}^{\text{Crystal}}$. Summing the three simulation legs yields the AMOEBA/FC deposition free energy $\mathrm{\Delta }{G}_{\text{AMOEBA}/\text{FC}}^{\text{Dep}}$

$$\mathrm{\Delta }{G}_{\text{AMOEBA}/\text{FC}}^{\text{Dep}}=\mathrm{\Delta }{G}_{\text{AMOEBA}\to \text{FC}}^{\text{Vapor}}+\mathrm{\Delta }{G}_{\text{FC}}^{\text{Dep}}+\mathrm{\Delta }{G}_{\text{FC}\to \text{AMOEBA}}^{\text{Crystal}}$$ Equation 5

Orthogonal Space Sampling of the Thermodynamic Paths

The Orthogonal Space Random Walk (OSRW) method builds up a time-dependent bias by depositing two-dimensional Gaussian-shaped repulsive potentials as a function of the state variable λ and the derivative of the potential energy with respect to λ (F_λ = ∂U/∂λ)^{77, 78}. The total potential energy is then given by

$$U_m=U_{\mathit{DFF}}(\lambda ,\mathbf{X})+f_m(\lambda )+g_m(\lambda ,F_{\lambda })$$ Equation 6

where g_m(λ, F_λ) is the sum of the repulsive potentials (i.e. hills) centered at states given by [λ(t_i), F_λ(t_i)]¹⁴:

$$g_m(\lambda ,F_{\lambda })=\sum _{t_i}h·e^{\left(\frac{{\mid \lambda -\lambda (t_i)\mid }^2}{2w_1^2}\times \frac{{\mid F_{\lambda }-F_{\lambda }(t_i)\mid }^2}{2w_2^2}\right)}$$ Equation 7

The additional biasing dimension promotes crossing of hidden barriers relative to the simpler one-dimensional bias of original metadynamics approaches.^{77, 78} We note that the gradient of U_m (i.e. the partial derivatives with respect to all atomic coordinates), which is needed to integrate equations of motion during OSRW dynamics, requires partial derivatives of the target function U_DFF(λ, X) that include ∂U_DFF(λ, X)/∂λ, ∂²U_DFF(λ, X)/∂λ² and ∂²U_DFF(λ, X)/∂λ ∂X. These are given by

$$\partial U_{\mathit{DFF}}(\lambda ,\mathbf{X})/\partial \lambda =U_{\text{AMOEBA}}(\mathbf{X})-U_{\text{FC}}(\mathbf{X})$$ Equation 8

$${\partial }^2{U}_{\mathit{DFF}}(\lambda ,\mathbf{X})/\partial {\lambda }^2=0$$ Equation 9

and

$${\partial }^2{U}_{\mathit{DFF}}(\lambda ,\mathbf{X})/\partial \lambda \partial X=\partial U_{\text{AMOEBA}}(\mathbf{X})/\partial X-\partial U_{\text{FC}}(\mathbf{X})/\partial X$$ Equation 10

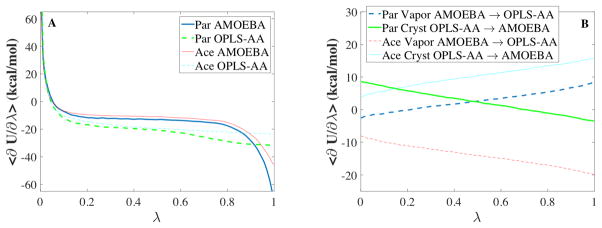
The first two results above (Equations 8 and 9) are the 1^st and 2^nd partial derivatives of the dual force field potential energy (Equation 3) with respect to λ, while the last result (Equation 10) is equivalent to the difference in the partial derivative for each force field with respect to atomic coordinate X. As shown in Figure 3, the ensemble average thermodynamic force 〈 ∂U/∂λ 〉 is smooth and well-behaved as resolutions between the OPLS-AA and AMOEBA force fields are sampled (i.e. for 0 ≤ λ ≤ 1). However, if this had not been the case (i.e. for force fields that are more dramatically different), higher powers of λ could be explored (i.e. in Equation 3 apply the substitution λ → λ²).

Figure 3.

The ensemble average thermodynamic force 〈∂U/∂λ〉 along the depositon path (Panel A) and dual force field paths (Panel B) are shown for paracetamol (Par) and acetanilide (Ace).

Simulations with Non-Crystallographic Symmetry

In cases where more than one molecule is present in the asymmetric unit (i.e. non-crystallographic symmetry), intermolecular interactions are smoothly turned off as the simulation transitions from the crystalline state to the vapor state. This allows each molecule to be independent in the vapor state (i.e. they can pass through each other). For example, due to non-crystallographic symmetry in the ethyl paraben crystal (Table 2), two molecules were simulated and computed deposition values normalized by a factor of two.

Results

Lattice Potential Energies

Displayed in Table 3 is the lattice energy for each compound using both OPLS-AA and AMOEBA force fields. The mean absolute difference for OPLS-AA relative to AMOEBA of 3.6 kcal/mol is significant relative to the goal of achieving chemical accuracy (i.e. ~1.0 kcal/mol). In particular, the three amide containing compounds (acetanilide, paracetamol and phenacetin) show increased crystalline stability of 4.0 to 6.6 kcal/mol under OPLS-AA relative to AMOEBA. The differences for the ester containing methyl and ethyl paraben compounds of 0.5 and 1.2 kcal/mol, respectively, are more modest.

Table 3.

OPLS-AA and AMOEBA lattice potential energies for each compound (kcal/mol).

Compound	OPLS-AA			AMOEBA			Diff.
	Crystal	Vacuum	Lattice	Crystal	Vacuum	Lattice
Acetanilide	−28.73	−2.01	−26.72	−38.05	−15.32	−22.73	3.99
Paracetamol	−44.45	−10.12	−34.32	−41.04	−13.35	−27.70	6.63
Methyl Paraben	−23.58	−0.13	−23.45	−30.77	−8.48	−22.29	1.16
Ethyl Paraben	−24.33	0.78	−25.11	−28.56	−3.98	−24.58	0.53
Phenacetin	−37.49	−5.70	−31.80	−36.05	−9.92	−26.13	5.67
Mean			−28.28			−24.68	3.60

Deposition Free Energy and Dual Force Field Corrections

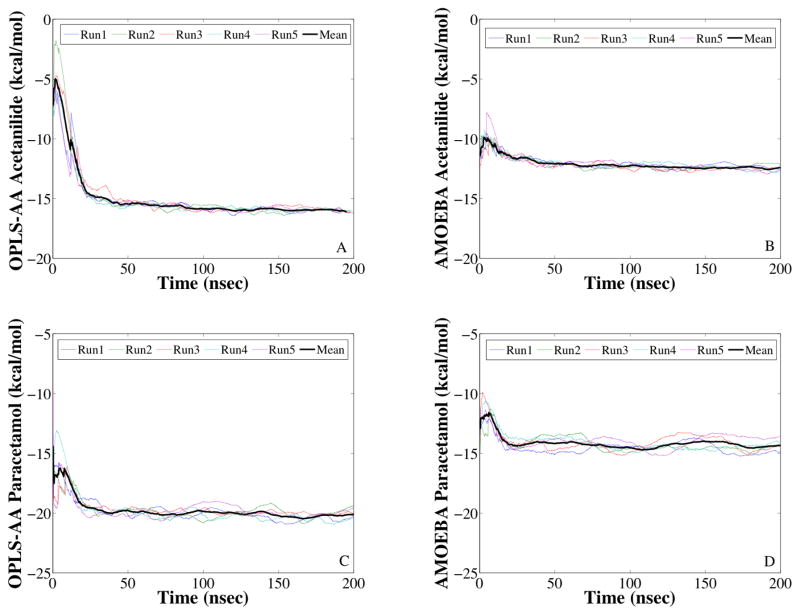
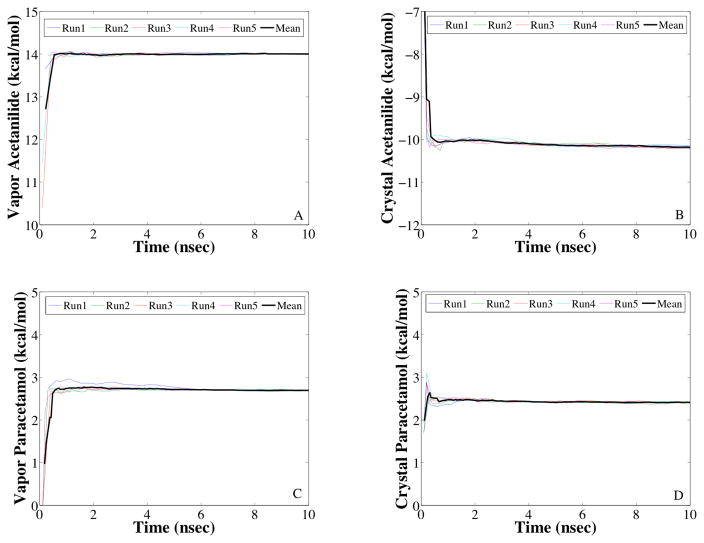
As shown in Figure 1 above, the accelerated thermodynamic pathway consists of three steps. First, the transition to the cheap force field is completed in the vapor state $\mathrm{\Delta }{G}_{\text{AMOEBA}\to \text{FC}}^{\text{Vapor}}$, followed by the deposition/sublimation phase transition for the asymmetric unit using the cheap force field $\mathrm{\Delta }{G}_{\text{FC}}^{\text{AU}\text{Dep}}$, and finally the transition back to the expensive force field in the crystalline state $\mathrm{\Delta }{G}_{\text{FC}\to \text{AMOEBA}}^{\text{Crystal}}$. Convergence of the independent deposition/sublimation phase transition trajectories for the asymmetric unit in both the expensive (i.e. AMOEBA) and cheap (i.e. OPLS-AA) force fields is presented in Figure 4 for both acetanilide and paracetamol. Convergence of the independent DFF transition trajectories in vapor and crystalline phases is shown in Figure 5 for both acetanilide and paracetamol. Free energy differences were computed by collecting the ensemble average thermodynamic force 〈 ∂U/∂λ 〉 for 200 equally sized bins along the λ parameterized thermodynamic path, followed by numerical thermodynamic integration. Simulation legs were considered to be converged once the mean free energy difference for the five independent trajectories changed by less than 0.1 kcal/mol for the last ¼ of the trajectory.

Figure 4.

Convergence of the deposition free energy is shown for alchemical simulations of the asymmetric unit of acetanilide (Panels A & B) and paracetamol (Panels C & D). Panels A & C use the OPLS-AA force field while Panels B & D use the AMOEBA force fields.

Figure 5.

Convergence of the free energy change for acetanilide (Panels A & B) and paracetamol (Panels C & D) dual force field simulations are shown. In Panels A & C, the AMOEBA force field is transformed into the OPLS-AA force field in vapor. In Panels B & D, the OPLS-AA force field is transformed into the AMOEBA force field in the crystalline environment.

The total DFF corrections in Table 4 follow the trend of the lattice potential energy differences shown in Table 3, albeit slightly smaller in magnitude in all cases. After 5 nsec of sampling for both of the dual force field legs, the mean standard deviation of the free energy difference had fallen to 0.05 kcal/mol (Table 4). The direct deposition/sublimation phase transitions for the asymmetric unit using OPLS-AA and AMOEBA¹⁵ are shown in Table 5. The differences between AMOEBA $\mathrm{\Delta }{G}_{\text{AMOEBA}}^{\text{AU}\text{Dep}}$ and OPLS-AA $\mathrm{\Delta }{G}_{\text{FC}}^{\text{AU}\text{Dep}}$ follow the trends seen in Table 3 for lattice potential energy differences, with OPLS-AA showing greater stabilization than AMOEBA. For example, the mean unsigned error of 3.1 kcal/mol is only slightly smaller than the mean lattice potential energy difference of 3.6 kcal/mol. The standard deviation for the phase transition free energy after 200 nsec of sampling was 0.41 kcal/mol for AMOEBA and 0.27 kcal/mol for OPLS-AA (Table 5). The DFF corrections from Table 4 were added to the pure OPLS-AA deposition values $\mathrm{\Delta }{G}_{\text{FC}}^{\text{AU}\text{Dep}}$ in Table 5 to yield corrected values denoted $\mathrm{\Delta }{\mathrm{G}}_{\text{AMOEBA}/\text{FC}}^{\text{AU}\text{Dep}}$.

Table 4.

DFF thermodynamic corrections for each compound in vapor $\mathrm{\Delta }{\mathbf{G}}_{\text{AMOEBA}\to \text{FC}}^{\text{Vapor}}$ and crystalline $\mathrm{\Delta }{\mathbf{G}}_{\text{FC}\to \text{AMOEBA}}^{\text{Crystal}}$ phases after 5 nsec of sampling (kcal/mol). Each value is the mean of 5 trials ± the standard deviation.

Compound	$\mathrm{\Delta }{\mathrm{G}}_{\text{AMOEBA}\to \text{FC}}^{\text{Vapor}}$	$\mathrm{\Delta }{\mathrm{G}}_{\text{FC}\to \text{AMOEBA}}^{\text{Crystal}}$	Total
Acetanilide	14.00±0.02	−10.12±0.02	3.87±0.03
Paracetamol	2.72 ±0.03	2.42±0.02	5.14±0.04
Methyl Paraben	8.48±0.01	−7.57±0.02	0.91±0.02
Ethyl Paraben	4.32±0.01	−4.14±0.03	0.18±0.03
Phenacetin	3.66±0.03	1.16±0.14	4.81±0.15

Table 5.

Shown are asymmetric unit absolute deposition free energy values for AMOEBA ( $\mathrm{\Delta }{\mathbf{G}}_{\text{AMOEBA}}^{\text{AU}\text{Dep}}$), OPLS-AA ( $\mathrm{\Delta }{\mathbf{G}}_{\text{FC}}^{\text{AU}\text{Dep}}$) and OPLS-AA corrected to AMOEBA ( $\mathrm{\Delta }{\mathbf{G}}_{\text{AMOEBA}/\text{FC}}^{\text{AU}\text{Dep}}$). In the latter case, the total DFF corrections (Table 4) have been added the OPLS-AA deposition values (kcal/mol).

Compound	$\mathrm{\Delta }{\mathrm{G}}_{\text{AMOEBA}}^{\text{AU}\text{Dep}}$	$\mathrm{\Delta }{\mathrm{G}}_{\text{FC}}^{\text{AU}\text{Dep}}$		$\mathrm{\Delta }{\mathrm{G}}_{\text{AMOEBA}/\text{FC}}^{\text{AU}\text{Dep}}$
		Deposition	UE	Deposition	UE
Acetanilide	−12.42±0.29	−16.06±0.12	3.64	−12.19±0.12	0.23
Paracetamol	−13.98±0.57	−19.43±0.29	5.45	−14.30±0.29	0.32
Methyl Paraben	−9.81±0.29	−10.80±0.16	0.99	−9.89±0.16	0.08
Ethyl Paraben	−10.31±0.71	−10.86±0.37	0.55	−10.68±0.37	0.37
Phenacetin	−14.47±0.21	−19.10±0.39	4.63	−14.29±0.40	0.18
Mean	−12.20±0.41	−15.25±0.27	3.05	−12.27±0.27	0.23

We note that the statistical uncertainty for the DFF AMOEBA/FC deposition is almost completely due to the OPLS-AA sublimation/deposition phase transition ( $\mathrm{\Delta }{G}_{\text{FC}}^{\text{AU}\text{Dep}}$) step of the thermodynamic cycle, and not from the DFF corrections. To further reduce the statistical uncertainty, this analysis suggests the focus should be on the OPLS-AA deposition/sublimation phase transition, which is further considered in the Conclusions below. Comparison of pure AMOEBA to the DFF AMOEBA/FC results show a mean unsigned error of only 0.2 kcal/mol, indicating successful application of the DFF thermodynamic path (Figure 1 and Eq. 5). Overall, the DFF method reduced the amount of condensed phase sampling in the more expensive AMOEBA force field by a factor of 40 (i.e. 200 nsec per trial per compound was reduced to only 5 nsec). Although the current version of FFX (1.0.0-beta) does not include optimized code for FC electrostatics, the wall clock time saved using OPLS-AA relative to AMOEBA was a factor of ~2 in this work due to elimination of the self-consistent field calculation (i.e. fixed multipole interactions with zero dipole and quadrupole components are computed for OPLS-AA). In the future, it is reasonable to expect the speed-up of the DFF AMOEBA/FC approach should reach a factor of ~5, based on codes that implement relatively optimized code paths for both fixed partial charge (i.e. OPLS-AA) and polarizable atomic multipole (i.e. AMOEBA) force fields such as TINKER⁷⁹.

Absolute Deposition Thermodynamics vs. Experiment

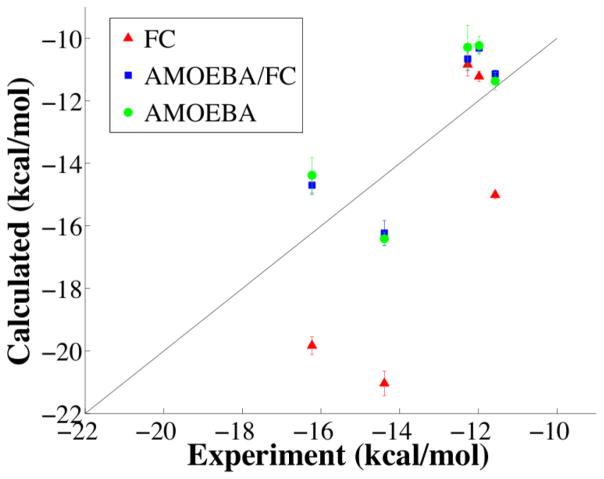
The AMOEBA and AMOEBA/FC asymmetric unit deposition free energy values given in Table 5 can be compared to experiment after addition of 1) an ideal gas correction to account for compressing a 1 molar vapor into the volume of the crystal and 2) a correction to account for removal of the perfect symmetry constraint applied during the sublimation/deposition phase transition simulations. This later correction, a part of the GAUCHE path, has been described previously.¹⁵ As shown in Table 6, both AMOEBA and AMOEBA/FC approaches produce absolute deposition free energy values that compare favorably to experiment, with mean unsigned errors of 1.6 and 1.4 kcal/mol, respectively. For all compounds, the difference between AMOEBA and the accelerated AMOEBA/FC DFF result is not significant based on Student’s t-test. While OPLS-AA and AMOEBA deposition thermodynamics are clearly different for some crystals, the results from the AMOEBA/FC dual force field path are not distinguishable from the direct AMOEBA path (Figure 6).

Table 6.

Shown are absolute deposition free energy values for AMOEBA and AMOEBA/FC after including ideal gas and GAUCHE corrections (kcal/mol). The unsigned errors (UE) are relative to experiment.

Compound	Expt.	Ideal Gas Correction	GAUCHE Correction	$\mathrm{\Delta }{\mathrm{G}}_{\text{AMOEBA}}^{\text{Dep}}$	UE	$\mathrm{\Delta }{\mathrm{G}}_{\text{AMOEBA}/\text{FC}}^{\text{Dep}}$	UE
Acetanilide	−11.57	1.30	−0.25±0.24	−11.37±0.38	0.20	−11.14±0.27	0.43
Paracetamol	−16.23	1.27	−1.67±0.18	−14.38±0.60	1.85	−14.70±0.34	1.53
Methyl Paraben	−11.98	1.32	−1.74±0.14	−10.23±0.32	1.75	−10.31±0.21	1.67
Ethyl Paraben	−12.27	1.21	−1.19±0.18	−10.29±0.73	1.98	−10.66±0.41	1.61
Phenacetin	−14.39	1.14	−3.08±0.36	−16.41±0.42	2.02	−16.23±0.54	1.84
Mean					1.56		1.42

Figure 6.

Absolute crystal deposition free energy values from FC (OPLS-AA), AMOEBA/FC dual force field approach and direct AMOEBA calculations are compared to experiment.

Decomposition into Enthalpic and Entropic Contributions

Crystal structure prediction and the ranking of polymorphs is often based on direct use of potential energy rather than thermodynamic stability (i.e. free energy)⁸⁰. Although efficient, methods that neglect entropic contributions are unable to describe changes in polymorph stability as a function of temperature. To overcome this common approximation, the GAUCHE procedure was developed to efficiently calculate absolute deposition free energy¹⁵. Insights into the origin of crystal stability differences can sometimes be obtained by decomposing free energy differences into enthalpic and entropic contributions using the relationships

$$\mathrm{\Delta }{\mathrm{H}}^{\text{Dep}}=\langle U_{\text{crystal}}\rangle -\langle U_{\text{vapor}}\rangle$$ Equation 11

and

$$-T\mathrm{\Delta }{\mathrm{S}}^{\text{Dep}}=\mathrm{\Delta }{\mathrm{G}}^{\text{Dep}}-\mathrm{\Delta }{\mathrm{H}}^{\text{Dep}}$$ Equation 12

where temperature (T) is 298 degrees Kelvin for the current work and the NVT ensemble was sampled using stochastic dynamics with experimental unit cell parameters (Table 1). The importance of entropic contributions is shown by comparing acetanilide to methyl and ethyl paraben in Table 7; while methyl and ethyl paraben have lower enthalpy of deposition under AMOEBA, acetanilide’s lesser entropic penalty results in a more favorable deposition free energy.

Table 7.

The decomposition of AMOEBA absolute deposition free energy values for each compound into enthalpic and entropic contributions at 298 degrees Kelvin.

Compound	$\mathrm{\Delta }{\mathrm{G}}_{\text{AMOEBA}}^{\text{Dep}}$	$\mathrm{\Delta }{\mathbf{H}}_{\text{AMOEBA}}^{\text{Dep}}$	$-T\mathrm{\Delta }{\mathrm{S}}_{\text{AMOEBA}}^{\text{Dep}}$
Acetanilide	−11.37±0.38	−20.81±0.15	9.44±0.40
Paracetamol	−14.38±0.60	−25.93±0.18	11.55±0.63
Methyl Paraben	−10.23±0.32	−21.19±0.23	10.96±0.39
Ethyl Paraben	−10.29±0.73	−23.30±0.24	13.01±0.77
Phenacetin	−16.41±0.42	−22.96±0.28	6.55±0.50
Mean	−12.54	−22.84	10.30

Conclusions

The DFF approach combines the strengths of both advanced polarizable atomic multipole force fields and efficient fixed partial charge models for organic crystal thermodynamics, while mitigating their primary weaknesses (i.e. FC accuracy limitations and the increased computational cost of AMOEBA). The AMOEBA/FC thermodynamic path was both accurate and cost effective for acetanilide, phenacetin, methyl parben, ethyl paraben and paracetamol crystals with a MUE of 1.4 kcal/mol relative to experiment, which is substantially less than the OPLS-AA MUE of 3.0 kcal/mol. Furthermore, the AMOEBA/OPLS-AA DFF method was statistically indistinguishable from using AMOEBA directly, with a MUE of only 0.2 kcal/mol relative to AMOEBA. Finally, the DFF protocol enabled sampling a path between energy functions with large inherent differences in both their bonded (i.e. equilibrium bond and angle values) and non-bonded functional forms (i.e. van der Waals, permanent electrostatics and explicit polarization). This serves to overcome limitations in reweighting procedures (e.g. the Zwanzig relationship) that require significant phase space overlap.

In future work, we plan to incorporate transition-tempering into the orthogonal space sampling algorithm (i.e. transition-tempered OSRW) to further reduce statistical uncertainty⁸¹, especially for the sublimation/deposition phase transition step. We also plan to replace the three discrete simulations that form the thermodynamic cycle described in Figure 1 with a single simulation that “on-the-fly” turns AMOEBA into OPLS-AA at the beginning of the thermodynamic path (i.e. in vacuum) and then back into AMOEBA at the end (i.e. in the crystalline state). This will serve to avoid any discrepancy in the optimal unit cell parameters or coordinates between force field resolutions for NPT ensembles. We also plan to explore the domain of applicability of DFF thermodynamic paths for applications beyond crystal thermodynamics, including acceleration of small molecule solvation thermodynamics⁸², protein/ligand binding⁸³ and protein folding stability.⁸⁴