A Bayesian Credible Subgroups Approach to Identifying Patient Subgroups with Positive Treatment Effects

Summary

Many new experimental treatments benefit only a subset of the population. Identifying the baseline covariate profiles of patients who benefit from such a treatment, rather than determining whether or not the treatment has a population-level effect, can substantially lessen the risk in undertaking a clinical trial and expose fewer patients to treatments that do not benefit them. The standard analyses for identifying patient subgroups that benefit from an experimental treatment either do not account for multiplicity, or focus on testing for the presence of treatment-covariate interactions rather than the resulting individualized treatment effects. We propose a Bayesian credible subgroups method to identify two bounding subgroups for the benefiting subgroup: one for which it is likely that all members simultaneously have a treatment effect exceeding a specified threshold, and another for which it is likely that no members do. We examine frequentist properties of the credible subgroups method via simulations and illustrate the approach using data from an Alzheimer's disease treatment trial. We conclude with a discussion of the advantages and limitations of this approach to identifying patients for whom the treatment is beneficial.

1. Introduction

Clinical trials have generally focused on demonstrating that an experimental treatment performs, on average, better than a control such as a placebo or the standard of care. Recently there has been greater attention paid to developing targeted or tailored therapies, that is, identifying a subgroup of the patient population for which the new treatment has the greatest benefit and the least risk. Finding personalized treatments is beneficial to all involved parties, including patients, practitioners, regulators, drug developers, and payers. Said another way, there is greater focus today on the heterogeneity of the treatment effect in the broad patient population. All invested parties are concerned that the treatment which performs best on average may not be the best choice for all patients.

Subgroup analysis investigates treatment effect heterogeneity among subsets of the study population defined by baseline characteristics. Challenges faced in subgroup analyses include lack of power, since the sizes of subgroups are necessarily smaller than that of the total study sample, and multiplicity, due to the large number of subgroups typically examined. Pocock et al. (2002) argue that a subgroup analysis procedure should begin with a test for treatment-covariate interaction, as such a test directly examines the strength of evidence for heterogeneity in the treatment effect. However, many studies are not sufficiently powered to detect a treatment-covariate interaction, and it is therefore potentially misleading to interpret failure to identify a significant interaction as sufficient evidence that none exist. Ruberg et al. (2010) note the deficiencies of this use of interaction tests and recommend data mining methods for variable selection and model building as exploratory techniques.

Although identifying treatment effect heterogeneity holds scientific interest, we argue that detecting this heterogeneity is often secondary to the question that regulators, physicians, drug developers, and payers primarily need answered, namely: for whom is there evidence that the proposed treatment is beneficial? Simon (2002) proposes using a linear model with skeptical priors on treatment-covariate interactions to reflect the belief that strong interactions are unlikely a priori. Inferences about patient-specific treatment effects are drawn from the posteriors of the treatment and treatment-covariate interaction parameters. However, the inferences suggested are non-simultaneous (do not account for multiplicity).

Another approach is through tree-based methods. Structures related to classification and regression trees (CART) (Breiman et al., 1984; Chipman et al., 1998) have the advantages of the straightforward “flowchart-style” often used by clinicians and the ability to capture complex and nonlinear relationships. Su et al. (2009) aim to partition the covariate space into two groups which show the greatest difference in treatment effect. Others (Foster et al., 2011; Lipkovich et al., 2011) search for areas of the covariate space in which patients display an enhanced treatment effect relative to the general population. However, tree structures face serious challenges with respect to stability, as small changes in the data can drastically change the structure of the fitted tree. While not necessarily a problem for prediction tasks, this renders suspect inference concerning the structure of underlying processes. Additionally, the ability of trees to capture complex and nonlinear relationships may in fact be a liability when such relationships are considered a priori unlikely, and may often result in overfitting. Finally, while these methods are interesting ways to identify heterogeneity, they do not directly address the question of identifying who benefits from treatment. Berger et al. (2014) partially address this by recommending tree-based priors for use in model selection from a space of linear models, which provides opportunities for a wide variety of posterior inferences, and SUBA (Xu et al., 2014) provides a tree-based algorithm for constructing subgroups and allocating patients adaptively to the best subgroup-specific treatments. Again, the tree-based methods in the literature do not address simultaneous inference.

Simultaneous inferences regarding subpopulations are statements concerning properties that all members of that subpopulation satisfy, the most pertinent example in this context being the statement that every member of a specific subpopulation (which may or may not be pre-specified) benefits from treatment. This is in contrast to the non-simultaneous methods described above, which make statements concerning properties of each individual (or covariate point) separately; for example, identifying members of the population who have each have a high marginal probability of benefiting from treatment. In certain cases a subpopulation for which there is probability p that every member simultaneously benefits is the same as the subpopulation in which for every member there is probability p′ ≥ p of benefiting individually, but this does not hold in general. Multiplicity is inherent in the problem of bounding the benefiting population because we implicitly test for a treatment effect at each point in the covariate space, and methods of simultaneous inference account for this multiplicity in order to avoid inflating the familywise type I error rate.

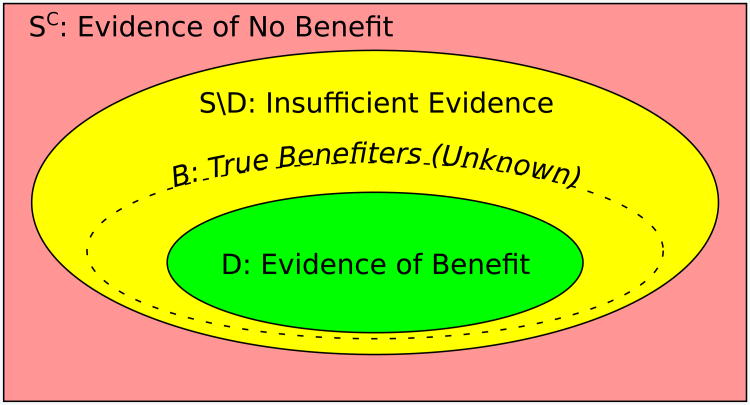
In this paper, we propose a Bayesian credible subgroups method for simultaneous inference regarding who benefits from treatment, and develop the procedure in the context of a hierarchical linear model. As illustrated in Figure 1, a credible subgroup pair (D, S) defines a trichotomy of the predictive covariate space, from which practitioners may conclude that all patients in D have treatment effect greater than a threshold δ and that those in the complement S^c of S have treatment effect at most δ, while deferring conclusions about patients in the uncertainty region S \ D (S remove D) until more evidence is available. First, in Section 2.1, we describe these credible subgroups in general terms. We describe our model in Section 2.2, and procedures for computing the bounds in Sections 2.3–2.5. Section 3.1 presents simulations evaluating the frequentist properties of our method and comparisons to non-simultaneous methods, while Section 3.2 illustrates our approach using data from an Alzheimer's disease treatment trial. Section 4 concludes and offers directions for future work.

Figure 1.

Interpretation of the trichotomy of the covariate space induced by the credible subgroup pair (D, S) relative to the true benefiting subgroup B.

2. Methods

The method of credible subgroups is a two-part procedure—inference on model parameters followed by construction of subgroup bounds from those inferences. In our development of methodology we will concentrate on linear models, especially in the normal error case.

2.1 The Credible Subgroups

For each subject i, let x_i = (x_i1, x_i2, …, x_ip) be a vector of prognostic covariates (affecting patient outcome regardless of treatment choice), z_i = (z_i1, z_i2, …, z_iq) be a vector of predictive covariates (interacting with treatment choice), t_i ∈ {0, 1} be the treatment indicator, and y_i be the response. Covariates may be both prognostic and predictive, and the covariate vectors may include intercept terms. Let β = (β₁, …, β_p) be parameters corresponding to the prognostic effects and γ = (γ₁, …, γ_q) be parameters corresponding to the predictive effects. Consider the linear model

$$\mathrm{E}[Y_i|{\mathit{x}}_i,{\mathit{z}}_i,t_i]={\mathit{x}}_i^{\prime }\mathit{\beta }+t_i{\mathit{z}}_i^{\prime }\mathit{\gamma }.$$ (1)

It is possible to use a generalized linear model or even a non-linear model, but we proceed with model (1) for simplicity. We are interested in identifying the characteristics of patients for whom the treatment outperforms the control by some specified margin of clinical significance δ, that is, the points z for which

$$\mathrm{\Delta }(\mathit{z})\equiv \mathrm{E}[Y|\mathit{x},\mathit{z},t=1]-\mathrm{E}[Y|\mathit{x},\mathit{z},t=0]={\mathit{z}}^{\prime }\mathit{\gamma }>\delta .$$ (2)

Note that (2) may not be the only requirement for use of a treatment. It may also be desired that E[Y|x, z, t = 1] > ε, but we focus here solely on the effect of the treatment relative to the control. It is also important to note that we are not searching for a subgroup such that the overall treatment effect in the subgroup is greater than δ, but rather a subgroup for which the treatment effect is greater than δ for every member of that subgroup.

Let B_γ be the benefiting subgroup, i.e. the set for which Δ(z) = z′γ > δ. One way of directly estimating B_γ is to take B̂_γ = {z : P(Δ(z) > δ|y) > 1/2}, which reflects a loss function that equally weights incorrect inclusions and exclusions. When incorrect exclusions are preferred over incorrect inclusions, the threshold of 1/2 may be replaced with 1 − α for some α ∈ (0, 1/2). The resulting subset is more akin to a probabilistic lower bound than a direct estimate, but does not account for multiplicity, or the uncertainty regarding the global properties of the subset (rather than the inclusion or exclusion of particular covariate points). However, it is possible to find α′ ≤ α such that D = {z : P(Δ(z) > δ|y) > 1 − α′} is a probabilistic lower bound for B_γ in the sense that P_Bγ (D ⊆ B_γ|y) ≥ 1 − α. Furthering this notion, we wish to find a pair of sets (D, S), called a credible subgroup pair, such that

$${\mathrm{P}}_{{\mathrm{B}}_{\mathit{\gamma }}}(\mathrm{D}\subseteq {\mathrm{B}}_{\mathit{\gamma }}\subseteq \mathrm{S}|\mathit{y})\ge 1-\alpha ,$$ (3)

where the probability measure for B_γ is induced by the probability measure for γ. We term D an exclusive credible subgroup, since the posterior probability that D contains only z for which Δ(z) > δ is at least 1 − α. Similarly, we call S an inclusive credible subgroup, since the posterior probability that S contains all z such that Δ(z) > δ is at least 1 − α. That is,

$${\mathrm{P}}_{\mathrm{\Delta }}[(\mathrm{\Delta }(\mathit{z})>\delta \text{for all}\mathit{z}\in \mathrm{D})|\mathit{y}]\ge 1-\alpha ,\text{and}{\mathrm{P}}_{\mathrm{\Delta }}[(\text{all}\mathit{z}\text{for which}\mathrm{\Delta }(\mathit{z})>\delta \text{are in}\mathrm{S})|\mathit{y}]\ge 1-\alpha .$$ (4)

While there are many ways of arriving at pairs which satisfy (3) and (4), taking the credible subgroups D = {z : P(Δ(z) > δ|y) > 1 − α′/2} and S = {z : P(Δ(z) > δ|y) > α′/2} is intuitive and yields unique pairs up to specification of α′. The two-sided threshold α′/2 is used here because we will construct our credible subgroups using symmetric simultaneous confidence bands, while (4) is a more conservative statement that holds in the general case. We discuss three methods for choosing α′.

First, for some level α ∈ (0,1), let G_α,y be a 1 − α highest posterior density credible region for γ|y. To every predictive parameter estimate γ̂ there corresponds a half-space B_γ̂ of the predictive covariate space with Δ̂(z) ≡ z′γ̂ > δ for all z ∈ B_γ̂. Let ℬ be the collection of all B_γ̂ corresponding to γ̂ ∈ G_α,y. Let D and S be the intersection and union, respectively, of all member sets of ℬ. Then (3) is satisfied, and equality holds if δ ≠ 0 and is bounded below by 1 − α if δ = 0. We further describe this highest posterior density (HPD) method of finding credible subgroups in Section 2.3.

The HPD method assumes that the entire covariate space is of interest, and thus is underpowered when only a subset of the covariate space is considered. Restrictions may include indicator variables that can only take values 0 or 1, and numerical covariates for which investigators are only concerned with values that lie at most k standard deviations from the mean. The restriction of the entire unbounded covariate space to a bounded one can drastically reduce the size of simultaneous credible bands for treatment effects, and thus the exclusive credible subgroup can often be expanded and the inclusive credible subgroup contracted. We discuss a restricted covariate space (RCS) procedure for handling these cases in Section 2.4.

The HPD and RCS methods take advantage of the fact that credible regions for the regression parameters asymptotically agree with the corresponding frequentist confidence regions under an uninformative prior. Thus not only is there at least 1 − α posterior probability that D ⊆ B_γ ⊆ S, but treating γ as fixed, 1 − α is an approximate lower bound on the frequency with which D ⊆ B_γ ⊆ S, often a desirable frequentist property. When such a frequentist property is not necessary and only a restricted covariate space is of interest, a larger exclusive credible subgroup and a smaller inclusive credible subgroup may be obtained for which the posterior probability that D ⊆ B_γ ⊆ S is closer to 1 − α. We discuss such a pure Bayesian (PB) procedure in Section 2.5.

2.2 A Normal Hierarchical Linear Model

We now review a normal hierarchical linear model setting for which we will develop examples of our benefiting subgroup selection tools. Let φ = (β₁,…, β_p, γ₁,…, γ_q) be the combined vector of effect parameters. Let X be the n × p prognostic design matrix with the ${\mathit{x}}_i^{\prime }$ as rows, Z be the n × q predictive design matrix with the ${\mathit{z}}_i^{\prime }$ as rows, and T be the n × n diagonal treatment matrix diag(t₁,…, t_n). It may often be the case that the columns of Z are a subset of the columns of X, and that one or both contain a column of 1's for an intercept or main effect of T. Consider the model

$$\begin{array}{c}\mathit{Y}|\mathbf{X},\mathbf{Z},\mathit{T},\mathit{\beta },\mathit{\gamma },{\sigma }^2\sim \mathcal{N}(\mathbf{X}\mathit{\beta }+\mathbf{T}\mathbf{Z}\mathit{\gamma },{\sigma }^2\mathbf{\sum }),\\ \mathit{\phi }|{\sigma }^2\sim \mathcal{N}(\mathit{\nu },{\sigma }^2\mathbf{R}),\\ {\sigma }^2\sim \mathcal{I}\mathcal{G}(a_0,b_0),\end{array}$$ (5)

where 𝒩 and ℐ𝒢 denote the normal and inverse-gamma distributions, respectively, and Σ, ν, R, a₀, and b₀ are hyperparameters assumed known. σ² is included in the prior scale for φ for conjugacy. With W = (X TZ) as the full design matrix, the first line of (5) becomes

$$\mathit{Y}|\mathbf{W},\mathit{\phi },{\sigma }^2\sim \mathcal{N}(\mathbf{W}\mathit{\phi },{\sigma }^2\mathbf{\sum }).$$ (6)

The posterior distribution of φ conditioned on σ² is then (Lindley and Smith, 1972)

$$\begin{array}{c}\mathit{\phi }|\mathit{y},\mathbf{W},{\sigma }^2\sim \mathcal{N}({\mathbf{H}}_{\mathit{\phi }}{\mathit{h}}_{\mathit{\phi }},{\sigma }^2{\mathbf{H}}_{\mathit{\phi }}),\\ {\mathbf{H}}_{\mathit{\phi }}^{-1}=({\mathbf{W}}^{\prime }{\mathbf{\sum }}^{-1}\mathbf{W}+{\mathbf{R}}^{-1}),\\ {\mathit{h}}_{\mathit{\phi }}=({\mathbf{W}}^{\prime }{\mathbf{\sum }}^{-1}\mathit{y}+{\mathbf{R}}^{-1}\mathit{\nu }),\end{array}$$ (7)

and the posterior distribution of σ² is

$$\begin{array}{c}{\sigma }^2|\mathit{y},\mathbf{W}\sim \mathcal{I}\mathcal{G}(a,b),\\ a=a_0+\frac{n}{2},\\ b=b_0+\frac{1}{2}({\mathit{y}}^{\prime }{\mathbf{\sum }}^{-1}\mathit{y}+{\mathit{\nu }}^{\prime }{\mathbf{R}}^{-1}\mathit{\nu }-{\mathit{h}}_{\mathit{\phi }}^{\prime }{\mathbf{H}}_{\mathit{\phi }}{\mathit{h}}_{\mathit{\phi }}).\end{array}$$ (8)

Thus the marginal posterior of φ is the multivariate Student's t distribution

$$\mathit{\phi }|\mathit{y},\mathbf{W}\sim t_{2a}({\mathbf{H}}_{\mathit{\phi }}{\mathit{h}}_{\mathit{\phi }},\frac{b}{a}{\mathbf{H}}_{\mathit{\phi }}),$$ (9)

and the marginal posterior of γ is

$$\mathit{\gamma }|\mathit{y},\mathbf{W}\sim t_{2a}(\mathbf{H}\mathit{h},\frac{b}{a}\mathbf{H})$$ (10)

where H is the submatrix of H_φ and Hh = γ̂ is the subvector of H_φh_φ corresponding to the coordinates of γ only.

2.3 The Highest Posterior Density (HPD) Method of Credible Subgroups

Let G_α,y be the highest posterior density (HPD) 1 − α credible set for γ. A given predictive covariate vector z is in D if and only if z′γ > δ for all γ ∈ G_α,y. For complicated models (e.g. generalized linear models) for which analytical descriptions of G_α,y are not available, a Monte Carlo sample may be used as an approximation. We proceed with a derivation of an analytical expression of the credible subgroups in the case of the model from Section 2.2.

Under the marginal posterior distribution (10), G_α,y is bounded by the ellipsoid

$${(\mathit{\gamma }-\mathbf{H}\mathit{h})}^{\prime }{\left(\frac{b}{a}\mathbf{H}\right)}^{-1}(\mathit{\gamma }-\mathbf{H}\mathit{h})=qF(1-\alpha ,q,2a),$$ (11)

where F(1 − α, q, 2a) is the 1 − α quantile of the F distribution on q numerator and 2a denominator degrees of freedom. If z′γ > δ for at least one γ ∈ G_α,y and there is no γ ∈ G_α,y such that z′γ = δ, then by the Intermediate Value Theorem z′γ > δ for all γ ∈ G_α,y. Additionally, the set of γ such that z′γ = δ, being a hyperplane, intersects G_α,y if and only if it intersects the boundary of G_α,y. Thus z ∈ D if and only if

$$\begin{array}{c}{\mathit{z}}^{\prime }\mathbf{H}\mathit{h}>\delta \text{and}\\ \{\mathit{\gamma }:{\mathit{z}}^{\prime }\mathit{\gamma }=\delta \text{and}{(\mathit{\gamma }-\mathbf{H}\mathit{h})}^{\prime }{\left(\frac{b}{a}\mathbf{H}\right)}^{-1}(\mathit{\gamma }-\mathbf{H}\mathit{h})=qF(1-\alpha ,q,2a)\}=\varnothing .\end{array}$$ (12)

Let P_z ≡ I − zz′/ ║z║² be the orthogonal projector onto span (z)^⊥. Since z′γ = δ if and only if ${\mathit{z}}^{\prime }(\mathit{\gamma }-\frac{\delta }{{\Vert \mathit{z}\Vert }^2}\mathit{z})=0$, the second condition of (12) is satisfied when the minimum of

$$Q_{\mathit{z}}(\mathit{\gamma })\equiv {({\mathbf{P}}_{\mathit{z}}\mathit{\gamma }+\frac{\delta }{{\Vert \mathit{z}\Vert }^2}\mathit{z}-\mathbf{H}\mathit{h})}^{\prime }{\left(\frac{b}{a}\mathbf{H}\right)}^{-1}({\mathbf{P}}_{\mathit{z}}\mathit{\gamma }+\frac{\delta }{{\Vert \mathit{z}\Vert }^2}\mathit{z}-\mathbf{H}\mathit{h})$$ (13)

is greater than qF(1 − α, q, 2a). Letting ⁻ denote the generalized matrix inverse,

$${\mathit{\gamma }}_{\mathit{min}}\equiv {arg\; min}_{\mathit{\gamma }}{Q}_{\mathit{z}}(\mathit{\gamma })={\left[{\mathbf{P}}_{\mathit{z}}^{\prime }{\left(\frac{b}{a}\mathbf{H}\right)}^{-1}{\mathbf{P}}_{\mathit{z}}\right]}^{-}{\mathbf{P}}_{\mathit{z}}^{\prime }{\left(\frac{b}{a}\mathbf{H}\right)}^{-1}(\mathbf{H}\mathit{h}-\frac{\delta }{{\Vert \mathit{z}\Vert }^2}\mathit{z}),$$ (14)

so D is the set of z such that z′Hh > δ and Q_z(γ_min) > qF(1 − α, q, 2a).

Conversely, z is not in S if and only if z′γ ≤ δ for all γ ∈ G_α,y. Following an argument similar to the above, z is in S unless z′Hh ≤ δ and Q_z(γ_min) ≥ qF(1 − α, q, 2a).

The credible subgroup pair (D, S) is then given by

$$\begin{array}{c}\mathrm{D}=\{\mathit{z}:{\mathit{z}}^{\prime }\mathbf{H}\mathit{h}>\delta \text{and}{Q}_{\mathit{z}}({\mathit{\gamma }}_{\mathit{min}})>qF(1-\alpha ,q,2a)\},\\ \mathrm{S}=\{\mathit{z}:{\mathit{z}}^{\prime }\mathbf{H}\mathit{h}>\delta \text{or}{Q}_{\mathit{z}}({\mathit{\gamma }}_{\mathit{min}})<qF(1-\alpha ,q,2a)\}.\end{array}$$ (15)

2.4 The Restricted Covariate Space (RCS) Method of Credible Subgroups

The HPD method of Section 2.3 is equivalent to finding the Scheffé simultaneous credible band (Scheffé, 1959) for Δ(z),

$$\mathrm{\Delta }(\mathit{z})\in {\mathit{z}}^{\prime }\widehat{\mathit{\gamma }}\pm \sqrt{qF(1-\alpha ,q,2a){\mathit{z}}^{\prime }\left(\frac{b}{a}\mathbf{H}\right)z},$$ (16)

and taking as D the points z for which the lower bound is greater than δ, and taking as S those for which the upper bound is at least δ. This band is exact for unrestricted z and conservative when only a subset C of the covariate space is of interest. In such a case, Uusipaikka (1983) observes that the substantially narrower band

$$\mathrm{\Delta }(\mathit{z})\in {\mathit{z}}^{\prime }\widehat{\mathit{\gamma }}\pm \sqrt{q{m}_{\alpha ,\mathrm{C}}^2{\mathit{z}}^{\prime }\left(\frac{b}{a}\mathbf{H}\right)z}$$ (17)

may be used in the same manner, where m_α,C is the 1 − α quantile of the distribution of

$$M_{\mathrm{C}}=\underset{\mathit{z}\in \mathrm{C}}{sup}\frac{|{\mathit{z}}^{\prime }(\mathit{\gamma }-\widehat{\mathit{\gamma }})|}{\sqrt{q{\mathit{z}}^{\prime }\left(\frac{b}{a}\mathbf{H}\right)z}}$$ (18)

The distribution of M_C is usually unknown, but m_α,C may be estimated via Monte Carlo methods by drawing a sample from the posterior (10) of γ and computing the corresponding values of M_C. When continuous covariates are present, a grid may be used for approximation. Additionally, when models other than our normal linear model are used, RCS credible subgroups may be constructed by replacing ${\mathit{z}}^{\prime }\left(\frac{b}{a}\mathbf{H}\right)$ in (17) and (18) by the more general expression Var [Δ(z)], perhaps estimated via MCMC.

2.5 The Pure Bayes (PB) Method of Credible Subgroups

The HPD and RCS methods leverage the frequentist properties of estimates of parameters and linear combinations of parameters to make frequentist coverage guarantees, but are conservative when considering posterior probabilities only. Exact credible subgroups may be obtained by replacing qF(1 − α, q, 2a) in equation (15) with some smaller value r². This yields a larger exclusive credible subgroup and a smaller inclusive credible subgroup.

Given a sample from the posterior of γ and a finite set C of points in the predictive covariate space, a Monte Carlo method estimates an appropriate value of r² via binary search:

1. Initialization: Set search bounds $r_L^2=0$ and $r_U^2=qF(1-\alpha ,q,2a)$.

2. Set the working value for r to ${\widehat{r}}^2=(r_L^2+r_U^2)/2$.

3. Substitute r̂² for qF(1 − α, q, 2a) in (15) to produce a working subgroup pair (D̂, Ŝ).

4. Use the posterior sample of γ to produce a sample of B_γ and estimate p̂ = P_Bγ (D̂ ⊆ B_γ ⊆ Ŝ|y).

5. If p̂ > 1 − α set $r_U^2={\widehat{r}}^2$, and if p̂ < 1 − α set $r_L^2={\widehat{r}}^2$.

6. If p̂ is in [1 − α, 1 − α + ε), set r² = r̂² and end; otherwise go to (2).

When the set C or the posterior sample size is small, the algorithm may not reach the target precision for p̂, in which case the smallest p̂ > p may be taken.

3. Results

3.1 Simulations

We perform a simulation study to evaluate certain frequentist properties of each method for finding credible subgroup pairs. The property of primary interest is the frequency with which D ⊆ B_γ ⊆ S under a fixed value of γ, which we refer to as total coverage. The total coverage is the frequentist counterpart to the Bayesian definition of the credible subgroup pair: that P_Bγ (D ⊆ B_γ ⊆ S|y) ≥ 1 − α.

We also wish to have a notion of the generalized width, or size, of the credible subgroup pair. A natural choice is to consider P_z (z ∈ S \ D|D, S), i.e. the proportion of the population included in the uncertainty region. Given a pair of credible subgroups, such a value may be estimated from the distribution of predictive covariates in the broad population.

We are also able to treat each of the credible subgroups as a diagnostic test and compute sensitivities and specificities for D and S. These quantities measure how well the credible subgroups align with the benefiting subgroup. The sensitivity of D, P_z(z ∈ D|z ∈ B_γ), is reported here, and other quantities in the Supplementary Materials.

In addition to comparing the three methods of constructing credible subgroups, we also include in our simulations two non-simultaneous methods of identifying benefiting subgroups. The first, which we call “pointwise,” uses the same normal linear model as our methods for constructing credible subgroups but does not account for multiplicity in constructing the credible subgroups; i.e., it takes as D the covariate points at which the posterior probability of Δ(z) > δ is greater than 1 − α and as S those at which the posterior probability of Δ(z) ≤ δ is at most α. The second is Bayesian additive regression trees (BART) (Chipman et al., 2010). Multiplicity adjustments for BART have not been developed in the literature, and Bonferroni-type corrections are likely to be highly conservative. We fit the BART model on all covariates plus the treatment indicator, and use as the fitted treatment effect the difference in fitted means between the treated and untreated patients at each covariate point. We again take as D the covariate points at which the posterior probability of Δ(z) > δ is greater than 1 − α and as S those at which the posterior probability of Δ(z) ≤ δ is at most α, using posterior draws from the BART fit. No multiplicity adjustment is made.

We simulate 1000 datasets each containing n = 40 subjects to reflect the size of our example dataset. Results for simulations with n = 100 and n = 350 are presented in the Supplementary Materials. Each subject i has a covariate vector x_i = (1,x_i2, x_i3) with x_i2 = 0, 1 with equal probability and x_i3 continuously uniformly distributed on [−3,3], a binary treatment indicator t_i taking values 0 and 1 with equal probability, and a normally distributed response y_i. The covariates are used as both prognostic and predictive covariates and denoted x_i and z_i in the respective situations. The response has mean ${\mu }_i={\mathit{x}}_i^{\prime }\beta +t_i{\mathit{z}}_i^{\prime }\mathit{\gamma }$ and variance σ² = 1. We fix β = 0 and use six different values for γ. We also present three simulations in which the effects of x₂ are nonlinear in order to evaluate the effects of misspecification. The “square root” configuration uses effects linear in $x_2^{\prime }=\sqrt{x_2+3}-\sqrt{3}$, “S-curve” uses $x_2^{\prime }=x_2^{1/3}$, and “inverted U” uses $x_2^{\prime }=1/2-{(x_2/3)}^2$.

We use a vague ℐ𝒢(10⁻³, 10⁻³) prior for σ² and a 𝒩(0, σ²R) prior on φ|σ² with R = diag(10⁴,10⁴,10⁴,10⁴,1,1), which is conservative with respect to interaction terms and vague with respect to other regression parameters. For the BART fits, we use the default settings in the BayesTree R package, with 500 posterior draws kept after 100 burn-in iterations. For each dataset we compute credible subgroup pairs using each of the three methods at the 80% credible level. To determine credible subgroups we use a grid search in which z₁ = 1, z₂ = 0,1, and z₃ ranges from −3 to 3 in steps of 0.1 and include or exclude each covariate point on the grid from the subgroups as they satisfy or fail to satisfy the conditions specified in Section 2. Where a sample from the posterior of γ is needed we use a sample of size 1000.

In order to compare the model fits of our linear model to those of BART, we compute the mean squared errors of the treatment effects by comparing the estimated treatment effects to the true values at each point on the covariate space grid. For the linear model, we also track how often an F test for treatment effect heterogeneity is significant.

Table 1 displays the average summary statistics for 80% credible subgroup pairs under nine generating models (n = 40). More results (n = 100, 350) are available in the Supplementary Materials. Moving from the PB to RCS to HPD methods, total coverage, pair size, and specificity of D increase, while sensitivity of D decreases. For both linear and non-linear data generating models the RCS and HPD methods have consistently conservative (≥ 80%) total coverage, while the PB method is sometimes conservative and at other times anticonservative.

Table 1. Average summary statistics for 80% credible subgroup pairs as well as pointwise (PW) and BART methods (n=40).

Truth	Method	Total Coverage	Pair Size	Sensitivity of D	Specificity of D	Effect MSE	Heterog. Tests
γ = (0, 0, 0)	PB	0.46	0.75	–	0.87	0.24	0.18
	RCS	0.88	0.95	–	0.97	0.24	0.18
	HPD	0.91	0.97	–	0.98	0.24	0.18
	PW	0.43	0.59	–	0.79	0.24	0.18
	BART	0.68	0.71	–	0.85	0.10	–
γ = (0, 0, 1)	PB	0.82	0.25	0.76	0.99	0.24	1.00
	RCS	0.94	0.34	0.67	1.00	0.24	1.00
	HPD	0.96	0.38	0.64	1.00	0.24	1.00
	PW	0.46	0.13	0.87	0.98	0.24	1.00
	BART	0.59	0.45	0.54	0.97	1.62	–
γ = (0, 1, 0)	PB	0.55	0.55	0.68	0.83	0.28	0.45
	RCS	0.87	0.78	0.38	0.95	0.28	0.45
	HPD	0.91	0.82	0.33	0.96	0.28	0.45
	PW	0.47	0.39	0.79	0.71	0.28	0.45
	BART	0.49	0.40	0.79	0.62	0.21	–
γ = (0, 1, 1)	PB	0.77	0.25	0.81	0.99	0.28	1.00
	RCS	0.92	0.35	0.75	1.00	0.28	1.00
	HPD	0.95	0.38	0.72	1.00	0.28	1.00
	PW	0.41	0.14	0.89	0.97	0.28	1.00
	BART	0.48	0.38	0.78	0.88	1.63	–
γ = (1, 0, 0)	PB	0.99	0.25	0.75	–	1.21	0.18
	RCS	1.00	0.50	0.50	–	1.21	0.18
	HPD	1.00	0.56	0.44	–	1.21	0.18
	PW	0.97	0.13	0.87	–	1.21	0.18
	BART	1.00	0.04	0.96	–	0.13	–
γ = (1, 1, 1)	PB	0.73	0.24	0.87	0.97	1.53	1.00
	RCS	0.92	0.33	0.82	0.99	1.53	1.00
	HPD	0.94	0.35	0.80	0.99	1.53	1.00
	PW	0.43	0.15	0.92	0.93	1.53	1.00
	BART	0.12	0.14	0.97	0.47	1.59	–
Square Root	PB	0.64	0.62	0.28	0.98	0.28	0.56
	RCS	0.92	0.84	0.13	1.00	0.28	0.56
	HPD	0.94	0.87	0.10	1.00	0.28	0.56
	PW	0.38	0.42	0.45	0.95	0.28	0.56
	BART	0.54	0.67	0.17	0.93	0.35	–
S-curve	PB	0.76	0.44	0.56	0.99	0.35	0.92
	RCS	0.93	0.61	0.40	1.00	0.35	0.92
	HPD	0.95	0.65	0.35	1.00	0.35	0.92
	PW	0.42	0.24	0.74	0.97	0.35	0.92
	BART	0.57	0.60	0.36	0.94	0.87	–
Inverted U	PB	0.20	0.73	0.21	0.81	0.37	0.18
	RCS	0, 80	0.93	0.06	0.95	0.37	0.18
	HPD	0.85	0.95	0.04	0.96	0.37	0.18
	PW	0.16	0.56	0.33	0.71	0.37	0.18
	BART	0.42	0.66	0.30	0.75	0.19	–

Note: Statistics are averaged without undefined values, e.g. sensitivity of D when B_γ is empty. Total coveragerates at or above 80% and low pair sizes (analogous to interval lengths for interval estimation) are desired. The heterogeneity test is a Bayesian F test for the null hypothesis γ₂ = γ₃ = 0.

The pointwise and BART methods yields generally tighter credible subgroups (smaller credible pair sizes) than the simultaneous methods, resulting in poorer coverage and specificity of D, but improved sensitivity of D. The BART model tends to fit better (with respect to effect MSE) when there is no heterogeneity or the heterogeneity is with respect to the binary covariate, but less well when heterogeneity is present with respect to the continuous covariate, with the exception of the inverted U scenario. This reflects BART's tendency to partition with respect to binary covariates rather than continuous ones. As the sample size increases (results shown in the Supplementary Materials) BART gains an advantage in nonlinear situations, however the linear model is competitive in smaller samples.

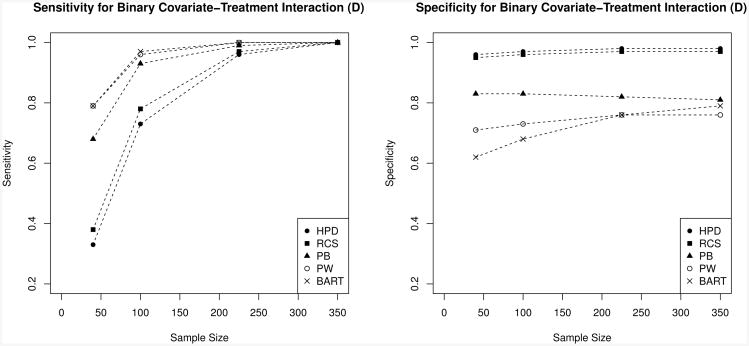
The primary advantage of the multiplicity-correcting methods is the high specificity of D and sensitivity of S, which are 100% whenever the coverage goal D ⊆ B_γ ⊆ S is met. However, the high specificity of D and sensitivity of S come at the price of lower sensitivity of D and specificity of S, especially for small samples. This trade-off may be favorable when extreme specificity is preferred over sensitivity (e.g. a regulatory setting). Figure 2 illustrates the trade-off for D in the particularly interesting case of γ = (0, 1, 0), a dichotomous predictive covariate for which one group has a constant positive benefit while the other has no benefit. Here the PB method is nearly as sensitive as the uncorrected methods, but only the fully corrected HPD and RCS methods deliver the extreme specificities desired by regulators.

Figure 2. Diganostic measure comparison in a case with a binary covariate-treatment interaction.

Sensitivity (left) and specificity (right) of D in the case γ = (0, 1, 0) (treatment effect is determined by a binary covariate). The multiplicity-correcting methods (HPD, RCS, and to a lesser extent PB) maintain extremely high specificity at the expense of sensitivity, especially for small sample sizes. Because the benefit is positive in one group and zero in its complement, the sensitivities of all methods approach 100% for large sample sizes while the specificities remain approximately constant.

Although the PB method is valid within a purely Bayesian context, we recommend against its use when strict frequentist guarantees are desired, and instead prefer the RCS or HPD methods. Further, we recommend the RCS method over the HPD method when the covariate space of interest is restricted, as the RCS method produces less conservative credible subgroup pairs and thus greater sensitivity of D. This advantage lessens as the covariate space becomes large and less discretized. In practical terms, the RCS method detects the most members within the benefiting population among methods that maintain the frequentist coverage guarantee. Finally, the linearity assumption should be carefully considered, especially at the larger sample sizes that can support nonparametric models such as BART.

3.2 Application to Alzheimer's Disease Data Set

We illustrate our method on data from a clinical trial of an Alzheimer's disease treatment developed by AbbVie. We compare a low-dose treatment to a placebo on a subset of patients of the sponsor's interest. There are 41 such patients, 25 receiving the placebo ( TREAT = 0) and 16 receiving the treatment ( TREAT = 1), excluding 2 subjects with incomplete observations.

In addition to the intercept, there are four baseline measurements of interest. SEVERITY measures the progression of disease at study entry (baseline), so that high values indicate severe cognitive impairment. AGE ranges from 58 to 90 at baseline, and SEX is approximately 37% male ( SEX = 1) and 63% female ( SEX = 0). CARRIER indicates the presence ( CARRIER = 1) or absence ( CARRIER = 0) of a genetic biomarker related to Alzheimer's disease, which 56% of the patients carry. The response of interest is CHANGE, the negative change in severity from baseline to end-of-study (that is, baseline minus end of study). This definition is used so that a positive value of CHANGE indicates a positive outcome (decreased cognitive impairment). We assume the responses are independent conditional on the covariates and there is no heteroskedasticity (Σ = I). We search for a population for which the treatment effect Δ(z) is greater than zero for all members simultaneously at the α = 0.05 credible level.

We use all of the above baseline covariates as both prognostic and predictive variables. We also include the SEX:CARRIER and TREAT:SEX:CARRIER interactions due to prior information that they may be important. The continuous covariates SEVERITY and AGE are standardized for computation and presentation of regression coefficients but are plotted in their original scales. An intercept and baseline treatment effect are also modeled.

We fit the Bayesian normal hierarchical linear model described in Section 2.2 with vague priors for prognostic effects and skeptical priors for predictive effects; specifically, R is diagonal with elements corresponding to prognostic effect variances set to 10,000 and those corresponding to predictive effect variances set to 1. The means ν of the prior distributions of all effects are set to 0. Hyperparameters a₀ = b₀ = 0.001 are used for a vague prior for σ². The credible subgroups are numerically obtained by a grid search where AGE ranges from 55 to 90 and SEVERITY ranges from 5 to 45, both as integers. Membership in a credible subgroup is determined for each point by the appropriate criterion from Section 2.

Table 2 gives the posterior mean and standard error of effect parameters. Note that the overall treatment effect and only the interaction of treatment and age would be identified as significant at the 95% credible level with no multiplicity adjustment. The conclusion we wish to avoid is that the only treatment interaction is with age. We consider this conclusion specious because a lack of evidence for strong interactions with sex, carrier status, and baseline severity does not imply a homogeneous treatment effect among levels of those covariates, and thus some patients may benefit from treatment while others may not. Instead, we wish to directly identify the baseline characteristics of patients for whom there is sufficient evidence of benefit from treatment, even when treatment-covariate interactions are weak.

Table 2.

Posterior summaries of selected effect parameters.

Effect	Posterior Mean	Posterior SE	Sig.
( Intercept)	−2.45	1.72
SEVERITY	0.64	1.03
AGE	−2.18	1.36
SEX	4.04	2.35
CARRIER	1.07	2.04
SEX:CARRIER	−4.60	3.29
TREAT	5.92	2.38	*
TREAT:SEVERITY	−0.88	1.33
TREAT:AGE	3.49	1.61	*
TREAT:SEX	−4.28	2.66
TREAT:CARRIER	−1.50	2.46
TREAT:SEX:CARRIER	−0.65	3.26

Note: Continuous covariates are standardized. Estimates greater than 1.96 standard errors from 0 are marked significant.

We restrict our interest to the region of the covariate space where SEVERITY and AGE are within the ranges observed in the study participants, and proceed with the RCS method of identifying credible subgroups. In order to estimate m_α,R we construct four integer grids in which SEVERITY and AGE span 5–45 and 55–90, respectively, one for each of the four combinations of levels of SEX and CARRIER. We then simulate 10,000 draws from the distribution of (18), and use the 80th percentile as m̂_α,R.

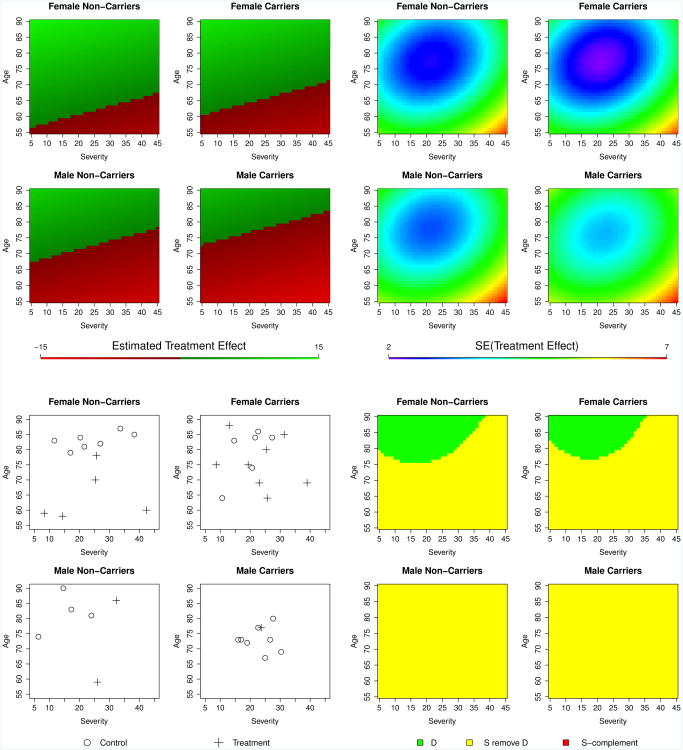
Figure 3 (bottom right) illustrates the region of the covariate space which constitutes the 80% exclusive credible subgroup, D. There is at least 80% posterior probability that the treatment effect is positive for all patients with covariates points in D, fully accounting for multiplicity and thus supporting regulatory approval for that subgroup. Also shown are point estimates and standard errors of the personalized treatment effects that are used to construct the credible subgroup pairs. Note that while the linear nature of the model produces linear treatment effect estimates, the ellipsoidal contours of the standard errors, centered around the main mass of data points, induce the curved boundaries of the credible subgroups.

Figure 3.

Visualizations of the 80% credible subgroup pair.

Top: Point estimates (left) and standard errors (right) of the personalized treatment effects. Bottom left: Locations of study subjects in the covariate space. Control subjects are represented as circles and treatment subjects as crosses. Bottom right: Credible subgroup pair. There is at least 80% posterior probability that all patients with covariate points in D have a positive treatment effect (δ = 0).

We see that we only have enough evidence to show that the oldest female patients with low-to-moderate severity benefit from the treatment versus the control. The PB and HPD methods yield similarly shaped regions that are larger and smaller, respectively. The uncertainty region S \ D indicates characteristics of patients who may or may not benefit and for whom more evidence is needed. Patients in this region may be the focus of subsequent trials using enrichment designs (Peace and Chen, 2010). A sensitivity analysis of a₀ and b₀ ranging from 1 to 1/100,000 resulted in nearly identical credible subgroups. Modifying R to set prior variances for interaction terms to a vague 100 also produced similar results, while shrinking interaction estimates even more strongly toward zero with prior variances of 1/100 resulted in a larger exclusive credible subgroup (figures shown in Supplementary Materials). Additionally, placing a vague inverse-Wishart prior on R centered at the value originally used gave results nearly identical to those obtained by using vague prior variances for interactions.

A BART model fit yields constant point estimates and standard errors within SEX-CARRIER strata. Estimated treatment effects (standard errors) are 3.62 (1.75) for female carriers, 3.53 (1.71) for female non-carriers, 2.89 (1.80) for male carriers, and 2.83 (1.76) for male non-carriers. Note that the BART fit displays a similar broad trend to the linear model, with the treatment being more effective for females and slightly moreso for carriers. However, the BART fit does not detect the significant effect heterogeneity with respect to age, and the standard errors do not reflect the covariate distribution of observations within SEX-CARRIER strata. The BART fit can in fact be represented by the linear model.

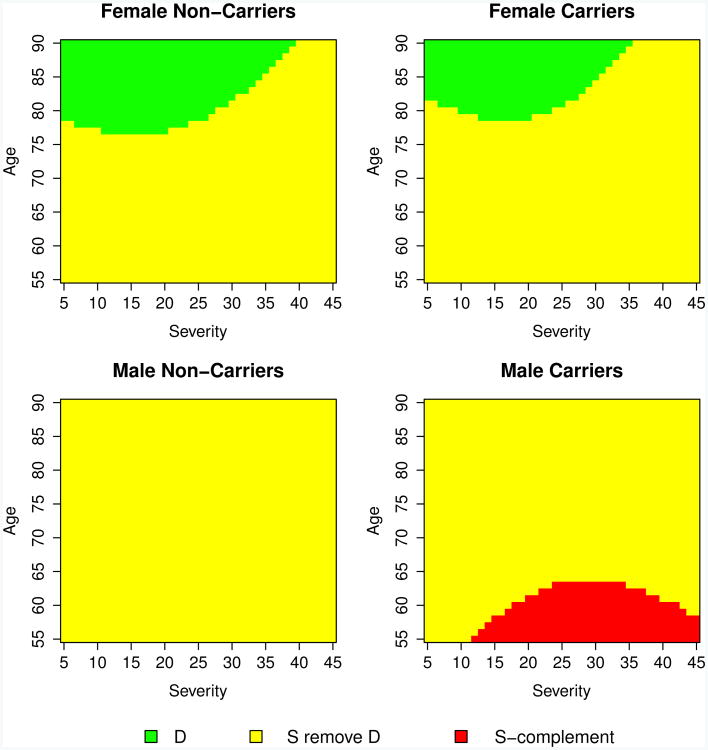
Figure 4 illustrates the results of a contrived analysis with credible level 1 − α = 0.50 and effect threshold δ = 2 that includes, in addition to D and S \ D, the complement S^c of the inclusive credible subgroup. There is at least 1 − α posterior probability that the treatment effects for patients with covariate vectors in this region (here, younger male carriers with moderate-to-high severity) are simultaneously at most δ, and investigators may wish to abandon efforts to show a beneficial treatment effect in this subgroup. However, S^c does not contain any data points, and is thus an extrapolation using the linear model and should therefore be interpreted with appropriate caution.

Figure 4.

Example showing all three regions D, S\D, and S^c. These form the 50% credible subgroup pair with treatment effect threshold δ = 2.

4. Discussion

When evaluating the performance of a treatment, one of the oft-made assumptions is that the treatment effect is homogeneous within the population. If the assumption of homogeneity is correct, then methods that make use of the assumption are valid and have more power for detecting treatment effects than methods that do not. However, the usual method for testing the assumption of homogeneity is the treatment-covariate interaction test, which is often underpowered. Therefore, it may be inappropriate to interpret the failure to reject the homogeneity hypothesis as sufficient evidence that heterogeneity is absent. The Bayesian paradigm offers a compromise between assuming treatment effect homogeneity and making no assumptions about it at all: skeptical priors for interaction terms in the linear model can be used to reflect the a priori belief that a large amount of heterogeneity is unlikely, while still allowing strong evidence of heterogeneity to overwhelm the prior.

The key advantage of the method of credible subgroups is its conclusion: that there is high posterior probability that all members of the exclusive credible subgroup D have a treatment effect exceeding δ, and no patients who are not members of the inclusive credible subgroup S have such a treatment effect. Such conclusions differ from those of the overall test: that the overall treatment effect exceeds δ, and, if the treatment effect is homogeneous, that it exceeds δ for everyone. The conclusions reached by the method of credible subgroups are not necessarily more restrictive than those of the overall test: it may be the case that the overall treatment effect is not positive, but there is a substantial subgroup which benefits from treatment. Additionally, deferring classification of the uncertainty region until more evidence is obtained allows for stronger statements about the classifications already made.

Due to the two-step regression-classification procedure for determining credible subgroup pairs, the methods described in this paper are extensible to non-normal and non-linear models as long as it is possible to obtain a sample from the joint posterior of the predictive effect regression parameters or the personalized treatment effects, though closed-form criteria for the HPD credible subgroups may not be available.

Another advantage of the method of credible subgroups is that it does not require pre-specification of subgroups for testing, but only a list of covariates which may have predictive value. Additionally, the credible subgroups method more fully and naturally accounts for the dependence structure of the implicit tests than do many methods of pre-specified subgroups which rely on Bonferroni or similar multiplicity adjustments which are often conservative. However, credible subgroups are not as simple to describe as most pre-specified subgroups, especially when there are multiple continuous predictive variables. This difficulty stems from the elliptical contours of the standard error of the treatment estimates, as shown in Figure 3. Furthermore, the inclusion of a large number of predictive variables reduces power and makes interpretation and summarizing difficult. Future work may include methods incorporating variable selection, such as the Bayesian lasso (Park and Casella, 2008), or formulations of credible subgroups to BART-style nonparametric recursive partitioning models.

Another challenge in using the method of credible subgroups is in trial design. The sample size and composition needed to detect a treatment effect depend not only on the average effect magnitude and the variance of the responses, but also on effect heterogeneity across the population. Adaptive designs (Berry et al., 2010) may be useful here. Additionally, enrichment designs (Peace and Chen, 2010) can shift the greatest power for detection to different areas of the covariate space. Trial design is a potential topic for later work.

Our example analysis shows that although the sample sizes needed to detect benefiting populations are higher for credible subgroups methods than for analyses assuming homogeneous treatment effects, they are not as high as those typically needed for detecting heterogeneities as in traditional subgroup analysis. The example data of size n = 41 is sufficient to form a non-empty exclusive credible subgroup at the 80% level, but requires a level near 50% to identify effect heterogeneity in the form of the presence of both nonempty exclusive and non-universal inclusive credible subgroups.

Finally, the method described here has important implications for developing tailored or targeted therapies. It identifies patients for whom there is sufficient evidence of benefit, rather than simply identifying an overall treatment effect. This allows therapies which benefit only a subpopulation to be used for that subpopulation and not outside of it, and allows patients and prescribers to be confident that a therapy works for the specific patient to whom it is prescribed. In the future, we hope to extend this work to multiple treatments and multiple outcomes, including safety-related outcomes, thereby allowing patients and prescribers to perform risk-benefit analyses and make even better informed treatment decisions.