Abstract
Dynamic light scattering can be used to measure the diffusivity of a protein within a formulation. The dependence of molecular diffusivity on protein concentration (traditionally expressed in terms of the interaction parameter kD) is often used to infer whether protein-protein interactions are repulsive or attractive, resulting in solutions that are colloidally stable or unstable, respectively. However, a number of factors unrelated to intermolecular forces can also impact protein diffusion, complicating this interpretation. Here, we investigate the influence of multicomponent diffusion in a ternary protein-salt-water system on protein diffusion and kD in the context of Nernst-Planck theory. This analysis demonstrates that large changes in protein diffusivity with protein concentration can result even for hard-sphere systems in the absence of protein-protein interactions. In addition, we show that dynamic light scattering measurements of diffusivity made at low ionic strength cannot be reliably used to detect protein conformational changes. We recommend comparing experimentally determined kD values to theoretically predicted excluded-volume contributions, which will allow a more accurate assessment of protein-protein interactions.
Introduction
Weak protein-protein interactions are a major determinant of protein stability and aggregation (1, 2, 3) and are therefore of great importance in the pharmaceutical industry. Since protein aggregation can reduce efficacy or, worse, elicit an immune response (4, 5, 6, 7), studies of weak protein-protein interactions can provide useful screening tools in early drug development. One measure of protein-protein interactions is the osmotic second virial coefficient B22, which describes the nonideal solution behavior resulting from two-body interactions between solutes (denoted by the subscript 2) (8, 9). B22 is often normalized against its hard-sphere (HS) value, B2HS. Values of B22/B2HS > 1 indicate net repulsive interactions between solutes, whereas values below unity indicate net attractive conditions relative to purely steric repulsion (10, 11, 12). Techniques such as static light scattering (SLS) and membrane osmometry have been developed to measure B22 (9, 10, 13, 14, 15). However, B22/B2HS is difficult to measure with high-throughput techniques and has limited applicability to protein-protein interactions under pharmaceutically relevant conditions, because it is a dilute-solution property (16).
Recently, the use of the interaction parameter kD has gained favor as a more high-throughput means to quantify protein-protein interactions (17). The interaction parameter can be obtained directly with such techniques as dynamic light scattering (DLS) (17, 18) or Taylor dispersion analysis (19) by measuring the dependence of protein diffusivity, Dm,2, on protein concentration, c:
| (1) |
where Ds,2, the single-particle diffusion coefficient, is a constant obtained at infinite dilution, and μ is the chemical potential. Subscripts follow Scatchard notation, where water is denoted as subscript 1, protein as subscript 2, and cosolute as subscript 3 (20). Under dilute conditions, where higher-order interactions can be neglected, kD is related to B22 through
| (2) |
where is the first-order concentration coefficient in the virial expansion of the frictional coefficient, M is the protein’s molecular weight, and is the protein’s partial specific volume (18). Thus, kD values reflect both thermodynamic and hydrodynamic interactions.
High-throughput DLS instruments have been developed to facilitate rapid determination of kD for colloidal stability screening during early drug development (21, 22, 23). However, multiple factors may affect interpretation of DLS data, some of which have not been explicitly investigated in the context of protein stability screening. In particular, proteins in solution are macroions whose Brownian diffusion can be perturbed by the presence of other ions. Indeed, multiple studies (24, 25, 26) have shown that when charged proteins undergo mutual diffusion with small, mobile counterions such as Cl−, charge separation is prevented, because diffusion-induced local electric fields slow the motions of the small counterions and speed those of the protein macroions. Thus, salt concentration gradients with tunable amplitude have been used to achieve strongly amplified particle migrations not representative of specific colloidal forces between proteins (24, 25, 26, 27). This effect is heightened at low ionic strengths, where chemical potential gradients of ionic species are consequential.
DLS measures diffusivity by probing relaxation times of microscopic concentration fluctuations in solution, whereas the mutual diffusion coefficient is best measured using classical techniques based on macroscopic concentration gradients (28). In general, this is not a practical issue, as demonstrated in past work stemming from the Onsager regression hypothesis (29, 30) that microscopic fluctuations give the same transport coefficients as those observed macroscopically (31, 32).
kD, as described in Eq. 2, can be separated into two components, a thermodynamic contribution and a hydrodynamic contribution. Because it includes hydrodynamic forces, kD has been used to probe solution behavior at high protein concentration, such as when measuring protein crystallization propensity (33), making it a useful tool for protein-based pharmaceuticals whose concentrations often exceed 100 g L−1 due to small volume requirements (34). However, caution should be taken when making conclusions regarding protein-protein interactions based on kD measurements under these conditions. At high concentration, where thermodynamic nonidealities, crowding effects, and higher-order interactions (e.g., B222) can alter net interactions (2, 35), collective behavior can be dramatically different from that observed under dilute conditions.
This study aims to address some of the limitations of using kD to measure protein-protein interactions. First, we highlight the dependence of protein diffusion on electrolyte concentrations and local electric potential gradients by using the Nernst-Planck equation to predict the effects of electrolytes on protein mutual diffusion coefficients. We then compare these predictions to experimental diffusivity results. We also show that changes in Ds,2 obtained from DLS at low ionic strength need not imply changes in protein conformation. Finally, a theoretical HS model is used to determine the effect of excluded volume on kD as a function of protein concentration. The results demonstrate the utility of comparing kD to its HS value to estimate the contribution of hydrodynamic interactions to kD.
Theory
Enumeration of components
For the protein-salt-water systems that we consider here, there are three ionic and one neutral species, which are the proteins lysozyme or mAb (P+), counterions (Cl−), coions (K+), and the neutral solvent species, water. We can neglect water dissociation, whereas KCl completely dissociates into K+ and Cl−. We assume that only Cl− counterions interact with the positively charged protein, whereas K+ diffuses freely. Although additional specific and nonspecific protein-solute interactions are possible, such as ligand binding to specific sites and salt-exclusion effects from the protein surface, we neglect them in the scope of this study (36, 37).
Modeling protein diffusion due to a chemical potential gradient
We model the multicomponent diffusion system composed of proteins, Cl−, and K+, using the Nernst-Planck equation, which describes the flux of charged species (Ni) under the influence of composition gradients and of an electric field (38, 39). The Nernst-Planck equation can be simplified by assuming steady state, the absence of an external electric potential gradient coupled with a net charge balance of zero, , and neglecting the effects of nonideality. Flux is then a function of only composition and local electric potential gradients. For a dilute solution comprised of three ionizable components (n = 3) with well-defined net charges, the equation combined with a multicomponent Fickian diffusion equation becomes (40):
| (3) |
where xi are the mole fractions of the three ionic species, zi are the net charges of each species, and Ds,i are the single-particle diffusion coefficients (for derivation, see Appendix A). Equation 3 enables us to calculate the mutual diffusion coefficients of each species, Dm,i, based solely on coupled transport due to chemical potential gradients. DLS measures the eigenvalues of the diffusion coefficient, Dm,p matrix, and the smallest eigenvalue is close to the protein mutual diffusion coefficient (41). Constants used in the model are Ds,i and zi. Ds,Cl- and Ds,K+ are 1.97 10−5 cm2 s−1 and 1.96 10−5 cm2 s−1, respectively. They are obtained from electrical conductivity measurements in water at infinite dilution and were corrected for temperature and viscosity (42, 43). Ds,P+ values obtained from DLS at high salt concentrations (500 mM) are used for lysozyme (1.20 10−6 cm2 s−1) and the mAb (4.40 10−7 cm2 s−1). The charges of K+ and Cl− ions are +1 and −1, respectively. Protein charge is determined from the literature, because calculations of net charge based on amino acid sequences often overestimate the magnitude of a protein’s overall charge (44, 45).
The variables in Eq. 3 are the mole fractions, xi, of each mobile species. To determine the appropriate values of xi corresponding to each experimental condition, a short explanation of sample preparation is necessary. Each protein was dialyzed at 23 mg mL−1 against the desired salt solution. During dialysis, unequal partitioning of ions occurred to neutralize the protein’s charge across the membrane due to the Donnan effect (46, 47, 48). The total concentration of ions on the retentate side (ret) of the membrane after dialysis is represented quantitatively in the Donnan equilibrium equations below (for derivation, see Appendix A):
| (4a) |
| (4b) |
where [P+] is the protein concentration on the retentate side, superscript perm indicates the permeate side during dialysis, and the amount of bound counterion on the retentate side is z(P+)[P+]. Under conditions of low total mobile ion concentration, unequal partitioning is relatively large, whereas it diminishes at higher mobile ion concentrations. In addition, electroneutrality dictates an excess of counterions and a shortage of coion on the retentate side of the dialysis membrane relative to permeate concentrations (49). If, after dialysis, the protein is diluted to lower concentrations, the final concentrations of coion K+ will increase with dilution, whereas the counterion Cl− concentrations will decrease.
Calculation of excluded-volume contributions to kD
High protein concentrations impose a limitation on the use of Eq. 2 as a measure of protein-protein interactions. This follows because for most solutions it is difficult to separate the contributions to kD from higher-order protein-protein interactions from those due to hydrodynamic effects. Attempts have been made to draw empirical relations between kD and B22 to extract friction coefficients, but in general, these relations are not universal, as is affected by molecular symmetry, shape, and type (21, 50, 51, 52, 53, 54, 55).
Solution viscosities are strongly dependent on protein concentration, and protein diffusivities have been empirically found to be proportional to the inverse of the solution viscosity (56). Thus, we postulate that at high protein concentration, viscous effects account for a large portion of kD, leading to negative kD values that are not truly representative of protein-protein attractive interactions. Although interactions other than volume exclusion may affect protein diffusion in concentrated solutions (57, 58, 59), past work (e.g., scaled particle theory (60, 61)) has shown that protein diffusion coefficients can be predicted at high protein concentration based on simple hard-particle models without interactions beyond excluded-volume contributions.
As the particle concentration in an HS suspension increases, the crowding reduces diffusional mobility—a hydrodynamic rather than thermodynamic consequence that impacts solution viscosity (62). The concentration dependence of the viscosity (η) of a solution containing an HS solute can be described by the generalized form of the Mooney equation (63),
| (5) |
where is the viscosity of the solvent, is the protein volume fraction in the solution, k is the self-crowding factor, and S is a parameter that depends on the shape of the protein, its hydrodynamic interactions, and temperature. The volume fraction can be expressed as , where mL g−1 (55, 64). For a HS, S = 2.5 and 1.35 ≤ k ≤ 1.91, where k depends on the packing density (63). Although the Mooney model offers reasonable prediction of viscosity using only excluded volume, in some cases, structural details can become important (65). For example, lysozyme and the monoclonal antibody (mAb) can be more accurately treated as ellipsoids of revolution than as HSs (66). When modeled in this fashion, values for S and k for lysozyme at 296 K have been determined experimentally by Monkos and are 3.01 and 2.91, respectively (67). For the mAb, S is 2.6; this value was calculated using dimensions a = 14 and b = 10 nm, following Eq. 13 in Monkos (67). The self-crowding factor, k, can be calculated by k = 1/<OSP>, where <OSP> is the average occluded surface packing. Using data from Fleming and Richards, k for the mAb was estimated to be 2.3 (68).
To provide an estimate of how protein diffusion depends on solution viscosity, we used the Stokes-Einstein equation for the diffusion of a spherical particle (43, 69):
| (6) |
where R is the protein hydrodynamic radius, kB is Boltzmann’s constant, and T is temperature. Equations 5 and 6 may be combined after substituting to yield
| (7) |
Following Eq. 1, and using the approximations that for a HS, D = Dm,2 and Ds,2 is the diffusion coefficient calculated from Eq. 6 at infinite protein dilution, the derivative of Eq. 7 is taken as a function of protein concentration and is divided by Ds,2 to estimate the contribution of viscosity to kDHS:
| (8) |
We note that this model for kDHS incorporates only HS interactions between proteins with no attractive and/or electrostatic repulsive forces as long as the distance between their respective centers exceeds the surface-contact distance. A similar equation modeling the concentration dependence of the mutual diffusion of HSs has been derived previously in Phillies (70). kDHS thus differs from kD, because it omits possible electroviscous effects due to protein-protein charge interactions as well as other protein-protein interactions. kDHS is analogous to the thermodynamic normalization factor, B22HS, and it can be used to normalize kD to facilitate comparisons between measurements of different protein types and/or at different protein concentrations.
Materials and Methods
Proteins and reagents
Chicken-egg-white lysozyme (molecular weight 14.3 kDa, rH = 1.89 nm, with >90% purity) was obtained from Sigma-Aldrich (St. Louis, MO) as a lyophilized powder and was reconstituted in 0.02 μm filtered deionized Milli-Q water to form a stock solution at a concentration of 30 mg mL−1. Purified mAb (molecular weight 145 kDa, rH = 5.1 nm) was donated by Medimmune (Gaithersburg, MD) at a stock concentration of 23 mg mL−1 in 10 mM NaAc. Analysis by size exclusion chromatography showed that the mAb and the lysozyme were pure and free of soluble aggregates (see Fig. S1 in the Supporting Material). Potassium chloride salt was obtained from Sigma-Aldrich (≥99.0% purity). All stock solutions were prepared with deionized Milli-Q water filtered with a 0.22 μm filter (Millipore, Billerica, MA).
Protein sample preparation
Proteins were exchanged into the final formulation using a bench-scale equilibrium dialysis kit by placing protein samples in 3.5 kDa MWCO dialysis cassettes (Pierce, Rockford, IL). They were dialyzed overnight against excess KCl solution adjusted to pH 6.0 with HCl. After dialysis, protein samples were diluted with 0.02 μm filtered KCl solution to desired protein concentrations. Protein concentrations were determined using a NanoDrop2000 spectrophotometer (ThermoScientific, Waltham, WA) at 280 nm with an extinction coefficient of 2.52 mL mg−1 cm−1 for lysozyme (71) and 1.45 mL mg−1 cm−1 for the mAb (72). Protein concentrations were measured in triplicate after each dialysis and/or dilution step. Finally, before light-scattering experiments, samples were filtered with 0.1 μm (Whatman, Maidstone, United Kingdom) filters to minimize light scattering due to impurities such as dust. All solutions were used within a week of preparation and their pH was checked the day of sample preparation.
DLS to obtain protein diffusion coefficients
DLS studies were conducted at 296 K using a DynaPro DLS instrument from Wyatt Technology (Goleta, CA) at a 90° scattering angle using a 830 nm diode laser. Protein samples were inserted into a 12 μL quartz cuvette (Wyatt Technology) and the cuvette was placed into the MicroSampler unit of the DLS instrument. Each sample was equilibrated for 2 min before measurements were recorded. Due to instrument limitations, protein concentration was varied from 2 mg mL−1 to 25 mg mL−1 for lysozyme and from 0.7 mg mL−1 to 23 mg mL−1 for the mAb. At least eight scans of 10 s each, with polydispersity <30% and sum of squares <2, were accumulated for each sample. The laser power was varied from 10% to 50% to achieve constant amplitudes of the autocorrelation function for all measurements. All samples were measured in triplicate. Temporal fluctuations of light intensity scattered at 90° were processed by a correlator, yielding the intensity autocorrelation function. The samples were monodisperse, so the method of cumulants was used to obtain the mutual diffusion coefficient, Dm,2 from the autocorrelation function (73). For a more detailed description of the theory behind the DLS and method of cumulants, see the detailed review in (17). Finally, Dm,2 was plotted against protein concentration to find kD.
CD spectroscopy to measure protein secondary structure
Far-ultraviolet (UV) circular dichroism (CD) spectra were collected to monitor protein secondary structure. Samples were placed in a 0.5 mm path-length quartz cuvette and spectra were recorded from 190 nm to 260 nm for solutions containing 2 mM and 10 mM KCl (pH 6.0). Samples with 90 mM KCl were monitored from 195 nm to 260 nm to keep the high-tension voltage below 600 V (74). Triplicate samples were analyzed, and 10 scans per sample were measured using a Chirascan-plus spectrometer (Applied Photophysics, Leatherhead, United Kingdom). After subtraction of a blank solution spectrum from the raw average signal, the spectra were normalized by calculating the mean residue ellipticity:
| (9) |
where is the observed ellipticity, residues is the number of amino acid residues per protein molecule, and L is the cell path length.
SLS to measure protein apparent molecular weight
A Brookhaven light-scattering system (Brookhaven Instruments, Holtsville, NY) was used to measure apparent molecular weights. Protein samples were prepared at concentrations ranging from 0.5 mg mL−1 to 5.0 mg mL−1 in formulations with defined ionic strengths at pH 6.0. The refractive index increment of the protein/solvent pair was assumed to be constant at 0.185 mL g−1 for the range of ionic strength studied (75). The scattering intensity was measured at 90° using a 2 mm pinhole size for lysozyme and a 1 mm pinhole size for the mAb at 296 K using a mini L-30 compact diode 637 nm laser. The absolute Rayleigh ratios of the samples were obtained using pure benzene as a calibration standard. Triplicate samples were prepared for each formulation condition, and scattering intensity was acquired for each sample replicate. Disturbances due to dust were minimized by using a built-in statistical dust rejection function.
Results
Nernst-Planck theory for noninteracting protein molecules accurately predicts experimentally determined diffusivities
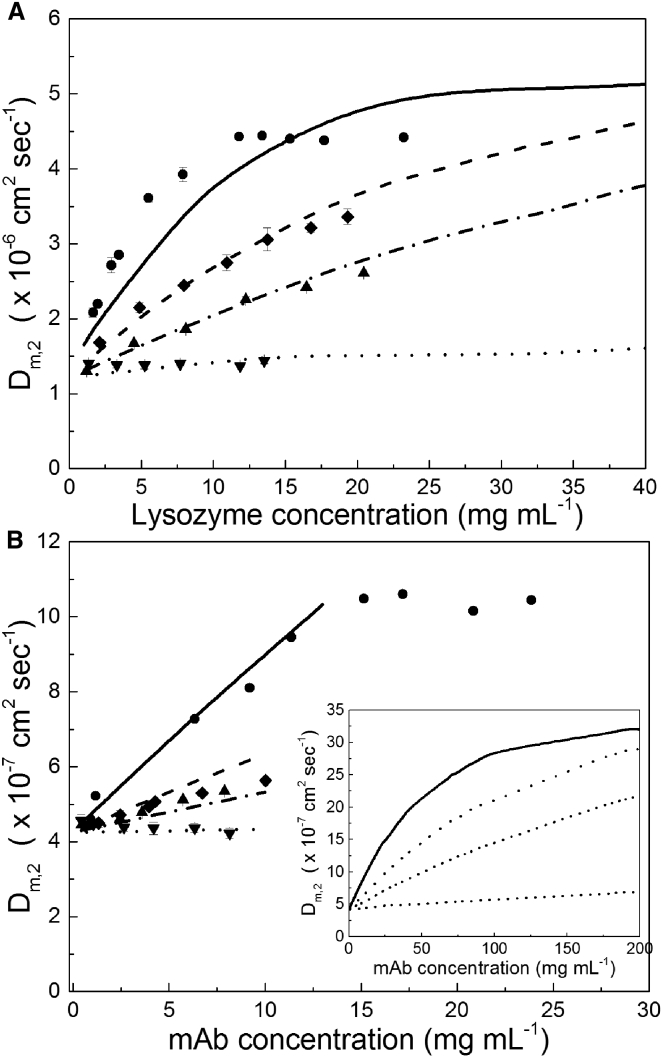
In Fig. 1, a and b, experimental DLS data for both lysozyme and mAb are compared to predictions of the multicomponent diffusion model described by Eq. 3. The predictions of the model, Dm,2 versus protein concentration, are shown as lines in both figures. Concentrations of ionizable species, which reflect experimental sample preparation, are input parameters in the model. The concentrations of K+ and Cl− ions present in solution after dialysis are calculated using Eqs. 4a and 4b, respectively. For example, after dialyzing a 23 mg mL−1 solution of lysozyme against 2.3 mM KCl, [K+,ret] is 0.5 mM, whereas [Cl−,ret] is 10 mM. In contrast, when this concentrated protein sample is diluted to a protein concentration of 1.5 mg mL−1 by adding 2.3 mM KCl, the concentrations of [K+,ret] and [Cl−,ret] are 2 mM and 2.7 mM, respectively. These resulting electrolytes and protein concentrations are used with Eq. 3 to calculate diffusivities.
Figure 1.
DLS data for lysozyme (A) and mAb (B) in 2 mM KCl (circles), 5 mM KCl (diamonds), 10 mM KCl (triangles), and 90 mM KCl (inverted triangles) at pH 6.0. Error bars represent the standard deviation of triplicate measurements. Most error bars are smaller than symbols. Lines show the fit of the model Dm,2 versus c, calculated using Eq. 3 in 2 mM KCl (solid line), 5 mM KCl (dashed line), 10 mM KCl (dash-dotted line), and 90 mM KCl (dotted line) at pH 6.0. The inset in (B) shows a zoomed-out version of the model to demonstrate curvature.
Both experimental and theoretical results demonstrate that at low ionic strength and low protein concentration, protein diffusivity increases with increasing protein concentration. At higher ionic strength, however, this trend becomes weaker, and at an ionic strength of 90 mM the diffusivity is essentially independent of protein concentration. The model fits well with DLS data for both proteins at low protein concentrations (up to ∼10–20 mg mL−1), but at higher concentrations of mAb, where protein-protein interactions neglected in the Nernst-Planck model likely become more important, the agreement is only qualitative, with experimental data showing a more sharply curved profile than the calculated model data (see Fig. 1 b, inset). The agreement between the model—which does not incorporate protein-protein interactions—and DLS data for both proteins demonstrates that local electric field gradients at low ionic strength account for the majority of protein mutual diffusion behavior (40). Tables 1 and 2 show the apparent kD values for lysozyme and the mAb, respectively, calculated from the slopes of experimental diffusivity versus concentration data in Fig. 1, a and b, using Eq. 10:
| (10) |
At low ionic strengths, kD values are obtained at different protein concentration ranges due to the nonlinearity of the experimental data. We chose popular protein concentration ranges commonly employed in the literature to calculate kD from the DLS data obtained at ∼2–12 mg mL−1 and ∼2–25 mg mL−1 protein concentrations (41, 53, 76, 77, 78), and noticed large discrepancies between kD values calculated over the two concentration ranges. This effect is due to the nonlinearity of the curves at low ionic strength and it highlights a potential problem that could arise when using diffusivity as a function of protein concentration to measure the strength of protein-protein interactions.
Table 1.
Apparent kD Values Obtained from Lysozyme Diffusivity Values by DLS
| Ionic Strength (mM KCl) | Lysozyme Concentration Range (mg mL−1) | Apparent kD (mL g−1) from DLS |
|---|---|---|
| 2 | 2–12 | 119.1 ± 18.7 |
| 2 | 2–25 | 45.6 ± 9.3 |
| 5 | 2–12 | 75.6 ± 4.8 |
| 5 | 2–25 | 59.0 ± 3.5 |
| 10 | 2–25 | 51.0 ± 2.8 |
| 90 | 2–12 | −1.5 ± 1.7 |
Error bars come from fitting error.
Table 2.
Apparent kD Values Obtained from mAb Diffusivity Values by DLS
| Ionic strength (mM KCl) | mAb Concentration Range (mg mL−1) | Apparent kD (mL g−1) from DLS |
|---|---|---|
| 2 | 2–12 | 85.0 ± 4.2 |
| 2 | 2–25 | 21.5 ± 5.2 |
| 5 | 2–12 | 29.9 ± 1.5 |
| 10 | 2–12 | 27.9 ± 1.0 |
| 90 | 2–12 | –7.8 ± 2.4 |
Error bars come from the fitting error.
Effect of net protein charge on protein diffusion
Both Donnan equilibrium equations and the multicomponent diffusion model are sensitive to net protein charge, so the accuracy of any predicted protein diffusivity is dependent on assumed protein charge. This sensitivity could explain some discrepancy between the models and experimental data, as the estimation of the net charge on the proteins is challenging (44, 45). Although protein charge as a function of solution pH is frequently estimated using the protein’s primary amino acid sequence and assumed pKa values for ionizable residues, this approach often overestimates the actual protein’s absolute net charge (79, 80, 81). Actual charges are likely to be different from theoretical values due to specific protein-salt interactions and the effects of ionic strength on the pKa values of amino acid residues (45, 79). Indeed, Lehermayr et al. (80) showed that the estimated net charge of a series of eight mAbs differed by up to 70% from their measured net charge at pH 6.0. Extrapolating from the data of Lehermeyer et al., the mAb used here would be predicted to have a net charge between +8 and +10 at the experimental pH of 6.0, in contrast to its theoretical value of +30.1 (based on sequence and assumed pKa values). We found that the “best-fit” charge of the model for all DLS results is +8.7, consistent with the extrapolation from the data of Lehermayr et al. At pH 6.0, in 0.1 M KCl, the net charge of lysozyme from titration curves is +7.5 (79), whereas under our low-ionic-strength conditions, we found the lysozyme “best-fit” effective charge to be +4.8. Again, it is likely that the two estimates vary due to the effects of protein conformation and ionic strength on the pKa values of amino acid residues.
Under low-ionic-strength conditions, conformational changes should not be inferred from DLS data
Protein conformational changes as a function of solution conditions have been inferred from measurements of protein diffusivity (e.g., Sarangapani et al. (78)) by extrapolating the infinite-dilution single-particle diffusion constant, Ds,2, from DLS data using the linear relationship between Dm,2 and Ds,2 (Eq. 10) (47). Protein size (i.e., hydrodynamic radius) is then calculated from Ds,2 using the Stokes-Einstein equation for a spherical particle (Eq. 6) and assuming D = Ds,2. However, because the mutual diffusivity of a protein depends not only on its concentration, but also on the ratio of its concentration to that of other ionic species, kD is not constant as a function of protein concentration. Thus, experimentally, the choice of protein concentrations used in the extrapolation of Eq. 10, as well as the ionic strength, will affect the apparent value of Ds,2. If Eq. 6 is then used to calculate the hydrodynamic radius of the protein, this in turn will result in artifactual implications of ionic-strength- or protein-concentration-dependent changes in protein conformation.
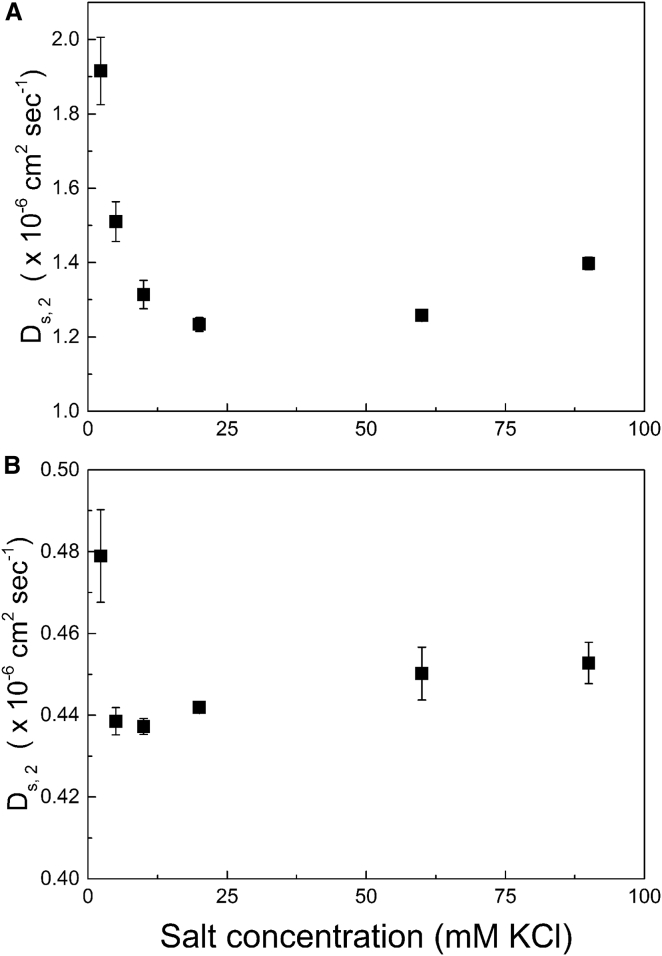
DLS experimental data from Fig. 1, a and b, were used to calculate Ds,2 by linear extrapolation to zero protein concentration. In solutions containing 2 mM KCl, only concentrations up to 12 mg mL−1 for lysozyme and 15 mg mL−1 for mAb were analyzed to maximize R2 of a linear fit. Ds,2 values at the lowest ionic strength were 50% higher for lysozyme and 10% higher for mAb compared to their respective Ds,2 values at higher ionic strengths (see Fig. 2, a and b). If interpreted in the context of the Stokes-Einstein equation, these dramatic changes in diffusivity as a function of ionic strength would yield the improbable implication that lysozyme is tightly folded at low ionic strengths but unfolds at moderate ionic strengths. In fact, when fully unfolded (e.g., in high concentrations of chaotrope), the diffusivity of lysozyme decreases by 55% (82), a similar drop to what occurs in Fig. 2 a.
Figure 2.
The self-diffusion coefficient, Ds,2, as a function of ionic strength calculated by linear extrapolation of DLS data for lysozyme (A) and mAb (B). Results are obtained by finding the intercept of the linear portion of DLS data in Fig. 1. Error bars represent the standard deviation of triplicate measurements and extrapolation to zero protein concentration.
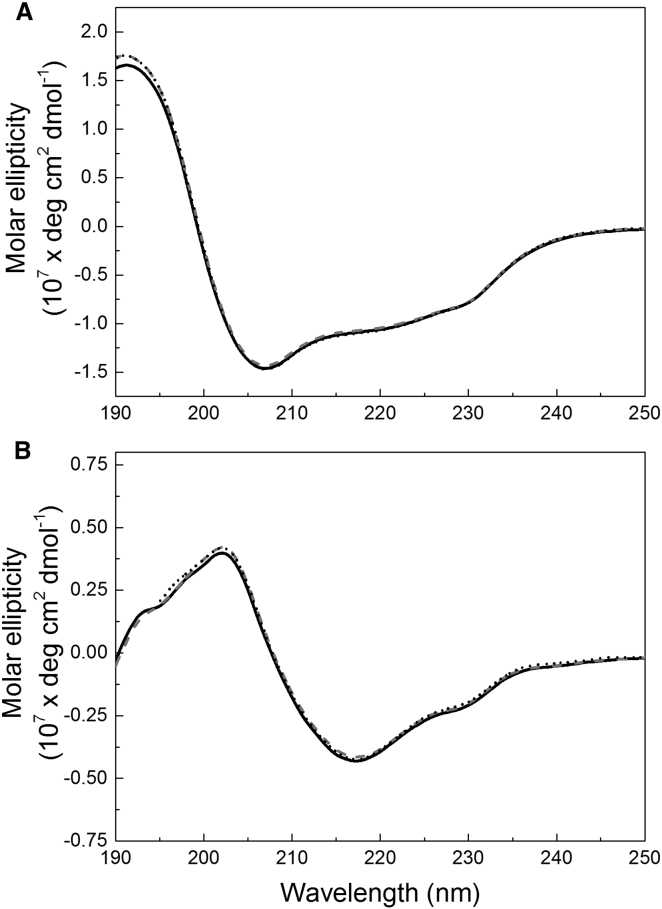
To confirm that ionic strength did not affect protein conformation, each protein’s secondary structure was examined by far-UV CD. The spectra for both lysozyme and mAb are shown in Fig. 3, a and b, after subtraction of the blank solution spectrum and conversion to molar ellipticity. The spectra at all three ionic strengths (2 mM, 10 mM, and 90 mM) overlap each other, indicating no change in protein secondary structure as a function of solution ionic strength for either protein. Finally, SLS was used to determine protein apparent molecular weight at dilute protein concentrations to check for potential monomer-dimer associations or aggregation across the range of ionic strength studied (2–90 mM). The apparent molecular weights for both proteins agreed with their respective theoretical molecular weights within 95% confidence intervals, consistent with a lack of dimerization or other oligomerization under these solution conditions (data shown in Figs. S2 and S3).
Figure 3.
Normalized far-UV CD spectra in KCl at pH 6.0 for lysozyme (A) and the mAb (B) at 2 mM KCl (solid black line), 10 mM KCl (dashed gray line), and 90 mM KCl (dashed black line), at pH 6.0. Each curve represents the average of triplicates of 10 scans each. Error bars are not shown, for clarity.
The excluded volume contribution to kD is always negative and becomes increasingly large at high protein concentration
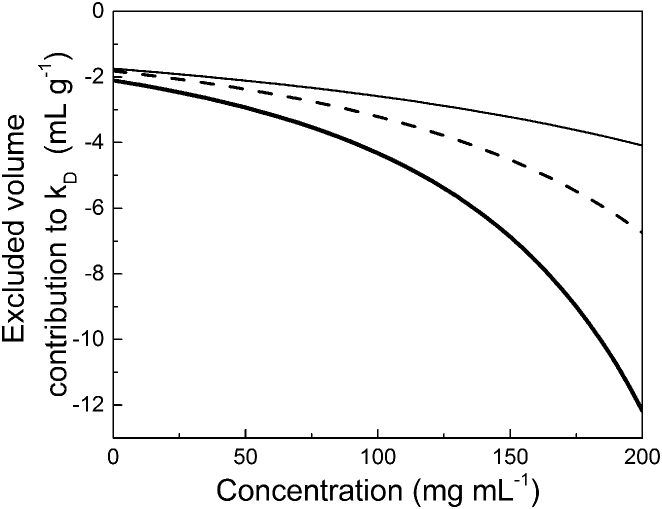
The influence of excluded volume on kD for proteins modeled as HSs is calculated using Eq. 8, where k = 1.35 for densely packed spheres (63, 83), such as in a face-centered cubic lattice (Fig. 4, thin black line). S and k parameters depend on protein shape and packing habits, respectively. S and k for lysozyme were determined experimentally by Monkos by treating lysozyme as a prolate ellipsoid of revolution, and he found that S = 3.01 and k = 2.91 (67). Those values were used to calculate excluded-volume contributions to kD for lysozyme as a function of protein concentration (Fig. 4, thick line). Excluded-volume contributions to kD were also calculated for the mAb by treating the protein as an ellipsoid of revolution with S = 2.6 and k = 2.3 (Fig. 4, dashed line). At zero protein concentration, kDHS is −1.75 mL g−1, whereas the excluded-volume contribution to kD for lysozyme and the mAb are −2.1 mL g−1.and −1.8 mL g−1, respectively. Interestingly, those values are negative, although they do not take into account any protein-protein interactions beyond simple steric effects. In addition, excluded volume increases with protein concentration, due to increasing solution viscosity based solely on volume fraction, making kD more negative in the process.
Figure 4.
Excluded-volume contribution to kD calculated using Eq. 8 for an HS with S = 2.5 and k = 1.35 (thin black line), for lysozyme modeled as a prolate ellipsoid with S = 3.01 and k = 2.91 (thick line), and for the mAb with S = 2.6 and k = 2.3 (dashed line).
Discussion
DLS is a high-throughput, automated technique that can measure protein colloidal stability, assess aggregation, and screen high-concentration protein solutions. These features make DLS a useful tool during protein screening in the formulation process. However, in formulations of low ionic strength, the protein concentration dependence of protein mutual diffusivities (e.g., as determined from DLS measurements) is dominated by effects resulting from cosolute chemical potential gradients, and at high volume fractions of protein, diffusivities are strongly affected by excluded-volume effects on solution viscosity. Thus, under either of these conditions, kD values do not quantitatively reflect protein-protein interactions.
Protein diffusion is influenced by the concentration of electrolytes
Protein diffusion is mediated by electrostatic interactions, hydrodynamic interactions, thermodynamic interactions, and intrinsic excluded-volume effects. The interaction parameter kD takes all of these interactions into account, so care should be taken when interpreting kD values in light of only one of the effects (e.g., protein-protein interactions (52, 84) or protein hydrodynamic size (78, 85)).
We used a Nernst-Planck multicomponent diffusion model to estimate the effect of electrostatics on kD. Electrostatic interactions are governed by ionic strength, counterion valence, protein concentration, and charge density. Our protein-salt-water model includes three ionic species, a positively charged protein and a monovalent salt that dissociates into co- and counterions K+ and Cl−. Many protein-based pharmaceuticals are formulated in low-ionic-strength buffers or prepared at high protein concentrations (34), where the molar concentration of coions and counterions is similar to that of the protein. In these regimes, electrochemical-potential gradients of the ionic species play an important role in driving electrolyte diffusion.
Comparing experimental DLS data to the multicomponent diffusion model demonstrates that the concentration dependence of protein diffusion for both lysozyme and the mAb is largely accounted for by electrochemical potential gradients. Even in the absence of protein-protein interactions, large and positive kD values are predicted to arise in solutions of low ionic strength. We believe that this is an important discovery, as kD is often interpreted as a measure of protein-protein intermolecular interactions to assess protein colloidal stability.
At lower ionic strengths, there is pronounced curvature in plots of diffusivity versus protein concentration obtained from both DLS experimental data and from the model. This phenomenon has been observed for α-chymotrypsinogen under low-ionic-strength conditions, and it was explained in terms of strongly repulsive protein-protein interactions (86). However, the curvature, which is readily apparent in the diffusivities calculated from the Nernst-Planck equation, is rather an indication of a decrease in the molar ratio of counterions to protein at higher protein concentrations that results in reducing electrostatically driven migration. In principle, this curvature could also be associated with nonideal behavior, reflecting monomer-dimer or monomer-trimer interactions. However, we can discount higher-order interactions as the cause of this curvature, which is seen under conditions where the volume fractions of both proteins are well below 2% and peaks from DLS are monodisperse. This curvature can cause inaccuracy when using DLS to measure protein colloidal stability, since apparent kD values depend on the experimental range of protein concentrations chosen, as highlighted in Table 1 and Table 2. This curvature is not limited to DLS experiments; indeed, measurements of lysozyme diffusion coefficients at low ionic strength by Taylor dispersion analysis, a microcapillary flow technique, also yield diffusivity-versus-concentration plots with a curvature similar to those observed by DLS (see Fig. S6).
For both proteins, the model a priori fits the data well. Discrepancies can be explained by the simplicity of the model and some major underlying assumptions. The model is sensitive to the protein’s net charge, which is treated as a constant but realistically expected to depend on solution ionic strength. We also neglected protein-salt specific interactions and mAb glycosylation, which could lead to asymmetric charge distributions on the protein’s surface and impact diffusion induced by a local electric field.
We also demonstrated that electrostatic interactions can impact not only the protein’s mutual diffusion coefficient but the infinite dilution single-particle diffusion constant, Ds,2, as well. Clearly, protein-protein interactions are negligible at infinite dilutions of protein molecules, but protein-cosolute interactions still cannot be neglected because, as is evident from Nernst-Planck theory, the presence of counterions induces dramatic effects on protein diffusion. Using experimental DLS data, we measured changes in Ds,2 without detecting any conformational changes by CD spectroscopy or monomer-dimer association by SLS. We postulate that the Stokes-Einstein equation is not applicable for DLS data at low ionic strength, as this equation neglects electrostatic interactions present in a ternary protein-salt-water system even at infinitesimal protein concentrations. This issue does not apply solely to light-scattering experiments, however, as large deviations in Ds,2 for lysozyme at low ionic strength have been seen in diffusivity measurements from pulsed-gradient spin-echo NMR studies (87). This is an important observation, since changes in protein diffusivity are often used in conjunction with the Stokes-Einstein equation to infer protein conformational changes such as unfolding. For example, Sarangapani et al. (78) concluded that bovine serum albumin (BSA) increased in size by 20% from pH 7.2 to 5.0 and by 40% from pH 7.2 to 3.0 based on fluctuations in Ds,2 values measured by DLS in 20 mM ionic strength buffers. Those findings are surprising considering that other studies did not observe such significant changes in the size of BSA as a function of pH (pH >2) under similar buffer conditions (88, 89). Furthermore, Tanford and Buzzell demonstrated that apparent size changes in BSA as a function of pH are due to electroviscous effects alone and not to the deformation of the BSA molecule (90).
kD can be strongly positive or negative with no attractive or repulsive forces present
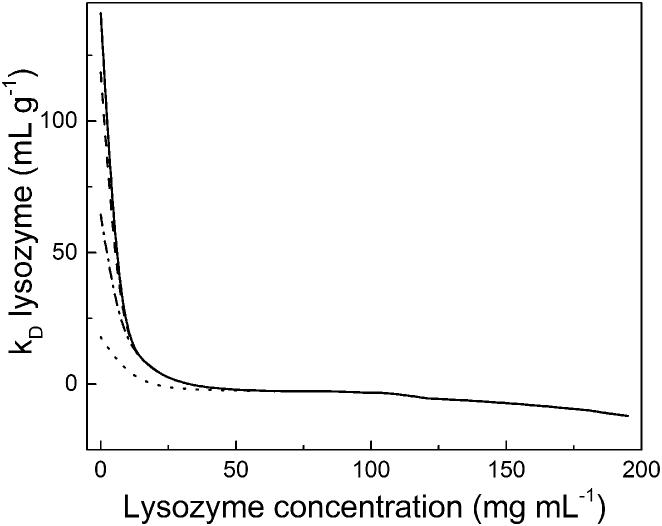
Thus far, we have discussed factors affecting kD measured at low protein concentrations. However, many protein-based pharmaceuticals are prepared in highly concentrated (100–200 mg mL−1) solutions (34, 91). At these high concentrations, electrostatic forces can become negligible compared to hydrodynamic forces from excluded volume (59, 92). We showed, using Eq. 8, that at high protein concentration, the excluded-volume contribution to kD becomes relatively large and negative. This effect is purely steric and not determined by underlying microscopic colloidal forces such as van der Waals interactions. This effect is even more dramatic when lysozyme and the mAb are modeled as prolate ellipsoids as opposed to spheres. To obtain a complete picture of kD for lysozyme as a function of protein concentration, with no repulsive or attractive forces present aside from steric forces, the multicomponent diffusion model was added to Fig. 4 (see Fig. 5). The electrophoretic impact on diffusion is evident at low protein concentration, whereas excluded-volume contributions dominate as protein concentration increases. This figure highlights the possibility of obtaining a wide range of apparent kD values, both positive and negative, even in the complete absence of actual attractive or repulsive forces.
Figure 5.
Theoretical kD values as a function of lysozyme concentration calculated by contributions from excluded volume and electrostatics using Eqs. 3 and 8, with 2 mM KCl (solid line), 5 mM KCl (dashed line), 10 mM KCl (dash-dotted line), and 90 mM KCl (dotted line) at pH 6.0.
Conclusions
kD is a parameter that can be measured with high throughput and is a promising tool for understanding solution behavior of protein formulations. However, because it reflects both hydrodynamic and thermodynamic effects on protein solutions, careful interpretation is needed if it is used to measure protein-protein interactions and colloidal stability of protein formulations. Especially at low ionic strength, kD values are dominated by electrophoretic effects rather than by protein-protein interactions. Likewise, at high protein concentrations, viscous effects arising from excluded volume may largely determine the value of kD. We recommend comparing experimentally determined kD values against calculated contributions to kD excluded-volume effects.
Author Contributions
All authors contributed extensively to this work. L.L.S and M.A.D conducted DLS experiments. L.L.S created the model and analyzed output data with contributions from T.W.R and D.K.S. L.L.S performed the remaining of the experiments (CD and SLS) and wrote the manuscript. T.W.R and D.K.S supervised and edited the article.
Editor: James Cole.
Footnotes
Six figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(16)30818-9.
Appendix A: Derivation of Equations 3 and 4
Equation 3
Diffusion of charged species is affected by composition and by electric potential gradients generated by the transport of ionizable species in solution. A charged protein in a solution of small and fast salt ions will create minute charge separations between the protein and oppositely charged ions. This scenario generates local electric potential gradients that accelerate the protein and slows down the oppositely charged ion. As more salt is added, however, the diffusion potential diminishes and trace amounts of the charged protein have a negligible influence on this phenomenon. For a quantitative understanding of the composition effects on protein diffusivity, it is necessary to start with the generalized Maxwell-Stefan equation (93, 94).
| (A1) |
where Fi is flux density of species i, and ui is mobility. Mobility can be expressed by diffusivity alone. Of all possible forces, only electric and composition gradients are included; this neglects effects of nonideality (activity coefficients are assumed to be unity) and pressure gradients. If only the friction between the solute and water is considered, which is applicable for dilute solutions, the above expression reduces to the Nernst-Planck equation:
| (A2) |
where is the electric potential, e is Faraday’s constant, R is the ideal gas constant, and T is temperature. For simplicity, it is assumed that the gradient takes place only in the z-direction. With a net charge of zero, without external electric potential gradient (where, in the current example, n = 3), can be determined as a function of the gradient in diffusion and can be substituted into the Nernst-Planck equation:
| (A3) |
Putting this in matrix form with three species in the structure of yields Eq. 3 (40). We note that Eq. 3 takes into account the fluxes of all three charged species (protein, coion, and counterion), but because species diffusivities are coupled and conditions of electroneutrality need to be maintained, Eq. 3 could have been reduced to a 2 × 2 Fickian diffusion matrix, as the counterion contribution is not needed (26).
Equations 4a and 4b
Assuming that the solution is ideal, the chemical potential of the salt is
| (A4) |
During dialysis, at equilibrium, the standard state chemical potential must be the same in both phases (48):
| (A5) |
The net charge of each phase must equal zero, a condition known as electroneutrality, which is expressed mathematically as
| (A6) |
| (A7) |
Substitution of Eq. A5 into Eq. A7 yields
| (A8) |
Equations A5 and A6 are substituted into the [Cl−,ret] term of Eq. A8, which gives Eq. 4a. Similar steps starting with Eq. A7 can be taken to obtain Eq. 4b.
Supporting Material
References
- 1.Geng S.B., Cheung J.K., Tessier P.M. Improving monoclonal antibody selection and engineering using measurements of colloidal protein interactions. J. Pharm. Sci. 2014;103:3356–3363. doi: 10.1002/jps.24130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Saluja A., Fesinmeyer R.M., Gokarn Y.R. Diffusion and sedimentation interaction parameters for measuring the second virial coefficient and their utility as predictors of protein aggregation. Biophys. J. 2010;99:2657–2665. doi: 10.1016/j.bpj.2010.08.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.He F., Woods C.E., Razinkov V.I. High-throughput assessment of thermal and colloidal stability parameters for monoclonal antibody formulations. J. Pharm. Sci. 2011;100:5126–5141. doi: 10.1002/jps.22712. [DOI] [PubMed] [Google Scholar]
- 4.Rosenberg A.S. Effects of protein aggregates: an immunologic perspective. AAPS J. 2006;8:E501–E507. doi: 10.1208/aapsj080359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.De Groot A.S., Scott D.W. Immunogenicity of protein therapeutics. Trends Immunol. 2007;28:482–490. doi: 10.1016/j.it.2007.07.011. [DOI] [PubMed] [Google Scholar]
- 6.Singh S.K. Impact of product-related factors on immunogenicity of biotherapeutics. J. Pharm. Sci. 2011;100:354–387. doi: 10.1002/jps.22276. [DOI] [PubMed] [Google Scholar]
- 7.Braun A., Kwee L., Alsenz J. Protein aggregates seem to play a key role among the parameters influencing the antigenicity of interferon alpha (IFN-α) in normal and transgenic mice. Pharm. Res. 1997;14:1472–1478. doi: 10.1023/a:1012193326789. [DOI] [PubMed] [Google Scholar]
- 8.Mcmillan W.G., Mayer J.E. The statistical thermodynamics of multicomponent systems. J. Chem. Phys. 1945;13:276–305. [Google Scholar]
- 9.McQuarrie D.A. Harper & Row; New York: 1976. Statistical Mechanics. [Google Scholar]
- 10.George A., Wilson W.W. Predicting protein crystallization from a dilute solution property. Acta Crystallogr. D Biol. Crystallogr. 1994;50:361–365. doi: 10.1107/S0907444994001216. [DOI] [PubMed] [Google Scholar]
- 11.Ruppert S., Sandler S.I., Lenhoff A.M. Correlation between the osmotic second virial coefficient and the solubility of proteins. Biotechnol. Prog. 2001;17:182–187. doi: 10.1021/bp0001314. [DOI] [PubMed] [Google Scholar]
- 12.George A., Chiang Y., Wilson W.W. Second virial coefficient as predictor in protein crystal growth. In: Carter C.W. Jr., Sweet R.M., editors. Methods in Enzymology, volume 276: Macromolecular Crystallography, Part A. Academic Press; New York: 1997. pp. 100–110. [DOI] [PubMed] [Google Scholar]
- 13.Zimm B.H. Application of the methods of molecular distribution to solutions of large molecules. J. Chem. Phys. 1946;14:164–179. [Google Scholar]
- 14.Tombs M.P., Peacocke A.R. Clarendon Press; Oxford, United Kingdom: 1974. The Osmotic Pressure of Biological Macromolecules. [Google Scholar]
- 15.King R.S., Blanch H.W., Prausnitz J.M. Molecular thermodynamics of aqueous two-phase systems for bioseparations. AIChE J. 1988;34:1585–1594. [Google Scholar]
- 16.Ben-Naim A. Plenum Press; New York: 1992. Statistical Thermodynamics for Chemists and Biochemists. [Google Scholar]
- 17.Hassan P.A., Rana S., Verma G. Making sense of Brownian motion: colloid characterization by dynamic light scattering. Langmuir. 2015;31:3–12. doi: 10.1021/la501789z. [DOI] [PubMed] [Google Scholar]
- 18.Harding S.E., Johnson P. The concentration-dependence of macromolecular parameters. Biochem. J. 1985;231:543–547. doi: 10.1042/bj2310543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Latunde-Dada S., Bott R., Leszczyszyn O.I. Methodologies for the rapid determination of the diffusion interaction parameter using Taylor dispersion analysis. Anal. Methods. 2016;8:386–392. [Google Scholar]
- 20.Scatchard G. Physical chemistry of protein solutions; derivation of the equations for the osmotic pressure. J. Am. Chem. Soc. 1946;68:2315–2319. doi: 10.1021/ja01215a054. [DOI] [PubMed] [Google Scholar]
- 21.Yadav S., Shire S.J., Kalonia D.S. Viscosity behavior of high-concentration monoclonal antibody solutions: correlation with interaction parameter and electroviscous effects. J. Pharm. Sci. 2012;101:998–1011. doi: 10.1002/jps.22831. [DOI] [PubMed] [Google Scholar]
- 22.He F., Becker G.W., Razinkov V.I. High-throughput dynamic light scattering method for measuring viscosity of concentrated protein solutions. Anal. Biochem. 2010;399:141–143. doi: 10.1016/j.ab.2009.12.003. [DOI] [PubMed] [Google Scholar]
- 23.Minton A.P. Recent applications of light scattering measurement in the biological and biopharmaceutical sciences. Anal. Biochem. 2016;501:4–22. doi: 10.1016/j.ab.2016.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Cadman A.D., Fleming R., Guy R.H. Diffusion of lysozyme chloride in water and aqueous potassium chloride solutions. Biophys. J. 1981;37:569–574. [PMC free article] [PubMed] [Google Scholar]
- 25.Annunziata O., Buzatu D., Albright J.G. Protein diffusiophoresis and salt osmotic diffusion in aqueous solutions. J. Phys. Chem. B. 2012;116:12694–12705. doi: 10.1021/jp307625d. [DOI] [PubMed] [Google Scholar]
- 26.Leaist D.G. The role of supporting electrolytes in protein diffusion. J. Phys. Chem. 1989;93:474–479. [Google Scholar]
- 27.Lin S.-C., Lee W.I., Schurr J.M. Brownian motion of highly charged poly(L-lysine). Effects of salt and polyion concentration. Biopolymers. 1978;17:1041–1064. [Google Scholar]
- 28.Tyrrell H.J.V., Harris K.R. Butterworth-Heinemann; London, United Kingdom: 1984. Diffusion in Liquids: A Theoretical and Experimental Study. [Google Scholar]
- 29.Onsager L. Reciprocal relations in irreversible processes. I. Phys. Rev. 1931;37:405–426. [Google Scholar]
- 30.Callen H.B., Welton T.A. Irreversibility and generalized noise. Phys. Rev. 1951;83:34–40. [Google Scholar]
- 31.Phillies G.D. Cambridge University Press; Cambridge, United Kingdom: 2011. Phenomenology of Polymer Solution Dynamics. [Google Scholar]
- 32.Berne B.J., Pecora R. Dover Publications; Mineola, NY: 2000. Dynamic Light Scattering with Applications to Chemistry,Biology, and Physics. [Google Scholar]
- 33.Wilson W.W. Monitoring crystallization experiments using dynamic light scattering: assaying and monitoring protein crystallization in solution. Methods. 1990;1:110–117. [Google Scholar]
- 34.Shire S.J., Shahrokh Z., Liu J. Challenges in the development of high protein concentration formulations. J. Pharm. Sci. 2004;93:1390–1402. doi: 10.1002/jps.20079. [DOI] [PubMed] [Google Scholar]
- 35.Alford J.R., Kwok S.C., Randolph T.W. High concentration formulations of recombinant human interleukin-1 receptor antagonist: I. Physical characterization. J. Pharm. Sci. 2008;97:3035–3050. doi: 10.1002/jps.21199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Zhang L., Tan H., Zhang J. Antibody solubility behavior in monovalent salt solutions reveals specific anion effects at low ionic strength. J. Pharm. Sci. 2012;101:965–977. doi: 10.1002/jps.22826. [DOI] [PubMed] [Google Scholar]
- 37.Boström M., Williams D.R., Ninham B.W. Specific ion effects: why the properties of lysozyme in salt solutions follow a Hofmeister series. Biophys. J. 2003;85:686–694. doi: 10.1016/S0006-3495(03)74512-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Krishna R., Wesselingh J.A. The Maxwell-Stefan approach to mass transfer. Chem. Eng. Sci. 1997;52:861–911. [Google Scholar]
- 39.Lightfoot E. Applicability of the Stefan-Maxwell equations to multicomponent diffusion in liquids. AIChE J. 1962;8:708–710. [Google Scholar]
- 40.Leaist D.G., Hao L. Diffusion in buffered protein solutions: combined Nernst-Planck and multicomponent Fick equations. J. Chem. Soc., Faraday Trans. 1993;89:2775–2882. [Google Scholar]
- 41.Annunziata O., Buzatu D., Albright J.G. Protein diffusion coefficients determined by macroscopic-gradient Rayleigh interferometry and dynamic light scattering. Langmuir. 2005;21:12085–12089. doi: 10.1021/la052147f. [DOI] [PubMed] [Google Scholar]
- 42.Nightingale E.R., Jr. Phenomenological theory of ion solvation. Effective radii of hydrated ions. J. Phys. Chem. 1959;63:1381–1387. [Google Scholar]
- 43.Robinson R.A., Stokes R.H. Butterworths Scientific; London, United Kingdom: 1959. The Measurement and Interpretation of Conductance, Chemical Potential and Diffusion in Solutions of Simple Electrolytes. [Google Scholar]
- 44.Gokarn Y.R., Fesinmeyer R.M., Brems D.N. Effective charge measurements reveal selective and preferential accumulation of anions, but not cations, at the protein surface in dilute salt solutions. Protein Sci. 2011;20:580–587. doi: 10.1002/pro.591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Filoti D.I., Shire S.J., Laue T.M. Comparative study of analytical techniques for determining protein charge. J. Pharm. Sci. 2015;104:2123–2131. doi: 10.1002/jps.24454. [DOI] [PubMed] [Google Scholar]
- 46.Stoner M.R., Fischer N., Kendrick B.S. Protein-solute interactions affect the outcome of ultrafiltration/diafiltration operations. J. Pharm. Sci. 2004;93:2332–2342. doi: 10.1002/jps.20145. [DOI] [PubMed] [Google Scholar]
- 47.Tanford C. Wiley; New York: 1961. Physical Chemistry of Macromolecules. [Google Scholar]
- 48.Donnan F.G. The theory of membrane equilibria. Chem. Rev. 1924;1:73–90. [Google Scholar]
- 49.Bull H. F.A. Davis; Philadelphia, PA: 1971. An Introduction to Physical Biochemistry. [Google Scholar]
- 50.Roberts D., Keeling R., Curtis R. The role of electrostatics in protein-protein interactions of a monoclonal antibody. Mol. Pharm. 2014;11:2475–2489. doi: 10.1021/mp5002334. [DOI] [PubMed] [Google Scholar]
- 51.Connolly B.D., Petry C., Gokarn Y.R. Weak interactions govern the viscosity of concentrated antibody solutions: high-throughput analysis using the diffusion interaction parameter. Biophys. J. 2012;103:69–78. doi: 10.1016/j.bpj.2012.04.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Menzen T., Friess W. Temperature-ramped studies on the aggregation, unfolding, and interaction of a therapeutic monoclonal antibody. J. Pharm. Sci. 2014;103:445–455. doi: 10.1002/jps.23827. [DOI] [PubMed] [Google Scholar]
- 53.Shi S., Uchida M., Shameem M. Method qualification and application of diffusion interaction parameter and virial coefficient. Int. J. Biol. Macromol. 2013;62:487–493. doi: 10.1016/j.ijbiomac.2013.09.033. [DOI] [PubMed] [Google Scholar]
- 54.Placidi M., Cannistraro S. A dynamic light scattering study on mutual diffusion coefficient of BSA in concentrated aqueous solutions. Europhys. Lett. 2007;43:476–481. [Google Scholar]
- 55.Yu Y.-X., Tian A.-W., Gao G.-H. Prediction of collective diffusion coefficient of bovine serum albumin in aqueous electrolyte solution with hard-core two-Yukawa potential. Phys. Chem. Chem. Phys. 2005;7:2423–2428. doi: 10.1039/b500371g. [DOI] [PubMed] [Google Scholar]
- 56.Gros G. Concentration dependence of the self-diffusion of human and Lumbricus terrestris hemoglobin. Biophys. J. 1978;22:453–468. doi: 10.1016/S0006-3495(78)85499-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Li L., Kumar S., Boardman D. Concentration dependent viscosity of monoclonal antibody solutions: explaining experimental behavior in terms of molecular properties. Pharm. Res. 2014;31:3161–3178. doi: 10.1007/s11095-014-1409-0. [DOI] [PubMed] [Google Scholar]
- 58.Anderson J.L., Reed C.C. Diffusion of spherical macromolecules at finite concentration. J. Chem. Phys. 1976;64:3240–3250. [Google Scholar]
- 59.Saluja A., Kalonia D.S. Nature and consequences of protein-protein interactions in high protein concentration solutions. Int. J. Pharm. 2008;358:1–15. doi: 10.1016/j.ijpharm.2008.03.041. [DOI] [PubMed] [Google Scholar]
- 60.Muramatsu N., Minton A.P. Tracer diffusion of globular proteins in concentrated protein solutions. Proc. Natl. Acad. Sci. USA. 1988;85:2984–2988. doi: 10.1073/pnas.85.9.2984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Han J., Herzfeld J. Macromolecular diffusion in crowded solutions. Biophys. J. 1993;65:1155–1161. doi: 10.1016/S0006-3495(93)81145-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Tokuyama M., Oppenheim I. Dynamics of hard-sphere suspensions. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 1994;50:R16–R19. doi: 10.1103/physreve.50.r16. [DOI] [PubMed] [Google Scholar]
- 63.Mooney M. The viscosity of a concentrated suspension of spherical particles. J. Colloid Sci. 1951;6:162–170. [Google Scholar]
- 64.Zimmerman S.B., Minton A.P. Macromolecular crowding: biochemical, biophysical, and physiological consequences. Annu. Rev. Biophys. Biomol. Struct. 1993;22:27–65. doi: 10.1146/annurev.bb.22.060193.000331. [DOI] [PubMed] [Google Scholar]
- 65.Hall D., Minton A.P. Macromolecular crowding: qualitative and semiquantitative successes, quantitative challenges. Biochim. Biophys. Acta. 2003;1649:127–139. doi: 10.1016/s1570-9639(03)00167-5. [DOI] [PubMed] [Google Scholar]
- 66.Squire P.G., Himmel M.E. Hydrodynamics and protein hydration. Arch. Biochem. Biophys. 1979;196:165–177. doi: 10.1016/0003-9861(79)90563-0. [DOI] [PubMed] [Google Scholar]
- 67.Monkos K. Concentration and temperature dependence of viscosity in lysozyme aqueous solutions. Biochim. Biophys. Acta. 1997;1339:304–310. doi: 10.1016/s0167-4838(97)00013-7. [DOI] [PubMed] [Google Scholar]
- 68.Fleming P.J., Richards F.M. Protein packing: dependence on protein size, secondary structure and amino acid composition. J. Mol. Biol. 2000;299:487–498. doi: 10.1006/jmbi.2000.3750. [DOI] [PubMed] [Google Scholar]
- 69.Einstein A. On the motion of small particles suspended in a stationary liquid, as required by the molecular kinetic theory of heat. Ann. Phys. 1905;17:549–560. [Google Scholar]
- 70.Phillies G.D. The second order concentration corrections to the mutual diffusion coefficient of Brownian macroparticles. J. Chem. Phys. 1982;77:2623–2631. [Google Scholar]
- 71.Davies R.C., Neuberger A., Wilson B.M. The dependence of lysozyme activity on pH and ionic strength. Biochim. Biophys. Acta. 1969;178:294–305. doi: 10.1016/0005-2744(69)90397-0. [DOI] [PubMed] [Google Scholar]
- 72.Gerhardt A., Bonam K., Randolph T.W. Ionic strength affects tertiary structure and aggregation propensity of a monoclonal antibody adsorbed to silicone oil-water interfaces. J. Pharm. Sci. 2013;102:429–440. doi: 10.1002/jps.23408. [DOI] [PubMed] [Google Scholar]
- 73.Koppel D.E. Analysis of macromolecular polydispersity in intensity correlation spectroscopy: the method of cumulants. J. Chem. Phys. 1972;57:4814–4820. [Google Scholar]
- 74.Kelly S.M., Jess T.J., Price N.C. How to study proteins by circular dichroism. Biochim. Biophys. Acta. 2005;1751:119–139. doi: 10.1016/j.bbapap.2005.06.005. [DOI] [PubMed] [Google Scholar]
- 75.Theisen A. Nottingham University Press; Nottingham, United Kingdom: 2000. Refractive Increment Data-Book for Polymer and Biomolecular Scientists. [Google Scholar]
- 76.Yadav S., Scherer T.M., Kalonia D.S. Use of dynamic light scattering to determine second virial coefficient in a semidilute concentration regime. Anal. Biochem. 2011;411:292–296. doi: 10.1016/j.ab.2010.12.014. [DOI] [PubMed] [Google Scholar]
- 77.Saito S., Hasegawa J., Fukui K. Behavior of monoclonal antibodies: relation between the second virial coefficient (B (2)) at low concentrations and aggregation propensity and viscosity at high concentrations. Pharm. Res. 2012;29:397–410. doi: 10.1007/s11095-011-0563-x. [DOI] [PubMed] [Google Scholar]
- 78.Sarangapani P.S., Hudson S.D., Pathak J.A. Critical examination of the colloidal particle model of globular proteins. Biophys. J. 2015;108:724–737. doi: 10.1016/j.bpj.2014.11.3483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Kuehner D.E., Engmann J., Prausnitz J.M. Lysozyme net charge and ion binding in concentrated aqueous electrolyte solutions. J. Phys. Chem. B. 1999;103:1368–1374. [Google Scholar]
- 80.Lehermayr C., Mahler H., Ader K.M., Fischer S. Assessment of net charge and protein—protein interactions of different monoclonal antibodies. J. Pharm. Sci. 2011;100:2551–2562. doi: 10.1002/jps.22506. [DOI] [PubMed] [Google Scholar]
- 81.Durant J.A., Chen C., Allison S.A. Use of T4 lysozyme charge mutants to examine electrophoretic models. Biophys. Chem. 2002;101-102:593–609. doi: 10.1016/s0301-4622(02)00168-0. [DOI] [PubMed] [Google Scholar]
- 82.Wilkins D.K., Grimshaw S.B., Smith L.J. Hydrodynamic radii of native and denatured proteins measured by pulse field gradient NMR techniques. Biochemistry. 1999;38:16424–16431. doi: 10.1021/bi991765q. [DOI] [PubMed] [Google Scholar]
- 83.Quillin M.L., Matthews B.W. Accurate calculation of the density of proteins. Acta Crystallogr. D Biol. Crystallogr. 2000;56:791–794. doi: 10.1107/s090744490000679x. [DOI] [PubMed] [Google Scholar]
- 84.Li S., Xing D., Li J. Dynamic light scattering application to study protein interactions in electrolyte solutions. J. Biol. Phys. 2004;30:313–324. doi: 10.1007/s10867-004-0997-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Yu Z., Reid J.C., Yang Y.-P. Utilizing dynamic light scattering as a process analytical technology for protein folding and aggregation monitoring in vaccine manufacturing. J. Pharm. Sci. 2013;102:4284–4290. doi: 10.1002/jps.23746. [DOI] [PubMed] [Google Scholar]
- 86.Blanco M.A., Perevozchikova T., Roberts C.J. Protein-protein interactions in dilute to concentrated solutions: α-chymotrypsinogen in acidic conditions. J. Phys. Chem. B. 2014;118:5817–5831. doi: 10.1021/jp412301h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Price W.S., Tsuchiya F., Arata Y. Lysozyme aggregation and solution properties studied using PGSE NMR diffusion measurements lysozyme aggregation. J. Am. Chem. Soc. 1999;121:11503–11512. [Google Scholar]
- 88.Jachimska B., Wasilewska M., Adamczyk Z. Characterization of globular protein solutions by dynamic light scattering, electrophoretic mobility, and viscosity measurements. Langmuir. 2008;24:6866–6872. doi: 10.1021/la800548p. [DOI] [PubMed] [Google Scholar]
- 89.Barbosa L.R.S., Ortore M.G., Itri R. The importance of protein-protein interactions on the pH-induced conformational changes of bovine serum albumin: a small-angle x-ray scattering study. Biophys. J. 2010;98:147–157. doi: 10.1016/j.bpj.2009.09.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Tanford C., Buzzell J.G. The viscosity of aqueous solutions of bovine serum albumin between pH 4.3 and 10.5. J. Phys. Chem. 1956;60:225–231. [Google Scholar]
- 91.Narasimhan C., Mach H., Shameem M. High-dose monoclonal antibodies via the subcutaneous route: challenges and technical solutions, an industry perspective. Ther. Deliv. 2012;3:889–900. doi: 10.4155/tde.12.68. [DOI] [PubMed] [Google Scholar]
- 92.Tomar D.S., Kumar S., Li L. Molecular basis of high viscosity in concentrated antibody solutions: strategies for high concentration drug product development. MAbs. 2016;8:216–228. doi: 10.1080/19420862.2015.1128606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Clerk Maxwell J. On the dynamical theory of gases. Phil. Trans. R. Soc. Lond. 1867;157:49–88. [Google Scholar]
- 94.Stefan J. Über das Gleichgewicht und die Bewegung, insbesondere die Diffusion von Gasgemengen. Sitzber. Akad. Wiss. Wien. 1871;63:63–124. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.