Influence of Ganglioside GM1 Concentration on Lipid Clustering and Membrane Properties and Curvature

Abstract

Gangliosides are a class of glycosphingolipids (GSLs) with amphiphilic character that are found at the outer leaflet of the cell membranes, where their ability to organize into special domains makes them vital cell membrane components. However, a molecular understanding of GSL-rich membranes in terms of their clustered organization, stability, and dynamics is still elusive. To gain molecular insight into the organization and dynamics of GSL-rich membranes, we performed all-atom molecular-dynamics simulations of bicomponent ganglioside GM1 in 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) phospholipid bilayers with varying concentrations of GM1 (10%, 20%, and 30%). Overall, the simulations show very good agreement with available experimental data, including x-ray electron density profiles along the membrane normal, NMR carbohydrate proton-proton distances, and x-ray crystal structures. This validates the quality of our model systems for investigating GM1 clustering through an ordered-lipid-cluster analysis. The increase in GM1 concentration induces tighter lipid packing, driven mainly by inter-GM1 carbohydrate-carbohydrate interactions, leading to a greater preference for the positive curvature of GM1-containing membranes and larger cluster sizes of ordered-lipid clusters (with a composite of GM1 and POPC). These clusters tend to segregate and form a large percolated cluster at a 30% GM1 concentration at 293 K. At a higher temperature of 330 K, however, the segregation is not maintained.

Introduction

Glycosphingolipids (GSLs), carbohydrate-bearing lipids, are found in the outer leaflet of the plasma membrane of most eukaryotic cells. GSLs may comprise up to 10−20 mol % of the lipid constituents of the membranes (1, 2, 3). More than 350 diverse carbohydrate headgroups have been characterized for mammalian GSLs, and the chain length and level of unsaturation in the ceramide tails vary greatly (4). With such structural diversity, GSLs are believed to play important roles in various dynamic cellular processes, such as cell-cell interactions and recognition, signal transduction, and membrane protein regulation (5, 6, 7).

One of the most important GSLs, ganglioside GM1, contains a sialic acid as part of its carbohydrate moiety (Fig. 1). GM1 is particularly abundant in neuronal plasma membranes (3, 4, 8), and historically, to mimic plasma membranes, experimental studies have incorporated as much as 30% of GM1 into lipid bilayers (9). Its interactions with cholera toxin B subunits (10) and amyloid beta (Aβ) in Alzheimer’s disease (11, 12) have been well studied. Along with other GSLs, GM1 has been reported to play an active and primary role in forming and stabilizing laterally segregated microdomains, e.g., cholesterol-dependent rafts or caveolae and cholesterol-independent glycosynapses in biological membranes (2, 13). For example, evidence has indicated that in patients with Alzheimer’s disease, clustering of GM1 on neuronal cell surfaces favors binding of Aβ to GM1 (12, 14).

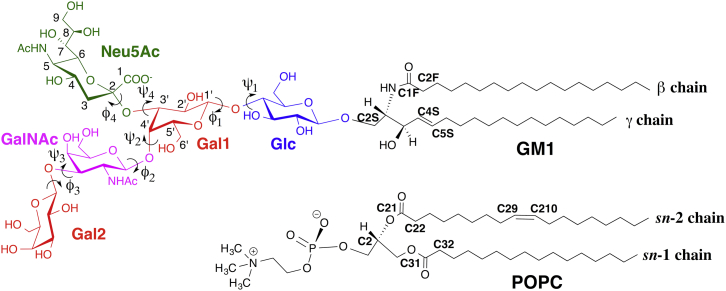
Figure 1.

Schematic representation of the bilayer components (ganglioside GM1 and POPC). Abbreviations: Glc, d-glucose; Gal, d-galactose; GalNAc, N-acetyl-d-galactosamine; Neu5Ac, N-acetyl neuraminic acid (sialic acid). To see this figure in color, go online.

Biochemical and biophysical studies using bi- and/or multicomponent lipid mixtures have been carried out to understand the basis of the organization that leads to segregated GSL-rich domains (2, 3). Experimental studies suggested that the formation and stabilization of GSL clusters or microdomains and their cellular roles at the membrane surface might be dictated by the molecular composition, i.e., the size of the oligosaccharide headgroup, length and saturation of the hydrophobic portion, and concentration of GSLs (3, 15, 16). Electron paramagnetic resonance and spin-labeled probes of gangliosides in phosphatidylcholine bilayers showed reduced fluidity and hydrocarbon chain mobility due to clustering of gangliosides (17, 18). A few other studies showed that at low concentrations, gangliosides are dispersed in phosphatidylcholine bilayers (19). However, a recent study showed ganglioside clustering in concentrations as low as 1% (20). In addition to experimental studies, several molecular-dynamics (MD) studies on GSL-containing membranes with different compositions and concentrations provided atomistic details regarding the structural and dynamic properties of these membranes (21, 22, 23, 24, 25). A few MD simulations indicated that GM1 cluster formation is specifically induced in the presence of cholesterol and sphingomyelin, and that cholesterol critically suppresses membrane fluidity and facilitates clustering of GM1 (22, 26). Nonetheless, a molecular-level understanding of GSL-rich membranes in terms of their basic organization, stability, and dynamics in the absence of cholesterol has remained elusive.

Considering that the lateral organization of GM1 and other GSLs plays a crucial role at the membrane surface, and such arrangements are determined by molecular forces within membrane constituents, it is important to explore the concentration-dependent structural and dynamic properties of GSL-rich membranes. In this study, considering that the suggested domain size in recent experimental work is rather large (300–900 lipids) (20), for practical reasons (i.e., with regard to the system size and simulation time), we performed all-atom MD simulations of bicomponent membrane systems with varying concentrations of GM1 (10%, 20%, and 30%) in 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) bilayers. Our results provide molecular-level insight into the effects of GM1 concentration on 1) membrane physicochemical properties, 2) carbohydrate-carbohydrate interactions and conformations of GM1 headgroups, 3) membrane curvature, and 4) lipid clustering. In addition, we also explored the dependence of lipid clustering on the system size and temperature.

Materials and Methods

System setup

Three different GM1 systems—GM1^10% (10% GM1 in POPC), GM1^20% (20% GM1 in POPC), and GM1^30% (30% GM1 in POPC)—were considered in this study (Fig. 2). Each system contained a total of 200 lipids at 293 K. In addition, to check the system size and temperature dependency, we also simulated larger systems with a total of 800 lipids at two different temperatures (293 K and 330 K): GM1^10%B, GM1^20%B, GM1^30%B, GM1^10%B-330K, GM1^20%B-330K, and GM1^30%B-330K. Details regarding the molecular composition of each system are given in Table S1 in the Supporting Material.

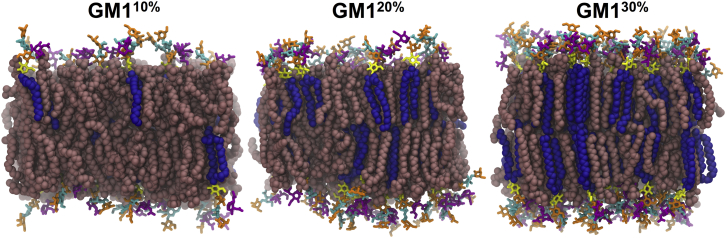
Figure 2.

Representative snapshots of systems GM1^10%, GM1^20%, and GM1^30%. The tails of GM1 and POPC are represented as blue and pink spheres, respectively. GM1 oligosaccharides are shown as sticks, with the following color code: Glc (yellow), Gal1 and Gal2 (orange), GalNAc (cyan), and Neu5Ac (purple). For clarity, only heavy atoms of GM1 and POPC are shown. Snapshots were taken at the end of the simulations (500 ns). To see this figure in color, go online.

All of the systems were built and equilibrated according to the general procedure of bilayer system building and equilibration in Membrane Builder (27, 28, 29) in CHARMM-GUI (27) (http://www.charmm-gui.org/input/membrane). The initial coordinate of GM1 was obtained from CHARMM-GUI Glycolipid Modeler (http://www.charmm-gui.org/input/glycolipid), which uses the internal coordinate information of common glycosidic torsion angle values, orients GM1 along the z axis (i.e., the membrane normal with z = 0 for the bilayer center), and performs Langevin dynamics with a cylindrical restraint potential to keep the GM1 molecule cylindrical in shape and aligned along the z axis. In the next step, we built GM1-POPC mixed bilayers by duplicating and randomly positioning GM1 so that the oligosaccharide portions were located above and below the POPC phosphates (on the z axis) in the top and bottom leaflets, respectively, and then adding POPC molecules in each leaflet around the GM1 molecules using the replacement method. The final building and assembly of each system were accomplished by addition of a TIP3P (30) bulk water box and K⁺ ions to neutralize the negatively charged GM1. These building steps were repeated five times for GM1^10%, GM1^20%, and GM1^30% with different random seed numbers to generate five independent replicas for all three systems to improve sampling and to check for simulation convergence. For GM1^10%B, GM1^20%B, GM1^30%B, GM1^10%B-330K, GM1^20%B-330K, and GM1^30%B-330K, we built and simulated only a single system for each, due to their system size and considerable requirement for computational resources.

MD simulations

We performed ∼2-ns equilibration simulations for each system using CHARMM (31) and CHARMM36 force fields for lipids (32, 33) and carbohydrates (34, 35, 36), employing a short NVT (constant particle number, volume, and temperature) simulation and then an NPT (constant particle number, pressure, and temperature) simulation. Various restraints were applied to the GM1, POPC, and water molecules, and additional dihedral angle restraints were applied to restrain all of the carbohydrate rings of GM1 to the pertinent chair conformation. These restraint forces were gradually reduced during the equilibration.

We carried out NPT production runs of 500 ns for GM1^10%, GM1^20%, and GM1^30%; 650 ns for GM1^10%B, GM1^20%B, and GM1^30%B; and 250 ns for GM1^10%B-330K, GM1^20%B-330K, and GM1^30%B-330K using NAMD (37) and input files generated by CHARMM-GUI (38). A time step of 2 fs using the SHAKE algorithm (39) was used for each system, and all other restraints, including the dihedral restraints for sugar rings used in equilibration simulations, were removed in the production run. The van der Waals interactions were smoothly switched off over 10–12 Å by a force-switching function (40), and long-range electrostatic interactions were calculated using the particle-mesh Ewald method (41) with a mesh size of ∼1 Å for fast Fourier transformation and a sixth-order B-spline interpolation. The pressure was held at 1 bar and different temperature conditions (293 K or 330 K) were applied as mentioned above. In the CHARMM simulations, Langevin temperature control was used for NVT dynamics (42). Temperature and pressure were controlled with a Hoover thermostat (43) and Langevin piston for NPT dynamics (44, 45). For the NAMD NPT simulations, Langevin dynamics was used to maintain constant temperature, with the Langevin coupling coefficient set to 1 ps⁻¹, and a Nosé-Hoover Langevin piston (46, 47) was used to maintain constant pressure with a piston period of 50 fs and a piston decay of 25 fs. The simulation results are presented for the last 300-ns trajectory of GM1^10%, GM1^20%, and GM1^30%. Most results are presented by the average of five independent runs and the standard error. For GM1^10%B, GM1^20%B, and GM1^30%B, the last 300-, 200-, and 100-ns trajectories were analyzed, respectively. For GM1^10%B-330K, GM1^20%B-330K, and GM1^30%B-330K, the last 150-ns trajectories were analyzed.

Analysis

Bilayer properties and interactions between lipids

The area per lipid (A_L) for each lipid type was calculated using a Voronoi tessellation approach with the following atom selections: C21, C31, and C2 atoms for POPC, and C1F, C5S, and C2S atoms for GM1 (Fig. 1) (48). In addition, the membrane hydrophobic thickness (d_H) was calculated by measuring the distance between the average z values of C22, C32 (POPC), C2F, and C4S atoms (GM1; Fig. 1) in each leaflet. Hydrogen bonding (H-bonding) analysis was carried out with the COOR HBOND utility in CHARMM (31) with a distance cutoff of 2.5 Å for D–H···A and an angle cutoff of 120° for D–H–A, where D is the donor and A is the acceptor. For each system, we calculated the NMR order parameter, $\left|S_{\text{CD}}\right|=\left|\langle 3{\text{cos}}^2{\theta }_{CH}-1\rangle /2\right|$ (where ${\theta }_{CH}$ is the time-dependent angle between the C-H bond vector and the z axis, and the angular bracket denotes a time and ensemble average), which is a common metric used to distinguish a liquid-disordered bilayer phase from a liquid-ordered phase. Effective proton-proton distances, $r_{\text{eff}}$, were computed for comparison with nuclear Overhauser effect measurements using $1/r_{\text{eff}}={\langle r_{\text{MD}}^{-6}\rangle }^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$6$}\right.}$. In our simulations, there was no system drift. Therefore, we calculated the lateral diffusion coefficients of GM1 and POPC along the membrane plane using the equation $D_{\text{L}}=\underset{t\to \infty }{\text{lim}}d\langle {\sum }_{\alpha }{\left({\mathbf{r}}_{\alpha }\left(t\right)-{\mathbf{r}}_{\alpha }\left(0\right)\right)}^2\rangle /4dt$ (where the bracket denotes an ensemble average and ${\mathbf{r}}_{\alpha }\left(t\right)$ represents the xy coordinate of the atom α at time t) after removing monolayer drifts.

Clustering of GM1 oligosaccharide conformations

We carried out conformational clustering of the GM1 oligosaccharide headgroup using an in-house-written clustering algorithm by aligning all heavy atoms, and extracting a total of 1000 snapshots from the last 200-ns trajectory of each run of GM1^10%, GM1^20%, and GM1^30%. The clustering was achieved in two steps, as our algorithm can only handle 1000 structures at a time. First, the 1000 individual structures for each GM1 molecule (e.g., 20 (GM1^10%), 40 (GM1^20%), and 60 (GM1^30%) GM1 molecules, respectively) were clustered using a 1-Å root mean-square deviation (RMSD) cutoff, and any cluster with more than 20 members was selected for each system. The resulting cluster conformations were then reclustered using the same 1-Å RMSD cutoff.

GM1-induced membrane curvature

The impact of GM1 concentration on the membrane curvature can be described by the free-energy derivative of each monolayer at the planar curvature, which can be calculated from the lateral pressure profile, $p\left(z\right)=p_L\left(z\right)-p_N\left(z\right)$, where $p_L\left(z\right)$ and $p_N\left(z\right)$ are the lateral and normal components of the pressure tensor, respectively, i.e., $p_L\left(z\right)=\left[p_{xx}\left(z\right)+p_{yy}\left(z\right)\right]/2$ and $p_N\left(z\right)=p_{zz}\left(z\right)$. The lateral pressure profile in the NAMD output is calculated using the Harasima contour (49), whose normal component $p_N\left(z\right)$ cannot be simply obtained (50). By noting that the bilayer systems were equilibrated (i.e., vanishing surface tension) and in mechanical equilibrium (uniform $p_N$), we estimated $p_N$ as

$$p_{\text{N}}=L_z^{-1}\underset{-L_z/2}{\overset{L_z/2}{\int }}dz{p}_{\text{L}}\left(z\right),$$ (1)

where the bilayer center is at z = 0 and L_z is the box size along the z axis. In pressure-profile calculations, the forces were evaluated at every 10 ps and p(z) was estimated according to a protocol suggested in a previous study of asymmetric bilayers (51). The calculated $p_N$ was close to the bulk pressure (≈1 bar) and its standard error from five replicas was <0.1 bar.

The leaflet free-energy derivative can be defined by the first moment of the pressure profile as (51, 52, 53)

$${\overline{F}}_{\text{T}}^{\prime }\left(0\right)=-\underset{0}{\overset{\infty }{\int }}dzzp\left(z\right)and{\overline{F}}_{\text{B}}^{\prime }\left(0\right)=\underset{-\infty }{\overset{0}{\int }}dzzp\left(z\right).$$ (2)

Here, we assume that the center of curvature for a given leaflet is located at the tail (headgroup) side for positive (negative) curvature (51). A leaflet (L = T or B for the top and bottom leaflets, respectively) would prefer a more positive curvature if ${\overline{F}}_{\text{L}}^{\prime }\left(0\right)<0$, whereas it would prefer a more negative curvature if ${\overline{F}}_{\text{L}}^{\prime }\left(0\right)>0$. The bilayer free-energy derivative is given by ${\overline{F}}^{\prime }\left(0\right)={\overline{F}}_{\text{T}}^{\prime }\left(0\right)-{\overline{F}}_{\text{B}}^{\prime }\left(0\right)$, which vanishes because of the symmetry in lipid composition between the leaflets.

GM1 clustering

We analyzed GM1 clustering at each concentration using a Voronoi tessellation approach (48), in which a cluster is composed of GM1s in the connected Voronoi cells. To analyze the contribution from the lipid chains and carbohydrates (CARB), lipids and CARB were separately tessellated. In the lipid tessellation, ceramide (CER) and POPC were represented by the atom selections used for A_L calculations. In the CARB tessellation, each CARB residue (a total of five in each GM1 molecule) was represented by its center of mass (COM) projected onto the xy plane. To properly tessellate CARB, supporting points around CARB were introduced, so that the area of Voronoi cells of CARB was bounded and comparable to that covered by heavy atoms of the corresponding CARB residue on the xy plane. The supporting points were chosen as follows: among six equally spaced points along a circle of radius 2d_cut centered at each CARB COM, supporting points were added only when they were neither within d_cut from COMs of other CARB nor within 1 Å from the already assigned supporting points. The value of d_cut was empirically adjusted and set to be 5 Å.

Using the resulting Voronoi tessellations for lipids and CARB from each snapshot of trajectories, we performed hierarchical GM1-GM1 clustering analyses. Initially, all GM1s (in the primary system) were assigned to different clusters. A pair of clusters (composed of GM1s in the primary system) was then merged when the shared border between Voronoi cells of each cluster was larger than d_cut (= 5 Å), where we considered GM1s both in the primary system and in their periodic images on the xy plane. The clustering was iterated until there was no cluster whose shared border with other clusters was longer than d_cut. We performed cluster analyses of CER-CER and CARB-CARB separately, and obtained the overall GM1-GM1 clusters as the union of the CER-CER and CARB-CARB clusters. We note that the size of an assigned cluster is bounded by the total number of GM1s in a leaflet, whereas the cluster may be connected to its own images and extended across the primary system (percolated).

Ordered-lipid clustering

To analyze the clustering of ordered lipids, we first obtained the time series of the ordered state for each lipid. We then clustered the ordered lipids using the ordered state maps onto the Voronoi tessellation of CER and POPC from each frame of trajectories. A similar approach was proposed for the identification of liquid-ordered regions of a bilayer on the basis of the local composition of the lipids (54).

In the first step of the analysis, we obtained the time series of the ordered state of lipids by using the hidden Markov model (HMM) for three observables: |S_CD|, monolayer thickness (d_M), and A_L, where the HMM consists of three hidden states (the lowest, intermediate, and highest ordered states) and nine emission states based on the value of the observables. As the terminology implies, 1) the (hidden) ordered states are not directly observable, but the emission states are observable; 2) the evolution of each lipid’s ordered state does not depend on its history (Markov process) and its transition to other states is modeled by a transition probability matrix; and 3) each ordered state has a set of probabilities over possible emission states, which is modeled by an emission probability matrix. Initially, the HMM was composed of a uniform transition probability matrix and an emission probability matrix deduced from the distribution of the observable of interest, where the observable space was partitioned into nine subspaces to assign discrete emission states. Using the input time series of the emission states for GM1 and POPC in a given leaflet, the HMM was trained by the Baum-Welch algorithm (55, 56) and the most likely ordered state sequence for each lipid was determined by the Viterbi algorithm (57).

The maps of the HMM-inferred ordered states for different observables on the Voronoi tessellation of lipid tails were correlated, and they varied significantly at 10% GM1 but agreed better at 30% GM1 (data not shown). To robustly determine a lipid-ordered state, we considered a combined ordered state from those for d_M and A_L because both are physically more transparent descriptors for the lipid order compared to the instantaneous |S_CD|. The combined ordered state of a lipid was deduced from a geometrical consideration of the lipid (expansion, compression, and tilt). The spatial distribution of ordered lipids (clusters) in a given frame was then investigated by clustering ordered lipids mapped onto the Voronoi tessellation of lipid tails, where the combined ordered states were estimated from exponential running averages of instantaneous ones over the previous 0.1 ns.

For the clustering, we first assigned ordered lipids from the map of the HMM-inferred ordered states on the Voronoi tessellation by the standardized Getis-Ord local spatial autocorrelation statistic $G_i^{\ast }$ (58, 59), where we assigned lipid i with $G_i^{\ast }>1$ as a member of the cluster core (i.e., statistical assignment of high-ordered-state lipids). Then, among unassigned lipids, we added POPC j with a positive $G_j^{\ast }$ and a sufficiently long shared border with the core GM1 (> d_cut), and the nearest neighbor GM1s to the assigned core (shared border > d_cut) iteratively. These tentatively assigned ordered lipids were clustered hierarchically with the same d_cut for the shared border between the clusters. After releasing POPC-only clusters, we obtained the ordered-lipid clusters, which we analyzed to calculate their size distribution and average compositions of GM1 and POPC. Similarly to the aforementioned GM1 clustering, in the cluster analysis, we determined the connectivity between a pair of clusters using the ordered lipids both in the primary system and in the images, where the size of an assigned cluster was given by the number of unique members (determined by using the lipid indices in the primary system).

Bilayer thickness of ordered and disordered regions

Using the results from the cluster analysis of ordered lipids, we calculated the d_H of ordered and disordered regions. To estimate the local d_H, for a lipid in a given leaflet, we assigned its nearest neighbor in the opposite leaflet as suggested by Pandit et al. (48). For the chosen lipid pair, we categorized the local bilayer properties into three classes: ordered (both lipids from ordered-lipid clusters), intermediate (only one lipid from ordered-lipid clusters), and disordered (no lipid from ordered-lipid clusters). In addition, we estimated the correlation of the ordered-lipid clusters between both leaflets by calculating the fraction of lipids in the ordered-lipid clusters whose nearest neighbor in the other leaflet belonged to the ordered-lipid cluster.

Results and Discussion

GM1-POPC bilayer structure and comparison with experiments

To get a general idea of lipid packing in the GM1-POPC membrane plane, we calculated the A_L and d_H of each lipid type (Table 1). The calculated A_L for POPC in GM1^10% (61.70 ± 0.05) was smaller than the experimental (62.7) (60) and calculated (63.7 ± 0.3) (61) A_L in a pure POPC bilayer system at 293 K. As shown in Table 1, A_L decreased for both POPC (from 61.70 ± 0.05 to 57.28 ± 0.47 Å²) and GM1 (from 55.75 ± 0.22 to 52.03 ± 0.30 Å²) with increasing GM1 concentration from 10% to 30% at 293 K. This correlates with the gradual increase in d_H: 29.2 Å (GM1^10%), 30.6 Å (GM1^20%), and 31.9 Å (GM1^30%), indicating an increase in lipid packing with increasing GM1 concentration.

Table 1.

Average Area per Lipid of POPC and GM1, the Thickness of Each System, and the Diffusion Coefficients of POPC and GM1

System	AL (Å2)		Thickness (Å)			DL (10−8 cm2/s)
	POPC	GM1	dH	dPP	dSS	POPC	GM1
GM110%	61.70	55.75	29.2	40.1 (39.0)	57.8	2.94	2.29
GM120%	59.30	53.84	30.6	41.1 (42.0)	59.0	1.48	1.16
GM130%	57.28	52.03	31.9	41.8 (40.6)	60.8 (61.7)	0.68	0.38

Experimental values obtained from McIntosh and Simon (9) are given in parentheses. The standard errors in A_L are <0.5 Å², and those in thicknesses are <0.25 Å from five independent runs. A_L, average area per lipid; D_L, diffusion coefficient; d_H, membrane hydrophobic thickness; d_PP, phosphate peak-to-peak distance; d_SS, oligosaccharide peak-to-peak distance.

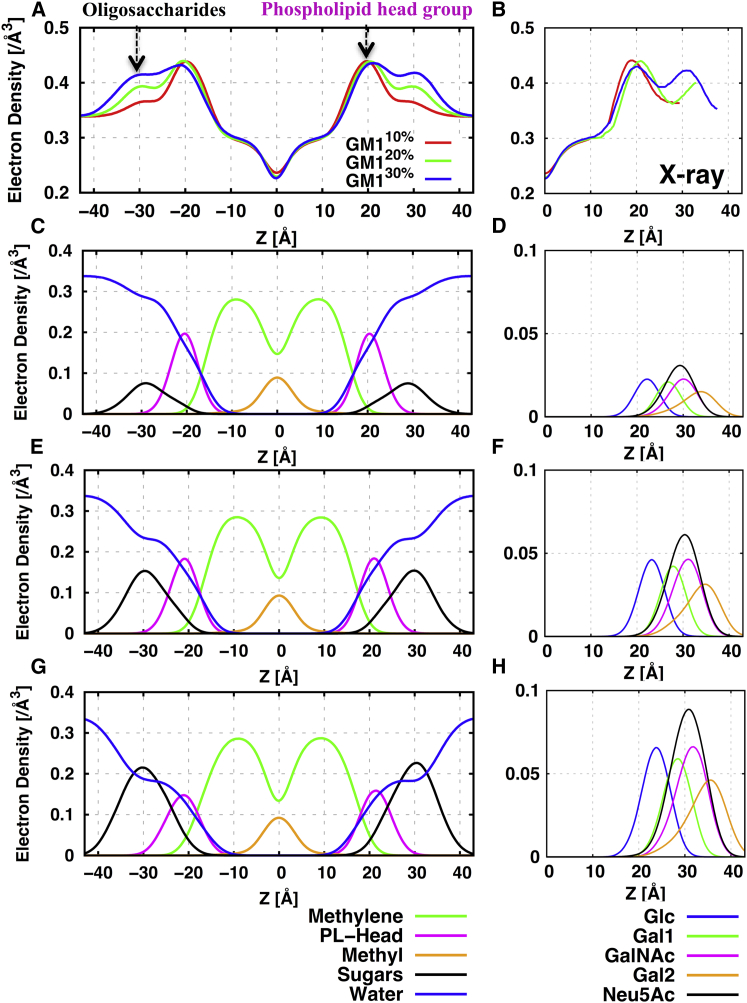
To elucidate the influence of GM1 concentration on the overall bilayer structure, we calculated electron density profiles (EDPs) along the membrane normal (i.e., the z axis). Fig. 3 shows the average locations of different molecular components, such as the terminal methyl group (at the bilayer center), methylene chains (medium density region around ±10 Å), phospholipid head (high density around ±20 Å), and GM1 oligosaccharide headgroup (peak around ±30 Å). The calculated EDPs were also compared with x-ray diffraction data (9) from multiwalled vesicles of egg phosphatidylcholine (EPC) with varying amounts of GM1 (10–30%). Consistent with the EDPs obtained from the x-ray experiment, there was a prominent effect on the overall bilayer structure between the maximal peaks with increasing GM1 concentration. Both the d_PP (phosphate peak-to-peak distance) and d_SS (oligosaccharide peak-to-peak distance) gradually increased with increasing GM1 concentration (Table 1). The calculated d_PP values in GM1^10% (40.1 ± 0.03 Å), GM1^20% (41.1 ± 0.06 Å), and GM1^30% (41.8 ± 0.24 Å) are in good agreement with the experimental d_PP values of 39.0 (GM1^10%), 42.0 (GM1^20%), and 40.6 Å (GM1^30%), considering the fact that the experimental measurements were done with EPC membranes (9). Although roughly 60% of membranes have acyl chains that match POPC (18:1/16:0), 30% of lipids have acyl chains that are 18:0 and 18:2, which would cause a slight difference in the values measured from our membranes. More importantly, McIntosh and Simon (9) suggested that the GM1 concentrations do not influence d_PP, implying that the experimental peak positions may have an uncertainty of ±1.5 Å (9). The calculated d_SS for GM1^30% (60.8 ± 0.25 Å) is slightly lower than the experimental d_SS of 61.7 Å, which may also be attributed to the membrane environments. The peak electron densities (Fig. 3) for the carbohydrate regions are 0.366 (GM1^10%), 0.393 (GM1^20%), and 0.416 (GM1^30%) electrons/ų, which are in excellent agreement with the experimental data (0.367, 0.394, and 0.410 electrons/ų). Similarly, the calculated phospholipid headgroup electron densities for GM1^10% (0.44), GM1^20% (0.44), and GM1^30% (0.43) are in excellent agreement with the experimental electron densities of 0.44 (10% and 20% GM1 in EPC bilayers) and 0.43 (30% GM1 in EPC bilayers) electrons/ų. In a recent experimental work (62), it was shown that EPC bilayers are nearly identical to pure POPC bilayers, and thus the agreement with experimental data is clear. GalNAc and negatively charged sialic acid (Neu5Ac) mainly contribute to the peaks related to the carbohydrate regions (Fig. 3). This contribution steadily increases with increasing GM1 concentration. Overall, the calculated differences between the d_H, d_PP, and d_SS values of GM1^10% and GM1^30% are 2.7 Å, 1.7 Å, and 3.0 Å, suggesting that notable changes occur in the overall bilayer structure with increasing GM1 concentration. In particular, the relatively greater differences in d_H and d_SS between GM1^10% and GM1^30% might suggest that an increase in clustering of GM1 leads to an increase in the hydrophobic chain order and more aligned carbohydrate orientations to the membrane normal.

Figure 3.

(A) Total EDPs along the membrane normal with increasing GM1 concentration. (B) Comparison with the x-ray data for z > 0. (C, E, and G) Electron density distribution for each membrane component (terminal methyl group, methylene chains of GM1 and POPC, phospholipid headgroup, GM1 oligosaccharide headgroup, and water) for GM1^10%, GM1^20%, and GM1^30%. (D, F, and H) Electron density distribution (z > 0) of each carbohydrate component in GM1^10%, GM1^20%, and GM1^30%. To see this figure in color, go online.

Oligosaccharide orientation and conformations

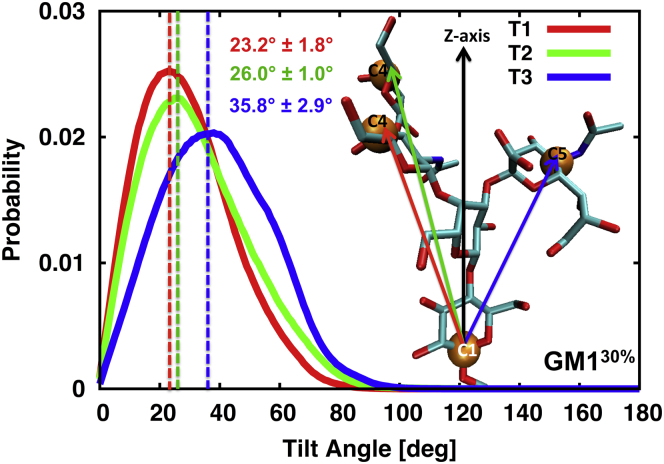
To determine the orientation of the GM1 oligosaccharide headgroup in the GM1-POPC membrane systems, we calculated the distributions of three tilt angles (T1, T2, and T3) from the membrane normal (Figs. 4 and S1). All three tilt angles are in the range of 0–90°, indicating the flexibility of the oligosaccharide orientation. The tilt-angle distributions in GM1^30% indicate that negatively charged Neu5Ac is more inclined toward the membrane. This is evident from the peak positions of T1 (23.2° ± 1.8°), T2 (26.0° ± 1.0°), and T3 (35.8° ± 2.9°).

Figure 4.

Tilt-angle distributions in GM1^30% with the peak tilt angles and standard deviations from the five replicas. T1 is a vector from the C1 carbon of residue Glc and the C4 carbon of GalNAc, T2 is a vector from the C1 carbon of residue Glc and the C4 carbon of residue Gal2, and T3 is a vector from the C1 carbon of residue Glc and the C5 carbon of residue Neu5Ac. The tilt-angle distributions in GM1^10% and GM1^20% are given in Fig. S1. To see this figure in color, go online.

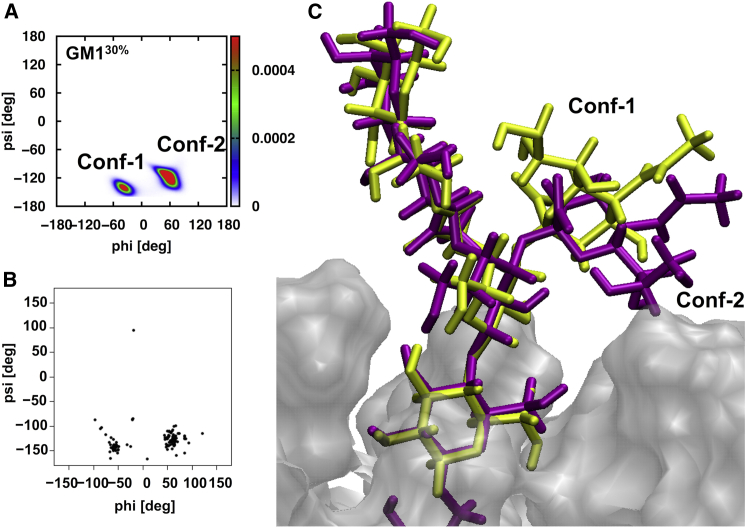
A comparison of the GM1 oligosaccharide conformations in the simulations and experiments (crystallographic and NMR structures) suggests an overall conformational rigidity that is independent of concentration. A cluster analysis of the oligosaccharide showed that the RMSD of the conformations explored by the oligosaccharide remained under 2 Å on the simulation timescale (Table S2). In addition, representative conformations of the top three clusters were also compared with the seven crystal structures of GM1 oligosaccharide, which were also found to be within 2 Å RMSD (Table S3). The conformational rigidity of the GM1 oligosaccharide is confirmed by the conformational space in the ϕ/ψ torsional distributions of glycosidic linkages (as defined in Fig. 1): β–Gal–(1→4)–β–Glc (ϕ₁/ψ₁; Fig. S2 A), β–GalNAc–(1→4)–β–Gal (ϕ₂/ψ₂; Fig. S2 B), β–Gal–(1→3)–β–GalNAc (ϕ₃/ψ₃; Fig. S2 C), and α–Neu5Ac–(2→3)–β–Gal (ϕ₄/ψ₄; Fig. 5 A). In solution, α–Neu5Ac–(2→3)–β–Gal may adopt three major low-energy conformations, as defined by their distinct ϕ₄ values (60°, –60°, and 180°) (63). Our simulations explored two main conformations: Conf-1 with ϕ₄ around –60° and Conf-2 with ϕ₄ around 60°, with a preference for Conf-2 (Fig. 5 A). As shown in Fig. 5 B, similarly to the current simulation, a PDB crystal structure survey of ϕ/ψ from 105 glycan structures containing α–Neu5Ac–(2→3)–β–Gal shows an overall preference for ϕ near 60° (Conf-2) over –60° (Conf-1). However, if the glycans only from GM1 x-ray structures are considered, the preference is shifted from Conf-2 to Conf-1. For example, Fig. 5 C shows an overlap of a Conf-2 simulation structure and a representative GM1 crystal structure (PDB: 3CHB). The oligosaccharide headgroup overlays well, with the only difference being in the orientation of Neu5Ac due to ϕ₄, and the overall RMSD of the two structures is only 0.9 Å. Interestingly, as the GM1 concentration increases, the population of the conformation with ϕ₄ ≈ –60° also increases (as shown in Fig. S3), which may be attributed to an increase in intermolecular CARB-CARB interactions (Fig. 2): the calculated CARB-CARB interaction energies are –12.15 ± 1.45 (GM1^10%), –26.85 ± 1.01 (GM1^20%), and –41.99 ± 1.26 kcal/mol (GM1^30%) (also see the following section). The effect of the different conformational preference of Neu5Ac is also reflected in minor differences between the calculated and experimental proton-proton distances (Table S4) (64, 65). The discrepancies associated with the proton-proton distances and ϕ₄/ψ₄ values of the GM1 crystal structures compared with the values calculated from the MD simulations could be related to 1) effects of phospholipid membranes, which may have altered the relative populations, as indicated by the tilt-angle distribution of Neu5Ac; 2) the crystal conformational preference, in particular for α–Neu5Ac–(2→3)–β–Gal linkage, may have been influenced by protein environments; 3) NMR nuclear Overhauser effect data, which were obtained from the carbohydrate-enriched surface of GM1-acetyl micelles and monomeric GM1 in DMSO; and 4) limited sampling of the dominant Conf-1 conformer observed experimentally.

Figure 5.

(A) The ϕ₄/ψ₄ (O6′–C2′–O_link–C3/C2′–O_link–C3–C2) torsion distribution of α–Neu5Ac–(2→3)–β–Gal of GM1 oligosaccharide in GM1^30%. (B) The ϕ/ψ distribution of α–Neu5Ac–(2→3)–β–Gal from 105 PDB crystal glycan structures with a resolution of <2.5 Å, obtained from the glycan fragment database (http://www.glycanstructure.org/fragment-db) (67). (C) Overlap of the top representative GM1 oligosaccharide Conf-2 simulation structure (purple) and the crystal conformation (PDB: 3CHB) representing Conf-1 (yellow). To see this figure in color, go online.

Lipid and carbohydrate H-bonding

As a unique structural feature among lipids, CER has both H-bonding donors (–NH and –OH) and acceptors (C=O and –OH), whereas POPC has only H-bonding acceptors ($-{\text{PO}}_4^{-}$ and C=O). We characterized lipid-lipid interactions in terms of H-bonding occupancy between CER-CER and POPC-CER, and the results are summarized in Table S5. On average, CER-CER H-bonding occupancy increased from 12% (GM1^10%) to 16.9% (GM1^20%) and 27.6% (GM1^30%). Compared to CER-CER, POPC-CER H-bonding was stronger and rather similar regardless of GM1 concentration: the average H-bonding occupancy was 42–44% in all of the systems, suggesting that POPC may play a role as a spacer between GM1s (see below). Increased interlipid H-bonding for CER-CER with constant POPC-CER H-bonding could explain the observed gradual decrease in A_L and D_L, as well as the increase in d_H, with increasing GM1 concentration (Table 1). As the oligosaccharide portion of GM1 also has both H-bonding donors and acceptors, we analyzed intermolecular H-bonding of GM1 in terms of CARB-POPC (five monosaccharides of GM1 interacting with POPC), CARB-CER (five monosaccharides of GM1 interacting with CER), and CARB-CARB (five monosaccharides of GM1 interacting with one of the five monosaccharides of another GM1), including intramolecular carbohydrate interactions (Table S5). There was a significant increase in the intermolecular H-bonding occupancies of CARB-CARB from ∼9% (GM1^10%) to ∼33% (GM1^30%), with one-third of contributions coming from Neu5Ac at all concentrations. Interestingly, the consistent increase in CER-CER and CARB-CARB H-bonding occupancies and interaction energies indicates that an increase in GM1 concentration facilitates GM1-GM1 interactions and thus GM1 clustering (see below).

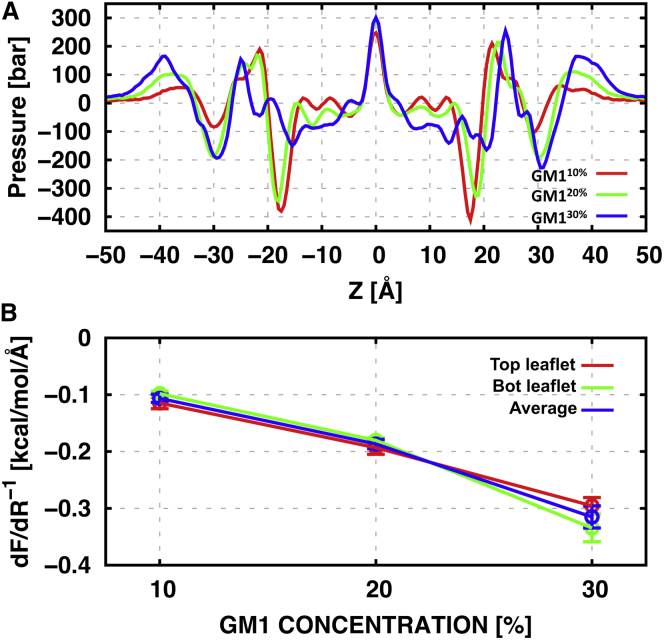
Impact of GM1 on membrane curvature

The lateral pressure along the membrane normal, p(z), is affected by GM1-GM1 and GM1-POPC interactions, and thus can alter the mechanical properties of bilayers, including their curvature. The effects of GM1 concentration on p(z) are shown in Fig. 6 A, where one can identify characteristic peaks due to chain entropy at the bilayer center, phospholipid-water interface around 20 Å, and GM1 carbohydrate-water interface around 40 Å. Between these peaks, there are characteristic dips due to phospholipid headgroup interactions (slightly below 20 Å) and GM1 carbohydrate interactions (∼30 Å). As the GM1 concentration increases, the peaks and dips associated with GM1 become stronger, whereas the dips associated with POPC become weaker. In addition, there is a noticeable shift of the outermost peaks toward bulk water. In GM1^30%, the pressure profile becomes notably asymmetric and shows a qualitatively different behavior compared to those obtained for GM1^10% and GM1^20% over 5–20 Å, which may be attributed to segregation of ordered lipids at 30% (Fig. 2 and see the next section).

Figure 6.

(A) Pressure profiles in GM1^10%, GM1^20%, and GM1^30%, calculated from the last 220 ns of the trajectories. (B) Derivative of the deformation free energy $\overline{F^{\prime }}\left(0\right)$ as a function of GM1 concentration. To see this figure in color, go online.

We investigated the effect of GM1 concentration on the membrane curvature by calculating the derivative of the deformation free energy $\overline{F^{\prime }}$(0) at the planar membrane curvature using Eq. 2, and found that it was negative for all bilayer systems and its magnitude increased with increasing GM1 concentration (Fig. 6 B). Negative $\overline{F^{\prime }}$(0) indicates that the bilayer prefers a positive curvature in the presence of GM1, which is consistent with experimental evidence for GM1-enriched microdomains in caveolae (3, 66) and the previously reported positive curvature for the N-palmitoyl-d-sphingomyelin bilayer system (33).

GM1 clustering and potential segregation

The arrangements of GSLs in phospholipid bilayers define their roles as recognition sites and in several other cellular processes (3, 6). To quantify the GM1 chain structures with increasing GM1 concentration, we calculated the chain order parameters of all systems. An increase in chain order parameters with increasing GM1 concentration indicates more ordered acyl chains due to increasing relative amounts of saturated acyl chains of GM1 (Figs. 2 and S4), which is consistent with a decrease in A_L and increase in d_H (Table 1). These observations imply that GM1s interact more with each other at higher GM1 concentrations, i.e., GM1s can form bigger clusters.

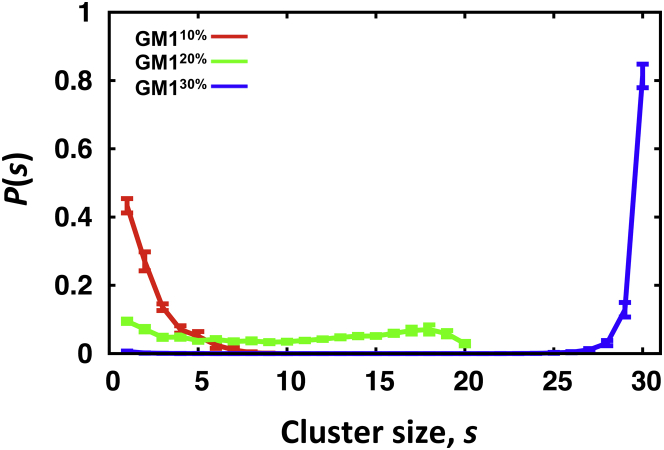
To assess the influence of GM1 concentration on GM1 clustering and cluster size, we analyzed GM1 clustering as a combination of CER-CER and CARB-CARB clusters at each concentration (see Materials and Methods). The size of the GM1 clusters was dominated by contributions from the CARB-CARB clusters, and the size of the CER-CER clusters remained small (<10) at all GM1 concentrations (data not shown). The GM1 clustering exhibited different characteristics at each GM1 concentration, as indicated by the probability that a GM1 belongs to an s-size cluster, P(s) (Fig. 7). In GM1^10%, the majority of GM1s belonged to small clusters (s < 5), which agrees with the reported P(s) for GM1 clusters in a study of coarse-grained plasma membrane model by Ingólfsson et al. (26). In GM1^20%, P(s) became broad, with a hump close to its maximum size. In GM1^30%, P(s) indicates that most GM1s belonged to a single big cluster. A percolated cluster (i.e., a continuous chain of GM1-GM1 contacts beyond the periodic boundaries) was observed occasionally in GM1^20% and, in GM1^30%, the cluster was strongly percolated, as illustrated in Fig. S5. Together with |S_CD| (Fig. S4), this indicates that CARB-CARB interactions are the main driving force for GM1 clustering.

Figure 7.

Probability that a GM1 belongs to a cluster of size s, P(s), in GM1^10% (red), GM1^20% (green), and GM1^30% (blue). The maximum cluster sizes are 10 (GM1^10%), 20 (GM1^20%), and 30 (GM1^30%). To see this figure in color, go online.

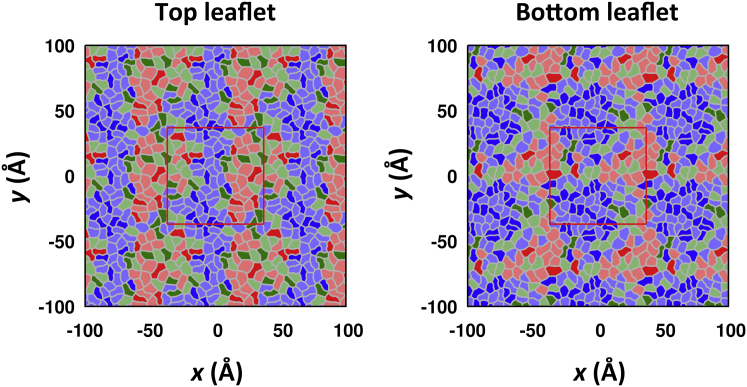
The impact of GM1-GM1 clustering on lipid packing was clearly observed, as shown in Fig. 2 and the overlay of |S_CD| for each GM1 and POPC molecule in Fig. S6, where more lipids have higher |S_CD| with increasing GM1 concentration and the overlay is wider toward higher |S_CD|, implying a coexistence of low- and high-ordered lipids. This observation raises a question about how ordered lipids are distributed, i.e., whether finite-sized clusters are dispersed or are aggregated into a big cluster. To get an idea of how the ordered lipids were distributed, we mapped instantaneous |S_CD| of lipids in each leaflet onto its Voronoi tessellation (Fig. 8), where the ordered-lipid cluster appeared to be aggregated in GM1^30%. However, it should be noted that the instantaneous |S_CD| for lipids away from the core of the ordered-lipid cluster fluctuated from low to high values, so statistically robust methods are required for a quantitative cluster analysis.

Figure 8.

|S_CD| maps in GM1^30%, illustrating the segregation of ordered lipids at the top and bottom leaflets for a final snapshot at 500 ns. The |S_CD| values are mapped onto a Voronoi tessellation with different colors: |S_CD| < 0.17 (red), 0.17 ≤ |S_CD| < 0.27 (green), and |S_CD| ≥ 0.27 (blue). POPC Voronoi regions are mapped with lighter colors to distinguish them from GM1 regions. The primary cell (simulation box) is shown as a red box. To see this figure in color, go online.

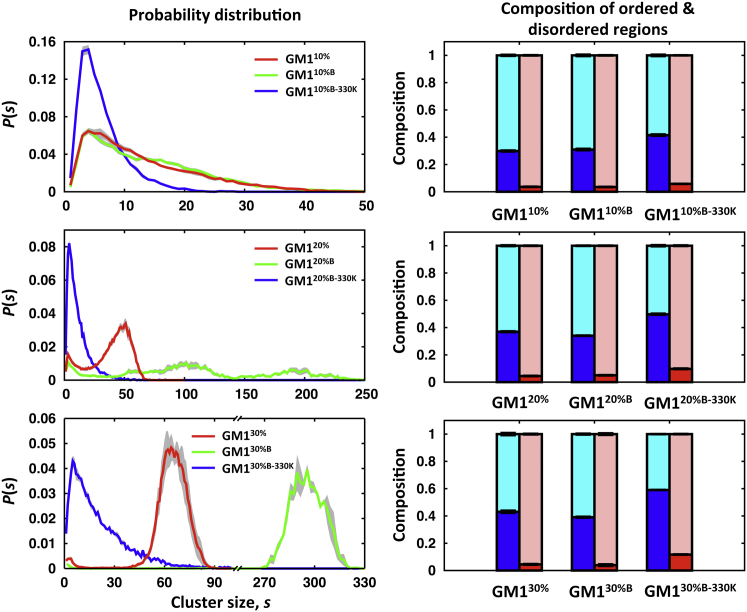
To quantify the clustering of ordered lipids (composite of GM1 and POPC) at each GM1 concentration, we performed a cluster analysis using ordered-state maps, where the ordered states were obtained by combining those determined from the HMM analyses of d_M and A_L (see Materials and Methods). The characteristics of ordered-lipid clusters at each GM1 concentration are consistent with those of GM1-GM1 clusters, which is shown by the probability of a lipid belonging to an s-size ordered-lipid cluster, P(s) (Fig. 9), i.e., finite-sized clusters (GM1^10%), a mixture of finite-size clusters and occasionally percolated cluster (GM1^20%), and strongly percolated cluster of ordered lipids (GM1^30%), as also shown in Fig. S5. The composition of GM1 in the ordered-lipid clusters increased from 30% (GM1^10%) to 43% (GM1^30%). A plausible explanation for this observation is that the POPCs that packed between GM1s were squeezed out from the clusters due to stronger interactions between GM1s at higher GM1 concentrations. The composition of GM1 in the outside of the clusters was low (<5%) and did not show a meaningful dependence on GM1 concentration.

Figure 9.

Cluster analysis of ordered lipids. The left panels show the probability of a lipid (POPC or GM1) belonging to an s-sized cluster, P(s), with the standard errors (shown as gray area). The right panels show the compositions of GM1 and POPC in the ordered-lipid clusters and outside the clusters. Blue, GM1 in ordered-lipid clusters; cyan, POPC in ordered-lipid clusters; red, GM1 outside the clusters; pink, POPC outside the clusters. Note that the maximum cluster sizes are 100 (GM1^10%, GM1^20%, and GM1^30%) and 400 (GM1^10%B, GM1^10%B-330K, GM1^20%B, GM1^20%B-330K, GM1^30%B, and GM1^30%B-330K), where superscript B and B-330K stand for fourfold larger systems at 293 K and 330 K, respectively. To see this figure in color, go online.

Using the results from the cluster analysis of ordered lipids, we calculated the d_H of ordered and disordered regions (Table 2). Consistent with the d_H and d_SS values given in Table 1, the d_H for ordered regions became larger with increasing GM1 concentrations as expected. However, the d_H for disordered regions was maintained up to 20% GM1 concentration and slightly decreased at 30% GM1 concentration. This may indicate that the bilayer properties of GM1^30% are qualitatively different from those of GM1^10% and GM1^20%. We attribute this to strongly percolated ordered-lipid clusters at the 30% GM1 concentration, which could explain the qualitative difference shown in p(z) (Fig. 6) and P(s) (Figs. 7 and 9) in GM1^30% compared to GM1^10% and GM1^20%. The fraction (f_O) of lipids in the ordered-lipid clusters whose nearest neighbor in the other leaflet belonged to the ordered-lipid cluster became greater with increasing GM1 concentration: 15% ± 1% (GM1^10%), 34% ± 2% (GM1^20%), and 54% ± 2% (GM1^30%). This indicates that the correlation between ordered-lipid clusters in two leaflets becomes higher as the GM1 concentration increases.

Table 2.

Average Bilayer Thickness, d_H, of Ordered and Disordered Bilayer Regions

System	Ordered	Intermediate	Disordered
GM110%	31.5 ± 0.2	29.9 ± 0.0	28.4 ± 0.1
GM120%	33.1 ± 0.3	30.7 ± 0.1	28.5 ± 0.1
GM130%	34.9 ± 0.4	30.5 ± 0.2	27.3 ± 0.3
$\Delta d_{\text{H}}$	3.4 ± 0.6	0.6 ± 0.2	−1.1 ± 0.4

The average d_H (Å) and its standard error were calculated over five independent runs. Δd_H is the thickness difference between GM1^30% and GM1^10%. The bilayer regions are categorized into three classes based on the local bilayer properties from a pair of the nearest neighboring lipids in the top and bottom leaflets (see Materials and Methods): ordered (both lipids from ordered-lipid clusters), intermediate (only one lipid from ordered-lipid clusters), and disordered (no lipid from ordered-lipid clusters).

Influence of system size and temperature on GM1 clustering

As the ordered-lipid clusters in GM1^20% and GM1^30% appeared to be extended over the simulation box, we made and simulated fourfold larger systems to determine whether the cluster size depends on the system size. This was done for all three concentrations at two different temperatures 293 K and 330 K (GM1^10%B, GM1^20%B, GM1^30%B, GM1^10%B-330K, GM1^20%B-330K, and GM1^30%B-330K). As shown in Fig. S7, there is no significant difference between P(s) for GM1-GM1 clusters in GM1^10% and GM1^10%B, and the overall shapes of P(s) in GM1^20% and GM1^30% are similar in different system sizes at 293 K: i.e., a broad range of their span (GM1^20%) and a predominant (percolated) big cluster near the maximum cluster size (GMI^30%). However, the cluster size increases with the system size in both GM1^20%B and GM1^30%B, suggesting that the GM1-GM1 clusters tend to aggregate. For systems at 330 K, P(s) becomes broadened and its peak is shifted to smaller cluster sizes, which is marginal and expected due to the higher thermal energy of lipids.

Similar to the case of GM1-GM1 clusters, the P(s) values for the ordered-lipid clusters in GM1^10% and GM1^10%B overlap well, and those for GM1^30% and GM1^30%B show the same characteristics in that there is a predominant (percolated) big cluster with different peak positions due to the system size difference (Figs. 9 and S8). However, the P(s) values in GM1^20% and GM1^20%B look completely different at first glance. Upon more careful examination, we found common patterns in P(s), e.g., P(s) in a range of 1–130 and 130–250 in GM1^20%B compared to a similar dual-peak pattern in GM1^20%. The largest clusters (with a size of ∼200) generally extended over the simulation box and occasionally were percolated. These behaviors suggest that ordered-lipid clusters at 20% GM1 concentration tend to be segregated, but their interactions are not strong enough to form a percolated cluster. The correlation between ordered-lipid clusters between leaflets is similar to that observed for the smaller systems, where f_O was estimated as 18% ± 1% (GM1^10%B), 44% ± 4% (GM1^20%B), and 65% ± 3% (GM1^30%B).

At a higher temperature of 330 K, the P(s) values in all systems indicate that the ordered-lipid clusters were fragmented into smaller clusters compared to those at 293 K (Figs. 9 and S9). In addition, percolated ordered-lipid clusters were not observed in all systems, though the percolation of GM1-GM1 clusters still occurred at 30% GM1 concentration (Fig S9 C). These results suggest that CARB-CARB interactions between GM1s are not strong enough to hold the aggregated ordered lipids, so small clusters are dispersed at 330 K up to 30% GM1 concentration. The differences between the systems at 293 K and 330 K are evident from the calculated d_H (Table S6), with a reduction in d_H for the ordered regions and smaller variations in d_H between different bilayer regions at 330 K. These differences are also reflected in the lower f_O values compared to the corresponding system at 293 K: 7% ± 1% (GM1^10%B-330K), 14% ± 0% (GM1^20%B-330K), and 22% ± 1% (GM1^30%B-330K). It should be noted that the observed differences between the systems at 293 K and 330 K are consistent with the results from ordered-lipid cluster analysis, whereas GM1-GM1 cluster analysis is not able to capture these differences due to the dominance of CARB-CARB interactions in it.

Conclusions

To gain molecular level insight into GM1-rich membranes, we performed all-atom MD simulations of GM1 in POPC phospholipid bilayer model systems. We validated the membrane bilayer structures in GM1^10%, GM1^20%, and GM1^30% by determining their EDPs and comparing them with those obtained from experiments. We then analyzed in detail the influence of the GM1 concentration (ranging from 10% to 30%) on the membrane physicochemical properties of the membrane, including the conformation and orientation of the oligosaccharide group of GM1, intermolecular interactions, membrane curvature, GM1 clustering, and ordered structure of the membrane. With increasing GM1 concentration, the lipids become packed more tightly, as reflected by 1) the increase in d_PP (and d_SS), the decrease in A_L and D_L, and higher |S_CD|; 2) the increase in interlipid H-bonding occupancy and GM1-GM1 (CER-CER and CARB-CARB) interactions; 3) the greater preference of GM1-containing membranes to have a positive curvature; and 4) the increase in the size of GM1-GM1 and ordered-lipid clusters. These observations indicate that the tighter lipid packing is mainly driven by inter-GM1 CARB-CARB interactions, which can induce segregation of ordered lipids and form a strongly percolated cluster at a 30% GM1 concentration at 293 K. At the higher temperature of 330 K, however, these interactions cannot maintain the segregation, which was successfully captured by the ordered-lipid cluster analysis, but not by the GM1-GM1 cluster analysis. The ordered-lipid cluster analysis presented here can be directly applied to various systems containing an order-inducing agent such as cholesterol.

Author Contributions

J.B.K. and W.I. designed research. D.S.P., S.P., and E.L.W. performed research. D.S.P., S.P., E.L.W., G.W., M.S.Y., J.B.K., and W.I. analyzed data. D.S.P., S.P., and W.I. wrote the manuscript, and all authors contributed to editing the manuscript.

Editor: Markus Deserno.