Kinetic Insights into the Binding between the nSH3 Domain of CrkII and Proline-Rich Motifs in cAbl

Abstract

The interaction between CrkII and cAbl is implicated in diverse cellular processes. This interaction starts with the binding of the N-terminal Src homology 3 (nSH3) domain of CrkII to the proline-rich motifs of cAbl (PRMs^cAbl). Despite its critical importance, the detailed binding mechanism between the nSH3 domain and PRMs remains elusive. In this study, we used nuclear magnetic resonance Carr-Purcell-Meiboom-Gill relaxation dispersion experiment to study the binding kinetics between the nSH3 domain of CrkII and PRMs^cAbl. Our results highlight that the nSH3 domain binds to three PRMs^cAbl with very high on- and off-rate constants, indicating the transient nature of the binding. To further characterize the binding transition state, we conducted the Eyring and linear free energy relationship analyses using temperature-dependent kinetic data. These data indicate that the binding transition state of the nSH3 domain and PRM is accompanied by small activation enthalpy, owing to partial desolvation of the transition state. These results also highlight the similarity between the transition and free states, in terms of structure and energetics. Although the binding of the nSH3 domain and PRM displays the features consistent with a diffusion-limited process within our experimental conditions, further tests are necessary to determine if the binding is a true diffusion-limited process.

Introduction

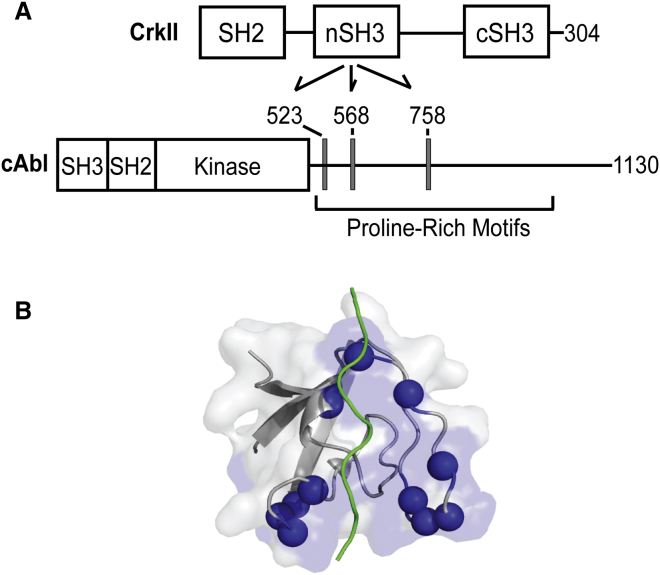
The interaction between CrkII and cAbl has been implicated in a number of cellular processes such as cell migration, proliferation, and apoptosis (1, 2, 3, 4, 5, 6). In addition, this interaction is highly significant in human cancer cells, as highlighted by various methods (7, 8). CrkII consists of three Src homology (SH) domains: SH2, and the N- and C-terminal SH3 (nSH3 and cSH3) domains (Fig. 1 A). The C-terminal half of cAbl protein mainly consists of structurally disordered regions and contains multiple proline-rich motifs (PRMs) (Fig. 1 A) (9). Recently, we identified that the nSH3 domain of CrkII recognizes three PRMs in cAbl (10). Although the interaction between CrkII and cAbl takes place at multiple sites in the two proteins (11, 12, 13), it is generally believed that binding through the nSH3 domain and PRMs is the first step of the interactions. Hence, it is important to understand the binding mechanism between nSH3 and PRM^cAbl.

Figure 1.

Interaction between CrkII and cAbl. (A) Domain organizations of CrkII and cAbl. (Arrows) Recognition of PRMs in cAbl by the nSH3 domain of CrkII. (Gray boxes) Three PRMs in human cAbl-1A are shown with residue numbers. (B) Crystal structure of nSH3:PRM⁷⁵⁸ (Protein Data Bank (PDB): 5IH2). (Blue spheres) Backbone amide nitrogen atoms that are used for NMR CPMG-RD experiments. (Green) PRM⁷⁵⁸. To see this figure in color, go online.

Intrinsically disordered proteins (IDPs) and proteins with intrinsically disordered regions (IDRs) play diverse roles in protein-protein interactions (14, 15, 16, 17). Many functional (or target-binding) regions in IDPs/IDRs are composed of short linear motifs (18), and PRMs are commonly found motifs in IDPs (19, 20). Hence, the interactions mediated by PRMs and their recognizing domains, such as SH3 and WW, constitute an important part of protein-protein interaction networks (21, 22, 23). In this light, the study of the interactions between the nSH3 domain and PRMs^cAbl is important to understand not only the interaction between CrkII and cAbl but also the binding mechanism of IDPs/IDRs-mediated protein-protein interactions. The study of binding mechanism of flexible proteins like IDPs is challenging, because association often accompanies large-scale conformational change or folding (16, 24, 25, 26, 27).

Investigation of the energetics and structure of the binding transition state is essential to elucidate the binding mechanism. A basic mechanism of interaction between a protein (P) and a ligand (L) consists of two steps:

$$P+L\rightleftharpoons P\cdot L^{\ast }\rightleftharpoons PL$$ (Scheme 1)

The first step corresponds to the association of two components, and the second step to the formation of a final complex structure. The loosely bound complex $\left(P\cdot L^{\ast }\right)$ is often called the transient or encounter complex (28, 29). The transition state takes place in between the transient and final product complexes. In the binding-induced folding mechanism of IDPs, the binding takes place through the formation of the encounter complex, i.e., the intermediate state, and subsequent folding to the final complex structure (24, 30). In some other cases, however, the two processes are not well separated, resulting in a single-step association—a so-called two-state binding process. For example, the interactions between SH3 domains and PRMs are typically described as a two-state process (31, 32). However, this does not automatically exclude the presence of an encounter complex. Instead, this indicates that the characteristics of the encounter complex and transition state must be very similar in the course of binding between SH3 and PRM, and that a particular experiment cannot distinguish the two binding steps.

Recently, we have identified that the nSH3 domain binds to three PRMs in cAbl with virtually identical affinities (K_d ≈ 1 μM) (10). This result naturally raises questions about the binding kinetics between the nSH3 domain and PRMs. Association and dissociation kinetics are important to understand the molecular basis of protein-protein interactions (14, 29, 33, 34, 35). Although a large number of thermodynamic studies of interactions between SH3 and PRM do exist, the molecular basis of their binding kinetics is not well understood. This is because the binding is so rapid that fast-mixing techniques, such as the stopped-flow method, are limited to low temperatures (32, 36).

Here, we investigated the binding kinetics of the nSH3 domain and all three PRMs^cAbl, using nuclear magnetic resonance (NMR) Carr-Purcell-Meiboom-Gill (CPMG) relaxation dispersion (RD) experiments (37, 38, 39). All the PRMs^cAbl bind to the nSH3 domain with k_on ≈ 10⁸ M⁻¹ s⁻¹ and k_off ≈ 500 s⁻¹. These results highlight the transient nature of the interactions between CrkII and cAbl. Furthermore, we investigated the binding transition state using temperature-dependent kinetic experiments. Overall, the binding transition state seems to be highly similar to the free state, in terms of the energetic and structural response to the temperature variation. Based on the analysis of viscosity-dependent kinetics, we also suggest that the association of the nSH3 and PRMs may proceed via an induced-fit binding mechanism.

Materials and Methods

Sample preparation

The protein samples used in this study were prepared as described in Bhatt et al. (10). Synthetic peptides were purchased in a crude form, and further purified using reverse-phase high-performance liquid chromatography in our laboratory. The N- and C-termini of peptides were acetylated and amidated, respectively. The peptide concentration was determined by measuring the UV absorption at 280 nm of a single tyrosine at the N- or C-terminal ends of the peptide.

NMR spectroscopy

All NMR experiments were conducted using protein samples in 20 mM sodium phosphate (pH 6.1), 80 mM NaCl, 0.02% sodium azide, 1 mM EDTA, 10 μM DSS (4,4-dimethyl-4-silapentane-sulfonate), and 10% D₂O at 25°C. NMR spectra were acquired on AVANCE 600 MHz and 800 MHz spectrometers (Bruker, Billerica, MA), equipped with a cryogenic probe. NMR spectra were processed with NMRPipe (40) and analyzed with NMRViewJ (One Moon Scientific, Westfield, NJ) and CARA (41). The assignment of ¹H, ¹³C, and ¹⁵N resonances was carried out using a set of experiments: (¹H, ¹⁵N) heteronuclear single quantum coherence (HSQC), (¹H, ¹³C) HSQC, HNCO (42), HNCACB (43), HN(CO)CA (44), HNCA (45), HN(CA)CO (46), CBCA(CO)NH (47), HBHA(CO)NH (48), and HC(C)H-TOCSY (49). ¹H chemical shifts were referenced with respect to DSS, and ¹³C and ¹⁵N chemical shifts were referenced indirectly (50). The temperatures of the NMR sample were calibrated using deuterated methanol-d₄ (51). The assignment of ¹H, ¹³C, and ¹⁵N resonances of the free nSH3 domain was deposited to the Biological Magnetic Resonance Bank (BMRB: 26870).

Binding kinetic measurements

The association and dissociation rate constants of nSH3:PRM complexes were measured using constant relaxation time Carr-Purcell-Meiboom-Gill (CPMG) single quantum relaxation dispersion (RD) experiments (37, 52). The concentration of the nSH3 domain was 200 μM. The molar ratios of nSH3 and PRMs were adjusted to make the population ratio of the complex become 5% of the entire nSH3 population. CPMG RD experiments were recorded with 14–16 different CPMG frequencies $\left({\nu }_{\text{CPMG}}\right)$, ranging from 50 to 1000 Hz, for each dispersion curve. CPMG RD data were acquired at two static magnetic fields (600 and 800 MHz). $R_{2,\text{eff}}\left({\nu }_{\text{CPMG}}\right)$ values were calculated from the peak intensities according to:

$$R_{2,\text{eff}}\left({\nu }_{\text{CPMG}}\right)=\frac{-1}{T_{\text{relax}}}\text{ln}\left[\frac{I\left({\nu }_{\text{CPMG}}\right)}{I\left(0\right)}\right],$$ (1)

where $T_{\text{relax}}$ is the length of relaxation delay, and $I\left(0\right)$ and $I\left({\nu }_{\text{CPMG}}\right)$ are the intensities of the peak at $T_{\text{relax}}=0$ and 40 ms with a given CPMG frequency, respectively. The uncertainty of $R_{2,\text{eff}}\left({\nu }_{\text{CPMG}}\right)$ was estimated by comparing the peak intensities of duplicated spectra of $I\left(0\right)$ and $I\left(50\text{Hz}\right)$. Using these differences in peak intensities, 100 Monte Carlo simulations were performed to measure the uncertainty: data fitting were repeated 100 times, and randomly selected uncertainties were added to peak intensities at each time. We assumed that the uncertainty is Gaussian distributed. In our experimental conditions, the uncertainties were ∼5% of $R_{2,\text{eff}}\left(50\text{Hz}\right)$. The estimated uncertainty was applied to all $R_{2,\text{eff}}\left({\nu }_{\text{CPMG}}\right)$. The CPMG-RD profiles were fitted using the Carver-Richards equation (Eq. 2) (53, 54) or the Luz-Meiboom equation (Eq. 3) (55) depending on the chemical exchange regime in the NMR timescale (56). The reported kinetic parameters are the results of the global fitting of multiple peaks using either the Carver-Richards or Luz-Meiboom equations:

$$R_2\left(v_{\text{CPMG}}\right)=0.5\left(R_{2,\text{free}}^{°}+R_{2,\text{bound}}^{°}+k_{\text{ex}}-2v_{\text{CPMG}}{\cosh }^{-1}\left(D_{+}\cosh \left({\eta }_{+}\right)-D_{-}\cosh \left({\eta }_{-}\right)\right)\right),D_{\pm }=0.5\left(\pm 1+\frac{\Psi +2\Delta {\omega }^2}{\sqrt{{\Psi }^2+{\xi }^2}}\right),{\eta }_{\pm }=\frac{\sqrt{\left(\pm \Psi +\sqrt{{\Psi }^2+{\xi }^2}\right)}}{2\sqrt{2}{v}_{\text{CPMG}}},\Psi =k_{\text{ex}}^2-\Delta {\omega }^2,\xi =-2\Delta \omega \left(p_{\text{free}}{k}_{\text{ex}}-p_{\text{bound}}{k}_{\text{ex}}\right).$$ (2)

$$R_2\left(v_{\text{CPMG}}\right)=R_2^{°}+\frac{{\Phi }_{\text{ex}}}{k_{\text{ex}}}\left(1-\frac{4v_{\text{CPMG}}}{k_{\text{ex}}}\tanh \left(\frac{k_{\text{ex}}}{4v_{\text{CPMG}}}\right)\right),R_2^{°}=p_{\text{free}}{R}_{2,\text{free}}^{°}+p_{\text{bound}}{R}_{2,\text{bound}}^{°},{\Phi }_{\text{ex}}=p_{\text{free}}{p}_{\text{bound}}\Delta {\omega }^2.$$ (3)

Binding assay

The dissociation constant (K_d) of nSH3:PRM⁷⁵⁸ complex was measured by monitoring the change of tryptophan fluorescence signal. Excitation wavelength was 295 nm. All binding assays were performed in a stirred 1 cm path-length cuvette using a QM-400 fluorimeter (Photon Technology International, HORIBA Scientific, Edison, NJ). Protein concentration used for the fluorescence-based binding assays was 0.1 μM. The measurements were done in 20 mM sodium phosphate (pH 6.1) and 80 mM or 1 M NaCl at 25°C. The K_d was calculated by assuming a 1:1 complex, and by the global fitting of the repeatedly measured fluorescence intensities to:

$$\Delta F=\Delta F_{\max }\left(\frac{\left[P_t\right]+\left[L_t\right]+K_d\pm \sqrt{{\left(\left[P_t\right]+\left[L_t\right]+K_d\right)}^2-4\left[P_t\right]\left[L_t\right]}}{2\left[P_t\right]}\right),$$ (4)

where ΔF and ΔF_max are the change and the maximum amplitude of signal change, respectively. P_t is the total protein concentration and L_t is the total ligand concentration at each titration point.

Results

The binding kinetics of nSH3 domain and PRMs^cAbl

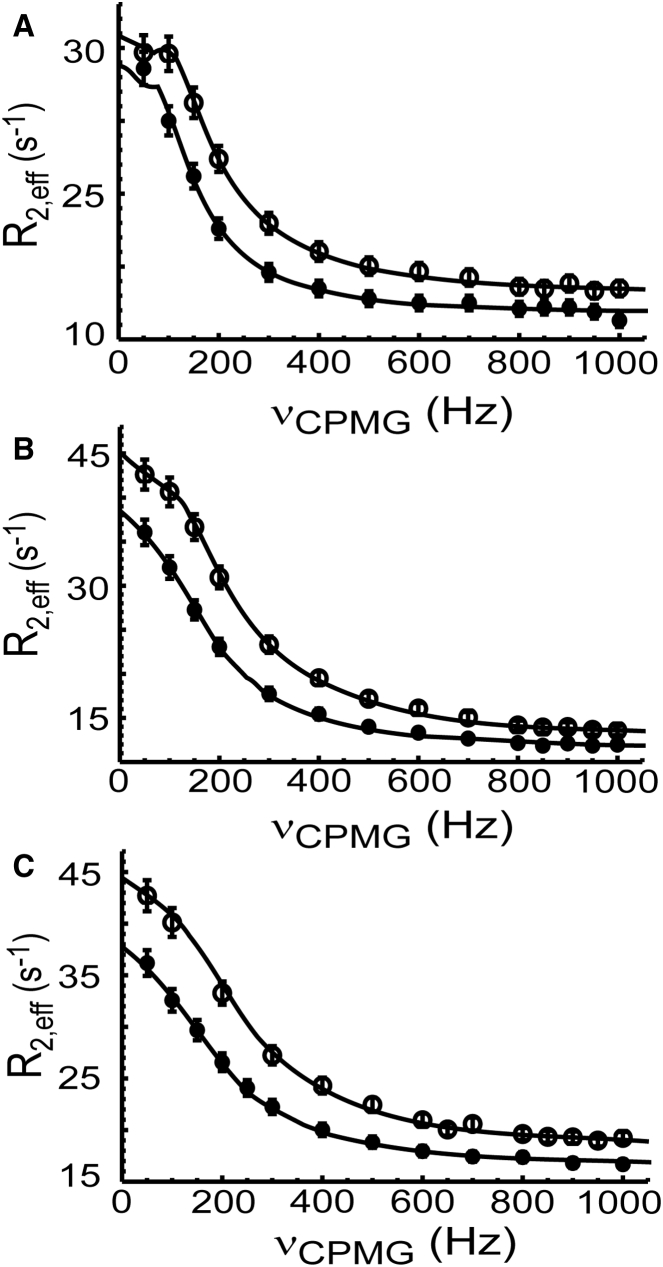
We have measured the binding kinetics of the nSH3 domain and PRMs using backbone ¹⁵N NMR CPMG-RD experiments (Figs. 1 B and 2). Overall, PRM⁷⁵⁸ binds and dissociates to the nSH3 domain slightly faster than other two PRMs (Table 1). The data fitting results for individual residues are shown in Fig. S1 and Table S1 in the Supporting Material. All three PRMs bound to the nSH3 domain with k_on close to the diffusion-limited rate constant (10⁸–10⁹ M⁻¹ s⁻¹) under some biasing forces such as electrostatics. Because our measurements were conducted with a low salt concentration (i.e., 80 mM NaCl), the measured k_on values are partially by long-range electrostatics (see Discussion). The dissociation rate constants (k_off) of the nSH3:PRM complexes also show modest variation, and this result indicates that the lifetime of the complexes is very short (∼1 ms).

Figure 2.

Representative ¹⁵N CPMG-RD profiles (W169) measured for the binding of the nSH3 domain to (A) PRM⁵²⁴, (B) PRM⁵⁶⁸, and (C) PRM⁷⁵⁸. Data obtained at 14.1 Tesla (solid circles) and 18.8 Tesla (open circles) magnetic fields. The population of PRM-bound nSH3 domain is adjusted to be 5% of the entire protein population.

Table 1.

Kinetic Parameters for the Interactions between the nSH3 Domain and PRMs at 298 K

PRMs	kon (108 M−1 s−1)	koff (s−1)
PRM524 (QAPELPTKTRTSY)	2.01 ± 0.58	345.2 ± 32.0
PRM568 (VSPLLPRKERGY)	2.38 ± 0.26	689.1 ± 60.5
PRM758 (YEKPALPRKR)	5.48 ± 0.20	933.5 ± 104.9

In the CPMG-RD experiments, we adjusted the population of the minor state (i.e., ligand-bound state) to 5% of the total population, based on the measured K_d values. Because the minor state population is small, a relatively small number of peaks displayed dispersion profiles. On average, we observed ∼12–15 peaks showing dispersion profile in each sample. However, considering the quality of dispersion profiles of the peaks as described below, several peaks from each sample were analyzed to measure the kinetic parameters (Table S1). Most of the peaks that showed dispersion behavior correspond to the residues at the nSH3:PRM interface (Fig. 1 B). In addition, these peaks showed gradual chemical shift changes during the titration of ligand to the nSH3 domain (Fig. S2). This demonstrates that they undergo chemical exchange in intermediate-to-fast NMR timescales. CPMG-RD profiles were analyzed using the Carver-Richards (53, 54) or Luz-Meiboom equations (55), depending on k_ex (= k_on(L) + k_off) relative to Δω (= ω_15N,free − ω_15N,complex) (56). Because of the complexity of the Carver-Richards equation, and interdependency between fitting parameters (57), the Carver-Richards equation was only applied when R_ex > 2.5 s⁻¹. The analyzed peaks did not display CPMG-RD profiles in the free and PRM-saturated nSH3 domains (Fig. S3).

The k_on and k_off values obtained for the nSH3:PRM^cAbl complexes agree well with those of nSH3:PRM^Sos, which were measured using NMR line-shape analysis (58). In addition, the k_on and k_off values measured for the nSH3:PRM^C3G complex were 1.0 × 10⁸ M⁻¹ s⁻¹ and 50 s⁻¹, respectively, using the stopped-flow fluorescence method (36). However, because of the fast binding kinetics, the authors measured the rate constants at 15°C. To compare this with our results, we assumed that the kinetic activation energy is between 3 and 10 kcal mol⁻¹. This assumption is valid based on the Eyring analysis (see below). In this range of activation energy, the rate constant doubles when the temperature increases by 10°C. Therefore, the estimated k_on and k_off values for the nSH3:PRM^C3G at 25°C agree well with our results. The binding kinetics of the Fyn SH3 domain and PRM has comparable temperature dependence (31). The binding kinetics was also measured for several other SH3:PRM interactions using NMR CPMG-RD experiment or line-shape analysis (31, 58, 59). Despite some variation in the experimental conditions, reported k_on and k_off values are ∼10⁸ M⁻¹ s⁻¹ and 100 s⁻¹, respectively.

Although surface plasmon resonance (SPR) has been used to measure the binding kinetics of SH3 domains and PRMs, the results are often significantly different from those obtained by NMR methods (31, 60). The difference was attributed to slow diffusion through the hydrated matrix in the SPR study. The binding kinetics of PRM derived from DOCK180 to nSH3 was measured by SPR. Although the direct comparison is not possible, because the sequence of PRM^DOCK180 is different from our PRMs^cAbl, the reported k_on and k_off of the nSH3:PRM^DOCK180 complex differ from our results by >1000-fold (60).

Validation of a two-state binding model of nSH3 and PRM interaction

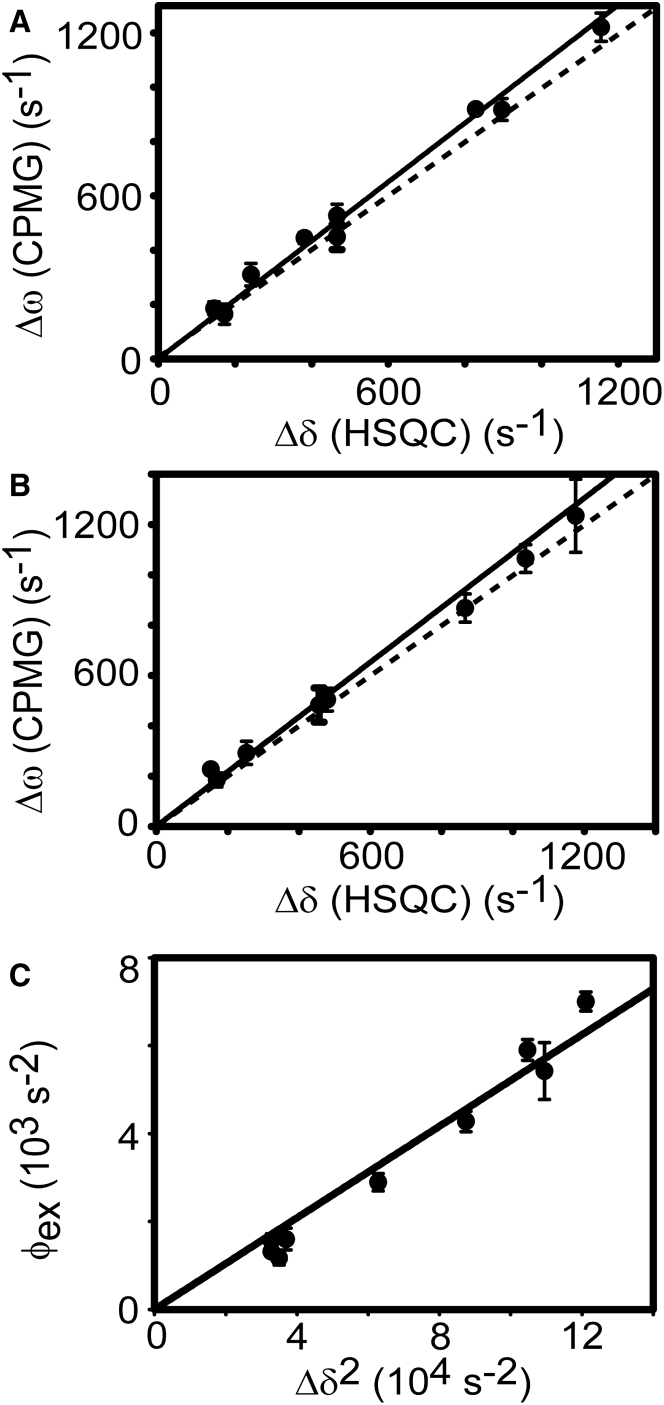
Fitting of the CPMG-RD profiles using the Carver-Richards or Luz-Meiboom equations provides additional parameters, Δω and ϕ_ex (= p₁p₂Δω²), respectively, in addition to k_ex. The value Δω is the ¹⁵N chemical shift difference between the major (p₁) and minor (p₂) conformational states. In the context of our study, the major and minor states correspond to the free and PRM-bound states, respectively. These parameters are useful for validation of the fitting model. Throughout this study, we use a two-state binding model. Hence, to examine if a two-state model is valid to study the binding of the nSH3 domain to PRMs, we compared the Δω from the data fitting with the Δδ measured by comparing HSQC spectra of free and ligand-saturated samples (Fig. 3, A and B). When a ligand binds to a protein in a two-state manner, the plot of Δω and Δδ is expected to form a linear curve with a slope of 1, as shown in Fig. 3. The observation of linear correlation between Δω and Δδ does not exclude the presence of the alternative binding model, and instead, these results demonstrate that the two-state model is appropriate for the analysis of CPMG-RD data.

Figure 3.

Correlation of the ¹⁵N chemical shift differences estimated by CPMG-RD and comparing HSQC spectra of free and PRM-saturated nSH3 domains: (A) PRM⁵²⁴-, (B) PRM⁵⁶⁸-, and (C) PRM⁷⁵⁸-bound nSH3 domains. The Δδ values were measured by comparing the HSQC spectra of free nSH3 and PRM-saturated nSH3 samples. Δω and ϕ_ex were estimated by applying the Carver-Richards and the Luz-Meiboom equations to the CPMG-RD data, respectively. The dotted lines in (A) and (B) are hypothetical diagonal lines and shown to guide the eye and are not regression curves. (Solid lines) Linear regression line.

The binding of the nSH3 domain and PRM⁷⁵⁸ was mainly analyzed using the Luz-Meiboom equation. The population of the minor (ligand-bound) state was calculated using the plot of ϕ_ex versus Δδ² (Fig. 3 C). The slope of this plot represents p₁p₂ and was calculated to be 0.051. This agrees well with the expected value (0.047), based on the K_d of the nSH3:PRM⁷⁵⁸ complex. This plot also provides experimental evidence for a two-state binding model. If the PRMs were binding to the nSH3 domain through a process more complicated than the two-state model, the plot would show a nonlinear curve.

Temperature-dependent chemical shift perturbation upon nSH3:PRM complexation

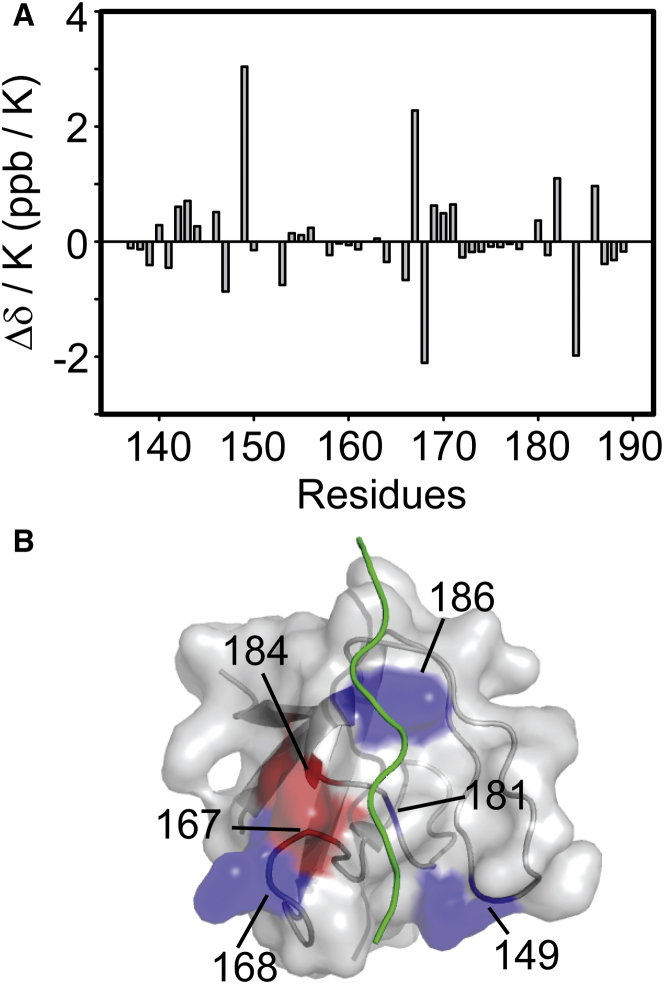
We measured the NMR chemical shift changes (Δδ) between the free and PRM⁷⁵⁸-bound states of the nSH3 domain at six different temperatures, ranging from 15 to 40°C. The purpose of this experiment is twofold. First, the observed Δδ (¹⁵N) values serve as important probes to monitor the quality of the data fitting results during the temperature-dependent CPMG-RD analysis. Second, the temperature coefficient of the amide proton chemical shift (Δδ (¹HN)/ΔT) provides information about the local melting of the structure as the temperature changes (61). When Δδ (¹HN)/ΔT is smaller than −4.5 ppb/K, the local structure is considered well-ordered and stable. The average temperature coefficients of the nSH3 domain (residues 134–189) in the free and PRM-bound states are –3.56 and –3.33 ppb/K, respectively. We excluded the residues in the N- and C-terminal tails in this analysis because the regions are structurally disordered. When the temperature coefficients of the free and PRM-bound nSH3 domains were compared, only six residues show the change in temperature coefficient >±1.0 ppb/K (Fig. 4). All these six residues are located in the binding interface with PRM, indicating structural changes upon complexation. These results suggest that the difference in temperature-dependent structural change between the free and PRM-bound states is minimal, and does not considerably influence the temperature dependence of K_d and association/dissociation rate constants. This provides an important structural basis to our Eyring and van’ t Hoff analysis.

Figure 4.

(A) Difference in Δδ/ΔT between the free and PRM⁷⁵⁸-bound nSH3 domains: ΔΔδ/ΔT = Δδ/ΔT(complex) – Δδ/ΔT(free). (B) The residues, whose ΔΔδ/ΔT values are >+1.0 ppb/K (blue) and <−1.0 ppb/K (red) in the structure of nSH3:PRM⁷⁵⁸. To see this figure in color, go online.

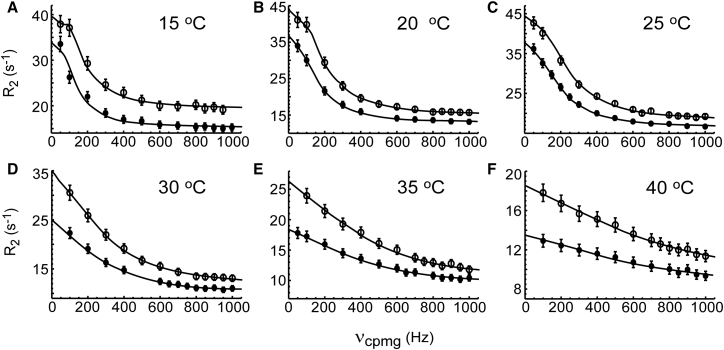
Temperature-dependent binding kinetics of nSH3 and PRM

To characterize the transition state of binding between the nSH3 and PRM, we conducted temperature-dependent binding kinetics measurements. We used PRM⁷⁵⁸ as a representative of other PRMs because detailed structure and thermodynamic characterizations of the nSH3:PRM⁷⁵⁸ interaction are available. We characterized the binding kinetics at six different temperatures ranging from 15 to 40°C, using NMR CPMG-RD experiments (Table 2; Fig. 5). Because k_ex changes with temperature, we applied the Carver-Richards equation to all the data obtained at 15 and 20°C and several residues at 25°C. We applied the Luz-Meiboom equation to the data obtained at 25, 30, 35, and 40°C. To confirm that the binding of the nSH3 domain and PRM maintains a two-state process over the temperature range, we compared the fitted parameters, Δω and ϕ_ex, with HSQC-derived Δδ. The good agreement of these parameters indicates that the two-state mechanism is a valid model for the binding between the nSH3 and PRM in this temperature range (Fig. S4).

Table 2.

Temperature-dependent Kinetic Parameters for the Interactions between the nSH3 Domain and PRM⁷⁵⁸

Temperature (K)	kon (108 M−1 s−1)	koff (s−1)	Kd (μM)a
288	4.39 ± 0.18	375.8 ± 44.0	0.85 ± 0.11
293	5.26 ± 0.14	648.1 ± 72.2	1.23 ± 0.10
298	5.48 ± 0.20	933.5 ± 104.9	1.70 ± 0.48
303	7.03 ± 0.18	1641.9 ± 72.7	2.34 ± 0.41
308	7.42 ± 0.18	2519.3 ± 299.2	3.39 ± 0.47
313	9.79 ± 0.25	4233.2 ± 380	4.32 ± 1.03

^aThe equilibrium dissociation constants were determined by detecting fluorescence intensity change of nSH3 domain upon binding to nSH3 domain (10).

Figure 5.

Representative ¹⁵N CPMG-RD profiles (W169) of the nSH3 domain partially saturated by PRM⁷⁵⁸ at (A) 15, (B) 20, (C) 25, (D) 30, (E) 35, and (F) 40°C. Data were obtained at 14.1 Tesla (solid circles) and 18.8 Tesla (open circles) magnetic fields. The population of the PRM-bound nSH3 domain is adjusted to be 5% of the entire protein population in NMR samples.

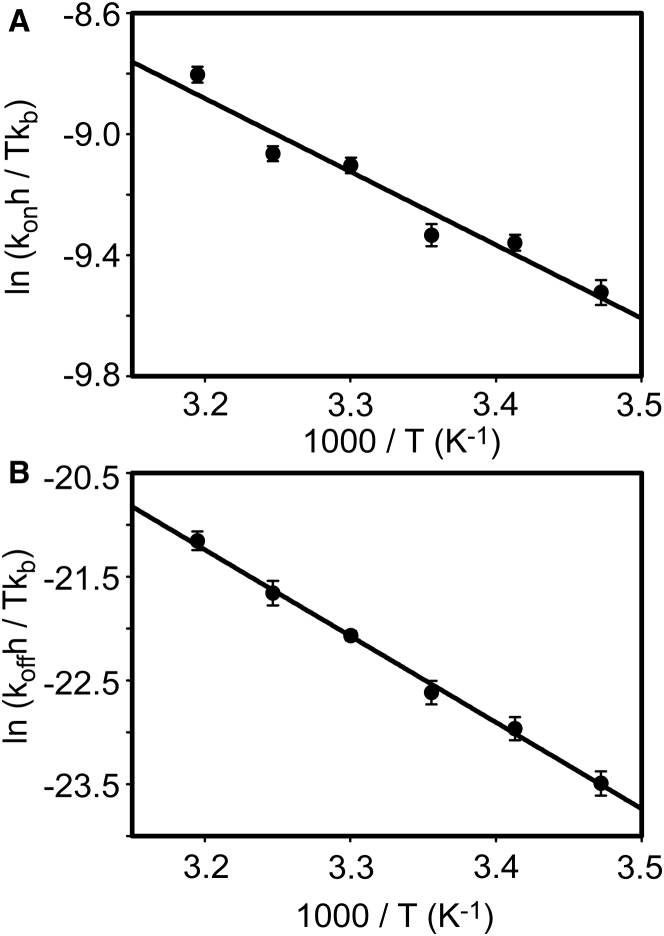
The temperature-dependent k_on and k_off values were analyzed using the Eyring equation. The Eyring plots of both k_on and k_off of the nSH3:PRM interaction showed no sign of curvature (Fig. 6). The nonlinear Eyring plot (or van’ t Hoff plot) indicates a considerable change in heat capacity upon protein-ligand complexation. Including the heat capacity term in the fitting equation did not result in statistically significant improvement of the result, based on the F-test, with α = 0.05. Similarly, the plot from our previous van’ t Hoff analysis of the nSH3:PRM⁷⁵⁸ interaction did not show curvature. Structure-based calculation yielded a ΔC_p of −200 cal mol⁻¹ K⁻¹ for nSH3:PRM⁷⁵⁸ complexation (10). Given the temperature range covered in this study, this value is too small to generate a statistically significant curvature in the Eyring plot. Hence, we used a linear Eyring equation to calculate the activation enthalpy and entropy associated with binding and unbinding of the nSH3 and PRM⁷⁵⁸. It is of note that the calculated activation entropy should not be considered inaccurate because the value is obtained by extrapolation of the data. Lente et al. (62) showed that the ΔS can be calculated from the slope, not from the intercept after simple rearrangement of the equation. The authors demonstrated that whether the ΔS is calculated from the slope or from the intercept, the result does not change significantly. We tested both methods and found that the calculated ΔS values do not differ. In addition, symmetric distribution of the temperature points at ∼298 K improves the reliability of the fit result.

Figure 6.

Eyring plots of the (A) association and (B) dissociation rate constants of nSH3 domain and PRM⁷⁵⁸.

The k_on value increases by approximately threefold over the temperature range of the experiment (from 15 to 40°C), resulting in the modest slope in the Eyring plot (Fig. 6 A). The slope and y intercept correspond to the activation enthalpy and entropy for association, $-\Delta H_a^{‡}/R$, and $\Delta S_a^{‡}/R$, respectively. Linear fit to the data yielded $\Delta H_a^{‡}$ = 4.81 ± 0.55 kcal mol⁻¹ and $\Delta S_a^{‡}$ = −2.22 ± 1.86 cal mol⁻¹ K⁻¹. These results indicate that the association of nSH3 and PRM is accompanied by an enthalpic activation barrier. The activation free energy of the association process was 5.47 kcal mol⁻¹ at 298 K. This value is very close to the theoretical activation energy (∼5 kcal mol⁻¹) for protein-small molecule reactions exhibiting a diffusion-limited binding (63, 64). This small enthalpic barrier is associated with a change in viscosity upon temperature change (28, 64).

The dissociation rate constant (k_off) was more sensitive to the change in temperature (Fig. 6 B). The linear fit to the data yielded $\Delta H_d^{‡}$ = 16.53 ± 0.46 kcal mol⁻¹ and $\Delta S_d^{‡}$ = 10.7 ± 1.53 cal mol⁻¹ K⁻¹. This suggests that the dissociation transition state of the complex is also characterized by a large enthalpic barrier and is only slightly compromised by a favorable entropy change. To further assess the quality of the activation parameters obtained from the Eyring analysis, we compared these results with those from the previous van’ t Hoff analysis. The ΔH_bind and TΔS_bind values associated with the nSH3:PRM⁷⁵⁸ interaction at 298 K were −11.5 ± 0.31 kcal mol⁻¹ and −3.64 ± 0.31 kcal mol⁻¹, respectively. The sum of $\Delta H_a^{‡}$ and $-\Delta H_d^{‡}$ yielded −11.72 ± 0.71 kcal mol⁻¹, and the sum of $T\Delta S_a^{‡}$ and $-T\Delta S_d^{‡}$ yielded –3.85 ± 0.72 kcal mol⁻¹ at 298 K. This is an exceptionally good agreement of results obtained by equilibrium and kinetic experiments, using two independent methods, fluorescence and NMR spectroscopy, respectively. This demonstrates that our data is internally consistent.

Discussion

Transient interactions between the nSH3 domain and PRM

In this study, we characterized the binding kinetics between the nSH3 domain of CrkII and three PRMs from cAbl. The nSH3 domain binds to all three PRMs with similar k_on and k_off values. Taken together with the previous results of equilibrium study (10), these data indicate that the three PRM sites are thermodynamically and kinetically equivalent in terms of interactions with CrkII. The functional significance of the binding of CrkII to individual PRM sites remains to be elucidated.

Transient protein-protein interactions are critical for many biochemical pathways (65, 66). Diffusion-limited association and fast dissociation of the nSH3 domain and PRMs highlight that the interaction between CrkII and cAbl is intrinsically transient. This suggests that the initial transient binding via nSH3 and PRM leads to different stable modes of interactions between CrkII and cAbl. For example, binding between CrkII and cAbl results in phosphorylation of CrkII (67). This leads to subsequent interaction between the SH3 domain of cAbl and the SH2 domain of CrkII (13). In this light, the transient nature of the nSH3:PRM interaction may play an important role in switching the binding modes, because a stable interaction might inhibit the facile transition between them.

Linear free energy relationship analysis indicates that the transition state is similar to the free state

Analysis of the binding transition state is essential to understand the molecular basis of protein-ligand interactions. Binding of PRM to the nSH3 domain is driven by a large favorable enthalpy. A small enthalpic activation barrier in the course of the association might be the result of temperature-dependent viscosity changes (63, 64). A small entropic barrier was observed in the association, which suggests that small positive entropy change upon partial desolvation of the binding interface might be compromised by the small unfavorable conformational entropy change. In addition, a positive entropy change in the course of dissociation indicates that the nSH3 domain and PRM maintain considerable conformational dynamics in the transition state.

To further characterize the transition state, we conducted the linear free energy relationship (LFER) analysis (68). Direct observation of the transition state is extremely difficult. Instead, this analysis provides information on the similarity between the transition and the ground states in terms of free energy change upon perturbations such as changes in pH and temperature or mutations. The resulting Leffler $\alpha \left(=\partial \Delta G_a^{‡}/\partial \Delta G_{\text{eq}}^{°}\right)$ value can be interpreted to assess the position of the transition state on the reaction coordinate (69, 70). However, it is of special note that the interpretation of this result critically depends on whether the perturbation predominantly affects either the free or ligand-bound states (see below) (71, 72, 73).

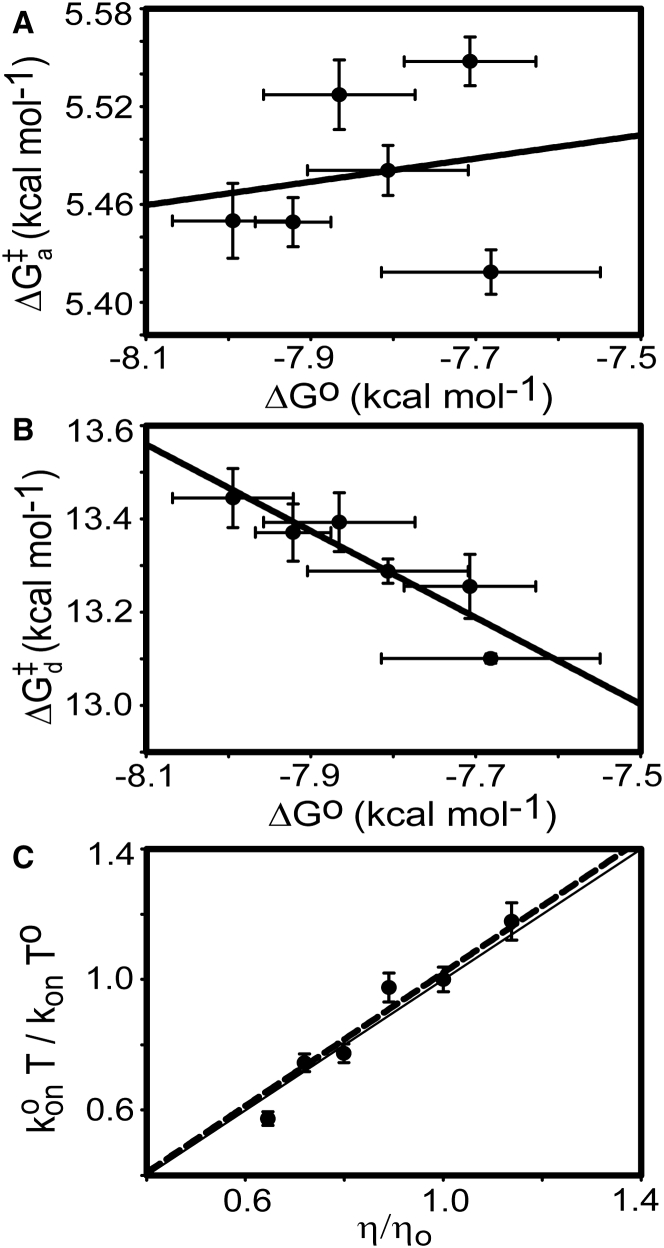
Previously, we reported the result of the van’ t Hoff analysis of the nSH3:PRM⁷⁵⁸ interactions (10). Here, we combine the results of the Eyring and van’ t Hoff analyses to perform LFER analysis. The plot of $\Delta G_d^{‡}$ versus ΔG° shows that the change in the ground state free energy is highly correlated with the change in the dissociation rate constant (α_d = −0.93 ± 0.20) (Fig. 7 A). This is a sharp contrast with the association transition state free energy (Fig. 7 B), in which $\Delta G_a^{‡}$ does not correlate at all with ΔG° (α_a = −0.07 ± 0.21). To rationalize the results, we postulate two different mechanisms (Fig. 8). The first mechanism assumes that the free energy of the PRM-bound state is destabilized (increased) as the temperature increases, whereas the free energy of the transition and free states do not change (Fig. 8 A). The free energy difference between the free and PRM-bound states decreases as the temperature increases. This mechanism implies that the transition state is highly similar to the free state, in terms of structure and energetics. On the other hand, a second mechanism assumes that the free energy of the PRM-bound state does not change, while the free and transition state energy level decrease similarly, as the temperature increases (Fig. 8 B). Both models explain why there is no correlation between $\Delta G_a^{‡}$ and ΔG°, whereas the $\Delta G_d^{‡}$ correlates well with ΔG°. A key difference between the two mechanisms is whether the temperature-dependent change in K_d is owing to the stabilization of the free state or destabilization of the PRM-bound state. However, it should be noted that both models indicate that the transition state is highly similar to the free state, rather than to the PRM-bound state. These results highlight that the interpretation of the LFER analysis should be cautious.

Figure 7.

LFER between equilibrium binding free energy (ΔG°) and transition state free energy of the (A) association $\left(\Delta G_a^{‡}\right)$ and (B) dissociation $\left(\Delta G_d^{‡}\right)$ processes. (C) Temperature-corrected viscosity plot. (Solid line) Expected relationship between $k_{\text{on}}^{0}T/k_{\text{on}}{T}^0$ and η/η₀, with slope = 1. (Dotted line) Linear regression line with a slope = 1.02 ± 0.19.

Figure 8.

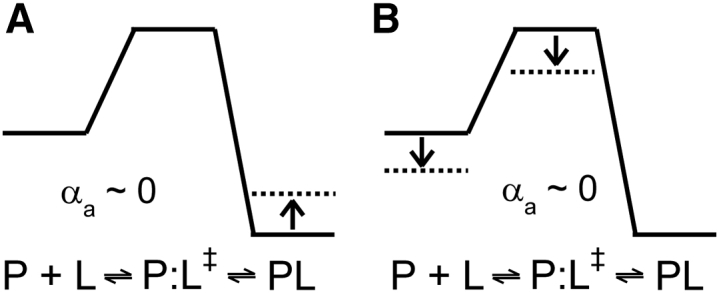
(A and B) Two potential scenarios to explain the result of LFER analysis. (Arrows) Change in the free energy level as temperature increases.

Because of the very fast binding kinetics, the Eyring analysis of binding between SH3 domain and PRM is rarely conducted. Demers and Mittermaier (31) conducted a careful study on the temperature-dependent binding kinetics of Fyn SH3 and PRM. The authors found that $\Delta H_a^{‡}$ = 3.4 ± 0.5 kcal mol⁻¹ for the binding of Fyn SH3 to PRM, which is consistent with our result. The authors also found that the activation barrier for dissociation of the FynSH3:PRM complex is accompanied by a considerable heat capacity change. This suggests that the transition state is only partially desolvated in the course of association. Recently, Xue et al. (58) reported the results of detailed molecular dynamics simulation of the nSH3 domain complexed with PRM derived from Sos. The authors found that the electrostatic interaction is the dominant player in the binding of nSH3 and PRM^Sos, but the encounter complex holds considerable conformational dynamics, resulting in a “fuzzy complex” (58). Partial electrostatic interactions might result in partial desolvation in the transition state. This is consistent with our result that the transition state is similar to the free state.

Is the nSH3:PRM binding a pure diffusion-limited process?

By determining if binding proceeds through a diffusion-limited process, we can provide an important clue to understand the binding mechanism between nSH3 domain and PRMs. Although the observed k_on values for all three PRMs are very close to the diffusion-limited rate constant, this is not sufficient evidence that binding is predominantly a diffusion-limited process (74). To test if the binding between the nSH3 and PRM is a diffusion-limited process, we investigated if the k_on linearly changes according to the change in viscosity. The diffusion-limited rate constant under the influence of electrostatic interaction during association is explained by (28, 29):

$$k=k_0\text{exp}\left(-{\langle U\rangle }^{\ast }/k_{\text{B}}T\right),$$ (5)

where k₀ is the basal rate constant in the absence of a biasing force such as long-range electrostatics. The effect of electrostatic interactions is treated by the Boltzmann factor (29). Hence, U is the interaction energy that is the sum of the energetically favorable (typically, long-range electrostatics) and unfavorable interactions. In the presence of high salt concentration, the diffusion rate constant is equivalent to the basal rate constant (k₀), which is proportional to the diffusion constant, $D=RT/N6\pi \eta r$ (28). The values R and N are the ideal gas constant and the Avogadro’s number, respectively; r is the Stokes’ radius of the transient complex; and η is solvent viscosity. Hence, the effect of changing solvent viscosity linearly affects the k₀.

The solvent viscosity can be changed by adding cosolutes, such as glucose or polymers, or changing the temperature. In the latter case, the linear relationship can be tested by plotting k_on versus T/η. Alternatively, the linearity can be tested by plotting the relative association rate constants $\left(k_{\text{on}}^{0}T/k_{\text{on}}{T}^0\right)$ versus the relative change in solvent viscosity (η/η₀) (74, 75). When solvent viscosity changes with varying temperature, this plot takes into account the effects from changes in both temperature and viscosity. The k⁰ and η₀ represent the corresponding values in the reference temperature, T⁰. In this study, we used T⁰ = 293 K because η₀ = 1 at this temperature. If the binding is a pure diffusion-limited process, then $k_{\text{on}}^{0}T/k_{\text{on}}{T}^0$ should be linearly dependent on η/η₀ with a slope of $\text{exp}\left[-\left(\langle U\rangle /R\right)\left({1/T}^0-1/T\right)\right]$. This plot is less sensitive to the effects of long-range electrostatics, relative to the plot of k_on versus T/η, which has an expected slope of $\text{exp}\left[-\left(\langle U\rangle /RT\right)\right]$. This is an additional benefit for us because the presence of a high salt concentration (>1 M) prevents the application of the high power CPMG pulse.

Fig. 7 C shows that $k_{\text{on}}^{0}T/k_{\text{on}}{T}^0$ agrees well with the temperature-induced relative viscosity changes, η/η₀. It should be noted that the activation enthalpy (ΔH^‡) probed by the Eyring analysis is taken into account by the change in viscosity of water (28). Hence, this agreement indicates that the result of the Eyring analysis is consistent with the effect of viscosity change on the association process. Furthermore, this result indicates that $\langle U\rangle$ is close to zero in the presence of 80 mM NaCl and that the basal rate constant, k₀, is high (∼10⁸ M⁻¹ s⁻¹) in the binding between nSH3 and PRM. Although it is not clear why the basal rate constant is so high for the binding between nSH3 and PRM, a recent study of binding between the Fyn SH3 domain and PRM also showed that the basal rate constant is very high (∼5 × 10⁷ M⁻¹ s⁻¹) (32). This may indicate that the binding transition state between SH3 domain and PRM is highly nonspecific and less restricted in translation/rotation, compared to other protein-protein binding processes. This interpretation is also consistent with the result of our LFER analysis.

To further examine the contribution of electrostatics in the binding between nSH3 and PRM, we measured the K_d value of the nSH3:PRM⁷⁵⁸ complex in the presence of 1 M NaCl. The K_d increased by sixfold in the presence of 1 M NaCl (Fig. S5), relative to that in 80 mM NaCl. The dissociation rate constant is typically determined by short-range electrostatics and hence, is not influenced significantly by the screening of long-range electrostatics using high salt concentration (29, 32, 76). If we assume that the change in k_off is modest upon the increase in salt concentration, this result implies that k_on would decrease by ∼10-fold in 1 M NaCl, relative to that in 80 mM NaCl, which is our experimental condition. This suggests that our estimated basal k_on would be ∼10⁷ M⁻¹ s⁻¹ in the presence of 1 M NaCl. Therefore, our result is consistent with that of binding between Fyn SH3 and PRM (32).

Although our results agree reasonably well with diffusion-limited binding, there are some caveats. First, the range of temperature-induced viscosity change is narrow. It is desirable to use cosolutes to change solvent viscosity, but the NMR signal intensity decreases as the cosolute concentration increases, owing to increased tumbling time. Hence, it is necessary to use higher protein concentrations to compensate the loss of signal intensity. However, it was reported that the nSH3 domain forms a mixture of a monomer and nonspecific dimers (or multimers) at high protein concentrations (58). This raised a concern about technical difficulties associated with analyzing multistate equilibria using NMR CPMG data. These limitations prevented us from using cosolutes to change viscosity. A systematic study will be required to address these problems. In this study, the protein concentration of our NMR experiments was kept low (200 μM) to prevent the nonspecific dimerization of the nSH3 domain. Second, we cannot exclude the possibility that a PRM undergoes a conformational exchange between binding-incompetent and -competent states before binding to the nSH3 domain. Our NMR experiments probe the signal from nSH3 domain, not from PRMs. Moreover, the concentration of PRM was only 5% of protein concentration in our NMR samples. Even if 10% of the entire PRM populated the binding-incompetent conformation, it constitutes only 0.1 × 0.05 = 0.5% of the entire population. Hence, it might be difficult to detect its effect on dispersion profiles.

The results of the Eyring and LFER analyses provided structural and energetic characteristics of the binding transition state between nSH3 and PRM. However, our data do not conclusively define that the binding between nSH3 and PRM is a diffusion-limited process. Observation of a fast k_on does not automatically grant diffusion-limited binding. Rogers et al. (74) reported that the binding of PUMA and MCL-1 also showed a nonlinear plot of $k_{\text{on}}^{0}T/k_{\text{on}}{T}^0$ versus η/η₀, although the basal rate constant was consistent with that of a diffusion-limited process.

Author Contributions

J.-H.C. conceived and coordinated the study and wrote the article; D.Z., Q.S., V.S.B., and J.-H.C. performed experiments; J.-H.C. analyzed experiments; and all authors reviewed the results and approved the final version of the article.

Editor: Jeff Peng.