Correlations for the Viscosity of 2,3,3,3-Tetrafluoroprop-1-ene (R1234yf) and trans-1,3,3,3-Tetrafluoropropene (R1234ze(E))

Abstract

Due to concerns about global warming, there is interest in 2,3,3,3-Tetrafluoroprop-1-ene (R1234yf) and trans-1,3,3,3-Tetrafluoropropene (R1234ze(E)) as potential replacements for refrigerants with high global warming potential (GWP). In this manuscript we survey available data and provide viscosity correlations that cover the entire fluid range including vapor, liquid, and supercritical regions. The correlation for R1234yf is valid from the triple point (220 K) to 410 K at pressures up to 30 MPa, and the correlation for R1234ze(E) is valid from the triple point (169 K) to 420 K at pressures up to 100 MPa. The estimated uncertainty for both correlations at a 95 % confidence level is 2 % for the liquid phase over the temperature range 243 K to 363 K at pressures to 30 MPa, and 3 % for the gas phase at atmospheric pressure.

1. Introduction

Concerns about climate change and global warming have led to interest in searching for replacement refrigerants with low global warming potential (GWP). R134a (1,1,1,2-tetrafluoroethane) has been widely used in automotive air conditioning systems, but has a high GWP. In response to this, European directive 2006/40/EC requires all new car platforms for sale in Europe to use refrigerants in their air conditioning systems with a GWP below 150. Other common refrigerants with high GWP’s will need to be considered for phase out as well. The present search for alternatives considers the possibility of using hydrofluorethers (HFE’s), and also unsaturated hydrofluorocarbons such as hydrofluoroolefins (HFO’s). Systematic searches have been done to identify if there may be other classes of compounds that may be suitable as well (Kazakov et al., 2012; McLinden et al., 2016). Viable candidate fluids must have other properties in addition to low GWP; they must have zero or very low ozone depletion potential, chemical stability, low toxicity, appropriate thermophysical properties, and must satisfy safety concerns regarding flammability. McLinden et al. (McLinden et al., 2016) identified 28 low-GWP fluids as potential pure-fluid replacements for unitary AC systems. These fluids included halogenated alkanes and oxygenates, hydrocarbons, halogenated nitrogen and sulfur compounds, inorganic compounds, and HFO’s. HFO’s were the largest group, with 10 compounds. Two promising HFO’s identified were 2,3,3,3-Tetrafluoroprop-1-ene (R1234yf, CAS 754-12-1) and trans-1,3,3,3-Tetrafluoropropene (R1234ze(E), CAS 29118-24-9).Kedzierski et al. (Kedzierski et al., 2015) evaluated cycle performance in a typical air conditioner for 39 refrigerants identified as low-GWP alternatives, and found R1234yf as one of the top three candidates. Mota-Babiloni and coworkers (Mota-Babiloni et al., 2015a) examined mixtures of R1234ze(E) and R134a as a drop-in replacement for R134a in a vapor compression plant. They also (Mota-Babiloni et al., 2015b) analyzed mixtures with R1234yf and R1234ze(E) as alternatives for refrigeration and HVAC systems and presented a review of R1234ze(E) systems for HVACR applications (Mota-Babiloni et al., 2015c). Other studies have focused on evaluating low-GWP fluids for power generation in organic Rankine cycles (ORC). Luo et al. (Luo et al., 2015) found mixtures with R1234yf and the pure fluids R1234ze(E) as promising candidates. Liu et al. (Liu et al., 2014) investigated the performance of eight different HFO’s including R1234yf and R1234ze(E) for application as working fluids in ORC’s for geothermal power applications.

In order to efficiently design refrigeration systems and power cycles, accurate models for thermophysical properties of the working fluids are needed. For R1234yf there currently are two high-accuracy equation of state formulations (Richter et al., 2011); Akasaka, 2011) available, and three for R1234ze(E) (Thol and Lemmon, 2016; McLinden et al., 2010; Akasaka, 2011). Wide-ranging correlations for the thermal conductivity of both fluids have been published (Perkins and Huber, 2011), and the surface tension of R1234ze(E) has been investigated (Tanaka and Higashi, 2013). Mulero et al. (Mulero et al., 2012) have developed a correlation for the surface tension R1234yf based on available literature data. However, there currently are few wide-ranging correlations for the viscosity of R1234yf or R1234ze(E). There is one extended corresponding states (ECS) model for the viscosity of R1234yf (Akasaka, 2010) and unpublished ECS models for both R1234yf and R1234ze(E) in REFPROP (Lemmon et al., 2013), and most recently a free-volume based model (He et al., 2015). In this work we develop correlations for the viscosity as a function of temperature and density that are valid over a wide range of fluid states including gas, liquid, and supercritical regions for R1234yf and R1234ze(E) and compare with known experimental data.

2. Viscosity Correlation

The viscosity η can be expressed (Dymond et al., 1996) as the sum of four independent contributions, as

$$\eta (\rho ,T)={\eta }_0(T)+{\eta }_1(T)\rho +\mathrm{\Delta }\eta (\rho ,T)+\mathrm{\Delta }{\eta }_{\mathrm{c}}(\rho ,T),$$ (1)

where ρ is the molar density and T is the absolute temperature. There is theoretical guidance for the first two terms, η₀(T) and η₁(T), that will be discussed below. The critical enhancement term, Δη_c(ρ,T), is confined to a small region, becoming relevant only at temperatures and densities very close to the critical point, and will not be included in this work. Finally, the term Δη(ρ,T), the residual term, must be handled empirically by fitting experimental data.

Table 1 summarizes, to the best of our knowledge, the experimental measurements of the viscosity of R1234yf and R1234ze(E), including sample purities, experimental method, and the uncertainties ascribed by the original authors. The sets marked in bold face were used in determining the coefficients of the correlations; other sets are included only for comparison purposes. The distribution of the experimental data and the phase boundary in the T,p plane are shown in Figures 1 and 2. For R1234yf, the densities and the phase boundary are calculated from the equation of state of Richter et al.(Richter et al., 2011) This equation is valid from 220 K (the triple-point temperature) to 410 K at pressures up to 30 MPa. We also incorporate the critical parameters from this equation of state, given in Table 2. For R1234ze(E), we calculate densities and the phase boundary with the equation of state of Thol and Lemmon (Thol and Lemmon, 2016). This equation is valid from 169 K (the triple-point temperature) to 420 K at pressures up to 100 MPa. The critical temperature and critical density are given in Table 2.

Table 1.

Experimental Measurements of the Viscosity of R1234yf and R1234ze(E)

1st author	Year Publ.	Technique employeda	Purity (%)	Uncertainty (%)	No. of data	Temperature range (K)	Pressure range (MPa)
R1234yf
Dang	2015a	MovP	99.9	1	25	283–321	0.6–1.3
Dang,b	2015b	FB	99	1.5	8	274–338	0.1
Zhaoc	2014	LScat	99.9	2–6	10	293–365	0.6–3.2
Meng	2013	VibW	99.9	2	110	243–363	0.1–30
Cousins	2012	SGCap	99.96	2.5–5	20	247–340	0.1–1.9
Hulse	2009	OscP	na	7–14	39	257–307	0.2–2.1
Yamaguchi	2009	RB	na	1.5	94	263–323	0.1–19.6
R1234ze(E)
Zhaoc	2014	LScat	99.9	2–6	9	295–373	0.5–3.1
Meng	2013	VibW	99.9	2	119	243–373	0.1–30
Cousins	2012	SGCap	99.96	2.5–5	20	247–340	0.1–1.5
Grebenkovd	2009	Cap	na	2.5	53	257–369	0.1–6.1

^aCap, Capillary; FB, Falling Ball; LScat, Light Scattering; MovP, Moving Piston; OscP, Oscillating Piston; RB, Rolling Ball; SGCap, Sealed Gravitational Capillary; VibW, Vibrating Wire.

^bAlso presented in conference paper (Arakawa et al., 2010)

^cKinematic viscosities, converted to absolute viscosity with the equation of state of Richter et al (R1234yf) and Thol and Lemmon (R1234ze(E))

^dGas phase data of Grebenkov were not used in regression.

Figure 1.

Distribution of experimental viscosity data for R1234yf in the T,p plane

Figure 2.

Distribution of the experimental viscosity data for R1234ze(E) in the T,p plane

Table 2.

Coefficients and parameters for Eqs. (1), (6)–(10).

	R1234yf	R1234ze(E)
Scaling parameters	ε/kB = 275 Κ σ = 0.531 nm	ε/kB = 340 Κ σ = 0.500 nm
Mw (g mol−1)	114.0416	114.0416
Tc(K)	367.85	382.513
ρc(mol L−1)	4.17	4.29
coefficients for Eq(6)
a0	−836950	−963382
a1	6336.28	9614.09
a2	−2.3547	−13.233
a3	0.039 556 3	0.0360562
a4	39509.1	122059
a5	121.018	−224.741
Coefficients bi for Eq. (9) from (Vogel et al., 1998) for both R1234yf, R1234ze(E)
b0 = −19.572 881	b1 = 219.73999	b2 = −1015.322 6
b3 = 2471.012 5	b4 = −3375.171 7	b5 = 2491.659 7
b6 = −787.260 86	b7 = 14.085 455	b8 = −0.346 641 58
Coefficients ci for Eq. (10)
c0	−0.194 259 10	8.61691913
c1	−2.079 577 245	0
c2	0	20.83024738
c3	−43.470 272 88	0
c4	0	0.542 43690
c5	0	−10.496 848 41
c6	0	−1.38137689
c7	−3.536 827 91	1
c8	1	0

2.1 The dilute-gas limit and the initial-density dependence terms

The dilute-gas limit viscosity, η₀(T), can be analyzed independently of all other contributions in Eq. (1) and is only a function of temperature. If there are accurate values for the gas thermal conductivity λ₀ and the ideal gas heat capacity at constant volume C_v,0, one can estimate the dilute-gas viscosity using the modified Eucken correlation (Reid, et al. 1987)

$$\frac{{\lambda }_0{M}_{\mathrm{w}}}{{\eta }_0{C}_{v,0}}=1.32+\frac{1.77}{C_{v,0}/R},$$ (2)

where R is the molar gas constant, (Mohr et al., 2015) 8.314 4598 J mol⁻¹ K⁻¹.For both R1234yf and R1234ze(E), there are correlations for the thermal conductivity of the dilute gas in the limit of zero density (Perkins and Huber, 2011), and the heat capacity at constant volume can be obtained from the equations of state for R1234yf (Richter et al., 2011) and R1234ze(E) (Thol and Lemmon, 2016). Assuming that the Lennard-Jones 12-6 potential is applicable, one can use Chapman-Enskog theory (Reid et al., 1987) to express the dilute-gas viscosity as

$${\eta }_0(T)=\frac{5}{16}{\left[\frac{M_{\mathrm{w}}RT}{\pi }\right]}^{1/2}\frac{1}{{\sigma }^2{\mathrm{\Omega }}^{(2,2)}},$$ (3)

where Ω^(2,2) is the Lennard-Jones collision integral that can be calculated by the empirical correlation developed by (Neufeld et al., 1972),

$${\Omega }^{*}(T^{*})=1.16145{(T^{*})}^{-0.14874}+0.52487{\mathrm{e}}^{-0.7732T^{*}}+2.16178{\mathrm{e}}^{-2.43787T^{*}}-6.435\times {10}^{-4}{(T^{*})}^{0.14874}\text{sin}[18.0323{(T^{*})}^{-0.7683}-7.27371],$$ (4)

with T*=k_BT/ε, ε is the Lennard Jones energy parameter, and σ is the Lennard Jones collision diameter. In engineering units this may be expressed as

$${\eta }_0(T)=0.026695693\frac{\sqrt{M_{\mathrm{w}}T}}{{\sigma }^2{\mathrm{\Omega }}^{(2,2)}},$$ (5)

where in Eq. (5) η₀ is in μPa s, M_w is in g mol⁻¹, T is in K and σ is in nm. We used Eqs. (2)–(5) to obtain the Lennard Jones parameters ε/k_B and σ, given in Table 2. For ease of use in calculations, η₀ was fit to a rational polynomial form:

$${\eta }_0(T)=\frac{(a_0+a_{1}T+a_2{T}^2+a_3{T}^3)}{(a_4+a_{5}T+T^2)},$$ (6)

where the units for η₀ are μPa s, T is in K and the a_i coefficients are in Table 2.

To represent the temperature dependence of the term η₁(T) in Eq. (1), we use a model presented by Vogel et al.(Vogel et al., 1986) expressed by means of the second viscosity virial coefficient B_η(T) as

$$B_{\mathrm{\eta }}(T)=\frac{{\eta }_1(T)}{{\eta }_0(T)},$$ (7)

The second viscosity virial coefficient can be obtained according to the theory of Rainwater and Friend (Friend and Rainwater, 1984; Rainwater and Friend, 1987) as a function of a reduced second viscosity virial coefficient, $B_{\mathrm{\eta }}^{*}(T^{*})$, as

$$B_{\mathrm{\eta }}^{*}(T^{*})=\frac{B_{\mathrm{\eta }}(T)}{N_{\mathrm{A}}{\sigma }^3},$$ (8)

where (Vogel et al., 1998)

$$B_{\mathrm{\eta }}^{*}(T^{*})=\sum _{l=0}^6{b}_i{(T^{*})}^{-0.25i}+b_7{(T^{*})}^{-2.5}+b_8{(T^{*})}^{-5.5}.$$ (9)

In the above equations, N_A is Avogadro’s constant (Mohr et al., 2015), 6.022 140 857×10²³ mol⁻¹. If the units for molar density in Eq. (1) are mol m⁻³ and the viscosity is in μPa s, then the size scaling parameter σ should be expressed in meters and B_η is in m³ mol⁻¹. The coefficients b_i from Vogel et al., 1998 are given in Table 2. Note that T* is a dimensionless temperature defined as T*=T/(ε/k_B), where ε/k_B and σ are energy and size scaling parameters for the Lennard Jones potential, given in Table 2.

2.2 The residual term

Theory is not available for the residual viscosity term Δη(ρ,T), and its evaluation is based entirely on experimentally obtained data. We used symbolic regression software (Nutonian, 2016) to fit the experimental data to determine the function and coefficients to represent the residual viscosity. This approach was used successfully for the viscosity surface of hydrogen (Muzny et al., 2013), benzene (Avgeri et al., 2014), toluene (Avgeri et al., 2015), hexane (Michailidou et al., 2013), and heptane (Michailidou et al., 2014). We follow those works and incorporate a form suggested by the hard-sphere model employed by (Assael et al., 1992), $\mathrm{\Delta }\eta ({\rho }_{\mathrm{r}},T_{\mathrm{r}})=({\rho }_{\mathrm{r}}^{2/3}{T}_{\mathrm{r}}^{1/2})F({\rho }_{\mathrm{r}},T_{\mathrm{r}})$, where the symbolic regression method was used to determine the functional form for F(ρ_r,T_r). The dilute-gas limit η₀(T) and the initial density dependence terms η₁(T)ρ were calculated for each experimental point (employing Eqs. (6) – (9)) and subtracted from the experimental viscosity to obtain the residual term. A simple expression was found:

$$\mathrm{\Delta }\eta (\rho ,T)={\rho }_{\mathrm{r}}^{2/3}{T}_{\mathrm{r}}^{1/2}(c_0+c_1{\rho }_{\mathrm{r}}+c_2{\rho }_{\mathrm{r}}^2+\frac{c_3{\rho }_{\mathrm{r}}+c_4{\rho }_{\mathrm{r}}^6+c_5{\rho }_{\mathrm{r}}{T}_{\mathrm{r}}^2+c_6{\rho }_{\mathrm{r}}^5{T}_{\mathrm{r}}}{c_7{T}_{\mathrm{r}}+c_8{\rho }_{\mathrm{r}}{T}_{\mathrm{r}}})$$ (10)

Coefficients c_i are given in Table 2 for both fluids. T_r is the reduced temperature T_r=T/T_c and ρ_r is the reduced density ρ_r=ρ/ρ_c, with Δη in μPa s.

2.3 Comparisons with Experimental Data

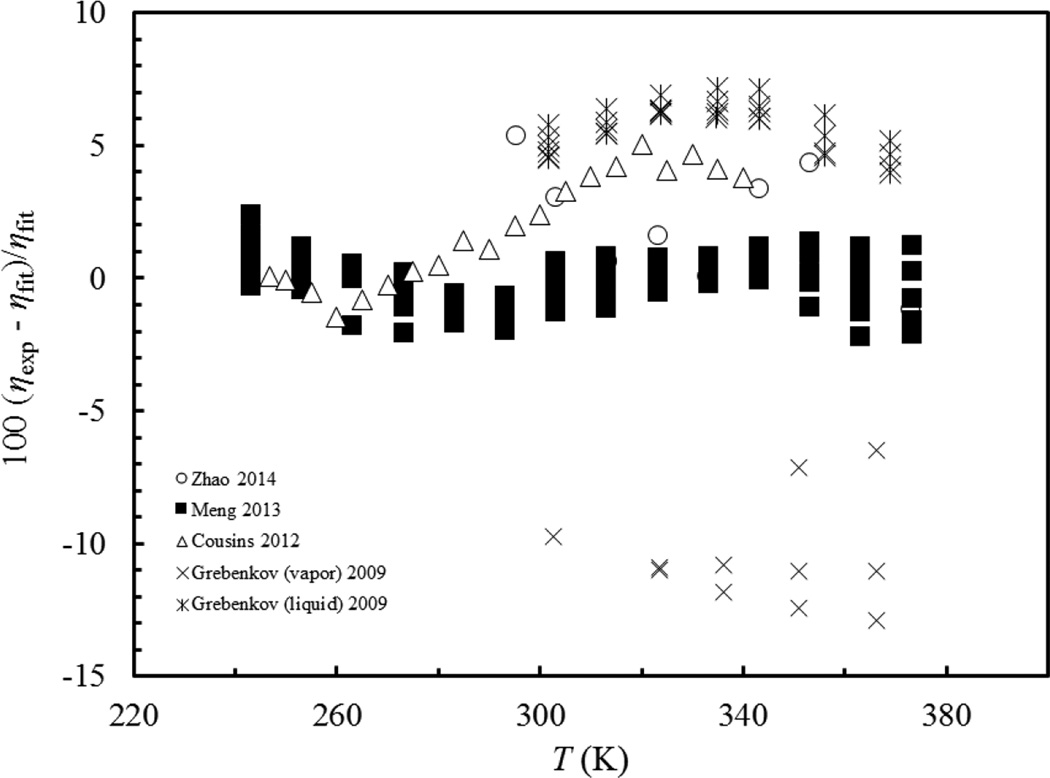
Table 3 summarizes comparisons of all experimental data with the correlations. In the Table we use percent deviation, PCTDEV = 100*(η_exp−η_fit)/η_fit, average absolute percent deviation (AAD), AAD = (∑|PCTDEV|)/n, and BIAS = (∑PCTDEV)/n, where η_exp is the experimental value of the viscosity, η_fit is the value calculated from the correlation, and the summation is over all n points. Figures 3 and 4 show the deviations of all data sets from the correlations for R1234yf and R1234ze(E) respectively. In both figures, the most comprehensive viscosity measurements are the measurements of Meng and coworkers (Meng et al., 2013) performed in an absolute vibrating-wire instrument with an uncertainty of 2 %. This set is backed by a full theory and is the most wide-ranging data set available, and the correlation represents those data sets to within experimental uncertainty. The other data sets generally have more scatter and larger deviations. To obtain an estimate of the uncertainty of the correlation, comparisons with the highest- quality data sets (those with the lowest uncertainty) are used. We estimated the uncertainty of the R1234yf correlation in the liquid phase at pressures up to 30 MPa to be 2 % at a 95 % confidence level over the temperature range 243 K to 363 K, based on the data of Meng et al. (Meng et al., 2013). In the gas phase, the best measurements are those of Dang et al. (Dang et al., 2015b) The correlation represents this set to within 3 %; there is much more scatter in the Yamaguchi data (Yamaguchi et al., 2009). Additional comparisons are available in Supplemental Information. Although the available experimental data only cover a limited temperature range, 243 K- 365 K, and pressures only to 30 MPa, the correlation extrapolates smoothly and in a physically reasonable manner, and can be used over the full range of the equation of state (Richter et al., 2011), from the triple point to 410 K and pressures up to 30 MPa; however uncertainties will be larger especially as the triple point is approached and at high pressures. Similarly we estimate the uncertainty of the liquid phase for R1234ze(E) to be 2 % at pressures up to 30 MPa (based on the data of Meng et al. (Meng et al., 2013)) and 3 % in the gas phase, with the correlation behaving in a physically reasonable manner up to the limits of the equation of state (420 K and 100 MPa), although the uncertainty may be larger in regions where no data were available.

Table 3.

Comparisons of the viscosity correlations with all experimental data.

1st author	Year Publ.	AAD	BIAS
R1234yf
Dang	2015a	1.18	−0.96
Dang	2015b	1.08	−0.13
Zhao	2014	3.19	−3.19
Meng	2013	0.95	−0.70
Cousins	2012	3.13	2.99
Hulse	2009	2.86	2.09
Yamaguchi	2009	3.10	1.82
R1234ze(E)
Zhao	2014	2.22	1.96
Meng	2013	0.77	−0.28
Cousins	2012	2.19	1.88
Grebenkov	2009	7.00	0.61

Figure 3.

Comparisons of all experimental data with the correlation for R1234yf

Figure 4.

Comparisons of all experimental data with the correlation for R1234ze(E)

2.4 Computer-Program Verification

To assist the user in computer-program verification, we provide the following numbers for checking calculations: For R1234yf at 300 K and 0 mol L⁻¹, the viscosity is 11.579 μPa s; at 300 K and 0.044 mol L⁻¹ it is 11.549 μPa s; and at 300 K and 10.522 mol L⁻¹ it is 217.97 μPa s. For R1234ze(E) at 300 K and 0 mol L^-1, the viscosity is 11.777 μPa s; at 300 K and 0.044 mol L⁻¹ it is 12.041 μPa s; and at 300 K and 10.522 mol L⁻¹ it is 217.89 μPa s.

3. Conclusions

We present correlations for the viscosity of R1234yf and R1234ze(E) based upon currently available experimental data. These correlations are valid over the entire fluid surface from the triple point to the upper temperature limit of the equation of state, at pressures up to the upper limit of the equation of state. The estimated uncertainty for both correlations is 2 % in the liquid phase for 243 K to 363 K at pressures up to 30 MPa, and 3 % in the gas phase. Both correlations behave in a physically reasonable manner up to the limits of the equation of state although the uncertainty may be larger in regions where no data were available for comparisons.