Abstract
The gradual loss of diversity and the establishment of clines in allele frequencies associated with range expansions are patterns observed in many species, including humans. These patterns can result from a series of founder events occurring as populations colonize previously unoccupied areas. We develop a model of an expanding population and, using a branching process approximation, show that spatial gradients reflect different amounts of genetic drift experienced by different subpopulations. We then use this model to measure the net average strength of the founder effect, and we demonstrate that the predictions from the branching process model fit simulation results well. We further show that estimates of the effective founder size are robust to potential confounding factors such as migration between subpopulations. We apply our method to data from Arabidopsis thaliana. We find that the average founder effect is approximately three times larger in the Americas than in Europe, possibly indicating that a more recent, rapid expansion occurred.
Keywords: Biogeography, gene flow, population genetics, population structure
A range expansion is the spread of a population from a geographically restricted region to a much larger region. Range expansions are a common occurrence in many species, and they happen on time scales that differ by several orders of magnitude; viruses and bacteria may spread across the globe in a few weeks (Brockmann and Helbing 2013), invasive species are able to colonize new habitats over decades (Davis 2009); and many species have dispersed into their current habitat over the last few millennia, following changes in environmental conditions (Taberlet et al. 1998; Hewitt 1999).
The population genetic theory of range expansion is based on two largely distinct types of models. The first type follows from the seminal papers of Fisher (1937) and Kolmogorov et al. (1937) and is often called the Fisher–Kolmogorov–Petrovskii–Piscounov (Fisher–KPP) model. These models describe the diffusive spread of alleles in continuous space, and they are analyzed with methods from statistical mechanics. The other type, called the serial founder model, assumes a collection of discrete locations that can be colonized (Cann et al. 1987; Austerlitz et al. 1997; Hewitt 1999; Ramachandran et al. 2005). This class of models is similar to the stepping stone models used in analyzing isolation by distance in equilibrium populations (Kimura 1964).
The Fisher–KPP model describes the change in allele frequency at a spatial location due to dispersal and fitness differences in a continuously distributed population. The model can be applied to range expansions by equating the advantageous allele with presence of a species, and the deleterious allele with its absence (see, e.g., Barton et al. 2013, for a recent review). The solution to the resulting partial differential equation has the form of a traveling wave and is similar in form to logistic growth. This model has been tested against data by Hallatschek et al. (2007), who compared growing colonies of E. coli to the predictions from the Fisher–KPP equation.
Some of the predictions of the Fisher–KPP model are inconsistent with observations of many macroscopic systems. In particular, the Fisher–KPP model predicts that local populations start with extremely small population sizes, which leads to strong genetic drift. In the experiments of Hallatschek et al. (2007), all local genetic variability was quickly eliminated, and no polymorphisms were shared between individuals sufficiently far from each other. This prediction does not fit what is seen in humans: An expansion of humans from Africa to Eurasia was suggested based on the topology of a mitochondrial-DNA tree (Cann et al. 1987). This finding has been replicated in numerous studies (Ramachandran et al. 2005; DeGiorgio et al. 2009; Henn et al. 2012), yet many genetic variants are shared by all human populations. The serial founder model does not lead to such extreme differentiation because the intensity of founder effect at each step is an independent parameter. Each group that founds a new population can be of any size and the pattern of population growth after founding can be adjusted arbitrarily. Austerlitz et al. (1997) and Ray et al. (2010) assumed logistic growth. DeGiorgio et al. (2011) and Slatkin and Excoffier (2012) assumed instantaneous growth after population founding.
A complete serial founder model, including selection, founder events, and migration between subpopulations, has so far been proven intractable. However, a recursion approach (Austerlitz et al. 1997) and simulations (Klopfstein et al. 2006; Burton and Travis 2008) have been successfully applied to investigate the behavior of the model. In addition to models that explicitly include spatial dependence, there are other approaches that make additional simplifications. Perhaps the simplest model of this kind is that of a demographic expansion without any spatial component. In this case, the expansion is fully described by a change in the rate of coalescence (Gravel et al. 2011; Li and Durbin 2011). This model is a good approximation for a range expansion when migration between subpopulations is very large. In that case, we would not expect the creation of any spatial structure.
A slightly more complicated model has been used to estimate the number of founder lineages of the population: If a new population is founded by colonists from a larger source population, the number of founders and the timing of the founding event can be estimated (Anderson and Slatkin 2007; Leblois and Slatkin 2007).
A further step is the infinite-island approximation (Excoffier 2004). In this model, an originally small, panmictic population expands instantly into a metapopulation with a large number of identical subpopulations. In this model, inference of demographic parameters can be based on the mismatch distribution and the difference in coalescent time distribution between and within subpopulations. However, while this model distinguishes within-deme from between-deme variation, it assumes that all subpopulations are exchangeable, so that the geographic locations of the subpopulations do not matter.
Slightly more realistic are the models of DeGiorgio et al. (2011) and Slatkin and Excoffier (2012). DeGiorgio et al. (2011) derived coalescence time distributions under a serial founder model, assuming a small bottleneck at each founder event. In the model of Slatkin and Excoffier (2012), the expansion is modeled as a spatial analog of genetic drift, where each founder event corresponds to a generation in a standard Wright-Fisher model. Neither of these models has been used for inference. The most elaborate methods for inference under a range expansion are simulation based. Techniques such as approximate Bayesian computation (Beaumont et al. 2002) can be used (Itan et al. 2009). However, these approaches tend to lead to a “black box.” Simulation models are difficult to validate and they generally do not lead to an intuitive understanding of the process.
In this article, we develop a serial founder model of a range expansion. We then develop some intuition about how allele frequencies are expected to behave under this model. Next, we introduce a branching process approximation and show how the resulting model leads to a simple prediction about the model’s behavior that can be the basis for inferring the net strength of a founder effect. We test the model and the validity of our approximations using simulations, and we apply our method to an Arabidopsis thaliana (L.) Heynh. Single nucleotide polymorphism (SNP) data set (Horton et al. 2012).
Results
RANGE EXPANSION MODEL
During a range expansion, individuals who colonize previously uninhabited space are descendants of those living close to the expansion front (Klopfstein et al. 2006; Hallatschek et al. 2007). Furthermore, as the name “serial founder model” implies, the movement into a previously unoccupied area is accompanied by founder effects. The reduction in effective size at the expansion front results in an increase in the intensity of genetic drift. Allele frequencies at the expansion front will have a higher variance, and alleles are more likely to become fixed or lost. In other words, genetic drift is stronger at the expansion front than away from the front. It is this difference in that we are aiming to describe and use for inference.
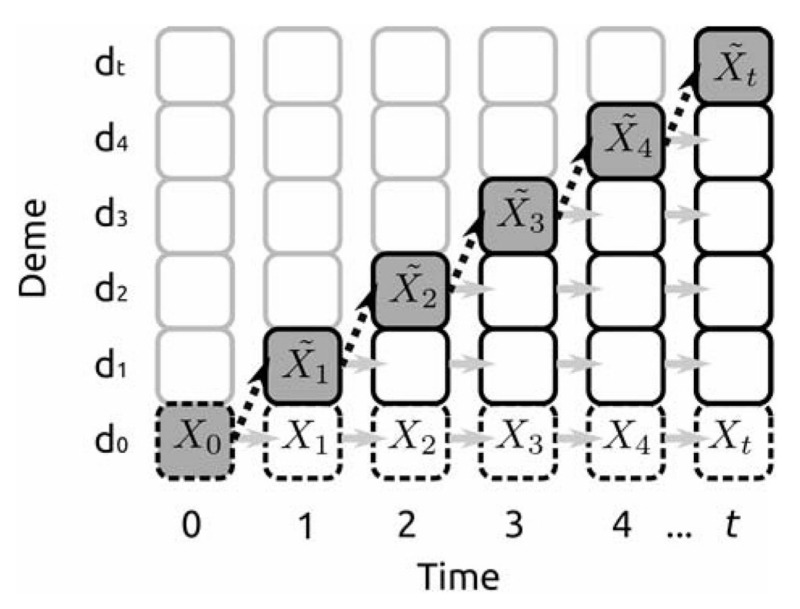
A schematic of the model is given in Figure 1. In brief, we assume that the population starts from a single deme in a one-dimensional (1D) array of empty locations and evolves in discrete generations. Every generation, the population expands to occupy a previously vacant location. The new deme is colonized by the offspring of individuals in the most recently founded deme. We assume that the colonizing process results in a founder event that temporarily reduces the effective population size. During the same time step, all other demes experience genetic drift at a rate determined by their effective population size, which is larger than the size of the colonizing group. At time step t, the deme at the expansion front will have experienced t founder events, whereas the population at the expansion origin will have experienced t generations of genetic drift. If we compare two populations r and s steps away from the origin at time t, (0 ≤ r < s ≤ t), the population at r will have experienced r founder events and t − r generations of genetic drift, and the population at s will have experienced s founder events and t − s generations of drift. Thus, the population at s will have experienced s − r more founder events and s − r fewer generations of genetic drift than the population at location r.
Figure 1.
Schematic of the expansion models studied. Each square corresponds to a subpopulation, with gray borders indicating subpopulations not colonized at a time step. Each time step, a new deme is colonized (black, dashed arrows), and other demes undergo neutral genetic drift (gray arrows). We compare the allele frequencies {Xt} at the expansion origin d0 (dashed borders) with the allele frequencies {} at the expansion front (shaded backgrounds).
Thus, if the order of large-drift founder effects and small-drift generations does not matter, the amount of drift a deme experienced will increase linearly with the distance from the origin. As shown in the section Discrete Time Expansion Model in the Appendix, this is indeed a good approximation for our model. The slope of the curve of allele frequency versus geographic distance will depend on the difference in the number of founder events experienced. The stronger the founder effects during each colonization, the larger the slope.
One way to measure the difference in the net effect of drift is to use the directionality index we introduced previously (Peter and Slatkin 2013). The directionality index ψ(A, B) for two populations A and B is defined as
| (1) |
Here, fA, j is the derived allele frequency of SNP j in population A, and we sum only over SNPs that have at least one derived allele in both populations. In Peter and Slatkin (2013), we showed using simulations that ψ increases approximately linearly with distance from the origin of colonization. Therefore, ψ captures the signal described above. If more than two locations are sampled, we compute the matrix of ψ for all pairs of locations sampled.
OVERVIEW OF THEORETICAL RESULTS
In this section, we summarize the formal analysis needed to support the claims made above. The derivations are given in the Appendix. We start by defining two stochastic processes, {Xt} and {}, for t = 0, 1, 2, …. Xt and describe the allele frequency in generation t at the expansion origin and the wave front, respectively (see Fig. 1). We are particularly interested in Zt = − Xt|Xt > 0, > 0 the difference in allele frequency between front and origin, conditioned on alleles being present in both populations. In the section section Discrete Time Expansion Model in the Appendix, we show that the expected difference in allele frequency is
| (2) |
where f0 is the initial frequency of the allele in deme X0, and L(t) and are the probabilities that an allele is lost by time t at the origin of the expansion and the wave front, respectively.
To make this result more explicit, we need to further specify {Xt} and {}. We assume that both processes evolve according to a branching process (Harris 1963) with mean one. Furthermore, let the offspring distributions of {Xt} and {} be F and , respectively. Making these assumptions, we show in the section Branching Process in the Appendix that equation 2 can be written as
| (3) |
In other words, we expect a linear increase in the difference in allele frequency with distance between samples, with the slope depending on the variances of the offspring distributions.
Because we assume that high-drift founder events occur at the expansion front, we expect it to have a higher offspring variance. Under a Cannings model (Ewens 2004), the effective size of a population is directly related to the offspring variance through the equation Ne = N/Var(F), where Ne and N denote the effective size and census size, respectively. Similarly, we can define an effective founder size ke, the effective size of the founder event process at the wave front, to be ke = N/Var(). Then, as shown in the section Effective Population Size in the Appendix, equation 2 can be written as
| (4) |
It is worth noting that in equation 4, only the ratio enters the equation. In some cases, it might be possible to interpret Ne and ke directly. For example, if we think of a species colonizing a system of islands, Ne corresponds to the effective population size of that species on a given island and ke corresponds to the effective number of founders that colonized that island. In a continuously distributed population, however, subpopulations are not clearly defined. We would get a different ratio for each choice of deme size. We can circumvent this problem either by arbitrarily choosing a deme size, and then presenting ke/Ne conditional on that deme size, or we can fix the founder effect size ke/Ne to a certain value (e.g., 0.99) and compare expansions using the distance over which that founder effect occurs (see the section Rescaling in the Appendix). The larger the distance, the weaker the founder effect. We may refer to a founder event that reduces the effective size at the front by n percent as a n%-founder effect, for example, a 1% founder effect has a ke/Ne ratio of 0.99.
Finally, in the section Estimation in the Appendix we show how we can estimate Zt from genetic data using ψ. As ψ is defined between pairs of populations, we can record the distance between pairs of samples and ψ for all pairs of populations. These results suggest that we can estimate the net founder effect that characterizes the loss of genetic diversity with increasing distance from the expansion origin by using a simple linear regression on the frequencies of shared alleles with increasing distance between samples.
SIMULATIONS
We validate our analytical results by performing extensive simulations under two different models. The first is the forward-in-time stepping stone model described by Slatkin and Excoffier (2012). The second model is a backward-in-time stepping stone model, based on the Kingman coalescent (Wakeley 2009).
Forward simulations
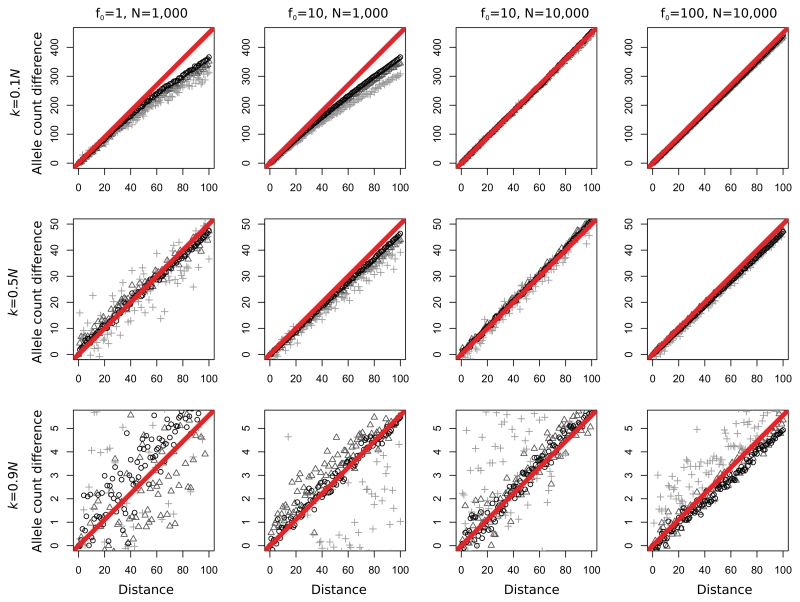
We first consider the discrete-time Wright–Fisher model. In Figure 2, we give results for various initial allele frequencies f0, setting ke = 0.1N (first row), ke = 0.5N (middle row), and ke = 0.9N (bottom row). Using equation 4, we would predict Zt to be 4.5t, 0.5t, and t/18, respectively. Those predictions are given by the red lines; the points represent the simulated data. We find that we get better estimates when (1) the effective founder size is low, (2) the time after the expansion is short, and (3) the effective population size is high. In particular, we find that the allele frequency difference between demes far apart is smaller than expected when the founder effect is very strong. In that case, many alleles become fixed, and the difference between the Wright–Fisher and the branching process models becomes quite apparent.
Figure 2.
Forward simulations. Expected (red line) and simulated (black circles, dark gray triangles, light gray crosses) allele frequency differences between deme t and the a sample from the origin. Circles, triangles, and crosses correspond to samples taken 0, 100, and 500 generations after the expansion reached the final deme 100. f0, initial allele frequency; k, effective founder size; N, effective deme size. Distance is measured in demes. Other parameters are time between expansion events: t = 2 and migration rate m = 0.
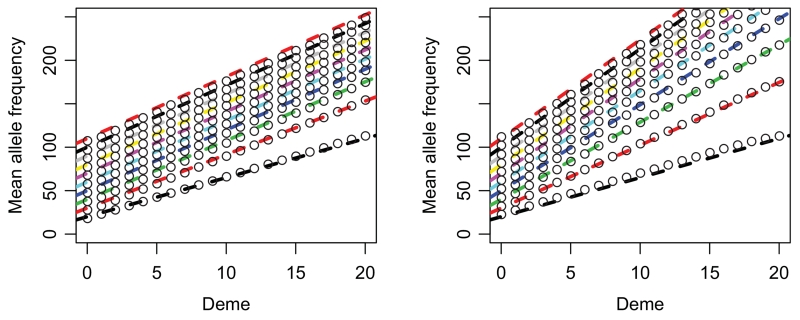
In Figure 3, we investigate the effect of demes growing to their carrying capacity via logistic growth, as opposed to instantaneous growth that we assume in most other cases. Here, we can apply the result that under nonconstant founder population sizes, the effective founder size is simply the harmonic mean of all founder sizes, divided by the number of generations. In Figure 3, simulations were performed with a carrying capacity of 10,000, and each new colony was founded with an initial propagule of 500 individuals.
Figure 3.
Comparison between WF-simulations and predictions from the branching process model under a logistic growth model. Growth rates were set to 1 (panel a) and 0.5 (panel b), respectively. Lines correspond to 1–10 generations of logistic growth per expansion step (from bottom to top). Dots correspond to the simulated data, and the dashed lines are the analytical predictions using the harmonic mean of the population sizes. Samples were taken immediately after the expansion finished.
Backward simulations
We also performed backward-in-time simulations (1) to test the robustness of the branching process predictions to migration, (2) to test the effect of estimation from a subsample, and (3) to remove the initial allele frequency as an explicit parameter. Coalescent simulations were performed in a continuous-time model with discrete expansion events. In particular, most of the time lineages merge according to the standard structured coalescent. The only exceptions are the expansion events, which are represented by a single generation of a Wright–Fisher model, followed by moving all lineages in the newly colonized deme back to the founder deme (see Methods section for details). Thus, unlike the Kingman coalescent, this model allows for multiple mergers at the wave front. Under this model,
| (5) |
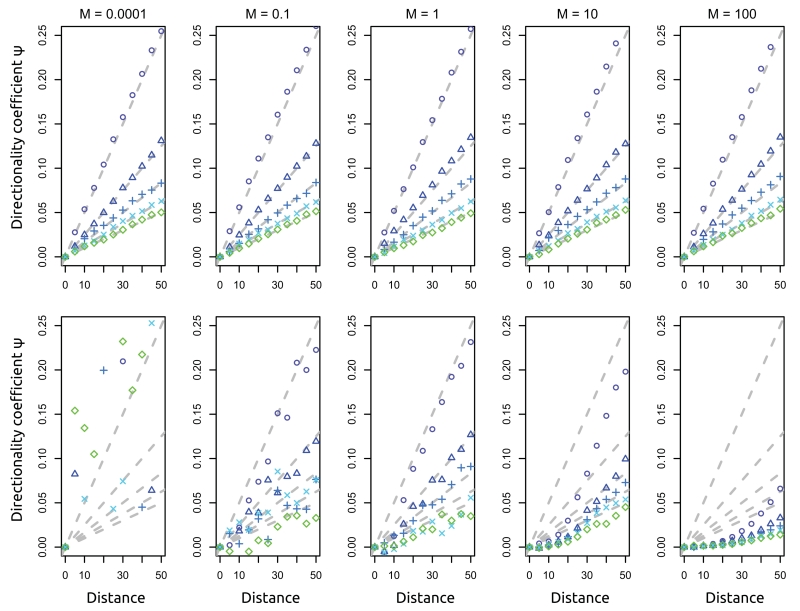
because the founder events result in an increase in the offspring variance by a factor of (2ke)−1. We estimate Zt using ψ defined in Peter and Slatkin (2013), which we justify in the section Estimation in the Appendix. Results are displayed in Figure 4. First, we show samples taken immediately after the expansion reaches the boundary of the habitat (top row). Second, we explore the limiting behavior of a very old expansion with samples taken 20N generations after the expansion finishes (bottom row). We find that recent expansions are detected easily, almost independently of the migration rate, and the simulated data closely follow the predictions from our approximate model. The bottom row shows how the signal deteriorates. We see different behaviors for high and low migration rates: in the low migration rate regime we do not have any power for inference, because lineages all coalesce within their demes before they have the opportunity to coalesce with lineages from other locations. The result is data sets in which there is almost no shared variation among populations. In that case, ψ is a poor summary statistic. For high migration rates (M = 100), we see a different decay pattern: The signal of expansion has almost vanished because migration has dispersed alleles almost evenly throughout the population. The result is that the signal of the range expansion is no longer apparent and the population approaches one in which there is isolation-by-distance at equilibrium.
Figure 4.
Effect of migration rate and subsampling. Each set of points corresponds to ψ estimated from simulations under a specific ke value; ke varies from 100 to 500 in increments of 100 (top to bottom: circles/triangles/plus signs/crosses/diamonds, blue to green). Gray dashed lines give the expectation from the branching process model. Top row: data sampled immediately after the expansion finished. Bottom row: data sampled a very long time (20 Ne generations) after the expansion finished. Other parameters are as follows: sample size n = 10, time between expansion events te = 0.0001Ne generations.
Two-dimensional simulations
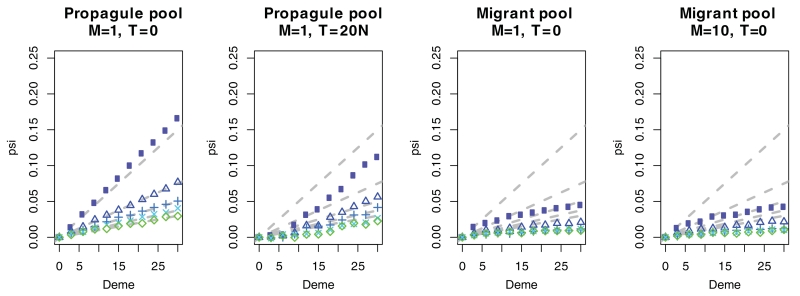
We also performed simulations on a two dimensional (2D) stepping stone model to investigate the robustness of our results in a 2D habitat. We simulated expansions both under a migrant pool model and a propagule pool model (Slatkin and Wade 1978). In a migrant pool model, all neighboring populations send migrants at equal rates to a newly colonized deme, whereas under the propagule pool model, one possible founder population is selected to send out a “propagule,” which colonizes the new deme. We find that if the sampling transect is parallel to the orientation of the stepping stone grid, then the choice of colonization model does not matter, and we obtain results similar to those from the 1D model. However, for a diagonal transect, the results differ between the two models: The propagule pool model again behaves similar to the 1D model, whereas the behavior of the migrant pool model is different (Fig. 5). The reason for this in the migrant pool model, there are many different pathways by which a deme can be colonized, and the number of pathways increases with distance from the origin. As a consequence, the amount of drift increases nonlinearly with increasing distance from the origin. In contrast, in the propagule pool model, only a single pathway is chosen. We also find that in the 2D model, the signal of the expansion disappears more quickly than in the 1D model if the migration rates are equal. In the 1D model at a migration rate of M = 1 the expansion is still detectable after 20N generations, but in the 2D model the population has almost reached equilibrium by that time.
Figure 5.
2D model simulations. Each set of points corresponds to ψ estimated from simulations under a specific ke value; ke varies from 100 to 500 in increments of 100 (top to bottom: circles/triangles/plus signs/crosses/diamonds, blue to green). Gray dashed lines give the expectation from the branching process model in one dimension.
APPLICATION TO A. THALIANA
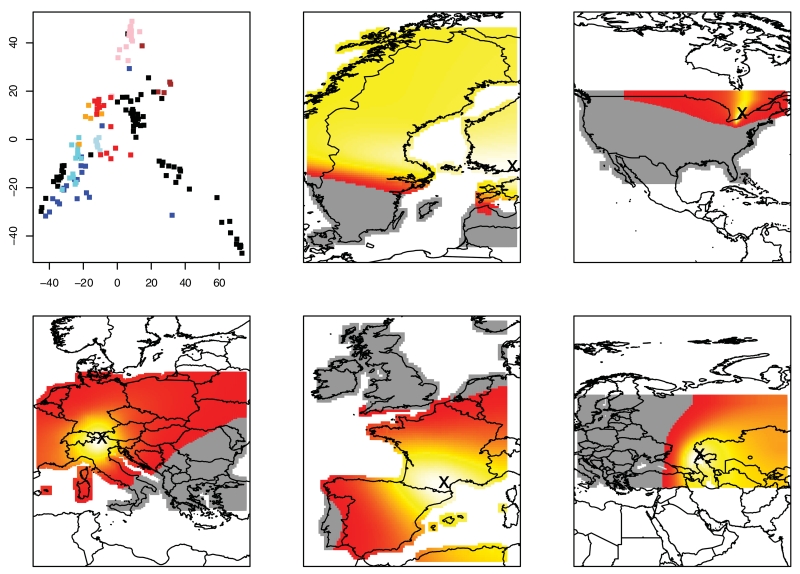
Arabidopsis thaliana is a small, annual plant thought to be native to Europe and introduced to North America and elsewhere (Jorgensen and Mauricio 2004). The biogeography and population structure of A. thaliana has been well studied (Jorgensen and Mauricio 2004; Nordborg et al. 2005; Horton et al. 2012). Although the earliest studies showed relatively little population differentiation on a global scale, genome-wide genetic data show evidence of widespread genetic differentiation among populations (Nordborg et al. 2005; Horton et al. 2012). Based on a principal component analysis (PCA) analysis (Fig. 6a), we defined five regions for further examination: Scandinavia, Americas, and Western, Central and Eastern Europe.
Figure 6.
Results for A. thaliana data set. Panel (a): PCA analysis of the 121,412 SNPs. Colors: green, Scandinavia; black, Americas; blue, UK; cyan, France; light blue, Spain and Portugal; red, North-Western Europe; orange, Switzerland and Italy; pink, Central Europe; brown, Russia, Lithuania, and Western Asia. Panels (b–f): Expansion for Scandinavia, United States, Central Europe, Western Europe, and Eastern Europe/Asia, respectively. Brighter yellow regions indicate more likely origin of expansion. Red and gray regions indicate unlikely origin.
In the Americas (Fig. 6c), we find a most likely origin of introduction is the Great Lakes region, not the east coast. But as we only have one sampling location on the east coast, support for this conclusion is weak. An additional problem is that, as we showed in our previous paper (Peter and Slatkin 2013), using ψ to infer an origin leads to biased results when the true origin is at the boundary of the habitat.
Scandinavia (green dots in Fig. 6 a, c) shows the most diversity within a region according to the PCA plot and the second highest founder effect size. The most differentiated samples, shown in the bottom left of Figure 6, are from Northern Sweden and Finland, whereas samples that cluster with the Central and Eastern European Accessions are predominately found in southern Sweden. We find evidence of immigration from the east, with the most likely origin of the Scandinavian accessions lying in Finland. Based on the PCA analysis, we might expect the accessions from southern Sweden to show evidence of a range expansion from the south, and that is indeed the case when we consider only these southern samples.
If we analyze these southern Scandinavian samples together with the samples from Austria, the Czech Republic, Russia, Lithuania, and Tajikistan (Fig. 6d, pink and brown dots in the PCA), we find evidence of an expansion out of eastern Asia, possibly from a refugium close to the Caspian Sea. For the Central European samples, we find an origin close to the border between Austria and Italy. This is likely a proxy for a refugium in either southern Italy or the Balkan region, as the inferred origin was covered by an ice sheet during the last glacial maximum. Finally, for the western European samples we find the weakest founder effect in the regions we analyzed, with a 1% founder effect at a scale of 38.6 km, almost an order of magnitude weaker than the strongest founder effect we inferred in the Americas. This difference may, however, be partly due to the aggregation of the British and continental samples. If we analyze only the French, Spanish, and Portuguese samples (excluding the British samples), we find a founder effect of 18.7, comparable to what we found for the other continental European regions. In contrast, if we analyze the British samples separately, we estimate an 1% decrease to occur over 47.8 km, and the slope in allele frequency is in fact not significantly different from isolation-by-distance at equilibrium.
Discussion
In this article, we study range expansions using a serial founder model to develop a method for inferring the net effect of founder events during a range expansion. A linear or approximately linear decline of genetic diversity with distance has been observed previously in humans (Ramachandran et al. 2005; DeGiorgio et al. 2009) and in simulations (DeGiorgio et al. 2009; Peter and Slatkin 2013). In previous work, we showed in simulations that the directionality index ψ, defined in equation 1, increases approximately linearly with distance from the origin of the range expansion (Peter and Slatkin 2013). In this article, we connect these empirical observations with a theoretical model that explains this decay in terms of differences in variance in the number of offspring per family. In populations with a higher offspring variance, the population’s effective size becomes smaller.
Although branching processes have a long history in population genetics (Ewens 2004), they differ from other commonly used models such as the Wright-Fisher model and the Kingman coalescent in that the total number of individuals in the population is not constant (or following a predetermined series of population sizes). Instead, only the expected number of individuals is constant, leading to different population dynamics. For example, a neutral branching process will eventually die out almost surely, something that cannot happen under the Wright–Fisher model. Therefore, the results presented here are valid only for parameters for which the branching process model provides a good approximation. Our approximation breaks down if there are only few shared variants between populations. However, in this case, phylogeographic methods are more appropriate than population-genetic ones. Otherwise, the branching process approximation appears to be useful as long as many variants have a most recent common ancestor during the expansion or before the expansion started. If that is not the case, as in the large-migration-rate simulations sampled 20N generations after the expansion finished as shown in Figure 4, we find that ψ will be very close to zero, because the signal of the expansion vanishes as time increases. Another parameter region where our approximation breaks down is when the mean allele frequencies become large (Fig. 2). In that case, allele frequencies stop increasing under the Wright–Fisher model as alleles become fixed. In the branching process model, allele frequencies continue to increase.
The effective founder size ke defined here is a variance effective size. The expected allele frequency difference Zt is largely independent of the expansion speed, conditional on ke. The reason is that, even though more segregating variants will be lost during a more rapid expansion, the difference between the expansion front and the rest of the population remains the same. Similarly, we find that Zt is independent of the exact sampling time; waiting after the expansion finishes will add the same amount of genetic drift in both populations. But as long as shared alleles are maintained, we will be able to detect the signal of the expansion if the migration rate is low. Our simulations showed that strong migration will return a population quickly to isolation-by-distance equilibrium.
Our main result summarized the genetic effect of a range expansion in terms of the net founder effect per unit distance. Although we are not able to separately determine the extent of genetic drift per founder event, we capture the combined effect when there is expansion into a large geographic area. If dispersal distances can be determined by some other means, then we can estimate how much smaller the founder size is than Ne.
The analysis of the A. thaliana data shows both the utility and some of the limitations of our approach. We are able to identify expansion origins and infer the strength of the founder effect from genetic data. In the A. thaliana data set, we find that the founder effect is much stronger in the Americas than in continental Europe. It would be interesting to find out if the same pattern is found for other introduced or invasive species. In Europe, our results are consistent with previous analyses by Nordborg et al. (2005) and Franois et al. (2008). Nordborg et al. (2005) found that Arabidopsis likely colonized Scandinavia both from the east, through Finland, and from the south. We similarly infer an eastern Scandinavian origin when analyzing all samples, and a southern origin when considering only the samples from southern Sweden or if we jointly analyze them with eastern European samples. Overall, we identify a likely ice-age refugium close to the Pyrenees in southern France or eastern Spain, a likely refugium near the Caspian sea and a refugium in central southern Europe, either in the Balkans or Italy. Denser sampling would be required to obtain a more accurate picture. In the Americas, we find that Arabidopsis experienced very strong founder effects, and we identify a most likely point of introduction on east coast.
Methods
FORWARD WF-SIMULATIONS
Forward simulations were performed using a simulator implemented in R. Simulations were started with a fixed initial frequency f0 and allowed to evolve for a fixed number of generations. Every t − 1 generations, colonists from the rightmost deme founded a new population, first with a single Wright–Fisher generation of size ke and then of size N afterwards. All demes except the newly founded one underwent t generations of random mating at the same time. Thus, after gt generations, g demes have been colonized. Zt was estimated from 106 replicate alleles. We also assumed logistic instead of instantaneous population growth (see Fig. 3).
BACKWARD SIMULATIONS
Backward-in-time simulations were performed under a structured coalescent model (Wakeley 2009) with migration and colonization. Migration is included in the structured coalescent by allowing lineages to move between neighboring subpopulations. Modeling colonization with a founder effect requires more care. Going forward in time, we want to first take a subsample of the most recent colonized population and let the resulting propagule establish the new deme. To simulate this process going backwards in time, we need to perform these steps in reverse order. We take all lineages from the most recently colonized deme and model the founder event by allowing additional coalescences. The founder event reduces the number of lineages according to the backwards transition probably of the Wright–Fisher model (Wakeley 2009, p. 62):
| (6) |
where ke is the effective founder size, Qt is the number of lineages at time t, (time measured backwards), is the Stirling number of the second kind, and N[j] is the jth falling factorial. If the number of lineages is reduced, we choose lineages to coalesce with equal probability. Then, the colonization step is modeled by moving all remaining lineages to a neighboring colonized deme. To compare predictions of this model to predictions from the branching process model, we have to consider the excess variance in offspring distribution resulting from these expansion events, which is , such that for this coalescent model
| (7) |
Thus, the smaller the effective founder size ke, the larger the allele frequency gradient will be. 1D and 2D simulations were performed using the same simulator. For 1D simulations, we simulated a population consisting of 141 demes, with the expansion starting in the center. A total of 11 samples of size n lineages were taken distances of 0, 5, 10, …, 50 from the origin.
For the 2D simulations, we sampled both a diagonal and horizontal transects. The horizontal transect, parallel to the demic structure, had length 30. The diagonal transect, where demes were colonized every time units, had length , so that demes on both transect are colonized in approximately the same time.
Application
The data set of Horton et al. (2012), along with the coordinates for the accessions, was downloaded from the project’s website at http://bergelson.uchicago.edu/regmap-data/. Genotypes of the sister species Arabidopsis lyrata kindly provided by Matthew Horton were used to determine the ancestral state for each SNP. SNPs for which we could not unambiguously determine the ancestral state, either because no homolog A. lyrata allele was found or the allele of A. lyrata was not present in A. thaliana, were removed. Similarly, we removed all individuals for which we did not have sampling coordinates. Because A. thaliana is a selfing plant and highly inbred accessions were sequenced, we had only a haploid genotype per individual. Because our methodology requires at least two sampled haplotypes, we restricted our analysis to locations with at least two accessions sampled. In addition, selfing may lead to closely related individuals. If only closely related individuals were sampled, our results might be biased because we had underestimated the effective population size of that sample. Therefore, we removed seven locations (all of which had only two samples) where the plants differed at less than 1.5% of sites (average heterozygosity of all locations was 7.1%, with a standard deviation of 3.2%). This resulted in a total of 149 locations with at least two samples, representing 855 individuals, with 121,412 SNPs genotypes remaining. As a single, uniform expansion throughout Europe seems rather unlikely, we performed a PCA analysis to find the main axes of population differentiation (Fig. 6a). The resulting pattern divided the samples broadly into five different groups, and we analyzed data from these groups separately. These groups are as follows: Americas (black), Western Europe (blue), Central Europe (red), Eastern Europe (brown), and Scandinavia (green). For each group, we inferred the origin of the range expansion using equation 5 of Peter and Slatkin (2013). For visualization, we evaluated this equation on a grid (with locations not falling on land excluded) and estimated the best fit for the slope parameter (v) using linear regression, with the location with the highest r2 corresponding to the least-squares estimate of the origin of the expansion (Fig. 6 b–f).
The expected value of ψ depends on the ratio of the effective founder size ke to the effective population size Ne and the number of demes that the population colonized. The number of demes is relevant, because if we divide the population into more demes, it will undergo more but weaker founder effects over the same physical distance. Conversely, if we assume that demes are large, then there are fewer founder events but each one is stronger. Using the model developed in this article, we cannot distinguish between these possibilities without additional information. If, however, the mean dispersal distance and local population densities were known, we could estimate ke relative to the neighborhood size. Alternatively, if the dispersal distance is unknown, we may fix the ratio r = ke/Ne to an arbitrary constant, and instead report the required distance xe over which the effective founder size is ke. This has the advantage that the resulting quantity does not require any assumptions about the demic structure of the population; the larger xe, the weaker the founder effect of the population. For illustration purposes, we calculate the ratio ke/Ne for deme sizes of 1, 10, and 100 km, as well as xe for all groups and report them in Table 1.
Table 1.
Analysis of A. thaliana data.
| Region | Longitude | Latitude | q | r 1 | r 10 | r 100 | x e | r 2 | p |
|---|---|---|---|---|---|---|---|---|---|
| Scandinavia | 24.16 | 60.32 | 0.00065 | 0.99869 | 0.9871 | 0.884 | 7.75 | 0.252 | 4.2×1055 |
| United States | −78.63 | 44.22 | 0.00118 | 0.99763 | 0.9768 | 0.808 | 4.26 | 0.242 | 6.8×1006 |
| Central Europe | 11.40 | 46.84 | 0.00035 | 0.99928 | 0.9928 | 0.932 | 14.05 | 0.171 | 8.3×1021 |
| Western Europe | 2.47 | 43.33 | 0.00013 | 0.99973 | 0.9973 | 0.974 | 38.60 | 0.264 | 4.7×1050 |
| Eastern range | 48.29 | 46.92 | 0.00028 | 0.99943 | 0.9943 | 0.946 | 17.80 | 0.115 | 3.6×1022 |
Notes: The table shows the inferred latitude and longitude of the origin. q, regression slope in km−1; ri , ke/Ne, for demes of size ikm; di, distance (in km) over which 1 − ke/Ne = 1%; r2 and p, adjusted coefficient of determination and Bonferroni-corrected P-value.
Supplementary Material
ACKNOWLEDGMENTS
We thank M. Horton for help with the data, and J. Wilkins, J. Schraiber, M. Yang, K. Harris, and two anonymous reviewers for helpful comments on earlier versions of this article. This work was supported by National Institutes of Health Grant R01-GMR0282 to MS.
Appendix: Derivation of main results
DISCRETE TIME EXPANSION MODEL
We model a range expansion in a 1D habitat with potential deme positions 0, 1, 2, … labeled di, i = 0, 1, …. All but deme d0 are empty at the start of the process. We denote the frequency of the derived allele of a biallelic marker in deme di at time t as fi(t), and we assume that f0(0) = f0, where f0 is some constant. The population behaves as a Markov process, so that the allele frequencies at time t depend only on frequencies at t − 1. Each time step, genetic drift will change allele frequencies according to some probability distribution. In addition, deme dt will become colonized by the offspring of individuals present at time t − 1 in deme dt−1 according to some other probability distribution. We assume there is no migration between demes.
Let {Xt} = { f0(0), f0(1), … f0(t)} and {} = { f0(0), f1(1), … ft(t)} be stochastic processes describing evolution away from the wave front and at the wave front, respectively. Because we disallow migration, {Xt} and {} are independent conditional on f0. The allele frequency of the demes di, 0 < i < t is described by the processes {} = { f0(0), f1(1), … fi(i), fi(i + 1) … fi(t)}. In words, demes are colonized when the wave front first reaches them, and the subsequent evolution depends only on the allele frequencies at the time when they are colonized. From this construction, it follows that for i < j, {} and {} are conditionally independent given fi(i). Together with the Markov property, this implies that the difference in allele frequency in two demes is a function of distance, that is, they obey
| (A1) |
Throughout this section, we assume that Xt|X0 = f0 is constant, which is satisfied if there are no new mutations and no selection, and we further assume that Var(Xt) < ∞. For example, for the critical branching process model we introduce in the following section Var(Xt) = σt, where σ is the offspring variance in one generation. Then, the autocovariance for s < t is,
| (A2) |
and similarly for , because {Xt}, {} are martingales.
Next, we define the conditioned processes {Yt} = {Xt|Xt > 0} and , which describes the evolution of allele frequencies conditional on the alleles not being lost.
Then, we have
| (A3) |
because
| (A4) |
Here, L(t) = (Xt = 0) denotes the probability that an allele is at frequency zero in generation t, and we remove the dependency of L(t) from f0 for notational convenience.
Using the conditional variance formula, we can compute the variance and autocovariance of {Yt}:
| (A5) |
| (A6) |
and covariance for s < t
| (A7) |
| (A8) |
| (A9) |
| (A10) |
The last quantity of interest is the difference Zt = Yt − , which gives the difference in allele frequency between the wave-front and the origin of the expansion, conditional on an allele surviving in both locations. We find that
| (A11) |
| (A12) |
| (A13) |
and
| (A14) |
| (A15) |
BRANCHING PROCESS
To further specify the moments derived in the previous section Discrete Time Expansion Model in the Appendix, we need to define Var(Xs), L(s), and f0, and the corresponding quantities at the wave front. Under a critical Galton–Watson branching process, individuals produce offspring independent from each other according to some offspring distribution F with mean one. Let Li(t) denote the probability that an allele has been lost by generation t, given that it started with i copies in generation 0. Kolmogorov (1938) showed that when t is large, L1 is well approximated by
| (A16) |
where F is the offspring distribution and Var(F) is assumed to be finite. We assume that a branching process with offspring distribution F describes neutral genetic drift away from the wave front, and that the colonization of new demes occurs according to a branching process with offspring distribution
If the initial frequency f0 of the allele is greater than one, the corresponding expression becomes
| (A17) |
by independence of individuals. Using a Taylor expansion around t = ∞ yields
| (A18) |
| (A19) |
Thus, we find that the expected difference in allele frequency between the expansion origin and the front of the population increases approximately linear with distance, the slope of the curve being the difference in offspring variance of individuals at the wave front and expansion origin. From the second term in the Taylor expansion, we see that the approximation is suitable when t > , that is, the number of demes between the two samples is large, and the frequency of the allele at the founding location is small.
EFFECTIVE POPULATION SIZE
The variance effective population size for a Cannings model is defined as
| (A20) |
where N is the absolute number of individuals per population. The branching process considered above is not a Cannings model; however, the evolution of the offspring of a single individual under a Cannings population is well approximated by a branching process. Fisher (1930) pioneered the modeling of population genetics using branching processes (Ewens 2004, p. 29). Under a Wright–Fisher model, the offspring distribution of a single individual has mean and variance very close to one. This allowed Fisher to approximate the evolution of an individual under the Wright–Fisher model as evolving according to a branching process with a Poisson(1) offspring distribution, which has offspring variance 1, a model we will also use here to model genetic drift away from the wave front.
To incorporate the reduced effective size of a founder effect at the wave front, we use a modified offspring model: with probability (1 − α), an individual at the wave front does not produce any offspring. With probability α, the number of offspring is Poisson distributed with parameter 1/α s.t. the overall expected number of offspring is still one and the variance is Var() = α−1. This allows us to define an effective founder size ke
| (A21) |
which measures the “increase” in genetic drift at the wave front.
Combining eq. A21 and eq. A19 yields
| (A22) |
From this, we see immediately that Zt = 0 if Ne = ke, and also that the effective founder size enters the equation only in the ratio , so that it makes sense to further define the relative founder size κ, which measures the strength of the founder effect.
RESCALING
The branching processes we used above assume that exactly one generation of genetic drift happens between each founder event. In this section, we show that the expected allele frequency difference between the expansion front and at the origin is invariant to additional generations between expansion events and to additional generations after the expansion finished.
Both of these results follow from the fact that for a branching process with mean one, the variances of subsequent generations can simply be added: Consider a nonhomogeneous critical branching process {Bt} and let us denote the generating function of the distribution of Bt with pt(s). Then, the variance of Bt is pt(1)″. Then, the generating function of Bt+1 is q(pt(s)), where q(s) is the generating function of the offspring distribution of that last generation. The variance in offspring after this additional generation is q(pt(1))″.
| (A23) |
because (1) = pt(1) = q(1) = q′ (1) = 1.
Thus, if individuals in the range expansion model have offspring variance v at the expansion front and variance away from the front, the total variance after t time steps with d expansion events is (t − d)v + .
Now from equation A19 we have (for f0 = 1),
| (A24) |
Adding T generations with neutral drift between each founder event and τ generations after the expansion stopped, changes this only to
which simplifies to eq. A19.
We can generalize our model to relax our assumptions about population growth, for example by allowing for an extended bottleneck or logistic growth. Again, this will result in an increase in Var(Xd) and Var() by the same amount, which cancels in the difference.
Furthermore, we can also change how we subdivide a population into demes. It is easy to see that a population with expansions at times 0, 1, 2, … and offspring variances Var(F) and Var() behaves similarly to a population with expansions occurring at times 0, δt, 2δt, … with offspring variances and in the sense that Zt will be the same for either population. Consequently, how we subdivide space into demes is not important, only the ratio of the founder size to the population size matters.
ESTIMATION
To estimate Zt from genetic data, we need to take subsampling into account, that is, we need to estimate . In particular, the probability that an allele is lost from the population (which we condition on in Zt) is not the same as it being absent from a sample (which we may observe in data). To model subsampling, we assume that the process starts with f0 copies of the derived allele and A0 copies of the ancestral allele, all evolving as independent branching processes. The expected number of ancestral alleles will be At = A0 in all generations, whereas the expected number of the derived allele, conditioned on it not being lost, is Yt. Hence, in generation t, the probability of drawing m copies of the derived allele out of n is approximately binomially distributed with parameters n and . The mean of the expected allele frequency, conditional of sampling at least one derived allele, is
| (A25) |
with the term normalizing to allele counts. Setting A0 ≈ 2N − Yt, we obtain the series representation
| (A26) |
Hence,
| (A27) |
and we see that we have a bias term that increases with sample size. Hence, the easiest way to proceed is to down-sample larger samples to a sample size of two, the case that is probably the most important for the analysis of genomic data.
To compare samples of size n1 and n2, recall that the 2D-site frequency spectrum is the n1 + 1 × n2 + 1-matrix S whose entries fi j represent the number of polymorphisms that are at frequency i in one population and at frequency j in the other (0 ≤ i ≤ n1, 0 ≤ j ≤ n2). We can calculate a reduced site frequency spectrum matrix S′ from the full site frequency spectrum using
| (A28) |
where P1 and P2 are (2 + 1) × (n1 + 1) and (2 + 1) × (n2 + 1) matrices (with indices starting at 0), respectively, with entries
| (A29) |
for 0 ≤ i ≤ n1 and 0 ≤ j ≤ 2 for P1. Entries in P2, are similar, except n1 is replaced by n2.
If we denote the entries of S′ with si j, we can write as
| (A30) |
This statistic is identical to the statistic defined in Peter and Slatkin (2013), where we did not give any theoretical justification.
Footnotes
Additional Supporting Information may be found in the online version of this article at the publisher’s website:
Figure S1: Robustness results.
LITERATURE CITED
- Anderson EC, Slatkin M. Estimation of the number of individuals founding colonized populations. Evolution. 2007;61:972–983. doi: 10.1111/j.1558-5646.2007.00080.x. [DOI] [PubMed] [Google Scholar]
- Austerlitz F, Jung-Muller B, Godelle B, Gouyon PH. Evolution of coalescence times, genetic diversity and structure during colonization. Theor. Popul. Biol. 1997;51:148–164. [Google Scholar]
- Barton NH, Etheridge AM, Kelleher J, Vber A. Genetic hitchhiking in spatially extended populations. Theor. Popul. Biol. 2013;87:75–89. doi: 10.1016/j.tpb.2012.12.001. [DOI] [PubMed] [Google Scholar]
- Beaumont MA, Zhang W, Balding DJ. Approximate Bayesian computation in population genetics. Genetics. 2002;162:2025–2035. doi: 10.1093/genetics/162.4.2025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brockmann D, Helbing D. The hidden geometry of complex, network-driven contagion phenomena. Science. 2013;342:1337–1342. doi: 10.1126/science.1245200. [DOI] [PubMed] [Google Scholar]
- Burton OJ, Travis JMJ. The frequency of fitness peak shifts is increased at expanding range margins due to mutation surfing. Genetics. 2008;179:941–950. doi: 10.1534/genetics.108.087890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cann RL, Stoneking M, Wilson AC. Mitochondrial DNA and human evolution. Nature. 1987;325:31–36. doi: 10.1038/325031a0. [DOI] [PubMed] [Google Scholar]
- Davis MA. Invasion biology. 1st ed. Oxford Univ. Press; Oxford/New York: 2009. [Google Scholar]
- DeGiorgio M, Jakobsson M, Rosenberg NA. Explaining worldwide patterns of human genetic variation using a coalescent-based serial founder model of migration outward from Africa. Proc. Natl. Acad. Sci. USA. 2009;106:16057–16062. doi: 10.1073/pnas.0903341106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeGiorgio M, Degnan JH, Rosenberg NA. Coalescence-time distributions in a serial founder model of human evolutionary history. Genetics. 2011;189:579–593. doi: 10.1534/genetics.111.129296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ewens WJ. Mathematical population genetics: theoretical introduction. Springer; New York: 2004. [Google Scholar]
- Excoffier L. Patterns of DNA sequence diversity and genetic structure after a range expansion: lessons from the infinite-island model. Mol. Ecol. 2004;13:853–864. doi: 10.1046/j.1365-294x.2003.02004.x. [DOI] [PubMed] [Google Scholar]
- Fisher RA. The wave of advance of advantageous genes. Ann. Eugen. 1937;7:355–369. [Google Scholar]
- Franois O, Blum MGB, Jakobsson M, Rosenberg NA. Demographic history of European populations of Arabidopsis thaliana. PLoS Genet. 2008;4:e1000075. doi: 10.1371/journal.pgen.1000075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gravel S, Henn BM, Gutenkunst RN, Indap AR, Marth GT, Clark AG, Gibbs RA, The 1000 Genomes Project. Bustamante CD. Demographic history and rare allele sharing among human populations. Proc. Natl. Acad. Sci. USA. 2011;108:11983–11988. doi: 10.1073/pnas.1019276108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hallatschek O, Hersen P, Ramanathan S, Nelson DR. Genetic drift at expanding frontiers promotes gene segregation. Proc. Natl. Acad. Sci. USA. 2007;104:19926–19930. doi: 10.1073/pnas.0710150104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris TE. The theory of branching processes. Springer-Verlag; Berlin: 1963. [Google Scholar]
- Henn BM, Cavalli-Sforza LL, Feldman MW. The great human expansion. Proc. Natl. Acad. Sci. USA. 2012;109:17758–17764. doi: 10.1073/pnas.1212380109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hewitt GM. Post-glacial re-colonization of European biota. Biol. J. Linn. Soc. 1999;68:87–112. [Google Scholar]
- Horton MW, Hancock AM, Huang YS, Toomajian C, Atwell S, Auton A, Muliyati NW, Platt A, Sperone FG, Vilhjalmsson BJ, et al. Genome-wide patterns of genetic variation in worldwide Arabidopsis thaliana accessions from the RegMap panel. Nat. Genet. 2012;44:212–216. doi: 10.1038/ng.1042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Itan Y, Powell A, Beaumont MA, Burger J, Thomas MG. The origins of lactase persistence in Europe. PLoS Comput Biol. 2009;5:e1000491. doi: 10.1371/journal.pcbi.1000491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorgensen S, Mauricio R. Neutral genetic variation among wild North American populations of the weedy plant Arabidopsis thaliana is not geographically structured. Mol. Ecol. 2004;13:3403–3413. doi: 10.1111/j.1365-294X.2004.02329.x. [DOI] [PubMed] [Google Scholar]
- Kimura M. Diffusion models in population genetics. J. Appl. Prob. 1964;1:177–232. [Google Scholar]
- Klopfstein S, Currat M, Excoffier L. The fate of mutations surfing on the wave of a range expansion. Mol. Biol. Evol. 2006;23:482–490. doi: 10.1093/molbev/msj057. [DOI] [PubMed] [Google Scholar]
- Kolmogorov A, Petrovskii I, Piscounov N. A study of the diffusion equation with increase in the amount of substance, and its application to a biological problem. Univ. Math. Mech. 1937;1:1–25. [Google Scholar]
- Leblois R, Slatkin M. Estimating the number of founder lineages from haplotypes of closely linked SNPs. Mol. Ecol. 2007;16:2237–2245. doi: 10.1111/j.1365-294X.2007.03288.x. [DOI] [PubMed] [Google Scholar]
- Li H, Durbin R. Inference of human population history from individual whole-genome sequences. Nature. 2011;475:493–496. doi: 10.1038/nature10231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nordborg M, Hu TT, Ishino Y, Jhaveri J, Toomajian C, Zheng H, Bakker E, Calabrese P, Gladstone J, Goyal R, et al. The pattern of polymorphism in Arabidopsis thaliana. PLoS Biol. 2005;3:e196. doi: 10.1371/journal.pbio.0030196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peter BM, Slatkin M. Detecting range expansions from genetic data. Evolution. 2013;67:3274–3289. doi: 10.1111/evo.12202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramachandran S, Deshpande O, Roseman CC, Rosenberg NA, Feldman MW, Cavalli-Sforza LL. Support from the relationship of genetic and geographic distance in human populations for a serial founder effect originating in Africa. Proc. Natl. Acad. Sci. USA. 2005;102:15942–15947. doi: 10.1073/pnas.0507611102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ray N, Currat M, Foll M, Excoffier L. SPLATCHE2: a spatially explicit simulation framework for complex demography, genetic admixture and recombination. Bioinformatics. 2010;26:2993–2994. doi: 10.1093/bioinformatics/btq579. [DOI] [PubMed] [Google Scholar]
- Slatkin M, Excoffier L. Serial founder effects during range expansion: a spatial analog of genetic drift. Genetics. 2012;191:171–181. doi: 10.1534/genetics.112.139022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slatkin M, Wade MJ. Group selection on a quantitative character. Proc Natl. Acad. Sci. USA. 1978;75:3531–3534. doi: 10.1073/pnas.75.7.3531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taberlet P, Fumagalli L, Wust-Saucy A-G, Cosson J-F. Comparative phylogeography and postglacial colonization routes in Europe. Mol. Ecol. 1998;7:453–464. doi: 10.1046/j.1365-294x.1998.00289.x. [DOI] [PubMed] [Google Scholar]
- Wakeley J. Coalescent theory: an introduction. Roberts & Co. Publishers; Greenwood Village, CO: 2009. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.