Variation in the Protective Effect of Higher Education Against Depression*

Abstract

Numerous studies document that higher education is associated with a reduced likelihood of depression. The protective effects of higher education, however, are known to vary across population subgroups. This study tests competing theories for who is likely to obtain a greater protective benefit from a college degree against depression through an analysis of data from the National Longitudinal Study of Adolescent Health and recently developed methods for analyzing heterogeneous treatment effects involving the use of propensity scores. The analysis examines how the effects of two “treatments” (at least some college education and attaining at least a four-year college degree) on latent depressive symptomology vary by background disadvantage, as indicated by having a low propensity for completing some college or attaining a four-year college degree. Results indicate that people from disadvantaged backgrounds realize a greater protective effect of higher education, either completing some college or attaining a four-year degree, against depressive symptomology than people from advantaged backgrounds. This pattern is more pronounced for people who attain at least a four-year degree than for people who complete at least some college education.

Introduction

Depression is one of the leading causes of disability in the United States with close to 10 percent of adults in the U.S. showing significant symptoms of depression in a given year (Strine et al. 2008). Education offers a degree of protection against depression as numerous studies have documented an inverse association between educational attainment and depression (see Lorant et al. (2003) for a meta-analysis). The inverse association in part reflects selection processes in which depression in childhood and adolescence influences both educational attainment and depression in adulthood (Fletcher 2008, 2010; McLeod and Fettes 2007), though some studies find that the selection processes are minimal or non-existent (Miech et al. 1999). Furthermore, although few studies attempt to account for selection processes when estimating the effect of education on depression, those that do generally continue to find a robust inverse association linking education and depression. For instance, studies relying on instrumental variables and natural experiments based on compulsory schooling laws report enduring associations between education and depression (Chevalier and Feinstein 2007; Crespo, López-Noval, and Mira 2013).ⁱ Twin studies, however, suggest that common genetic causes of both education and depression may be a source of confounding (Fujiwara and Kawachi 2009), though there are some concerns that these studies are underpowered (Madsen and Osler 2009).

The protective effect of education against depression is known to vary across subgroups of the population. Studies have examined whether the effects of education on depression are conditional on age (Bjelland et al. 2008; Miech and Shanahan 2000; Schaan 2014), sex (Ross and Mirowsky 2006), race/ethnicity (Hudson et al. 2012; Williams et al. 2007; Williams, Takeuchi, and Adair 1992), family socioeconomic resources in childhood (Schaan 2014), and the level of education itself (Bracke, Pattyn, and von dem Knesebeck 2013). In general, education has a greater protective effect for women than for men, for whites than for blacks, and for people growing up in families with limited socioeconomic resources. Over the life course, the protective effect of education against depression appears to follow a curvilinear pattern with larger effects among young adults and the elderly, but this remains an active area of inquiry because of conflicting results across studies. In addition, there is evidence that the protective effect of education diminishes with increasing levels of education, particularly for people who are overeducated for their job.

Past studies of the conditional protective effects of education against depression typically focus on one or two factors at a time. In this study I adopt an alternative analysis strategy that involves analyzing whether the protective effects of educational attainment are conditional on a summary measure that encapsulates background advantage/disadvantage, i.e., the likelihood of completing some college or attaining a college degree. In particular, I adopt methods developed by Xie et al. (2012) to examine whether a treatment effect varies across the propensity (likelihood) of attaining the treatment. These analysis strategies have proven fruitful in a number of empirical studies examining heterogeneity in the returns to education (Bauldry 2014; Brand and Davis 2011; Brand and Xie 2010; Brand 2010; Musick, Brand, and Davis 2012; Schafer, Wilkinson, and Ferraro 2013).

This study draws on data from the National Longitudinal Study of Adolescent Health (Add Health) (Harris et al. 2009) and recently developed models for analyzing heterogeneous treatment effects (Xie et al. 2012) to examine how the protective effect of a college degree against depression among young adults varies across the likelihood of completing some college or attaining a college degree. The next section reviews two competing hypotheses of who is more likely to benefit from higher education. The third section describes the Add Health data and the models used to analyze heterogeneous effects. The fourth section presents the results of the analysis and the final section contextualizes the results.

Who Benefits More from Education

In a series of papers, Ross and Mirowsky developed and tested competing hypotheses of who is likely to benefit more from higher levels of education with respect to health in general (Ross and Mirowsky 2006, 2010a, 2010b, 2011). The first hypothesis, referred to as “resource multiplication,” posits that higher education will be more beneficial for people from advantaged backgrounds. With respect to depression, this hypothesis would hold if people from advantaged backgrounds obtained a greater protective effect from higher education than people from disadvantaged backgrounds.

People from advantaged backgrounds may obtain a greater protective effect from higher education for a few reasons. First, prior to attending college people from advantaged backgrounds are more likely to have healthy lifestyles and the resources to support them that promote mental health (Cockerham 2005). Attaining a college degree may further reinforce these healthy lifestyles, thus garnering a greater protective effect against depression than that realized by people from disadvantaged backgrounds.

Second, one of the pathways linking higher education to lower levels of depression is through the attainment of more fulfilling careers and higher wages. Such jobs provide economic resources and a work environment that can mitigate financial stress, support healthy lifestyles, and thereby promote mental health (Link, Lennon, and Dohrenwend 1993; Mirowsky and Ross 2003; Turner and Lloyd 1999; Turner, Wheaton, and Lloyd 1995; Zimmerman, Christakis, and Vander Stoep 2004). People from advantaged backgrounds can draw on additional resources (e.g., economic support and social capital) to help ensure that they obtain the sorts of careers that promote mental health. In contrast, people from disadvantaged backgrounds may have less flexibility (e.g., the economic resources to support working in an unpaid internship) and less social capital to draw upon to help ensure that higher education leads to careers that promote mental health.

Third, another pathway linking higher education to lower levels of depression is through the development of a sense of mastery and self-efficacy, which in turn helps people cope with life’s problems and stresses (Kohn and Schooler 1982; Mirowsky and Ross 2003; Pearlin 1989; Pearlin et al. 1981; Thoits 1995; Turner and Lloyd 1999; Wheaton 1980). Prior to attending college, people from disadvantaged backgrounds are more likely to lack a sense of mastery and self-efficacy (Conger et al. 2009; Ross and Mirowsky 2013). Furthermore, adolescence is a critical period for the development of mastery and self-efficacy (Erol and Orth 2011), thus it is possible that higher education is less effective at instilling these important psychological resources for people from disadvantaged backgrounds than for people from advantaged backgrounds.

The second hypothesis, referred to as “resource substitution,” posits that instead of magnifying preexisting advantages higher education instead compensates for preexisting disadvantages. With respect to depression, this hypothesis would hold if people from disadvantaged backgrounds obtained a greater protective effect from a college degree than people from advantaged backgrounds. As with resource multiplication, there are a couple plausible explanations for why people from disadvantaged backgrounds may benefit more from higher education with respect to depression than people from advantaged backgrounds.

First, although people from advantaged backgrounds can draw on more resources to help ensure they obtain a career that supports their mental health, it is possible that this would have been true even without higher education. In other words, people from advantaged backgrounds may have to less to gain from higher education than people from disadvantaged backgrounds. In support of this possibility, a recent study finds that the economic returns to a college degree are greater for people from disadvantaged backgrounds (Brand and Xie 2010). This result stems from the fact that people from disadvantaged backgrounds who do not obtain a college degree have particularly poor labor market outcomes.

Second, following a similar logic, it could be that the improved sense of mastery and self-efficacy associated with higher education is less meaningful for people from advantaged backgrounds than people from disadvantaged backgrounds. Although adolescence is a critical period for developing a sense of mastery and self-efficacy, it is possible that even the potentially smaller gains during college are more meaningful for people from disadvantaged as opposed to advantaged backgrounds. For instance, the possibility that people from disadvantaged backgrounds overcame significant odds to attend college or attain a college degree may in itself support a sense of mastery and self-efficacy.ⁱⁱ As with the economic returns, it may be that the “psychological” returns to higher education are greater for people from disadvantaged backgrounds due to the potentially poor prospects for people from disadvantaged backgrounds who do not obtain a college degree.

Empirical evidence to date has generally supported the resource substitution hypothesis over the resource multiplication hypothesis. In a study of the varying effects of education on depression by sex using data from the 1995 Aging, Status, and Sense of Control survey, Ross and Mirowsky (2006) found that women had a greater protective benefit from education against depression than men. They conceptualize women as a disadvantaged group relative to men in economic terms and thus consider the results supportive of resource substitution. In another study of the effects of education on depression with socioeconomic resources in childhood as the measure of advantage/disadvantage using data from the multiple waves of the Survey of Health, Ageing, and Retirement in Europe, Schaan (2014) also found that people from poor families benefited more from education than people from better-off families, a pattern that remained consistent over the later life course (ages 50 and up). Additional evidence in support of the resource substitution hypothesis comes from analyses examining the effects of education on physical health (Ross and Mirowsky 2011; Schafer et al. 2013); however, Bauldry (2014) found support for resource multiplication in an analysis of self-rated health among young adults.

In contrast to the Ross and Mirowksy (2006) and Schaan (2014) studies, the present study draws on propensity scores of completing some college and attaining a four-year college degree as key summary measures of advantage/disadvantage and adopts a recently developed approach for identifying heterogeneous treatment effects. In contrast to the Schafer et al. (2013) and Bauldry (2014) studies that draw on similar models for heterogeneous treatment effects, the present study focuses on mental rather than physical health, in particular, depressive symptomology. In addition, the present study examines heterogeneity in the effect of both completing some college education and attaining a four-year college degree.

Data and Methods

Sample

Data for the present study come from Waves I and IV of the National Longitudinal Study of Adolescent Health (Add Health). Add Health is a nationally representative study of adolescents in the United States in grades 7 through 12 that began in 1995 and to date has continued for four waves (Harris et al. 2009). The 1995 Wave I in-home interview consisted of a sample of 20,745 adolescents along with 17,713 parents of the adolescents. The 2008 Wave IV in-home interviews followed-up with 15,701 respondents of the original Wave I respondents now aged 24 to 34. The analysis sample consists of respondents who participated in Wave IV with valid sample weights (N = 14,800), non-missing educational attainment (N = 14,796), non-missing for all measures of depression at Wave IV (N = 14,793), and with complete data for all covariates except parent income (N = 13,120). With the exception of parent income, most of the covariates are missing for less than 0.5 percent of the respondents and none are missing for more than 5 percent of the respondents.

Parent income is missing for a substantial proportion of respondents (22 percent of the analysis sample). Ideally, one would use multiple imputation to address this missing data (as well as among the other covariates); however, the analytical approaches to estimate heterogeneous treatment effects have not been developed for multiply imputed data. As an alternative, I use a single imputation strategy employed by Brand (2010) to impute parents’ income based on regressing logged income on all covariates. The imputation procedure did not produce any outliers and only slightly reduced the mean and variance of the measure. The original logged parent income measure has mean 3.57 and standard deviation 0.84, and the measure with imputed values has mean 3.54 and standard deviation 0.78.

Measurement

The outcome for the following analysis is a latent variable for depressive symptomology measured by a subset of the 10 questions from the Center for Epidemiologic Studies Depression Scale (CES-D) asked of respondents at Wave IV (Radloff 1977). A study of the psychometric properties of the CES-D items using Wave I of Add Health found that four of the ten items are the most suitable indicators of depressive symptomology (Perreira et al. 2005). In addition, a measurement analysis of the 10 CES-D items available at Wave 4 indicated that subset of four items identified as suitable indicators produced a better fitting model than using all 10 indicators (results available upon request). The four items begin with the stem “[d]uring the past seven days:” and included (1) “you could not shake off the blues, even with the help from your family and friends” [blues] (2) “you felt depressed” [depressed] (3) “you felt happy” [happy] and (4) “you felt sad” [sad] (see Table 1). Treating depressive symptomology as a latent variable allows one to address measurement error in the indicators.

Table 1.

Weighted means or proportions for measures of depressive symptomology and covariates (N = 13,120).

	Overall	Some College			Four-Year Degree
		No	Yes	Dif.	No	Yes	Dif.
		M/P	M/P		M/P	M/P
Blues	0.31	0.42	0.25	***	0.37	0.19	***
Depressed	0.38	0.50	0.32	***	0.44	0.25	***
Happy	2.18	2.06	2.24	***	2.12	2.30	***
Sad	0.56	0.66	0.50	***	0.60	0.46	***
Depressive symptomology	0.00	0.09	−0.05	***	0.04	−0.09	***
Demographics
Age at wave IV	28.34	28.35	28.33		28.34	28.35
Female	0.49	0.42	0.53	***	0.46	0.54	***
White	0.67	0.61	0.70	***	0.64	0.74	***
Black	0.15	0.19	0.14	***	0.17	0.11	***
Hispanic	0.11	0.15	0.10	***	0.13	0.07	***
Other race	0.07	0.06	0.07		0.06	0.08	**
Native born	0.95	0.95	0.95		0.95	0.95
Both bio parents	0.56	0.46	0.61	***	0.50	0.70	***
Family background
Par edu: < HS	0.11	0.20	0.07	***	0.15	0.04	***
Par edu: HS or GED	0.27	0.38	0.21	***	0.33	0.15	***
Par edu: some college	0.30	0.30	0.31		0.33	0.25	***
Par edu: 4-year degree	0.18	0.09	0.22	***	0.14	0.26	***
Par edu: > 4-year degree	0.14	0.03	0.19	***	0.06	0.30	***
Family income (log)	3.54	3.24	3.71	***	3.37	3.93	***
Indicator for imputed income	0.20	0.21	0.20		0.20	0.20
Academic factors
Adolescent GPA	2.81	2.41	3.03	***	2.59	3.31	***
Adolescent PVT	102.06	95.74	105.42	***	99.04	108.65	***
Adolescent aspirations	4.44	3.97	4.69	***	4.25	4.84	***
Health and health behaviors
Adolescent self-rated health	2.10	2.26	2.02	***	2.21	1.88	***
Adolescent BMI	22.48	22.95	22.23	***	22.80	21.79	***
Adolescent smoker	0.21	0.28	0.17	***	0.25	0.11	***
Adolescent drinking	1.09	1.15	1.06	*	1.12	1.01	**
Mental health
Adolescent dep. sym.	−0.02	0.04	−0.05	***	0.01	−0.09	***
Adolescent counseling	0.13	0.17	0.11	***	0.15	0.09	***

Notes: Means and proportions are weighted by the Wave I/Wave IV longitudinal Add Health sample weights. Depressive symptomology and adolescent depressive symptomology are the factor score measures. Significance tests are based on Wald tests for the difference between weighted means or proportions.

Two treatment conditions are considered in the following analysis. The first is completing some college education and the second is attaining a four-year college degree. Any respondent who reported some college education or higher at Wave IV or any respondent who reported attaining a college degree or higher at Wave IV are considered in the respective treatment conditions. Sixty eight percent of Add Health respondents reported completing some college education and 33 percent of Add Health respondents reported attaining at least a four-year college degree (weighted 65 and 31 percent respectively).

Given that at Wave IV respondents ranged in age from 24 to 34, it is possible that some respondents had not had the opportunity to enroll in college or complete their education at the time of the interview. With respect to attaining a college degree, Add Health includes a question about whether respondents are currently enrolled in college, but it is unknown what proportion of these respondents will complete a college degree. An auxiliary analysis excluding people who reported being enrolled in college and had not yet attained a four-year degree (N = 1,438; 11 percent of the sample) was conducted and found the same pattern of results (available upon request).

The analysis strategy for estimating the protective effect of completing some college or attaining a college degree rests on the assumption that, conditional on a set of covariates, the probability of completing some college or attaining a college degree is independent of depression, which is known as the conditional independence assumption or ignorability (Heckman 2005; Morgan and Winship 2007; Rosenbaum and Rubin 1983). In practice, this assumption is unlikely to hold, but a rich set of covariates predicting completing some college or attaining a college degree can make the assumption more plausible and less likely to be substantially violated.

The model to estimate propensities for completing some college or attaining a college degree includes five conceptually distinct sets of covariates (see Table 1). The first set of covariates includes sociodemographic measures known to be associated with higher education and depression: age at wave IV, sex, race (indicators for black, Hispanic, and other races with white as the referent), nativity status, and family structure (an indicator for living with a both biological parents). The second set of covariates includes family resources: parent education and family income at Wave I. Parent education ranges from 1 “less than a high school degree” to 5 “professional training beyond a 4-year college or university.” Indicators for each level were entered with “professional training beyond a 4-year college or university” as the referent group in order to allow for a nonlinear association with completing some college or attaining a college degree. Family income is the log of pre-tax income measured in thousands of dollars and includes imputed values as discussed above. I also include an indicator for cases with imputed values for logged income.

The third set of covariates includes academic measures: GPA, cognitive ability, and educational aspirations. GPA is based on self-reported grades in up to four classes (English or language arts, mathematics, history or social studies, and science) for the most recent grading period at Wave I. The Peabody Vocabulary Test is used as a measure of cognitive ability (Dunn and Dunn 1981). Educational aspirations is based on a Likert scale item asking respondents how much do you want to go college and how likely is it that you will go to college respectively. The responses range from 1 “low” to 5 “high.”

The fourth set of covariates includes measures of adolescent health and health behaviors taken from Wave I: self-rated health, BMI, an indicator for ever having smoked regularly, and frequency of alcohol consumption. Self-rated health is based on the standard five-point scale ranging from 5 “excellent” to 1 “poor” asked of the respondents at Wave I. BMI is calculated from self-reported weight and height. The indicator for ever having smoked regularly captures respondents who reported ever smoking at least a cigarette a day for 30 days. The frequency of alcohol consumption captures drinking behavior in the last year and ranges from 0 “never” to 6 “almost every day.”

The fifth set of covariates includes a measure of depressive symptomology in adolescence and an indicator for having received psychological or emotional counseling in the past year. To maintain as much consistency as possible with the outcome measure of latent depressive symptomology, a measurement model was specified for adolescent depressive symptomology using the same items (i.e., the items that Perreira et al. (2005) identified as the best measures) as used at Wave IV, and factor scores were constructed using the regression method which maximizes the correlation between the factor scores and the underlying latent variable (Thomson 1939). The correlation between the factor scores for adolescent depressive symptomology and the latent variable is 0.91. This is an important set of covariates to include in the propensity score models given the potential social selection processes in which mental health in adolescence may influence educational attainment and mental health in adulthood (Fletcher 2008, 2010; McLeod and Fettes 2007).

Analysis Strategy

The analysis of variation in the protective effects of higher education against depression draws on two approaches developed by Xie et al. (2012) and used in a number of papers by Brand and colleagues examining heterogeneity in the effects of education across a range of social outcomes (Brand and Davis 2011; Brand and Xie 2010; Brand 2010; Musick et al. 2012). The first analytic strategy for this analysis, the stratification-multilevel method of estimating heterogeneous treatment effects, proceeds in four steps (Xie et al. 2012).

The first step is to estimate propensity scores for completing some college and attaining a college degree by specifying probit models with the sets of covariates discussed above (Rosenbaum and Rubin 1983). The second step is to group respondents into propensity score strata based on achieving balance within each stratum separately for the two treatments. Balance within a stratum is achieved when the difference in means for all covariates between people who completed and did not complete a college degree are not statistically significant (Rosenbaum and Rubin 1984).ⁱⁱⁱ For this analysis, the threshold for determining whether the means of the covariates differ between the people with and without some college and with and without a college degree is set at p < 0.001, which is consistent with past studies in this area (Brand and Xie 2010; Schafer et al. 2013). Balanced propensity score strata are identified using the algorithm outlined and implemented in the Stata user-written program pscore (Becker and Ichino 2002).

This step also involves identifying the range of propensity scores that includes both people who did and did not receive the treatment, which is known as the region of common support. Ideally, one identifies respondents for the full theoretical range of propensity scores that did and did not receive the treatment (e.g., both people with a low propensity of attaining a four-year college degree but who did attain a degree and people with a high propensity of attaining a four-year degree but who did not attain a degree). If there are ranges of propensity scores for which either no treatments or no controls exist, then it is unadvisable to use cases in these ranges as they are not well matched with either treatments or controls. In this analysis, the region of common support for completing some college ranges from propensity scores of 0.020 to 0.999 and admits the use all but 17 respondents with estimated propensity scores outside this range. Similarly the region of common support for attaining a four-year college degree ranges from propensity scores of 0.001 to 0.994 and admits the use of all but 145 respondents with estimated propensity scores outside this range.

The third step is to estimate the effects of completing some college and attaining a college degree on latent depressive symptomology within each propensity score stratum (stratum-specific treatment effects). For depressive symptomology, this step involves first specifying a measurement model linking the indicators to latent depressive symptomology within each propensity score stratum and then regressing the latent variable on a treatment indicator. The model is given by

$${\eta }_{ik}={\alpha }_k+{\beta }_{1k}{T}_{ik}+{\epsilon }_{ik}$$ (1)

$$x_{\mathit{ijk}}={\alpha }_{jk}+{\lambda }_{jk}{\eta }_{ik}+{\delta }_{\mathit{ijk}},$$ (2)

where i indexes individuals, j indexes the four indicators of depressive symptomology, and k indexes propensity score, η_ik is latent depressive symptomology, T_ik is an indicator for completing some college or attaining a college degree, x_ijk is the j^th indicator of depressive symptomology, ε_ik and δ_ijk are error terms, α_k and α_jk are intercepts, λ_jk is the factor loading for j^th indicator, and β_1k is the effect of the treatment on depressive symptomology.

The fourth step is to evaluate a trend across propensity score strata using variance-weighted least squares to regress the stratum-specific estimates of the effects of completing some college or attaining a college degree on the stratum rank. This is the key step in identifying any patterns in the treatment effects across the propensity score strata. Since the scaling indicator for depressive symptomology is coded such that higher values indicate more depressive symptoms, the average effect of higher education should be negative. If some college or a college degree compensates for background disadvantages, then we should see a positive trend in the stratum-specific treatment effects, as this would indicate that the protective effects against depression are greater (i.e., more negative) among respondents with lower propensity scores. Alternatively, if some college or a college degree augments preexisting advantages, then we should see a negative trend in the stratum-specific treatment effects.

One limitation of the stratification-multilevel method of analyzing heterogeneous treatment effects is the assumption that treatment effects are homogenous within a limited number of strata. Another limitation is that due to the small number of propensity score strata, it is difficult to assess potential nonlinear patterns across the treatment effects. The matching-smoothing method for assessing heterogeneous treatment effects overcomes these limitations but at the cost of addressing measurement error in the indicators of depressive symptomology (Xie et al. 2012). To maximize consistency with the stratification-multilevel method, I construct factor scores for latent depressive symptomology using the regression method that maximizes the correlation between the factor scores and the latent variable. The correlation between the factor scores for young adult depressive symptomology and the latent variable is 0.92.

The matching-smoothing method proceeds in four steps. The first step involves estimating propensity scores for completing some college or attaining college degree for all respondents. The second step involves matching treatments to controls based on the estimated propensity scores. For this step, I use a nearest-neighbor matching algorithm with replacement that allows for each treatment to be matched with up to five controls and I set a caliper of 3 percent (i.e., the difference in propensity scores between treatments and controls can be no greater than 0.03). I use the Stata user-written program psmatch2 to implement the matching algorithm (Leuven and Sianesi 2003).

The third step involves calculating the difference in depressive symptomology factor scores for each match and plotting the differences across the range of propensity score values. For treatments matched with multiple controls, the value of depressive symptomology for controls is the average value among the matched controls. The fourth step involves examining the pattern in differences between matched treatments and controls across the range of propensity scores using a local polynomial regression, a non-parametric smoothing device that allows for nonlinear relationships. Following Xie et al. (2012), I specify the local polynomial regression with degree 1, the Epanechnikov kernel, bandwidth 0.2, and bandwidth 0.3 for variance estimation.

The propensity score models and the models for heterogeneous treatment effects are weighted by longitudinal sample weights provided by Add Health that address unequal probabilities of selection and sample attrition between Waves I and IV.

Results

Propensity Score Strata

The first two steps of the analysis involve estimating probit models to obtain propensity scores and identifying balanced propensity score strata. Appendix 1 includes a table with the estimates from the probit models predicting completing some college and attaining a four-year college degree along with a brief discussion of the models. With one exception, the respondents were grouped into 14 propensity score strata in which the means of the covariates did not significantly differ between those who did and did not complete some college or attain a college degree (Becker and Ichino 2002). The one exception is that it was not possible to achieve balance under the given criteria for growing up with two biological parents in stratum 14 for completing some college. To help address the lack of balance for this covariate, I added the indicator for two biological parents to the model estimating the effect of some college on depressive symptomology in stratum 14 (Bang and Robins 2005).

As noted above, a small number of cases were excluded due to lying outside the region of common support. All of these cases were people who had a very low propensity of completing some college or attaining a college degree (less than 0.020 and 0.001 respectively). Table 2 reports the number and percentage of respondents without and with some college and without and with a four-year college degree by propensity score strata. Most of the strata include at least 40 respondents with or without some college or a four-year degree. The top strata for some college and attaining a college degree have few respondents who did not complete some college (N = 12) or attain a college degree (N = 24). Auxiliary analyses combining strata 13 and 14 did not reveal a different pattern of results.

Table 2.

Balanced propensity score strata for completing some college and attaining a four-year college degree.

	Some College
	No		Yes		Total
	N	%	N	%
Stratum 1: [0.02, 0.1)	221	5.2%	38	0.4%	259
Stratum 2: [0.1, 0.2)	402	9.5%	126	1.4%	528
Stratum 3: [0.2, 0.3)	521	12.3%	237	2.7%	758
Stratum 4: [0.3, 0.4)	552	13.1%	333	3.7%	885
Stratum 5: [0.4, 0.5)	632	15.0%	469	5.3%	1,101
Stratum 6: [0.5, 0.6)	543	12.9%	674	7.6%	1,217
Stratum 7: [0.6, 0.7)	488	11.6%	958	10.8%	1,446
Stratum 8: [0.7, 0.75)	221	5.2%	613	6.9%	834
Stratum 9: [0.75, 0.8)	201	4.8%	726	8.2%	927
Stratum 10: [0.8, 0.85)	182	4.3%	805	9.1%	987
Stratum 11: [0.85, 0.9)	125	3.0%	1,020	11.5%	1,145
Stratum 12: [0.9, 0.95)	88	2.1%	1,249	14.1%	1,337
Stratum 13: [0.95, 0.975)	34	0.8%	791	8.9%	825
Stratum 14: [0.975, 0.999)	12	0.3%	842	9.5%	854
Total	4,222		8,881		13,103

	Four-Year Degree
	No		Yes		Total
	N	%	N	%
Stratum 1: [0.001, 0.025)	1,425	16.5%	48	1.1%	1,473
Stratum 2: [0.025, 0.05)	898	10.4%	54	1.2%	952
Stratum 3: [0.05, 0.1)	1,201	13.9%	116	2.7%	1,317
Stratum 4: [0.1, 0.15)	954	11.1%	120	2.8%	1,074
Stratum 5: [0.15, 0.2)	740	8.6%	151	3.5%	891
Stratum 6: [0.2, 0.25)	563	6.5%	167	3.8%	730
Stratum 7: [0.25, 0.3)	512	5.9%	217	5.0%	729
Stratum 8: [0.3, 0.4)	792	9.2%	385	8.8%	1,177
Stratum 9: [0.4, 0.5)	574	6.7%	493	11.3%	1,067
Stratum 10: [0.5, 0.6)	426	4.9%	529	12.2%	955
Stratum 11: [0.6, 0.7)	256	3.0%	563	12.9%	819
Stratum 12: [0.7, 0.8)	175	2.0%	552	12.7%	727
Stratum 13: [0.8, 0.9)	84	1.0%	616	14.2%	700
Stratum 14: [0.9, 0.994)	24	0.3%	340	7.8%	364
Total	8624		4351		12,975

Notes: 17 cases are excluded from the analysis of some college and 145 cases are excluded from the analysis of four-year degrees due to lying outside the region of common support.

Measurement Models for Depressive Symptomology

The next step of the analysis is to specify and test measurement models for depressive symptomology within each stratum defined by the two different treatments. The baseline specification follows equation (2) with depressed set as the scaling indicator to identify the model. Table 3 reports the overall chi-square test statistics, p-values, and BICs for the baseline measurement models within each stratum. For most of the strata, the chi-square test statistics are not significant or only significant at the 0.05 level, and the BICs are all negative with the exception of strata 12 and 14 for some college and stratum 14 for attaining a four-year degree. This pattern indicates that the baseline measurement model is adequate, but the model fit can be improved by adding a correlation between the errors for depressed and blues, in which case the chi-square test statistics are all non-significant and the BICs are all negative. This correlated error, however, is not theoretically motivated and may be capitalizing on idiosyncrasies in the data. Both the baseline measurement model and the model allowing for the errors for depressed and blues to be correlated were used in estimating the within stratum-specific treatment effects and the resulting estimates were virtually identical. The following results for depressive symptomology are based on the baseline measurement model.

Table 3.

Model fit statistics of measurement models for latent depressive symptomology within propensity score strata.

	Some College			BIC
	Chi-square	df	p-value
Stratum 1: [0.02, 0.1)	0.53	2	0.768	−10.58
Stratum 2: [0.1, 0.2)	0.10	2	0.950	−12.44
Stratum 3: [0.2, 0.3)	2.42	2	0.298	−10.84
Stratum 4: [0.3, 0.4)	6.59	2	0.037	−6.98
Stratum 5: [0.4, 0.5)	8.49	2	0.014	−5.52
Stratum 6: [0.5, 0.6)	5.87	2	0.053	−8.34
Stratum 7: [0.6, 0.7)	0.95	2	0.621	−13.60
Stratum 8: [0.7, 0.75)	0.59	2	0.005	−2.87
Stratum 9: [0.75, 0.8)	7.75	2	0.021	−5.92
Stratum 10: [0.8, 0.85)	2.43	2	0.296	−11.35
Stratum 11: [0.85, 0.9)	8.79	2	0.012	−5.29
Stratum 12: [0.9, 0.95)	14.59	2	0.001	0.19
Stratum 13: [0.95, 0.975)	8.02	2	0.018	−5.41
Stratum 14: [0.975, 0.999)	29.16	2	0.000	15.66

	Four-Year Degree			BIC
	Chi-square	df	p-value
Stratum 1: [0.001, 0.025)	5.47	2	0.065	−9.12
Stratum 2: [0.025, 0.05)	4.78	2	0.092	−8.94
Stratum 3: [0.05, 0.1)	7.90	2	0.019	−6.47
Stratum 4: [0.1, 0.15)	6.19	2	0.045	−7.77
Stratum 5: [0.15, 0.2)	0.07	2	0.966	−13.52
Stratum 6: [0.2, 0.25)	7.75	2	0.021	−5.44
Stratum 7: [0.25, 0.3)	3.71	2	0.156	−9.47
Stratum 8: [0.3, 0.4)	7.25	2	0.027	−6.89
Stratum 9: [0.4, 0.5)	7.59	2	0.023	−6.36
Stratum 10: [0.5, 0.6)	4.83	2	0.090	−8.90
Stratum 11: [0.6, 0.7)	8.62	2	0.013	−4.79
Stratum 12: [0.7, 0.8)	5.53	2	0.063	−7.64
Stratum 13: [0.8, 0.9)	11.28	2	0.004	−1.82
Stratum 14: [0.9, 0.994)	22.55	2	0.000	10.75

Treatment Effects

Table 4 reports the average effect of completing some college and attaining a four-year college degree on depressive symptomology assuming homogenous treatment effects, stratum-specific effects, and estimates of the trend across stratum-specific effects. Beginning with the effect of completing some college, we see, as expected, that the average effect is negative – i.e., people who completed some college have fewer symptoms of depression. The average effect, however, obscures a notable degree of variation across the propensity score strata. With the exception of the estimate for the first stratum, which has a significantly larger standard error than the estimates for any of the other strata, we a see a generally increasing trend (b = 0.02) in the estimates across strata indicative of a decrease in the protective effects of completing some college. There is no evidence of a significant protective effect for respondents with propensities of 0.8 or higher of completing some college.

Table 4.

Estimated treatment effects from regressing latent depressive symptomology on completing some college or attaining a college degree.

	Some College		Four-Year Degree
	Est	95% CI	Est	95% CI
Average effect	−0.10***	[−0.14, −0.06]	−0.09***	[−0.13, −0.06]
Stratum-specific effects
Stratum 1	0.30	[−0.44, 1.03]	−0.23*	[−0.44, −0.03]
Stratum 2	−0.11	[−0.27, 0.06]	−0.09	[−0.32, 0.14]
Stratum 3	−0.21**	[−0.37, −0.06]	−0.24***	[−0.37, −0.11]
Stratum 4	−0.02	[−0.19, 0.14]	−0.16+	[−0.32, 0.00]
Stratum 5	−0.06	[−0.19, 0.06]	−0.09	[−0.24, 0.06]
Stratum 6	−0.13**	[−0.22, −0.04]	−0.11+	[−0.22, 0.01]
Stratum 7	−0.15**	[−0.24, −0.06]	−0.16**	[−0.26, −0.05]
Stratum 8	−0.07	[−0.21, 0.07]	−0.11*	[−0.20, −0.02]
Stratum 9	−0.22**	[−0.35, −0.08]	−0.06	[−0.15, 0.03]
Stratum 10	0.02	[−0.10, 0.14]	−0.13**	[−0.22, −0.04]
Stratum 11	0.04	[−0.07, 0.15]	−0.05	[−0.15, 0.04]
Stratum 12	−0.16	[−0.34, 0.01]	0.02	[−0.09, 0.13]
Stratum 13	0.09	[−0.02, 0.20]	−0.07	[−0.24, 0.10]
Stratum 14	−0.03	[−0.34, 0.27]	0.13*	[0.00, 0.26]
Linear trend
slope	0.17**	[0.01, 0.03]	0.20***	[0.01, 0.03]
constant	−0.21***	[−0.30, −0.11]	−0.26***	[−0.35, −0.17]

Notes:

⁺p < 0.10,

^*p < 0.05,

^**p < 0.01,

^***p < 0.001 (two-tailed tests).

The parameters were estimated using the Wave I/Wave IV Add Health longitudinal sample weights. 17 cases are excluded from the analysis of some college and 145 cases are excluded from the analysis of four-year degrees because they were outside the region of common support.

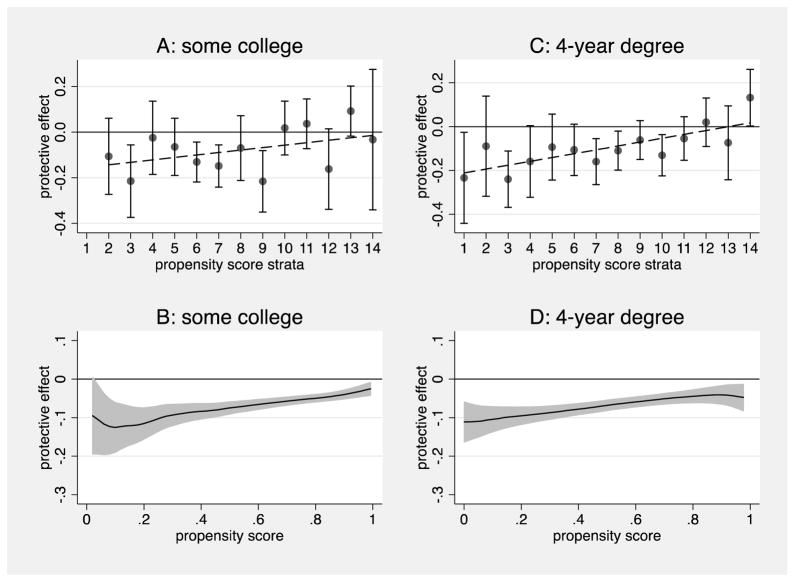
Figure 1, Panel A illustrates the stratum-specific protective effects of completing some college against depressive symptomology along with 95 percent confidence intervals for strata 2 through 14 (stratum 1 is not included due to the large confidence interval). Although the trend is imperfect, the estimates appear roughly to follow a linear trajectory across propensity score strata. With the exception of the first couple strata, this appearance is largely confirmed in Figure 1, Panel B, which shows the results of the matching-smoothing approach to assessing heterogeneous treatment effects. The solid line provides the difference in average depressive symptomology between people with and without some college across the range of propensity scores (within the region of common support noted above) and the shading provides a 95 percent confidence band. We see a significant degree of uncertainty in the estimates of the effects at low propensity scores, but this uncertainty tapers off into the middle of the propensity score distribution and the same pattern of a generally linear upward sloping trend in the protective effect with increasing propensity score strata emerges. The particular pattern of effects from both the stratification-multilevel method and the matching-smoothing method is consistent with the resource substitution hypothesis that people from disadvantaged backgrounds, as indexed by a low propensity for completing some college, realize a greater protective benefit from higher education against depression than people from advantaged backgrounds.

Figure 1.

Stratification-multilevel estimates (Panels A and C) and matching-smoothing estimates (Panels B and D) of heterogeneous effects for some college and completing a four-year degree on latent depressive symptomology. Bars and shading provide 95% confidence intervals/bands. Stratum 1 is excluded from Panel A due to the large confidence interval.

Turning to completing a four-year degree, we see a similar, albeit more pronounced, pattern of effects as with completing some college. The average effect of completing a four-year degree is negative (i.e., people who completed a four-year degree have fewer symptoms of depression) and, interestingly, is about the same magnitude as the effect of completing some college. This suggests that on average completing some college produces a similar protective effect against depression as attaining a four-year degree.

Once again, the average effect of a four-year degree, however, obscures a notable degree of variation across propensity score strata. Across the propensity score strata we see a relatively clear increasing trend (b = 0.02) that suggests the protective effect of a college degree diminishes with the increasing likelihood of attaining a college degree. There is no evidence of a protective effect of college degree completion for people with propensities above 0.6. In fact, in the top stratum, the estimated effect is positive and statistically significant, though one should be cautious in interpreting this estimate in light of the small number of people without a college degree in this stratum.

Figure 1, Panel C illustrates the stratum-specific protective effects of completing some college against depressive symptomology along with 95 percent confidence intervals. The stratum-specific estimates appear to follow a linear trajectory across propensity score strata (b = 0.02). This appearance is confirmed in Figure 1, Panel D, which shows the results of the matching-smoothing approach to assessing heterogeneous treatment effects. In contrast to the estimates for some college, we see less uncertainty and a clearer linear trajectory across propensity scores for the protective effect of attaining a four-year degree. Once again, the particular pattern of effects from both the stratification-multilevel method and the matching-smoothing method is consistent with the resource substitution hypothesis that people from disadvantaged backgrounds, as indexed by a low propensity for attaining a four-year college degree, realize a greater protective benefit from higher education against depression than people from advantaged backgrounds.

Discussion

This study makes several contributions to the growing body of work examining systematic patterns of heterogeneity in the benefits of higher education. First, in contrast to past studies focusing specifically on depression (Ross and Mirowsky 2006; Schaan 2014), this study relies on propensity scores of completing some college and attaining a four-year college degree as key summary measures of advantage/disadvantage and recently developed approaches for identifying heterogeneous treatment effects. In the process this study also adjusts for a wider array of potential confounders than in past studies and, with the matching-smoothing estimator, considers potential nonlinear heterogeneous treatment effects. Finally, this study draws on data representative of a younger age group and a more recent birth cohort than has been examined in past studies.

Even with the broader measure of advantage/disadvantage, the more rigorous approach to identifying heterogeneous treatment effects, and the different ages and birth cohorts of the respondents, the results are consistent with past studies of who benefits more from higher education. In particular, people from disadvantaged backgrounds realize a greater protective effect from both completing some college and attaining a four-year degree than people from advantaged backgrounds, a pattern that is consistent with the resource substitution hypothesis.

Two past studies have used similar methodological approaches as this study in examining heterogeneity in the beneficial effect of a college degree with respect to physical heath outcomes (Bauldry 2014; Schafer et al. 2013). In contrast to the work on depression, these studies have come to opposite conclusions. One study found people from disadvantaged backgrounds realized a greater protective effect from higher education with respect to cardiovascular disease and mortality than people from advantaged backgrounds, while the other study found that people from advantaged backgrounds realized a greater protective effect from higher education with respect to self-rated health than people from disadvantaged backgrounds. Furthermore, the study finding evidence of resource multiplication for self-rated health used the same data as the present study and thus is based on the same age group and cohort. In combination with the present study, the differing pattern of results across mental and physical health outcomes indicates that who benefits more from higher education appears to vary depending on the specific outcome examined.

More work is needed across different mental health outcomes (e.g., major depressive disorder, anxiety disorders, seeking treatment) and different populations (e.g., older populations, different birth cohorts) to determine whether people from disadvantaged backgrounds consistently realized greater protective effects from higher education or if the pattern in who benefits more is outcome dependent even with respect to mental health. At this stage it remains unclear whether the conflicting results for patterns in who benefits more from higher education with respect to physical health outcomes will extend to different mental health outcomes and whether the conflicting patterns reflect different theoretical processes across mental and physical health outcomes.

There are a couple limitations of the present study that are important to keep in mind. The analytic framework relies on the estimation of propensity scores. In the analysis the estimated propensity scores are treated as if they are measured without error. This is implausible, but, to date, methods for incorporating measurement error into propensity scores that are then used in the stratification-multilevel method or the matching-smoothing method have not been developed. In addition, the analytic framework relies on the assumption that all confounders of the association between higher education and depression are included in the propensity score model (i.e., the ignorability assumption). This also is implausible; however, the longitudinal nature of Add Health allows for prospective measures to be included in the propensity score model that capture a wide array of potential confounders.

Understanding who obtains a greater protective effect from higher education against depression is important for understanding population-level mental health disparities. This is particularly true given the expansion of higher education in the latter half of the twentieth century and the changing composition of the population attending college. In addition, as noted in past studies of heterogeneity in the effects of education (Ross and Mirowsky 2011; Schafer et al. 2013), the particular pattern of who benefits more from higher education has implications for policy. If people from disadvantaged backgrounds have more to gain from higher education with respect to reducing symptoms of depression, then policies promoting college access might help reduce mental health disparities in the population as these policies typically target people with a low likelihood of attending college. In addition, programs that help reduce the likelihood of college attrition may also help reduce mental health disparities as these programs also target people with a low likelihood of completing a four-year college degree. The possibility remains, however, that for some health outcomes people from advantaged backgrounds obtain a greater benefit from higher education and thus policies promoting college access and reducing the likelihood of attrition may do little to reduce population health disparities with respect to these health outcomes.

Appendix 1

Table A1 reports the estimates from the propensity score models used to construct propensity scores of completing some college or attaining a college degree for each respondent. It is difficult to interpret individual estimates because the models include many potentially endogenous measures in the service of obtaining good estimates for the propensity scores. For instance, in the models being black (relative to white) has a positive significant effect on completing some college or attaining a four-year college degree, which is counter to intuition. The estimates, however, are the direct effects after adjusting for a number of endogenous factors (e.g., GPA, college aspirations). The bivariate association between being black and attaining a college degree is −0.35 with a standard error of 0.04, as one would expect. Similarly, we do not find significant direct effects for adolescent depressive symptomology, but this is again due to including other endogenous variables in the model and the bivariate associations are statistically significant.

Table A1.

Estimates from probit models regressing completing some college or attaining a college degree on selected covariates (N = 13,120).

	Some College		Four-Year Degree
	Est	95% CI	Est	95% CI
Age at wave IV	0.03**	[0.01, 0.06]	0.05***	[0.03, 0.07]
Female	0.31***	[0.24, 0.38]	0.17***	[0.09, 0.24]
Black	0.19***	[0.09, 0.29]	0.20***	[0.10, 0.31]
Hispanic	0.06	[−0.07, 0.18]	−0.01	[−0.14, 0.12]
Other race	−0.04	[−0.19, 0.11]	0.05	[−0.09, 0.18]
Native born	−0.39***	[−0.56, −0.22]	−0.24**	[−0.42, −0.07]
Both bio parents	0.11**	[0.04, 0.19]	0.15***	[0.07, 0.23]
Par edu: < HS	−0.97***	[−1.15, −0.80]	−0.88***	[−1.07, −0.69]
Par edu: HS or GED	−0.89***	[−1.04, −0.75]	−0.86***	[−0.99, −0.74]
Par edu: some college	−0.63***	[−0.77, −0.49]	−0.75***	[−0.86, −0.63]
Par edu: 4-year degree	−0.28***	[−0.44, −0.13]	−0.39***	[−0.51, −0.27]
Family income (log)	0.15***	[0.09, 0.20]	0.29***	[0.22, 0.35]
Indicator for imputed income	0.05	[−0.03, 0.14]	0.14**	[0.06, 0.23]
Adolescent GPA	0.41***	[0.36, 0.47]	0.65***	[0.59, 0.70]
Adolescent PVT	0.02***	[0.02, 0.03]	0.02***	[0.01, 0.02]
Adolescent aspirations	0.26***	[0.21, 0.30]	0.26***	[0.21, 0.31]
Adolescent self-rated health	−0.05*	[−0.09, 0.00]	−0.11***	[−0.16, −0.07]
Adolescent smoker	−0.23***	[−0.32, −0.14]	−0.40***	[−0.51, −0.29]
Adolescent drinking	0.03	[0.00, 0.05]	0.03*	[0.00, 0.06]
Adolescent BMI	0.00	[−0.01, 0.01]	−0.01	[−0.02, 0.00]
Adolescent dep. sym.	−0.02	[−0.10, 0.06]	0.07	[−0.02, 0.16]
Adolescent counseling	−0.12*	[−0.24, −0.01]	−0.13*	[−0.25, −0.02]
_constant	−4.59***	[−5.35, −3.84]	−6.77***	[−7.58, −5.97]
pseudo R-square	0.26		0.32

Notes:

^*p < 0.05,

^**p < 0.01,

^***p < 0.001 (two-tailed tests).

The model was estimated using the Wave I/Wave IV longitudinal Add Health sample weights.