Measurement of Latent Cognitive Abilities Involved in Concept Identification Learning

Abstract

Introduction

We used cognitive and psychometric modeling techniques to evaluate the construct validity and measurement precision of latent cognitive abilities measured by a test of concept identification learning: the Penn Conditional Exclusion Test (PCET).

Method

Item response theory parameters were embedded within classic associative- and hypothesis-based Markov learning models and fitted to 35,553 Army soldiers' PCET data from the Army Study To Assess Risk and Resilience in Servicemembers (Army STARRS).

Results

Data were consistent with a hypothesis-testing model with multiple latent abilities— abstraction and set shifting. Latent abstraction ability was positively correlated with number of concepts learned, and latent set shifting ability was negatively correlated with number of perseverative errors, supporting the construct validity of the two parameters. Abstraction was most precisely assessed for participants with abilities ranging from one-and-a-half standard deviations below the mean to the mean itself. Measurement of set shifting was acceptably precise only for participants making a high number of perseverative errors.

Conclusions

The PCET precisely measures latent abstraction ability in the Army STARRS sample, especially within the range of mildly impaired to average ability. This precision pattern is ideal for a test developed to measure cognitive impairment as opposed to cognitive strength. The PCET also measures latent set shifting ability, but reliable assessment is limited to the impaired range of ability reflecting that perseverative errors are rare among cognitively healthy adults. Integrating cognitive and psychometric models can provide information about construct validity and measurement precision within a single analytical framework.

The field of clinical neuropsychology has a long tradition of inferring latent neurocognitive processes from psychometrically sound measures (Lezak, Howieson, Bigler, & Tranel, 2012; Milberg, Hebben, & Kaplan, 2009; Reitan & Wolfson, 2009). Yet the validation of inferences about latent processes and the evaluation of measurement precision are generally pursued in distinct studies (Erikson, 1995; Lezak et al., 2012). Moreover, the popularity of classical psychometric methods to assess measurement precision has slowed the adoption of modern psychometric techniques (see Embretson & Reise, 2000; Thomas, 2011), which explicitly link measurement precision to latent constructs. In this paper we provide an example of how cognitive and psychometric modeling approaches can help assess both the construct validity and measurement precision of estimates of latent ability within a single analysis.

The focus of the analysis is a measure of concept identification learning: the Penn Conditional Exclusion Test (PCET; Kurtz, Ragland, Moberg, & Gur, 2004). Impaired concept formation is common among patients with neuropsychiatric disorders, especially those with frontal lobe dysfunction (Axelrod et al., 1996; Berg, 1948; Grant & Berg, 1948; Heaton, 1981; Luria, 1973; Milner, 1964; Reitan & Wolfson, 2009; Weigl, 1941). The assessment of concept identification is therefore central to most neuropsychological evaluations (Lezak et al., 2012). PCET examinees are required to decide which of four objects does not belong with others based on one of three sorting principles (or concepts): e.g., line thickness, shape, or size (i.e., “Odd Man Out”; see Flowers & Robertson, 1985). A PCET item is shown in Figure 1; the examinee must recognize that the 2nd object (large star) is the only object with a unique line thickness. Examinees are not told which concept to use or what concepts to choose from for any particular trial, but are given feedback as to the correctness of their choice. Complexity is added by changing the concept each time the examinee achieves 10 consecutive correct responses.

Figure 1.

Example of a Penn Conditional Exclusion Test item where examinees are instructed to “Click on the object that does not belong.” Line thickness (object 2) is the correct answer.

Since the publication of papers by Vygotsky and Goldstein, clinical neuropsychologists have interpreted poor performance on tests of concept identification as resulting from a cognitive strategy that differs from the more efficient, abstract, hypothesis-testing approach presumably typical of healthy adults (Goldstein & Scheerer, 1941; Vygotsky, 1962). Goldstein attributed this loss of abstract attitude to a form of concreteness; however, his definition of concreteness has been difficult to operationalize (Chapman & Chapman, 1973; Goldstein & Scheerer, 1941). Vygotsky provided more specific criteria for types of inefficient concept identification and, in particular, described associative learning of item-category links as a less effective cognitive strategy than hypothesis testing (Vygotsky, 1962). Similarly, Kendler (1979) theorized that slowly evolving associative learning of stimulus-response links formed the basis of inefficient concept formation among young children. Supporting this, Schmittmann, Visser, and Raijmakers (2006) compared associative and hypothesis testing models of learning in data collected on children and young adults, finding that the proportion of participants who employed rational, hypothesis-based learning increased with age, reaching nearly complete saturation by young adulthood.

The assumption that the performance of healthy adults on tests of concept formation reflects the cognitive strategy of hypothesis testing, rather than associative learning, is rarely tested in clinical neuropsychological research. Rather, investigators typically present total test scores or group-averaged learning curves that can be accounted for by either the slow build-up of associations across trials or by a saltatory increase in performance as hypotheses are deduced at different learning rates in different individuals (Batchelder, 1975; Heaton, 1981). Moreover, tests of Vygotsky's theory of conceptual learning using expert ratings of object sorting behavior found that the strategy of sorting based on a conceptual rule was not characteristic of many healthy participants (Hanfmann & Kasanin, 1942). Although these results might have been specific to the sorting tests studied, they suggest a need to determine whether healthy controls use hypothesis-testing strategies to deduce concepts on other tests of concept formation, rather than assume such rule-based strategies.

Even if it can be assumed that hypothesis testing accurately characterizes the response data of healthy adults, it remains to be determined whether a single or multiple cognitive processes underlie the strategy (e.g., Dehaene & Changeux, 1991). Zable and Harlow (1946) were among the first to acknowledge that concept identification might engage multiple cognitive processes. Today, it is commonly assumed in clinical settings that the total number of concepts learned reflects an underlying process of abstraction, whereas the total number of perseverative errors—choosing the same concept on consecutive trials despite negative feedback—reflects deficiencies in mental set shifting (Kongs, Thompson, Iverson, & Heaton, 2000; Lezak et al., 2012). Although observed indicators of these assumed underlying processes are invariably correlated—likely indicating a general executive ability—they can be uniquely diagnostic of specific impairments. For example, perseverative errors are often associated with frontal lobe lesions (e.g., Janowsky, Shimamura, Kritchevsky, & Squire, 1989).

Confirming that abstraction and set shifting might underlie hypothesis-based learning on particular neuropsychological tests does not guarantee that individual differences in the latent abilities enabling these processes can be precisely measured. A longstanding psychometric concern made clear by item responses theorists (Lord, 1980) is that the degree to which estimates of latent ability reflect random error instead of “true” ability—standard error of estimate (SE_θ)— is a function of the difference between examinee ability and item or task difficulty. SE_θ is typically a “U”-shaped function of ability; items or tasks that are too hard or too easy lead to imprecise measurement (Thomas, 2011). For example, if the conceptual features of stimuli were effortlessly identified by a sub-sample of PCET examinees, we would not obtain precise measurements of individual differences in concept formation within that sub-sample.

Addressing concerns of cognitive process multidimensionality and measurement precision has direct bearing on the use of concept identification tasks in clinical research. Psychologists have long judged the test performance of neuropsychiatrically impaired individuals in comparison to the test performance of cognitively healthy adults. Similarly, measurements obtained over time in longitudinal studies, or repeated clinical observations, allow for interpretation of inter- and intra-individual differences in change relative to baseline. The Army Study to Assess Risk and Resilience in Servicemembers (Army STARRS) is an example of such a study. Army STARRS is a multi-component epidemiological research study designed to inform data-driven approaches to reducing U.S. Army suicides and advance understanding of the psychosocial and neurobiological determinants of suicidality (Kessler et al., 2013; Ursano et al., 2014). As part of this effort, researchers will explore whether the PCET, as a measure of executive abilities, predicts the development of psychiatric distress as is suggested in the literature (Bondi, Salmon, & Kaszniak, 2009; Burton, Vella, Weller, & Twamley, 2011; Testa & Pantelis, 2009; Marzuk, Hartwell, Leon, & Portera, 2005; Westheide et al., 2008). Yet, reliable assessment of individual differences or of individual change in concept formation can vary by the match of ability to difficulty and by the dimension of performance under investigation. Thus, to more accurately interpret the PCET's Army STARRS results and maximize test use, careful examinations of the test precision and underlying latent cognitive abilities are required.

In the present work, our goals are to assess aspects of the PCET's construct validity and precision in the Army STARRS sample by answering three related measurement questions: 1) Are Army soldiers' PCET data more consistent with associative or hypothesis-based models of learning?; 2) Does a single or multiple cognitive processes underlie this learning strategy?; and 3) Can individual differences in the latent cognitive abilities supporting these processes be precisely measured? To answer these questions we conducted cognitive and psychometric modeling analyses of the Army STARRS' PCET data by combining elements of item response theory (e.g., Embretson & Reise, 2000; Lord, 1980; Thomas, 2011) with classic associative- and hypothesis-based Markov models of concept identification learning (see Atkinson, Bower, & Crothers, 1965; Millward & Wickens, 1974; Raijmakers, 1981; Schmittmann, Visser, & Raijmakers, 2006; Wickens & Millward, 1971). Prior research and theory (e.g., Kongs, Thompson, Iverson, & Heaton, 2000; Schmittmann, Visser, & Raijmakers, 2006) suggests that a multidimensional, hypothesis-based model ought to fit PCET response data best.

Method

Participants

Army soldiers were recruited to volunteer without compensation for the Army STARRS New Soldier Study—a component of the larger Army STARRS project (see Heeringa et al., 2013; Kessler, Colpe, et al., 2013; Kessler, Heeringa, et al., 2013; Ursano et al., 2014)—prior to the start of basic combat training. Participants were recruited from three Army bases in the United States (Kessler, Colpe, et al., 2013). Sample biases were small (Ursano et al., 2014). All soldiers were asked to provide informed, written consent prior to participation in research. Of new soldiers selected to attend the survey consent session, approximately 96% consented to conduct the survey and approximately 87% completed all questionnaires. Army commanders provided sufficient time to complete all surveys and tests, which were administered in a group format using laptop computers. Proctors monitored the testing environment and assisted with questions and technical difficulties. Surveys and tests were administered in a fixed order during two 90-minute sessions over two days of testing. The PCET was administered on the second day.

A total of 39,031 Army soldiers recruited into the New Soldier Study were administered the PCET. Of these, 3,478 cases were removed from the current analyses due to invalid response data (i.e., technical problems, failure to complete the test, or aberrant responding). Automated rules for identifying aberrant data were developed based on previous large-scale studies using the Penn Computerized Neurocognitive Battery (Gur et al., 2010). Automated quality control is required due the complexities of validating thousands of individual response profiles (cf. Hoerger, Quirk, & Weed, 2011). Within the sample, the average age of the soldiers was 21 years, 84% were male, and 87% were right-handed (11% left-handed; 2% ambidextrous). Most had high school diplomas (56%), followed by post-high school education without a certificate (21%), 4-year degree (7%), 2-year degree (6%), GED (5%), post-high school education with a certificate (4%), and some graduate school (1%). The majority of soldiers were White (70%), followed by Black or African American (20%), other (6%), Asian (3%), American Indian or Alaskan Native (1%), and Native Hawaiian or Pacific Islander (< 1%).

Measure

The PCET was administered as part of a neurocognitive battery designed for efficient computerized assessment (Gur et al., 2010). Administration followed the tests' standard protocol, which resembles that of similar measures of concept identification learning (e.g., Heaton, 1981). The test draws from a pool of 72 total item displays—each consisting of 4 display objects (see Figure 1)—for a total of 24 unique items per concept. Objects vary by line thickness (heavy or light), shape (square, triangle, circle, or star), and size (large or small). For each item, only one object has a unique property for the current concept. All objects are presented in blue on a black background. For each trial, participants are instructed to “Click on the object that does not belong.” Their responses are followed by feedback (“Correct” or “Incorrect”) presented in white font. Item administration for each concept continues until the examinee chooses 10 consecutive correct answers or has been administered 48 items total (i.e., 2 repetitions of the 24 unique items per concept). If participants fail to choose 10 consecutive correct answers in 48 items for the first concept, test administration ends. If participants fail to choose 10 consecutive correct answers in 48 items for the second concept, they automatically continue onto the third concept. Thus, participants are administered either 1 or 3 concepts total. These starting and stopping rules improve exam efficiency and tolerability, particularly for neurologically impaired examinees, and are common for neuropsychological tests of concept identification learning, (e.g., Heaton, 1981).

Analyses

Models

Models fitted to the PCET data were based on Markov models of concept identification learning that have previously been explained in the literature (Wickens, 1982). In the models, learning was characterized by transitions between discrete states of knowledge. These included learned, guessing, and perseverative states. In the learned state, or L, examinees were assumed to have identified the concept and therefore always responded correctly to each new trial. In the guessing state, examinees were assumed to have not yet identified the concept and therefore responded correctly only by chance, with a probability of 0.25 (i.e., one over the number of response options). In the perseverative state, examinees were assumed to have responded correctly with a probability far less than chance; that is, we assumed that perseverating on a past concept led examinees to consistently choose incorrect stimuli. However, because of rare instances in which a stimulus displayed unique attributes with respect to both the previous and the current concepts, the probability of responding correctly while in the perseverative state was estimated from the data rather than fixed to zero.

Models of associative learning and hypothesis testing were constructed that included either 1) guessing and learned states only, or 2) guessing, learned, and perseverative states. To facilitate parameter estimation and model comparisons, guessing was separated into a guessing after an error response state, or GE, and a guessing after a correct response state, or GC; similarly, perseveration was separated into a perseveration after an error response state, or PE, and a perseveration after a correct response state, or PC. The models are depicted in Figure 2. Each circle represents a discrete state of learning. The arrows between states represent transitions that can occur after each trial of PCET testing. The associative learning models allowed examinees to transition between guessing, perseverative, and/or learned states after either positive or negative consequences, compatible with the law of effect (Hill, 1971, pp. 58-59). In contrast, hypothesis testing models allowed transitions between states only after an error response, compatible with the win-stay/lose shift strategy (Wickens, 1982, pp. 28-29). It should be noted that although Figure 2 represents the Markov models in a manner that is similar to more commonly used methods of analysis (e.g., RAM diagrams in structural equation models), rules governing total effects, identification, and nesting are dissimilar. It is reasonable to find that a model with fewer apparent “paths” (i.e., the arrows are not paths in a regression sense) can produce a better fitting log-likelihood (e.g., Schmittmann, Visser, & Raijmakers, 2006).

Figure 2.

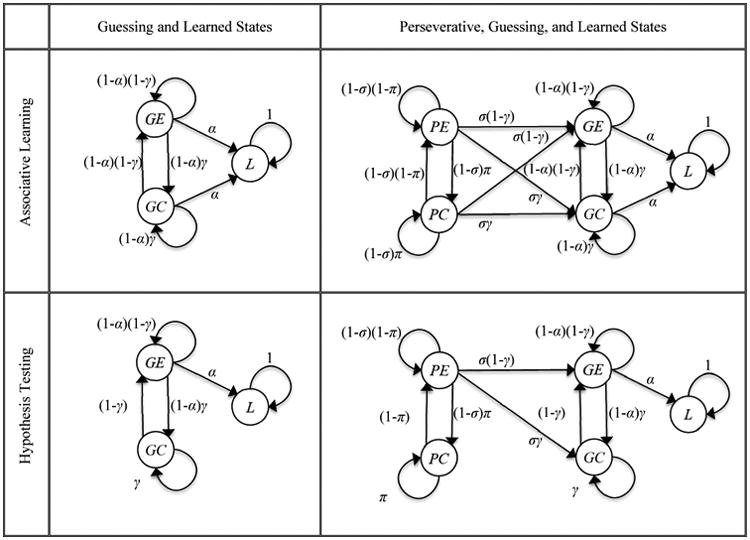
Associative learning and hypothesis testing Markov learning models. L = learned state; GE = guessing after an error response state; GC = guessing after a correct response state; PE = perseveration after an error response state; PC = perseveration after a correct response state; γ = probability of answering correctly while in the guessing state; α = the probability of moving to the learned state (i.e., abstraction); σ = the probability of leaving the perseverative state (i.e., set shifting); π = the probability of answering correctly while in a perseverative state. In the hypothesis testing models, examinees can only transition to the guessing and/or learned states after an error. In the associative learning models, examinees can transition to the guessing and/or learned states after an error or after a correct response.

The transition probabilities are parameters of the models. Of these parameters, only γ— the probability of answering correctly while in the guessing state—was fixed (see above). All other parameters were estimated from the data. The probability of moving from the guessing state to the learned state is symbolized by the Greek letter α (for abstraction), the probability of moving from the perseverative state to the guessing state is symbolized by the Greek letter σ (for set shifting), and the probability of answering correctly while in a perseverative state is symbolized by the Greek letter π. Although π was derived from data, it was assumed to be constant over examinees and concepts. This assumption reflects the view that variation in perseverative responses following concept attainment was a function of individual differences in the set shifting ability parameter σ and not due to stimulus differences related to the concepts tested or to a transitory coupling of an individual's perseverative tendency with particular stimuli. In contrast to π, the parameters α and σ were hierarchically related to unique latent abilities (θ) for each examinee and to unique latent difficulties (β) for each task concept. Higher θ values convey greater ability and higher β values convey greater difficulty. The parameters α and σ are expressed in Equations 1 and 2 for each individual i and task concept j, similarly to a one-parameter item response model (Lord, 1980):

$${\alpha }_{ij}=N(0_{\alpha i}-{\beta }_{\alpha j})$$ (1)

$${\sigma }_{ij}=N(0_{\sigma i}-{\beta }_{\sigma j}),$$ (2)

where N is the cumulative normal function, θ_αi represents the ability of individual i to form abstract concepts, θ_σi the ability of individual i to shift mental set, β_αj represents the difficulty in abstracting concept j, and β_σj the difficulty in shifting mental set from concept j. Equations 1 and 2 link the cognitive and psychometric aspects of the analysis by relating the latent cognitive parameters, α and σ, to the more basic parameters of ability and difficulty, θ and β. Because concepts were always administered in the same order, we could not separate concept difficulties from order effects.

It should be noted that although Equations 1 and 2 have a similar form to a one-parameter item response model, these do not, alone, determine the item response probabilities (i.e., they are not item response functions). Rather these functions determine the transition probabilities within the frameworks of the associative- and hypothesis-based Markov models described above. It is the complete Markov framework, not just the transition probabilities governed by the psychometric relationship between θ and β, which determines the probability of a correct item response.

Models that included guessing and learned states assumed unidimensional cognitive ability (i.e., that individual differences in item responding were explained by a single latent dimension); models that included perseverative, guessing, and learned states assumed multidimensional cognitive ability (i.e., that individual differences in item responding were explained by multiple latent dimensions). Additionally, all models assumed equal discrimination (i.e., that the weighted difference between ability and difficulty affects the Markov transition probabilities equally across all items and all concepts). Finally, it was assumed that a Markov, or memoryless process—as described above—adequately explained learning from one trial to the next.

We assumed that latent θ and β parameters were normally distributed for simplicity in estimation and interpretation. A technical description of the models and their parameters is provided in Appendix A. Appendix B describes how parameters were estimated using Bayesian methods. For models that included guessing and learned states, we estimated one ability per person and one difficulty per concept. For models that included perseverative, guessing, and learned states, we estimated two abilities per person (abstraction and set shifting), one abstraction difficulty per concept, and one set-shifting difficulty for the second and third concepts only (i.e., perseveration could not occur on the first concept; see above).

Model fit

Models were compared in terms of their deviance values (-2*log-likelihood) as well as their Wantanabe-Akaike Information Criterion values (WAIC; Gelman, Carlin, Stern, Dunson, Vehtari, & Rubin, 2013). Lower deviances and lower WAICs both indicate better fit. WAIC is a Bayesian index that adjusts for complexity by penalizing models using the effective number of parameters (pD). Because Bayesian estimation relies on prior information (see Appendix B), WAIC typically has a smaller penalty term compared to the more traditional Akaike Information Criterion (AIC; Gelman et al., 2013). Local independence, assessed by calculating residual autocorrelations, did not appear to be seriously violated for any Markov model.

The models were also compared in terms of their ability to predict errors (see Appendix A). We used the Kolmogorov-Smirnov distance (K-S D; Wilcox, 1997) function implemented in R (R Development Core Team, 2011) to compare the observed and expected cumulative distributions of errors over examinees. K-S D gives the maximum difference between two cumulative distributions and ranges from 0 (good fit) to 1 (poor fit). For comparison, we also calculated the deviance and K-S D statistics for a guessing model (i.e., where the probability of correct response was fixed to 0.25 for all examinees on all items) and for a threshold (or mean) model (i.e., where the probability of a correct response was fixed for each examinee to one minus the average number of errors made over items within each concept). Although the number of parameters estimated within each model is high (see Table 1), this is mainly due to the large sample size. Because of the assumption of local independence, the large number of examinees helps, not hurts the overall model fitting processes. Guessing and threshold model parameters were either fixed (guessing) or descriptive (threshold) and thus no estimation was required.

Table 1. Fit Statistics for Guessing, Threshold, Associative Learning, and Hypothesis Testing Models of Concept Identification Learning.

	Fit Statistics
Model	Parameters	Deviance	pD	WAIC	K-S D Errors
Guessing	0	3,945,960.00	--	--	0.77
Threshold	101,785	2,376,306.00			0.00
Associative Learning
Guessing and Learned	35,556	1,862,407.00	24,816.66	1,923,774.00	0.13
Perseverative, Guessing, and Learned	71,111	1,832,287.00	29,067.85	1,904,628.00	0.12
Hypothesis Testing
Guessing and Learned	35,556	1,844,850.00	22,528.04	1,902,575.00	0.13
Perseverative, Guessing, and Learned	71,111	1,803,620.00	28,024.10	1,876,088.00	0.12

Note. Parameters = total number of parameters; Deviance = -2log-likelihood; pD = effective number of parameters; WAIC = Wantanabe-Akaike information criterion; K-S D Errors= Kolmogorov-Smirnov distance comparing observed and model expected cumulative distributions of total errors. Guessing and Threshold model parameters were not estimated, and thus these have no pD or WAIC values.

Precision of ability estimates

After evaluating model fit, we determined regions of ability with relatively better or worse standard error of estimate (SE_θ)². Interpretations of SE_θ focus on the pattern of association between ability estimates and error rather than a summary index. However, for the sake of providing an approximate quantitative marker of precision, SE_θ values near or less than 0.55 were considered adequate, corresponding, on average, to a reliability index of 0.70 or greater (see Embretson & Reise, 2000).

Results

Model Fit

Model fit results (deviance and WAIC) are reported in Table 1. Table 1 also reports K-S D values comparing observed and model predicted cumulative distributions of errors over examinees. The order of model fit, from best to worst WAIC values, was as follows: 1) the hypothesis testing model that included perseverative, guessing, and learned states, 2) the hypothesis testing model that included guessing and learned states, 3) the associative learning model that included perseverative, guessing, and learned states, 4) the associative learning model that included guessing and learned states, 5) the threshold model, and 6) the guessing model. In terms of predicting cumulative distributions of errors, the guessing model fitted worst and the threshold model fitted best. The latter result is a trivial finding given that threshold model parameters were defined by total errors (i.e., zero degrees of freedom). Among the Markov models, there were no differences between the associative learning and hypothesis testing models in terms of predicting errors, but the three state models had a slight edge.

Overall, the Markov-based learning models outperformed the guessing and threshold models suggesting that models accounting for learning over trials are superior to models that do not. Within each Markov approach, models that included a perseverative state fitted better than models that did not; models that assumed a hypothesis-based learning approach fitted better than models that assumed an associative-based learning approach. However, the differences in fit among Markov models were small relative to the differences between Markov and non-Markov (non-learning) models. Also, differences in terms of predicting errors were negligible. This underlines that allowing mechanisms for dynamic learning was the best determinant of fit.

In the hypothesis testing model that included perseverative, guessing, and learned states, the abstraction difficulty parameters (β_α)—where larger values imply greater difficulty—were 0.11 for concept 1 (line thickness), 0.67 for concept 2 (shape), and 1.56 for concept 3 (size). Or, translated into the probability of transitioning from the guessing state to the learned state after each trial, 0.46, 0.25, and 0.06 at mean ability. Because concepts 1 through 3 were administered in this fixed order, we cannot comment on whether these difficulties reflect innate features of each concept, general features of the task (e.g., fatigue), or a combination of both. The set shifting difficulty parameters (β_σ) were 0.12 for the shift after concept 1 and -0.12 for the shift after concept 2. That is, a 0.45 probability of shifting after the first concept and a 0.55 probability of shifting after the second concept at mean ability. The probability of responding correctly while in the perseverative state (π) was estimated to be .03, which is consistent with our prior assumption that perseveration should result mostly in errors.

Figure 3a presents estimates of abstraction ability (θ_α) by the standard errors of these estimates (SE_θ) for the hypothesis testing model that included perseverative, guessing, and learned states. The latent abilities were standardized; thus, -3.0 on the x-axis indicates low abstraction ability, 0.0 indicates average abstraction ability, and 3.0 indicates high abstraction ability. Lower SE_θ values indicate greater precision. The solid black line running through the figure indicates values of SE_θ predicted by θ_α. As expected, SE_θ varied as a “U”-shaped function of θ_α. The abilities of very poor learners and very good learners were estimated less precisely than the abilities of moderate learners. SE_θ appeared to reach a minimum at approximately one standard deviation below the mean (i.e., the 16^th percentile). Ability estimates in the region between -1.5 and 0.0—where SE_θ hovers around 0.55—were most precise. The points in Figure 3a are color-coded according to the number of concepts learned. There was a strong positive association between abstraction ability and the number of concepts learned (r = 0.78). Examinees who identified 1 or 2 concepts (yellow and green points) tended to have more precise ability estimates than examinees who identified 0 or 3 concepts (red and blue points). Also, there was a floor effect, where θ_α estimates of many examinees who learned 0 concepts converged around -3.0. Finally, it is noteworthy that although some examinees who learned 0 concepts were estimated to have abstraction abilities at or above the abilities of examinees who learned 1, 2, or 3 concepts, the former were consistently associated with higher SE_θ. It is possible that these examinees misunderstood task instructions, employed an unexpected learning strategy, or somehow otherwise produced odd patterns of response data.

Figure 3.

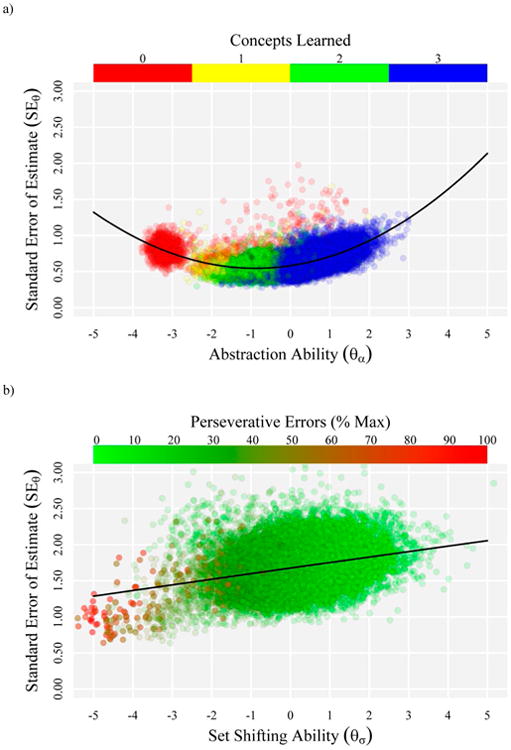
a) Estimates of abstraction ability (θ_α) by the standard errors of these estimates (SE_θ) for the hypothesis testing model that included perseverative, guessing, and learned states. The points in Figure 3a are color-coded according to the number of concepts learned. b) Estimates of set shifting ability (θ_σ) by the standard errors of these estimates (SE_θ) for the hypothesis testing model that included perseverative, guessing, and learned states. The points in Figure 3b are color-coded according to the number of perseverative errors made (i.e., percentage of maximum errors made). Abilities (x-axes) are reported in a standardized metric where higher values indicate better ability. Solid black lines indicate values of SE_θ as predicted by θ.

Figure 3b presents estimates of set shifting ability (θ_σ) by the standard errors of these estimates (SE_θ) for the hypothesis testing model that included perseverative, guessing, and learned states. Data were excluded for examinees that were discontinued after the first concept, as these individuals did not have the opportunity to perseverate on a previous concept. The points in Figure 3b are color-coded according to the number of perseverative errors made (i.e., percentage of maximum). There was a strong negative association between set shifting ability and perseverative errors (r = -0.68). In contrast to abstraction, estimates of latent set shifting abilities were much less precise. Only the abilities of examinees who demonstrated very poor set shifting (i.e., θ_σ values < -3.0) were estimated with a reasonable level of precision. Moreover, the correlation between θ_α and θ_σ was 0.73, indicating that latent abstraction and set shifting abilities were not highly dissociable in the sample.

Discussion

Our results indicate that: 1) Army soldiers' PCET data were better fitted by hypothesis-rather than associative-based models of learning; 2) multiple cognitive processes facilitated the hypothesis-based learning strategy; and 3) although the PCET assessed multiple cognitive processes in the Army STARRS sample, assessment was acceptably precise for only one latent cognitive process, abstraction, in the sample. Overall, the results are consistent with prior research suggesting that hypothesis testing during concept formation accurately characterizes the response data of cognitively mature, neurologically healthy learners (e.g., Schmittmann, Visser, & Raijmakers, 2006). Non-impaired test takers are expected to identify unique attributes among stimuli and employ a rational process of elimination, based on feedback, to decide which response category is correct. To the extent that response data differ from this assumed hypotheses-based learning approach, theory suggests the presence of cognitive immaturity or neurological disease (Ashby et al., 1998). Soldiers participating in Army STARRS represent a normative sample of adult test takers; thus, better fit of the hypothesis testing model was expected.

It is important to note that the largest determinant of model fit was whether or not a model included a mechanism for learning over concept identification trials. Specifically, we compared several dynamic models of learning to non-dynamic models—that is, the guessing and threshold (or mean) models— and found that the ability to learn improved a model's capacity to predict PCET response strings. Indeed, differences in fit between models that included a single versus multiple cognitive processes or models featuring hypothesis- versus associative-based learning were less impressive compared to differences in fit between learning and non-learning models.

Notwithstanding the prior comments, the hypothesis testing model that included multiple cognitive processes, presumably abstraction and set shifting, outperformed a model that included just a single process. This result is consistent with clinical heuristics commonly used to interpret test data produced by concept identification measures (Lezak et al., 2012). However, we found that individual differences only in abstraction ability, not set shifting ability, could be precisely measured in the current sample. Specifically, standard error of estimate was much higher for the latter. Moreover, estimates of abstraction were most precise for examinees in the impaired to average range of latent ability (see Figure 3a). This precision pattern is ideal for a test developed to measure cognitive impairment as opposed to cognitive strength. Ability estimates outside of the impaired to average range were less precise, though still useful for clinical research. In contrast, Figure 3b suggests that set shifting on the PCET was generally too easy for Army soldiers, and estimates of set-shifting abilities were acceptably precise only for examinees with the greatest number of perseverative errors. This finding is consistent with the clinical literature, where perseverative errors are generally regarded as a hallmark of neurological disease as opposed to a normative occurrence (Lezak et al., 2012). The PCET would thus be expected to produce much more precise estimates of set shifting abilities in clinical samples. It may also be possible to increase the difficulty of set shifting on the PCET, to avoid measurement ceiling effects, by providing more ambiguous, perhaps even probabilistic feedback. Importantly, abstraction and set shifting abilities were highly correlated, suggesting that a general executive ability predominantly influenced item responding in this normative sample of test takers. Because to our knowledge this study represents the first item-level, modern psychometric analysis of a test of concept identification learning, we cannot comment explicitly on how well these findings compare to similar types of measures (e.g., Wisconsin Card Sorting Test).

Our modeling approach combined elements of psychometric theory with elements of cognitive theory. The use of item response theory (one-parameter) functions in our approach was exclusively restricted to modeling the probability that an individual examinee, on an individual item within a PCET concept, would transition between discrete states of knowledge (i.e., abstraction and set shifting processes). Another way of stating this is that the psychometric parameters determined the probability that an examinee successfully completed the underlying cognitive processing steps assumed by the associative- or hypothesis-based Markov models. In turn, it was the cognitive architecture that determined how cognitive processes interacted to produce observed item response data.

Of course, no model is entirely correct. Both the overall strategy and the specific processes of learning specified in the models are open to debate. Moreover, additional latent abilities may become statistically apparent in impaired samples (e.g., Su, Lin, Kwan, & Guo, 2008). Dehaene and Changeux (1991) identified three components of learning: the ability to rapidly change the current concept when a negative reward occurs, the ability to memorize previously tested concepts and to avoid testing them twice, and the ability to reject some concepts a priori by reasoning on the possible outcomes of using one rule or the other. Bishara et al. (2010) identified processes of attention shifting following reward, attention shifting following punishment, and decision-consistency. The model employed by Bishara and colleagues is notable for predicting response choices, as opposed to accuracy, which may improve the ability to quantify perseverative responding. Neural computational models of concept identification have also been constructed, mimicking cortical and subcortical brain systems assumed to underlie test performance—typically the striatum and frontal/temporal lobes (e.g., Amos, 2000; Dehaene & Changeux, 1991; Levine & Prueitt, 1989; Monchi, Taylor, & Dagher, 2000). In measurement theory as well, several models of learning and change have been developed (e.g., Andersen, 1985; Embretson, 1991; Fischer, 1976; Martin & Quinn, 2002). In particular, Verhelst and Glas (1993) presented a dynamic item response Rasch model for estimating individual differences in the ability to learn from feedback.

The choice of a specific model, or modeling framework, is best determined by the purpose of analysis. In this study, we sought to compare classic Markov learning models in order to determine whether Army soldiers' PCET data were more consistent with an associative learning or a hypothesis-testing (rule-based) learning strategy, reflecting two longstanding neuropsychological theories about how individuals might learn concepts (Goldstein & Scheerer, 1941; McCarthy & Warrington, 1990; Vygotsky, 1962; Walsh, 1978) and continue to be relevant in psychometric interpretations of concept identification test data (Su, Lin, Kwan, & Guo, 2008). Verification of the cognitive strategies that examinees use to meet task demands is considered a form of construct validity known as construct representation (Whitely, 1983). Our finding that hypothesis testing is a better model of concept formation on the PCET compared to associative learning supports the construct representation of the PCET as a measure of hypothesis testing abilities, at least among healthy controls. Further, the strong correlations of the abstraction parameter (α) with the number of concepts obtained and of the set shifting parameter (σ) with number of perseverative errors support the validity of these parameters as measures of abstraction and set shifting abilities (Kongs et al. 2000; Lezak et al., 2012). To further establish the construct validity of α and σ, theoretically motivated experimental manipulations could be conducted, showing predicted differential impact on the two model parameters (e.g., Brown, Turner, Mano, Bolden, & Thomas, 2013). Psychometric studies of convergent and discriminant validity, possibly using a multitrait-multimethod approach, could also be carried out to support the nomothetic span and specificity of these parameters in differentially measuring the constructs of abstraction and set-shifting (Whitely, 1983). Nonetheless, the joining of clinical and mathematical models of concept identification is a significant strength of this study, and adds to the interpretability of the measured constructs.

Limitations

Limitations of the current study include that data were not explicitly gathered for the purpose of latent variable modeling. The PCET makes use of starting and stopping rules meant to improve testing efficiency and tolerability. Although these rules are beneficial for the purpose of collecting data, they are not optimal for modeling analyses. Also, approximately 9% of the participants' data were removed from the analyses due to technical problems, failure to complete the test, or aberrant responding based on automated rules. Although automated quality control is required due to the complexities of validating tens of thousands of individual response profiles, and is not uncommon (e.g., Hoerger, Quirk, & Weed, 2011), it is possible that some valid data were incorrectly flagged. Finally, as mentioned above, the models fitted to the PCET data in the current study are only approximations of reality. To the extent that our models misfitted the data or that our model assumptions were unfounded, our interpretations, parameter estimates, and the standard errors of those estimates may also be inaccurate. Yet, unlike verbal theories, the assumptions that are made in cognitive modeling are explicit and can be quantitatively tested and compared.

Future Directions

For Army STARRS, the current paper reported on a foundational analysis meant to describe calibration of data that will later be used in substantively driven analyses. The study includes integration and analysis of several Army and Department of Defense administrative data systems, as well as cross-sectional and prospective survey, genetic data, and neurocognitive assessments, including the PCET. Broadly, the PCET is a measure of executive functions, which are thought to play important roles in the diagnosis and treatment of many neuropsychiatric disorders (Testa & Pantelis, 2009; Bondi, Salmon, & Kaszniak, 2009), and may help distinguish between suicidal and non-suicidal individuals (Burton, Vella, Weller, & Twamley, 2011; Marzuk, Hartwell, Leon, & Portera, 2005; Westheide et al., 2008). Army STARRS researchers hope to use PCET measurements, among other predictors, to develop models of risk and resilience that can reduce suicidal behavior and other stress-related disorders among Army soldiers. Modeling results from the current study can become used as part of these predictive models in future cross-sectional and potentially longitudinal studies. It will be of particular interest to consider the possibility that changes in learning strategy, processes, or abilities could all predict or otherwise be associated with negative psychiatric or neurological events.

As psychologists increasingly apply formal computational methods to neurocognitive test data in studies of psychiatric and neurological diseases, neuroimaging studies, or in translational science (e.g., Batchelder, Chosak-Reiter, Shankle, & Dick, 1997; Brown, Lohr, Notestine, Turner, Gamst, & Eyler, 2007; McKenna, Brown, Drummond, Turner, & Mano, 2013; Sanislow et al., 2010; Thomas et al., 2013), the need for models capable of simultaneously quantifying mental strategies, processes, and abilities will increase. Latent variable modeling that integrates cognitive and psychometric theories (see Batchelder, 2010) may constitute a fruitful medium for this research.

Appendices

Appendix A: Calculation of likelihoods and summary statistics

A brief description of the Markov models is presented here. Readers interested in a full derivation of the formulas should refer to Wickens (1982; pp. 77-107). The models are expressed in terms of starting probabilities, transition probabilities, and response probabilities. Matrix algebra provides computationally efficient methods for calculating likelihoods and other summary statistics for the models. To begin, we define matrices of sub-matrices and vectors of sub-vectors that correspond to either learned (L; i.e., absorbed and always correct), transient correct (C), or transient error (E) states in each model.

The vector S of starting states is expressed as:

$$\mathrm{S}=[\begin{array}{ccc}{\mathrm{S}}_{\mathrm{L}}& {\mathrm{S}}_{\mathrm{C}}& {\mathrm{S}}_{\mathrm{E}}\end{array}],$$ A.1

where S_L is a row vector of probabilities to start the test in any of the learned states, S_C is the row vector of probabilities to start in any of the transient correct states, and S_E is the row vector of probabilities to start in any of the transient error states. The exact number of starting states differed between models.

The transition matrix T is defined by probabilities of moving from any of the learned, transient correct, or transient error states on the current trial (t) to any of the learned, transient correct, or transient error states on the next trial (t + 1). It is expressed as:

$$\mathrm{T}=\begin{array}{cccc}& {\mathrm{L}}_{\mathrm{t}+1}& {\mathrm{C}}_{\mathrm{t}+1}& {\mathrm{E}}_{\mathrm{t}+1}\\ {\mathrm{L}}_{\mathrm{t}}& 1& (0)& (0)\\ {\mathrm{C}}_{\mathrm{t}}& \mathrm{A}\prime \mathrm{c}& \text{Qcc}& \text{Qce}\\ {\mathrm{E}}_{\mathrm{t}}& \mathrm{A}\prime \mathrm{e}& \text{Qec}& \text{Qee}\end{array},$$ A.2

where Qee is the matrix of probabilities of moving from any transient error state on trial t to any transient error state on trial t + 1; Qec is the matrix of probabilities of moving from any transient error state on trial t to any transient correct state on trial t + 1; Qce is the matrix of probabilities of moving from any transient correct state on trial t to any transient error state on trial t + 1; and Qcc is the matrix of probabilities of moving from any transient correct state on trial t to any transient correct state on trial t + 1. Because the learned state is assumed to be absorbing (i.e., it cannot be left), the probability of remaining in the learned state is always fixed to 1 and the probabilities of moving from the learned state to any of the transient correct or transient error states are always fixed to 0. A′c and A′e are the matrices of probabilities of moving from any of the transient correct states to the learned state and from any of the transient error states to the learned state, respectively. As with the starting vector, the exact number of transition states differed between models.

The response vector R may be expressed for all models as:

$$\mathbf{R}=[{\mathbf{R}}_{\mathbf{L}}¦{\mathbf{R}}_{\mathbf{C}}¦{\mathbf{R}}_{\mathbf{E}}]=[1¦1¦0],$$ A.3

where R_L, R_C, and R_E are the responses provided by the examinees when in the learned state, transient correct states, and transient error states, respectively. Because examinees in the learned states or in any of the transient correct states always respond with a correct answer, the values of R_L and R_C are set to 1; and because examinees in any of the transient error states always respond with an incorrect answer, the value of R_E is set to 0.

The starting vectors and transition matrices differed between the associative learning model and the hypothesis testing model, and also depending on the inclusion of the perseveration state. The models included combinations of the following states: learned state (L), guessing after a correct response (GC), guessing after an error response (GE), perseveration after a correct response (PC), and perseveration after an error response (PE). The starting vectors and transition matrices are expressed below as a function of γ (the probability of answering correctly while in the guessing state), α (the probability of transitioning to the learned state), σ (the probability of transitioning from the perseverative state to the guessing state), and π (the probability of answering correctly while in a perseverative state).

For the associative learning model with learned and guessing states, the starting vector was expressed as:

$$\mathrm{S}=[\begin{array}{ccc}0& \gamma & (1-\gamma )\end{array}],$$ A.4a

and the transition matrix as:

$$\mathrm{T}=\begin{array}{cccc}& L_{t+1}& {\mathit{\text{GC}}}_{t+1}& {\mathit{\text{GE}}}_{t+1}\\ L_t& 1& 0& 0\\ {\mathit{\text{GC}}}_t& \alpha & (1-\alpha )\gamma & (1-\alpha )(1-\gamma )\\ {\mathit{\text{GE}}}_t& \alpha & (1-\alpha )\gamma & (1-\alpha )(1-\gamma )\end{array}.$$ A.4b

For the hypothesis testing model with learned and guessing states, the starting vector was also expressed as:

$$\mathrm{S}=[\begin{array}{ccc}0& \gamma & (1-\gamma )\end{array}],$$ A.5a

but the transition matrix as:

$$\mathrm{T}=\begin{array}{cccc}& L_{t+1}& {\mathit{\text{GC}}}_{t+1}& {\mathit{\text{GE}}}_{t+1}\\ L_t& 1& 0& 0\\ {\mathit{\text{GC}}}_t& 0& \gamma & (1-\gamma )\\ {\mathit{\text{GE}}}_t& \alpha & (1-\alpha )\gamma & (1-\alpha )(1-\gamma )\end{array}.$$ A.5b

For the associative learning model with learned, guessing, and perseverative states, the starting vector for the first PCET concept was expressed as:

$$\mathrm{S}=[\begin{array}{ccccc}0& \gamma & 0& (1-\gamma )& 0\end{array}],$$ A.6a

and for second and third concepts as:

$$\mathrm{S}=[\begin{array}{ccc}0& \sigma \gamma (1-\sigma )\pi & \sigma (1-\gamma )(1-\sigma )(1-\pi )\end{array}].$$ A.6b

The transition matrix for this model was expressed as:

$$\begin{array}{cccccc}& L_{t+1}& {\mathit{\text{GC}}}_{t+1}& {\mathit{\text{PC}}}_{t+1}& {\mathit{\text{GE}}}_{t+1}& {\mathit{\text{PE}}}_{t+1}\\ L_t& 1& 0& 0& 0& 0\\ {\mathit{\text{GC}}}_t& \alpha & (1-\alpha )\gamma & 0& (1-\alpha )(1-\gamma )& 0\\ {\mathit{\text{PC}}}_t& 0& \sigma \gamma & (1-\sigma )\pi & \sigma (1-\gamma )& (1-\sigma )(1-\pi )\\ {\mathit{\text{GE}}}_t& \alpha & (1-\alpha )\gamma & 0& (1-\alpha )(1-\gamma )& 0\\ {\mathit{\text{PE}}}_t& 0& \sigma \gamma & (1-\sigma )\pi & \sigma (1-\gamma )& (1-\sigma )(1-\pi )\end{array}.$$ A.6c

For the hypothesis testing model with learned, guessing, and perseverative states, the starting vector for the first PCET concept was expressed as:

$$\mathrm{S}=[\begin{array}{ccccc}0& \gamma & 0& (1-\gamma )& 0\end{array}],$$ A.7a

and for second and third concepts as:

$$\mathrm{S}=[\begin{array}{ccccc}0& \sigma \gamma & (1-\sigma )\pi & \sigma (1-\gamma )& (1-\sigma )(1-\pi )\end{array}].$$ A.7b

The transition matrix for this model was expressed as:

$$\begin{array}{cccccc}& L_{t+1}& {\mathit{\text{GC}}}_{t+1}& {\mathit{\text{PC}}}_{t+1}& {\mathit{\text{GE}}}_{t+1}& {\mathit{\text{PE}}}_{t+1}\\ L_t& 1& 0& 0& 0& 0\\ {\mathit{\text{GC}}}_t& 0& \gamma & 0& (1-\gamma )& 0\\ {\mathit{\text{PC}}}_t& 0& 0& \pi & 0& (1-\pi )\\ {\mathit{\text{GE}}}_t& \alpha & (1-\alpha )\gamma & 0& (1-\alpha )(1-\gamma )& 0\\ {\mathit{\text{PE}}}_t& 0& \sigma \gamma & (1-\sigma )\pi & \sigma (1-\gamma )& (1-\sigma )(1-\pi )\end{array}.$$ A.7c

For each model, the likelihood of a given response sequence was calculated as the product of the probability of the response sequence prior to learning (i.e., all responses through the last error) and the probability of then entering the learned state (i.e., never return to the transient errors states after entering a transient correct state). The probability B′e of entering the learned state was expressed using the following equation (Wickens, 1982):

$$\mathrm{B}\prime \mathrm{e}=\mathrm{A}\prime \mathrm{e}+\text{Qec}{(\mathrm{I}-\text{Qcc})}^{-1}\mathrm{A}\prime \mathrm{c}.$$ A.8

For example, when learning occurred, the likelihood of the response sequence X = 0, 1, 1, 0, 1, 1, …, where 1 implies correct, 0 implies incorrect, and the ellipsis implies no further error, is given by:

$$\text{Likelihood}=P(\mathbf{X})=\mathbf{\text{Se}}\times \mathbf{\text{Qec}}\times \mathbf{\text{Qcc}}\times \mathbf{\text{Qce}}\times \mathbf{B}\prime \mathbf{e}.$$ A.9

When learning did not occur, the final term was replaced with a column vector of 1s with as many rows as there are columns in matrix Qce.

The expected number of errors prior to learning was then calculated using the following equation (Wickens, 1982):

$$E(\text{Errors})=\mathrm{f}\times {(\mathrm{I}-\mathrm{D})}^2\times \mathrm{B}\prime \mathrm{e},$$ A.10

where f is the probability of the examinee entering any of the error states, expressed with

$$\mathrm{f}=\text{Se}+\text{Sc}\times {(\mathrm{I}-\text{Qcc})}^{-1}\times \text{Qce},$$ A.11

and D is the matrix of probabilities governing eventual passages from one error state to another, expressed with

$$\mathrm{D}=\text{Qee}+\text{Qec}\times {(\mathrm{I}-\text{Qcc})}^{-1}\times \text{Qce}.$$ A.12

We used augmented rather than raw response strings to calculate the likelihoods. Specifically, because some item responses appeared to be accidental incorrect answers, any examinee who responded with 5 consecutive correct answers, and then made no more than 1 error over the next 5 consecutive responses, was considered to have met criteria for learning on the current concept. This method avoided over-penalizing examinees for slips in terms of parameter estimation (a similar rule was used by Schmittmann, Visser, and Raijmakers, 2006). Augmented data strings consisted of the raw response data from test start to the last error, followed by 10 consecutive 1s if the learning criteria had been met.

To adapt the Markov models to a psychometric framework, we assumed that individual differences in the α and σ parameters were determined by unique latent abilities (θ) for each examinee as well as unique latent difficulties (β) for each PCET concept. Specifically, the abstraction rate α_ij for examinee i on concept j was specified as the cumulative normal function (N) of the difference between abstraction ability and abstraction difficulty,

$${\alpha }_{ij}=N({\theta }_{\alpha i}-{\beta }_{\alpha j})$$ A.13

and the set shifting rate σ_ij for examinee i on concept j was specified as the cumulative normal function of the difference between set shifting ability and set shifting difficulty,

$${\sigma }_{ij}=N({\theta }_{\sigma i}-{\beta }_{\sigma j}).$$ A.14

We further assumed that ability remained constant for a given person and that difficulty remained constant for a given concept. Use of the cumulative normal function ensured that the learning rate parameter varied between 0 and 1.

Appendix B: Parameter estimation

A Bayesian (see Fox, 2010; Levy, 2009) Markov chain Monte Carlo (MCMC) procedure was used for parameter estimation. The goal was to find values for the latent parameters that maximized their posterior probability given the observed data. A Metropolis-Hastings-within-Gibbs sampler was used in the current study. The Gibbs procedure is a type of divide-and-conquer approach where the posterior probability of each parameter of interest is iteratively sampled conditioned on previously drawn values of all other latent parameters. The algorithm proceeds by making stochastic “jumps” around the parameters' posterior distributions. Each jump contributes a new link in the MCMC chains, that, when allowed to iterate for a sufficient period of time are expected to converge to stationary distributions (Gelman et al., 2013). Technical descriptions of the algorithm are found elsewhere (Chib & Greenberg, 1995; Metropolis, Rosenbluth, Rosenbluth, Teller, & Teller, 1953).

Estimation began by setting starting values for all θ and β parameters using random samples from their prior distributions (see below). Next, we iteratively drew parameter states for the MCMC chains using Metropolis sampling. This two-step process involved drawing candidates from symmetric proposal distributions (i.e., normal distributions with means set to the current states; see Levy, 2009; Patz & Junker, 1999) and then accepting or rejecting candidate draws based on their posterior probabilities relative to the posterior probabilities of the current draws. The candidate draws were always accepted if their posterior probabilities were greater than the posterior probabilities of the current draws. If the posterior probabilities of the candidate draws were worse, they were accepted with probabilities equal to the ratio of candidate to current posterior probabilities. If the candidate draws were not accepted, the chains remained in their current states. The variances of the proposal distributions were adaptively tuned to control acceptance rates.

We assumed multivariate normal (MVN) prior distributions for θ and β: θ ∼ MVN(μ_θ, Σ_θ); β ∼ MVN(μ_β, Σ_β). For β, the parameters of the prior distribution were fixed to be non-informative. Specifically, the vector of means (μ_β) was fixed to zeros and the covariance matrix (Σ_β) was fixed to an orthogonal matrix with variances of 100. For θ, the vector of means (μ_θ) was also fixed to zeros and the covariance matrix (Σ_θ) was fixed such that latent abilities had a variance of 1.00 and a covariance of 0.70. For models with perseveration, we additionally estimated a π parameter, the probability of responding correctly while in the perseverative state. The π parameter, a value that must range between 0.00 and 1.00, was held constant over examinees and concepts, and given a beta prior with shape parameters 2 and 20.

We constructed the MCMC chains using a Metropolis-Hastings-within-Gibbs sampler (Chib & Greenberg, 1995) programmed in R (R Development Core Team, 2011). For samples of the programming code, refer to the appendices of Gelman et al. (2013) and Patz and Junker (1999). Three separate MCMC chains were run until each converged to a stationary distribution. Geweke's (1992) diagnostic was used to determine that burn-ins of 500 iterations for each parameter were sufficient. Because of autocorrelation, we thinned all chains by retaining every 50th draw. Chains were run for a total of 1,000 iterations each, resulting in a total of 10 draws per chain (30 draws per parameter) after burn-in and thinning. Convergence was established by monitoring traceplots and potential scale reduction factors (PSRF) for each parameter (Brooks & Gelman, 1998; Gelman & Rubin, 1992). For all models, average PSRFs were close to 1 and no value was larger than 1.10 for individual parameters. Visual inspection of the traceplots for each model further suggested that convergence was adequate.