Cell chirality: emergence of asymmetry from cell culture

Abstract

Increasing evidence suggests that intrinsic cell chirality significantly contributes to the left–right (LR) asymmetry in embryonic development, which is a well-conserved characteristic of living organisms. With animal embryos, several theories have been established, but there are still controversies regarding mechanisms associated with embryonic LR symmetry breaking and the formation of asymmetric internal organs. Recently, in vitro systems have been developed to determine cell chirality and to recapitulate multicellular chiral morphogenesis on a chip. These studies demonstrate that chirality is indeed a universal property of the cell that can be observed with well-controlled experiments such as micropatterning. In this paper, we discuss the possible benefits of these in vitro systems to research in LR asymmetry, categorize available platforms for single-cell chirality and multicellular chiral morphogenesis, and review mathematical models used for in vitro cell chirality and its applications in in vivo embryonic development. These recent developments enable the interrogation of the intracellular machinery in LR axis establishment and accelerate research in birth defects in laterality.

This article is part of the themed issue ‘Provocative questions in left–right asymmetry’.

1. Introduction

In vitro models have been widely used in biomedical research. In the past century, Petri dishes have been a simplistic model for cell culture and provided great insights into biophysical and biochemical properties of cells in living organisms. Transwell membranes are used for epithelial cell culture to create the proper apicobasal polarity found in vivo, which is characterized by the strong expression of actin and atypical protein kinase C at the apical surface, and the deposition of basement extracellular matrix at the basal surface. The in vitro scratch assay, a simple scrape in a cellular monolayer generating a strip-shaped gap, allows for studying cell migration during wound healing and analysing the front-rear polarity. With these tools, apicobasal and front-rear polarity have been extensively studied in numerous literatures, and now scientists have a comprehensive understanding of molecular mechanisms, owing to these simple in vitro models. The polarity along a third axis, the left–right (LR) axis, has yet to be studied in-depth at a cellular level in a well-controlled manner, until the recent development of several in vitro cell chirality systems [1–7].

The establishment of the LR axis is critical for living organisms [8]. In fact, all vertebrates exhibit asymmetry along the midline of the body (also known as handedness or chirality) in the positioning and morphology of internal organs. A deviation from such an arrangement often has severe consequences, especially when one or two organs are in mirror positions (i.e. situs ambiguous). When all internal organs are on the opposite side of the body (i.e. situs inversus), the individual can be healthy, although some may suffer from diseases such as Kartagener syndrome. Previously with animal embryos, several models have been established to account for different mechanisms that drive symmetry breaking by considering dominant factors such as the leftward fluid flow on the ventral node driven by the directional rotation of cilia [9–11], voltage gradients resulting from asymmetric expression of ion channels [12–14] and asymmetric vesicular transport via unconventional myosin ID along actin cable networks [15–17]. Defects in laterality are observed in over 0.1% of live births [14,18]. The actual percentage could be higher as poor axis establishment of fetuses often leads to miscarriages. Therefore, studying LR axis establishment has significant clinical implications.

Increasing evidence suggests that cell chirality may have significant implications in the LR asymmetry of embryonic development. Traditionally, an object (e.g. D-glucose and DNA) is considered chiral when it is distinguishable from its mirror image. Mathematically, cell chirality is the nature of the relationship (i.e. left or right handedness) between the LR axis and the predefined apicobasal (usually resulting from two-dimensional cell attachment) and front-rear axes (often defined by the nuclear-centrosomal axis for polarized cells). Chirality can also be observed as the directional rotation of cellular organelles, cytoskeleton and cells as a whole. As individual cells often demonstrate strong randomness in morphology and movement, cell chirality is often statistically defined as a population property at subcellular, cellular and multicellular levels, and quantified from directional biases of cell organelle positioning, cytoskeleton dynamics, cell shape, cell alignment and cell migration [1,3,4,6,7,19]. Cell chirality has been reported in multiple biological systems in developmental biology. For instance, cleaving Xenopus embryos and parthenogenetically activated eggs treated with myosin ATPase inhibitor, 2,3-butanedione monoxime exhibited a large-scale chiral torsion of actin structures [20]. In the hindgut looping of Drosophila, the chirality of planar cell shape was found to be responsible for directional looping [19,21]. Similar results were found for Drosophila genitalia rotation [22,23]. Formin, a critical scaffolding protein related to cell chirality, was found to be associated with the LR asymmetry of the pond snail and frog [7,24].

LR asymmetry research has benefited from in vitro cell chirality models. First, in vitro models incorporate minimal cues by excluding possible confounding factors, and greatly facilitate the discovery of molecular mechanisms. Second, similar to Petri dishes, in vitro systems are typically easy to use, and imaging and molecular assays can be performed reliably. Third, these systems are potentially more efficient for screening teratogens and environmental factors associated with birth defects in laterality. Finally, using human cells, in vitro analyses may provide insights into patient-specific mechanisms associated with malformations.

In this review article, we focus on recent developments of in vitro experimental models of LR asymmetry and theoretical modelling. Starting with a brief review of earlier reports on the formation of chiral structures, we discuss recent progresses in in vitro cell chirality systems and several mathematical models describing different aspects of biophysical mechanisms of cell chirality.

2. In vitro chirality systems

(a). Earlier in vitro studies on cellular chirality

Chirality of cells and biological tissues has previously been observed in several organisms ranging from bacteria to mammalian systems. Bacterial colonies, under stressed conditions, develop chiral morphology in which the colony consists of twisted branches, all with the same handedness (figure 1a) [25]. This phenomenon is attributed to the microscopic chirality and handed rotation of the flagella, along with cell–cell interaction between the bacteria. Retinal explants from goldfish, when cultured on two-dimensional poly-lysine substratum, grow in a clockwise manner (figure 1b) [26]. The directionality is observed in the region of the growing tips of the neurites. The apparent directionality is believed to be an intrinsic helical property of the neurons, and independent of external guidance cues. The authors proposed that interaction of a right-handed helix with a planar surface generates a clockwise curvature of the central axis. In a recent study, Tamada et al. demonstrated that a unidirectional rotation of growth cone filopodia rendering the growth cone intrinsically asymmetric explains the chiral elongation of neurites (figure 1c) [27]. Growth cone filopodia of neurons cultured on two-dimensional substrates rotate in the right-screw direction, driven by interactions of myosin V (a and b) and actin filaments. While these studies are intriguing, the universality of chirality as a basic cell property is still undetermined and the biological significance is still unexplored.

Figure 1.

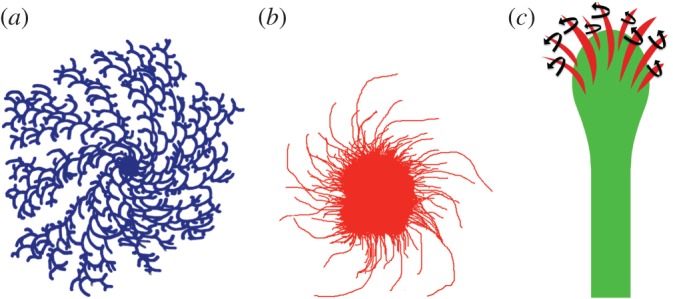
Chiral behaviour in diverse systems. (a) Bacterial colonies exhibit chiral morphology consisting of twisted branches with same handedness. (b) Retinal explants grow in a clockwise pattern on two-dimensional substrates. (c) Growth cone filopodia of cultured neurons rotate in a right-screw direction (red arrows). (Online version in colour.)

(b). Recent engineered systems for in vitro cell chirality

Recently, the development of in vitro chirality systems ranging from the single cellular level to more complex multicellular structures (table 1) has led to substantial evidence that cellular chirality is a fundamentally intrinsic property of most cells, if not all.

Table 1.

In vitro systems for detecting chirally biased structures and tissues, cell types used and major experimental results.

system	references	cell types	major results
single cells with fluorescently labelled centrosome and nucleus	Xu et al. [4]	blood neutrophil-like differentiated HL60 (dHL60)	single dHL60 cells had a migrational bias towards the left of nucleus–centrosome axis directional bias in cell alignment is microtubule-dependent and may be related to the chiral structure of the centrosome directional bias was altered by disruption of Cdc42/Par6 polarity pathway, but reversed with the activation of GSK-3β
ring-shaped and linear strip micropatterns	Wan et al. [28]	C2C12, NIH 3T3, MC3T3, rat cardiac fibroblast, hSkMC, hUVEC, hASC, hMSC, human primary fibroblast, human skin fibroblast, human skin cancer fibroblast	all cells tested are chiral in their alignment on micropatterned surfaces multicellular chirality is phenotype-specific expression of chirality is dependent on proximity to ring boundaries actin treadmilling inhibitors reversed chirality in CCW or leftward biased cells inhibition of tubulin function or actomyosin contractility does not affect cell chirality
ring-shaped micropatterns	Singh et al. [29]	hUVEC, C2C12	chirality is impaired by the treatment of CNTs at approximately 5 µg ml−1, which is far below the widely reported toxic concentration of 100 µg ml−1 the loss of chirality can be recovered with the inhibition of oxidative stress the disoriented nuclear–centrosome and enhanced focal adhesion may be responsible for the loss of chirality
linear strip micropatterns	Worley et al. [30]	MDCK	direction of biased collective migration is opposite on appositional boundaries disruption of adherens junctions diminishes chiral cell alignment and the migration bias, but increases cell motility cells remain polarized on the boundaries, but chiral bias cannot be transmitted deep into the interior region
ring-shaped micropatterns	Worley et al. [30] (SB3C, 2015)	MDCK	induced epithelial–mesenchymal transmission in vitro resulted in a decrease or even a loss in cell chirality
alternated strips of fibronectin and PEG	Chen et al. [1]	vascular mesenchyaml cells, bovine vascular endothelial cells, NIH 3T3, ST2	asymmetry in cell multicellular alignment and migration propagates across large two-dimensional surfaces consistent rightward-biased organization of cells exhibited at line boundaries where there was stress fibre accumulation. multicellular chirality, cell polarity and stress fibre accumulation were abolished with inhibition of Rho kinase and non-muscle myosin-II
three-dimensional hollow spheroids of epithelial cells	Chin et al. [2]	MDCK	microtissues exhibited chirally biased directionality in collective rotational behaviour in three-dimensional culture disruption of actin polymerization reversed the directional bias
single-cell circular patterns	Tee et al. [7]	human foreskin fibroblast	actomyosin network in single cells exhibits definite handedness radial actin fibres tilt in a positive or negative angle resulting in anticlockwise or clockwise swirling of the actin cytoskeleton, respectively α-actinin-rich RFs extend from the focal adhesions centripetally in a formin-dependent manner level of α-actinin-1 cross-linking regulate handedness of the chiral pattern
binucleated single cells	Yamanaka et al. [6]	zebrafish (Danio rerio) melanophore	melanophores exhibit intrinsic chiral bias nuclei and apical cell surface consistently rotate in an anticlockwise direction, and actin filaments rotate in a clockwise direction. disruption of actin dynamics inhibits chiral rotation nuclear rotation is enhanced with disruption of microtubule network

(i). Biased migration revealed by organelle labelling

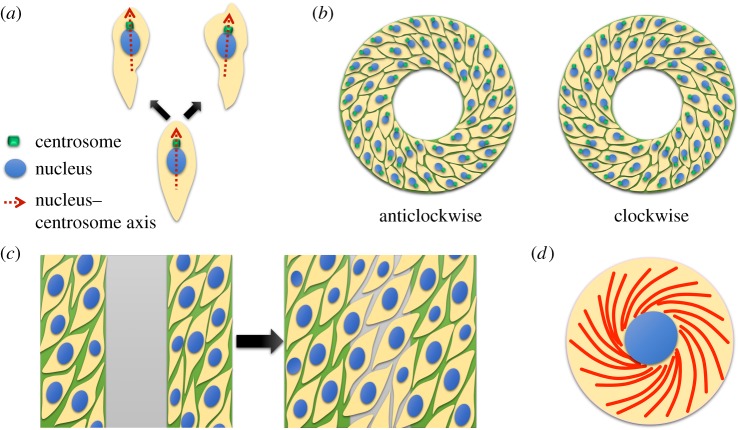
The intrinsic LR bias of individual cells has been revealed with live imaging of cells with fluorescently labelled cell organelles (i.e. nucleus and centrosome; figure 2a) [4]. The blood neutrophil-like differentiated HL60 (dHL60) cells were seeded sparsely on a substrate, and a uniform attractant concentration of f-Met-Leu-Phe (fMLP) was used to initiate cell polarization. The individual cells exhibited a directional bias in locomotion, and migrated leftward of an axis defined from the nucleus to the centrosome. As the cells were seeded sparsely as single cells, there was no influence by neighbouring cells on the bias of polarity. The directional bias was found to be microtubule-dependent with the treatment of Nocodazole, a microtubule polymerization inhibitor. The investigation of Cdc42/Par6 polarity signalling pathway revealed that the interference of upstream regulators such as Cdc42 and Par 6 leads to the loss of polarity altogether, while disrupting the downstream effectors results in a randomized chirality, but a proper polarity. Surprisingly, perturbing the polarity pathway Cdc42/Par6 via constitutive activation of glycogen synthase kinase-3β reversed the directional bias of dHL60 polarity. Later on, with this system, tubulin mutation in human cells was found to lead to a loss in their chiral bias, demonstrating the non-ciliary role of microtubule proteins in LR patterning across biological kingdoms beyond plants, nematodes and frogs [31].

Figure 2.

In vitro cell chirality systems. (a) Polarized single cells exhibit biased directional migration either leftward or rightward of the nucleus–centrosome axis. (b) Ring-shaped micropatterns induce multicellular chirality observed by LR asymmetry in cell alignment and migrational direction. (c) Coherent multicellular LR asymmetry emerged while confined to linear strip micropatterns and propagated while migrating to neighboring strips. (d) Chiral self-organization of actin cytoskeletal fibres (red) in single cells on circular micropatterns. (Online version in colour.)

(ii). Chiral alignment and migration between micro-printed appositional boundaries

Cell chirality has also been observed at the multicellular level in vitro [5,28]. Wan et al. have developed a well-controlled and highly reproducible technique for accurate determination of multicellular chirality by characterizing cell alignment and migration on micropatterned surfaces (figure 2b) [3]. In this in vitro system, cells were confined between appositional boundaries (approx. several hundred micrometres apart) to form ring (or strip) geometries [32,33]. Upon confluency, the cells were primarily aligned along the circumferential direction, but make a small biased angle. This angular bias of cell alignment was analysed using an automated custom-written MatLab program based on the intensity gradient in phase contrast images of the cells. Cell alignment was identified as either clockwise- or anticlockwise-biased. Interestingly, cell migration was biased towards opposite directions on two appositional boundaries, possibly due to the opposite polarity of the cells found on boundaries.

Using this micropatterning system, the chirality of various cell types was analysed, and cell chirality was determined to be phenotype-specific. With the over 10 cell phenotypes tested, two types of skeletal muscle cells showed an anticlockwise bias, while the rest such as endothelial cells were biased to the clockwise direction. The possible role of major cytoskeletal components was investigated with small inhibitory drugs. The destabilization of microtubules with drugs such as Nocodazole did not alter cellular chiral bias, but interfering with actin function with drugs such as Latrunculin A reversed the chiral cellular alignment as well as directional migration on boundaries.

Subsequently, this assay was used for detecting cellular toxicity of nanomaterials. In a recent study, we used single-walled carbon nanotubes (CNTs) as a model, and found cellular exposure to CNTs leads to a loss in cell chirality, which can be recovered with the inhibitors of oxidative stress [29]. In-depth analyses revealed that the loss of cell chirality was related to disintegrated centrosomes, disorganized microtubules and matured adhesion complexes. Such alterations impaired cell migration and led to a loss of chirality. Overall, this study has demonstrated that cell chirality can potentially be used as an in vitro measure for evaluating nanomaterial toxicity for embryonic development.

With linear strip micropatterns, effects of cell–cell adhesion on multicellular chirality were investigated with MDCK (Madin–Darby canine kidney) epithelial cells [30]. The chirality was observed as opposite migration direction of the cells on the appositional boundaries and as a chiral alignment pattern. When adherens junctions were disrupted with ethylene glycol tetraacetic acid (EGTA), the cells remained polarized at the boundary of the linear micropattern, the cell alignment and directional migration became increasingly randomized. Fluorescence staining demonstrated that with EGTA treatment, the definite cellular polarization was increasingly localized to the proximity of the boundaries, decreasing the capability of transmission of chiral bias into the interior region. The loss of cell chiral bias was also found with the epithelial–mesenchymal transition (EMT) of MDCK cells induced by the treatment of transforming growth factor-β1 (TGF-β1) and epidermal growth factor [34]. This was attributed to the decrease in E-cadherin expression and gradual loss of adherens junctions during EMT, similar to what was found with the EGTA treatment.

Recently, we have also improved the imaging analysis of multicellular chirality. We developed a Python-based algorithm which is able to identify and quantify immunofluorescence-labelled individual epithelial cells on multicellular patterns [35]. This approach can not only determine the chirality of a multicellular pattern, but also captures morphological properties of individual cells and their organelles, such as sizes and aspect ratios. Cell nuclei were also found to have the same alignment bias as the cell. Together with live cell imaging, this new imaging analysis approach can be very useful for analysing the polarity and chirality of individual cells within multicellular structures.

(iii). Scalable chiral morphogenesis using degradable hydrogels

Multicellular chirality was distinctly demonstrated in a larger in vitro system by Chen et al. (figure 2c) [1]. Adult vascular mesenchymal cells were cultivated on linear strips assembled in parallel. The strips were coated with fibronectin, separated by regions of polyethylene glycol (PEG). Cells were able to bind to the fibronectin lanes, proliferate and chirally align similar to the aforementioned work [3,30]. The PEG hydrogel underwent degradation over time and the cells migrated out of the fibronectin lane and into the PEG domains where the cells exhibited a coordinated alignment at a 20° orientation. Migration of the cells across the PEG region exhibited the propagation of cellular chirality. The authors proposed that the boundaries of the micropattern strips provide mechanical cues that prompt LR asymmetry breaking, since the loss of chiral alignment was observed with the inhibition of Rho kinase with small drugs.

(iv). Chiral intracellular actin dynamics of single cells on circular patterns

Recently, Tee et al. revealed that at a single-cell level, the chiral bias in actin cytoskeleton originates through temporal self-organization of the α-actinin-enriched radial fibres (RFs) and myosin-IIA-enriched transverse fibres (figure 2d) [7]. The authors studied distinctive patterns of actin self-organization in single cells confined to circular adhesive islands, using dynamic imaging of fluorescently labelled actin filaments. They demonstrated that, in an isotropic, circular cell, actin cytoskeleton consists of a self-organizing network of radial and transverse fibres, which transform progressively from a radial to a linear pattern, with an intermediate chiral stage with distinct handedness. The transient chiral form is a result of unidirectional tilting of the RFs, subsequently accompanied by tangential shift in the retrograde movement of transverse fibres. The RFs are equivalent to dorsal stress fibres of migrating cells and grow centripetally from focal adhesions in a formin-dependent manner. The authors defined the tilt direction of the RFs as positive or negative based on the deviation from initial position, generating anticlockwise or clockwise swirling of the actin cytoskeleton, respectively. In fibroblast cells, the RFs consistently tilt in the positive direction resulting in anticlockwise swirling. The authors further demonstrated that cross-linking levels of α-actinin-1 regulate the directionality of the tilt in the RFs. Cells with low levels of α-actinin-1 display positive tilting of RFs, giving rise to an anticlockwise swirling. Cells with elevated levels of α-actinin-1 expression exhibit negative tilting of the RFs, resulting in clockwise swirling of the actin cytoskeleton. Overall, this study suggests that the chirality in the self-organizing actin cytoskeleton could be a potential mechanism to regulate cell chirality itself. However, it will be interesting to observe how this chiral pattern of actin filaments manifests itself in a multicellular system and communicates with the polarizing cues in the microenvironment.

(v). Rotation of binucleated pigment cells

In some special cases, cells can exhibit chiral behaviour without patterning. Using a transgenic zebrafish that expresses nuclear-localized fluorescent protein in the melanophores, Yamanaka & Kondo [6] demonstrated that the nuclei of isolated melanophores rotate consistently in an anticlockwise manner. Furthermore, fluorescent beads were placed on the apical cell surface to show that the apical cell surface rotates in the same direction as the nuclei. By contrast, protrusions in the peripheral regions of the cells appear to be static, indicating that the apical portion of the cells is twisting against the basal portion. This chirality is inherent to the melanophores, as basement extracellular matrices do not affect the direction of the cellular rotation. The authors then proposed that the chirality of the actin cytoskeleton generates the biased cellular rotation. Using another transgenic fish that expresses fluorescently labelled F-actin, they demonstrated that the actin bundles rotate clockwise, whereas the nuclei rotate anticlockwise. These observations suggest that the cellular rotation is generated as a counter action of the clockwise rotation of the actin bundles and that clockwise movement of actin filaments is extremely critical for determining cellular chirality. On the other hand, Nocodazole enhances the rotation of the nuclei. The authors concluded that the radial microtubule network extending from the centrosome impedes the rotation of the nuclei. Interestingly, the authors proposed that chiral movement of pigment cells at tissue boundaries during development could generate the characteristic parallel striped pattern of the zebrafish skin.

(vi). Directional rotation of cells between a graded hydrogel

Recently, we were able to detect the chirality of in vitro three-dimensional cellular structures [2]. MDCK cells were encapsulated at the interface of a bilayer Matrigel system and formed multicellular hollow microspheroids after culturing for several days. These spheroids displayed a coordinated rotational behaviour, which had a directional bias that correlated with the chirality of MDCKs on micropatterned rings. Three-dimensional systems may provide a more physiologically relevant platform to examine cellular behaviour. Disruption of actin polymerization, by the drug Latrunculin A, induced a switch in directional bias for both the three-dimensional spheroids and the two-dimensional ring patterns. The consistency suggests that the rotational behaviour is also a product of the inherent cellular chirality.

In summary, individual cells are intrinsically chiral as demonstrated by organelle positioning of migrating neutrophils as well as the intracellular actin swirling and nuclear rotation of patterned single cells and binucleated pigment cells. The chirality of multicellular structures has been determined with micro-contact printing techniques, and can be scaled up with switchable substrate or degradable polymers. Most of these assays require the front-rear polarization and associated cell migration to work properly, such as in the formation of multicellular chiral alignment. The recent development of a three-dimensional cell rotation assay will allow for determining the chirality of less polarized or less adhesive cells. The connection between various systems (e.g. multicellular chiral alignment on patterned surfaces and chiral actin dynamics in patterned individual cells) is worthy of further investigation. All these new tools provide unprecedented opportunities to study biophysical mechanisms of embryonic LR asymmetry development at a subcellular, cellular and multicellular level.

3. Mathematic models for chirality

Several mathematical models have been proposed for in vitro cell chirality (table 2). These models vary greatly with respect to their complexity and level of analysis, depending on which key components are considered with respect to their influence on cell chirality.

Table 2.

Mathematical models for the formation of chirally biased structures and tissues, their basic features and major simulation results.

model type	reference	features of model	major outcomes
formin-dependent actin swirling model	Tee et al. [7]	RFs modelled as elastic rods originating from focal adhesions, polymerize in a formin-dependent manner towards the cell centre. polymerization kinetics related to the mechanical stresses within fibres transverse fibres (TF) acting as active contractile actomyosin elements in the model are an inherent contractile stress alternating binding and unbinding events between RFs and TFs physical property parameters of radial and transverse elements suggested by experimental results	computational model illustrated a similar spontaneous transition from a radial actin pattern to a chiral pattern formation of the chiral pattern is seen as a direct result of the polar and helical properties of actin filaments
reaction–diffusion based directional migration model	Chen et al. [1]	reaction–diffusion kinetics consider the following factors: a slow diffusing activator, a rapidly diffusing inhibitor, cell density, proliferation, cytokinetic diffusion and chemotactic migration adjustable coefficients to model differential migration rates along the principal axes	a model taking into account reaction–diffusion and anisotropic migration can describe the formation of unidirectional ridges similar to that seen in vitro
vertex-based anisotropic line tension model	Taniguchi et al. [19]; Hatori et al. [21]	hindgut tube represented by two epithelial sheets composed of cuboidal cells represented as Voronoi cells representing the dorsal and ventral arcs of the tube along corresponding with boundary cells PCC modelled through constriction of cell boundaries; maximized at −45° to the AP axis two-staged simulation: 1. application of biased elastic tension energy and 2. relaxation and dynamic rotation mosaic hindgut created through modifications in maximum angle and line tension between model cells	reproduced the 90° left-handed rotation of the epithelial hindgut tube in silico using only LR-biased cell constriction introduction of a Myo31DF mosaic hindgut failed to recreate a 90° rotation observed in vivo, indicating the absence of some necessary parameter(s)
	Sato et al. [22,23]	vertex model using symmetry arguments for a particle model two-dimensional cell sheet, confined by parallel boundaries with periodic boundary conditions direction-dependent contraction and spatial variation of cell properties repeated junction remodelling between cells arising from polarized contraction at cell boundaries	modelled epithelial cells exhibit continuous shear movement when undergoing directionally dependent contraction when the friction is large at one boundary, the entire sheet could undergo unidirectional movement driven by chirality. applied to the directional cell movement of epithelial cells associated with genitalia rotation of drosophila

(a). Formin-dependent actin swirling model

Tee et al. [7] developed a mathematic model at a subcellular level to explore the mechanism behind the chiral swirling of actin within a single cell on a circular micropattern [7]. This swirling was formin- and myosin-IIA–dependent and could be altered by changing α-actinin-1 expression levels. The simulation started with a uniform circular stage similar to that observed in vitro, with radial and transverse actin fibres in addition to focal adhesions. By varying the radial fibre growth rate and the relative rate of transverse-radial fibre motion, they were able to recapitulate the chiral pattern seen in experiments. To explain the role of α-actinin-1 in cell chirality, for an unconstrained filament, formin immobilized at a focal adhesion results in a uniform ‘stair-stepping’ right-handed twisting of the actin filament as the fibre elongates. When the filament is constrained, such as during the binding of α-actinin-1, the filament adopts a ‘screw-stepping’ left-handed rotation during the radial fibre elongation. The difference in the handedness of filament rotation leads to the opposite chirality of actin swirling inside the cells observed at different expression levels of α-actinin-1. This in vitro single-cell work combined with their actin cytoskeleton modelling illustrates a role and mode of action for several cytoskeleton regulators in the establishment of chiral actin patterns.

(b). Reaction–diffusion-based directional migration model

The majority of available models attempt to understand intrinsic chiral behaviour at the multicellular level. Chen et al. uses a reaction–diffusion-based mathematic model to describe the chiral morphogenesis of the cells observed in vitro on alternated fibronectin and PEG micropatterned strip lines [1]. This model assumes that there exist two morphogens: a slowly diffusing activator, BMP-2, and a rapidly diffusing inhibitor, matrix γ-carboxyglutamic acid protein (MGP). Within two-dimensional morphogen patterns, the cells are assumed to migrate towards the high concentration of activators, but importantly have a consistent directional bias, which is ultimately responsible for the observed chirality of cell alignment. Therefore, while the reaction–diffusion component produces the observed parallel cellular patterns at a high cell density, the main influencing factor in the mathematical model is the inclusion of anisotropic cellular migration, which resulted in diagonal stripes, compared to the random patterning caused by isotropic cell migration.

(c). Vertex-based anisotropic line tension model

A comprehensive and widely used model for multicellular chirality is based on the vertex model often used to describe the dynamics of epithelial sheets [36–39]. In a vertex model, the cells are approximated by polygons in a two-dimensional plane, with shared edges between neighbouring cells. The points where edges meet are called ‘vertices’, whose positions and connections determine cell arrangement inside the epithelial cells. The movement of the vertices is governed by the minimization of the total potential energy, which consists of a potential energy associated with cell area change, an elastic energy from cell perimeter change, and a line tension energy from the change in edge length. The latter is often assumed to be directional or anisotropic with a maximal value at a preferred angle.

One application is modelling the directional looping of the Drosophila hindgut. By focusing on the chiral behaviour, a two-dimensional model was performed with two cellular sheets moving along immobile boundary cells. Prior to the modelling, Taniguchi et al. initially analysed the presence of DE-cadherin and myosin ID in cells of the Drosophila hindgut, and noted that an LR asymmetric chiral shape of these cells, referred to as planar cell-shape chirality (PCC), was dependent on DE-cadherin distribution [19]. The simulation mimicked the in vivo number of cells and included a restriction in boundary angles to mimic PCC. This resulted in a progressive transition of cell shape and ultimately the ability of the model to capture the 90° left-handed rotation seen in vivo. Further work from the same group modified this simulation to allow for cells of different types to be analysed [21]. They modelled Myo31DF mosaic hindguts through modification of maximum angle and line tension parameters. The resulting simulations illustrated the need for differences in line tension for each type of cell boundary with the requirement that there be higher line tension between rescued cells than between mutant cells in order to accurately model hindgut rotation.

In addition, with the vertex model, cell chirality was shown to induce directional collective cell migration in epithelial sheets [22,23]. This finding is associated with one of the important features of the vertex model, neighbour exchange, also known as T1 transition. In this process, when an edge length is smaller than a critical value, the edge is rotated by 90°, and the connection rules of the vertices related to the edges are changed. Sato et al. [23] modelled cell migration in epithelial sheets confined between parallel boundaries, similar to those grown on line micropatterns [3,30]. When the interface tension was enhanced in a specific direction tilted from the major axis of the tissue, cell rearrangement through T1 transition occurred, leading to spontaneous and continuing shear movement of epithelial cells with opposite directions at two boundaries. If the cells have large friction at one of the boundaries, this could generate unidirectional cell migration of cell sheet, driven by cellular chirality. This concept was applied to model the directional cell movement of epithelial cells associated with genitalia rotation of Drosophila [22].

In summary, these three models attempt to describe different facets of biophysical mechanisms behind cell chirality. The first one aimed to examine the intracellular origin of cell chirality through actin dynamics. In comparison of the latter two multicellular models, both have introduced a chiral term, either the directional bias of cellular response to a chemical gradient or the directional preference of strong line tension, and successfully recapitulated multicellular chiral alignment. Exact mechanisms associated with the directional bias are still not explicitly described in the models. In the future, multiscale modelling will be necessary to connect the intracellular cytoskeletal chirality with the multicellular collective behaviour for realistic representation of LR asymmetry breaking both in vitro and in vivo. Only such a model can attribute an alternation in LR asymmetry at a tissue level to cytoskeleton reorganization. This could result in mathematical models with higher predictive power in which gene expression information alone could be able to predict cytoskeleton remodelling, biased cell migration and chiral tissue morphogenesis.

4. Conclusion

The recent development of in vitro culture systems that measure cell chirality may create a new paradigm for studying cellular and molecular mechanisms associated with LR asymmetry in development. Together with mathematical modelling, these in vitro systems are becoming powerful tools for studying biological chirality at subcellular, cellular and multicellular levels. Although the association between in vitro cell chirality and LR asymmetry in development needs to be further examined, if successful, these systems can provide deep insights of LR symmetry breaking in embryonic development. Finally, as some micro-contact printing-based approaches are high-throughput in nature, they could be used for teratogen screening to prevent birth defects in laterality.

Authors' contributions

L.Q.W. outlined, wrote and edited the review article. A.S.C. and P.R. primarily wrote the section In Vitro Chirality Systems. K.E.W. primarily wrote the section Mathematic Models for Cell Chirality. All authors gave final approval for publication.

Competing interests

We have no competing interests.

Funding

The authors would like to thank the National Institutes of Health, National Science Foundation, American Heart Association and March of Dimes for funding Support. L.Q.W. is a Pew Scholar in Biomedical Sciences, supported by the Pew Charitable Trusts.