Abstract
Purpose
The purpose of this study was to compare two inverse planning algorithms for cervical cancer brachytherapy and a conventional manual treatment planning according to the MUW (Medical University of Vienna) protocol.
Material and methods
For 20 patients, manually optimized, and, inversely optimized treatment plans with Hybrid Inverse treatment Planning and Optimization (HIPO) and with Inverse Planning Simulated Annealing (IPSA) were created. Dosimetric parameters, absolute volumes of normal tissue receiving reference doses, absolute loading times of tandem, ring and interstitial needles, Paddick and COIN conformity indices were evaluated.
Results
HIPO was able to achieve a similar dose distribution to manual planning with the restriction of high dose regions. It reduced the loading time of needles and the overall treatment time. The values of both conformity indices were the lowest. IPSA was able to achieve acceptable dosimetric results. However, it overloaded the needles. This resulted in high dose regions located in the normal tissue. The Paddick index for the volume of two times prescribed dose was outstandingly low.
Conclusions
HIPO can produce clinically acceptable treatment plans with the elimination of high dose regions in normal tissue. Compared to IPSA, it is an inverse optimization method which takes into account current clinical experience gained from manual treatment planning.
Keywords: brachytherapy, cervix, inverse planning, HIPO, IPSA
Purpose
Inverse optimization algorithms were implemented into external beam therapy (EBRT) several years ago [1, 2]. Their main benefits are the reduction of treatment planning time, good reproducibility and the creation of treatment plans which provide both, better target coverage and sufficient sparing of organs at risk (OARs). In brachytherapy (BT), the development of inverse optimization algorithms, inverse planning procedure and their integration into clinical routine is just being established. Inverse planning algorithms are widely used by several institutions, but only in prostate cancer BT [3–12]. For other carcinomas, basic research, development of concepts, definition of constraints and clinical adaptation of the procedure are still necessary [13, 14].
The use of inverse plan optimization methods has been recently introduced into cervical cancer BT [13, 15–18]. The typical pear shaped dose distribution has been used for decades and results in very good clinical outcomes [19, 20]. With the integration of 3D imaging devices (CT, MRI), the dose distribution can be adapted to the individual anatomical situation [21, 22]. The aim of inverse planning is to achieve the best possible dose distribution for the target structures, the organs at risk and un-diseased tissue. However, even with dose adaptation methods, the typical pear shaped dose distribution should be preserved. Such a distribution consists of high dose regions concentrated within the tumour bearing uterus while not spreading into the adjacent normal tissue [14, 23]. Therefore, several issues remain to be addressed in preserving this concept with inverse planning [14].
Nowadays, two algorithms are commercially available. One of them is the HIPO algorithm which has been especially fine-tuned for use in cervical cancer BT [14, 24]; i.e. specific features have been incorporated into the inverse planning process in order to achieve smoother dose distribution. Further, sophisticated procedure was developed to preserve the typical form of the dose [25] and to keep the high dose regions just within the target structures. The second algorithm is the IPSA which is a more general algorithm [26]. No specific tools to control the spatial dose distribution of high dose regions for cervical cancer BT have been integrated into the inverse planning process with IPSA.
The purpose of this study was to compare the inverse planning algorithms dedicated to the treatment planning in cervical cancer BT and moreover, to compare both of them to the manual planning method. We placed a special emphasis on the high dose regions because they play an important role and the most significant differences were expected in this particular area.
Material and methods
Patients and treatment
The same group of 20 patients as in [14] was used for this study. The patients underwent 45 to 50.4 Gy whole pelvic EBRT followed by 4 fractions of HDR BT with prescribed dose (PD) of 7 Gy [23]. Ten patients were treated with the intracavitary MR/CT compatible Vienna tandem/ring (T/R) applicator (mean HR CTV 30 cm3). For the remaining ten patients, where the coverage of HR CTV was not sufficient with the T/R applicator alone, additional interstitial needles (T/R + N) were implanted (mean HR CTV 40 cm3) [27, 28]. For each patient, one fraction planned with an MRI based treatment planning approach was included in this analysis [23].
The applicator reconstruction was based on predefined applicator geometries consisting of the scanned outer dimensions of the applicator in relation to the source path [29]. Contouring of HR CTV, GTV, bladder, rectum and sigmoid colon was performed according to the GYN GEC ESTRO recommendations [30, 31]. IR CTV was not delineated. The dose volume constraints used for each patient are presented in Table 1 [32]. For the reasons of this study, EBRT dose of 45 Gy was used for all patients to acquire the same dose constraints.
Table 1.
The dose-volume constraints used for our treatment schedule; the given doses are physical doses per one BT fraction, the doses in brackets are biologically weighted doses to be reached [32]
| HR CTV: D90 (Gy) | > 7 Gy/fr. | (> 85 Gy) |
| HR CTV: V100 (%) | > 90% | |
| Bladder: D2cc (Gy) | < 6.2 Gy/fr. | (< 90 Gy) |
| Rectum: D2cc (Gy) | < 4.4 Gy/fr. | (< 70 Gy) |
| Sigmoid: D2cc (Gy) | < 4.4 Gy/fr. | (< 70 Gy) |
For all patients, three different treatment plans were created. The first plans were manually optimized which were clinically used for patient treatment. The other two were retrospectively created inverse optimized treatment plans with HIPO and with IPSA.
Manual treatment planning
Manual treatment planning workflow for cervical cancer BT at the Medical University of Vienna (MUW) has already been described in detail [14, 23, 27, 32]. All manual plans were done in the PLATO v14.3 TPS.
Inverse planning: HIPO
The Hybrid Inverse treatment Planning and Optimization algorithm (HIPO) is an advanced, anatomy-based optimization algorithm developed by Karabis, Giannouli and Baltas [24]. The adaptation of inverse planning with HIPO to meet the specific requirements for the dose distribution in cervical cancer BT treatments have been already described elsewhere [14]. HIPO features, such as automatically generated individual anatomy based loading patterns, dwell time gradients, normal tissue constraints and separate optimization of the interstitial and intracavitary parts of an implant, have the potential to support the pear-shaped dose distribution [14].
All HIPO plans were done in the Oncentra GYN v0.9.14 and based on the MUW workflow with the optimization settings introduced in [14] and presented in Table 2.
Table 2.
Sets of objectives – dose limits and importance factors for HIPO [14]
A) T/R applicator alone
dwell time gradient: 0.5
| VOI | Dmin (% PD) | Imp. factor | Dmax (% PD) | Imp. factor |
|---|---|---|---|---|
| HR CTV | 100 | 50 | 300 | 1 |
| GTV | 150 | 15 | 300 | 0.1 |
| Bladder | – | – | 88 | 10 |
| Rectum | – | – | 60 | 10 |
| Sigmoid colon | – | – | 60 | 15 |
| Normal tissue | – | – | 200 | 0.1 |
B) T/R applicator (from the combined intracavitary /interstitial implant)
dwell time gradient: 0.5
| VOI | Dmin (% PD) | Imp. factor | Dmax (% PD) | Imp. factor |
|---|---|---|---|---|
| HR CTV | 100 | 10 | 300 | 2 |
| GTV | 150 | 15 | 300 | 0.1 |
| Bladder | – | – | 88 | 20 |
| Rectum | – | – | 60 | 20 |
| Sigmoid colon | – | – | 60 | 20 |
| Normal tissue | – | – | 200 | 0.1 |
C) needles (from the combined intracavitary/interstitial implant)
dwell time gradient: 0.2
| VOI | Dmin (% PD) | Imp. factor | Dmax (% PD) | Imp. factor |
|---|---|---|---|---|
| HR CTV | 100 | 40 | 300 | 1 |
| GTV | – | – | – | – |
| Bladder | – | – | 88 | 10 |
| Rectum | – | – | 60 | 10 |
| Sigmoid colon | – | – | 60 | 10 |
| Normal tissue | – | – | 200 | 1 |
Inverse planning: IPSA
The Inverse Planning Simulated Annealing (IPSA) is an algorithm developed by the UCSF group [15, 17]. This advanced inverse optimization technique is used for prostate BT in several centres and favourable results have been presented [3–12]. Some institutions also use it for cervix BT. The algorithm is implemented in the Plato TPS (from v14.3, Nucletron B.V., Veenendaal, The Netherlands) and the OncentraBrachy (from v1.0, Nucletron B.V., Veenendaal, The Netherlands). The implementation of the algorithm into TPS does not integrate any additional specific tools for different brachytherapy treatment sites [15].
Inverse treatment planning with IPSA was performed in Plato. Before optimization, all dwell positions in the intracavitary and interstitial parts of the implant were activated. All parts of the applicator were included into the optimization at the same time. The optimization always uses the optimization settings from the UCSF [15–17] for both types of applicators. In case of an unsatisfactory dose distribution, the optimization parameters were adjusted and the calculation was repeated again until our objective was achieved. The average adjusted optimization settings which led to the best dose distributions are presented in Table 3. Moreover, the additional help structure around the ring part of the implant was contoured and integrated into the inverse optimization in order to obtain more contribution from the ring, and therefore to reduce the contribution from the interstitial needles to the whole dose distribution [14, 23].
Table 3.
Average dose objectives and weighting factors used for IPSA
| Dmin (cGy) | Mmin | Dmax (cGy) | Mmax | |
|---|---|---|---|---|
| HR CTV | 700/700 | 100/100 | 750/750 | 0/0 |
| GTV | 700/700 | 100/100 | 1050/1050 | 0/0 |
| Help structure | 1050/0 | 20/0 | 2800/2800 | 0/0 |
| Bladder | 0/0 | 0/0 | 470/470 | 20/20 |
| Rectum | 0/0 | 0/0 | 400/400 | 20/20 |
| Sigmoid | 0/0 | 0/0 | 400/400 | 40/40 |
Both, the dose objectives and weighting factors are in the form of surface/volume
Dmin = minimum dose, Dmax = maximum dose, Mmin = slope of penalty function for violating minimum dose constraint, Mmax = slope of penalty function for violating maximum dose constraint [17]
Evaluation
For each treatment plan, the dosimetric parameters based on the GYN GEC ESTRO recommendations were evaluated [17]. Additionally, absolute volumes V100, V200 and V400 of normal tissue receiving a dose of PD, 2 × PD and 4 × PD per fraction respectively, were evaluated (absolute volume of the reference dose with the exclusion of the absolute volumes of HR CTV and the applicator volume outside HR CTV receiving reference dose. The part of the tandem inside of HR CTV was included in HR CTV in keeping with the current practice in most of the centres).
In order to find out the portion of the dose coming from the interstitial needles in case of the T/R + N applicator, the absolute loading times of the tandem, ring and all needles were evaluated.
To evaluate how accurately HR CTV was covered and to estimate the amount of dose received by the surrounding tissue including OARs, two conformity indices were used. The first conformity index was proposed by Paddick [33] as a measure of how well the prescribed isodose conforms to the size and shape of a target volume. It was defined as:
where Vref,TV is a volume of a reference dose covering the target volume, TV is the target volume and Vref is a volume of a reference dose. Its ideal value is equal to 1. Paddick’s indices for reference doses of 1 × PD, 2 × PD and 4 × PD were evaluated to acquire relative comparisons of the ratios between the target volumes and sizes of high dose regions.
The second index used for evaluation was a modified COIN index as proposed by Baltas et al. [34, 35]. It was based on an evaluation of dose-volume histograms. It measures the overall quality of a treatment plan and is defined as product of three coefficients:
The coefficient c1 describes how accurately the target volume is covered by a reference dose Dref, i.e. PD.
where Vref,TV is a volume of a reference dose covering the target volume and TV is the target volume. The ideal value of c1 is equal to one.
The coefficient c2 is also a measure how accurately the target volume covered by the reference dose Dref. Moreover, it measures how much of normal tissue volume outside of the target volume receives the reference dose Dref:
The volume Vref is a volume of reference dose.
The last coefficient, c3, evaluates how much irradiation is received by OARs. It is defined as:
where VOAR is a volume of OAR and VOARcrit is a volume of OAR receiving critical dose Dcrit, i.e. 90%, 63% and 100% of PD for bladder, rectum/sigmoid and vagina wall, respectively. The product is taken over all OARs that should be included into the evaluation. These relative values are related to the total dose constraints used at the MUW, and are only valid for specific treatment schedule of four times 7 Gy BT plus 45 Gy EBRT.
The statistical significance of the results was proven with a two sided paired t-test with a level of significance at 0.05 [36]. All statistical calculations were done using the STATISTIKA (StatSoft, Inc.) package.
Results
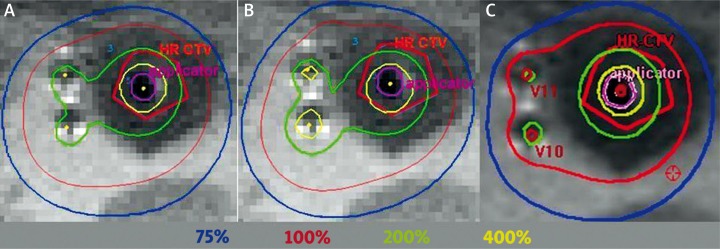
Figure 1 shows the example of typical dose distribution after manual, HIPO and IPSA optimization. All three plans were created for the same patient treated by combining the T/R applicator with 3 interstitial needles. From this example, the main difference among all three approaches can be seen. After the manual optimization, most of the dose comes from the intracavitary T/R applicator and the interstitial needles have very low loading just to cover the missing parts of extensive HR CTV which was not possible to cover with the intracavitary part alone. After inverse optimization with HIPO and toggling between two different optimization sets, the resulting dose distribution is almost the same as after the manual optimization. HIPO was even able to reduce high dose regions around interstitial needles. After IPSA inverse optimization, where all parts of the implant have the same importance, the overloading of needles can be seen. This is an unwanted result as it can lead to complicated side effects.
Fig. 1.
An example of the dose distribution after manual (A), IPSA (B) and HIPO (C) optimization
The average values of dosimetric parameters are presented in Table 4. The intracavitary T/R and combined intracavitary/interstitial treatment T/R + N were analysed separately. IPSA as well as HIPO were able to produce dosimetrically acceptable treatment plans for both kinds of treatments. In case of the T/R applicator, HIPO optimization leads to the best clinical dosimetric parameters for both, target structures and OARs. However, only the differences in V100 for HR CTV and D2cc for the rectum were statistically significant. In case of the T/R + N implant, HIPO optimization resulted in significantly better sparing of the bladder and sigmoid compared to the manual optimization. Moreover, both bladder and rectum were more spared as compared to IPSA optimization. The whole implant volume was the lowest after HIPO optimization in both implant modalities. IPSA led to the unnecessarily blown up high dose regions affecting normal tissue.
Table 4.
Summary of dosimetric results (mean ± st. dev.) of manual optimization and inverse optimization with HIPO and IPSA for a single fraction; all doses are physical doses. Numbers 1, 2 and 3 represent manual, HIPO and IPSA optimization, respectively
| T/R | 1 | 2 | 3 | p (1-2) | p (1-3) | p (2-3) |
|---|---|---|---|---|---|---|
| HR-CTV: V100 (%) | 95.8 ± 3.5 | 97.9 ± 2.3 | 96.4 ± 3.1 | 0.006 | 0.153 | 0.030 |
| HR-CTV: D90 (Gy) | 8.2 ± 1.1 | 8.6 ± 0.9 | 8.3 ± 1.1 | 0.138 | 0.607 | 0.368 |
| HR-CTV: D100 (Gy) | 5.2 ± 1.0 | 5.8 ± 0.7 | 5.6 ± 0.7 | 0.011 | 0.145 | 0.315 |
| Bladder: D2cc (Gy) | 5.2 ± 0.9 | 5.0 ± 1.2 | 5.6 ± 0.8 | 0.248 | 0.146 | 0.114 |
| Rectum: D2cc (Gy) | 3.5 ± 1.0 | 3.1 ± 0.8 | 3.7 ± 0.7 | < 0.001 | 0.238 | < 0.001 |
| Sigmoid c.: D2cc (Gy) | 4.2 ± 0.4 | 4.0 ± 0.5 | 4.1 ± 0.4 | 0.059 | 0.740 | 0.211 |
| Implant: VPD (cm3) | 81.1 ± 16.0 | 76.3 ± 19.4 | 93.4 ± 32.9 | 0.284 | 0.109 | 0.034 |
| T/R + N | 1 | 2 | 3 | p (1-2) | p (1-3) | p (2-3) |
| HR-CTV: V100 (%) | 94.7 ± 3.3 | 95.7 ± 2.5 | 95.8 ± 2.5 | 0.123 | 0.194 | 0.794 |
| HR-CTV: D90 (Gy) | 8.0 ± 0.9 | 8.1 ± 0.7 | 7.9 ± 0.5 | 0.429 | 0.783 | 0.296 |
| HR-CTV: D100 (Gy) | 4.7 ± 1.0 | 4.8 ± 1.0 | 5.2 ± 0.8 | 0.714 | 0.124 | 0.126 |
| Bladder: D2cc (Gy) | 5.4 ± 0.5 | 4.8 ± 0.8 | 5.4 ± 0.6 | 0.018 | 0.913 | 0.049 |
| Rectum: D2cc (Gy) | 3.7 ± 0.7 | 3.4 ± 0.8 | 3.8 ± 0.6 | 0.085 | 0.573 | 0.050 |
| Sigmoid c.: D2cc (Gy) | 4.2 ± 0.9 | 3.9 ± 1.0 | 3.9 ± 0.7 | 0.016 | 0.030 | 0.589 |
| Implant: VPD (cm3) | 95.4 ± 13.6 | 81.1 ± 23.4 | 94.5 ± 17.1 | 0.003 | 0.744 | 0.006 |
The comparison of the absolute volumes of normal tissue receiving certain reference doses are listed in Table 5. There was no significant difference in any volume for T/R. For the T/R + N configuration, normal tissue receiving the prescribed dose was significantly lower after HIPO optimization compared to the manual optimization as well as after IPSA optimization compared to manual. The difference between IPSA and HIPO in favour of the HIPO algorithm was not statistically significant.
Table 5.
Absolute volumes V100, V200 and V400 (mean ± st. dev.) of normal tissue receiving a dose of PD, 2 × PD and 4 × PD per fraction. Numbers 1, 2 and 3 represent manual, HIPO and IPSA optimization, respectively
| T/R | 1 | 2 | 3 | p (1-2) | p (1-3) | p (2-3) |
|---|---|---|---|---|---|---|
| V100 (cm3) | 31.4 ± 10.5 | 29.2 ± 10.9 | 35.4 ± 15.6 | 0.587 | 0.440 | 0.210 |
| V200 (cm3) | 3.9 ± 2.3 | 3.5 ± 2.1 | 3.8 ± 2.5 | 0.648 | 0.945 | 0.691 |
| V400 (cm3) | 0.5 ± 0.6 | 0.1 ± 0.6 | 0.4 ± 0.4 | 0.185 | 0.474 | 0.185 |
| T/R + N | 1 | 2 | 3 | p (1-2) | p (1-3) | p (2-3) |
| V100 (cm3) | 35.7 ± 9.3 | 28.8 ± 12.4 | 31.3 ± 9.2 | 0.036 | 0.024 | 0.343 |
| V200 (cm3) | 4.0 ± 1.7 | 2.7 ± 2.3 | 3.0 ± 1.8 | 0.115 | 0.091 | 0.544 |
| V400 (cm3) | 0.5 ± 0.4 | 0.6 ± 0.8 | 0.3 ± 0.3 | 0.599 | 0.095 | 0.225 |
The absolute loading times in each part of the implant and the whole implant loading are summarized in Table 6. All times are normalized to a source strength of 40820 cGy.cm2.h-1. The total loading times, as well as loading times of the ring and tandem, were significantly different between IPSA and HIPO. The HIPO optimization algorithm increases the loading time for the tandem whereas it reduces the loading time of the ring compared to manual and IPSA optimizations. In 9 out of 10 patients, the total loading time for all interstitial needles, as well as the time of the maximally loaded needle was noticeably reduced with HIPO compared to manual and IPSA optimizations.
Table 6.
Absolute average loading times (mean ± st. dev.) of tandem, ring and additional interstitial needles for T/R and T/R + N patients; these times are sums over all dwell positions in a given part of the implant. Regarding the needles, the sum is over all dwell positions in all needles together. Maximum needle loading time refers to one needle in which the sum of all dwell positions was highest compared to other needles loaded in a given patient. Numbers 1, 2 and 3 represent manual, HIPO and IPSA optimization, respectively
| T/R | 1 | 2 | 3 | p (1-2) | p (1-3) | p (2-3) |
|---|---|---|---|---|---|---|
| Total treatment time (s) | 374 ± 49 | 357 ± 63 | 404 ± 92 | 0.241 | 0.173 | 0.038 |
| Ring (s) | 206 ± 48 | 166 ± 43 | 239 ± 71 | 0.035 | 0.139 | 0.028 |
| Tandem (s) | 168 ± 52 | 191 ± 58 | 166 ± 56 | 0.164 | 0.850 | 0.038 |
| T/R + N | 1 | 2 | 3 | p (1-2) | p (1-3) | p (2-3) |
| Total treatment time (s) | 403 ± 38 | 351 ± 92 | 396 ± 44 | 0.056 | 0.459 | 0.101 |
| Ring (s) | 199 ± 20 | 151 ± 79 | 206 ± 48 | 0.105 | 0.700 | 0.086 |
| Tandem (s) | 144 ± 25 | 170 ± 59 | 122 ± 39 | 0.261 | 0.033 | 0.065 |
| Σ needles (s) | 60 ± 37 | 31 ± 18 | 68 ± 43 | 0.037 | 0.465 | 0.008 |
| Max. needle (s) | 32 ± 17 | 19 ± 10 | 42 ± 25 | 0.045 | 0.198 | 0.006 |
The conformity indices are presented in Table 7. For both T/R modalities, with or without needles, HIPO had the highest mean value of both conformity indices. For T/R patients, only the difference in the COIN index between IPSA and HIPO reached statistical significance. For T/R + N patients, low value of the Paddick index for the volume of 2 × PD after the IPSA optimization is particularly noteworthy.
Table 7.
Results of Paddick’s and COIN conformity index (mean ± st. dev.) for T/R and T/R + N applicator. Numbers 1, 2 and 3 represent manual, HIPO and IPSA optimization, respectively
| T/R | 1 | 2 | 3 | p (1-2) | p (1-3) | p (2-3) |
|---|---|---|---|---|---|---|
| Paddick: PD | 0.34 ± 0.07 | 0.36 ± 0.09 | 0.31 ± 0.06 | 0.315 | 0.208 | 0.092 |
| Paddick: 2 × PD | 0.22 ± 0.06 | 0.25 ± 0.08 | 0.18 ± 0.08 | 0.409 | 0.180 | 0.094 |
| Paddick: 4 × PD | 0.04 ± 0.03 | 0.05 ± 0.03 | 0.04 ± 0.02 | 0.560 | 0.493 | 0.265 |
| COIN: PD | 0.25 ± 0.07 | 0.28 ± 0.10 | 0.20 ± 0.06 | 0.111 | 0.112 | 0.031 |
| T/R + N | 1 | 2 | 3 | p (1-2) | p (1-3) | p (2-3) |
| Paddick: PD | 0.38 ± 0.06 | 0.44 ± 0.10 | 0.39 ± 0.05 | 0.047 | 0.187 | 0.081 |
| Paddick: 2 × PD | 0.27 ± 0.04 | 0.29 ± 0.10 | 0.19 ± 0.06 | 0.582 | 0.002 | 0.007 |
| Paddick: 4 × PD | 0.04 ± 0.01 | 0.05 ± 0.04 | 0.03 ± 0.02 | 0.400 | 0.028 | 0.113 |
| COIN: PD | 0.25 ± 0.07 | 0.33 ± 0.15 | 0.25 ± 0.06 | 0.074 | 0.993 | 0.069 |
Discussion
The aim of manual optimization in cervical cancer brachytherapy is to achieve a typical pear shaped dose distribution with a specific pattern of high dose regions. This dose distribution results in high local control and low side effects [19, 37]. Because of these good clinical results, it is important to try to preserve such a dose distribution after inverse optimization. The spatial distribution of high dose regions has to be taken into account by inverse optimization algorithms to avoid unexpected high doses in the parametrium or vaginal wall. High doses are not undesirable but they should be concentrated inside the cervix and uterus where the tumour is located. It is important to enable to control a spatial dose distribution of high dose regions even with automatic optimization tools.
Several papers have been already published about IPSA but they have not considered this important issue [13, 15, 17]. Only Chajon et al. [13] concludes that not only dose volume constraints for volumes of interest have to be integrated into the inverse optimization. They mention that there is a need for additional parameters in order to force the optimizer to produce more homogeneous dwell time distribution and to prevent hot spots within the treated volume. Kim et al. [18] presented a clinical report with 2 years follow up of 51 patients that were planned with IPSA. The treatment was well tolerated with minimal toxicities and good local control. However, they used either intracavitary [15, 16] or the interstitial applicator [17]. Combined applicator was not a part of investigation. And especially in case of combined intracavitary/interstitial applicator the spatial distribution of high dose regions plays an important role.
To this end, the department of radiotherapy at the MUW is aware of the need to conserve the pear-shaped dose distribution and of avoiding high dose regions in normal tissue. One publication about the challenging issues occurring during the inverse planning process and their possible solutions using HIPO and specific workflows has already been described in details [14]. The anatomy based loading patterns, the dwell time gradients, normal tissue constraints, locking of catheters and different optimization settings for the intracavitary and the interstitial parts of the implant are used to fine-tune HIPO algorithm. Including such parameters enables us to mimic a similar dose distribution to that of a result after manual optimization. Further, these parameters create differences in the results between IPSA and HIPO. With both inverse optimization algorithms, it was possible to create a treatment plan which was comparable to manually optimized plan. Note, however, that only HIPO was able to reduce high dose regions around interstitial needles. When using HIPO without these additional tools (dwell time gradient equal to 0, all parts of implant optimized together, no normal tissue constraint, no anatomy based loading patterns) the contribution from needles, and therefore the presence of high dose regions was higher.
IPSA seems to work properly and with solid set of parameters in case of prostate treatments [3–12]. Although in case of cervical cancer treatment further developments of optimization with IPSA are necessary. In our set of patients UCSF constraints [15–17] did not lead to a satisfactory dose distribution in any patient and we had to find out our set of constraints. A detailed analysis of patient cases should be performed in order to find a solid set of constraints or class solutions to improve the performance of IPSA optimization.
In order to focus on the distribution of high dose regions, the absolute volumes of normal tissue receiving the reference doses were evaluated (Table 5). The only significant difference was observed in T/R + N approach for a volume of PD where HIPO optimization resulted in the lowest volume. However, this parameter provides no information about the location of high dose regions, only about their size. More relevant parameters are normalized loading times of each part of the implant (Table 6). According to the number of seconds that a source stays in certain dwell position it is possible to obtain an estimation how the dose regions will be distributed along each catheter. In case of the T/R applicator, there is a significant difference between IPSA and HIPO in the tandem as well as in the ring part of the applicator. The total treatment time is significantly lower after HIPO optimization compared to IPSA. The comparison of loading times in case of T/R + N is more important. Manual treatment planning approach delivers most of the dose from the T/R applicator while only about 20-30% of the dose comes from needles [23, 27]. Whereas the T/R applicator delivers dose to the cervix and uterus part of HR CTV, needles are responsible for the high dose in parametrium part of HR CTV where hot spots should be avoided. From the dwell time analysis it is clear to see that treatment plans optimized with HIPO also tend to cover most of HR CTV with the dose coming from T/R. The dose from the interstitial needles is low, even lower than in manually optimized plans. In contrast, IPSA results in significant overloading of needles. The mean sum of all absolute dwell times in all needles is higher than in manually optimized plans and more than two times higher than with HIPO optimized plans. The reason is that IPSA includes T/R and needles into the calculation at the same time and with the same weight. In contrast, HIPO enables separate optimization of each of the part of an implant. In this study, for example, T/R was optimized at first and the needles were included afterwards to cover only the missing parts of HR CTV. This explains why hot spots, as shown in Fig. 1, can occur with IPSA. While IPSA is a more general optimization algorithm, heavily dependent on the geometry of the structures, HIPO was adapted specifically for cervical cancer brachytherapy. Some other HIPO features, like dwell time gradient restriction and normal tissue objective, enable it to meet clinical requirements more effectively [14]. However, IPSA can be used for inverse optimization of intracavitary BT. In this case, it is necessary to introduce additional structures as a help structures, such as contours around the applicator and sub volumes of HR CTV both inside and outside the uterus. A constraint for these structures will suppress high dose areas more effectively [13]. In our study we have introduced the help structure around the ring part of the applicator. Without this help structure, IPSA optimizer reduced the dose coming from the ring and loaded fully the needles because the ring is not a part of HR CTV in contrast to needles. With such defined help structure it was possible to achieve more doses from the ring and consequently reduce the needles loading.
With the objective to carry out a quantitative evaluation of dose distribution, two conformity indices were calculated, Paddick’s and the COIN index. None of these indices is intended for intracavitary BT because the conformal dose coverage of target structures due to the steep dose gradient fall is not possible. However, these quality indices served as relative parameters to distinguish between alternative 3D treatment plans by taking into account the coverage of HR CTV and high doses inside and outside the target volume.
Paddick’s index is primarily used for stereotactic treatments to accurately describe the conformity of the plan. In BT, ideal conformal treatments occur very seldom [38]. For all evaluated reference doses (PD, 2 × PD and 4 × PD), HIPO had the highest mean value of conformity index for both implant modalities. It confirms that with HIPO we can achieve more conformal plans. In case of Paddick index for 2 × and 4 × PD the volume of a given isodose has to be also considered. From Table 5 it is apparent that all three optimization approaches lead to some amount of high dose regions. Therefore it is desired that the value of Paddick index is as high as possible because it correspond to the localization of high dose volume inside of HR CTV. The significantly low Paddick’s index value for IPSA optimized plans, especially for reference dose equal to two times prescribed dose, verifies that IPSA is overloading needles and a big part of the high dose is located in normal tissue.
The same results were obtained with more complex the COIN index evaluation. The partial indices c1 and c2 were quite close for all treatment optimization modalities. The c3 including OARs irradiation was critical. The main contribution was from the vagina wall which was contoured for the reasons of the COIN index calculation. Although anatomical and/or dosimetric assessment of the vagina wall is influenced by major uncertainties and therefore no dose volume parameters are recommended for prospective treatment planning [39], the vaginal wall can be used as a relative parameter to reflect the dose distribution outside of HR CTV, in the immediate vicinity of the T/R applicator [14].
Conclusions
The analysis of the patients used in this study shows that HIPO algorithms and its specific implementation into the Oncentra GYN enables to mimic the manual treatment planning approach for cervical cancer BT. It produces clinically acceptable treatment plans and enables the reduction of high dose regions in the immediate vicinity of HR CTV. The IPSA algorithm is also able to produce dosimetrically acceptable treatment plans. But in comparison to HIPO it does not integrate any additional features that would enable to control spatial dose distribution of high dose regions, especially to control the loading of interstitial needles. The appropriate integration of IPSA and the development of controlling tolls for cervical cancer BT need to be defined.
Acknowledgement
This project was sponsored from FWF (Project number L562-B19).
Conflict of notification
The Department of Radiotherapy at the Medical University of Vienna receives financial and/or equipment support for research and educational purposes from Nucletron B.V., Varian Medical Systems, Inc., and Isodose Control B.V. For the development of Oncentra GYN, Christian Kirisits was a consultant to Nucletron B.V.
References
- 1.Bortfeld T. Optimized planning using physical objectives and constraints. Semin Radiat Oncol. 1999;9:20–34. doi: 10.1016/s1053-4296(99)80052-6. [DOI] [PubMed] [Google Scholar]
- 2.Georg D, Kroupa B, Georg P, et al. Inverse planning - a comparative intersystem and interpatient constraint study. Strahlenther Onkol. 2006;182:473–480. doi: 10.1007/s00066-006-1531-y. [DOI] [PubMed] [Google Scholar]
- 3.Citrin D, Ning H, Guion P, et al. Inverse treatment planning based on MRI for HDR prostate brachytherapy. Int J Radiat Oncol Biol Phys. 2005;61:1267–1275. doi: 10.1016/j.ijrobp.2004.11.024. [DOI] [PubMed] [Google Scholar]
- 4.Jacob D, Raben A, Sarkar A, et al. Anatomy-Based Inverse Planning Simulated Annealing Optimization in High-Dose-Rate Prostate Brachytherapy: Significant Dosimetric Advantage Over Other Optimization Techniques. Int J Radiat Oncol Biol Phys. 2008;72:820–827. doi: 10.1016/j.ijrobp.2008.02.009. [DOI] [PubMed] [Google Scholar]
- 5.Kim Y, Hsu IC, Lessard E, et al. Class solution in inverse planned HDR prostate brachytherapy for dose escalation of DIL defined by combined MRI/MRSI. Radiother Oncol. 2008;88:148–155. doi: 10.1016/j.radonc.2007.11.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kolkman-Deurloo IK, Deleye XG, Jansen PP, et al. Anatomy based inverse planning in HDR prostate brachytherapy. Radiother Oncol. 2004;73:73–77. doi: 10.1016/j.radonc.2004.08.014. [DOI] [PubMed] [Google Scholar]
- 7.Lachance B, Beliveau-Nadeau D, Lessard E, et al. Early clinical experience with anatomy-based inverse planning dose optimization for high-dose-rate boost of the prostate. Int J Radiat Oncol Biol Phys. 2002;54:86–100. doi: 10.1016/s0360-3016(02)02897-3. [DOI] [PubMed] [Google Scholar]
- 8.Lessard E, Kwa SL, Pickett B, et al. Class solution for inversely planned permanent prostate implants to mimic an experienced dosimetrist. Med Phys. 2006;33:2773–2782. doi: 10.1118/1.2210565. [DOI] [PubMed] [Google Scholar]
- 9.Lessard E, Pouliot J. Inverse planning anatomy-based dose optimization for HDR-brachytherapy of the prostate using fast simulated annealing algorithm and dedicated objective function. Med Phys. 2001;28:773–779. doi: 10.1118/1.1368127. [DOI] [PubMed] [Google Scholar]
- 10.Pouliot J, Kim Y, Lessard E, et al. Inverse planning for HDR prostate brachytherapy used to boost dominant intraprostatic lesions defined by magnetic resonance spectroscopy imaging. Int J Radiat Oncol Biol Phys. 2004;59:1196–1207. doi: 10.1016/j.ijrobp.2004.02.055. [DOI] [PubMed] [Google Scholar]
- 11.Raben A, Sammons S, Sim S, et al. Initial comparison of inverse optimization, modified peripheral technique, and geometric optimization as real-time intraoperative computer planning options for permanent seed implantation of the prostate. Brachytherapy. 2007;6:238–245. doi: 10.1016/j.brachy.2007.08.001. [DOI] [PubMed] [Google Scholar]
- 12.Morton GC, Sankreacha R, Halina P, et al. A comparison of anatomy-based inverse planning with simulated annealing and graphical optimization for high-dose-rate prostate brachytherapy. Brachytherapy. 2008;7:12–16. doi: 10.1016/j.brachy.2007.10.001. [DOI] [PubMed] [Google Scholar]
- 13.Chajon E, Dumas I, Touleimat M, et al. Inverse planning approach for 3-D MRI-based pulse-dose rate intracavitary brachytherapy in cervix cancer. Int J Radiat Oncol Biol Phys. 2007;69:955–961. doi: 10.1016/j.ijrobp.2007.07.2321. [DOI] [PubMed] [Google Scholar]
- 14.Trnkova P, Potter R, Baltas D, et al. New inverse planning technology for image-guided cervical cancer brachytherapy: description and evaluation within a clinical frame. Radiother Oncol. 2009;93:331–340. doi: 10.1016/j.radonc.2009.10.004. [DOI] [PubMed] [Google Scholar]
- 15.Dewitt KD, Hsu IC, Speight J, et al. 3D inverse treatment planning for the tandem and ovoid applicator in cervical cancer. Int J Radiat Oncol Biol Phys. 2005;63:1270–1274. doi: 10.1016/j.ijrobp.2005.07.972. [DOI] [PubMed] [Google Scholar]
- 16.Kubicky CD, Yeh BM, Lessard E, et al. Inverse planning simulated annealing for magnetic resonance imaging-based intracavitary high-dose-rate brachytherapy for cervical cancer. Brachytherapy. 2008;7:242–247. doi: 10.1016/j.brachy.2008.01.003. [DOI] [PubMed] [Google Scholar]
- 17.Lessard E, Hsu IC, Pouliot J. Inverse planning for interstitial gynecologic template brachytherapy: truly anatomy-based planning. Int J Radiat Oncol Biol Phys. 2002;54:1243–1251. doi: 10.1016/s0360-3016(02)03802-6. [DOI] [PubMed] [Google Scholar]
- 18.Kim DH, Wang-Chesebro A, Weinberg V, et al. High-dose rate brachytherapy using inverse planning simulated annealing for locoregionally advanced cervical cancer: a clinical report with 2-year follow-up. Int J Radiat Oncol Biol Phys. 2009;75:1329–1334. doi: 10.1016/j.ijrobp.2009.01.002. [DOI] [PubMed] [Google Scholar]
- 19.Potter R, Dimopoulos J, Georg P, et al. Clinical impact of MRI assisted dose volume adaptation and dose escalation in brachytherapy of locally advanced cervix cancer. Radiother Oncol. 2007;83:148–155. doi: 10.1016/j.radonc.2007.04.012. [DOI] [PubMed] [Google Scholar]
- 20.Patel FD, Rai B, Mallick I, et al. High-dose-rate brachytherapy in uterine cervical carcinoma. Int J Radiat Oncol Biol Phys. 2005;62:125–130. doi: 10.1016/j.ijrobp.2004.09.017. [DOI] [PubMed] [Google Scholar]
- 21.Potter R, Kirisits C, Fidarova EF, et al. Present status and future of high-precision image guided adaptive brachytherapy for cervix carcinoma. Acta Oncol. 2008;47:1325–1336. doi: 10.1080/02841860802282794. [DOI] [PubMed] [Google Scholar]
- 22.Potter R, Fidarova E, Kirisits C, et al. Image-guided adaptive brachytherapy for cervix carcinoma. Clin Oncol (R Coll Radiol) 2008;20:426–432. doi: 10.1016/j.clon.2008.04.011. [DOI] [PubMed] [Google Scholar]
- 23.Kirisits C, Potter R, Lang S, et al. Dose and volume parameters for MRI-based treatment planning in intracavitary brachytherapy for cervical cancer. Int J Radiat Oncol Biol Phys. 2005;62:901–911. doi: 10.1016/j.ijrobp.2005.02.040. [DOI] [PubMed] [Google Scholar]
- 24.Karabis A, Giannouli S, Baltas D. HIPO: A hybrid inverse treatment planning optimization algorithm in HDR brachytherapy. Radiother Oncol. 2005;76(Suppl. 2):S29. [Google Scholar]
- 25.ICRU (International Commission of Radiation Units and Measurements) ICRU Report 38. Bethesda: 1985. Dose and volume specification for reporting intracavitary therapy in gyneacology. [Google Scholar]
- 26.Pouliot J, Lessard É, Hsu I-C. Brachytherapy Physics. Second Edition. M.P. Publishing, AAPM-ABS; 2005. Chapter 21 - Advanced 3D plan; pp. 393–413. [Google Scholar]
- 27.Kirisits C, Lang S, Dimopoulos J, et al. The Vienna applicator for combined intracavitary and interstitial brachytherapy of cervical cancer: design, application, treatment planning, and dosimetric results. Int J Radiat Oncol Biol Phys. 2006;65:624–630. doi: 10.1016/j.ijrobp.2006.01.036. [DOI] [PubMed] [Google Scholar]
- 28.Dimopoulos JC, Kirisits C, Petric P, et al. The Vienna applicator for combined intracavitary and interstitial brachytherapy of cervical cancer: clinical feasibility and preliminary results. Int J Radiat Oncol Biol Phys. 2006;66:83–90. doi: 10.1016/j.ijrobp.2006.04.041. [DOI] [PubMed] [Google Scholar]
- 29.Berger D, Dimopoulos J, Potter R, et al. Submitted to Radiother Oncol. 2009. Direct reconstruction of the Vienna applicator on MRI images. [DOI] [PubMed] [Google Scholar]
- 30.Haie-Meder C, Potter R, Van Limbergen E, et al. Recommendations from Gynaecological (GYN) GEC-ESTRO Working Group (I): concepts and terms in 3D image based 3D treatment planning in cervix cancer brachytherapy with emphasis on MRI assessment of GTV and CTV. Radiother Oncol. 2005;74:235–245. doi: 10.1016/j.radonc.2004.12.015. [DOI] [PubMed] [Google Scholar]
- 31.Potter R, Haie-Meder C, Van Limbergen E, et al. Recommendations from gynaecological (GYN) GEC ESTRO working group (II): concepts and terms in 3D image-based treatment planning in cervix cancer brachytherapy-3D dose volume parameters and aspects of 3D image-based anatomy, radiation physics, radiobiology. Radiother Oncol. 2006;78:67–77. doi: 10.1016/j.radonc.2005.11.014. [DOI] [PubMed] [Google Scholar]
- 32.Lang S, Kirisits C, Dimopoulos J, et al. Treatment planning for MRI assisted brachytherapy of gynecologic malignancies based on total dose constraints. Int J Radiat Oncol Biol Phys. 2007;69:619–627. doi: 10.1016/j.ijrobp.2007.06.019. [DOI] [PubMed] [Google Scholar]
- 33.Paddick I. A simple scoring ratio to index the conformity of radiosurgical treatment plans. Technical note. J Neurosurg. 2000;93:219–222. doi: 10.3171/jns.2000.93.supplement. [DOI] [PubMed] [Google Scholar]
- 34.Lahanas M, Schreibmann E, Baltas D. Multiobjective inverse planning for intensity modulated radiotherapy with constraint-free gradient-based optimization algorithms. Phys Med Biol. 2003;48:2843–2871. doi: 10.1088/0031-9155/48/17/308. [DOI] [PubMed] [Google Scholar]
- 35.Milickovic N, Lahanas M, Papagiannopoulo M, et al. Multiobjective anatomy-based dose optimization for HDR-brachytherapy with constraint free deterministic algorithms. Phys Med Biol. 2002;47:2263–2280. doi: 10.1088/0031-9155/47/13/306. [DOI] [PubMed] [Google Scholar]
- 36.Meloun M, Militký J. Academia Praha. 2001. Kompendium statistického zpracování dat. ISBN 80-200-1008-4. [Google Scholar]
- 37.Dimopoulos JC, Potter R, Lang S, et al. Dose-effect relationship for local control of cervical cancer by magnetic resonance image-guided brachytherapy. Radiother Oncol. 2009;93:311–315. doi: 10.1016/j.radonc.2009.07.001. [DOI] [PubMed] [Google Scholar]
- 38.Baltas D, Kolotas C, Geramani K, et al. A conformal index (COIN) to evaluate implant quality and dose specification in brachytherapy. Int J Radiat Oncol Biol Phys. 1998;40:515–524. doi: 10.1016/s0360-3016(97)00732-3. [DOI] [PubMed] [Google Scholar]
- 39.Berger D, Dimopoulos J, Georg P, et al. Uncertainties in assessment of the vaginal dose for intracavitary brachytherapy of cervical cancer using a tandem-ring applicator. Int J Radiat Oncol Biol Phys. 2007;67:1451–1459. doi: 10.1016/j.ijrobp.2006.11.021. [DOI] [PubMed] [Google Scholar]