Reconciling Statistical and Systems Science Approaches to Public Health

Abstract

Although systems science has emerged as a set of innovative approaches to study complex phenomena, many topically focused researchers including clinicians and scientists working in public health are somewhat befuddled by this methodology that at times appears to be radically different from analytic methods, such as statistical modeling, to which the researchers are accustomed. There also appears to be conflicts between complex systems approaches and traditional statistical methodologies, both in terms of their underlying strategies and the languages they use. We argue that the conflicts are resolvable, and the sooner the better for the field. In this article, we show how statistical and systems science approaches can be reconciled, and how together they can advance solutions to complex problems. We do this by comparing the methods within a theoretical framework based on the work of population biologist Richard Levins. We present different types of models as representing different tradeoffs among the four desiderata of generality, realism, fit, and precision.

Rooted in the “mathematically based” disciplines such as engineering, computational sciences, and operations research, systems science has emerged as a family of methodologies appropriate for studying complex systems in society and nature (Sterman, 2006). Although systems science has proved to be an innovative way to study complex phenomena, many empirical researchers in the disciplines where it is being applied are perplexed by this methodology that at times appears to be lacking the scientific rigor of statistical approaches to which the researchers are accustomed. Here, and throughout this article, we use the terms statistics and statistical models to refer specifically to a subset of statistics, Null Hypothesis Significance Testing (NHST), except where indicated. Carefully collected statistical data are used for testing a small number of hypotheses that are identified by the researcher a priori. Indeed, as a reductionist approach, statistical modeling gears toward falsifying a well-defined null hypothesis such as “There is no difference between the mean responses to Drug A and the placebo.”

In contrast, systems science methodologies are used to address a range of goals including the following: (1) Knowledge Synthesis (summarizing information across a range of domains to represent the “big picture” view of the system or problem); (2) Heuristic (to aid in understanding the dynamics underlying the system or problem); (3) Hypothesis Generation (to generate new hypotheses and/or narrow the list of plausible hypotheses); (4) Forecasting (to generate a range of plausible future scenarios, based on explicit assumptions); (5) Identify and Prioritizing Research Gaps (use sensitivity analysis to determine knowledge gaps that, if addressed, would narrow the confidence band associated with model outcomes); and (6) Virtual Experimentation (conduct experiments in silico, saving time and money). Systems science methodologies are often employed for policy analysis and design—to examine tradeoffs of implementing different policy options; to generate and test dynamic hypotheses—could the Behavior X be generated by Causal Structure Y (i.e., a set of causal relationships); for anticipating future behavior modes—what is the expected future trajectory of variables of interest under specified conditions; and when exploration is the goal—what system behaviors (some of which may be unanticipated) emerge from dynamic simulation. Systems science models often rely on the conceptual framework and heterogeneous qualitative and quantitative data sources, and the consistency of the data may not be comparable to the sort of data that are demanded by statistical approaches. Furthermore, systems science models often emphasize generative explanation and emergent behaviors of systems whereas statistical models focus on the notion of causality (e.g., in clinical trials) and consistencies of models with carefully collected data sets from designed experiments and empirical studies.

In this article, we demonstrate how statistical and systems science approaches can be reconciled, and how together they can advance solutions to complex problems especially those related to public health. We build our work on the basic insight that different modeling approaches may pursue different goals, and none can achieve all the relevant goals simultaneously. Therefore, a systems modeling choice that seems like a poor practice to a statistical modeler may be motivated by the pursuit of goal different from what the statistical modeler is used to, and vice versa. For example, some models may target point prediction, and others may seek insight generation, descriptive accuracy, hypothesis testing, relevance to policy questions, or other goals (Randers 1980). Appreciating these differences in modeling goals and approaches is crucial for communication across disciplinary boundaries and for increasing consistency among policy conclusions that emanate from model-based analysis (Andersen, 1980). To this end, we employ a generality-realism-fit-precision paradigm motivated by the work of population biologist Richard Levins (1966) and later expanded by other biologists (Matthewson & Weisberg, 2009; Odenbaugh, 2006; Weisberg, 2006), which we referred to as the Levins Framework. Briefly, our framework considers four attributes, or desiderata of models: generality, realism, fit, and precision. We present different modeling applications as each representing a different balance, or what we shall call set of tradeoffs, between the four desiderata.

Tradeoffs in Modeling: Generality, Realism, Fit, and Precision

Meanings of Generality, Realism, Fit, and Precision

Precision, in the Levins framework, is not a property of a statistical estimate (e.g., in terms of the width of its confidence interval) but rather is the “fineness of model specification.” That is, precision is the level of specific details about model parameters, functional forms of relationships between variables, details about its components, and so on. By this definition, a model that can generate numerical outputs is precise, whereas broad qualitative models score low on precision. More operational qualitative models may be medium on this dimension. Realism in the original Levins framework refers to both the predictive accuracy of a model and to the level of accuracy to which the model reflects reality. Here we distinguish between qualitative realism, for which we retain the descriptor “realism,” and quantitative realism, which we refer to as “fit.” The former suggests consistency of the model with the mental models of experts and the latter consistency of the model with real data. Specifically, qualitative realism refers to the degree to which a model is perceived to be realistic by experts in the field, because it reflects the relevant real-world mechanisms and variables (i.e., to be realistic is to have face validity). On the other hand, quantitative realism (a.k.a. fit), refers to how well a model fits the data both in terms of goodness-of-fit of the model to historical data and predictive accuracy. Models such as complex black-box models in machine learning often have high level of fit but low level of qualitative realism. Generality refers to the extent to which a model can be applied across circumstances and phenomena. In the Levins framework, relative to less general models, a more general model would be one in which parameters are not specified as precisely, causal forces are described at higher levels of abstraction, and model variables are represented more qualitatively and less quantitatively. Examples of highly general models include the multilevel behavioral model (Glass & McAtee, 2006) and the social ecological (Emmons, 2002; see also Langille & Rogers, 2010) and ecosocial (Krieger, 2001) models, which forgo quantitative representation altogether.

One challenge of using the Levins framework for looking at the space of modeling approaches is that there is vast diversity even within each class of models. For example, NHST notwithstanding, the field of statistical modeling has emerged to include complex multimodal, multilevel, and temporal models, which are difficult to discuss in the same vein as t test and simple linear model. In the following section, we provide several illustrations of the Levins framework with three archetypical modeling approaches: statistical models, agent-based models (ABMs), and system dynamics models. Within each archetype, we use two examples to highlight the diversities that exist within the archetype. Table 1 provides a summary of their characteristics within the Levins framework.

Table 1.

Examples of Different Modeling Approaches Within the Levins Framework.

Model	Generality	Realism	Fit	Precision
Statistical model
Simple linear regression	Moderate	Low	Low	High
Large-scale tree-based model for handwriting recognition	Low	Low	High	High
Agent-based model
Small-scale specific application for bird flocking behavior	Moderate	High	Low	Low
Large-scale agent-based model for human pandemic	Moderate	High	Moderate	Moderate
System dynamics model
Mathematical modeling	High	Low	Low	Moderate
System dynamics model for relating energy imbalance to weight change	Moderate	High	Moderate	High
Socioecologic model (qualitative)	High	High	Low	Low

Note. Generality: applicability of model to phenomena other than that for which it was developed. Realism: degree to which the model reflects reality as viewed by experts in the field. Fit: degree to which the model output matches historical data and has predictive accuracy. Precision: fineness of model and level of details specified.

Examples of Models to Illustrate the Levins Framework

Statistical models

Statistical models are designed to be instantiated—that is, model parameters are assigned numeric values—such that statistical prediction can be achieved. The level of precision (e.g., specific functional form, parameter definition and instantiation, control for confounding factors) for practically useful statistical models is typically high. The dose of realism in statistical models, however, is a function of the type of research question that the model is designed to answer. Typically, statistical modeling follows a question-data-analysis sequence (Cox, 2006). In the question-formulation stage, the extent to which the designed model would be a representation of the real world—its realism—is determined. Indeed, the Levins framework asserts that at most three desiderata—for example, precision, fit, and realism—but not all four, can be simultaneously maximized by any model. Thus, it is still possible to construct complex and highly precise statistical models that are both realistic and have good fit to empirical data. However, in practice, increasing both the (qualitative) realism and fit in statistical modeling (and all types of modeling for that matter) has its upper boundaries, which are, at a minimum, related to the cognitive limitations for comprehending the model. The realism-fit-precision tradeoff can also be viewed from the perspective of a complexity-parsimony balance in model fitting, as discussed in Rodgers (2010a, 2010b) and elsewhere (Roberts & Pashler, 2000, 2002). From that vantage point, useful models are judged against their goodness-of-fit to data, which is analogous to the fit criterion, as well as their parsimony, which is analogous to realism and precision (more complex implies higher level of model fineness or precision but less qualitative realism).

Table 1 shows two forms of statistical models that achieve different tradeoffs in the four desiderata. All statistical models are high in precision, because they need to be specified with enough precision to allow the generation of numerical outputs. Simple linear regression is a relatively coarse model, and the lack of fineness often renders it not to be considered a realistic representation of the world (existence of multiple confounding factors, noise not normally distributed, etc.). Historically, perhaps the most well-known example of simple linear regression is Sir Francis Galton’s study of the relationship between the height of parents and their offspring (Galton, 1886). However, except in straightforward cases, it is rare to find high level of fit of simple regression model to empirical data. Although such models can be used to describe phenomena in many fields, it is restricted to phenomena that exhibit a linear relationship between two variables, and thus has limited generality. On the other hand, complex statistical models such as an ensemble of tree-based models (e.g., Random Forest; see Breiman, 2001) could be high on the accuracy dimension (good fit to the data) but low in generality (limited in terms of the populations it can be applied to) as well as low in realism (difficult to interpret).

Agent-based models

As a computational methodology, ABM uses computer programs to simulate the behaviors of heterogeneous “actors” across multiple scales and through time (Epstein, 2006). ABMs strive to represent reality by including (to a greater or lesser degree) social networks, complex geographies, environmental variations, and evolution. Thus, the computational model underlying a “realistic” ABM might contain thousands of rules and model parameters. Whereas the goals of statistical approaches are to test hypotheses, ABMs are often employed to generate hypotheses and to see if the resulting simulation is consistent with hypotheses. Because of the different goals of ABM, the ways parameters are instantiated differ from those of statistical approaches. Good modeling practices suggest instantiating the model parameters with empirical data whenever possible. When such data are not available, models may be parameterized based on values derived from subject matter experts. As a last resort, the parameters for which there are no data or even expert opinion may be left unspecified. The relative importance of quantifying unspecified (free) parameters can be assessed using sensitivity analysis of simulation data, which demonstrates the magnitude of the impact the missing information is likely to have on the model outcomes of interest. Moreover, ABM and other systems science methodologies are capable of handling realistic reciprocal relationships (i.e., bidirectional relationships or feedback loops); nonlinear, networked relationships; and heterogeneity in actors and factors, which are difficult to handle using statistical methods. Indeed, mimicking reality is regarded as the hallmark of the ABM approach.

Table 1 shows two forms of ABM—one built for small-scale specific problems and another for large-scale general problems. An example of specific ABM is the simulation of the flocking behavior of bird flying (Reynolds, 1987). Using an amazingly small number of rules (limited precision), the ABM approach could mimic flying patterns of birds in real life (high realism) but not necessarily fitting real data (low fit). Such models could be useful for generating explanations of phenomena that are challenging to directly model mathematically. An example of a large complex ABM system is a simulation study of the vaccine allocation for the H1N1 pandemic (Lee et al., 2010). In these more complex systems, there may be a greater need for the model to match some aspects of real data well (e.g., means and variances of important outcomes) and thus requiring a higher level of fit. Also some model parameters may be left unspecified (moderate precision) and explored through sensitivity analysis. Generally speaking, ABMs are designed to achieve a relatively high level of realism in the sense that users can interact with the model to make judgment about the degree to which the model reflects the real world.

System dynamics models

System dynamics models represent systems as interconnections between stocks, flows, and feedback loops (bidirectional relationships). These interconnections are represented mathematically using algebra and calculus (i.e., differential equations; Sterman, 2000). Here in Table 1 we use the term mathematical modeling to refer to formulations that make use of mathematical constructs to highlight formal, abstract, and general concepts. For example, a second-order differential equation can be used to describe harmonic oscillators under various damping conditions. One of the best known textbook examples of a mathematical model is that of a mechanically oscillating spring system but such general formulation can be adapted to model systems that exhibit alternating behaviors, from economic cycles to supply chain instability (Sterman, 1986, 2000). One such adaptation is in psychology of which the notion of feedback as a regulator of human and animal behavior is being modeled as an oscillating system (Levine & Fitzgerald, 1992; Ramsay, 2006). As some abstract representation of mechanisms, mathematical models are characterized by a high level of generality and medium realism and low fit. The fineness of the model (precision) depends on the kind of mathematical model.

Table 1 also shows a more specific example under the heading System Dynamics modeling. In a nutshell, typical system dynamic models use differential equations to capture dynamic phenomena. Stock (state) variables aggregate inertial concepts in a system, such as population groups. The goal is to identify and capture a broad set of feedback processes that regulate the rates of change in these stock variables. For example, Abdel-Hamid (2002) uses a system dynamics model to integrate nutrition, metabolism, hormonal regulation, body composition, and physical activity of a single individual as they relate to weight gain and loss. The model is then used for conducting different hypothetical dieting and exercise experiments that can inform obesity interventions in general and inspire new laboratory experiments that tease out effects otherwise unnoticed by empirical researchers. The model can also be calibrated to individual data for designing personalized obesity interventions. This model enjoys a high level of precision, since it is fully specified and can be simulated to generate individual weight change trajectories. It is also rather high on realism, as it strives to capture many biological processes in the body that underlie weight dynamics. The model’s fit is more moderate, because its free parameters are estimated based on a small sample of human subjects. The model’s generality may also be assessed as moderate, since its core mechanisms and structures carry over different individuals and populations, but model parameters require tweaking for application to different populations.

For comparison purpose, Table 1 also includes the qualitative multilevel ecologic model (i.e., a conceptual map by Glass & McAtee, 2006; to be discussed later), which is high on both generality and realism but low on fit and precision.

In summary, our revision to Levins framework offers a lens to view the potential strengths and challenges of different modeling assumptions. It reveals inherent limitations in how far one can create a representation of the real world through model building in that (1) no model can simultaneously achieve all four generality-realism-fit-precision desiderata without sacrificing one or more of the four and (2) models that occupy a single desiderata may not be highly useful; for example, a model of extreme generality can become too general in that it says nothing of interest regarding its targets and thereby loses explanatory power (Matthewson & Weisberg, 2009), or a model could be fine-tuned to precisely fit a dataset at the expense of being predictive for any other population group. It is worth reiterating that tremendous diversities exist within each class of models discussed in Table 1. This diversity suggests that, for example, one may find systems models that are closer to some statistical models than many more common systems models. Such models that better reflect the core strengths and challenges in other paradigms could act as useful bridges to introduce one paradigm to the practitioners of the other.

Using different strategies of modeling in the four-way tradeoff would lead to a range of what Weisberg (2006) called representational ideals of the world. In this sense, statistical models and computational models can be viewed as different representational ideals of the real world by playing the tradeoff game differently. Thus, the different modeling paradigms, while seeming to be contradictory, may indeed be complementary.

Potential Synergy Between Modeling Approaches

We present an example in childhood obesity research to illustrate the synergy that could be generated by taking advantage of the respective strengths in statistical modeling and ABM. As a social epidemic, childhood obesity is one of the most challenging public health issues that many countries currently face. A growing literature is pointing to treating childhood obesity as a systems problem that requires the study of multiple chains of causal influences including dynamic processes affecting the energy balance in a child within specific populations and environments including schools and communities (Hammond, 2009; Huang, Drewnowski, Kumanyika, & Glass, 2009; Huang & Glass, 2008). The Envision Network (www.nccor.org/envision) is a federally funded professional network comprising 11 research teams addressing various obesity questions with mathematical/computational modeling, including ABM, micro-simulation, system dynamics modeling, and statistical modeling projects. An aim of Envision is to support integrated modeling efforts between statistical and systems science teams in order to gain insight into the most effective ways of preventing childhood obesity.

An initial barrier of integrating systems approaches and statistical modeling for studying childhood obesity is the lack of a common language among the network researchers, as well as a lack of a common way of conceptualizing research questions and strategies for addressing them. The Levins framework served as an important starting point for bridging across these divides. Discussion of the relative strengths of statistical modeling and ABM led to a panel discussion at the 2013 International Conference on Social Computing, Behavioral-Cultural Modeling and Prediction (Mabry, Hammond, Huang, & Ip, 2011).

Several forms of interaction between the two broad classes of modeling strategies were identified: (1) statistical modeling results as input to ABMs, (2) use of statistical methods for evaluating output from ABMs, (3) ABM outputs (including hypotheses generated) as input to statistical modeling and methods, (4) ABM for evaluating statistical results, and (5) joint applications of ABM and statistical modeling as comparative studies to examine the same problem from different perspectives. Table 2 summarizes a sample of possible interactions for (1) to (4). Although space does not permit us to elaborate on all the activities listed in Table 2, we highlight two interactions as examples. The first example refers to ways of using ABM to explore micro-foundations that underlie empirical patterns (Cell (3)a in Table 2). It is possible to use ABMs to generate social phenomena such as the emergence of political actors (Axelrod, 1995) and the dynamics of retirement (Axtell & Epstein, 1999). In such cases, ABMs are used as computational exploratory tools to generate theory. Based on new conjectures developed from ABM, statistical models can then be applied to existing data or the new theories can be used to guide data collection for subsequent formal statistical testing. Statistical models can also contribute to ABM for example in simulation of agents through its deep roots in the study of diverse distribution types (Cell (1)d). Distributional assumptions can make or break the performance of an ABM in terms of qualitative reality. For example, in simulating firm formation in the U.S. economy, firm sizes and firm growth rates were set up to follow specific observed distributions (Axtell, 1999).

Table 2.

Interaction Between Statistical Modeling (SM) and Agent-Based Modeling (ABM).

Possible Synergistic Activity	(1) SM to ABM Input	(2) SM to ABM Output	(3) ABM to SM Input	(4) ABM to SM Output
a	Explore potential mechanism by fitting models to data	Assess goodness-of-fit of ABM to real data	Explore micro-foundations that underlie empirical patterns	Assess generative sufficiency
b	Provide effect strength in the form of estimated input parameters	Provide tools for assessing theory for long-term behavior in simplified models	Prioritize data gap—that is, identify “weak spots” within a system where new data are needed	Test statistical tools as in virtual epidemics
c	Identify relevant factors for inclusion in ABM through statistical variable selection	Provide techniques in exploratory data analysis for seeking unexpected patterns	Create synthetic data for testing robustness of statistical model for alternative data sets	Visualize statistical results, especially long-term dynamics
d	Provide advanced simulation techniques of high- dimensional numerical data such as Bayesian method and Markov chain Monte Carlo	Provide formal measure of uncertainty (e.g., confidence bands) on plausible outcomes	Integrate data from different sources	Provide retrodiction— that is, use current models to infer/ explain past phenomena

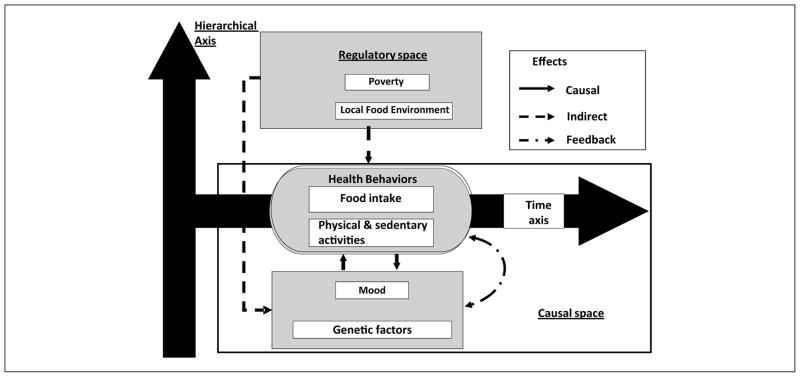
As an example for joint application of ABM and statistical modeling (5), we highlight a statistical modeling endeavor within the Envision Network and a potential comparative study using ABM. The statistical modeling approach, the Dynamic Multi-chain Graphical Model (DMGM; Ip, Zhang, Lu, Mabry, & Dube, 2013; Ip, Zhang, & Williamson, 2012; Ip, Zhang, Schwarz, et al., in press), is an attempt to operationalize a highly general model—the multilevel ecologic model conceptualized in Glass and McAtee (2006). The multilevel ecologic model can be envisioned as a system that contains two primary axes: time (as the horizontal axis) and multiple levels of subsystems from genes, to organs, behavior, social networks, and communities (as the vertical axis). Within the context of childhood obesity, the ecologic-conceptual model would capture both temporal influences on body weight during the life course of the child, as well as changes in his/her behavior as influenced by the multiple levels of proximal and distal risk factors. Almost as a direct mapping exercise of Glass and McAtee’s conceptual model to an empirically falsifiable mathematical model, the DMGM separates direct (causal) risk behavior for obesity (e.g., sedentary lifestyle) and stable but distal contextual risk regulators (e.g., environmental factors such as the density of fast food restaurants in the neighborhood) as two distinct constructs. An analytic tool—the dynamic Bayesian network (Ghahramani, 1997)—is then used to model direct temporal and causal mechanisms within what is termed a causal space, whereas generalized linear-mixed models are used to capture stable but distal risk factors within another space of interest, which is termed a regulatory space. Figure 1 graphically depicts the two spaces and some relevant variables. One can think of parameters for the regulatory space as “knobs” for tuning assumptions about the environment, which up- or downregulate the probability of specific obesity-related behaviors.

Figure 1.

Operationalizing the socioecological model in Glass and McAtee (2006) for the LA Health Study.

Data from an intervention study, the Louisiana Health Study (LA Health Study; Williamson et al., 2008) were used to provide numeric estimates of model parameters. The LA Health Study was a randomized clinical trial that enrolled N = 2,201 school students across 17 rural school clusters in the state of Louisiana. The school- and community-based intervention program consisted of modification of environmental cues, enhancement of social support, promotion of self-efficacy for health behavior change, and an Internet-based educational program reinforced with classroom instruction and counseling via email. Data from the original study, which included measures of psychosocial status, dietary composition, and sedentary and physical activities over time, were enhanced by environmental data collected at a later time point through secondary sources such as Google Maps and census tract–level data. The statistical modeling efforts yielded a set of model-parameter estimates and their associated uncertainties, as indicated by the confidence intervals of the estimates (Ip et al., 2012). Techniques for fitting this model and other similar models can be found elsewhere (Altman, 2007; Ip, Snow-Jones, Heckert, Zhang, & Gondolf, 2010; Ip, Zhang, Rejeski, Harris, & Kritchevsky, in press; Ip, Zhang, Schwarz, et al., in press; Shirley, Small, Lynch, Maisto, & Oslin, 2010; Zhang, Snow Jones, Rijmen, & Ip, 2010).

The instantiated, application-specific DMGM could not achieve much along the generality desiderata. Although high on the precision and fit scales, the DMGM has a moderate level of realism. While the temporal and causal mechanisms of the socioecological concept can be captured with reasonable assumptions (e.g., the Markov assumption), one important deficit of the model in realism is the lack of social network input and potential feedback mechanisms. By assuming individuals behave independently instead of as a unit within a social network, as most statistical models do, the DMGM lacks input in interactions between student–student, student–teacher, and parent–student. It also lacks the capacity to model the reciprocal effects (feedback) between psychosocial factors and behaviors related to energy intake and expenditure.

Systems science methods such as ABM and social network analysis (Wasserman & Faust, 1994) have the potential to enhance statistical models in realism and generality. Just designing an ABM for agents (students) for the above example could literally force statistical modelers to consider the micro-foundations that realistically underlie the dynamics of intervention—how student behaviors could have changed through the influence of fellow students, teachers, and parents. Continuing to use the social network example, one would argue for a “contagion” model for obesity among students, that is, students within a close social network would affect each other’s behaviors and that may lead to obesity “contagion” (Christakis & Fowler, 2007). A potential solution to build in contagion into a statistical model is to employ the following hybrid modeling strategy: (1) conduct a small-scale social network analysis to understand the network structure of students; (2) simulate agents that interact with each other according to the network structure discovered from Step 1, and explore different underlying ABMs (e.g., first-order logic for agent interaction) to mimic the influence of social network on behavior and weight; and (3) construct a formal probabilistic model to refine the contagion model in Step 2.

Discussion

Systems science is a relatively new class of methodologies that could appear to be intimidating to social and behavioral scientists working in the public health field. Because they often have limited exposure to anything other than statistical models that excel along the precision dimension, such as regression and ANOVA, the transition to a broader view of modeling and to a new paradigm of system science thinking will require overcoming some initial barriers. During the Envision meetings, one question that was often directed to ABM researchers was, “Where are the data?” Other frequent questions were “How valid is the model?” or “How do you validate the model?” Although there are some published articles that address these issues (e.g., Caro, Briggs, Siebert, & Kuntz, 2012; Grimm et al., 2010; Rahmandad & Sterman, 2012; Sterman, 1984), our framework perhaps could be an additional way to help people think about models as imperfect representations of the world. The framework could also be used to help convey the point that modelers often have to work under time and resource constraints such that a balance has to be made among generality, realism, fit, and precision for answering the question at hand.

Recently, the choice of computational and statistical models has also attracted much attention in the field of cognition (Pitt, Myung, & Zhang, 2002; Roberts & Pashler, 2000, 2002; Rodgers & Rowe, 2002). Multiple criteria for selecting computational and stochastic models for cognition were discussed, and some of them bear strong resemblance to the generality-realism-fit-precision paradigm, although in the cognition context the term model was used in a more restricted way. Jacobs and Grainger (1994) summarized the criteria for model choice into the following: (1) plausibility (are the assumptions of the model biologically and psychologically plausible?), (2) explanatory adequacy (Is the theoretical explanation reasonable and consistent with what is known?), (3) interpretability (does the model and its parts—e.g., parameters—make sense?), (4) descriptive adequacy (does the model provide a good description of observed data?), (5) generalizability (does the model predict well the characteristics of data that will be observed in the future?), and (6) complexity (does the model capture the phenomenon in the least complex—i.e., simplest—possible manner?). Pitt et al. (2002) argued that computational models usually satisfied the first three criteria during their course of evolution, leaving the latter three to be the primary criteria on which they are evaluated. The first three criteria are components of the concept of internal validity, which are related to qualitative realism in the Levins framework. On the other hand, the latter three criteria can be conveniently—though with imperfection—mapped onto the fit, generality, and precision desiderata of the our framework. Generalizability in Jacobs and Grainger (1994) is related to the property of external validity, which is more restrictive than what the generality desiderata in Levins framework intends to cover. Generalizability concerns whether the model can be applied to data (in a targeted population) other than the sample at hand, or to similar data collected in the future. In contrast, the generality desiderata in Levins framework pertains to a broader schema; here generality refers to the quantity and variety of phenomena a model or set of models successfully relate to (Matthewson & Weisberg, 2009). The reader is encouraged to read other authors who tackle the subject of systems science methodologies as contrasted with statistical ones (Andersen, 1980; Harlow, 2010; Robinson & Levin, 2010; Rodgers, 2010a, 2010b; Weisberg, 2007) and to read elaborations of the Levins framework (Matthewson & Weisberg, 2009).

From a dialectical world view, how we break up a phenomenon into parts, and what features we choose to include and not to include in our model, and what data we choose to use, must be a function of our modeling goals. Reliance on one specific modeling approach is unlikely to accomplish a comprehensive understanding of a phenomenon. A more pragmatic solution for modeling building could be based on a pluralistic modeling strategy. There is already evidence that hybrid modeling strategies are increasingly used. For example, MCMC and Bayesian statistical methods (see Table 2) were used in system dynamics models for exploring model calibration (Vrugt et al., 2009). With a long history of developing sampling theory and constructing precise models, statistics could perhaps benefit from systems science methodology as much as it can contribute to systems science. Encouraging synergistic activities between systems scientists and statisticians is a key to bringing mutual benefits to the stakeholders and accelerating the pace of moving the field of systems science forward.