Review of Thawing Time Prediction Models Depending
on Process Conditions and Product Characteristics

Summary

Determining thawing times of frozen foods is a challenging problem as the thermophysical properties of the product change during thawing. A number of calculation models and solutions have been developed. The proposed solutions range from relatively simple analytical equations based on a number of assumptions to a group of empirical approaches that sometimes require complex calculations. In this paper analytical, empirical and graphical models are presented and critically reviewed. The conditions of solution, limitations and possible applications of the models are discussed. The graphical and semi--graphical models are derived from numerical methods. Using the numerical methods is not always possible as running calculations takes time, whereas the specialized software and equipment are not always cheap. For these reasons, the application of analytical-empirical models is more useful for engineering. It is demonstrated that there is no simple, accurate and feasible analytical method for thawing time prediction. Consequently, simplified methods are needed for thawing time estimation of agricultural and food products. The review reveals the need for further improvement of the existing solutions or development of new ones that will enable accurate determination of thawing time within a wide range of practical conditions of heat transfer during processing.

Introduction

A growing and wide range of foodstuffs is frozen in order to be further processed or used after thawing. In the modern industrial practice food produce are frozen to stabilize the original quality, and also in case of excessive supply or when they have to be shipped over long distances. In general, the deep frozen produces are thawed and later processed into a large array of products ready for consumption. The knowledge of thawing time is essential for the optimization of existing processes but also for the development of new products and new types of equipment. Precisely determined thawing time enables the improvement of raw material quality through the reduction of drip loss or tissue dehydration, prevention of undesired enzymatic and non-enzymatic processes and, notably, contribution to reduced energy input. Therefore, it is crucial to develop appropriate mathematical solutions for the estimation of thawing time of food materials, especially equations that take into account the complex technological conditions of the processes. Despite the increasing knowledge and understanding of the thawing process and many existing theoretical and analytical models, there is no single and fully universal analytical equation available; in addition, all these models must be used in conjunction with data provided for specific limitations and simplifications. The application of artificial neural networks (ANN), or the tools for modelling complex systems offer basically a solution to the problem. The problem with these systems however is that they require considerable sets of test and experimental data that have to be used for training of the networks and the verification of the results (1). Computer-based and -assisted problem solving still involves the use of analytical models based on the laws of physics, empirical models based on the results of test measurements and graphical models developed through numerical simulation of the wide range of thawing operations performed on given food types. This study aims to characterize the applicability and a possible utilization of selected models of food thawing time calculations under industrial conditions.

Analytical and Analytical-Empirical Models

In most freezing and thawing processes of food products, changes in material water content induced by heat (mass) exchange are considered minor and may be omitted. Thus, heat exchange during freezing, thawing and chilling generally consists in heat conduction within a product associated with convection and radiation occurring between the object and ambient environment. The temperature gradient T in a function of time τ and displacements in the coordinate system x, y and z characterize heat conduction that within the food volume can be described by the Fourier equation as below (2):

where q is internal heat source, e.g. respiration heat (in W/kg), and x, y and z are coordinates of the system (m).

If heat conductivity k of food is constant, the above equation can be written as follows:

where:

is thermal diffusivity.

In order to obtain a solution to a differential equation of transient heat conduction in solids, the conditions for uniqueness of the solutions need to be specified. The conditions comprise initial and boundary ones. The initial conditions describe temperature distribution at the start moment of the process, whereas boundary conditions characterize heat exchange at the outer surfaces of the product.

As for freezing/thawing process, the initial condition is the uniform temperature within the whole volume of the object (2):

while the boundary conditions are as follows: Dirichlet boundary condition of the first type is assumed if the entire boundary (x=0) or its part has a prescribed temperature:

Neumann boundary condition of the second type is assumed when a function defining heat flow density at the boundary is specified:

Fourier boundary condition of the third type based on the balance of heat flow intensity through the boundary is assumed when conduction heat flux through the boundary is equal to the convection one:

With reference to the boundary and initial conditions, the solution of the above equation of transient heat exchange is available, as well as complete description of heat exchange during freezing or thawing.

To describe the course of freezing and thawing, the following two physical models are commonly used: the model of continuous change of properties k(T) and c_p(T), and the model of mobile phase transition front, so-called ice front model. The second model is based on a concept of the movement of phase transition boundary with concurrent change of thermophysical properties and release of whole latent heat of freezing. The boundary is always at cryoscopic temperature. Specification of the boundary movement in the case of one dimensional heat exchange takes the following form (3):

where x_f is the distance from the surface to the phase change front (in m).

Freezing and thawing description necessitates precise values of thermophysical properties of food. The most essential are heat conductivity k, density ρ, specific heat c_p, enthalpy H, latent heat of freezing L_f and initial cryoscopic temperature T_cr. As thermophysical property values are not constant and are primarily the function of material temperature, it is imperative that these properties are studied separately at each stage of material freezing and thawing process. Besides, the effect of phase transition of water to ice or vice versa should be taken into account (3).

The most widely known and used solution is the Plank’s model developed for food freezing time prediction and adapted for thawing (4). The Plank’s equation was derived from the basic laws of heat transfer and it serves as the basis for a number of solutions to the problem of freezing and thawing time calculations (5, 6). The basic equation for the model adapted to estimate food thawing time is as follows:

In the first version, the shape factors P and R were calculated from equations provided by the author. In a later publication (6), Plank’s equation was used to define the shape factors, where P and R are equal to 1 and 1/2 for one-side-heated infinite slab, 1/2 and 1/8 for two-side- -heated infinite slab, 1/4 and 1/16 for infinite cylinder, and 1/6 and 1/24 for sphere. For practical reasons Eq. 9 can also be presented in dimensionless form.

The shape factor values were derived by Plank (4) from the ratio A·d/2V, i.e. 6, 3 and 2 for slab, cylinder and sphere, respectively, according to the shape of the frozen product. The shape factors can be applied if and only if the frozen product surface is isothermal during the process, irrespective of its position.

During the thawing of biological material, this condition is met when the thawed portion of the product has the same geometrical shape as the part which is still frozen. Since Eq. 9 takes into account only latent heat of thawing, the estimated thawing time values tend to be lower than the real thawing times. Because of this deficiency, the general agreement is that Eq. 9 should not be applied, as depending on the situation, the thawing times calculated by this equation may be up to 30% shorter than the actual values (3, 7). To correct the deficiencies, modifications have been suggested through the adjustment of the equation to specific cases or thawing conditions. Since the heat transfer from air to the product surface during thawing is characterized by high Biot numbers (Bi>>1), Pham (8) proposed to simplify the Plank’s equation:

where E is the shape factor (1 for slab, 2 for cylinder and 3 for sphere).

When the heat transfer situation is characterized by the heat conductivity of the thawed material (Bi<<1), the equation takes the form:

The standard Plank’s solution was repeatedly written in a dimensionless form. To allow for thawing time estimation of irregularly shaped products, empirical equations have been recommended (6).

Like very few other analytical models, Konchakov’s model (9), as a purely analytical solution, considers the thawing of a slab-shaped product. The development of this model involved the third type boundary condition and assumed that thawing comprises two stages: the heating of a frozen product until it reaches the cryoscopic temperature at the surface, and thawing that lasts until the whole product is thawed. Meat isotropy was also assumed, as well as a constant ambient temperature and a heat transfer controlled by the surface heat transfer coefficient. The final equation acquires the form:

with:

An advantage of this solution, in contrast to other purely theoretical analytical models that require the knowledge of hard-to-measure thermophysical product properties, is its practical applicability for the evaluation of the thawing process of meat in air during natural convection. The thawing time for half carcass, including heating of the product up to 1 °C, can be calculated by multiplying the equation by the shape factor of 0.57 and by the coefficient of 1.3. According to Konchakov (9) the prediction accuracy of beef half carcass thawing time was ±5% compared with the experimental data.

Another approach based on the third kind boundary conditions is a model by Nagaoka et al. (10). The authors aimed to improve the accuracy of thawing time estimation by inserting into the Plank’s equation (Eq. 9) the dependencies on the initial and final heating of the product. According to the authors, the P and R shape factors can be calculated from the equation presented by Plank (4):

The model was proposed for estimating the thawing time of fish. Nagaoka et al. (10) pointed to the fact that there are no considerable differences between the general thermophysical properties of fish and other food products of similar fat contents; therefore, the equation can also be applied to predict thawing time of other food material.

Piotrowicz (11) used a different approach to the Tchigeov’s model (12). The basic equation of the Tchigeov’s model comprises an addition that accounts for the heat accumulated by the thawed material layer:

Eq. 16 also accounts for a number of simplifying assumptions, e.g. omitting the initial thawing time and assuming that the thawing ends when the central part of the product reaches the cryoscopic temperature and, finally, that the thermophysical properties of the product are not temperature-dependent.

Kluza and Góral (13) presented a model that allows to calculate the time to reach a given product temperature of an originally frozen product on the basis of the thawing time and the time to reach the pre-set temperature, Eqs. 17–20:

where t_F corresponds to a characteristic freezing temperature at which 70% of water content of the product is frozen. Temperature t_F was given by Kluza et al. (14, 15) who provided it by means of the modified Riedel’s equation (16) as follows:

By the use of t_F instead of the cryoscopic temperature major errors related to the inconsistencies in estimating the thawing temperature of individual products are avoided. The equation used for the calculation of the thawing time was based on the modified standard Plank’s equation:

It is recommended by the authors that the time of the third stage, the heating of the product to a pre-set temperature required for technological purposes, be based on the equation:

The entire process time can be calculated by the following equation:

where C is volumetric heat capacity, B and D are simplices of temperature, and ε is the function of the Biot number.

To respond to the needs of food industry, in the years 1965–79, a number of analytical models were proposed for calculation of thawing times for individual types of food. An analytical solution to estimate thawing time of fish immersed in water was discussed by Usvijat et al. (17). Similar to the model proposed by Nagaoka et al. (10), the model considers a heating phase from the initial product temperature t_a to the cryoscopic temperature t_cr:

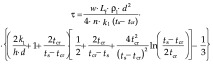The mass fraction of frozen out water can be estimated by the following equation:

It is assumed in the model that the shape of fish is an infinite cylinder. Deviations from the real time were adjusted empirically by means of the coefficient n introduced into the formula. The coefficient n was derived from 200 experimental industrial thawing operations in fish processing plant in Sukhumi, Georgia with various types of fish (17). The values of the coefficient depend on the size of fish (d/n=0.05/2.3, 0.06/1.9, 0.07/1.6, 0.08/1.4, 0.09/1.5, 0.10/1.7 and 0.11/1.9).

Another example of a specialized model is the equation to predict thawing times of lamb shoulders, proposed by Vanichseni et al. (18). It is assumed that the shoulder is an equivalent of a parallelepiped with the dimensions d×2d×2.5d. The characteristic dimension is derived from a regression analysis of the relation d vs. the mass m of the carcass:

Vanichseni et al. (18) provide two adapted modifications of the Plank’s equation (Eq. 9) to estimate the thawing time of shoulders immersed in water, Eq. 25, and a simplified Eq. 26:

The extensions in both above equations consider a heating phase from the initial product temperature t_a to the cryoscopic temperature t_cr, introducing the correction factor (1.1–1.2) depending on the product and the change of the product enthalpy ΔH between the initial and final temperature of its centre, instead of latent heat of thawing L_f.

Due to the difficulties in presenting an accurate analytical solution to predict thawing time of frozen materials, more advanced and more universal analytical-empirical models were developed in the late 1970s. Among them, the model of Cleland et al. (6, 19) is one the best known. The authors modified the Plank’s equation using the Stefan and Plank numbers:

where:

With the empirical shape factors P₁ and R₁ (Eqs. 28 and 29) and the equivalent heat transfer dimensionality (EHTD), the following equations were obtained:

Eq. 27 was developed to calculate the thawing time of any food product of regular shape. Attempts to improve the accuracy of this equation through the introduction of Eqs. 28 and 29 by Cleland et al. (19), using regression equations were not really successful; the discrepancies between the calculated and the actual thawing times were still significant.

The first mainly empirical solution that allows quite an accurate calculation of thawing time for a number of food materials is the model by Calvelo (20). The formula was expressed in dimensionless terms by Cleland et al. (19):

The only deficiency of Eq. 33 is that it yields slight error in case of slow thawing processes up to product temperatures of 0 °C. This equation was also used by other authors to develop the empirical solutions for thawing time predictions (5, 21–27).

Pham (28) proposed an analytical-empirical approach that is characterized by the absence of any numeric constants:

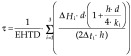where:

and

Eq. 34 accounts separately for the three thawing phases similarly to the model proposed by Kluza and Góral (13), an approach which is very helpful with respect to hygienic requirements where the knowledge of individual heating times is being asked for. Furthermore, the method allows to calculate and model the individual heat loads transferred to the product at each processing phase. A major drawback of the model is certainly the large number of dependencies, which, consequently, reduces the possibility of fast calculations of thawing time.

According to Cleland (6), Eq. 34 is only applicable provided the following conditions are maintained: 0.6<Bi<57.3, 0.085<Ste<0.768, and 0.065<Pk<0.272.

Cleland et al. (21, 22, 24) modified the Calvelo (20) equation into a dimensionless form for infinite slabs, among others, by correcting some values and coefficients based on experimental evidence, and by using the statistical analysis method:

The explicit thawing time has to be derived from the Fourier number Fo. In the case of shapes other than a slab, shape factors have to be introduced:

where G_1,2,3 are geometric constants, and E_1,2 and M_1,2,3 are variables used for shape coefficient estimation.

The coefficients EHTD and mean conducting path (MCP) were derived from nonlinear regression analyses for the numerical results of thawing time calculations realized according to the model systems (6).

Mathematically, the shape factor presented in the work of Hossain et al. (25–27) is inconvenient to use. In a different approach the authors introduced shape factor E, based on the laws of heat transfer, that can be inserted in Eq. 46. In the case of a parallelepiped with the dimensions d×β₁d× β₂d, the factor can be derived from the equation:

The coefficient E, which is more accurate than the factors used previously, allows for more correct calculations of thawing times. However, because of the need to use the Bessel functions and tables to determine the variables z_n, z_m and z_nm as a function of the Bi number, the inclusion of Eq. 49 into the models for fast calculations of the thawing time is somehow inconvenient. In order to simplify the situation, Hossain et al. (25–27) proposed the introduction of a coefficient E_AS instead of the coefficient E. The coefficient E_AS can be calculated as follows for a parallelepiped--shaped product with the dimensions d×2β₁d×2β₂d:

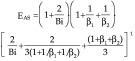Eq. 50 can only be applied for Biot numbers smaller than 0.16 (25).

As in the work of Góral and Kluza (7), results of investigations on thawing time (211 experiments) of a wide range of regularly shaped foods were analyzed. Taking into account availability of reliable experimental data and complete characteristics of thawing parameters, the data were taken from Cleland et al. (29) and Ilicali (30). The calculations were performed based on the following analytical--empirical models: Cleland et al. (19) (Eq. 27), Piotrowicz (11) (Eq. 16), Calvelo (20) (Eq. 46), Nagaoka et al. (10) (Eq. 14) and Pham (28) (Eq. 34). The results including the statistical evaluation of relative error of thawing time prediction were analyzed using StatGraphics packet (31) (Table 1).

Table 1. Relative error of thawing time calculations.

	Cleland et al. (19)	Piotrowicz (11)	Calvelo (20)	Nagaoka et al. (10)	Pham (28)
N(sample) Mean/% Variance/% Minimum/% Maximum/% Error range/%	211 3.82 97.59 –44.02 24.85 68.87	211 26.58 833.81 –11.31 252.10 263.42	211 40.78 309.69 –43.68 69.76 113.44	211 73.62 1688.72 7.52 179.67 172.15	211 17.47 441.54 –22.62 65.67 88.29

The examination of relative error of calculations leads to the conclusion that the statistically best results were obtained according to the model of Cleland et al. (19). The mean values and the range of minimum and maximum errors confirm this. However, the model of Nagaoka et al. (10) produced the results that highly differed from others.

All calculation results were subjected to the analysis of variance in order to point out the prediction models that give the best approximation to the real thawing times (Table 2). Test of equality of experimental and analytical mean values for 95% confidence interval led to rejection of the models of Piotrowicz (11), Calvelo (20) and Nagaoka et al. (10) because of statistically significant differences of the mean values.

Table 2. Variance analysis of experimental thawing time vs. times calculated according to different models.

	Experimental thawing time/min	Cleland et al. (19)	Piotrowicz (11)	Calvelo (20)	Nagaoka et al. (10)	Pham (28)
N(sample) Mean/min Variance/min Difference mean/min Variance ratio Mean equality for 95% confidential interval	211 6.43 33.2	211 6.75 37.43 –0.32 0.89 yes	211 8.73 76.75 –2.30 0.43 no	211 9.35 77.35 –2.93 0.43 no	211 12.59 181.92 –6.17 0.18 no	211 7.62 57.02 –1.20 0.58 yes

Graphical and Semi-graphical Models

Analytical and empirical solutions are practicable and relatively accurate in the situations when a heat transfer coefficient h and ambient temperature T_a are constant and there is no heat generation (internal heat sources) in the object (e.g. respiration heat of some biological material). Modelling of a process based on the thermophysical properties of the product needs implementation of numerical methods. Numerical solutions to the problem are based on Fourier’s equation (Eq. 1). Several numerical methods are grounded on breaking this equation into two parts, each linked with a different coordinate system. In the heat flow problems (considering only diffusion part), the space and time coordinates are discretized (8, 32). In that case finite difference schemes are used and the Crank- -Nicolson and Euler methods are employed most frequently (33). The Crank-Nicolson scheme does not enforce additional constraints with respect to time and space because of the midpoint method applied (central difference approximation):

The second space derivative is defined at the intermediate point that enables approximations averaging at the beginning (τⁱ) and the end (τⁱ⁺¹) of the time interval and, consequently, provides far higher accuracy than other methods:

and

It is required that mathematical approximations are centrally symmetric in both time and space. Combining these approximations means that difference equations can be written for any space node in the grid and that, in turn, facilitates prediction of complete temperature history in time in all the nodes (8, 32). In the finite element method (FEM), the domain of interest is gridded into a certain finite number of geometrically simple subdomains called finite elements. It is assumed that elements are interconnected at the finite number of points at their perimeters, most often these are placed at each element’s apices (nodes). The temperature values at each node make a parameter that should be essentially established. A temperature is approximated within each element by a function (polynomial) that is determined via nodal temperature values. The function is defined so that temperature continuity on element boundaries is preserved, while nodal temperature values ensure the optimal approximation for the actual temperature field. This is achieved by means of minimization of the functional (functional is a function from a vector space into its underlying scalar field, or a set of functions of the real numbers) corresponding to the differential equation of heat conduction (Fourier’s equation). The minimization process can be performed through direct minimization technique as well as be based on the necessary condition for extremum of a function. In the latter case, determination of nodal temperature values should be made using a set of algebraic equations. A number of equations in the set is equal to the number of nodes multiplied by the number of degrees-of-freedom at nodes, i.e. the number of unknown nodal temperature values. The next step is to insert the boundary conditions to the set of equations through the appropriate modifications of coefficient matrix of the equation set and the right-hand-side vector. Finally, the set of equations is solved and the nodal temperature values searched for are obtained (34, 35).

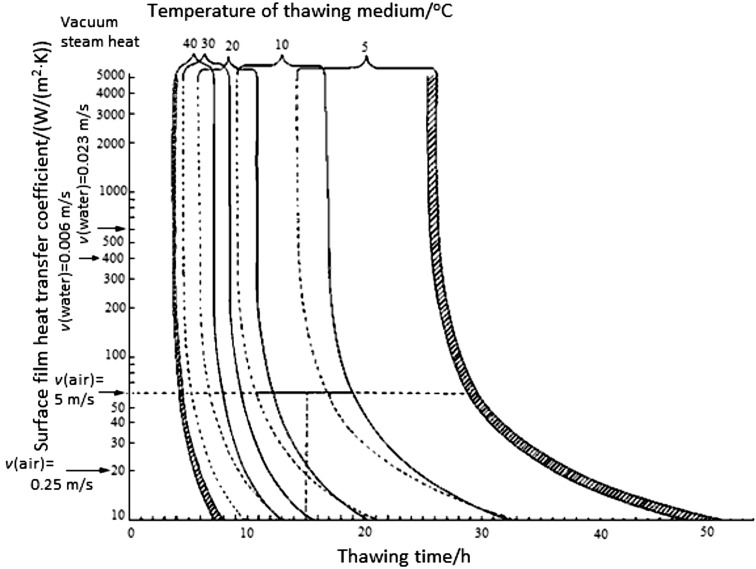
Besides the analytical-empirical models, a number of graphical solutions have been developed to estimate thawing times of biological materials. Bailey et al. (36, 37) proposed a model based on a numerical solution. To obtain the graphical solution for estimating the thawing time for pork legs, the authors (36, 37) conducted the numerical analysis (according to Dusinberre’s method) of the one-dimensional heat transfer for a sphere. The obtained chart allows predicting thawing times of pork legs to a temperature range between –30 and 0 °C when the convection heat transfer coefficient h follows the condition 10<h<5000 W/(m²·K), and the ambient temperature rises to 5, 10, 20, 30 or 40 °C (Fig. 1). The authors report that the error of this procedure was between 0.02 to 0.35%. The largest error occurred with low convection heat transfer coefficient and low thawing temperatures.

Fig. 1.

Thawing time prediction chart according to the model of Bailey and James (36) for 3-kg pork leg from –30 to 0 °C, 6-kg leg from –30 to 0 °C and thawing from –10 to 0 °C. Shaded area shows reduction in thawing time at initial temperature of –10 °C under the fastest and slowest thawing conditions

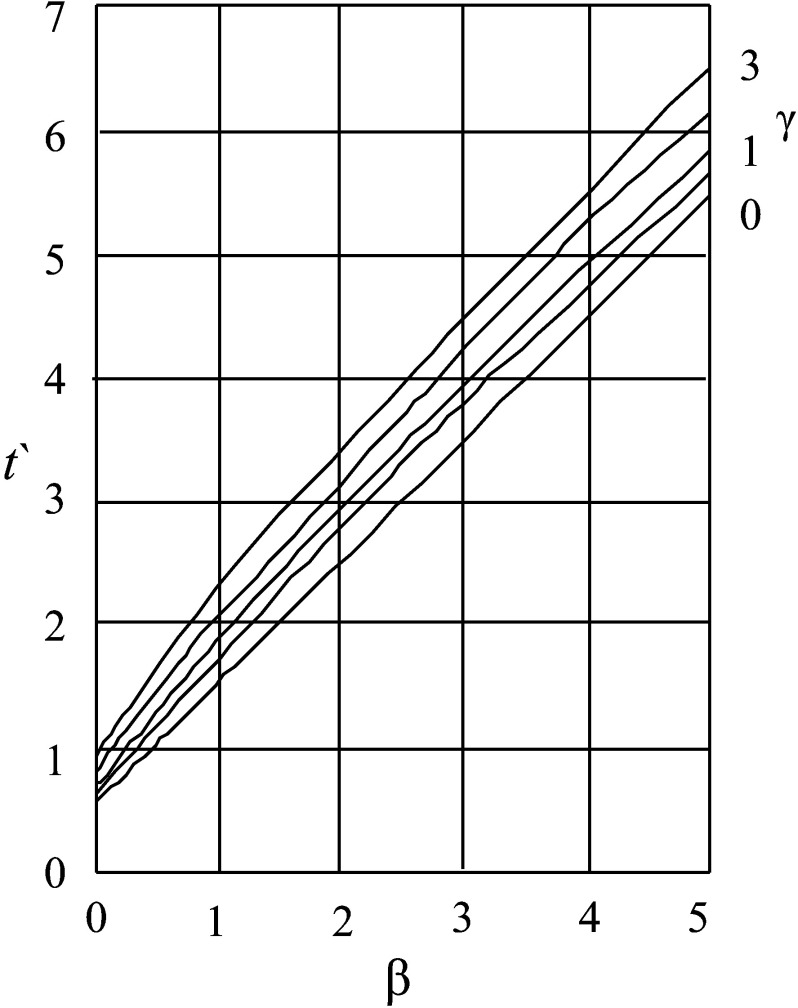
A similar model was proposed by Tao (38). The author developed a chart to analyze thawing time of products shaped as plate, cylinder or sphere. The chart was derived from the numerical solution of the dissolved Fourier’s equation:

The t’ value has to be read from the chart (Fig. 2; 39) using the variables β and γ (Eqs. 55 and 56), characteristic for each product:

Fig. 2.

Exemplary chart of Tao method for thawing time prediction of infinite slab. β and γ=dimensionless variables (39)

The model suggested by Tao (38) is based on the simplified assumptions that thawing time can only be determined for three simple geometric shapes (infinite slab, infinite cylinder or sphere); that the temperature of the ambient heat source does not change over time; and that the thawing process starts from the cryoscopic temperature of the product to be thawed.

Salvadori and Mascheroni (40, 41) proposed a method of calculating thawing times of food products exposed to a wide range of processing conditions commonly used in the food industry. The graphical solution is based on the relationship between the changing central product temperature and one-dimensional variable X. The basic equation in this model is as follows:

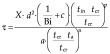and the values of n, p and c coefficients are given in Table 3, besides the product shape, for the basic conditions of the process.

Table 3. Values of n, p and c coefficients in the model of Salvadori and Mascheroni (40).

Shape	Thawing conditions				Coefficients
	Temperature/°C		Biot number		n	p	c
	initial	ambient
Slab Cylinder Sphere	–10 to –31 –10 to –35 –10 to –35	5–35 5–45 5–45	1–151 1–44 1–44		0.74 0.74 0.715	0.03 0.05 0.03	0.45 0.47 0.45

The model by Salvadori and Mascheroni (40, 41) was developed to predict thawing times of food materials with a high water content. Its great advantage is that in order to perform the calculations, it requires only the thermophysical properties of a product in the unfrozen state, which markedly reduces the number of needed data.

In the former Soviet Union, many simple solutions to estimate thawing times for fish were developed (42–45). One of the most common solutions presented by Stefanovski and Chomczenko (43–45) is based on a nomogram developed for a fast estimation of thawing times of fish under the conditions of vacuum pressure-assisted thawing and/or thawing in convectional water. The method requires only the knowledge of fish body mass, ambient temperature of water and the initial temperature of a product. A major advantage of the nomogram used in this model is the possibility to compare the high pressure thawing process with the traditional thawing process in water.

The graphical and semi-graphical methods are derived from numerical methods. It should be mentioned at this point that besides the models reviewed in this work, there are several other similar methods for thawing time estimation (46–48). These solutions have been developed for special situations and they are usually appropriate and accurate for only one selected product or its shape, which limits the scope of their use.

Conclusions

Most of the presented analytical-empirical models are derived from the original Plank’s equation, which is based on the principle laws of heat transfer under the conditions of the freezing/thawing process. All numerical solutions for the estimation of thawing times have a reduced range of applicability because of the complexity of the process.

To allow for standardized calculations, different types of shape coefficients are used. The most common coefficients, P and R, which were introduced by Plank, were derived from the ratio of volume to area of objects subjected to the freezing process. The A·d/2V ratio is accurate for all the shapes if the Biot number approaches zero. In the case of large Bi numbers, a good and simple shape factor does not exist. Substitution of complex geometric shapes of products with a sphere or slab of the same characteristic dimension is limited due to impossibility to determine an appropriate correlation without experimental studies. A known coefficient EHTD is valid for Bi→0, similar to the MCP coefficient developed by Pham. However, these coefficients imply systematic errors because they depend on environmental conditions. Furthermore, it is difficult to use the mathematically complex coefficient E, especially under production conditions.

Another source of inaccuracy is that analytical models consider thermophysical properties of products as constant, without considering their changes with the changing temperatures. In the models, the initial cryoscopic temperature of thawing corresponds to the cryoscopic temperature of the freezing of product in question, which is not correct.

Graphical methods are time-consuming and prone to errors caused by inaccurate reading of charts, and they prevent the automatic calculations by computer software.

Numerical methods predict thawing time more accurately; however, they require the control of numerical error, which depends on parameters like size of grid, change in boundary conditions and material properties, time step, etc. Another problem with numerical methods, in the case of thawing analysis, is the necessity to provide precise data on physicochemical properties of a product, which may be challenging because of its anisotropy and lack of homogeneity. A number of commercial programs based on numerical methods do not do reasonably well because of temperature-dependent product properties. On the other hand, analytical methods are encumbered with numerical error. In this case, however, a far more serious error may be committed at the stage of problem formulation.

Furthermore, using the numerical methods is not always possible as running calculations takes time, whereas the specialized software and equipment are not always cheap. For these reasons, the application of analytical-empirical models is more useful for engineering. The review has demonstrated that there is no simple, accurate and feasible analytical method for thawing time prediction, and its derivation takes into account the third kind boundary condition. Consequently, simplified methods are needed for thawing time estimation of agricultural and food products.

Nomenclature

α

thermal diffusivity, m²/s

A

surface area of food item, m²

B, D

simplices of temperature (Eq. 21)

Bi

Biot number,

C

volumetric heat capacity, J/(m³·K)

c_p

specific heat of food, J/(kg·K)

d

characteristic dimension, m

Fo

Fourier number,

G

constant for calculation of EHTD and MCP

h

heat transfer coefficient, W/(m²·K)

H and ΔH

enthalpy and enthalpy change, J/m³

k

thermal conductivity, W/(m·K)

L_f

latent heat of freezing, J/kg

m

mass of the carcass, kg

M

variables used for shape coefficient estimation

n

coefficient depending on the size of fish (Eq. 22)

n, p, c

coefficients from Table 3

Glossary

P, R, EHTD, E, MCP

shape factors

Pk

Plank number,

Q

heat, J/kg

q

internal heat source, J/kg

Ste

Stefan number,

t

temperature, °C

T

temperature, K

t’

value from the chart (Fig. 2)

Glossary

v

characteristic velocity, m/s

V

volume, m³

w

freezable water content, %

W

water content of meat (Eq. 13), %

W₁, W₂

functions depending on the Biot number 
 (Eqs. 31 and 32)

X

one-dimensional variable (Eq. 57)

x, y, z

coordinates of system, m

z

function of the Biot number

β, β₁, β₂

ratio of dimension to characteristic dimension

ρ

density, kg/m³

γ

value characteristic for a product

ε

function of the Biot number (Eq. 21)

τ

time, s

Subscripts

a

ambient

ave

average

c

thermal centre, end of process

cr

cryoscopic

fr

frozen

in

initial state

l

unfrozen

s

surface

slab

value for slab