Effect of Host Species on Topography of the Fitness Landscape for a Plant RNA Virus

ABSTRACT

Adaptive fitness landscapes are a fundamental concept in evolutionary biology that relate the genotypes of individuals to their fitness. In the end, the evolutionary fate of evolving populations depends on the topography of the landscape, that is, the numbers of accessible mutational pathways and possible fitness peaks (i.e., adaptive solutions). For a long time, fitness landscapes were only theoretical constructions due to a lack of precise information on the mapping between genotypes and phenotypes. In recent years, however, efforts have been devoted to characterizing the properties of empirical fitness landscapes for individual proteins or for microbes adapting to artificial environments. In a previous study, we characterized the properties of the empirical fitness landscape defined by the first five mutations fixed during adaptation of tobacco etch potyvirus (TEV) to a new experimental host, Arabidopsis thaliana. Here we evaluate the topography of this landscape in the ancestral host Nicotiana tabacum. By comparing the topographies of the landscapes for the two hosts, we found that some features remained similar, such as the existence of fitness holes and the prevalence of epistasis, including cases of sign and reciprocal sign epistasis that created rugged, uncorrelated, and highly random topographies. However, we also observed significant differences in the fine-grained details between the two landscapes due to changes in the fitness and epistatic interactions of some genotypes. Our results support the idea that not only fitness tradeoffs between hosts but also topographical incongruences among fitness landscapes in alternative hosts may contribute to virus specialization.

IMPORTANCE Despite its importance for understanding virus evolutionary dynamics, very little is known about the topography of virus adaptive fitness landscapes, and even less is known about the effects that different host species and environmental conditions may have on this topography. To bridge this gap, we evaluated the topography of a small fitness landscape formed by all genotypes that result from every possible combination of the first five mutations fixed during adaptation of TEV to the novel host A. thaliana. To assess the effect that host species may have on this topography, we evaluated the fitness of every genotype in both the ancestral and novel hosts. We found that both landscapes share some macroscopic properties, such as the existence of holes and being highly rugged and uncorrelated, yet they differ in microscopic details due to changes in the magnitude and sign of fitness and epistatic effects.

INTRODUCTION

The effects of mutations can be influenced by their interactions with other mutations, with the environment, or both. Epistatic interactions among genetic loci determine the ruggedness of fitness landscapes. In the absence of epistasis, landscapes are single peaked and smooth (1). For such simple landscapes, predicting the result of evolution is an easy task. In contrast, epistatic interactions create curvature in the landscape, and if they are of the sign or reciprocal sign type, they create multiple peaks separated by low-fitness valleys (1–3). The reproducibility of evolution in such complex landscapes, and therefore our ability to predict its outcome, diminishes as the number of possible peaks, that is, the ruggedness of the landscape, increases. Therefore, epistasis strongly determines the pace, reproducibility, and predictability of adaptive walks on fitness landscapes.

Mutations not only interact among themselves in determining fitness but also interact with the external environment, making phenotypes plastic (4, 5). In practical terms, in the case of viruses the environment mostly reduces to the host, although environmental factors, such as temperature, or the presence of other coinfecting viruses or cellular pathogens may affect the replication of viruses as well. Not all potential hosts in the host range (different species or different genotypes of the same species) of a virus are equally susceptible to infection, and it is generally assumed that a tight match may exist between host genotypes and virus genotypes to allow a virus to successfully infect a host (6). Indeed, a substantial amount of data supports the idea that by evolving in a single host species or genotype, viruses become specialists (7–10), whereas by evolving in multiple host species, the result may be no-cost generalists (7, 11–13).

Furthermore, epistasis and phenotypic plasticity mutually interact in a very intricate manner (14–16). The evolutionary consequences of these interactions are important. For example, by changing the pattern of epistasis it is possible to access mutational pathways that may be maladaptive in one environment but not so in another (17–20). Understanding the roles that environmental changes and landscape topology have in the number and nature of adaptive pathways would allow prediction of the potential avenues of future evolution. Despite this importance, how environmental heterogeneity affects the topography of fitness landscapes is still poorly understood, and only a few recent studies have started to tackle this problem, mostly in the context of the evolution of antibiotic resistances (20–23) or during experimental adaptation of Escherichia coli to an artificial glucose-limited environment (24).

The aim of the present study was to explore the effects of environmental changes on the topography of an empirical fitness landscape in a biologically relevant context, namely, an RNA virus and its eukaryotic multicellular hosts. Previously, we constructed the 2⁵ (i.e., 32) genotypes that comprise all possible combinations of the first five mutations (Table 1) fixed by Tobacco etch virus (TEV; genus Potyvirus, family Potyviridae) during experimental evolution in a novel host, Arabidopsis thaliana (25). In previous work, we evaluated the topography of this fitness landscape in the novel host (26), showing that it was rugged and contained holes created by the existence of a lethal genotype. We also showed that higher-order epistasis, that is, interactions between more than pairs of mutations, contributed in a significant manner to the architecture of fitness (26). For the present study, we followed up the previous work by evaluating the fitness of all 32 genotypes in the ancestral host, Nicotiana tabacum. By comparing both fitness landscapes, we found that some features remained similar among hosts, such as the existence of lethal genotypes and the prevalence of epistasis creating a highly rugged topography. However, we also observed significant differences in the fine-grained details between the two landscapes due to host-specific effects on both fitness and epistasis.

TABLE 1.

Set of mutations included in this study

Label	Mutation	Gene	Amino acid changea
●○○○○	U357C	P1	Synonymous
○●○○○	C3140U	P3	A999V
○○●○○	C3629U	6K1	T1162M
○○○●○	C6037U	VPg	L1965F
○○○○●	C6906U	NIaPro	Synonymous

^aNumeration is according to the amino acid residue in the polyprotein.

MATERIALS AND METHODS

Generation of viral genotypes.

All 32 TEV mutant genotypes used in this study were constructed by successive rounds of site-directed mutagenesis starting from the template plasmid pMTEV, which contains a full copy of the genome of a wild-type TEV strain isolated from tobacco (GenBank accession no. DQ986288) (27), using mutagenic primers with specific single-nucleotide mismatches (26) and Phusion high-fidelity DNA polymerase (Finnzymes). The PCR mutagenesis profile consisted of 30 s of denaturation at 98°C followed by 30 cycles of 10 s at 98°C, 30 s at 60°C, and 3 min at 72°C, with a final 10-min elongation at 72°C. Next, the PCR mutagenesis products were incubated with DpnI (Fermentas) for 2 h at 37°C to digest the methylated parental DNA template. E. coli DH5α electrocompetent cells were transformed with 2 μl of reaction product and plated on LB agar plates supplemented with 100 μg/ml ampicillin. Bacterial colonies were inoculated into 8 ml LB-ampicillin liquid medium and grown for 16 h in an orbital shaker (37°C, 225 rpm). Plasmid preparations were done using a Pure Yield plasmid maxiprep system (Promega) following the manufacturer's instructions. Incorporation of each mutation was confirmed by sequencing of a ca. 800-bp fragment circumventing the mutagenized nucleotide. The plasmid DNA was linearized with BglII and in vitro transcribed using an mMessage mMachine SP6 kit (Ambion) in order to obtain infectious RNA of each virus genotype (28).

Plant inoculation.

N. tabacum L. cv. Xanthi NN plants were used for production of a large stock of virus particles for each of the 32 genotypes. Batches of 8-week-old N. tabacum plants were inoculated with 5 μg of RNA of each viral genotype by abrasion of the third true leaf. At 10 days postinoculation (dpi), the whole infected plants were collected and pooled for each virus genotype. Next, plant tissue was frozen with liquid N₂, homogenized using a mortar and pestle, and aliquoted in 1.5-ml tubes. Saps were prepared by adding 1 ml of 50 mM potassium phosphate buffer (pH 8.0) per g of homogenized plant tissue and then centrifuged at 4°C and 10,000 × g for 10 min, and the upper liquid phase was taken and mixed with 10% Carborundum (wt/vol).

The viral stocks were used to mechanically inoculate between 3 and 31 (median, 12) A. thaliana L. ecotype Ler-0 plants, at growth stage 3.5 according to the Boyes scale (29), or 6 4-week-old N. tabacum plants. Plants were maintained in a biosafety level 2 greenhouse at 25°C with a 16-h light period. Infection status was determined by one-step reverse transcription-PCR (RT-PCR) at 21 dpi for A. thaliana.

Lethal genotypes and failed experiments produce the same result: a lack of infection. To deal with this possible source of error, we proceeded as described elsewhere (5, 26, 28). In short, we estimated the probability of failing an inoculation experiment using RNA transcripts from wild-type pMTEV and a large number of plants. Then, using this probability, we applied the Bernoulli probability distribution to evaluate the likelihood of failing all inoculation experiments after a given number of trials. In all cases, this probability was <0.01.

Virus genomic RNA purification and quantification of viral load.

RNA extraction from 100 mg of tissue per plant was performed using Agilent Plant RNA minikits (Agilent Technologies) following the manufacturer's instructions. The concentration of total plant RNA extract was adjusted to 100 ng/μl for each sample, and the quantification of viral load was done by absolute real-time reverse transcription-quantitative PCR (RT-qPCR), using standard curves (30). Standard curves were constructed using 10 serial dilutions of the TEV genome, produced as described above and diluted in total plant RNA obtained from healthy tobacco or arabidopsis plants treated like all other plants in the experiment. Quantification amplifications were done in a 20-μl volume, using an ABI StepOnePlus real-time PCR system (Applied Biosystems), a GoTaq 1-Step RT-qPCR system (Promega), and the following cycling conditions: the RT phase consisted of 15 min at 37°C and 10 min at 95°C; the PCR phase consisted of 40 cycles of 10 s at 95°C, 34 s at 60°C, and 30 s at 72°C; and the final phase consisted of 15 s at 95°C, 1 min at 60°C, and 15 s at 95°C. Amplifications were performed in 96-well plates, with each plate containing the RNA samples necessary to build the corresponding standard curve; quantifications were performed in triplicate for each sample from different plaques. Quantification results were examined using StepOne software v. 2.2.2 (Applied Biosystems).

Fitness determinations and statistical analyses.

Total RNA was extracted and virus accumulation quantified by RT-qPCR as described above and detailed previously (30). Virus accumulation (in picograms of TEV RNA per 100 ng of total plant RNA) was quantified at 21 dpi for infected A. thaliana plants and at 5 dpi for infected N. tabacum plants to ensure that viral populations were at the exponential growth phase in both cases (TEV reaches a quasi-stationary plateau faster in N. tabacum than in A. thaliana). These values were then used to compute the fitness of the mutant genotypes relative to that of the wild-type genotype on each host species, using the expression $W=\sqrt[t]{R_t/R_0}$, where R₀ and R_t are the ratios of accumulations estimated for the mutant and reference viruses at inoculation and after t days of growth, respectively (28).

A generalized linear model (GLM) was fitted to the fitness data. The model incorporated the following three random factors: host species (H), virus genotype (G), and plant (P), which represents the unit of biological replication (different individual plants from host species H were infected with viral genotype G). H and G were considered orthogonal factors, whereas P was nested within the interaction of H and G. The model equation reads as follows: W_ijkl = μ + G_i + H_j + (G × H)_ij + P(G × H)_ijk + ξ_ijkl, where μ is the grand mean value and ξ_ijkl is the error associated with the individual measure l (estimated from the technical replicates from the RT-qPCRs). The statistical significance of each factor was evaluated using a likelihood ratio test (LRT) that asymptotically follows a χ² distribution. The magnitude of effects was evaluated using the ${\eta }_p^2$ statistic, the ratio of variance explained by the effect while controlling for the other effects. Effects with an ${\eta }_p^2$ value of 0.25 or greater are considered large. Variance components were estimated by the maximum likelihood method. Statistical analyses were performed with IBM SPSS software, version 23.

Representation of fitness landscapes.

A simple way to represent fitness landscapes is in the form of a graph where each node corresponds to a specific genotype. Instead of representing genotypes in terms of nucleotides or amino acids, one can indicate only whether the wild-type or mutant allele is present at a given site, i.e., the possible entry at each site is ○ or ●, respectively, giving rise to a binary graph. With this notation, wild-type TEV is represented by ○○○○○, while the Arabidopsis-adapted isolate is represented by ●●●●●. Edges in the binary graph represent mutational steps of size 1, that is, connecting genotypes that differ in only one allele.

Evaluation of landscape ruggedness.

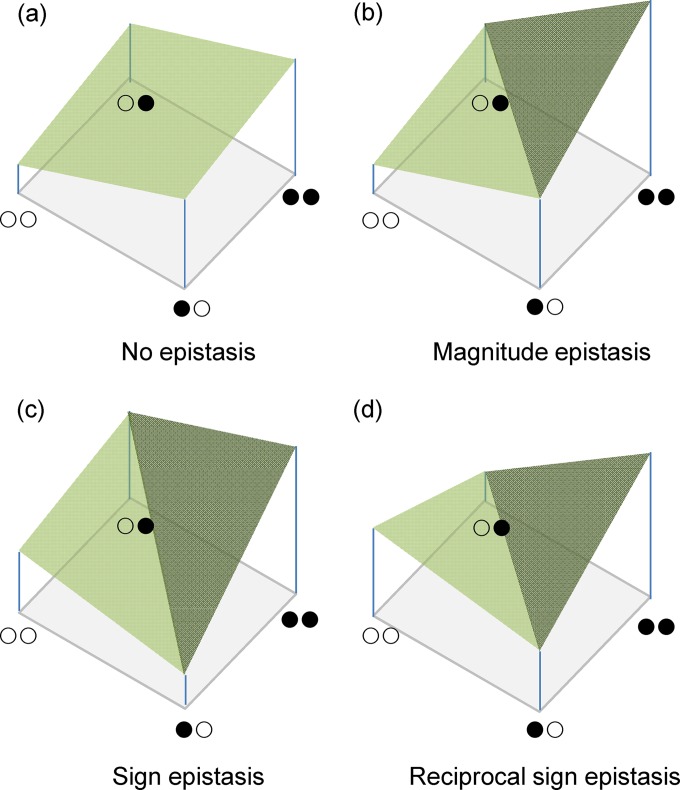
The ruggedness of the landscapes of the two hosts was evaluated using the following three different approaches: (i) the mean slope-to-roughness ratio, θ (31); (ii) the correlation between neighbors' fitness levels, ρ (32); and (iii) the frequencies of different types of epistatic interactions. θ measures how much the slope of a given peak spikes out from the average surface in which it exists. A θ value of ≫1 means that a peak emerges from an otherwise flat surface, similar to a Mount Fuji landscape; in contrast, a θ value of ≤1 indicates that the peak's slope does not differ substantially from the background surface, that is, it is surrounded by many small peaks with similar slopes (31). ρ measures the similarity between the fitness levels of genotypes that occupy nearby positions in the landscape. If this correlation is perfect (ρ ≈ 1), then the landscape is absolutely smooth; as epistasis becomes more and more prevalent, this correlation is reduced, and the ρ value is <0 in the case of sign or reciprocal sign epistasis (Fig. 1) (32).

FIG 1.

Different types of epistasis between two loci defining the fitness of a genotype. ○, wild-type allele; ●, mutant allele. (a) In the case of no epistasis, the fitness of the double mutant (●●) results from multiplying the fitness effects of both mutations in the wild-type genetic background (i.e., the fitness levels for genotypes ●○ and ○●). (b) If magnitude epistasis exists, the fitness of the double mutant (●●) is different from the multiplicative expectation. In the example, the observed fitness of ●● is larger than expected as a consequence of positive epistasis. In the cases of both no epistasis and magnitude epistasis, the effects of mutations ●○ and ○● are unconditionally beneficial. (c) If the effect of one of the mutations is conditionally beneficial (i.e., beneficial in one genetic background but deleterious in another), then we have the situation of sign epistasis. (d) Finally, if both mutations ●○ and ○● are deleterious by themselves but beneficial when combined, we have the situation of reciprocal sign epistasis.

In terms of their effects on landscape topography, four different types of epistatic interactions can be defined (Fig. 1). If magnitude epistasis exists, the fitness of the double mutant is different from the multiplicative expectation (see below for a mathematical definition of this condition). In the example shown in Fig. 1b, the observed fitness of the double mutant is larger than expected (positive epistasis); in the case of no epistasis (Fig. 1a) or magnitude epistasis (Fig. 1b), the effects of both mutations are unconditionally beneficial. If the effect of one of the mutations is conditionally beneficial (i.e., beneficial in one genetic background but deleterious in another), then we have the situation of sign epistasis (Fig. 1c). Finally, if both mutations are deleterious by themselves but beneficial when combined, we have the situation of reciprocal sign epistasis (Fig. 1d). The more common the cases of sign and reciprocal sign epistasis, the more rugged the landscape becomes.

The graphical representation of the two landscapes and the estimation of the above parameters describing their topography were obtained using the MAGELLAN Web server (33).

Computation of epistasis.

The magnitude of epistasis among mutations i and j was calculated as follows: ε_ij = W₀₀W_ij − W_i0W_0j, where W_i0 and W_0j are the relative fitness levels of genotypes carrying each single mutation, W_ij is the relative fitness of the double mutant, and W₀₀ is the fitness of the wild type (34, 35). The second term on the right-hand side of the equation corresponds to the expected fitness which, under the hypothesis of multiplicative independent effects, equals the observed fitness, resulting in an ε_ij value of 0. Deviations from the null hypothesis indicate antagonistic (ε_ij > 0) or synergistic (ε_ij < 0) epistasis. For genotypes containing more than two mutations, a very similar equation can be used, i.e., ε_i(k) = W₀₀W_i(k) − W_iW_(k), but in this case, W_i(k) corresponds to the fitness of the genotype containing k mutations into which mutation i has been introduced and ε_i(k) is the epistasis between mutation i and the genetic background containing the k mutations. For example, genotype ●○●●○ could be constructed in three ways, i.e., by inserting mutation ○○○●○ into genetic background ●○●○○, mutation ○○●○○ into genetic background ●○○●○, or mutation ●○○○○ into genetic background ○○●●○, meaning that we can test for three cases of epistasis for this genotype. This decomposition of interactions generated 75 possible genetic combinations for which epistasis was tested. Following the mathematical conditions given previously (36), we evaluated whether the cases for which we estimated a significant epistasis coefficient also corresponded to sign or reciprocal sign epistasis.

Higher-order epistasis was also evaluated using Walsh coefficients, as proposed previously (37), using the MAGELLAN Web server (33). Walsh coefficients have their equivalent in classic population genetics (37): (i) zero-order Walsh coefficients represent the mean fitness across all genotypes; (ii) first-order Walsh coefficients are equivalent to the selection coefficients, which represent the fitness effects of single mutations; (iii) second-order Walsh coefficients are equivalent to pairwise epistatic coefficients, i.e., ε_ij; and (iv) higher-order Walsh coefficients are thus equivalent to higher-order epistatic interactions among the >2 mutations present in a genotype. In the case of multiplicative fitness landscapes, all Walsh coefficients for orders of ≥2 are equal to zero, and thus the landscape is smooth. In contrast, ruggedness is maximal in a fully random landscape, with many local peaks representing all types of epistatic interactions. Real fitness landscapes lie between these two extremes, being neither smooth nor maximally rugged (37).

RESULTS

Landscape topographies and first descriptive statistics.

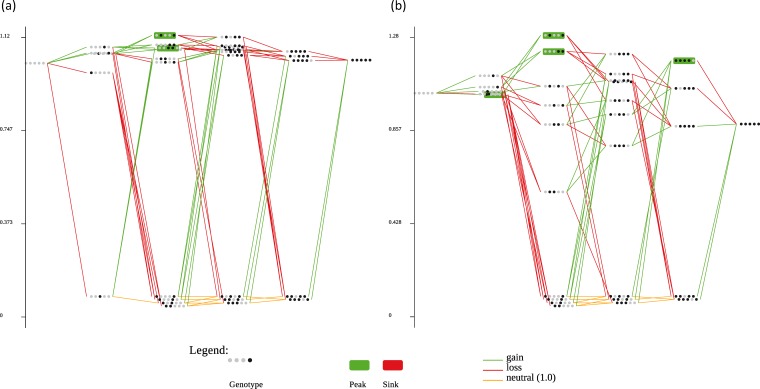
Figure 2 shows both estimated landscapes, and Table 2 contains some statistics describing their topographies. With a peak defined as representing a genotype such that all neighbors have a lower fitness, for A. thaliana the 32 genotypes define a landscape with two peaks (genotypes ○●○○● and ○○●●○) of different heights (26), whereas four peaks are defined for the ancestral host N. tabacum (genotypes ●○○○○, ○●○○●, ○○○●●, and ●●●●○). The ruggedness of the landscape can be evaluated using several different measures (Table 2). For instance, the ratio of mean slope to roughness, θ, (31) showed similar values for both hosts, and in both cases the values were >1, indicating that the landscapes are rugged in relationship to the average slope of the peaks. A recently proposed measure of epistasis is the correlation between fitness effects of a given genotype and all their one-step neighbors, i.e., ρ (32). In our case, both ρ values were positive and small (close to zero), suggesting the existence of many cases of magnitude epistasis. Another very intuitive measure of the ruggedness of a landscape is to compute the frequency of each type of epistatic interaction among all possible pairs of mutations: for a smooth landscape, the fraction of multiplicative interactions should be maximal, and as the ruggedness of the landscape increases, cases of sign and reciprocal sign epistasis should become more common (2, 36). Table 2 indicates that most mutations interacted epistatically in both hosts, with magnitude epistasis being the most common type of interaction in both landscapes. Sign epistasis was the second most common type of epistasis in A. thaliana, while reciprocal sign epistasis was the second most common type for the ancestral host N. tabacum. Taken together, these results suggest that the landscape defined by the five mutations is more rugged in the ancestral host than in the new one. We further expand these results in the next sections.

FIG 2.

Empirical fitness landscapes evaluated for the first five mutations fixed by TEV during its experimental adaptation to A. thaliana. The fitness of the 32 genotypes was evaluated in the novel host (a) and in the original one, N. tabacum (b). Each string of dots represents a genotype. Black dots represent a mutation in the corresponding locus, while white dots correspond to the wild-type allele at that locus. Genotypes in a green box correspond to local fitness peaks. Green lines correspond to beneficial mutations, red lines to deleterious mutations, and orange lines to neutral changes (in the direction from genotype ○○○○○ to genotype ●●●●●). Graphs were generated with the MAGELLAN Web server (33).

TABLE 2.

Summary statistics describing the topographies of both landscapes

Statistical parametera	Value
	A. thaliana	N. tabacum
General statistics
No. of peaks	2	4
No. of sinks	0	0
Epistasis statistics
Mean slope-to-roughness ratio (θ)	1.902	1.697
Correlation between neighbors' fitness levels (ρ)	0.119	0.111
Frequency of multiplicative interactions	0.013	0.013
Frequency of magnitude epistasis	0.662	0.575
Frequency of sign epistasis	0.212	0.188
Frequency of reciprocal sign epistasis	0.113	0.225

^aComputed using the MAGELLAN Web server (33).

Fitness correlations and antagonistic pleiotropy among hosts.

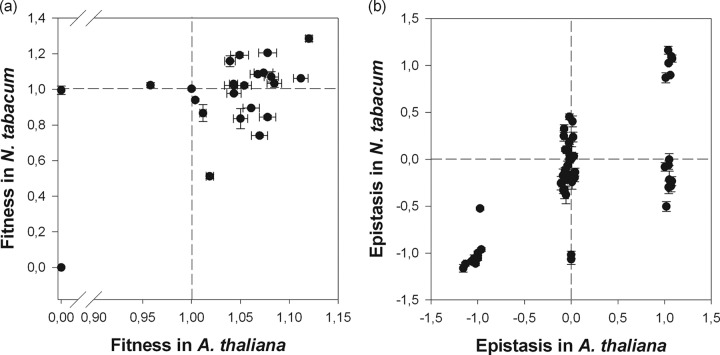
To further explore the relationship between the topographies of both landscapes shown in Fig. 2, we evaluated the similarity of the fitness effects estimated for each genotype in each host species (Fig. 3a). The fitness values are significantly correlated between the two landscapes (Pearson's r = 0.891; 30 df; P < 0.001). However, this correlation is entirely driven by the existence of a group of genotypes that are lethal in both hosts. If these genotypes are removed from the analysis, the correlation is no longer significant (r = 0.338; 20 df; P = 0.124). The dashed lines in Fig. 3a represent the relative fitness of wild-type TEV in both hosts. These lines divide the fitness space into four regions, with each region corresponding to genotypes with fitness values larger or smaller than that of the wild type (○○○○○) for each host. Twelve genotypes had fitness values larger than that of the wild type for both hosts and thus were unconditionally beneficial. In contrast, 10 genotypes were unconditionally deleterious, with fitness values smaller than that of the wild type for both hosts. Nine of them were lethal in both hosts, and genotype ○○●○○ was lethal in A. thaliana but only slightly deleterious (−0.5% effect) in N. tabacum. Together, these 22 genotypes, occupying the upper right and lower left quadrants of Fig. 3a, account for the above-described correlation. The cases in the other two quadrants are more interesting, as they represent examples of antagonistic pleiotropy, i.e., genotypes beneficial in one host that are deleterious in the alternative one. Genotype ●○○○○ was beneficial in N. tabacum but deleterious in A. thaliana. Eight genotypes had fitness values larger than that of the wild type in A. thaliana but were deleterious in the original host. Given their low fitness in the ancestral host, these genotypes most likely were generated and selected during the process of adaptation to the new host.

FIG 3.

Fitness values and epistasis coefficients for both hosts. (a) Fitness values estimated for the 32 genotypes shown in Fig. 2 for both hosts. For both hosts, fitness is expressed relative to that of the wild-type genotype (○○○○○). Dashed lines correspond to the fitness of the wild type in each host. The 0,0 dot includes the nine cases of unconditionally lethal genotypes. (b) Distribution of epistasis for both hosts. Dashed lines correspond to the case of multiplicative fitness effects (no epistasis). Error bars correspond to ±1 standard deviation (SD).

Prior to any further statistical analyses, fitness data were checked for violation of the assumptions of normality and homoscedasticity of variances. We found that the data were not normally distributed (one-sample Kolmogorov-Smirnov test; D = 0.248; P < 0.001), nor were variances homogeneous among groups (Levene test; F_229,399 = 13.980; P < 0.001). The GLM described above, with a gamma distribution and a log-link function (chosen because it had the minimal Bayes information criterion among a set of alternatives tested), was fitted to the fitness data to evaluate the relative contributions of genotypes and host species to the observed variability in fitness. Table 3 shows the results of this analysis. Overall, highly significant differences exist among the 32 genotypes (P < 0.001), which largely contribute to the observed differences in fitness (${\eta }_p^2$ = 0.860). The percentage of total variance explained by true genetic differences among viral genotypes is as large as 77.8%. The net contribution of host species to viral fitness is also significant (P = 0.037), although the magnitude of the effect is very small (${\eta }_p^2$ = 0.006; variance explained by the host, only 0.2%), and consequently the statistical power associated with this test is too low to make the result reliable. However, a highly significant effect (P < 0.001) of host species that depends on each genotype exists, and the magnitude of this interaction effect is also large (${\eta }_p^2$ = 0.500; variance explained by interaction, 16.7%). The fact that the interaction between viral genotype and host species contributes to fitness to a much larger extent than that for host species itself has an important consequence: the two landscapes differ in fine-grained details more than they do in coarse-grained details. Finally, the differences among plants of each host species inoculated with the same viral genotype are also significant (P < 0.001) and have a magnitude comparable to that of the main virus effect (${\eta }_p^2$ = 0.848), but they explain a relatively minor fraction of the total observed variance (4.2%).

TABLE 3.

Summary of the GLM fitted to the data

Factor	LRT resulta	df	P value	${\eta }_p^2$ valueb	1 − βc
Intercept	3,979.285	1	<0.001	0.982	1
G	2,397.695	31	<0.001	0.860	1
H	4.341	1	0.037	0.006	0.183
G × H	1,344.481	20	<0.001	0.500	1
P(G × H)	1,168.930	177	<0.001	0.848	1

^aLRT, likelihood ratio test.

^bMagnitude of effects associated with each model factor.

^cStatistical power of the corresponding tests.

Differences in epistasis and landscape ruggedness between hosts.

Next, we explored the congruency between epistasis values and types across host species for all genotypes carrying two or more mutations. Computing epistasis between pairs of mutations is straightforward, but for genotypes carrying more than two mutations, the computation becomes slightly more complicated. For example, for a triple mutant, we must consider the three different cases in which each single mutation is introduced into the corresponding complementary double mutant genotypes (see Materials and Methods for an example). By doing so, we have to analyze a total of 75 different possibilities (26). Figure 3b shows these data and illustrates the existence of a significant correlation between epistasis coefficients measured for both hosts (r = 0.718; 73 df; P < 0.001). However, a substantial number of interactions do not fit the diagonal expected under the hypothesis of no host effect on epistasis. Most of these cases (10 cases) had negative epistasis in N. tabacum that changed into multiplicative effects or even positive epistasis in A. thaliana.

Genetic interactions in A. thaliana can be classified as follows: 40 cases of multiplicative interactions, 26 of magnitude epistasis, 4 of sign epistasis, and 5 of reciprocal sign epistasis (26) (Table 4). For N. tabacum, the counts are as follows: 46 cases of multiplicative interactions, 11 of magnitude epistasis, 7 of sign epistasis, and 11 of reciprocal sign epistasis. The distributions of counts per category are significantly different between the hosts (χ² = 10.050; 3 df; P = 0.018), with an excess of cases of sign and reciprocal sign epistasis for N. tabacum. The epistasis transition matrix (Table 4) shows the effects that experimental adaptation to A. thaliana had on the different types of epistasis. Most of the interactions remained of the same type for both hosts (65.3%; binomial test P = 0.011), mainly due to the congruency in the number of multiplicative cases. Interestingly, among those that changed the type of epistasis, 57.5% did so in the direction of reducing the ruggedness of the landscape (e.g., from sign or reciprocal sign epistasis to magnitude epistasis) in A. thaliana.

TABLE 4.

Epistasis transition matrix

Epistasis type for N. tabacum	No. of cases for A. thaliana
	No epistasis	Magnitude epistasis	Sign epistasis	Reciprocal sign epistasis
No epistasis	37	8	1	0
Magnitude epistasis	2	9	0	0
Sign epistasis	1	4	0	2
Reciprocal sign epistasis	0	5	3	3

Seeking a mechanistic understanding of these changes in the patterns of epistasis, we focused on pairwise interactions due to their simplicity. Five combinations of two mutations resulted in a reduction of the landscape's ruggedness for A. thaliana compared to that for N. tabacum, in three cases from reciprocal sign epistasis to magnitude epistasis and in one case from sign epistasis to multiplicative effects. Note that four of these five cases involved the synonymous mutation P1/U357C (●○○○○). No obvious explanation can be brought forward to explain why the effect of a synonymous mutation depends so strongly on the presence of mutations in other genes. Another interesting case is the nonsynonymous mutation 6K1/T1126M (○○●○○). The 6K1 small peptide is required for viral replication and colocalizes with chloroplast-bound viral replicase elements 6K2 and NIb at early stages of infection (38). The fitness effects resulting from the interaction between this particular mutation at 6K1 and all four other mutations were always host dependent. For this mutation in combination with the synonymous mutation P1/U357C or the nonsynonymous mutation P3/A999V (○●○○○), interactions changed from sign epistasis in N. tabacum to multiplicative interactions or magnitude epistasis in A. thaliana. However, when this mutation was combined with the nonsynonymous mutation VPg/L1965F (○○○●○) or with the synonymous mutation NIaPro/C6906U (○○○○●), it increased the ruggedness in the novel host, from multiplicative interactions to sign or magnitude epistasis, respectively. Again, no obvious mechanism can be brought forward to explain why the effect of this mutation depends on synonymous mutations in other genes. The fitness effect of the 6K1/T1126M mutation was alleviated in the presence of the P3/A999V mutation in the novel host, suggesting some form of interaction between these two genes (either direct or indirect) that has not yet been detected experimentally (39). The beneficial fitness effect of the 6K1/T1126M mutation was potentiated in the presence of the VPg/L1965F mutation in the novel host, also suggesting that these two proteins may have tightly coordinated actions in determining TEV fitness in the novel host. A direct interaction between these proteins has not been confirmed experimentally (39). However, in both cases, an indirect interaction mediated by the CI protein may still be possible (39).

So far, we have focused on pairwise interactions between individual mutations or between one mutation and a group of mutations. Weinreich et al. (37) pointed out that this approach must be misleading, as the products of many genes interact in complex manners to determine the fitness of individuals, and thus higher-order epistasis must be a fundamental component of the genetic architecture of fitness. Using the Walsh coefficient approach proposed previously (37), we evaluated the contribution of higher-order epistasis to the two landscapes. Figure 4 compares the weight of each Walsh coefficient to the fitness variability observed in both landscapes. The zero-order coefficients represent the mean fitness across all genotypes. In this case, mean fitness is higher in the novel host than in the ancestral one. This is logical, since these genotypes, at least those that may have a real existence in the evolving population, were positively selected in A. thaliana. First-order coefficients correspond to selection coefficients for single mutations. In both landscapes, up to four-order interactions contribute in a noticeable manner to the observed pattern of fitness, illustrating the complexity of interactions between genes in determining TEV fitness in both hosts. Interestingly, second-order interactions, which correspond to pairwise epistasis coefficients, seem to be qualitatively more important in A. thaliana, while third-order interactions, representing the effect of a given mutation on the curvature of the surface defined by two other mutations (i.e., second-order interactions), appear to be more important in N. tabacum. The different weights of second- and third-order interactions in the hosts further support the idea that the landscape is less rugged in the novel host than in the ancestral one. Four-order interactions also appear to be qualitatively more important in A. thaliana than in N. tabacum. Four-order coefficients reflect the effect that a surface defined by a pair of mutations exerts on the surface defined by another pair of mutations. Unfortunately, we cannot provide an intuitive visualization of this numerical result.

FIG 4.

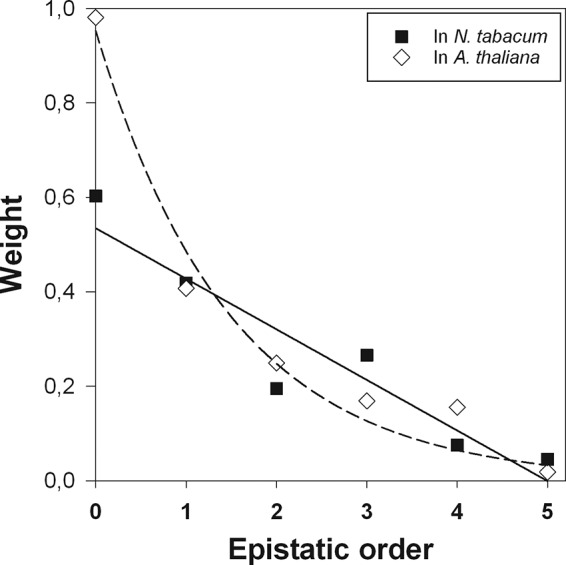
The zero-order Walsh coefficient gives the mean fitness across all genotypes; fitness values were normalized to make this figure equal to 1. First-order and second-order coefficients are analogous to selection coefficients and pairwise epistasis, respectively. Higher-order terms are equivalent to epistasis among increasing numbers of mutations. Walsh coefficients were computed with the MAGELLAN Web server (33).

Relationship between antagonistic pleiotropy and the sign of epistatic interactions.

Pleiotropy and epistasis have strong parallelisms because the effect of an allele depends on the context in both cases, i.e., the host species for pleiotropy and the viral genetic background for epistasis. Indeed, it has been postulated that pleiotropy is a prerequisite for epistasis (3, 40). This dependence is obvious for the case of sign pleiotropy, where mutations with a positive effect in the new host have a negative effect in the primary one (13). Furthermore, in the context of compensatory evolution, antagonistic pleiotropy is a precondition for sign epistasis because it allows for the negative pleiotropic effects of previously selected mutations to be compensated by additional ones (3). Therefore, it was of interest to test whether the 8 genotypes showing evidence of antagonistic pleiotropy (see comments above for Fig. 3a), all of them carrying the nonsynonymous mutation 6K1/T1126M, also changed the sign of their epistatic interactions in both hosts. Indeed, all 8 genotypes showed a change in the sign of their epistatic interactions: genotype ○●●○○ from negative to positive and the other 7 genotypes from positive to negative. In contrast, among the 18 genotypes not showing evidence of antagonistic pleiotropy, 14 did not change the sign of their epistatic interactions between host species, and 4 did change (3 from negative to positive and only 1 from positive to negative). Fisher's exact test confirms that changes in the sign of epistasis are significantly enriched among genotypes showing antagonistic pleiotropy compared to genotypes that do not show it (P < 0.001).

DISCUSSION

The results described above clearly illustrate that changes in host species result in perturbations in the topography of the fitness landscape of an RNA virus. The first five mutations fixed during experimental evolution of TEV in the novel host A. thaliana conformed a landscape in the original host, N. tabacum, that was significantly more rugged than the landscape in the novel host. Differences between the two landscapes, however, were local rather than global, with particular genotypes changing their relative heights in the landscape and resulting in different patterns of epistatic interactions with their neighbors. This dependence of the topography of the fitness landscape on the host supports the notion of dynamic landscapes (17) or seascapes (19) rather than static ones. Nonetheless, both landscapes share common features, such as the existence of fitness holes due to unconditionally lethal genotypes or the presence of pervasive epistatic interactions. The topographies of both empirical landscapes match pretty well with the expectations from a random uncorrelated landscape, lying somewhere between the extreme case of the house-of-cards model (31, 41), in which the fitness of each genotype is absolutely independent of the fitness of the other genotypes, and the less radical case of the rough Mount Fuji model (31, 42), which combines properties of both the house-of-cards model and a purely multiplicative landscape.

Antagonistic pleiotropic fitness effects have been reported widely for RNA viruses adapting to different hosts and are generally accepted as the main cause of fitness tradeoffs among hosts that drive virus specialization to novel hosts (reviewed in reference 43). Here we found that ∼26% of genotypes had a pleiotropic fitness effect, with all but one of these cases corresponding to genotypes beneficial in the novel host but deleterious in the ancestral one. These results further stress the importance of antagonistic pleiotropy in driving adaptation to a local new host at the cost of a reduced fitness in the ancestral one. Other authors, however, consider that fitness tradeoffs have been overrated as the mechanism explaining virus specialization toward a host (44, 45). Indeed, it has been proposed that incongruent fitness landscapes may be a better explanation for the evolution of specialist viruses infecting alternative hosts (45). Our results show that these two hypotheses can be conciliated: some genotypes represent clear examples of antagonistic pleiotropy, while both landscapes are incongruent in some particular details. Indeed, both hypotheses are not mutually exclusive, as antagonistic pleiotropy largely contributes to the incongruence among landscapes.

We also found that antagonistic pleiotropy in host usage and epistasis at the genomic level go hand in hand, thus corresponding to a situation defined as epistatic pleiotropy (13). Indeed, we previously reported a similar result when we analyzed the fitness and epistatic interactions of a larger collection of random mutations in the TEV genome (16). Epistatic pleiotropy has two important implications. First, unlike either sign or magnitude pleiotropy in the absence of epistasis, epistatic pleiotropy allows for the evolution of either specialist or no-cost generalist viruses, depending on the virus population's host. Second, and very important for limiting the emergence of new viruses, when epistasis is in the form of reciprocal sign epistasis, the ruggedness of the adaptive landscapes diminishes the ability of viral populations to escape from specialism to a situation of no-cost generalism. A long history of evolution in the primary host may result in an adaptive walk toward a host-specific fitness peak involving most, if not all, viral loci. Such a population could find itself many mutational steps away from reaching a generalist peak.

In recent years, evolutionary biologists have started to tackle the topography of fitness landscapes from an empirical perspective (reviewed in reference 1). Unfortunately, the amount of information about fitness landscapes is still very limited. Empirical fitness landscapes have been explored thoroughly only for another virus, HIV-1, for mutations allowing access to an alternative cell surface chemokine coreceptor (46–48) and for adaptation to different antiviral drugs (49). In both cases, ruggedness has been proved to be common due to the pervasiveness of epistasis. In the latter case, results suggested that the coarse-grained details of the topography were only weakly dependent on environmental conditions, in this case the presence of different antiretroviral drugs (49). Our results are in good agreement with these previous findings.

How can a viral population reach the global fitness maximum in such a highly rugged landscape and not be trapped in suboptimal fitness peaks? Here we have shown that by a change of the host species, the landscape has been flattened, facilitating access to certain peaks that otherwise may remain inaccessible in the ancestral host. There are other possible mechanisms for efficiently improving fitness in such landscapes that do not necessarily require moving one step at a time. These long-range jumps are known as stochastic tunneling in large populations (50). Recombination is the most obvious mechanism for such a tunneling effect, as it may combine beneficial mutations into a single genotype. At least for TEV, the recombination rate is in the same ballpark as the mutation rate (51), and high recombination rates are not rare among positive-sense single-stranded RNA (ssRNA) viruses (52). The typically high mutation rates of RNA viruses, usually in the vicinity of one per genome and replication round (53), combined with their very high replication rates and large population sizes, make it likely that a double mutant carrying two beneficial mutations can be created, thus allowing for the tunneling effect. In the case of TEV, the genomic mutation rate (U) is 0.601 (54). Assuming that only a very minor fraction of all possible individual mutations are beneficial, say only one per genome, the lower-bound probability of finding a genome carrying two such beneficial mutations would be $U_b^2$ = (0.601/9,539)² = 3.97 × 10⁻⁹. From an evolutionary perspective, the number that matters is the product ${NU}_b^2$, where N is the population census size. This product gives the number of individuals in the population that are double mutants. For TEV, N strongly varies among hosts, but in the case of susceptible A. thaliana ecotypes, it is always greater than 10⁸ and can be as large as 10¹⁰ genomes per plant (55), thus making ${NU}_b^2$ very likely to be >1 during the course of most infections.

Some readers may consider the following to be caveats of this study: (i) A. thaliana is not a natural host of TEV, and (ii) all our experiments were performed under controlled greenhouse conditions that may be optimal for virus replication and accumulation. We do not consider the first to be a real problem, as this study, and all previous ones performed with the same experimental pathosystem (25, 26, 30, 55–59), deal with the evolutionary determinants and consequences of viral emergence and adaptation to a fully novel host. The second may certainly be an issue to be considered. It is well known that wild A. thaliana, and wild hosts in general, support less replication than crops or hosts grown under greenhouse conditions (60). In this sense, our arguments above for efficient landscape exploration based on stochastic tunneling may not work well in the wild if replication levels are reduced. Therefore, generalizing our findings and conclusions to a natural ecological context may not be straightforward…as might be the case for almost every experimental evolution study, at least, if not for every laboratory experiment.

As a closing consideration, gathering information on the structure and topology of RNA virus adaptive landscapes, on their dependence on external factors, and on how they modulate virus evolution may be central to developing new antiviral strategies and personalized clinical treatments and predicting and containing emerging diseases with a viral etiology.

Funding Statement

This project was funded by grants BFU2012-30805 and BFU2015-65037P from the Spanish Ministry of Economy and Competitiveness (MINECO), PROMETEOII/2014/021 from the Generalitat Valenciana, and EvoEvo (ICT610427) from the European Commission 7th Framework Program to S.F.E. H.C. was supported by contract BES2013-065595 from MINECO. J.L. was supported by a JAE-pre contract from CSIC.