Structure–Reactivity Effects on Intrinsic Primary Kinetic Isotope Effects for Hydride Transfer Catalyzed by Glycerol-3-phosphate Dehydrogenase

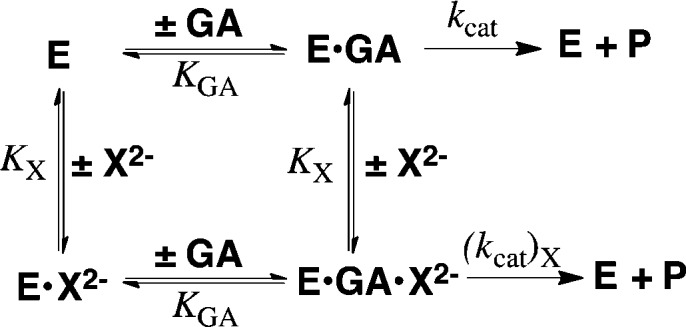
Abstract

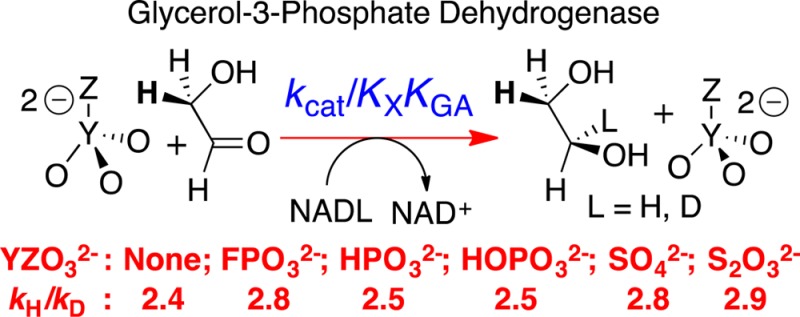
Primary deuterium kinetic isotope effects (1°DKIE) on (k_cat/K_GA, M^–1 s^–1) for dianion (X^2–) activated hydride transfer from NADL to glycolaldehyde (GA) catalyzed by glycerol-3-phosphate dehydrogenase were determined over a 2100-fold range of enzyme reactivity: (X^2–, 1°DKIE); FPO₃^2–, 2.8 ± 0.1; HPO₃^2–, 2.5 ± 0.1; SO₄^2–, 2.8 ± 0.2; HOPO₃^2–, 2.5 ± 0.1; S₂O₃^2–, 2.9 ± 0.1; unactivated; 2.4 ± 0.2. Similar 1°DKIEs were determined for k_cat. The observed 1°DKIEs are essentially independent of changes in enzyme reactivity with changing dianion activator. The results are consistent with (i) fast and reversible ligand binding; (ii) the conclusion that the observed 1°DKIEs are equal to the intrinsic 1°DKIE on hydride transfer from NADL to GA; (iii) similar intrinsic 1°DKIEs on GPDH-catalyzed reduction of the substrate pieces and the whole physiological substrate dihydroxyacetone phosphate. The ground-state binding interactions for different X^2– are similar, but there are large differences in the transition state interactions for different X^2–. The changes in transition state binding interactions are expressed as changes in k_cat and are proposed to represent changes in stabilization of the active closed form of GPDH. The 1°DKIEs are much smaller than observed for enzyme-catalyzed hydrogen transfer that occurs mainly by quantum-mechanical tunneling.

The most important metric for transition state structure for enzyme-catalyzed hydride transfer is the effect of substitution of −D for −H at NADH on the activation barrier ΔG^‡. This is reported as the intrinsic isotope effect on the appropriate kinetic parameter.¹ In the many cases where evolutionary pressures have equalized the relative barriers to isotope-independent substrate binding and product release steps and to isotope-dependent hydride transfer steps,² no single step is rate determining and the intrinsic kinetic isotope effect (KIE) is suppressed.³ Apparent intrinsic 1°DKIE have been reported for enzymatic hydride transfer at nonphysiological substrates,⁴ or for catalysis by enzymes crippled by site-directed mutagenesis.^4b The effect of these perturbations in substrate and enzyme structure on the intrinsic 1°DKIE for the unperturbed reaction is unclear.

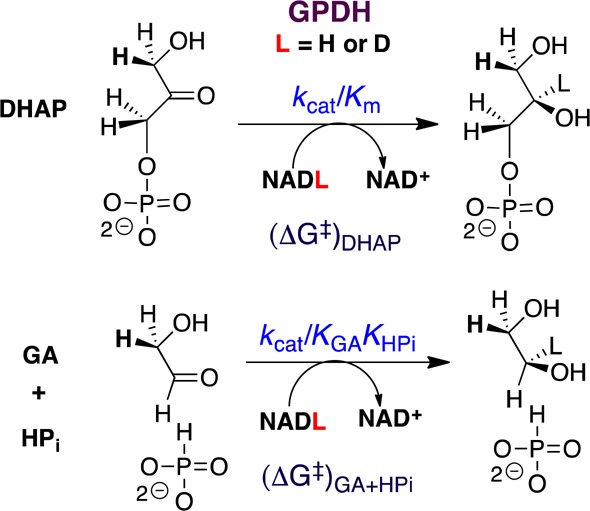
The ratio of rate constants k_cat/K_m = 4.6 × 10⁶ M^–1 s^–1 for human liver glycerol-3-phosphate dehydrogenase (hlGPDH)-catalyzed reduction of the whole substrate dihydroxyacetone phosphate (DHAP) by NADH and k_cat/K_dK_HPi = 1.6 × 10⁴ M^–2 s^–1 for the phosphite dianion (HP_i) activated reduction of glycolaldehyde (GA) gives the connection energy (ΔG)_S = 3.3 kcal/mol (eq 1).⁵ This shows that cutting the substrate into pieces reduces the total ligand binding energy but maintains the high substrate reactivity. The many observations that the reactivity of whole phosphodianion substrates is recovered in catalysis of reactions of the component pieces expand the horizon for the study of enzyme mechanisms.⁶

1

The tight binding of DHAP (K_m = 50 μM)⁷ to hlGPDH favors slow release of the bound substrate, rate determining substrate binding, and suppression of the 1°DKIE. By contrast, the weak binding of the pieces GA (K_d = 5 mM) and HP_i (K_X = 70 mM) favors fast and reversible ligand binding, and observation of intrinsic 1°DKIE on hydride transfer. We confirm this prediction and show that the observed 1°DKIEs on hlGPDH-catalyzed reduction of the physiological substrate DHAP are smaller than the intrinsic 1°DKIE (k_H/k_D) = 2.7 ± 0.3 for dianion activated hlGPDH-catalyzed reduction of GA.

The sources of reagents and the experimental methods are given in the Supporting Information (SI) for this communication. The experiments with NADH and 4S-[4-²H₁]-NADH (NADD) were conducted in parallel using the same solutions. Initial velocities (v_obs) for hlGPDH-catalyzed reduction of DHAP and truncated substrate GA by NADL were determined at 25 °C and pH 7.5 (triethanolamine (TEA) buffer) by monitoring the reduction of DHAP by NADL at 340 nm.^6aFigure S1 shows Michaelis–Menten plots of v_obs/[E] against [NADH] or [NADD] for hlGPDH-catalyzed reduction of DHAP at 25 °C, pH 7.5 and different fixed [DHAP]. The nonlinear least-squares fit of these data to eq 2 for reactions of NADH (F_i = 0) and NADD (F_i = 1.0), derived for an ordered reaction mechanism where NADH binds first followed by DHAP,⁸ gave the kinetic parameters reported in Table S1. The values of E_X (1°DKIE – 1) from Table S1 gave the following 1°DKIE; (E_V/Kb + 1) = 1.5 ± 0.1, (E_V/Ka + 1) = 1.2 ± 0.1, and (E_V + 1) = 1.5 ± 0.1. These 1°DKIEs are smaller than the calculated intrinsic 1°DKIEs for enzyme-catalyzed hydride transfer to aldehydes, when hydride transfer is fully rate determining.⁹

2

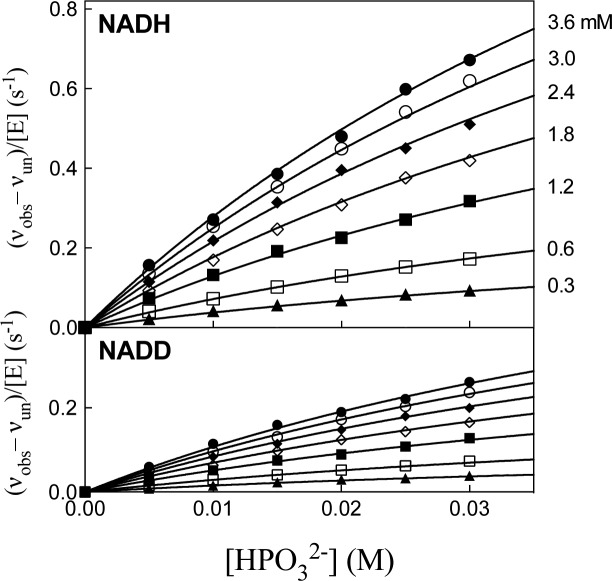
Figure 1 shows the dependence of v_un/[E] (s^–1) on [GA] for unactivated reduction of GA by 0.2 mM ≫ K_m NADH (F_i = 0) or NADD (F_i = 1.0) catalyzed by hlGPDH at pH 7.5 (10 mM TEA), 25 °C, and I = 0.12 (NaCl). The solid lines show the nonlinear least-squares fits of these data to eq 3, derived for Scheme 2 ([X^2–] = 0). Table 1 reports the kinetic parameters and 1°DKIE for unactivated hlGPDH-catalyzed reduction of GA obtained from these fits. Figure 2 shows the dependence of (v_obs – v_un)/[E] (s^–1) on [HPO₃^2–] for HP_i activated reduction of GA by saturating 0.2 mM NADH (top graph) or by 0.2 mm NADD (bottom graph) catalyzed by hlGPDH at pH 7.5 (10 mM TEA), 25 °C, and I = 0.12 (NaCl). The values of v_un for the unactivated reaction, determined using the kinetic parameters from Table 1 and K_X = 70 mM for HP_i, are ≤1% the value of v_obs. The solid lines in Figure 2 show the nonlinear least-squares fit of the experimental data to eq 4, derived for Scheme 2.⁸Table 1 reports the kinetic parameters and 1°DKIE obtained from the fit of the kinetic data to eq 4. Figures S2–S5 show, respectively, the dependence of (v_obs – v_un)/[E] (s^–1) on [X^2–] for fluorophosphate, sulfate, phosphate, and thiosulfate dianion activated reduction of GA by 0.2 mM NADH or by 0.2 mm NADD catalyzed by hlGPDH at pH 7.5 (10 mM TEA), 25 °C, and I = 0.12 (NaCl). Table 1 reports the kinetic parameters and 1°DKIE for these dianion activated reactions obtained from the nonlinear least-squares fit of the kinetic data to eq 4.

3

4

Figure 1.

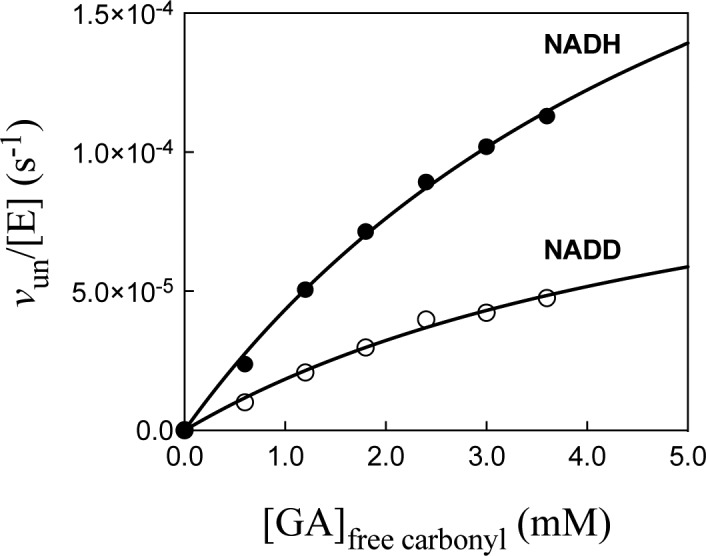
Dependence of v_un/[E] (s^–1) on [GA] (eq 3) for hlGPDH-catalyzed reduction of GA by NADH or NADD (0.2 mM) at pH 7.5, 25 °C, and I = 0.12 (NaCl).

Scheme 2.

Table 1. Kinetic Parameters (Scheme 2) for Glycerol Phosphate Dehydrogenase-Catalyzed Dianion Activated Reduction of GA by NADH and NADD and 1°DKIE on Enzyme-Catalyzed Hydride Transfer^a.

oxydianion activator	(kcat/KGA)/KX (M–2 s–1)b	ΔΔG† (kcal/mol)	KGA (10–3 M)	KX (10–3 M)	D(kcat/KGA)c	kcat (10–4 s–1)	D(kcat)c
none			6.2 ± 0.7		2.4 ± 0.2	3.0 ± 0.3	2.4 ± 0.4
FPO32–	75000 ± 6000	0	5.0 ± 0.2	17 ± 1	2.8 ± 0.1	(6.4 ± 0.2) × 104	2.8 ± 0.2
HPO32–	16000 ± 1300	0.9	4.9 ± 0.2	73 ± 3	2.5 ± 0.1	(5.7 ± 0.2) × 104	2.8 ± 0.1
SO42–	1100 ± 200	2.5	4.5 ± 0.3	70 ± 7	2.8 ± 0.2	(3.5 ± 0.3) × 103	3.2 ± 0.3
HOPO32–	200 ± 20	3.5	4.1 ± 0.2	39 ± 2	2.5 ± 0.1	(3.2 ± 0.1) × 102	3.1 ± 0.2
S2O32–	35 ± 5	4.6	5.0 ± 0.2	105 ± 10	2.9 ± 0.1	(1.8 ± 1.2) × 102	3.0 ± 0.2

^aFor reactions at pH 7.5 (10 mM TEA), 25 °C, and I = 0.12 (NaCl). Kinetic parameters for Scheme 2 were determined by analyses of data from Figure 2 and Figures S2−S5, as described in the text. The uncertainty in these values are the standard errors provided by the fitting program.

^bThe third-order rate constant for dianion activation of hlGPDH-catalyzed reduction of GA (Scheme 1).

^cThe primary kinetic isotope effect on this kinetic parameter.

Figure 2.

Dependence of (v_obs – v_un)/[E] (s^–1) on [GA] for HPO₃^2–-activated hlGPDH-catalyzed reduction of GA by 0.2 mM NADH or NADD at pH 7.5 (10 mM TEA), 25 °C, and I = 0.12 (NaCl). The individual curves compare dianion activation of reactions of NADH or NADD at the fixed [GA] shown on the right-hand side of the top panel.

Scheme 1.

The free energy profiles shown in Figure 3 are drawn for Scheme 3 to rationalize the experimental observations from Table 1 described below.

Figure 3.

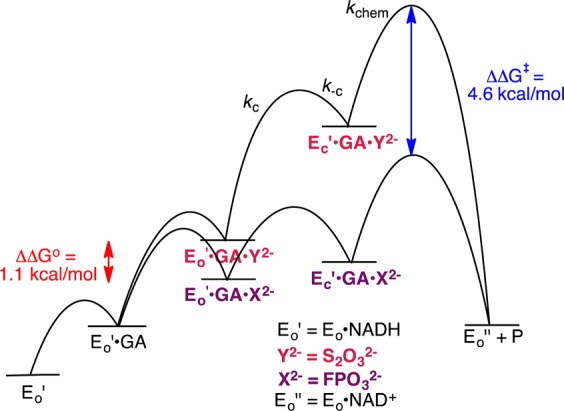
Hypothetical free energy profiles for activation of hlGPDH-catalyzed reduction of GA by FPO₃^2– and S₂O₃^2– drawn for Scheme 3 to show the difference in the relative ground state (ΔΔG^o = 1.1 kcal/mol) and transition state (ΔΔG^‡ = 4.6 kcal/mol) binding energies. The reactions are carried out in the presence of saturating [NADH], so that cofactor binding is not a kinetically significant step.

Scheme 3.

(1) The large dissociation constants K_GA for GA (6 mM) and K_X for X^2– (17–105 mM) require fast and reversible ligand binding to hlGPDH, so that similar rate-determining steps control k_cat/K_GA and k_cat. This provides a rationalization for the observation of similar 1°DKIE on these two kinetic parameters (Table 1). The 1°DKIE on HP_i activated reactions does not change significantly as the reaction barrier is increased by 4.6 kcal/mol for activation by S₂O₃^2–. This shows that hydride transfer is rate determining (Figure 3) for all reactions and that the observed 1°DKIEs (Table 1) are intrinsic 1°DKIEs. Cutting substrates into pieces has little effect on the structure of the transition state for reactions catalyzed by triosephosphate isomerase¹⁰ and orotidine 5′-monophosphate decarboxylase.¹¹ We propose a similarity in transition state structures for hlGPDH-catalyzed reactions of the whole substrate and pieces that gives rise to similar intrinsic 1°DKIEs.

(2) Dianion activators are released from hlGPDH with similar K_X (Figure 3). Therefore, the large differences in dianion affinity for binding to the hydride transfer transition state complex, required to account for the large differences in dianion activation, are expressed mainly as changes in the kinetic parameter k_cat. We conclude that the initial Michaelis complex to these dianions [E′_o·X^2–·GA] is unreactive toward hydride transfer and is converted to an active complex by a conformational change that optimizes transition state protein·dianion interactions.^5b,7,12 This conformational change is related to that observed for conversion of the binary E·NAD⁺ to the ternary E·NAD⁺·DHAP complex.¹² The dominant enzyme motion is closure of an open loop (Leu292–Leu297) over the phosphodianion of DHAP, which locks the ligand in a protein cage of low dielectric constant relative to water.¹³ The effect of formation of such protein cages will optimize stabilizing electrostatic interactions,^6e which in this case are dominated by the interaction between the R269 side chain cation and the anionic transition state for hydride transfer.^5b

(3) The activation barrier for turnover of the initial Michaelis complex [E′_o·X^2–·GA], with rate constant k_cat, is the sum of the thermodynamic barrier to the uphill enzyme conformational change (K_c = k_c/k_–c) and the activation barrier to hydride transfer (k_chem). The stepwise reaction (Figure 3) will be strongly preferred to as a competing concerted process in which the large enzyme conformational change is coupled to hydride transfer from NADL to GA because there is no advantage to coupling a large enzyme conformational change to hydride transfer. This coupling is required to reduce the barrier for the concerted process below that of the competing stepwise reaction.¹⁴ If the enzyme conformational change is cleanly separated from the hydride transfer step, then it will not influence the isotope effects reported in Table 1. Our results do not exclude the possibility that restricted local protein motions in the region of the transferred hydride at E_c·X^2–·GA·NADH are coupled to hydride transfer from NADL to GA, as has been proposed to occur for alcohol dehydrogenase.^9c

(4) The observation that the observed 1°DKIE is essentially independent of the magnitude of dianion activation (Table 1) provides strong support for the conclusion that these dianions afford different stabilization of the reactive closed enzyme conformation, which undergoes hydride transfer from NADL to GA through a common rate-determining transition state. This builds on our model for dianion activation: dianions play the active role of providing the necessary binding energy to lock enzymes into their catalytically active conformations,^6d−6f but serve as spectators while substrates GA and NADL are transformed to the transition states for hydride transfer.^10,11,15

The magnitude of these intrinsic 1°DKIE for hlGPDH-catalyzed reductions of GA by NADL (2.7 ± 0.3, Table 1) are slightly smaller than the calculated intrinsic 1°DKIE of ∼3.6 for hydride transfer catalyzed by alcohol dehydrogenase (ADH).^9aTable 1 offers novel and attractive targets for modeling experimental results by high-level ab initio calculations and presents a stringent test of the ability of calculations to generate a rate-determining transition state that reproduces the effect of dianion activators on the 1°DKIE for hlGPDH-catalyzed reduction of GA.

The experimental and calculated 1°DKIE on hydride transfer catalyzed by ADH and GPDH reflect the greater loss of zero-point energy for −H compared with −D, but require that a significant fraction of the ground state C–L zero-point energy be maintained at the transition state.^9a We note that the intrinsic 1°DKIEs from Table 1 are much smaller than for many enzyme-catalyzed hydrogen transfer reactions that occur mainly by quantum-mechanical tunneling through an energy barrier.¹⁶ Computational studies are consistent with quantum-mechanical tunneling of the transferred −H and −D at close to the top of the semiclassical free energy barrier to hydride transfer, but the resulting “tunnel correction” leads to only a modest increase in the velocity for transfer of −H compared to −D and in the 1°DKIE.^9a,9b These experimental and computational results show that the energy surfaces for enzymatic hydride transfer differ substantially from the surfaces for reactions where tunneling of −H compared with −D is strongly favored by the longer quantum mechanical wavelength for −H.¹⁷

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.6b07028.

• Procedures for preparation of hlGPDH, kinetic protocols, Michaelis–Menten-type plots of v_obs against [NADH] or [NADD] for hlGPDH-catalyzed reduction of DHAP, table of kinetic parameters derived from the fit of these data, Michaelis–Menten-type plots for FPO₃^2–, SO₄^2–, HOPO₃^2–, and S₂O₃^2– activated hlGPDH-catalyzed reduction of GA by NADH and NADD (PDF)

The authors declare no competing financial interest.