Heterozygosity Ratio, a Robust Global Genomic Measure of Autozygosity and Its Association with Height and Disease Risk

Abstract

Greater genetic variability in an individual is protective against recessive disease. However, existing quantifications of autozygosity, such as runs of homozygosity (ROH), have proved highly sensitive to genotyping density and have yielded inconclusive results about the relationship of diversity and disease risk. Using genotyping data from three data sets with >43,000 subjects, we demonstrated that an alternative approach to quantifying genetic variability, the heterozygosity ratio, is a robust measure of diversity and is positively associated with the nondisease trait height and several disease phenotypes in subjects of European ancestry. The heterozygosity ratio is the number of heterozygous sites in an individual divided by the number of nonreference homozygous sites and is strongly affected by the degree of genetic admixture of the population and varies across human populations. Unlike quantifications of ROH, the heterozygosity ratio is not sensitive to the density of genotyping performed. Our results establish the heterozygosity ratio as a powerful new statistic for exploring the patterns and phenotypic effects of different levels of genetic variation in populations.

CHARACTERIZING genetic diversity across individuals and populations is crucial for reconstructing recent human evolution and for understanding the genetic basis of complex diseases (Collins et al. 2003). Genome-level variability has most often been defined in terms of quantification of homozygosity, and the measure most commonly used today is the total length of runs of heterozygosity (ROH) (Gibson et al. 2006). The rationale for assessing ROH is that it quantifies inbreeding and that extended homozygosity regions increase the probability of homozygosity of rare deleterious variants (Szpiech et al. 2013). Most recently, a study found an inverse association between ROH and height (Joshi et al. 2015). Additionally, ROH has been associated with several diseases, especially those with neuropsychological traits (Keller et al. 2012; Gamsiz et al. 2013; Ghani et al. 2013; Gandin et al. 2015). However, the evidence is mixed, and several replication studies have found no significant associations of ROH with the same phenotypes (Vine et al. 2009; Sims et al. 2011; Heron et al. 2014). For example, Lencz et al. (2007) and Keller et al. (2012) reported that ROH was implicated as a risk factor for schizophrenia, but Heron et al. (2014) found no evidence to support this finding. Ghani et al. (2013) found connection between Alzheimer’s disease and ROH, but no evidence was found by Sims et al. (2011). This failure of replication has been blamed on the variability of the ROH calculation with the genotyping platform used, which is based on how uniformly the single-nucleotide polymorphism (SNP) probes on the platform are distributed throughout the genome (Ferencakovic et al. 2013; Power et al. 2014).

The genome-wide patterns of heterozygosity provide a valuable and often overlooked resource for examining human genetic diversity and evolutionary history. The argument for why genome-wide heterozygosity should associate with disease phenotypes is essentially the reverse of the argument given above. High levels of heterozygosity should correspond to lower risks of reinforcing rare deleterious variants, leading to protection from disease. Higher heterozygosity has been associated with lower blood pressure and cholesterol (Campbell et al. 2007; Govindaraju et al. 2009) and lower plasma cortisol (Zgaga et al. 2013). However, a recent study failed to find any significant associations of a heterozygosity measure and a range of endophenotypes with coronary heart disease (Mukamal et al. 2015).

Several different measures of heterozygosity have been used. Recently, Wang et al. (2015) defined a genome-wide measure of heterozygosity as the ratio of the number of heterozygous SNPs divided by the number of nonreference homozygous SNPs. We refer to this normalized measure of heterozygosity as the heterozygosity ratio. The normalization by the number of nonreference SNPs is intended to make this measure consistent across genome regions and between genotyping platforms. Guo et al. (2014b) presented an argument based on Hardy–Weinberg equilibrium (HWE) that the heterozygosity ratio should have a numerical value of 2, meaning that on average there should be twice the amount of heterozygous SNPs compared to nonreference homozygous SNPs. This argument is based on the assumptions of HWE, including random mating, that are often not true for real populations. A study has shown that the heterozygosity ratio is highly population dependent (Wang et al. 2015). The same study, based on 1000 Genomes phase 2 data, showed that African populations had the most genetically diverse population (heterozygosity ratio ≈2.0), East Asian populations had the lowest diversity (heterozygosity ratio ≈1.4), and American (heterozygosity ratio ≈1.7) and European (heterozygosity ratio ≈1.6) populations were intermediate (Wang et al. 2015). In addition, it was observed that unlike the transition/transversion ratio, the heterozygosity ratio is not dependent on genomic location, meaning that the heterozygosity ratios computed from SNPs from any particular regions (for example, the exome, intergenic regions, etc.) of the genome or from a sampling of SNPs [such as genome-wide association study (GWAS) data] remain equal (Wang et al. 2015). The heterozygosity ratio has been proposed as a quality control parameter for SNP data (Guo et al. 2014b,c) due to its stability within a race.

In this study, we report how the heterozygosity ratio varies across a broader range of populations, including the special population of first-generation admixture between European and African ancestry parents. We show that the heterozygosity ratio is positively correlated with height, a highly polygenic trait. We also carry out a phenome-wide association study (PheWAS) of the heterozygosity ratio and show that heterozygosity is protective against several pathogenic conditions.

Materials and Methods

Data set

To examine the population diversity of the heterozygosity ratio, we conducted thorough genetic analyses, using two independent data sets. The first data set is the SNP data released from the 1000 Genomes Project (1000G) phase 3 (Durbin et al. 2010) in May 2013, which contains 2504 individuals and 13,424,776 SNPs from 5 major geographic populations and 26 subpopulations (Table 1). We refer to this as the 1000G data set.

Table 1. Data set descriptions.

Data set	Population	Subpopulation abbreviation	No. of subjects	Median heterozygosity ratio	Heterozygosity ratio SD
1000G	AFR	ACB	96	2.00	0.04
		ASW	61	2.04	0.10
		ESN	99	1.92	0.03
		GWD	113	1.94	0.07
		LWK	99	1.96	0.02
		MSL	85	1.95	0.02
		YRI	108	1.92	0.02
	AMR	CLM	94	1.63	0.11
		MXL	64	1.55	0.13
		PEL	85	1.31	0.18
		PUR	104	1.70	0.09
	EUR	CEU	93	1.55	0.02
		FIN	103	1.52	0.02
		GBR	105	1.54	0.02
		IBS	104	1.56	0.03
		TSI	99	1.56	0.02
	EAS	CDX	99	1.31	0.04
		CHB	99	1.31	0.02
		CHS	91	1.31	0.02
		JPT	107	1.31	0.03
		KHV	107	1.33	0.02
	SAS	BEB	86	1.57	0.03
		GIH	103	1.55	0.03
		ITU	102	1.55	0.08
		PJL	96	1.57	0.09
		STU	102	1.54	0.08
BioVU	AFR	NA	4,751	1.73	0.13
	AMR	NA	1,233	1.63	0.19
	EUR	NA	30,851	1.55	0.07
	ASN	NA	426	1.36	0.05
	AFR-EUR	NA	412	2.16	0.51

ACB, African Caribbean in Barbados; AFR, African; AFR-EUR, African-European; AMR, American; ASN, Asian; ASW, African ancestry in Southwest United States; BEB, Bengali in Bangladesh; CDX, Chinese Dai in Xishuangbanna, China; CEU, Utah residents with Northern and Western European ancestry; CHB, Han Chinese in Bejing, China; CHS, Southern Han Chinese, China; CLM, Colombian in Medellin, Colombia; EAS, East Asian; ESN, Esan in Nigeria; EUR, European; FIN, Finnish in Finland; GBR, British in England and Scotland; GIH, Gujarati Indian in Houston; GWD, Gambian in Western Division, The Gambia; IBS, Iberian populations in Spain; ITU, Indian Telugu in the United Kingdom; JPT, Japanese in Tokyo; KHV, Kinh in Ho Chi Minh City, Vietnam; LWK, Luhya in Webuye, Kenya; MSL, Mende in Sierra Leone; MXL, Mexican Ancestry in Los Angeles; PEL, Peruvian in Lima, Peru; PJL, Punjabi in Lahore, Pakistan; PUR, Puerto Rican in Puerto Rico; SAS, South Asian; STU, Sri Lankan Tamil in the United Kingdom; TSI, Toscani in Italy; and YRI, Yoruba in Ibadan, Nigeria.

The second data set is a genotyping data set from the Vanderbilt University Medical Center’s electronic medical record and biobank, BioVU (Mosley et al. 2014), which contains 37,673 subjects with large-scale genotyping data available. We refer to the SNP data from BioVU as the BioVU data set. The BioVU data set was genotyped using the Illumina Human Exome Beadchip 12v1, which contains a total of 247,901 features (247,733 SNPs). The BioVU data primarily consist of Caucasian subjects (N = 30,851), but include Asian (N = 426), Hispanic (N = 1233), and African ancestry subjects (N = 4751). Important for our analysis, our BioVU data set also includes 412 individuals with nearly equal amounts of European and African ancestry that are likely a first-generation admixture (Table 1).

The BioVU data set was processed by Vanderbilt Technologies for Advanced Genomics Analysis and Research Design. The entire protocol for quality control and processing of the Exome chip data has been published (Guo et al. 2014a). Briefly, quality control tests were conducted in Illumina Genome Studio and in PLINK (Purcell et al. 2007). In Genome Studio, we filtered all subjects by a 98% call rate and SNPs by a 95% call rate, and we conducted manual reclustering based on multiple parameters, such as GenTrain score and cluster separation. All SNPs on the exome chip were converted to the HG19 reference genome forward strand. In PLINK, we quality controlled the BioVU data set for gender mismatches, relatedness, HWE, heterozygosity rate, and Mendelian error as stated in our protocol (Guo et al. 2014a). In addition to BioVU Exome chip data, a second Exome chip data set of 10,906 (case N = 5852, control N = 5054) Chinese subjects from the Shanghai Breast Cancer Genetic Study (SBCGS) (Cai et al. 2014) was used to test the association between heterozygosity ratio and height.

Principle component analysis

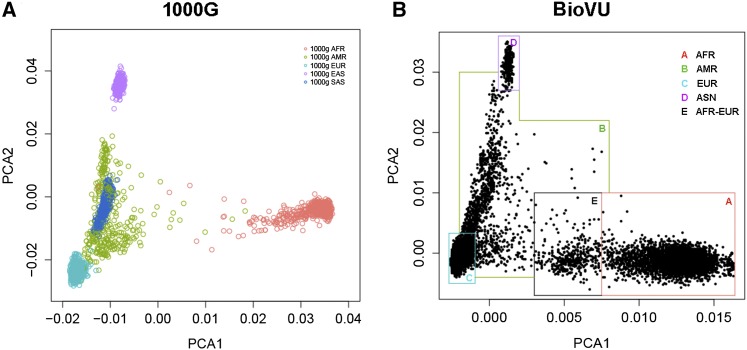
Clinical and demographic information, such as race, is subject to self-reporting and data recording errors. Often, simple race labels do not adequately describe complex situations, such as people of mixed ancestry. To quantify ancestry in the BioVU data set, we utilized principle component analysis (PCA) on the 2945 ancestry informative markers (AIMs) included on the Exome chip, and we distributed ∼1 marker per megabase across the autosomes and chromosome X. These markers were selected because they demonstrated strong differentiation power between African and European ancestry samples sequenced in the 1000 Genomes Project. We performed PCA on these AIM SNPs, using EIGENSTRAT (Price et al. 2006). A subject’s genetic ancestry, or race, can be determined by the location on the scatter plot drawn from the first and second principle components of all subjects (Figure 1). The genetically determined ancestry was then used in our analysis.

Figure 1.

(A) Scatter plot of PC1 and PC2 from 1000G data. (B) Scatter plot of PC1 and PC2 from of the BioVU data set. Boundaries were chosen by eye to define subpopulations for further analysis.

Heterozygosity ratio and structure analysis

The heterozygosity ratio for each subject was computed as the ratio between the number of genotyped heterozygous SNPs and the number of nonreference homozygous SNPs based on the GRCh37 reference sequence. Structure analyses were carried out using Structure 2.3.4 (Hubisz et al. 2009). ROH measures for 1000G data were computed using PLINK. The ROH for BioVU data were not computed due to the lack of density in SNPs of the Illumina Exome chip.

Genetic admixture for each population was computed using the Shannon entropy, using the formula $\text{admixture}={\displaystyle {\sum }_{i=1}^K\left(p_i{\log }_k{p}_i\right)}$, where K is the number of ancestry groups, and $p_i$ is the ancestry proportion of membership. For any population, the sum ${\displaystyle {\sum }_{i=1}^K\left(p_i\right)}$ should be equal to 1.

Allele frequency ratio

Based on Hardy–Weinberg equilibrium, we hypothesized that the distribution of allele frequency in a population can be used as an estimate of the median heterozygosity ratio in that population. To test this, we computed an estimated heterozygosity ratio defined as ${\displaystyle \sum 2p\left(1-p\right)}/{\displaystyle \sum p^2}$, where $p$ is the allele frequency of the nonreference allele and the sum is taken over all genotyped SNPs. The numerator is the sum of the probability of being heterozygous at each site, and the denominator is the sum of the probability of being a nonreference homozygote. Note that this estimate is computed over a population, and the actual heterozygosity ratio is computed on each subject individually.

Height association analysis and genetic score

We evaluated the association between the heterozygosity ratio and height in the BioVU exome chip data set, using a linear regression model in R v3.2.0, with height as the outcome and heterozygosity ratio as the predictor, adjusting for gender and a genetic score (GS) of height. The first five principal components were also included as covariates to correct for potential effects of population stratification within each population. In regressions including all subjects without stratification by listed race, the first five principle components were also included as covariates. SNPs associated with variation in height were identified from the U.S. National Human Genome Resource Institute (NHGRI) Catalog of Published Genome-Wide Association Studies in April 2014 (Hindorff et al. 2009) and were used to define a height GS. Only SNPs associated with height in a population of European ancestry were selected for this study. We selected independent SNPs, defined as pairwise linkage disequilibrium (LD) r² < 0.1 based on the International HapMap Project phase 3 data. For any two SNPs with an r² ≥ 0.1, the SNP with the lower P-value for association with height was selected. In total, 68 SNPs were selected for analysis from the exome chip (Supplemental Material, Table S1). An externally weighted GS was computed using the formula $\mathrm{GRS}={\displaystyle {\sum }_{i=1}^N{W}_i\mathrm{SN}{\mathrm{P}}_i}$, where N is the number of SNPs associated with height and available in the BioVU Exome chip data, $\mathrm{SN}{\mathrm{P}}_i$ is the genotype of the effect allele (coded as 0, 1, 2) of the ith SNP, and $W_i$ is the weight of the ith SNP. Two additional GSs were computed as a sensitivity analysis: an unweighted GS (uwGS) and an internal effect size weighted GS (iwGS). For the externally weighted height GS (ewGS), $W_i$ is the reported effect size (converted to the same unit) reported by published literature. For the uwGS, $W_i$ = 1; for iwGS, $W_i$ is the effect determined from BioVU data using a linear regression model with height as the outcome and SNP as the predictor and with adjustments made for gender and PC1–PC5. The GS analyses were limited to Caucasian subjects in BioVU, since the majority of the subjects are Caucasian and the majority of the reported height SNPs were also from Caucasian studies.

PheWAS analysis

BioVU has the advantage of containing electronic medical records from the Vanderbilt Medical Center. These records can be used in a PheWAS to test the relation of a specific genetic feature to the range of phenotypes captured by the medical record (Carroll et al. 2014). We used a PheWAS to test the relationship of one genetic predictor to multiple phenotypes (Denny et al. 2010). International Classification of Disease version 9 (ICD.9) codes and the dates on which they were coded were downloaded for each individual in our data set. These ICD.9 codes were aggregated into PheWAS codes, using the PheWAS package in R 3.2.0 (Carroll et al. 2014). An individual who had two or more ICD.9 codes on different days that contribute to the same PheWAS code was considered a case for that PheWAS code. Individuals who never had an occurrence of an ICD.9 code within a PheWAS code were considered controls for that group. Individuals who had only one occurrence of any ICD.9 code within a PheWAS group were excluded from analysis. Individuals who did not have an ICD.9 code within a PheWAS category, but who had related codes, were also exclusions for a category. We utilized PheWAS code groups that have been previously defined (Carroll et al. 2014). Associations were performed using logistic regression with the individual’s heterozygosity ratio as the predictor. PheWAS code statuses were used as the outcomes in all regressions. Gender and the median age of recorded ICD.9 codes were used as covariates. Subjects were classified as European or African ancestry based on principle components as described above and were tested separately. Since phenotypes captured by ICD.9 codes are highly correlated and therefore not independent, Bonferroni correction for multiple testing is overly conservative. To include the correlation structure of the phenotypes, we use the simple M method for multiple-testing correction (Gao et al. 2010).

Data availability

The 1000G data set used in this study is freely downloadable from http://www.1000genomes.org/. The heterozygosity ratios, relevant phenotype data from the BioVU data sets, are provided as supplementary material. R script for analyzing the height association data is also provided as supplemental files. The script used for PheWAS analysis can be found at https://medschool.vanderbilt.edu/cpm/center-precision-medicine-blog/phewas-r-package.

Results

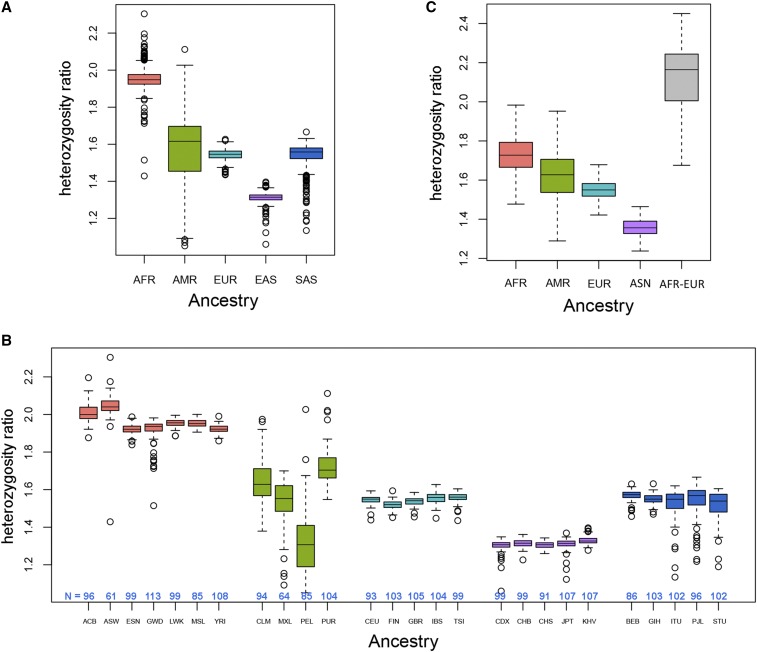
We first computed the heterozygosity ratio using the 1000 Genomes data. As expected, we found that the heterozygosity ratio was strongly associated with human ancestry. Africans had the highest heterozygosity ratio with a median of 1.95, followed by Americans, South Asians, and Europeans with median values of 1.62, 1.56, and 1.55, respectively. East Asians had the lowest heterozygosity ratio with a median of 1.31 (Figure 2, A and B). South Asian heterozygosity ratios were more similar to the European and American values than were East Asian values. Note that only the African population had a value close to the theoretical value of 2. In the 1000G project, five subpopulations of South Asian ancestry were available, two of which were Indian (Gujarati Indian from Houston and Indian Telugu from the United Kingdom). It has been shown that the Indian and European populations share common ancestry (2008) (Auton et al. 2009; Metspalu et al. 2011). Our analysis results based on the heterozygosity ratio suggest that the South Asians [Gujarati Indian from Houston (GIH), Punjabi in Lahore, Pakistan (PJL), Bengali in Bangladesh (BEB), Sri Lankan Tamil in the United Kingdon (STU), and Indian Telugu in the United Kingdom (ITU)] selected for the 1000G project have statistical genome characteristics that are more similar to Europeans and Americans than those of their East Asian neighbors.

Figure 2.

(A) Heterozygosity ratio distributions for the 5 major populations in 1000G. (B) Heterozygosity ratio distributions for the 26 subpopulations in 1000G. (C) Heterozygosity ratio distribution for the 4 major populations plus the first-generation admixed population (AFR-EUR) in BioVU.

Similar patterns for the heterozygosity ratio distribution were observed for the BioVU data compared to the 1000G data (Figure 2C). Subjects of primarily African ancestry (defined by PCA as described in Materials and Methods) had the highest (1.73) heterozygosity ratio, and subjects of Asian ancestry had the lowest heterozygosity ratio (1.36) with American (1.63) and European ancestry (1.55) in the middle. One interesting phenomenon is that the assumed first-generation admixture group between African and European ancestry had the highest heterozygosity ratio at 2.16. This high heterozygosity ratio should be expected for the first generation of admixture between two previously separated populations. The SNPs that are highly different in frequency between the African and European populations (those that we use as AIMs) will result in a higher number of heterozygous SNPs and a lower number of nonreference homozygous SNPs in the first-generation admixture offspring, thereby increasing the ratio.

The African ancestry subjects had the highest heterozygosity ratio in both the 1000G and the BioVU data except for the BioVU first-generation admixture group. This is caused by the higher number of available alternative alleles existing in the more diverse African population. To assess this, we counted the number of possible alternative alleles in each population for both the 1000G and BioVU data sets. After normalizing to sample size by population, Africans had the highest number of available alternative alleles, followed closely by the first-generation admixture group from BioVU (Figure S1). Europeans had the lowest number of available alternative alleles, followed by East Asians, South Asians, and Americans.

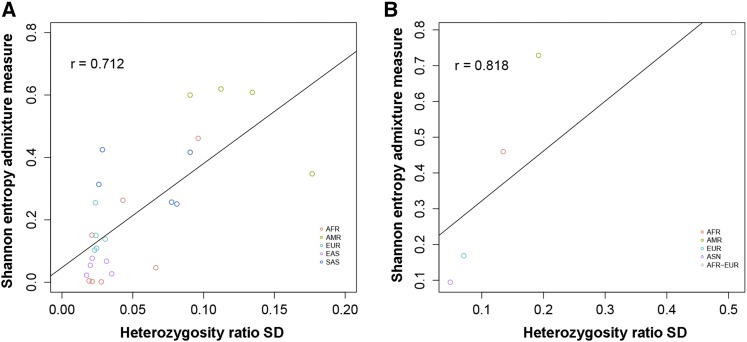
The 1000G American populations showed the highest variation (SD = 0.13) in heterozygosity ratio compared to other major populations (Table 1). Within American subjects, four subpopulations [Mexican ancestry in Los Angeles (MXL), Puerto Rican in Puerto Rico (PUR), Colombian in Medellin, Colombia (CLM), and Peruvian in Lima, Peru (PEL)] were included in 1000 Genomes. There were distinct differences within the four American subpopulations (Figure 1B). Peruvians had the lowest heterozygosity ratio (1.31), which is on the same level as the East Asian populations. The American populations in both 1000 Genomes and BioVU had large variation in the heterozygosity ratio (Figure 1, A and B). Structure analysis (Figure S2) showed that the American group has more ancestry groups than the other continental populations. We hypothesized that there is an association between the amount of genetic admixture of a population and the variability across individuals in the heterozygosity ratio. To test our hypothesis, we quantified the genetic admixture for each population based on Shannon entropy. The admixture measure ranges from 0 to 1, where 0 means that a single ancestry group is present, and 1 means all K ancestry groups are equally present. The scatter plot between the 26 subpopulations’ genetic admixture and the standard deviation of the heterozygosity ratio shows a strong positive correlation (1000G Spearman r = 0.712, BioVU Spearman r = 0.818) (Figure 3, A and B). Correlation analysis for the heterozygosity ratio itself (not the standard deviation) vs. admixture shows no significant correlation (Figure S3).

Figure 3.

(A) Scatter plot and correlation for the admixture measure vs. the standard deviation of the heterozygosity ratio based on the 26 subpopulations in 1000G. (B) Scatter plot and correlation for admixture vs. heterozygosity based on the 5 populations in BioVU.

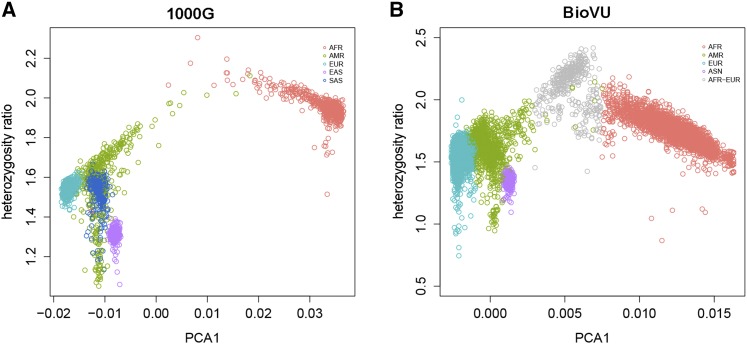
The heterozygosity ratio shows a very strong nonlinear relationship with the first principle component in both the 1000 Genomes and the BioVU data sets (Figure 4). In both sets, the first principle component separates European ancestry (to the negative side) from African ancestry (to the positive side). The heterozygosity ratio shows a strong inverted V pattern with PCA1. The peak heterozygosity value is in subjects with nearly equal European and African ancestry, and the heterozygosity ratio decreases linearly (with different slopes) as subjects extend to either extreme of pure African or European ancestry.

Figure 4.

(A) Scatter plot of heterozygosity ratio vs. PC1 in 1000G. (B) Scatter plot of heterozygosity ratio vs. PC1 in BioVU.

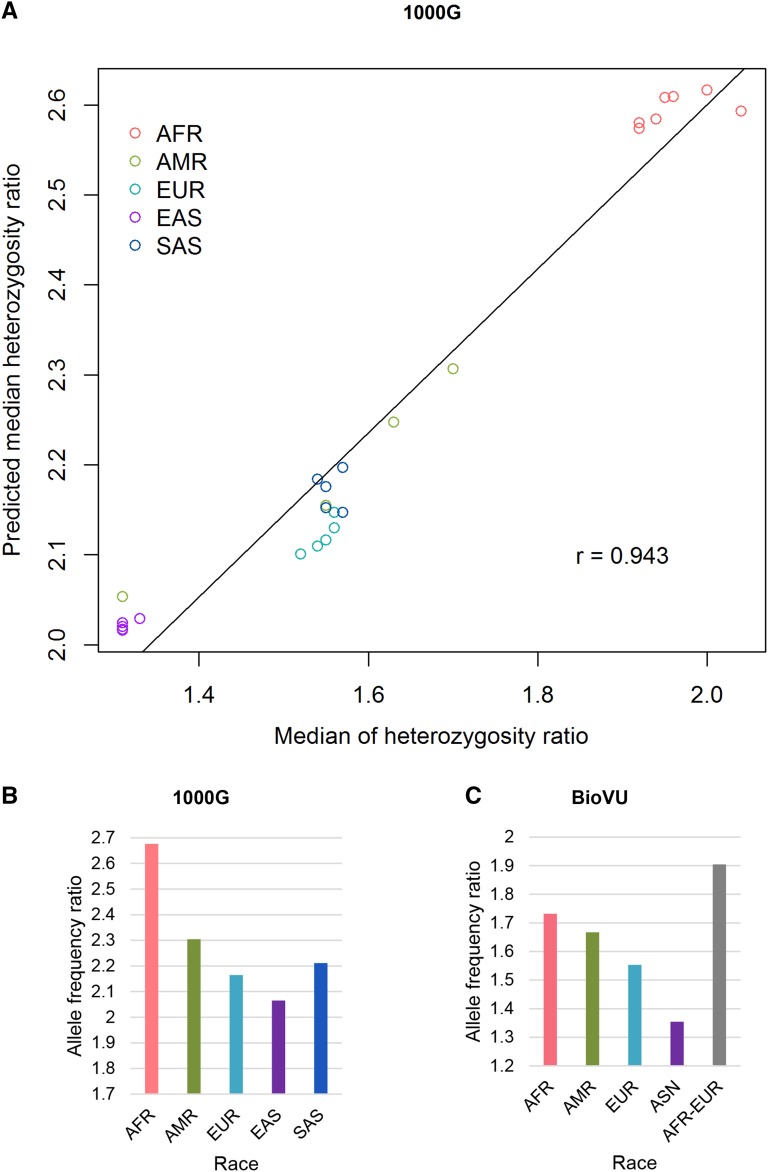
We hypothesized that the median heterozygosity ratio within a population could be estimated from the allele frequencies in that population based on predicted numbers of heterozygote and nonreference homozygote sites (see Materials and Methods for details). To test this, we computed the predicted ratio from the allele frequencies for the 1000G subpopulation data (Figure 5A). As expected, a high correlation was observed between the predicted ratios and the median measured heterozygosity ratios (Spearman r = 0.976). However, the predicted ratios based on allele frequencies were consistently higher than the median measured heterozygosity ratio. When comparing between the 1000G and BioVU exome chip data sets for comparable population groups, we observed large differences between the predicted ratios from allele frequencies (Figure 5, B and C), although the trends across population groups were similar between the two data sets.

Figure 5.

(A) Scatter plot between median measured heterozygosity ratio (x-axis) and the predicted median value based on allele frequencies in that population. (B) Predicted median heterozygosity ratios from the 1000G data set for major populations. (C) Predicted median heterozygosity ratios from the BioVU Exome chip data set for major populations. There is large difference in magnitude between the predicted ratios for the comparable populations computed in the two different data sets.

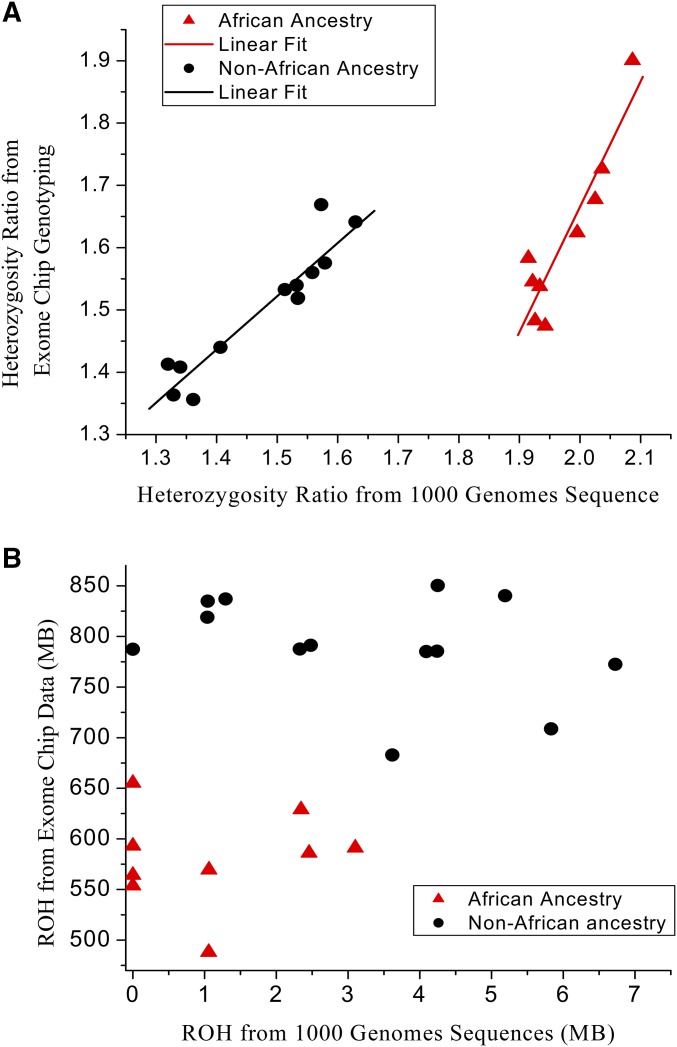
An alternative measure of genome-level variability is the ROH measure. Large values of ROH indicate a lack of genetic variability in the individual. Broadly, one would expect that ROH and the heterozygosity ratio should have an inverse relationship. We tested this by computing the ROH for the 1000 Genomes data to compare against the heterozygosity ratio values. The BioVU data were not used in this test since only Exome chip data were available for that group and we found that SNP distribution across the chromosomes on that chip was not dense enough for a reliable ROH calculation. Based on our previous study, which proved that the heterozygosity ratio is independent of genomic regions (Wang et al. 2015), we hypothesized that the heterozygosity ratio is independent of SNP density in contrast to ROH, which is highly dependent on SNP density. The 1000G data contain ∼13,424,000 SNPs, whereas the BioVU data contain ∼240,000 SNPs, a 56-fold difference. The ROH computed from 1000G data are predicted to be much smaller due to the higher SNP density. On the other hand, the heterozygosity ratio should not be affected much, since its definition as a ratio of two measures allows it to be estimated from a sampling of SNPs. To test our hypothesis, we examined the heterozygosity ratio and ROH for 22 HapMap samples [9 African (AFR), 4 American (AMR), 4 East Asian (EAS), and 5 European (EUR)] measured from five different genotyping sources (1000G, Exome chip, Metabo Chip, OMNI1, and OMNI5). We computed the intraclass correlation (ICC) for the heterozygosity ratio and the ROH computed from all five sources (Table S2). The heterozygosity ratio achieved an ICC of 0.80 and the ROH had an ICC of only 0.17. The heterozygosity ratio is clearly more consistently computed than was ROH across these highly diverse genotyping platforms. Using the two SNP sources (1000G vs. Exome chip) with extreme SNP density difference as an example, there is a strong linear relationship for the heterozygosity ratio, but no linear relationship for ROH (Figure 6). An interesting phenomenon observed was that AFR subjects form their own group for both the heterozygosity ratio and ROH. For the heterozygosity ratio, there is a shift of −0.4 to −0.5 for AFR subjects. We suspect this is caused by the density of the SNPs and the fact that the selection of the SNPs on the Exome chip is more focused on rare SNPs, which will affect the ROH measure in people of African and European ancestry differently.

Figure 6.

(A) Scatter plot of heterozygosity ratio for 22 HapMap samples measured from both Exome chip and 1000G genotyping data. (B) Scatter plot of ROH for the same 22 HapMap samples measured from Exome chip and 1000G data.

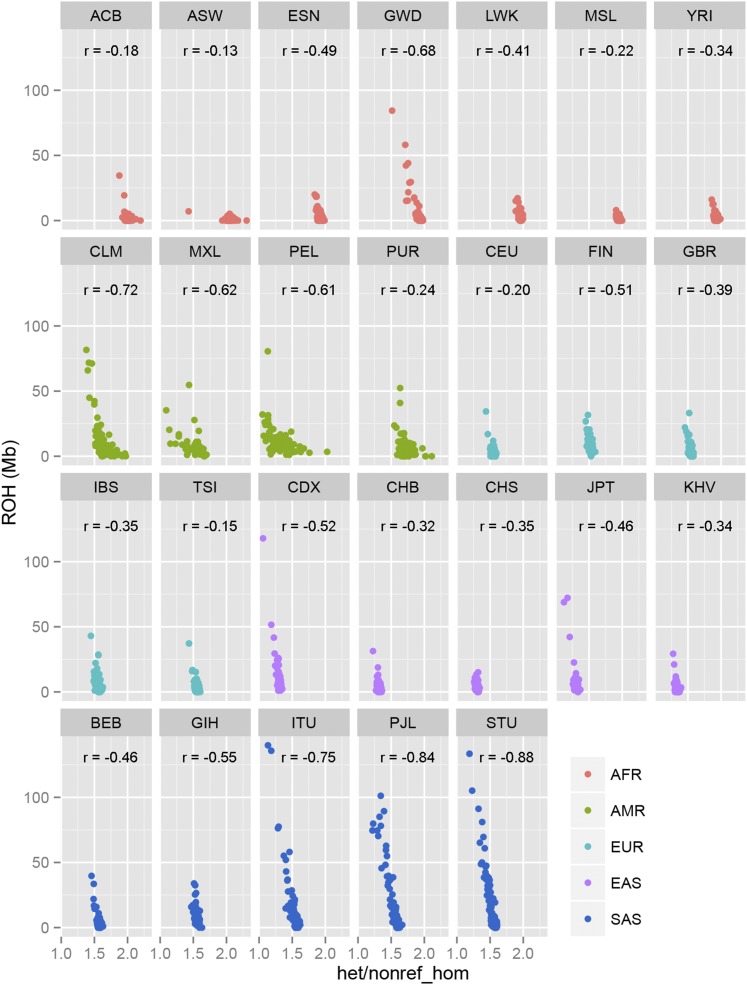
Additionally, using 1000G data as an example, we show that the heterozygosity ratio is highly negatively correlated with ROH in all subpopulations (Figure 7). To further demonstrate that the heterozygosity ratio is a more stable measure than ROH we conducted a subsampling test by randomly selecting 50,000 SNPs 50 times from the same aforementioned 22 HapMap subjects that were genotyped on Illumina’s Exome chip. Using these SNPs, we compared the heterozygosity ratio and ROH computed from these 50,000 SNPs to the heterozygosity ratio and ROH computed using all SNPs and found that the subsampled heterozygosity ratio was much more close to the initial value than was ROH (Figure S4).

Figure 7.

Scatter plots of 26 1000G subpopulations between the heterozygosity ratio and ROH.

Lower genetic variability may have deleterious effects. As a simple test of this hypothesis, we considered height as an easily quantified highly polygenic trait. Height has been negatively associated with higher ROH (McQuillan et al. 2012; Joshi et al. 2015). Based on this, we predicted that height would increase with a greater heterozygosity ratio. Using the clinical data within BioVU, we restricted our analysis to adults, determining the height for each individual with birth dates before 1980. Using linear regression of height with the heterozygosity ratio and adjusting for gender and PCs, we found in subjects of European ancestry a significant positive association of height with heterozygosity ratio, with an increase of 5.43 cm in height per unit increase of heterozygosity ratio (P = 1.18 × 10⁻⁸) (Table 2). Since the heterozygosity ratio is calculated using all available SNP data, it contains specific SNPs that have been associated with height. To test whether the significant association of the heterozygosity ratio is due to the known height GWAS hits, we constructed an ewGS based on published SNP associations (see Materials and Methods for details). After adjusting for the height ewGS (weighted and unweighted), the heterozygosity ratio remained positively significantly associated with height (P = 1.37 × 10⁻⁸), indicating that the heterozygosity ratio contributes new significant predictive power beyond what is captured by known height SNPs. After stratifying European subjects by gender, significant positive associations remained. The effect is stronger in EUR female subjects (P = 1.16 × 10⁻⁶) than in male subjects (P = 0.002). The sensitivity analyses using unweighted and internally weighted GS also reached the same conclusion (Table S3). In the African population of the BioVU Exome chip data set and the Asian female population in the SBCGS data sets, no significant association between heterozygosity ratio and height was observed.

Table 2. Associations between height and HR.

Subjects	Predictor	Effect	SE	P
EUR all (N = 19,545)	HR	5.4289	0.9515	1.18 × 10−8
	ewGS + HR	5.2940	0.9502	1.37 × 10−8
EUR male (N = 8,827)	HR	4.5482	1.4694	0.0020
EUR female (N = 10,718)	HR	6.0522	1.2440	1.16 × 10−6
AFR all (N = 1,964)	HR	3.1035	2.9578	0.29
AFR male (N = 747)	HR	7.1570	4.8740	0.14
AFR female (N = 1,217)	HR	−0.3538	3.7132	0.92
CHN female (N = 7,629)	HR	−0.2651	1.0601	0.80

Subjects used in the models were with date of birth >1980. In all models, gender and PC1–PC5 were also adjusted for models that used all subjects. AFR, African; CHN, Chinese; EUR, European; HR, heterozygosity ratio.

A PheWAS uses the ICD.9 billing codes contained in each individual’s electronic medical record as a proxy for the medically relevant phenotypes of that patient. Similar ICD.9 codes are grouped together into phenotype categories (Denny et al. 2010). In a PheWAS analysis on the BioVU data set in subjects of European ancestry adjusting for gender and PCs, the heterozygosity ratio showed a significant association in four phenotypes: disturbances of amino acid transport, abscess of oral soft tissue, renal colic, and open wounds of extremities (significance determined with simple-m adjustment for multiple-phenotype testing). In the smaller group of African ancestry subjects, one phenotype was significantly associated with the heterozygosity ratio: iron deficiency anemia. Data for these results are given in Table S1. All five significant effects were protective, with individuals of higher heterozygosity having fewer cases of the disease phenotype. This uniform protective effect against deleterious phenotypes is consistent with the hypothesis that higher heterozygosity is protective. The strongest association was with disturbances of amino acid transport (P = 2.00 × 10⁻⁵) (Table 3).

Table 3. Significant phenome-wide association study results for the heterozygosity ratio.

Phenotype	Population	Cases	Controls	ICD.9 codes	β	SE	P
Disturbances of amino acid transport	EUR	48	22,276	270, 270.1, 270.2, 270.3	−6.15	1.4	1.90 × 10−5
Cellulitis and abscess of oral soft tissues	EUR	29	22,096	527.3, 528.3	−6.82	1.8	0.0001
Renal colic	EUR	27	21,962	788	−6.7	1.8	0.0002
Open wounds of extremities	EUR	599	20,877	880, 881, 884, 890, 891, 894, 905.8, 906.1	−2.61	0.7	0.0002
Iron deficiency anemias	AFR	284	1,454	280	−2.54	0.7	0.0002

AFR, Africans; EUR, Europeans; SE, standard error.

Discussion

In this study, we thoroughly examined the intrinsic relationship of heterozygosity ratio across ethnic groups. Using 1000G data, we were able to compare 26 subpopulations and observed different levels of variation for the heterozygosity ratio among the subpopulations within a major ancestry. The highest heterozygosity ratio displayed by subjects of African ancestry can be explained by the high level of genetic diversity in Africans (Campbell and Tishkoff 2008). Using BioVU’s Exome chip data, we showed that the first-generation admixture group between African and European ancestry had an elevated heterozygosity ratio in comparison to their parental populations. We hypothesize that the different homozygous loci between subjects of European and African ancestry (the parents of this population) create additional heterozygous loci in these subjects, pushing the heterozygosity ratio upward. Carrying this concept over to the global 1000G data set, we showed that the variation in the heterozygosity ratio is correlated with the levels of genetic admixture of each subpopulation.

The heterozygosity ratio is defined as the number of heterozygous sites divided by the number of homozygous nonreference sites. The numerator of the ratio will not be changed by the choice of the reference sequence. The denominator will change depending on the reference. Individuals from populations genetically farther from the reference sequence will tend to have more nonreference homozygous sites and thus smaller ratios. However, that potential bias due the choice of the reference sequence (currently of European descent) is not strongly affecting the global population data (Figure 2). Europeans do not have the largest median heterozygosity ratio. The patterns that are present, with highest heterozygosity ratios in the recently admixed populations followed closely by the highly diverse African population, are clearly driven by population differences in the numerator of the ratio, the number of heterozygous sites.

Our result in Figure 4 shows that the predicted median heterozygosity ratio, based on the principles of Hardy–Weinberg equilibrium, from allele frequencies in the population is highly correlated with the median measured heterozygosity ratio within a data set when values across several populations were compared. However, this approach can predict only the median value within a population and does not tell us anything about the heterozygosity ratio of a particular individual within that population.

An ROH is defined as a genomic region where no heterozygous loci are observed, and this measure has been the subject of interest in genetic association studies (Vine et al. 2009; Sims et al. 2011; Keller et al. 2012; Gamsiz et al. 2013; Ghani et al. 2013; Heron et al. 2014; Gandin et al. 2015; Joshi et al. 2015). Here, we demonstrated that ROH is an unstable measurement and is highly dependent on the density of the SNP measurements. More densely measured SNP data naturally tend to produce smaller segments of ROH. This imprecision of ROH measurement probably has contributed to the lack of success in verification of some of the association findings for ROH (Vine et al. 2009; Sims et al. 2011; Heron et al. 2014). In contrast, we showed that the heterozygosity ratio is a much more reliable measurement because it does not greatly vary by genotyped SNP density. The heterozygosity ratio is a global measure of genetic variation that can be calculated reliably on a single individual. In contrast, a measure such as principle components represents how an individual relates to a larger population, without containing any direct information about the level of genetic variation in the individual. Ideally, the ROH measure should be closely and inversely related to the heterozygosity ratio. The ROH of an individual is mainly affected by very recent inbreeding or population bottlenecks, leading to increased homozygosity. As we have shown in this article, the heterozygosity ratio is strongly affected by the overall genetic variability of the individual’s pool of ancestors. However, ROH suffers from a strong sensitivity to genotyping density, while the heterozygosity ratio can be consistently calculated over several different choices of SNPs (Table S2).

Our findings show that the heterozygosity ratio is positively associated with height in subjects with European ancestry. The association is strongest within European ancestry female subjects. We speculate that the null association observed for Asian female subjects was caused by the inherent smaller standard deviation in height and heterozygosity ratio in this population, and the null association observed in African subjects was due to small sample size. Through PheWAS analysis, we also observed associations between several disease phenotypes and heterozygosity ratios. Height is a classic example of a polygenic trait, with large numbers of genes contributing to the eventual adult height. As a global genomic measurement, the heterozygosity ratio has the potential to represent highly polygenic traits well. One simple example of the strength of this method is to consider how much height difference is explained by 1 SD difference in the heterozygosity ratio for a population, compared to a SD change in the height GS. In our complete European ancestry data set, the SD of the heterozygosity ratio was 0.07, giving a change of (5.083 × 0.07 = 0.36 cm) based on the model in Table 2. The SD of the height ewGS was 1.77, giving a change of (0.108 × 1.77 = 0.19 cm). Thus, the heterozygosity ratio explains more of the range of height than did the ewGS.

Other polygenic traits may also tend to be associated with the heterozygosity ratio, as we have shown for height. Our analysis shows that the genomic heterozygosity ratio carries useful information that is lost in genetic scores based on a limited selection of significant SNPs and may help explain some of the questions still remaining concerning heritability, particularly missing heritability. Given the simplicity and the robustness of the computation of heterozygosity ratio, it should not be overlooked in future genetic studies.