Different Mechanisms of Longevity in Long-Lived Mouse and Caenorhabditis elegans Mutants Revealed by Statistical Analysis of Mortality Rates

Abstract

Mouse and Caenorhabditis elegans mutants with altered life spans are being used to investigate the aging process and how genes determine life span. The survival of a population can be modeled by the Gompertz function, which comprises two parameters. One of these parameters (“G”) describes the rate at which mortality accelerates with age and is often described as the “rate of aging.” The other parameter (“A”) may correspond to the organism’s baseline vulnerability to deleterious effects of disease and the environment. We show that, in mice, life-span-extending mutations systematically fail to affect the age-dependent acceleration of mortality (G), but instead affect only baseline vulnerability (A). This remains true even when comparing strains maintained under identical environmental conditions. In contrast, life-span-extending mutations in C. elegans were associated with decreases in G. These observations on mortality rate kinetics suggest that the mechanisms of aging in mammals might fundamentally differ from those in nematodes.

THE aging process can be studied by investigating genetic variants that alter life span in model organisms (Finch and Ruvkun 2001; Hekimi 2006). For example, the fact that mutations of genes involved in the insulin/insulin-like signaling pathway can extend life span in Caenorhabditis elegans, Drosophila, and mice is considered to imply a role for this pathway in the aging process (Kenyon 2010). Likewise, a role for mitochondrial function in aging is suggested by the finding that impairments to mitochondrial function can extend lifespan in C. elegans and mice (Ewbank et al. 1997; Feng et al. 2001; Dillin et al. 2002; Lee et al. 2003; Liu et al. 2005; Hughes and Hekimi 2011; Wang and Hekimi 2015).

Another point of view is provided by the study of mutations in a number of genes that induce segmental progeroid syndromes and shorten life span in mice. The short life span of these mutant mice is accompanied by the accelerated expression of some of the phenotypes commonly encountered in aging (Mounkes et al. 2003; Wong et al. 2003; Baker et al. 2004; Chang et al. 2004; Trifunovic et al. 2004). While these have often been presented as representing alterations to the aging process, it remains possible that their shorter life spans are caused by the induction of specific pathologies that only mimic aspects of the actual aging process (Harrison 1994; Miller 2004).

It has also been argued that an extension of life span may not necessarily be concrete evidence of a retardation of the aging process (Orr et al. 2003; De Magalhaes et al. 2005; Ladiges et al. 2009). In this view, a life-span-extending intervention may simply remedy deficiencies in the environment or in the genetic makeup of one particular strain. The intervention would therefore extend life span by correcting specific flaws rather than altering the aging process. These considerations create a conundrum: If life span is not a reliable measure of aging, how can we confirm that a particular manipulation truly affects the aging process? One approach is to assess physiological phenotypes that are known to deteriorate with age, such as cognition or the functioning of the cardiovascular or immune systems, to detect similarities or discrepancies with the patterns observed in control strains. An alternative criterion is to consider whether a particular manipulation changes how mortality rates increase with age (Sacher 1977; Finch et al. 1990; De Magalhaes et al. 2005; Yen and Mobbs 2010). This is based on the hypothesis that the increased incidence of the age-related pathological changes that characterize the aging process is reflected in changing mortality rates.

Human mortality rates increase exponentially with age, as first noted and quantified by Benjamin Gompertz in 1825 (described by Olshansky and Carnes 1997). This property has subsequently been observed for the mortality rates of model organisms including mice, Drosophila, and C. elegans (Johnson 1987; Gavrilov and Gavrilova 1991; De Magalhaes et al. 2005). The Gompertz model of mortality is commonly expressed by the following equation, where the mortality rate (R) can be represented at any age (t) for a given population by

$$\mathit{R}\left(\mathit{t}\right)=\mathit{A}{\mathit{e}}^{\mathit{Gt}}.$$

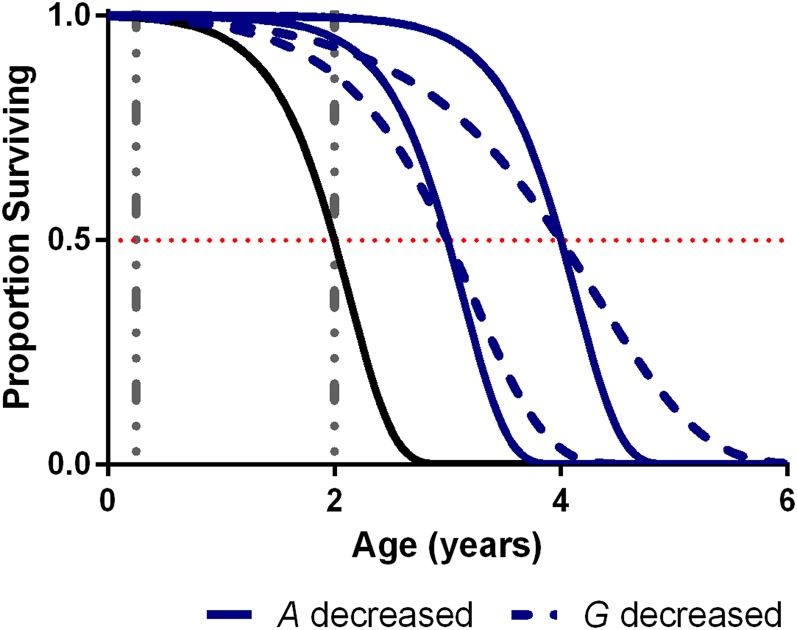
“G” describes the rate at which mortality rates accelerate with age and “A” represents the initial mortality rate at time 0 (Finch 1990). “A” is strictly theoretical as a mortality rate, since there can be no actual mortality at time 0. Instead, it can be determined by extrapolation from mortality rates at greater ages and does not necessarily correspond to true mortality rates at birth or during youth. Figure 1 shows how changes to the Gompertz parameters affect the survival curve of a hypothetical population of mice with a median life span of 2 years (solid black line). Decreasing A (solid blue lines) extends life span by shifting the inflection point of the curve rightward, such that it occurs proportionally later in age, relative to maximum life span. There is no change in the apparent “slope” of the curve. In contrast, decreasing G (dashed blue lines) decreases the slope.

Figure 1.

The effect of changing Gompertz parameters on the appearance of survival curves. A “baseline” survival curve with a median life span of 2 years is shown in black [G = 2.6, ln(A) = −4.6]. Increased life spans (median life span of 3 and 4 years) obtained by decreasing A [ln(A) of −7.2 and −9.8] while keeping G fixed are shown as solid blue lines. Increased life spans obtained by decreasing G (to 1.6 and 1.1) while keeping A fixed are shown as dashed blue lines. Vertical dashed lines show typical ages used for assessment of changes to age-dependent pathologies in mice.

A has been described as measuring the vulnerability to disease unrelated to the onset of aging (Sacher 1977) or the effect of the environment on mortality (Finch et al. 1990). Changes to A will alter mortality rates evenly across the life span of the population. In contrast, since the parameter G can be considered a rate constant for the age-related increase of mortality of a sample or population, it is often given a preeminent role as an indicator of the “rate of aging” (Sacher 1977; Finch et al. 1990). This is a logical hypothesis, since an increased or decreased G would likely reflect the rate at which physiological conditions are declining with age. Therefore it is often assumed that interventions that extend life span by slowing aging, rather than by alleviating some age-independent pathology, will be associated with a decreased G; likewise, those that accelerate aging would be associated with an increased G (Takeda et al. 1981; Finch et al. 1990; Honda et al. 1993; Pletcher et al. 2000; De Magalhaes et al. 2005; Merry 2005; Yen et al. 2008; Tricoire and Rera 2015). It should be noted, however, that some have argued against this viewpoint and suggest that G should not be assigned a dominant role as a measure of aging (Driver 2001; Masoro 2006).

Although the Gompertz model seems to fit survival curves for many human and model organisms, it can be modified to provide a better fit. It can include additional terms that account for mortality rates that plateau at later ages (logistic model), deaths due to exogenous, non-aging-related environmental causes (Makeham model), or both (i.e., logistic–Makeham) (Wilson 1994). Some caution is necessary, however, when interpreting survival curves that appear to be better fitted by more complex variants. For example, if the survival curve of a population is not optimally fitted by a particular model, then the addition of further parameters will naturally allow for more flexibility to adjust the model to the survival curve, without necessarily being informative about the underlying biology (Wilson 1994). Furthermore, a population of ≥100 is necessary to reliably determine which model best fits a particular distribution (Wilson 1994). Since most life span studies in mice use fewer animals than this, it is reasonable to use the simplest possible model in these cases, i.e., the Gompertz model.

Using this model, some studies observed a decreased G in cohorts of long-lived mice (Lapointe et al. 2009; Hughes and Hekimi 2011). However, a recent analysis of 29 published life span studies found this to be relatively rare in mice subjected to life-span-extending dietary or genetic manipulations (Yen et al. 2008). Instead, it was changes in A, not G, that were most frequently observed, with 4 of 12 long-lived strains having a statistically significant increase in A, but only 1 of 12 having a decreased G. Strikingly, the remainder did not exhibit any statistically significant changes in Gompertz parameters. Life-span-shortening interventions were somewhat more likely to be associated with decreases in G, with 6 of 15 short-lived strains associated with a statistically significantly decrease in G and 5 with a decrease in A. We theorized that actual changes in the parameters are being masked by the relatively small sample sizes that often characterize life span studies in mice and that looking at individual studies by this method will fail to reveal systemic relationships between changes to life span and Gompertz parameters.

Since a substantial number of studies reporting changes in mouse life span resulting from genetic manipulations have now been published, we hypothesized that a correlation-based approach may be a more powerful technique to search for patterns in Gompertz parameter shifts. For example, a negative correlation between life span and G across long-lived lines of mice would suggest that their extended longevity was due to a decreased rate of aging.

Dramatic changes in mortality rate trajectories have been reported across different species (Jones et al. 2014), demonstrating the importance of studying these phenomena in diverse model organisms. The nematode roundworm C. elegans has been used to identify many life-span-extending and -shortening mutations. The strength of invertebrate model systems such as C. elegans for aging research is their short life span and the possibility to repeatedly carry out experiments with very large cohorts, as well as the possibility to identify mutants with very large increases in life span. Early studies with this organism established that C. elegans mortality patterns apparently followed the Gompertz model (Johnson 1990; Honda and Matsuo 1992; Vanfleteren et al. 1998), with variations depending on growth conditions (Vanfleteren et al. 1998). Later studies investigated whether the environment and mutations could alter Gompertz parameters in this organism (Lenaerts et al. 2007; Wu et al. 2009; Yen and Mobbs 2010). We therefore elected to analyze short- and long-lived C. elegans as a comparator to our analysis of mice.

By the straightforward method of plotting Gompertz parameters against life span we found that most of the genetically driven variability in life span between normal- and long-lived groups of mice was due to changes in A, not G. In fact, G remained remarkably invariant for different groups of wild-type mice as well as for mice with genetic variations that extend life span. The only exceptions to this trend were some interventions that acutely shortened life span. We also found this to be true for a collection of inbred mouse strains studied under uniform conditions as part of the Mouse Phenome Database at The Jackson Laboratory (Yuan et al. 2009). Thus, with the exception of some severe life-span-shortening interventions, life span in laboratory mice is largely determined by factors that affect initial vulnerability, rather than age-dependent mortality rate acceleration. In contrast to mice, we found life span to be associated with changes in G, not A, among long-lived C. elegans mutants. This was true as a trend across long-lived mutants and was also observed by analyzing changes to Gompertz parameters among numerous replicate studies of the well-characterized daf-2, isp-1, and eat-2 mutants.

Materials and Methods

Estimation of Gompertz parameters

To estimate Gompertz parameters, numerical survival data were extracted from published Kaplan–Meier survival curves, using Engauge Digitizer 6.2 (Mark Mitchell, http://markummitchell.github.io/engauge-digitizer/). Survival data were divided into 10- or 1-day intervals for mice and C. elegans, respectively, and Gompertz parameters were determined by maximum-likelihood estimation (MLE) using WinModest 1.0.2 (Pletcher 1999), according to the Gompertz or logistics hazard functions (Pletcher et al. 2000):

$$\text{Gompertz:}\hspace{1em}\mathit{R}\left(\mathit{t}\right)=\mathit{A}{\mathit{e}}^{\mathit{Gt}}$$

$$\text{Logistic:}\hspace{1em}\mathit{R}\left(\mathit{t}\right)=\left(\mathit{A}{\mathit{e}}^{\mathit{Gt}}\right)/\left[\text{1}+\mathit{L}\left(\mathit{A}/\mathit{G}\right)\left({\mathit{e}}^{\mathit{Gt}}\mathrm{-}\text{1}\right)\right].$$

All estimates had associated inform values of “0,” indicating that the maximum-likelihood procedure was able to successfully resolve parameters within the given range and that asymptotic confidence intervals could be calculated. For all groups, the accuracy of the estimation was graphically confirmed by overlaying the resulting Gompertz survival function on the raw survival data, using Prism 6 (GraphPad Software).

For C. elegans, initial analysis using the logistic model yielded a clear bimodal distribution of values across strains for the logistic parameter “L”, with clusters of value >0.01 and <1 × 10⁵. Parameters in this lower group were more difficult to determine by MLE, with many appearing to resolve to arbitrarily small values without resulting in further changes to A or G. We therefore set these values to 0.

Model comparison

We used WinModest’s likelihood theory-based tools to determine which model (among Gompertz, logistic, Makeham, and logistic–Makeham) provided the best fit for C. elegans survival curves. This methodology takes into account the fact that models with additional parameters will naturally be less constrained when attempting to fit to a data set and therefore identifies the mortality model with the fewest parameters that fits the data sufficiently. This method is therefore superior to simple comparison of correlation coefficients obtained by regression-based methods.

General statistics

Nonparametric Spearman correlation was used to quantify the relationship between life span and Gompertz parameters. Prism was used to determine Spearman correlation coefficients and perform significance tests. For all tests a P-value <0.05 was taken to indicate statistical significance.

For pairwise comparisons between values of mutant and control parameters, differences (mutant minus control) were used rather than ratios because of the presence of negative or extremely low values. The nonparametric Wilcoxon signed-rank test was used to determine whether the average effect size was significantly different from 0. As an additional method of investigating the role of Gompertz parameters in alterations to life span, we used WinModest’s longevity decomposition tool to determine the extent to which the differences in Gompertz parameters between control and mutant groups contributed to changes in life span (Pletcher et al. 2000).

VBA code used to generate the simulated data described in supplemental figures is provided in File S2, as a macro-enabled workbook for Microsoft Excel 2010.

Data availability

The authors state that all data necessary for confirming the conclusions presented in the article are represented fully within the article or Supplemental Material (File S1).

Results

Life span of normal or genetically modified long-lived mice is largely determined by changes to A, not G

To calculate Gompertz parameters, one requires numerical survival data beyond what is typically provided in published reports. Gompertz parameters for a number of short- and long-lived strains have previously been determined (Yen et al. 2008), and we included those in our analysis (set 1, summarized in Table S1; note that we did not include calorically restricted groups in our analysis). We divided the mice into groups based on their life spans. Short-lived mice were defined as those subjected to genetic manipulations that shortened life span relative to that of controls. We also included in this group lines of mice known to have average life spans markedly shorter than those of conventional lines of laboratory mice, namely NZB/W mice, which are known to suffer from severe autoimmune disease (Partridge et al. 2005), and senescence-accelerated mice (SAM) as well as their “senescence-resistant” (SRM) controls (Avraam et al. 2013). Normal-lived mice were defined as those of the control strains, with life spans typical of laboratory mouse strains. Median “normal” life spans varied considerably (from 550 to 960 days), presumably dependent upon genetic background or husbandry. Lines of mice were defined as long lived if their life span was extended relative to that of normal-lived controls.

This compilation was published in 2008, and the increasing ease of mouse genetic manipulations and continued interest in understanding the causes of aging have meant that the number of long-lived strains has continued to grow. We therefore obtained numerical survival data from the published survival curves of an additional 32 separate studies comparing 31 separate long-lived mutants (set 2, summarized in Table 1). We did not search for additional short-lived strains of mice.

Table 1. Maximum-likelihood estimations of the Gompertz parameter values determined from published survival curves (set 2).

			Control				Mutant
Gene and allele or strain	Sex	Backgrounda	Median life span (D)	n	ln(A)	G	Median life span (D)	n	ln(A)	G	Source
AC5−/−	M+F	129/SvJ-C57BL/6	755	25	−6.74	3.46	990	13	−11.73	4.72	Yan et al. (2007)
cIGF-1tg	M	FVB/N	705	39	−3.54	1.73	880	38	−4.05	1.72	Li and Ren (2007)
IRS1−/−	F	C57BL/6	750	21	−5.11	2.73	970	14	−6.85	2.83	Selman et al. (2008)
	M		785	35	−6.84	3.50	860	13	−20.25	9.28
Klotho+46	M	C3H	785	29	−4.09	2.18	890	22	−5.61	2.53	Kurosu et al. (2005)
Klotho+48	M						1000	22	−6.24	2.55
Klotho+46	F		735	25	−4.30	2.41	840	28	−6.54	3.13
Klotho+48	F						825	29	−5.91	2.83
MTtg	M	FVB	850	55	−4.78	2.28	980	55	−4.26	1.58	Yang et al. (2006)
FGF21tg	M	C57Bl/6J	840	32	−4.56	1.94	1100	37	−7.24	2.57	Zhang et al. (2012)
S6K1−/−	F	C57BL/6	820	23	−4.43	2.15	975	29	−6.07	2.45	Selman et al. (2009)
Hcrt-UCP2	F	C57BL/6	550	31b	−2.91	2.07	660	26b	−4.06	2.42	Conti et al. (2006)
	M		720	36b	−3.24	1.75	815	53b	−4.85	2.37
MIF−/−	F	C57BL/6J-129/SvJ	740	24	−4.60	2.51	900	39	−5.01	2.17	Harper et al. (2010)
IRS1−/−	F	C57BL/6	780	16	−6.57	3.41	870	15	−4.18	1.86	Selman et al. (2011)
	M		770	37	−6.27	3.22	890	12	−5.88	2.58
GHRH−/−	M	C57BL6-129SV	610	56	−2.24	1.38	920	39	−6.18	2.67	Sun et al. (2013)
	F		660	52	−3.55	2.16	960	58	−4.67	1.90
IGF-1R+/−	F	C57BL/6J	800	38	−5.35	2.62	870	34	−6.45	2.84	Xu et al. (2014)
bIGF-1+/−	M	129/Sv×C57BL/6	830	20	−5.15	2.32	975	9	−13.98	5.70	Kappeler et al. (2008)
	F		850	22	−5.54	2.63	880	18	−6.70	2.99
Ptentg	M	C57BL6-CBA (75%:25%)	780	49	−4.77	2.56	880	32	−5.35	2.40	Ortega-Molina et al. (2012)
	F		790	63	−6.17	3.11	910	32	−7.82	3.45
Akt1+/−	F	C57BL/6	780	79	−5.40	2.85	870	80	−6.42	2.99	Nojima et al. (2013)
	M		840	101	−5.84	2.77	895	103	−5.17	2.29
mTOR∆/∆	M	129S1-C57BL/6Ncr	680	10	−5.44	3.19	830	17	−5.39	2.57	Wu et al. (2013)
	F		800	24	−3.59	1.74	960	26	−6.95	2.89
bSirt1tg	F	C57BL/6J	795	43	−5.81	2.91	930	34	−7.40	3.25	Satoh et al. (2013)
	M		855	47	−5.73	2.71	925	33	−8.35	3.53
Sirt6tg-55	M	C57BL/6J-BALB/c	865	35	−6.15	2.86	985	23	−6.41	2.54	Kanfi et al. (2012)
Sirt6tg-108	M		730	36	−4.08	2.18	790	25	−4.86	2.23
Gpx4+/−	M	C57BL/6	960	50	−6.33	2.68	1030	50	−8.81	3.57	Ran et al. (2007)
mGsta4−/−	F	C57BL/6	740	50	−4.12	2.18	840	50	−6.36	3.06	Singh et al. (2010)
hMTH1tg	M+F	C57BL/6	790	42	−7.89	4.02	910	34	−6.78	2.94	De Luca et al. (2013)
TRXtgc	M	C57BL/6	890	60	−4.15	1.73	950	60	−5.20	2.09	Pérez et al. (2011)
TgTerttgd	?	C57BL6-DBA/2	690	68	−3.91	2.24	1010	27	−7.83	3.14	Tomás-Loba et al. (2008)
UCP1tg	M+F	C57BL/6	820	53	−4.85	2.29	940	51	−6.30	2.76	Gates et al. (2007)
Dgat−/−	F	C57BL/6J	750	30	−4.34	2.30	940	30	−7.38	3.20	Streeper et al. (2012)
PKA RIIβ−/−	M	C57BL/6	900	20	−9.53	4.33	970	20	−6.68	2.79	Enns et al. (2009)
IκB-αDN	M	C57BL/6	880	23	−11.26	5.28	965	31	−9.31	3.92	Zhang et al. (2013)
BubR1tg	M+F	C57BL/6-SV129	630	60	−3.12	2.00	730	57	−3.36	1.70	Baker et al. (2013)
AT1A−/−	M	C57BL/6×129/SvEv	760	20b	−9.98	5.36	940	20	−12.57	5.30	Benigni et al. (2009)
ETA−/−	M	C57BL/6J	730	34	−3.82	1.74	920	28	−3.90	1.49	Ceylan-Isik et al. (2013)
AgRP−/−	M+F	C57BL/6J-129Sv	650	16	−5.03	3.45	710	21	−5.66	3.36	Redmann and Argyropoulos (2006)
Arf/p53tg	?	C57BL/6J	840	111	−5.12	2.47	950	25	−8.16	3.51	Matheu et al. (2007)
Mclk1+/−	M+F	129/Svj-BALB/c	764	14	−8.87	4.61	900	54	−5.2	2.35	Lapointe et al. (2009)
PAPP-A−/−	F	C57BL/6-129Sv/E	670	50	−3.48	2.00	880	38	−4.77	2.08	Conover et al. (2010)
	M		680	45	−2.71	1.45	830	40	−3.98	1.75

M, male; F, female.

^aDash denotes a mix of the indicated backgrounds; “×” denotes F₁ cross.

^bSample size approximated from survival curve.

^cCohort 2, male.

^dSp53/Sp16/SArf/TgTert^tg vs. Sp53.

The two sets together therefore encompass a diverse collection of genetic manipulations that have been shown to extend life span and likely comprise a majority of published reports of long-lived strains of mice (Yuan et al. 2009; Selman and Withers 2011; Liao and Kennedy 2014). The affected genes include those playing a role in oxidative stress response, signaling (mTOR, insulin/insulin-like, or growth hormone), metabolism, genomic integrity, mitochondrial function, and cellular proliferation. One strain of mice, Atg5 transgenics (Pyo et al. 2013), was excluded from further analysis because the parameter estimates [G of 8–14 and a ln(A) of −14 to −25] were so markedly different from those of the remainder of the strains (Table 1).

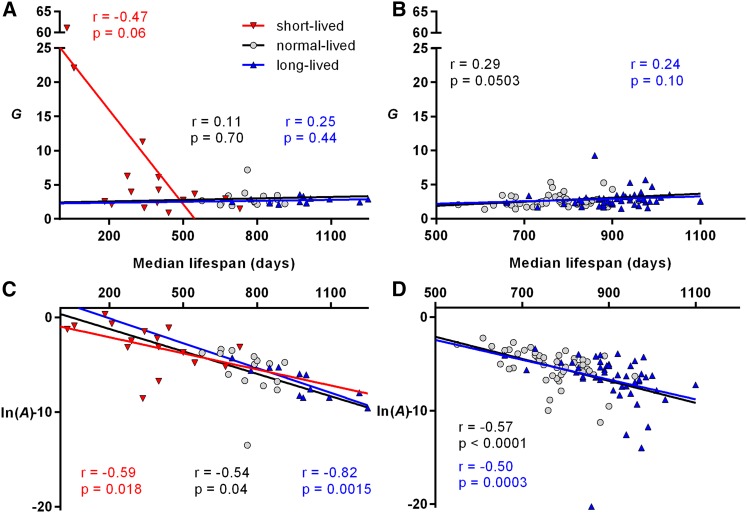
To determine whether either Gompertz parameter changed systematically with changes in longevity, we examined the relationship between median life spans and Gompertz parameters for each cohort. In short-lived mice the correlation of G with life span approached statistical significance (Figure 2A: r = −0.47, P = 0.06). However, this was largely due to the two shortest-lived lines (Klotho and Lmna mutants), with median life spans <2 months (if they were excluded, r = −0.22, P = 0.46). These two lines also had by far the largest G (22 and 61, respectively, compared to a median value of 3.3 for short-lived mice). There was no correlation between life span and G for normal- or long-lived mice in set 1 (Figure 2A: r = 0.11, P = 0.70 and r = 0.25, P = 0.44, respectively). For set 2 (Figure 2B: r = 0.29, P = 0.0503 and r = 0.24, P = 0.10 for normal- and long-lived groups, respectively), we saw no negative correlation and a borderline statistically significant positive correlation (underscoring that the changes in G in this set are not responsible for the increased life spans).

Figure 2.

MLE estimations of the Gompertz parameter values plotted against median life span for lines of mice with varying life spans (the symbols are as presented in the key in A). Lines of best fit, Spearman correlation coefficients (r), and associated P-values are shown in colors corresponding to the data points. Parameters determined previously (set 1) are shown in A and C; parameters determined as part of the current study (set 2) are shown in B and D. Note that the line of best fit (determined by linear regression) is shown as an aid for the reader, and the P-values shown were determined separately by nonparametric methods.

In contrast to G, there was a clear negative correlation between life span and ln(A). This was apparent for short-, normal-, and long-lived lines in set 1 (Figure 2C: r = −0.59, P = 0.018; r = −0.54, P = 0.04; and r = −0.82, P = 0.0015, respectively) and for normal- and long-lived lines in set 2 (Figure 2D: r = −0.57, P < 0.0001 and r = −0.50, P = 0.0003, respectively).

Combining sets 1 and 2 together yields similar results to those when they are analyzed separately, with no statistically significant effect on G (Figure S1A) and a negative correlation between ln(A) and lifespan (r = −0.65, P < 0.0001) (Figure S1B). Likewise, analyzing males and females separately (Figure S2) does not affect the Gompertz parameter–life span relationship, with a negative correlation between ln(A) and life span (r = −0.69 and −0.55 for females and males, respectively, P < 0.0001). The same relationship was also apparent when restricting the analysis to those studies carried out in the most commonly used background strain, C57BL/6, where there was a weak positive correlation between G and life span (r = 0.29, P = 0.04) and a strong negative correlation between ln(A) and life span (r = −0.60, P < 0.0001) (Figure S3).

Estimation of Gompertz parameters can be subject to biases resulting in systematic under- or overestimations (Promislow et al. 1999), especially for smaller samples sizes, potentially introducing statistical artifacts into our analysis. Correction for potential systematic biases in parameter estimations (determined using standard resampling techniques), as well as removal of possible outliers, did not change the effects described above (see Figure S4 and its legend).

Genetic differences underlie the relationship between A and life span in a panel of inbred mice

The results shown in Figure 2 imply that the biological mechanisms that determine life span in laboratory mice are largely those associated with changes to A, rather than G. As described above, A has been interpreted as representing the effect of age-independent factors on life span. It is therefore possible that the systematic decrease in A with increased life span that is apparent in Figure 2 could be due to environmental differences between studies, with more beneficial environments resulting in decreased aging-independent mortality rates and, consequently, longer life spans. Indeed, differences in the quality of husbandry have been raised as a potential confounding variable in aging studies (Liang et al. 2003; Ladiges et al. 2009).

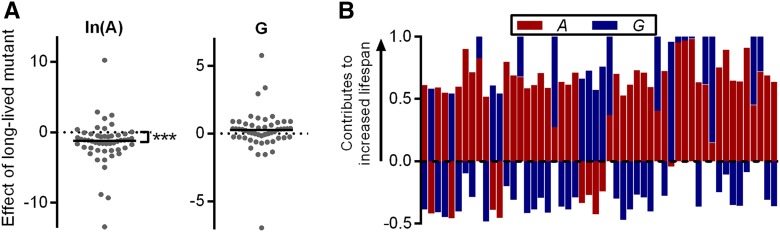
To address this question, we conducted a pairwise comparison, within studies, of Gompertz parameters for normal- and long-lived lines in set 2 of mice. Among 52 long-lived lines (males and females analyzed separately), A was decreased relative to normal-lived controls in 43 lines. Within-study ln(A) values decreased by an average of −1.504 units in the long-lived group (P < 0.0001 vs. 0 by Wilcoxon signed-rank test). In contrast, G was increased by an average of 0.26 units (P = 0.08 vs. 0) (Figure 3A).

Figure 3.

Pairwise comparison within studies of long-lived mouse strains relative to normal-lived controls (set 2). (A) Difference in Gompertz parameter values between long-lived and control groups within studies (males and females analyzed separately). A positive value corresponds to an increase in parameter value for long-lived mice and a negative value to a decrease. (B) Fractional contribution of each parameter change to the extended life span of long-lived groups of mice. Each bar is 1 unit long. A positive value indicates that the change in parameter value contributes to the increased life span. Negative values indicate that the parameter change acts to shorten life span. *** P < 0.0001 vs. 0 by Wilcoxon signed-rank test.

The above analysis considers A and G separately, when, in reality, changes in both parameters cooperate to establish a new survival trajectory when the survival curve of a population is shifted. It is possible to determine the contribution of each parameter to changes in average longevity (longevity decomposition), revealing the extent to which each parameter is responsible for the shift in life span (Pletcher et al. 2000). Thus, among the long-lived strains of set 2, changes to A account for the majority of the life span increase in 38 of 52 long-lived strains (Figure 3B; P = 0.0009 vs. expected by chance, by chi-square test).

To further differentiate between environmental and genetic effects we determined the relationship between the Gompertz parameters and life span among a group of 31 inbred strains of mice of various average life spans that were maintained under uniform conditions. Complete survival data were obtained from the Mouse Phenome Database, maintained by The Jackson Laboratory (Bogue et al. 2016). The 31 inbred strains used in this study were selected to encompass the greatest possible genetic diversity (Yuan et al. 2009, 2012) and included wild-derived strains as well as representatives from the seven genetically related groups that comprise laboratory mice (Yuan et al. 2009).

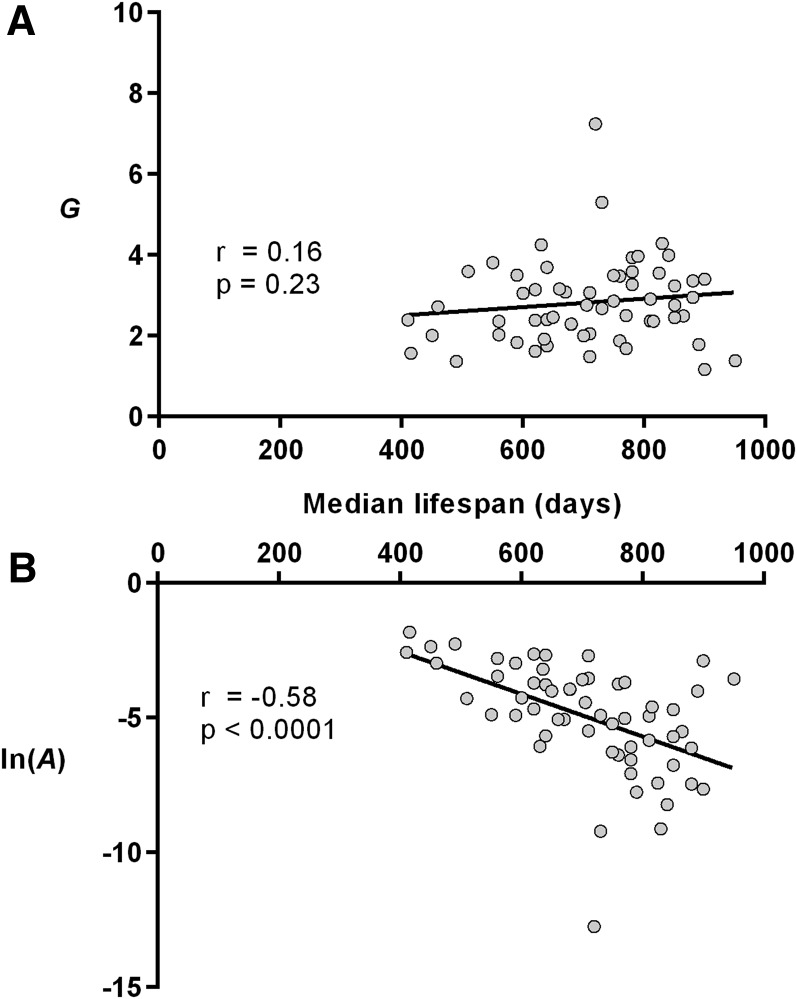
In this data set (Figure 4, Table S2), there was no correlation between median life span and G (r = 0.16, P = 0.23), but life span was correlated with ln(A) (r = −0.58, P < 0.0001). These relationships were unchanged when we corrected for systematic bias in parameter estimations, as well as upon removal of possible outliers (Figure S5).

Figure 4.

Maximum-likelihood estimations of the Gompertz parameter values plotted against median life span for strains maintained as part of the mouse phenome project at The Jackson Laboratories (see Table S2 for numeric values and descriptions of lines). Lines of best fit, Spearman correlation coefficients (r), and associated P-values are shown. (A) Gompertz parameter G, acceleration of mortality rates with age. (B) Natural logarithm of A, baseline mortality. Note that the line of best fit (determined by linear regression) is shown as an aid for the reader and that the P-values shown were determined separately by nonparametric methods. n = 13–32, average = 30.1.

As an additional test, we determined the relationship between the Gompertz parameters and life span among a group of 44 recombinant inbred strains of mice of various average life spans that were maintained under uniform conditions (males and females analyzed separately) (Liao et al. 2010). Although the small sample size of these groups (n = 5) limits the reliability of Gompertz parameter estimation, we still observed the same pattern of relationships between Gompertz parameters and life span, with no correlation between G and life span (r = 0.14, P = 0.2) and a negative correlation between ln(A) and life span (r = −0.38, P = 0.0006) (Figure S6, Table S3).

Life span in C. elegans mutants is associated with changes to G, not A

We wondered whether other classic model organisms commonly used for aging research would demonstrate a similar invariance for G with increased life span. The nematode C. elegans is one of the most widely used model organisms for the study of aging (Antebi 2007; Li and Ren 2007; Van Raamsdonk and Hekimi 2010). We calculated Gompertz parameters from published survival curves of 39 long-lived and 8 short-lived mutants, along with the 20 associated wild-type (N2) controls (Table 2). These mutants were chosen to affect a diverse collection of biological pathways including, but not limited to, mitochondrial function, insulin/insulin-like signaling, nutrient uptake, stress resistance, sensory perception, and autophagy. All life span experiments were carried out at 20° on agar plates and had an associated N2 control. Because of the large number of long-lived worm mutants that have been identified, this represents only a limited subset of potentially usable strains. For comparison, the GenAge database of aging-related genes (Tacutu et al. 2013) currently lists 112 long-lived C. elegans mutants (although survival experiments for these mutants were not all conducted in a manner that would have satisfied our inclusion criteria).

Table 2. Maximum-likelihood estimates of the logistic model mortality parameters for short- and long-lived C. elegans mutant and N2 control strains.

		N2					Mutant
Gene(s)	Allele(s)	Median life span (D)	n	ln(A)	G	L	Median life span (D)	n	ln(A)	G	L	Effect on life span	Source
hsf-1	sy441	20	42	−8.00	0.342	0.282	12	42	−7.98	0.633	1.441	0.600	Hajdu-Cronin et al. (2004)
gas-1	fc21	19	100	−8.61	0.426	1.358	12	100	−7.87	0.668	2.442	0.632	Suthammarak et al. (2013)
skn-1	zu129	15	75	−6.49	0.371	1.535	10	75	−24.72	3.093	11.184	0.667	An and Blackwell (2003)
mev-1	kn1	19	100	−8.61	0.426	1.358	13	100	−5.35	0.291	0.226	0.684	Suthammarak et al. (2013)
jnk-1	gk7	16	386	−8.90	0.537	1.997	12	333	−14.39	1.270	4.723	0.750	Ezekowitz (2014)
daf-16	m26	20	19	−7.54	0.345	1.186	15	37	−14.57	0.995	3.603	0.750	Kenyon et al. (1993)
jkk-1	km2	16	386	−8.90	0.537	1.997	13	189	−13.51	1.063	2.651	0.813	Ezekowitz (2014)
sir-2.1	ok434	19	70	−5.63	0.188	0.000	16	94	−7.28	0.358	0.014	0.842	Berdichevsky et al. (2006)
clk-2	qm37	18	50a	−14.95	0.839	2.666	18	50a	−14.93	0.945	6.160	1.000	Van Raamsdonk et al. (2010)
ctbp-1	ok498	19	254	−7.35	0.325	0.659	22	236	−8.52	0.330	0.492	1.158	Chen et al. (2009)
cep-1	gk138	17	115	−9.33	0.493	0.856	20	116	−10.08	0.496	2.446	1.176	Tavernarakis et al. (2008)
age-1	hx546	34	50	−7.18	0.142	0.000	42	50	−6.94	0.110	0.000	1.235	Yanase et al. (2002)
clk-5	qm152	18	50a	−14.95	0.839	2.666	24	50a	−14.83	0.585	2.479	1.333	Van Raamsdonk et al. (2010)
clk-8	qm162	18	50a	−14.95	0.839	2.666	24	50a	−8.57	0.325	1.383	1.333	Van Raamsdonk et al. (2010)
daf-19	m86	18	347	−8.45	0.475	2.471	24	35	−6.96	0.203	0.258	1.333	Apfeld and Kenyon (1999)
mec-8	e398	18	347	−8.45	0.475	2.471	24	46	−8.08	0.219	0.996	1.333	Apfeld and Kenyon (1999)
egl-30	ad806	18	50	−19.95	1.502	9.977	25	62	−6.12	0.146	0.000	1.389	Ch’ng et al. (2008)
arr-1	ok401	12	180	−5.38	0.331	0.457	17	210	−4.83	0.176	0.075	1.417	Palmitessa and Benovic (2010)
cdc-48.1; atx-3	tm544;gk193	19	312	−7.24	0.317	0.704	27	222	−6.95	0.184	0.382	1.421	Kuhlbrodt et al. (2011)
clk-3	qm38	18	50a	−14.95	0.839	2.666	26	50a	−10.41	0.341	0.884	1.444	Van Raamsdonk et al. (2010)
clk-1	qm30	18	309	−8.91	0.451	0.982	26	112	−21.52	0.903	7.037	1.444	Van Raamsdonk and Hekimi (2009)
che-13	e1805	18	347	−8.45	0.475	2.471	26	36	−5.89	0.142	0.206	1.444	Apfeld and Kenyon (1999)
che-2	e1033	18	347	−8.45	0.475	2.471	26	33	−25.00	1.560	19.645	1.444	Apfeld and Kenyon (1999)
daf-6	e1377	18	347	−8.45	0.475	2.471	26	75	−5.83	0.138	0.193	1.444	Apfeld and Kenyon (1999)
osm-1	p808	18	347	−8.45	0.475	2.471	26	17	−7.21	0.195	0.000	1.444	Apfeld and Kenyon (1999)
daf-4	e1364	15	60	−13.21	0.851	1.699	22	71	−11.14	0.479	1.927	1.467	Shaw et al. (2007)
nuo-6	qm200	22	150	−12.51	0.535	0.818	33	120	−10.38	0.288	1.743	1.500	Yang and Hekimi (2010)
clk-10	qm169	18	50a	−14.95	0.839	2.666	28	50a	−6.66	0.154	0.292	1.556	Van Raamsdonk et al. (2010)
clk-6	qm158	18	50a	−14.95	0.839	2.666	28	50a	−11.78	0.398	2.622	1.556	Van Raamsdonk et al. (2010)
clk-9	qm164	18	50a	−14.95	0.839	2.666	28	50a	−10.79	0.354	1.282	1.556	Van Raamsdonk et al. (2010)
sod-2	ok1030	18	309	−8.91	0.451	0.982	28	373	−8.44	0.255	0.805	1.556	Van Raamsdonk and Hekimi (2009)
che-11	e1810	18	347	−8.45	0.475	2.471	28	27	−6.02	0.126	0.000	1.556	Apfeld and Kenyon (1999)
daf-10	e1387	18	347	−8.45	0.475	2.471	29	30	−8.89	0.252	0.877	1.611	Apfeld and Kenyon (1999)
osm-6	p811	18	347	−8.45	0.475	2.471	30	30	−8.53	0.220	0.000	1.667	Apfeld and Kenyon (1999)
clk-7	qm159	18	50a	−14.95	0.839	2.666	32	50a	−8.03	0.212	1.109	1.778	Van Raamsdonk et al. (2010)
osm-3	p802	18	347	−8.45	0.475	2.471	32	133	−7.86	0.195	0.556	1.778	Apfeld and Kenyon (1999)
egl-3	nr2090	18	46	−11.13	0.704	4.043	32	63	−7.27	0.163	0.452	1.778	Ch’ng et al. (2008)
clk-4	qm151	18	50a	−14.95	0.839	2.666	34	50a	−5.99	0.095	0.033	1.889	Van Raamsdonk et al. (2010)
eat-2	ad1116	18	309	−8.91	0.451	0.982	35	156	−13.18	0.366	2.838	1.944	Van Raamsdonk and Hekimi (2009)
tax-4	p678	18	347	−8.45	0.475	2.471	37	105	−8.90	0.186	0.299	2.056	Apfeld and Kenyon (1999)
che-3	p801	18	347	−8.45	0.475	2.471	40	31	−9.17	0.192	0.509	2.222	Apfeld and Kenyon (1999)
isp-1	qm150	18	309	−8.91	0.451	0.982	42	114	−6.66	0.097	0.487	2.333	Van Raamsdonk and Hekimi (2009)
clk-1; sod-2	ok1030	18	309	−8.91	0.451	0.982	44	147	−9.36	0.169	0.687	2.444	Van Raamsdonk and Hekimi (2009)
osm-5	p813	18	347	−8.45	0.475	2.471	44	46	−6.74	0.092	0.000	2.444	Apfeld and Kenyon (1999)
daf-2; clk-9	e1370; qm164	21	200b	−7.72	0.303	0.265	59	200b	−8.43	0.130	0.429	2.810	Van Raamsdonk et al. (2010)
daf-2; clk-2	e1370; qm37	15	200b	−10.90	0.720	2.747	48	200b	−6.08	0.055	0.313	3.200	Van Raamsdonk et al. (2010)
daf-2	e1370	18	309	−8.91	0.451	0.982	63	168	−7.38	0.074	0.000	3.500	Van Raamsdonk and Hekimi (2009)

Note that some mutant strains were compared to the same N2.

^aTwenty worms per plate were examined with three trials per strain.

^bSum of at least three independent trials and an initial number of 80 worms per strain per trial.

Initial observations showed that the standard Gompertz model poorly fitted the survival of many groups of worms. In line with this, an automated life span analysis performed on populations of C. elegans with very large sample sizes (>200 animals) has recently shown that the exponential increase in mortality rates that characterize the Gompertz survival model largely ceases at later ages (Stroustrup et al. 2016). Thus, logistic models that account for late-life mortality rate deacceleration provide a better fit for C. elegans survival data. Indeed, of the 11 groups of N2 worms with n > 100 [at which sample size the actual population model can be reliably determined from the sample (Wilson 1994)] all but 1 were best described by the logistic model (see Materials and Methods for details of the model comparison method). Of the 18 mutant strains with n > 100, 16 were best fitted by the logistic model. We therefore used this model to analyze all C. elegans survival curves.

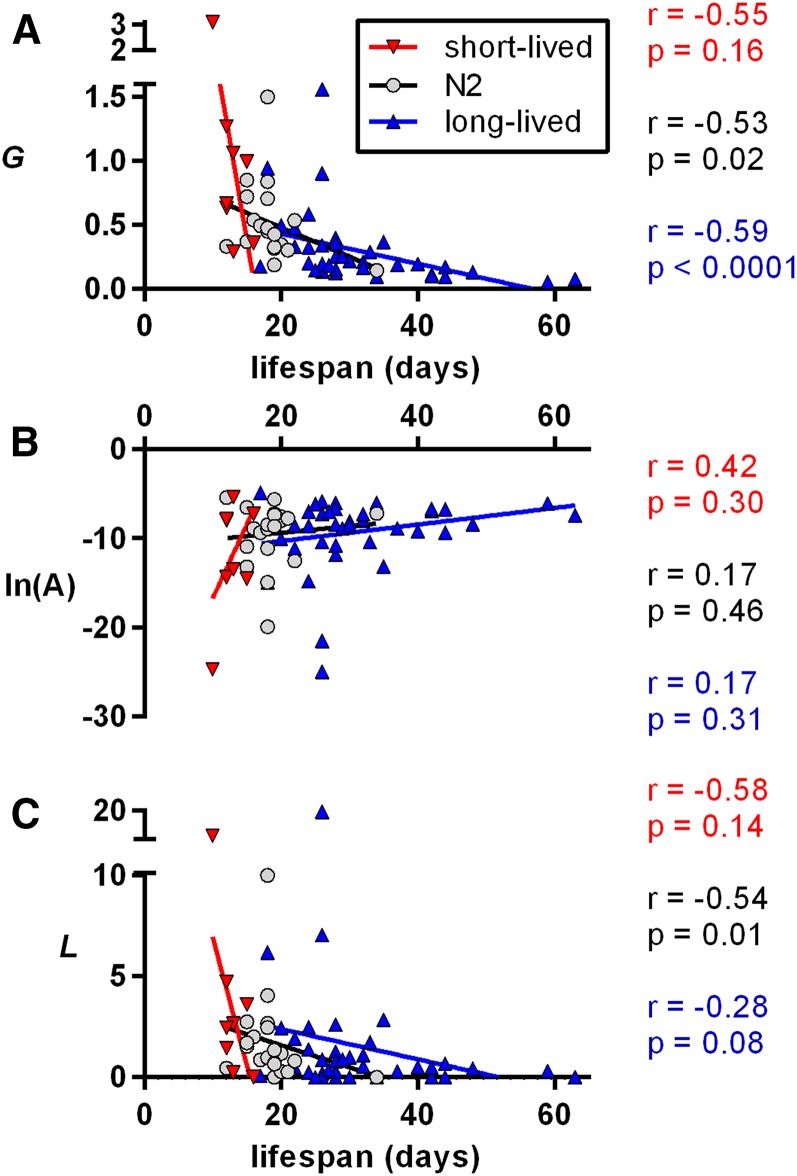
For C. elegans, median life span for short-lived strains exhibited a trend toward a negative correlation with G (r = −0.55, P = 0.16), and there was a statistically significant negative correlation between G and lifespan for control N2 or long-lived worms (r = −0.53, P = 0.02 and r = −0.70, P < 0.0001, respectively) (Figure 5A). In contrast to what we repeatedly observed in mice, there was no statistically significant relationship between ln(A) and life span (Figure 5B). There was an inverse relationship between the logistic parameter L and median life span for N2 worms (r = −0.54, P = 0.01), but this relationship did not reach statistical significance for short- or long-lived strains (Figure 5C). These relationships were unchanged when we corrected for systematic bias in parameter estimations, as well as upon removal of possible outliers (Figure S7). Thus, changes to the rate-of-aging parameter G seem to account for the bulk of the life span increase in C. elegans.

Figure 5.

Logistic parameter values for short-lived, long-lived, and wild-type control (N2) lines of C. elegans. Lines of best fit, Spearman correlation coefficients, r, and associated P-values are shown. (A) MLE estimations of the Gompertz parameter G, describing the age-related acceleration of mortality rates. (B) Natural logarithms of the MLE estimations of the Gompertz parameter A, the baseline mortality rate. (C) MLE estimations for the late-stage mortality rate deacceleration parameter L. Note that the line of best fit (determined by linear regression) is shown as an aid for the reader, and the P-values shown were determined separately by nonparametric methods.

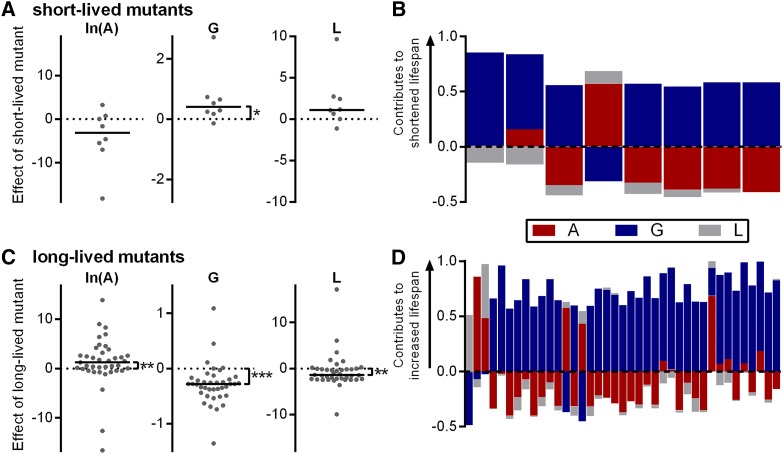
Within studies, pairwise comparisons between mutant and N2 control worms reveal that G is increased and that changes to G make the greatest contribution to the increase in average life span, for 6 of 7 short-lived strains (Figure 6, A and B). Among long-lived mutant strains, ln(A) values were actually increased by an average of 1.24 (P = 0.0044 vs. 0 by Wilcoxon signed-rank test) and the value of the L parameter changed by an average of −1.38 (P = 0.0022 vs. 0). These effects (which by themselves would decrease life span) were offset by a decrease in G (−0.28, P < 0.0001 vs. 0) (Figure 6C). Accordingly, changes to G made the greatest contribution to the increased average life span in 33 of 39 long-lived strains (Figure 6D).

Figure 6.

Pairwise comparison within studies of short- and long-lived C. elegans strains relative to their normal-lived N2 controls. (A) Differences in Gompertz parameter values between short-lived and N2 groups within studies. A positive value corresponds to an increase in parameter value for the mutant and a negative value to a decrease. (B) Fractional contribution of each parameter change to the shortened life span of short-lived lines of worms. Each bar is 1 unit long. A positive value indicates that the change in parameter value contributes to the shortened life span of the mutant. Negative values indicate that the parameter change acts to lengthen life span. (C) Differences in Gompertz parameter values between long-lived and N2 groups within studies. (D) Fractional contribution of each parameter change to the lengthened life span of long-lived lines of worms. A positive value indicates that the change in parameter value contributes to the increased life span of the mutant. Negative values indicate that the parameter change acts to shorten life span.

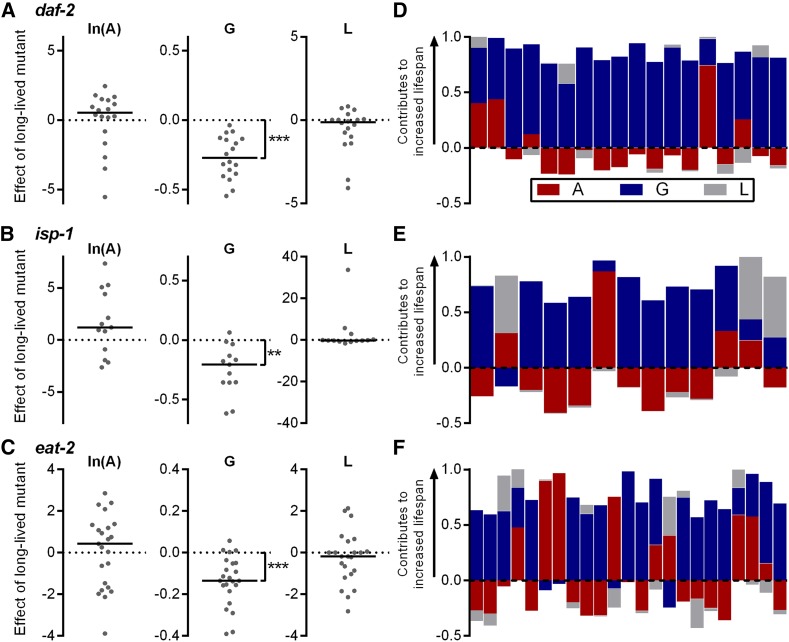
Due to the inherent variability in any one study, it would be difficult to reliably conclude whether a particular long-lived strain has a certain characteristic effect on the Gompertz parameters. For example, unique environmental or methodological issues could subtly influence the pattern of mortality in a particular study. We therefore analyzed survival results from multiple studies for three long-lived mutants that have been widely studied. We chose daf-2(e1370) as a model of impaired insulin/insulin-like signaling (Kenyon et al. 1993; Murphy and Hu 2013), isp-1(qm150) as a model of impaired mitochondrial function (Feng et al. 2001; Dancy et al. 2015; Wang and Hekimi 2015), and the feeding-impaired eat-2(ad1116) mutant as a model of caloric restriction (Lakowski and Hekimi 1998; Lan et al. 2015). We identified 18 daf-2 studies, 13 isp-1 studies, and 23 eat-2 studies and determined the Gompertz parameters from published survival data (Table S4). There were decreases in G for the long-lived mutants relative to normal-lived N2 controls for each group of mutants (Figure 7, A–C, P ≤ 0.0012 vs. a change of 0 by Wilcoxon signed-rank test) and no statistically significant effects on A or L (Figure 7, A–C). Likewise, decomposition of the contribution of each parameter to the increased longevity of each mutant revealed that, in the majority of studies for each mutant, changes to G were the dominant contributor to the increased average life span (Figure 7, D–F). We therefore conclude that daf-2, isp-1, and eat-2 mutations can be reliably said to extend life span through decreases to the age-dependent acceleration of mortality rates.

Figure 7.

Pairwise comparison of Gompertz parameters within studies of long-lived daf-2, isp-1, and eat-2 mutants (tabulated data in Table S4). (A–C) Differences in Gompertz parameter values between N2 and (A) daf-2(e1370), (B) isp-1(qm150), and (C) eat-2(ad1116) mutants within studies. A positive value corresponds to an increase in parameter value for the mutant and a negative value to a decrease. (D–F) Fractional contribution of each parameter change to the lengthened life span of (D) daf-2, (E) isp-1, and (F) eat-2 mutant worms. Each bar is 1 unit long. A positive value indicates that the change in parameter value contributes to the increased life span of the mutant. Negative values indicate that the parameter change acts to shorten life span. ** P = 0.0012, *** P < 0.0001 vs. 0 by Wilcoxon signed-rank test.

Discussion

We found that the age-dependent acceleration of mortality rate, G, remained essentially invariant throughout the wide range of life spans that characterized normal and genetically long-lived mice (Figure 2). This is consistent with earlier findings that G is reasonably constant between different human populations and among a small number of inbred strains of laboratory mice (Finch 1990), as well as among wild-caught strains of Drosophila (Spencer and Promislow 2005), and that life-span-extending interventions in mice had a tendency to be associated with statistically significant changes in A, rather than G (Yen et al. 2008). We have shown that this effect is systematic, rather than sporadic, and can be observed even in homogenous environmental conditions, where the genetic makeup of the strains is the only variable (Figure 4). Thus it appears that most variation in mouse life span—save for extreme shortenings—is largely due to mechanisms that affect initial vulnerability. Importantly, this is true among populations of both wild-type control strains and those with experimentally introduced or spontaneous single-gene mutations that extend life span.

The apparent invariance of G for mice (Figure 2 and Figure 4) suggests that it is fixed within a relatively narrow band, with both increases and decreases likely to be associated with dramatically shortened life spans. Indeed, for the data set containing short-lived mice, the three lowest G values, as well as the seven largest, were associated with shortened life spans (Table S1 and Figure 2A). Interestingly, even decreases in G associated with extended life span may be accompanied by signs of early frailty relative to wild type. For example, young Mclk1^+/− mice have impaired mitochondrial function and increased mitochondrial oxidative stress that is not apparent in aged Mclk1^+/− mice (Lapointe and Hekimi 2008; Lapointe et al. 2009). This is associated with increased mortality relative to that of wild-type siblings that is reversed at ∼2 years of age (made dramatically apparent by a crossing over of the survival curves at midlife), coupled with an increased A (Lapointe et al. 2009). Similarly, young Prop1^df/df mice (with decreased G, Table S1) exhibit some marked physiological deficiencies in addition to their dwarf stature, including infertility, decreased ambulatory activity, and early frailty exemplified by a requirement for a prolonged nursing period and group housing (Conover and Bale 2007), along with a trend toward an increased A. Thus, observations in these two strains are consistent with decreases to G in mice being associated with detrimental effects of varying severity. These may be counterbalanced by protective effects over the long term, resulting in an increased life span.

Short-lived lines of mice demonstrated great variability in terms of the relationship between the Gompertz parameters and life span (Figure 2). This is consistent with the view that some or all of these lines may be short lived due to sicknesses distinct from aging and that the diversity of possible causes of mortality in this group combined to prevent the establishment of any clear pattern.

The remarkable invariance of G across a great range of mouse life spans would imply that these differences in life span do not reflect changes to the underlying biological aging process. This would seem to suggest that the vast majority of variation to life span seen in normal or long-lived mice—whether due to single-gene mutations or the more complex genetic heterogeneity among different strains—is not associated with any change in the aging process, but rather to aging-independent physiological features. Thus, Bub1b mutants (G = 2.55; median life span = 6 months), C57Bl/6 controls for Trx transgenic mice (G = 2.67; life span = 19 months), and Prop1^df/df mice (G = 2.89; life span = 41 months) could be said to be aging at essentially the same rate. This is a surprising finding, since several long-lived strains of mice have been found to be resistant to the development of age-dependent pathologies (Flurkey et al. 2001; Kinney et al. 2001a,b; Ladiges et al. 2009), including several strains in which G was not decreased. For example, long-lived AC5^−/− mice (G of 4.72 vs. 3.46 in controls) were protected from aging-induced cardiomyopathy (Yan et al. 2007), and both long-lived female Irs1^−/− mice (G of 2.83 vs. 2.73 in controls) and S6K1^−/− mice (G of 2.45 vs. 2.15 in controls) exhibited superior maintenance of motor skills and immune function into old age relative to their wild-type controls (Selman et al. 2008, 2009). Such signs of delayed biological aging have also been observed in FIRKO (Katic et al. 2007) and αMUPA (Gutman et al. 2011; Yanai et al. 2011) mice, both of which were found to be long lived with a statistically significant decrease in A and a trend toward an increased G (Table S1).

It would seem surprising that a population that is not aging slower would consist of individuals showing a slower rate of biological aging. How can we explain long-lived mice with fewer age-dependent pathologies but an unchanged rate of population aging? One possible explanation for this apparent paradox is that these interventions are delaying the age of onset of age-related pathologies, rather than slowing their progression. Pathological analysis carried out at a single young and old age (represented by the vertical dashed lines in Figure 1), as is common in murine life span studies, would not differentiate between delays in pathology onset and a change in the rate at which they worsen. Interestingly, a delayed onset of age-related pathology would also mirror the changes to mortality patterns for populations where life span increases due to changes to A, in which the rapid increase in mortality rates that characterizes mid- to old-age animals is delayed (Figure 1, solid blue lines). It has also been suggested that such a “rectangularization of the survival curve” in human populations would be associated with decreased durations of morbidity and hence beneficial (Fries 1980).

It is also worth noting that, although the theory behind the Gompertz model has been well explored (Gavrilov and Gavrilova 2001; Ricklefs and Scheuerlein 2002; Milne 2008), the role of G as a measure of the rate of aging does not seem to have been subject to experimental validation (Driver 2001; Masoro 2006). As an alternative to the traditional view of G as a measure of aging, it has been suggested that a reduction in age-specific mortality throughout most of adult life would be sufficient evidence of a slower rate of aging, even if the rate at which it increased with age was unaffected (Masoro 2006). If future studies were to find that long-lived lines of mice display convincing evidence of a slower rate of accumulation of age-dependent pathology (i.e., slower biological aging), despite alterations to A rather than G, this may be cause to rethink our conventional understanding of the meaning behind the Gompertz parameters.

The extended life spans of long-lived C. elegans mutants were found to be associated with decreases in the Gompertz parameter G, the rate of aging. This is in striking contrast to what we observed in mice. Such species-specific differences should perhaps not be unexpected: Although C. elegans has important advantages as a model organism for the study of aging, they are (unlike mammals) poikilothermic and self-fertilizing hermaphrodites (Brenner 1974; Hekimi et al. 2001), and aspects of their aging process are clearly distinct from those of mammals (Gruber et al. 2014). For example, the last portion of worm life span is often spent lying immobile on its plate, moving only rarely or if prodded (in some long-lived mutants, they can spend one-quarter of their life in this state) (Van Raamsdonk et al. 2010). This is not observed in mice, where immobility is cause for immediate euthanasia. Nematodes are also tolerant of physiological states that would be lethal in mammals, such as extreme hypoxia and hyperoxia (Van Voorhies and Ward 2000).

Another striking difference between long-lived worm and mouse mutants is the degree to which life span can be extended. Among the studies analyzed here, the average percentage of increase in life span was 76% for worms [with a maximum of 250% for daf-2(e1370) mutants and eight other strains with a >100% increase] vs. 20% for mice (including sets 1 and 2). Among mice, the two strains showing the greatest increase in life span showed increases of 92% and 51%, respectively, substantially less than observed for long-lived C. elegans (Figure S8A). It is possible that dramatic physiological shifts are required for the greatest increases in life span and that these are associated with changes to G rather than A. Thus we could predict that long-lived strains of C. elegans or mice with equivalent increases in life span relative to their controls might show similar changes to their Gompertz parameters. This is difficult to test because of the limited overlap in the degree of life span extension between the two species (Figure S8B). However, at the point of greatest overlap (C. elegans and mice with median life spans extended between 1.3 and 1.4 times relative to their controls), while there does not appear to be a difference in the effects on G, the effects on ln(A) are significantly different between the two species [P = 0.0317 by Mann–Whitney test, with ln(A) tending to be increased in long-lived worms and decreased in long-lived mice]. This suggests that the interspecies difference in parameter effects is not simply due to the degree of life span extension.

The trends that we have described in this study do not rule out the existence of long-lived mouse mutants with decreases in G rather than A or long-lived worms with changes to A rather than G. Such exceptions would in fact be valuable comparators to lines showing the more stereotyped pattern of changes and may help relate changes in mortality trends to underlying biological mechanisms. Interestingly, one environmental intervention, caloric restriction, seems to increase life span in mice via decreases to G, rather than A (Simons et al. 2013).

C. elegans, in particular, are attractive model organisms for identification of short- or long-lived strains that exhibit atypical Gompertzian behavior because their short life span and minimal requirements for uptake allow for higher-throughput life span experiments with greater sample sizes. Indeed, a recent study used a novel automated imaging system to collect high-precision survival data for multiple replicate populations of ≥500 animals (Stroustrup et al. 2016). Intriguingly, the authors found that life-span-shortening or -extending mutations resulted in survival curves that could be mapped onto control survival curves by application of a single temporal scaling parameter. The mortality rate models used here were constructed using a parameterization that is incompatible with such investigations of temporal scaling (Stroustrup et al. 2016), but it is tempting to imagine using this tool to identify strains of C. elegans that have extended life spans characterized by decreases to A, rather than G.

In conclusion, our principal finding is the interspecies variation in mortality rate kinetics in response to genetically driven changes to life span. In normal and long-lived mutant mice, there was a remarkable invariance of the age-dependent acceleration of mortality rate, represented by the Gompertz parameter G, across a wide range of median life spans. Although genetic manipulations are capable of increasing G in mice, such changes are more likely to result in shortened than in lengthened life span. Genetic alterations that extend life span, or affect life span within the normal range, almost invariably act through changes to the age-independent Gompertz parameter A. This appears to be true for single-gene mutations, as well as for the more complex changes that affect life span in various laboratory strains. This indicates that the vast majority of mouse life span extensions achieved via genetic manipulation are due to a delay in the onset of age-dependent mortality, rather than a slowing of the aging rate itself. This was not, however, conserved across species, with long-lived C. elegans exhibiting a decreased G. It is perhaps not surprising that the nature of life span extension may be fundamentally different between these species, given the substantial differences in physiology and environmental niche occupied, as well as life spans that differ by orders of magnitude.