Nonequilibrium all-atom molecular dynamics simulation of the bubble cavitation and application to dissociate amyloid fibrils

Abstract

The cavitation of gas bubbles in liquids has been applied to different disciplines in life and natural sciences, and in technologies. To obtain an appropriate theoretical description of effects induced by the bubble cavitation, we develop an all-atom nonequilibrium molecular-dynamics simulation method to simulate bubbles undergoing harmonic oscillation in size. This allows us to understand the mechanism of the bubble cavitation-induced liquid shear stress on surrounding objects. The method is then employed to simulate an Aβ fibril model in the presence of bubbles, and the results show that the bubble expansion and contraction exert water pressure on the fibril. This yields to the deceleration and acceleration of the fibril kinetic energy, facilitating the conformational transition between local free energy minima, and leading to the dissociation of the fibril. Our work, which is a proof-of-concept, may open a new, efficient way to dissociate amyloid fibrils using the bubble cavitation technique, and new venues to investigate the complex phenomena associated with amyloidogenesis.

I. INTRODUCTION

A bubble in liquids is a spherical volume of gas. Due to the high compressibility of gas, a bubble, if subjected to external forces, may undergo oscillations in size. If the oscillation is slow then the contraction and expansion of size are approximately symmetric. This phenomenon, called stable cavitation, produces rapid flows of liquid around the bubble and induces shear stress on nearby objects. In contrast, a fast oscillation may lead to asymmetric contraction and expansion followed by a violent collapse called inertial cavitation. This generates a very high temperature, pressure and releases a shock wave that propagates at supersonic speed radially from the collapse site.¹ Both phenomena have been extensively studied and applied to different disciplines in life and natural sciences as well as in technologies.² Examples include ultrasound cleaning devices where dirt particles are flushed away through microstreaming generated by bubble cavitation,³ contrast agents for ultrasound imaging in medicine,⁴ therapeutic applications such as sonoporation, tumor ablation, sonothrombolysis,⁵ and delivery of drugs to treat the brain diseases.⁶ Hence, it is important to understand the molecular mechanism of the bubble cavitation and nucleation.

Experimental investigation of physical properties of bubbles is very difficult due to their tiny sizes and fragility which limit measurements under laboratory conditions.⁷ Molecular dynamics (MD) simulation is a useful tool to investigate microscopic structures and dynamics with fine time resolutions, resulting in a wealth of information on the bubble nucleation and cavitation. The common approach for simulating the bubble inertial cavitation dynamics is to remove some molecules in the simulation cell, therefore generating an empty hole to mimic a bubble.^8,9 During the simulation the empty hole is compressed by the surrounding molecules and then collapses. To simulate the bubble nucleation, usually some selected molecules are locally heated and thus scattered from non-heated molecules, generating an empty space considered as a bubble.¹⁰ Alternatively, the bubble nucleation can also be formed by reducing pressure in the simulation cell,¹¹ or applying a time-dependent oscillating external pressure to the system. When the pressure is negative, bubbles are formed in the liquid and crashed when the pressure becomes positive.¹² All these techniques have been developed and employed to study the bubble nucleation,^11,13–15 to investigate the nanobubble collapse in water,¹⁶ and to validate the well-known Rayleigh-Plesset equation^17,18 which was theoretically developed to describe the bubble dynamics driven by a low amplitude sound wave in an infinity fluid.^8–10,19

As mentioned above, methods for simulating the bubble inertial cavitation have been developed, but to our best knowledge, there are currently no methods for simulating the bubble stable cavitation, where bubbles undergo harmonic vibration in size, and the first aim of this work is to develop such a method. It can be used, for example, to simulate experiments where encapsulated stable gas bubbles in liquid undergo stable vibration in size due to external forces such as ultrasound. This method allows us to understand the microscopic effects of shear flows induced by the bubble stable cavitation, but not the inertial cavitation, on the surrounding objects. We then employ the method to simulate the stable cavitation effect on an amyloid β (Aβ) fibril model of Alzheimer’s disease.²⁰ Experimentally, amyloid fibrils can be detected and removed with chemicals such as guanidine hydrochloride or dimethyl sulfoxide.²¹ Since these chemicals are highly toxic and harmful, alternative methods using ultrasound^12,22,23 and infrared laser excitation^24–28 have been developed. It has been shown that amyloid fibrils are fragmented due to the ultrasound-induced bubble inertial cavitation. Our simulation shows that amyloid fibrils can also be dissociated under bubble stable cavitation, thus the second aim of this work is to suggest a proof-of-concept for the development of a new method to remove amyloid fibrils.

II. METHODOLOGY

A. The bubble model

In our method, a bubble is represented by a particle with low mass, no charge. The interaction with surrounding water molecules is represented by a time-dependent Lennard-Jones potential

$${\displaystyle V[r,\sigma \left(t\right)]=4ϵ\left[{\left(\frac{\sigma \left(t\right)}{r}\right)}^{12}-{\left(\frac{\sigma \left(t\right)}{r}\right)}^6\right],}$$ (1)

where r is the distance between the center of the bubble and the oxygen atom or the hydrogen atoms of a water molecule. This potential prevents water molecules to approach the particle, creating an empty spherical space which mimics a bubble with a radius R(t) = σ(t). To mimic the stable expansion and contraction of the bubble, the time-dependent bubble radius is expressed as a harmonic vibration

$${\displaystyle R\left(t\right)=R_0\left[2+cos\left(\frac{2\pi t}{\tau }+\pi \right)\right],}$$ (2)

where τ is the vibrational frequency of the bubble radius. The amplitude of the bubble varies between R₀ at t = nτ and 3R₀ at t = (n + 1/2) τ, where n = 0, 1, 2, 3⋯ is the periodicity. This way, the time-dependent potential [Eqs. (1) and (2)] changes harmonically during the simulation, pushing waters back and forth to bubbles, thus fluid flows are generated. Being very light, the mass of the bubble particle should be very small. However, to ensure simulation stability, a mass of 1 au is used.

B. System and simulation details

Having defined a model for the bubble, we carry out nonequilibrium molecular-dynamics (NEMD) simulations for a representative pentamer fibril [Fig. 1] formed by the Alzheimer’s Aβ_17–42 peptide [(Aβ_17–42)₅].²⁹ This model (PDB: 2BEG) is one of the most cited Aβ fibrillar structures deposited in the protein data bank, and widely used in MD simulations of Aβ aggregation.²⁰ The fibril is modeled by the AMBER-f99SB-ILDN force field,³⁰ and centered in a cubic box with edge length of 7.0 nm, field with around 8000 TIP3P water molecules. Starting from this structure, about 240 water molecules (≈3%) are randomly replaced by bubble particles. The bubble radius is allowed to vibrate with the frequency τ = 50 ps and the amplitudes R = 0.2–0.6 nm (R₀ = 0.2 nm). The GROMACS program³¹ including our code for simulating bubble vibration is employed. The bond lengths with hydrogen atoms are fixed with the SHAKE algorithm³² and the equations of motion are integrated with a time step of 0.2 fs using the leapfrog algorithm. The electrostatic interactions are calculated using the particle mesh Ewald method and a cutoff of 2.0 nm.³³ A cutoff of 1.2 nm is used for the van der Waals interaction between water-water, water-fibril, and fibril-fibril molecules. A time-dependent cutoff, which is equal to the bubble radius R(t) [Eq. (2)], is used for the van der Waals interaction between water molecules and bubbles. This guarantees that a bubble interacts only with water molecules on the bubble surface. The nonbonded pair lists are updated every 10 fs. The system volume and temperature are maintained at equilibrium using the Berendsen coupling procedures.³⁴ We carry out 10 NEMD simulations starting from different initial configurations, each runs for 5 ns and results are averaged over 10 trajectories.

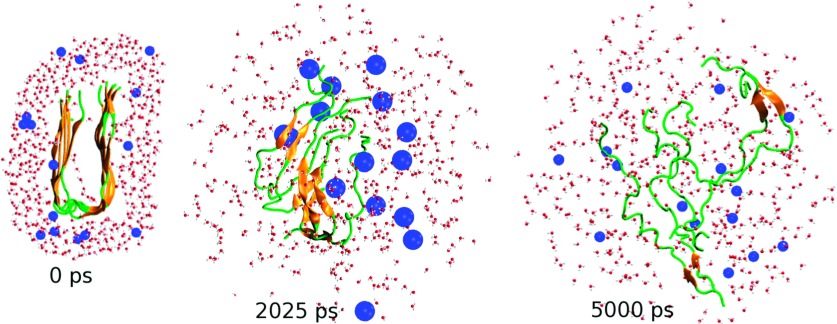
FIG. 1.

(0 ps) The initial structure of the fibril with the surrounding waters and bubbles. Shown are also two selected snapshots at 2025 ps and 5000 ps where the bubbles reach maximum and minimum radii of 0.6 nm 0.2 nm, respectively. For clarity, only a cross section and some selected waters, bubbles (blue spheres) are shown. The total number of bubbles in the system is 240.

III. RESULTS

Fig. 1 shows three selected snapshots during the simulation. For clarity, only cross sections of the fibril, surrounding water molecules and bubbles (blue spheres), are displayed. Initially, the fibril consists of a very stable cross-β sheet (orange segments) stabilized by backbone hydrogen bonds (H-bonds), there are no waters in the interior of the fibril and bubbles are randomly distributed in water. After 40 vibrational periods, each of 50 ps, we see that at t = 2025 ps, the radius of bubbles is largest (R_max = 0.6 nm), the fibril is partially dissociated with chains still adopting β-hairpin-like structures but separated from each other, allowing some bubbles to enter the interior of the fibril. Together with the bubbles on the surface, these interior bubbles exert efficiently the water pressure on the fibril from inside, breaking up the β-hairpins, converting them into the random coil states, and finally dissociating the whole fibril after 100 periods (t = 5000 ps).

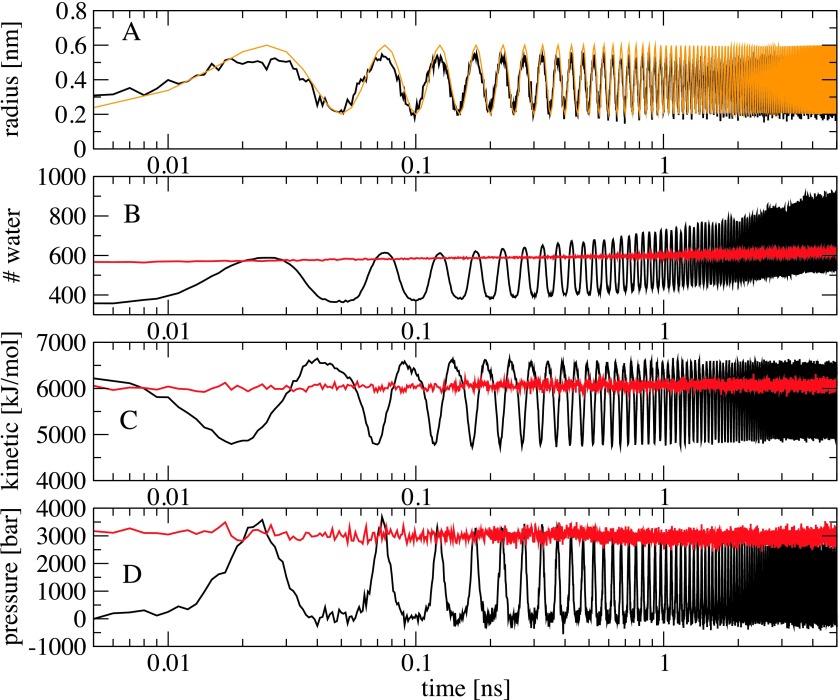
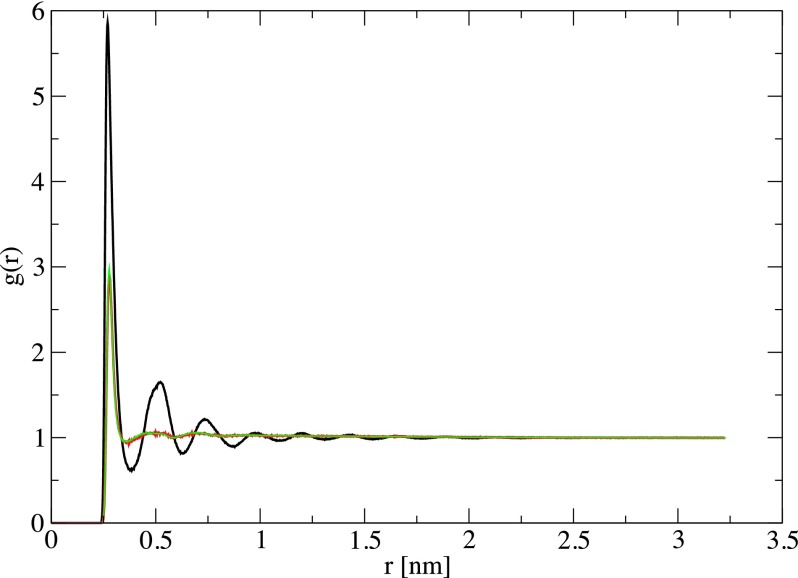
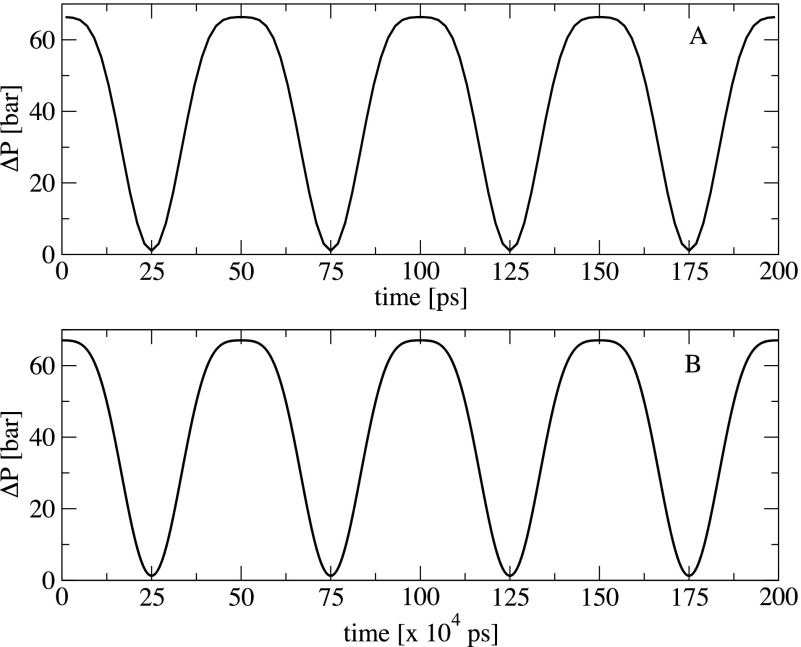
To investigate the effects of the bubble cavitation on the water structure and fibril dissociation mechanism, we first show in Fig. 2(a) the time-evolution (log-scale) of the radius of a selected bubble. It is calculated as the minimum distance between the center of the bubble to the surrounding waters. As seen, it fits perfectly the analytical curve [Eq. (2), orange line], and exhibits a harmonic vibration between 0.2 nm at t = n × 50 ps and 0.6 nm at t = (n + 1/2) × 50 ps with τ = 50 ps being the vibrational frequency, and n is the number of periodicity. To characterize the water structure, we calculate the pair radial distribution function (RDF) between the center-of-mass of water molecules during the bubble vibration. For a comparison, we also calculate RDF of pure water, i.e., without bubbles. As seen from Fig. 3, when the size of the bubbles is minimum (R_min = 0.2 nm), the RDF exhibits a typical water structure with a dominant peak at r = 0.27 nm, corresponding to the first water shell, and a much lower peak at r = 0.5 nm, representing the second shell. This RDF is virtually identical to its counterpart obtained without bubbles, indicating that the presence of ≈3% of bubbles with the radius of 0.2 nm hardly affects the water structure. However, when the bubbles are expanded to their maximum sizes of R_max = 0.6 nm, they occupy more space in the simulation cell, water molecules become closer, and this changes the spatial long-range correlation in water as reflected by the oscillations in RDF with dominant peaks at the first, second, and third water shells. The expansion of the bubble size also pushes waters far away, thus waters approach more closely to the fibril. But then waters move back following the bubble contraction. This is seen clearly from Fig. 2(b) which shows the time-evolution of the total number of water molecules within the cutoff distance of 0.3 nm from any atoms of the fibril. For example, at 25 ps the bubbles reach their maximum sizes, and the number of waters around the fibril also reaches the maximum value of ≈600, which then decreases to ≈400 at 50 ps after the bubble contraction. This change in the water density around the fibril generates fluctuations in the water pressure on the fibril. We have employed the force-decomposition method³⁵ to calculate the local pressure on the fibril, and the result shown in Fig. 2(d) exhibits an in-phase correlation with the number of waters, that is, the more the water molecules the higher the pressure on the fibril. We find that bubbles are rarely in contact with the fibril, thus this pressure is not due the direct bubble-fibril interaction but rather due to waters. An intuitive thinking could expect that the expansion of bubbles generates water flows which accelerate the fibril movement, resulting in the increase of the fibril kinetic energy. However, as shown in Fig. 2(c) the kinetic energy of the fibril is out-of-phase with the bubble vibration: when the bubbles reach the maximum radius, the kinetic energy of the fibril is the lowest ≈4700 kJ/mol. This is simply explained by the fact that under high pressures, the motion of atoms of the fibril is reduced, resulting in the decrease of the kinetic energy.

FIG. 2.

Time-evolution of the radius of a bubble obtained from the simulation (black) and the analytical Eq. (2) (orange) (a), the number of water molecules (b) and their kinetic energy (c) within spheres with a cutoff distance of 0.3 nm from any atoms of the fibril, (d) the pressure exerted on the fibril. Shown are ensemble averaged results obtained from 10 NEMD simulations with the bubble radius oscillating between R_min = 0.2 nm and R_max = 0.6 nm, frequency τ = 50 ps (black), and from 10 equilibrium MD simulations with a constant pressure of 3000 bars (red).

FIG. 3.

The radial distribution functions of the TIP3P water when the bubbles reach the maximum (R_max = 0.6 nm, black) and minimum (R_min = 0.2 nm, red) sizes. Shown is also the result in the absence of bubbles (green).

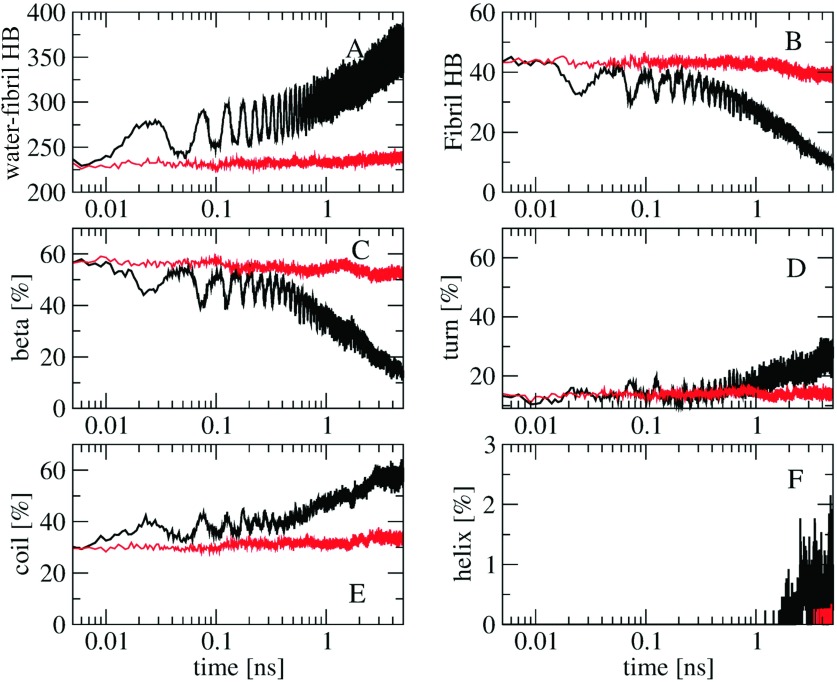
It is of interest to see how the bubble vibration breaks down the fibril. To this end, we show in Fig. 4 the time-evolution (log-scale) of various structural quantities of the fibril. As expected, the time-dependence of the number of H-bonds between fibril and waters [Fig. 4(a)] is in phase with that of the number of waters around the fibril shown in Fig. 2(b): the more waters the more H-bonds are formed. The number of intramolecular fibril H-bonds shown in Fig. 4(b) reveals clearly that the dissociation of the fibril is caused by the oscillating water pressure exerted on the fibril: at 25 ps the pressure on the fibril is maximum [Fig. 2(d)] and the fibril is destabilized with the number of fibril H-bonds decreasing from 45 to 32 H-bonds [Fig. 4(b)]. At 50 ps the bubbles are contracted to their minimum sizes, the water pressure decreases, the fibril has higher kinetic energy [Fig. 2(c)], and is further dissociated. This process continues and eventually results in the full dissociation of the fibril [Fig. 1]. The time evolution of the total population of various secondary structures calculated using the STRIDE³⁶ program shown in Figs. 4(c)–4(f) reveals the dissociation process in more detail. After the first bubble expansion cycle (t = 25 ps), the β-structure is reduced from ≈60% to ≈45%, and this is balanced with the increases of ≈5% and 10% of the turn and coil populations, respectively. During the bubble contraction (t ≥ 25 ps), the β content is increased again to ≈52% as the pentamer tends to refold back to the fibril structure, and the turn and coil contents are reduced. This process continues and ends up at 5 ns with only ≈12% of β, and significant amounts of turn (≈30%), coil (≈57%), together with a small (≤1%) population of α-helices.

FIG. 4.

Time-evolution of the number of H-bonds between water and fibril (a), the number of the intra-fibril H-bonds (b), and the content of various secondary structures including β (c), turn (d), coil (e), and helix (f). Shown are ensemble averaged results obtained from 10 NEMD simulations with the bubble radius oscillating between R_min = 0.2 nm and R_max = 0.6 nm, frequency τ = 50 ps (black), and from 10 equilibrium simulations with a constant pressure of 3000 bars (red).

IV. DISCUSSION AND CONCLUSIONS

We have presented a comprehensive method for performing stable bubble cavitation simulations. The method is quite general, simple, and can be readily implemented into any simulation packages. Thus, a wide range of applications is foreseen. Technical aspects and the implications of the method can be discussed as follows. First, although the method is developed for stable bubble cavitation simulations, it is straightforward to use it for simulating the inertial cavitation. To this end, one can carry out a NEMD simulation where bubbles are initially allowed to vibrate according to Eqs. (1) and (2). Then, at time t = (n + 1/2) τ when the bubbles reach the maximum sizes, the interaction potential between the bubbles and surrounding water molecules is turned off (V[r, σ(t)] = 0), and the bubbles collapse immediately, resulting in the inertial cavitation. Second, two parameters of our model: the bubble vibrational frequency, τ = 50 ps, and the equilibrium bubble radius, R_eq = 0.4 nm, are chosen to observe the bubble cavitation in a reasonable simulation time scale, and these values are different from those in real experiments. For example, in the widely used ultrasound induced blood-brain-barrier opening method,⁶ intravenously injected bubbles are much larger with the radii ranging from 0.5 to 4 μm, and undergo a much slower vibration in size at frequencies ranging from 0.3 to 8 MHz (3333–125 ns).^37–40 We acknowledge that with the current computer power, we cannot perform our all-atom NEMD simulations on the μs time scale to realize, at least, several ultrasound cycles using a box size of several μm to contain, at least, one real bubble. Nevertheless, despite the significant difference between our parameters and experiments, we expect that the mechanism that the bubble cavitation exerts shear stress on surrounding objects should be the same. To show this, let us estimate the pressure, generated by the bubble vibration, at the surface of a bubble. To this end, we employ the Rayleigh-Plesset equation^17,18 which describes the expansion and contraction of a bubble,

$${\displaystyle R\ddot{R}+\frac{3}{2}{\dot{R}}^2=\frac{1}{\rho }\left\{p_g(R,t)-p_{\infty }-p_s\left(t\right)-\frac{2\eta }{R}\right\},}$$ (3)

where $\dot{R}$ and $\ddot{R}$ represent respectively the first- and second-order time derivatives of the bubble radius R(t), p_g(R, t) is the pressure at the bubble surface, p_∞ is the hydrostatic pressure, p_s(t) is the ultrasound pressure, ρ and η are the density and surface tension of the bulk water, respectively. From Eq. (3), the difference between the pressure at the bubble surface and the hydrostatic pressure is

$${\displaystyle \mathrm{\Delta }p(R,t)\equiv p_g(R,t)-p_{\infty }=\rho \left\{R\ddot{R}+\frac{3}{2}{\dot{R}}^2\right\}+p_s\left(t\right)+\frac{2\eta }{R}.}$$ (4)

The ultrasound pressure, which must be out-of-phase with the bubble radius vibration [Eq. (2)], takes the form

$${\displaystyle p_s\left(t\right)=p_0\left[2+cos\left(\frac{2\pi t}{\tau }\right)\right],}$$ (5)

where p₀ is the ultrasound pressure amplitude. We calculate Δp(R, t) using our parameters of R_eq = 0.4 nm, τ = 50 ps, and compare the result with that obtained using typical experimental parameters of R_eq = 4 μm, τ = 2 MHz (500 ns), and p₀ = 2 MPa (20 bars).^37–40 Because the shorter the radius, the weaker the bubble surface tension, we approximate η(R_eq = 0.4 nm) = 0 mN/m and η(R_eq = 4 μm) = 72 mN/m which correspond to the surface tension of bulk water at 300 K.⁴¹ Using the analytical forms of the time-dependent radius R(t) [Eq. (2)] and ultrasound pressure p_s(t) [Eq. (5)], the pressure difference Δp(R, t) is calculated from Eq. (4) for the two cases and the results are shown in Fig. 5. As seen, during the bubble expansion [Fig. 2(a)] the pressure at the bubble surface is reduced as reflected by the decrease in Δp(R, t). At time t = (n + 1/2) τ, the bubble reaches the maximum size, and the surface pressure is equal to the hydrostatic pressure (Δp(R, t) = 0), and then increases until t = nτ due to the bubble contraction. Most importantly, the time-behavior and amplitude of the surface pressure of the small and large bubbles are almost the same. This suggests that the water pressure emitted by the vibration of the bubble surface pressure, at a distance r from the bubble surface, is similar for both small and large bubbles. Therefore, we expect that the mechanism that waters exert shear stress on objects surrounding the bubbles should be the same. As seen, the only difference between Figs. 5(a) and 5(b) is the time scale. This indicates that for the 100 ultrasound cycles used in this work, we should run a simulation of 50 μs to obtain the same effect if we use a larger bubble radius (0.4 μm) and a slow ultrasound frequency of 2 MHz.

FIG. 5.

Time-evolution of the difference between the pressure at the bubble surface and the hydrostatic pressure. Shown are results obtained for bubble and ultrasound parameters R_eq = 0.4 nm, τ = 50 ps (upper) and R_eq = 4 μm, τ = 2 MHz (lower). The ultrasound pressure amplitude of 2 MPa is used in both cases. For clarity, only four vibrational periods are shown for each case. Note the difference between the time scale in the panels (a) and (b).

In addition, nano-bubbles with radii ranging from 10 to 100 nm have recently been fabricated from polymeric micelles,⁴² and used to improve site-specific drug delivery in ultrasound-mediated cancer therapy.⁴³ In this context, simulations using coarse-grained force fields such as MARTINI⁴⁴ for large systems with simulation box edges of ∼100 nm, containing several nano-bubbles are doable on time scales of ∼100 μs, covering about 100 vibrational periods. This will allow us to simulate directly real experiments and confirm further the above theoretical arguments. This work is underway.

To understand the effects of the bubble stable cavitation on the surrounding objects, the method is demonstrated with the (Aβ₁₇₋₄₂)₅ fibril model. Several MD simulations have shown that this fibril is very stable under ambient equilibrium conditions,^20,28,45 and can only be dissociated under external forces such as ultrasound,¹² laser excitation,²⁸ or binding with molecular compounds.⁴⁶ The result displayed in Fig. 2(d) shows that when the bubbles reach the maximum size the highest pressure exerted on (Aβ₁₇₋₄₂)₅ is about 3000 bars. Several experimental studies have shown that fibrils can be dissociated under high pressures.^47–51 This raises a question whether (Aβ₁₇₋₄₂)₅ is dissociated due to high pressures. To this end, we carry out 10 equilibrium bubble-free MD simulations at the constant pressure of 3000 bars, using the same initial structures of the NEMD simulations. The ensemble average of the number of waters, the pressure, and the fibril kinetic energy obtained from these equilibrium MD simulations, shown in Fig. 2 (red lines), is quite similar to that obtained from NEMD simulations at time t = (n + 1/2) τ when the bubbles reach the maximum size of R_max = 0.6 nm. However, as seen from Fig. 4, the equilibrium MD simulation does not result in the dissociation of the fibril as reflected by the stable time-evolution of the number of H-bonds as well as the secondary structures (red lines). This indicates that the high pressure ∼3000 bars is not responsible for the dissociation of, at least, our (Aβ₁₇₋₄₂)₅ fibril. As shown in Fig. 2, the (Aβ₁₇₋₄₂)₅ fibril in our NEMD simulations is compressed and decompressed periodically due to the local oscillating water pressures generated by the bubble stable cavitation. This yields to the deceleration and acceleration of the fibril kinetics, which in turn, facilitate the conformational transition between local free energy minima, and finally to the dissociation of the fibril. This mechanism is qualitatively consistent with the recent experimental finding, which has shown that consecutive cycles of compression-decompression pressure lead to the reversible dissociation of the TTR and α-sysnuclei fibrils.⁴⁸ Taken together, we conclude that the oscillating pressure, but not the constant high pressure, is the essential factor that induces the dissociation of the fibril. Finally, the fact that the fibril kinetic energy is reduced when the bubbles expand [Fig. 2(c)] indicates that the dissociation is not due to the bubble inertial cavitation, which otherwise, would transfer high temperatures and accelerate the kinetic energy of the fibril.

Recently, Goto and colleagues have shown experimentally that ultrasonication accelerates the depolymerization of fibrils into monomers.^22,23 It was postulated that the inertial cavitation may occur and disrupt the fibrils. To explain this finding, Okumura and Itoh have carried out NEMD simulations under a time-dependent sinusoidal external pressure for a 12-mer Aβ fibril model. They have shown that when the pressure was negative a large bubble was formed at hydrophobic residues, but when the pressure became positive, the bubble collapsed. This generates water jets flowed out from hydrophilic residues to hydrophobic counterparts, leaving an empty water space around hydrophilic residues, thus the fibril was disrupted.¹² Therefore, the dissociation mechanism is essentially due to the presence of an empty water space around the hydrophilic residues. The direct interaction between jet flows and the fibril was not shown in their study. In our simulations, only ≈3% of bubbles are in the box and we find that bubbles do not make any direct contact with the fibril, neither at the hydrophobic nor hydrophilic residues. This confirms that our dissociation mechanism is not due to the destabilization of the fibril induced by the air-water bubble interface around hydrophilic residues. Taken together, the physics of the fibril dissociation mechanisms observed by Okumura et al. and our simulations is quite different.

In terms of applications, the use of ultrasonic irradiation to dissociate the amyloid fibril usually requires high-intensity ultrasound, because it is not clear whether bubbles are formed and the inertial cavitation occurs when the sonication frequency is lower than 2 MHz.⁵² However, a high-intensity ultrasound and the collapse of bubbles may induce damage not only to fibrils but also to the surrounding molecules due to overheating. In contrast, if gas-filled bubbles are injected into the liquid containing fibrils then bubbles absorb and concentrate energy from the ultrasound wave into a microscopic shear stress. This reduces the ultrasound intensity by many orders of magnitude from that required to induce the same effects without the bubbles.⁵³ Thus, the overheating is avoided. Moreover, the use of bubbles also allows one to achieve a repeatable and controlled cavitation environment which is important for repeatable experiments. Taken together, our method may provide an efficient approach for dissociating fibrils using the bubble stable cavitation technique, and open up new avenues to investigate the complex phenomena associated with amyloidogenesis.