Abstract
Multivariate synchronization index (MSI) has been proved to be an efficient method for frequency recognition in SSVEP-BCI systems. It measures the correlation according to the entropy of the normalized eigenvalues of the covariance matrix of multichannel signals. In the MSI method, the estimation of covariance matrix omits the temporally local structure of samples. In this study, a new spatio-temporal method, termed temporally local MSI (TMSI), was presented. This new method explicitly exploits temporally local information in modelling the covariance matrix. In order to evaluate the performance of the TMSI, we performs a comparison between the two methods on the real SSVEP datasets from eleven subjects. The results show that the TMSI outperforms the standard MSI. TMSI benefits from exploiting the temporally local structure of EEG signals, and could be a potential method for robust performance of SSVEP-based BCI.
Keywords: Steady-state visual evoked potential (SSVEP), Brain-computer interface (BCI), Multivariate synchronization index (MSI), Temporally local information
Introduction
Brain-computer interface (BCI) is an emerging technology that could provide an novel communication channel for human brain to control the external devices or environment without depending on the normal output pathways of peripheral nerves and muscles (Wolpaw et al. 2002; Lance et al. 2012; Freeman 2007b). In a BCI system, EEG was the most common noninvasive brain imaging techniques to monitor brain activity that coding the intent of a user. There exists several BCI modalities developed to utilize various brain responses, event-related potential (ERP) (Zhang et al. 2012a; Xu 2013; Long et al. 2011), sensorimotor rhythm (SMR) (Xu et al. 2011; He et al. 2015; Yuan and He 2014; Huang et al. 2010), and steady-state visual evoked potential (SSVEP) (Chen et al. 2015; Chang et al. 2016; Gao et al. 2014; Zhang et al. 2015), etc. Due to little user training and the higher information transfer rate(ITR), SSVEP-based BCI has attracted increasing attention.
For the SSVEP-based BCI, the researchers mainly focus on the target coding paradigm and the frequency recognition algorithm. In order to generate enough targets, several methods are presented, such as the Multiple frequencies sequential coding (MFSC) (Zhang et al. 2012b), frequency and phase mixed coding (Jia et al. 2011), and the sampled sinusoidal stimulation method (Chen et al. 2014), etc. Accurately translating the EEG signal poses some challenges in SSVEP-based BCI system. The single channel algorithms, such as power spectral density analysis (PDSA) (Cheng et al. 2002) and and stability coefficients (SC) (Wu and Yao 2007), need relatively long time window to yield a robust performance. In recent years, multichannel recognition methods have becoming popular. This kind of methods could efficiently exploit multichannel EEG signals to extract more robust features, then achieve higher detection accuracy. The minimum energy combination (MEC) (Friman et al. 2007), canonical correlation analysis (CCA) (Lin et al. 2006) and multivariate synchronization index (MSI) (Zhang et al. 2014a) are the mainly methods adopted in recent SSVEP-based BCI systems. The aim of MEC is to find optimized spatial filters to minimize the nuisance signals and noise as much as possible (Friman et al. 2007). The CCA-based method adopts the classical multivariate statistical method, i.e. CCA, to calculate the canonical correlation coefficients as the features between the multiple signals and the preconstructed reference signals (Lin et al. 2006). This method shows better performance than that of MEC (Nan et al. 2011). Recently, several extended CCA method have been proposed, such as individual template based CCA (IT-CCA) (Nakanishi et al. 2015), multiset canonical correlation analysis (MCCA) (Zhang et al. 2014c), L1-regularized version of MCCA (Zhang et al. 2013b). The MSI is a novel method to estimate the synchronization index between the multiple signals and the preconstructed reference signals as the classification feature (Zhang et al. 2014a). The MSI showed the best performance among the three method (Zhang et al. 2014a; Tello et al. 2014a, b). Although the MSI method provides satisfactory performance, it completely ignores the temporal information of the EEG signal in the covariances modelling.
Previous researches have confirmed that the utilizing the temporally local information of signals could significantly improve algorithm performance. The improved common spatial patterns (CSP) algorithm (Wang et al. 2012; Zhang et al. 2013b), and maximum signal fraction analysis(MSFA) artifact removal algorithm (Wang 2010) were both improved when the temporally local information was considered. EEG signals are nonstationary, and often contaminated by virous artifacts. It is beneficial to consider the temporally intrinsic manifold of EEG signals when modelling the covariance matrix which could make the algorithms effectively capture the discriminative feature (Wang et al. 2012; Wang and Xu 2012). Motivated by the ideas, in this study, we explicitly take temporally local information of EEG signals into account in the calculation of the covariance matrix of the MSI to further enhance the SSVEP frequency recognition accuracy. We term the new method as temporally local MSI (TMSI). EEG data from eleven subjects were adopted to validate the performance of TMSI. Experimental results demonstrate that the proposed TMSI outperforms the MSI, especially when short time windows are used.
Materials and methods
The standard MSI method
The MSI was proposed based on the theory of S-estimator. The S-estimator was based on the entropy of the normalized eigenvalues of the correlation matrix of multivariate signals (Carmeli et al. 2005). In the MSI method, the S-estimator was used to provide a synchronization index for frequency detection. Let and denote two multivariate signals. is the number of channels, M is the number of samples. Without loss of generality, X and Y are normalized to have a zero mean and unitary variance. Then, a covariance matrix of concatenation of X and Y can be calculated as
| 1 |
where
| 2 |
| 3 |
| 4 |
To reduce the influences of the autocorrelation of X and Y on the future computing, the following linear transformation is adopted (Joudaki et al. 2012):
| 5 |
Then, the transformed correlation matrix is
| 6 |
In fact, we can firstly use the matrices and to whiten the original data matrices X and Y respectively, and then obtain the covariance matrix R directly. Let be the eigenvalues of matrix R. Then, the normalized eigenvalues are calculated as follows:
| 7 |
where . Then, the synchronization index between two sets of signals can be calculated as follows:
| 8 |
With the formula (8), we can implement the frequency recognition for SSVEP-based BCI. Any matrix of X and Y, e.g. X, can be chosen to be the multichannel EEG signal, then Y can be the reference signal, which can be constructed with formula (9). The reference signal for each frequency in the stimulus frequency set is constituted by the following formula:
| 9 |
where denotes the number of harmonics, Fs is the sampling rate. With formula (1)–(8), K indices ( ) can be obtained with the K stimulus frequencies. Then, the targets could be identified by the rule as shown in formula (10). Namely, the frequency of the target is the frequency of the reference signal with the maximal index to the EEG signal.
| 10 |
Temporally local MSI
Previous studies demonstrate that the temporal structure information of signals can enhance the performance of signal processing algorithm, such as sparse signal recovery (Zhang et al. 2014d), artifact removal (Wang 2010), feature extraction (Wang et al. 2012; Wang and Xu 2012), etc. Covariance formulation is frequently used operation for deducing algorithms. Conventional covariance matrix omits the temporal information of signals. Temporally local covariance could be beneficial to capture the discriminative temporal structure of EEG signals and improve the performance of artifact removal and the CSP for motor imagery BCI (Wang et al. 2012; Wang 2010; Zhang et al. 2013b). Although the MSI is a potential method for frequency recognition, it is a time-independent method which may be its drawback. In this study, we try to improve the original MSI method by integrating the temporal structure information of signals into the covariance matrix. We expect that the time-dependent covariance modelling of the EEG signals could yield more robust features for frequency recognition for SSVEP-based BCI system.
Denote the weight matrix (or termed adjacency matrix) by , multivariate signals by respectively. M is the number of recording samples, and N are the number of variables or channels. Then, the temporally local covariance matrix is expressed as follow (Wang 2010):
| 11 |
The formula (11) can be further expressed as
| 12 |
where L is the Laplacian matrix and is a diagonal matrix with the diagonal elements being the row sums of W, i.e. for .
There are several choices to generate the weight matrix W. In this study, the Tukeys tricube weighting function is adopted (Cleveland 1979):
| 13 |
Here, defines the temporally local range, and it could character the manifold of the EEG signals.
| 14 |
is an monotonously decreasing function such that two temporally closer data points have larger weight between them. Similar to the study by Cleveland (Cleveland 1979), we set in the current study. When was generated, we can use the formula (5)–(8) to calculate the synchronization index, and also use the formula (10) to implement the frequency recognition. Therefore, the core operation for the temporal MSI is to model the covariance matrix which could deliver more discriminative information than the counterpart for the standard MSI.
SSVEP datasets
The TMSI was evaluated on the Eleven datasets used in our previous study (Zhang et al. 2014a). Eleven healthy subjects (two female and nine male, aged from 21 to 25 years) were recruited to participate in this study, which was approved by the Human Research and Ethics Committee of the University of Electronic Science and Technology of China. Before the experiment,all participants signed an informed consent form. All subjects were right handed, and had normal or corrected-to-normal vision.
During the experiment, the subjects were seated in a comfortable armchair, 60 cm away from the center of the laptop monitor. The experiment was performed in a normal room without electromagnetic shielding. Four frequencies (7.5, 8.6, 10, and 12 Hz) were adopted in the offline experiment. The flickering stimuli were displayed on a laptop with a 13” screen and a 60 Hz refresh rate. The subjects were instructed to gaze binocularly at each frequency stimulus for 30 s, followed by a rest period of approximately 1–2 min.
EEG signals were recorded at 1000 Hz sampling rate with a band-pass filter from 0.5 to 30 Hz and a 50 Hz notch filter. Eight Ag/AgCl recording electrodes covering occipital-parietal region were used to collect data with Symtop Amplifier (NIL System, Chengdu, China). Fcz was adopted as the reference, and Afz was adopted as the ground. The location of these electrodes is shown in Fig. 1. All the raw EEG signals were recorded for further offline analyses. All data epochs were further down-sampled to 250 Hz.
Fig. 1.
Electrode placement on the scalp for EEG recordings
Performance measurement
With the datasets, we evaluated the performance of MSI and TMSI with various time window lengths. The time windows (TW) ranged from 0.5 s to 3 s with an interval of 0.5 s. For each time window length, non-overlapping segments were extracted from the data of each frequency respectively, and then pooled all the segments of the four frequencies together. After the procedure, both methods were used to compute the classification accuracy which was the ratio of the number of segments correctly classified to the number of total segments. Only the classification accuracy was used to evaluate the performances of the two methods in this study.
Results
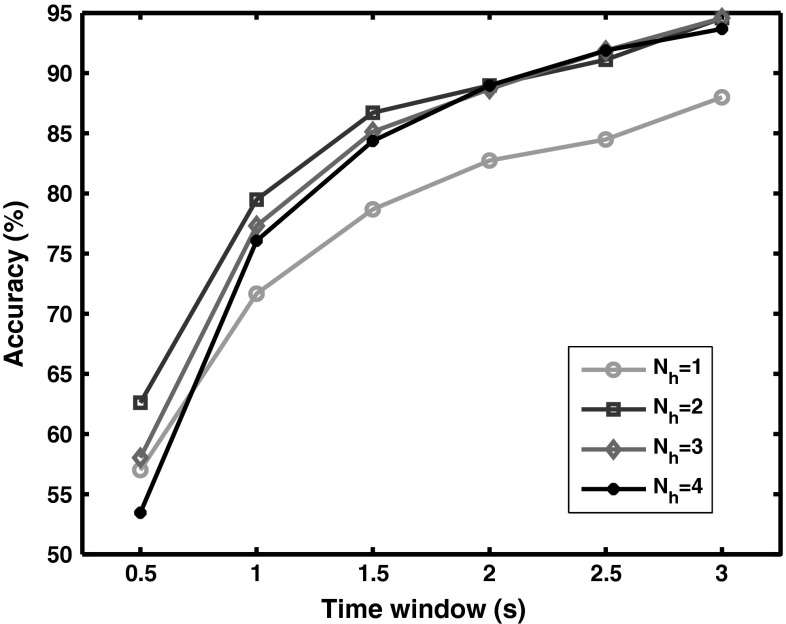
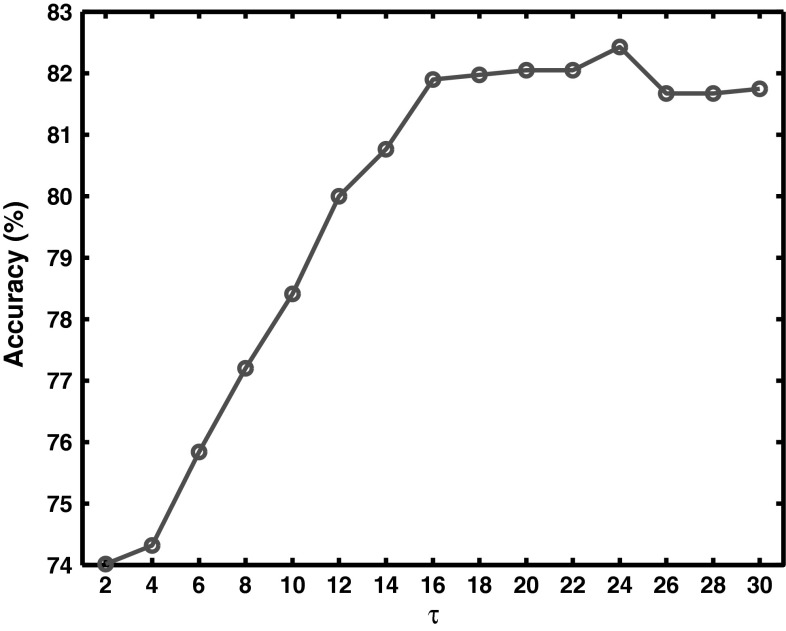
For the TMSI, we need to set the two parameters, i.e., in the weight matrix W and the number of the harmonics (). In current study, was determined using numbers ranged from 1 to 4 with the MSI method. In Fig. 2, provided the most satisfactory classification accuracy. Therefore, we set to be 2 in the following procedures for both methods. For the parameter , it was fixed by a grid search method,where was limited to [2 30] with an interval of 2, and the time window was 1 s. In Fig. 3, the results shows that yielded the highest accuracy. Therefore, this setting was used for further analysis of the TMSI method. Both TMSI and MSI methods were implemented on Matlab 2012a on a desktop computer with a 3.0 GHz CPU (4 GB RAM).
Fig. 2.
Classification accuracy of MSI method using different numbers of harmonics
Fig. 3.
Classification accuracy of TMSI method using different numbers for the with the time window being 1 s
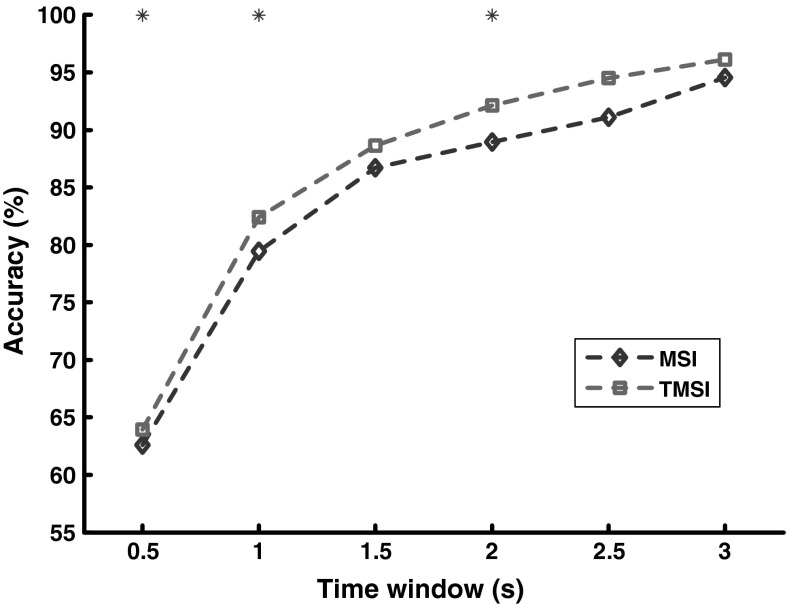
Table 1 and Fig. 4 show the classification accuracy of each subject and the averaged accuracy of all subjects with the two methods respectively. For all the TWs, the TMSI achieved better performance than the MSI according to the averaged accuracy. Furthermore, statistical analysis was implemented for the accuracy difference between the two methods with the paired-sample t-test (). The results demonstrated that the TMSI method yielded significantly higher accuracy than that of the MSI method in three TWs, and especially when time window was less than 1.5 s (see Fig. 4). The short time window required by the method can improve the response speed of the BCI system and reduce the visual fatigue of the subjects.
Table 1.
Classification accuracy (%) obtained with the MSI and TMSI at different time window (TW) respectively
| TW | Method | Subject | Average | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 | S11 | |||
| 0.5 s | MSI | 57.1 | 67.5 | 37.9 | 70.8 | 81.3 | 87.1 | 56.7 | 38.8 | 63.8 | 46.3 | 81.3 | 62.6 ± 17.0 |
| TMSI | 57.9 | 66.3 | 39.6 | 74.2 | 81.7 | 87.5 | 61.3 | 40.8 | 62.9 | 50.4 | 80.8 | 63.9 ± 16.2 | |
| 1 s | MSI | 71.7 | 88.3 | 50.8 | 89.2 | 95.8 | 98.3 | 74.2 | 52.5 | 85.8 | 71.7 | 95.8 | 79.5 ± 16.7 |
| TMSI | 71.7 | 93.3 | 50.0 | 94.2 | 98.3 | 97.5 | 79.2 | 56.7 | 90.0 | 79.2 | 96.7 | 82.4 ± 16.9 | |
| 1.5 s | MSI | 88.8 | 96.3 | 62.5 | 95.0 | 100 | 100 | 82.5 | 60.0 | 95.0 | 75.0 | 98.8 | 86.7 ± 14.8 |
| TMSI | 86.3 | 97.5 | 63.8 | 96.3 | 98.8 | 100 | 82.5 | 66.3 | 96.3 | 88.8 | 98.8 | 88.6 ± 13.0 | |
| 2 s | MSI | 90.0 | 100 | 66.7 | 93.3 | 98.3 | 100 | 85.0 | 61.7 | 98.3 | 85.0 | 100 | 88.9 ± 13.5 |
| TMSI | 93.3 | 100 | 71.7 | 96.7 | 98.3 | 100 | 91.7 | 73.3 | 100 | 88.3 | 100 | 92.1 ± 10.5 | |
| 2.5 s | MSI | 95.8 | 100 | 72.9 | 97.9 | 100 | 100 | 83.3 | 62.5 | 100 | 89.6 | 100 | 91.1 ± 12.9 |
| TMSI | 97.9 | 100 | 72.9 | 100 | 100 | 100 | 95.8 | 75.0 | 100 | 97.9 | 100 | 94.5 ± 10.3 | |
| 3 s | MSI | 97.5 | 100 | 82.5 | 100 | 100 | 100 | 87.5 | 72.5 | 100 | 100 | 100 | 94.5 ± 9.5 |
| TMSI | 100 | 100 | 85.0 | 100 | 100 | 100 | 95.0 | 80.0 | 100 | 97.5 | 100 | 96.1 ± 7.0 | |
Fig. 4.
Average accuracies of the two methods for different time window lengths. The asterisk denotes the significant difference between two methods (paired t-test, )
Discussion and conclusion
For the SSVEP-based BCI, multichannel classification methods could achieve roubst performance, and have received increasing attention. The main idea of these methods is to exploit the information from multichannel EEG signals to generate more robust features which could improve the performance of the methods (Lin et al. 2006; Friman et al. 2007; Wang et al. 2016; Zhang et al. 2014a, b). But, they completely ignores the temporal information of the EEG signal. Previous literatures have confirmed that the utilizing the temporally local structure of signals could significantly improve the algorithm performance (Wang et al. 2012; Wang 2010). To our knowledge, the issue has not been considered in the SSVEP-based BCIs.
In this study, we proposed a novel method which explicitly take temporal structure information of the EEG signals into account when developing the method based on the MSI in this study. The temporal structure information was considered by modelling the covariance matrix with a adjacency matrix constraint which incorporates the temporally intrinsic manifold. The Tukeys tricube weighting function is adopted to model the temporally local relationship between the signal samples. For this function, the parameter need to be specified, which determines the temporally local range. Although this function could reflect that two temporally closer data points have larger correlation between them, it could not reflect the real relationship between the two signal waveforms at different time points. In current study, we obtained the optimal value of by grid search. More efficient approaches should be adopted to determine this parameter for future study. Alternatively, other methods to calculate the weight matrix W need to be explored in future studies so that the W could be calculated automatically by the algorithms with the available data. Beside, the number of the harmonic () in the reference signals have impact to the recognition accuracy as shown in Fig. 2. Therefore, we need to determine the optimal () according to the available data, or use some modern methods to construct natural reference signals with the real SSVEP signals (Zhang et al. 2013b, 2014).
The experimental results show that the TMSI achieve better performance than the MSI, and have significant difference between them when the TW is shorter than 1.5 s. To see more details of the results, Fig. 5 compares the averaged accuracy across all the subjects between the two methods at each of the stimulus frequency. In most cases, TMSI outperformed MSI for all of the four stimulus frequencies at the six TWs. These experimental results indicated that TMSI is a promising method for the frequency detection in SSVEP-based BCI. There are only four frequencies in this study, which could be used for controlling the limbs of the robot (Zhang et al. 2014a). In our future study, we need to investigate the performance of the TMSI and compare it with other algorithms in the system with larger number of stimulus targets.
Fig. 5.
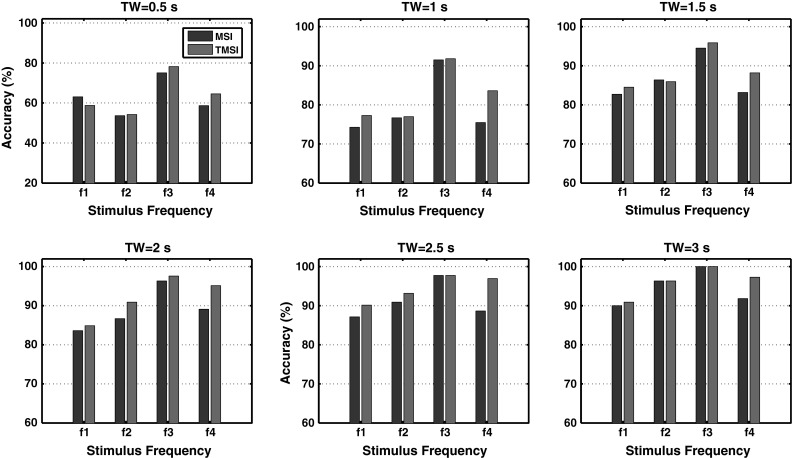
Average accuracies of each of the stimulus frequency at different time window (TW)
Furthermore, the computational time taken by the two method at different time windows were presented in Table 2. The results show that the TMSI and MSI could be implemented efficiently within 0.1 s. The online performance of the TMSI will be investigated in future studies.
Table 2.
The average computational time (s) of MSI and TMSI for classification at time window (TW) from 1 to 3 s, respectively
| TW | Method | |
|---|---|---|
| MSI | TMSI | |
| 0.5 s | 0.0039 | 0.0068 |
| 1 s | 0.0045 | 0.0129 |
| 1.5 s | 0.0052 | 0.0253 |
| 2 s | 0.0058 | 0.0410 |
| 2.5 s | 0.0064 | 0.0666 |
| 3 s | 0.0069 | 0.0946 |
In summary, we proposed a novel frequency recognition method(TMSI) by incorporating the temporal information from the multichannel EEG signals into the algorithm based on the MSI. The experimental results based on EEG data from eleven subjects showed the TMSI method outperformed the standard MSI method. TMSI could be a promising alternative for frequency recognition in the SSVEP-based BCI systems.
Acknowledgments
This work is supported in part by the National Natural Science Foundation of China (Nos. 81401484, 61527815, 81571770, 61305028) the Doctoral Fund of Southwest University of Science and Technology (Grant No. 15zx7115),and Shanghai Chenguang Program under Grant 14CG31.
Contributor Information
Yangsong Zhang, Email: zhangysacademy@gmail.com.
Daqing Guo, Email: dqguo@uestc.edu.cn.
References
- Chang MH, Lee JS, Heo J, Park KS. Eliciting dual-frequency SSVEP using a hybrid SSVEP-P300 BCI. J Neurosci Methods. 2016;258:104–113. doi: 10.1016/j.jneumeth.2015.11.001. [DOI] [PubMed] [Google Scholar]
- Cheng M, Gao X, Gao S, Xu D. Design and implementation of a brain-computer interface with high transfer rates. IEEE Trans Biomed Eng. 2002;49:1181–1186. doi: 10.1109/TBME.2002.803536. [DOI] [PubMed] [Google Scholar]
- Chen X, Chen Z, Gao S, Gao X. A high-ITR SSVEP-based BCI speller. Brain Comput Interf. 2014;1:181–191. doi: 10.1080/2326263X.2014.944469. [DOI] [Google Scholar]
- Chen X, Wang Y, Nakanishi M, Gao X, Jung TP, Gao S. High-speed spelling with a noninvasive brain-computer interface. Proc Natl Acad Sci USA. 2015;112(44):E6058–E6067. doi: 10.1073/pnas.1508080112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cleveland WS. Robust locally weighted regression and smoothing scatterplots. J Am Stat Assoc. 1979;74:829–836. doi: 10.1080/01621459.1979.10481038. [DOI] [Google Scholar]
- Carmeli C, Knyazeva MG, Innocenti GM, De Feo O. Assessment of EEG synchronization based on state-space analysis. Neuroimage. 2005;25:339–354. doi: 10.1016/j.neuroimage.2004.11.049. [DOI] [PubMed] [Google Scholar]
- Freeman WJ. Definitions of state variables and state space for brain-computer interface. Part 2: extraction and classification of feature vectors. Cognit Neurodyn. 2007;1:85–96. doi: 10.1007/s11571-006-9002-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friman O, Volosyak I, Graser A. Multiple channel detection of steady-state visual evoked potentials for brain-computer interfaces. IEEE Trans Biomed Eng. 2007;54:742–750. doi: 10.1109/TBME.2006.889160. [DOI] [PubMed] [Google Scholar]
- Gao S, Wang Y, Gao X, Hong B. Visual and auditory brain-computer interfaces. IEEE Trans Biomed Eng. 2014;61:1436–1447. doi: 10.1109/TBME.2014.2321007. [DOI] [PubMed] [Google Scholar]
- He B, Baxter B, Edelman BJ, Cline CC, Ye WW. Noninvasive brain-computer interfaces based on sensorimotor rhythms. Proc IEEE. 2015;103:907–925. doi: 10.1109/JPROC.2015.2396991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang G, Liu G, Meng J, Zhang D, Zhu X. Model based generalization analysis of common spatial pattern in brain computer interfaces. Cognit Neurodyn. 2010;4:217–223. doi: 10.1007/s11571-010-9117-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jia C, Gao X, Hong B, Gao S. Frequency and phase mixed coding in SSVEP-based brain-computer interface. IEEE Trans Biomed Eng. 2011;58:200–206. doi: 10.1109/TBME.2010.2068571. [DOI] [PubMed] [Google Scholar]
- Joudaki A, Salehi N, Jalili M, Knyazeva MG. EEG-based functional brain networks: does the network size matter? PLoS One. 2012;7:e35673. doi: 10.1371/journal.pone.0035673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lance BJ, Kerick SE, Ries AJ, Oie KS, McDowell K. Brain-computer interface technologies in the coming decades. Proc IEEE. 2012;100:1585–1599. doi: 10.1109/JPROC.2012.2184830. [DOI] [Google Scholar]
- Lin Z, Zhang C, Wu W, Gao X. Frequency recognition based on canonical correlation analysis for SSVEP-based BCIs. IEEE Trans Biomed Eng. 2006;53:2610–2614. doi: 10.1109/TBME.2006.886577. [DOI] [PubMed] [Google Scholar]
- Long J, Gu Z, Li Y, Yu T, Li F, Fu M. Semi-supervised joint spatio-temporal feature selection for P300-based BCI speller. Cognit Neurodyn. 2011;5:387–398. doi: 10.1007/s11571-011-9167-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nan W, Wong CM, Wang B, Wan F, Mak PU, Mak PI, Vai MI (2011) A comparison of minimum energy combination and canonical correlation analysis for SSVEP detection. In: Proceedings of 5th international IEEE EMBS conference on neural engineering, pp 469–472
- Nakanishi M, Wang Y, Wang Y, Jung TP. A comparison study of canonical correlation analysis based methods for detecting steady-state visual evoked potentials. PLoS One. 2015;10:e0140703. doi: 10.1371/journal.pone.0140703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tello RM, Muller SM, Bastos-Filho T, Ferreira A (2014a) A comparison of techniques and technologies for SSVEP classification. In: Proceedings of 5th ISSNIP-IEEE biosignalling and biorobotics conference on biosignal and robot better safer living, pp 1–6
- Tello RM, Torres Muller SM, Bastos-Filho T, Ferreira A (2014b) Comparison of new techniques based on EMD for control of a SSVEP-BCI. In: IEEE 23rd international symposium on industrial electronics (ISIE), pp 992–997
- Wang H. Temporally local maximum signal fraction analysis for artifact removal from biomedical signals. IEEE T Signal Proces. 2010;58:4919–4925. doi: 10.1109/TSP.2010.2052047. [DOI] [Google Scholar]
- Wang H, Xu D. Comprehensive common spatial patterns with temporal structure information of EEG data: minimizing nontask related EEG component. IEEE Trans Biomed Eng. 2012;59:2496–2505. doi: 10.1109/TBME.2012.2205383. [DOI] [PubMed] [Google Scholar]
- Wang H, Tang Q, Zheng W. L1-norm-based common spatial patterns. IEEE Trans Biomed Eng. 2012;59:653–662. doi: 10.1109/TBME.2011.2177523. [DOI] [PubMed] [Google Scholar]
- Wang H, Zhang Y, Waytowich N, Krusienski D, Zhou G, Jin J, Wang X, Cichocki A. Discriminative feature extraction via multivariate linear regression for SSVEP-based BCI. IEEE Trans Neural Syst Rehabil Eng. 2016;24(5):532–541. doi: 10.1109/TNSRE.2016.2519350. [DOI] [PubMed] [Google Scholar]
- Wolpaw JR, Birbaumer N, McFarland DJ, Pfurtscheller G, Vaughan TM. Brain-computer interfaces for communication and control. Clin Neurophysiol. 2002;113:767–791. doi: 10.1016/S1388-2457(02)00057-3. [DOI] [PubMed] [Google Scholar]
- Wu Z, Yao D. Frequency detection with stability coefficient for steady-state visual evoked potential (SSVEP)-based BCIs. J Neural Eng. 2007;5:36. doi: 10.1088/1741-2560/5/1/004. [DOI] [PubMed] [Google Scholar]
- Xu P, Yang P, Lei X, Yao D. An enhanced probabilistic LDA for multi-class brain computer interface. PLoS One. 2011;6:e14634. doi: 10.1371/journal.pone.0014634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu M, et al. Channel selection based on phase measurement in P300-based brain-computer interface. PLoS One. 2013;8:e60608. doi: 10.1371/journal.pone.0060608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan H, He B. Brain-computer interfaces using sensorimotor rhythms: current state and future perspectives. IEEE Trans Biomed Eng. 2014;61:1425–1435. doi: 10.1109/TBME.2014.2312397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Zhao Q, Jin J, Wang X, Cichocki A. A novel BCI based on ERP components sensitive to configural processing of human faces. J Neural Eng. 2012;9:026018. doi: 10.1088/1741-2560/9/2/026018. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Xu P, Liu T, Hu J, Zhang R, Yao D. Multiple frequencies sequential coding for SSVEP-based brain-computer interface. PLoS One. 2012;7:e29519. doi: 10.1371/journal.pone.0029519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang R, Xu P, Liu T, Zhang Y, Guo L, Li P, Yao D. Local temporal correlation common spatial patterns for single trial EEG classification during motor imagery. Comput Math Methods Med. 2013;2013:591216. doi: 10.1155/2013/591216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Zhou G, Jin J, Wang M, Wang X, Cichocki A. L1-regularized multiway canonical correlation analysis for SSVEP-based BCI. IEEE Trans Neural Syst Rehabil Eng. 2013;21:887–896. doi: 10.1109/TNSRE.2013.2279680. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Xu P, Cheng K, Yao D. Multivariate synchronization index for frequency recognition of SSVEP-based brainCcomputer interface. J Neurosci Methods. 2014;221:32–40. doi: 10.1016/j.jneumeth.2013.07.018. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Dong L, Zhang R, Yao D, Zhang Y, Xu P. An efficient frequency recognition method based on likelihood ratio test for SSVEP-based BCIs. Article ID: Comput Math Methods Med; 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Zhou G, Jin J, Wang X, Cichocki A. Frequency recognition in SSVEP-based BCI using multiset canonical correlation analysis. Int J Neural Syst. 2014;24:1450013. doi: 10.1142/S0129065714500130. [DOI] [PubMed] [Google Scholar]
- Zhang Z, Jung T-P, Makeig S, Pi Z, Rao B. Spatiotemporal sparse Bayesian learning with applications to compressed sensing of multichannel physiological signals. IEEE Trans Neural Syst Rehabil Eng. 2014;22:1186–1197. doi: 10.1109/TNSRE.2014.2319334. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Zhou G, Jin J, Wang X, Cichocki A. SSVEP recognition using common feature analysis in brain-computer interface. J Neurosci Methods. 2015;244:8–15. doi: 10.1016/j.jneumeth.2014.03.012. [DOI] [PubMed] [Google Scholar]