Proton-Coupled Electron Transfer in Organic Synthesis: Fundamentals, Applications, and Opportunities

Abstract

Proton-coupled electron transfers (PCETs) are unconventional redox processes in which both protons and electrons are exchanged, often in a concerted elementary step. While PCET is now recognized to play a central a role in biological redox catalysis and inorganic energy conversion technologies, its applications in organic synthesis are only beginning to be explored. In this chapter we aim to highlight the origins, development and evolution of PCET processes most relevant to applications in organic synthesis. Particular emphasis is given to the ability of PCET to serve as a non-classical mechanism for homolytic bond activation that is complimentary to more traditional hydrogen atom transfer processes, enabling the direct generation of valuable organic radical intermediates directly from their native functional group precursors under comparatively mild catalytic conditions. The synthetically advantageous features of PCET reactivity are described in detail, along with examples from the literature describing the PCET activation of common organic functional groups.

Introduction

‘Proton-coupled electron transfer’ (PCET) describes any elementary step (or series of elementary steps) in which both a proton and an electron are exchanged [1-9]. Within this broad definition, further distinctions may be drawn: if the proton and electron move simultaneously, the elementary step is referred to as a concerted PCET. Alternatively, if electron transfer precedes a rapid proton-transfer event (or vice versa), the series of elementary steps is said to be stepwise. The proton and electron in a PCET process need not originate from the same bond, or even the same molecule: when the proton and electron are delivered to two separate acceptors or arrive from two distinct donors, the PCET event is said to be multisite.

In recent years PCET has been shown to play a central role in important biological redox processes, such as photosynthetic water oxidation [10], ribonucleotide reduction in DNA biosynthesis [11-12], oxygen reduction by cytochrome C oxidase [13], enzymatic C-H bond oxidation [14-15], natural product biosynthesis [16], DNA photolyase activity [17], and numerous synthetic inorganic technologies for small molecule activation [18-19]. Concurrently, extensive physical and theoretical studies have provided a number of important insights into PCET reaction mechanisms [20-21]. However the applications of PCET as a mechanism of substrate activation in organic synthesis have only recently begun to be explored. The focus of this review is to highlight both the basic reactivity trends and beneficial attributes of concerted PCET reactions for synthetic applications, and to discuss the chemistry of common organic functional groups known to engage in concerted PCET reactivity. This review is not meant to serve as a comprehensive overview of documented PCET processes in biology or an exhaustive overview of their physical origins. Rather, it is meant as a primer for organic chemists who may wish to design or utilize PCET reactions in their own work, or to become acquainted with the synthetically relevant literature in this large and diverse area of research. The structure of this review starts with an introductory discussion of the energetics of PCET reactions, followed by mechanistic discussion as organized by functional groups. Where applicable, synthetic examples are included to demonstrate the capacity of PCET to furnish desirable radical synthons and explore their often unique selectivities.

Energetic Characteristics of PCET Activation

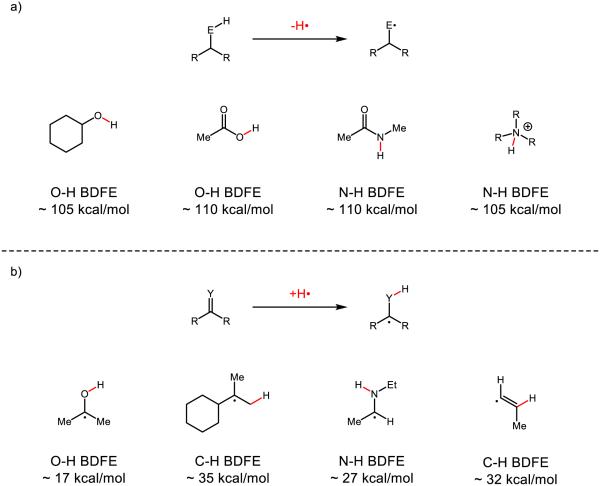
From a synthetic perspective, multisite PCET is similar to traditional hydrogen atom transfer (HAT) reactions in that both involve the addition or removal of the elements of H• to furnish a neutral free radical product. However, PCET has the potential to enable the direct homolytic activation of many common organic functional groups that are energetically inaccessible using conventional H-atom transfer platforms. In HAT reactions, the thermodynamic driving force is taken to be proportional to the difference in bond strengths of the bonds being broken and formed in the exchange. As such, cleaving a strong bond to hydrogen in the donor requires formation of a similarly strong or even stronger bond to hydrogen in the acceptor. Similar constraints apply in the reactions of H-atom donors, wherein the new bond to hydrogen formed upon HAT to an acceptor must be of similar strength (or stronger than) the bond to hydrogen in the donor. These energetic constraints present a significant challenge to developing effective catalysts for the homolytic activation of many common organic functional groups (Figure 1). With respect to oxidative HAT activation, the bonds to hydrogen in many of the most common protic organic functional groups (including alcohols, amides, ammonium ions, and carboxylic acids) feature bonds strengths well in excess of 100 kcal mol⁻¹ (Figure 1a). As such, even the most powerful molecular HAT reagents, such as the ferryl groups in metalloproteins such as cytochrome P450, do not possess a sufficient driving force to activate many polar N-H and O-H bonds [22]. Moreover, these polar functional groups are often embedded in hydrocarbon frameworks containing much weaker aliphatic C-H bonds that are often preferentially activated by strong H-atom acceptors.

Figure 1.

a) Examples of strong bonds of common organic functional groups b) examples of weak bonds vicinal to radical centers derived from common organic functional groups

Similarly, for the reductive HAT activation of π-systems, the new bond to hydrogen is dramatically destabilized by virtue of being vicinal to an unpaired electron (Figure 1b). As such, few if any HAT donors have been shown to be competent to activate ketones, imines, arenes, or certain classes of olefins [23-26] via HAT. In fact, the weakest, well-characterized metal hydride is Norton’s H-V(CO)₄(dppb), which features a V-H BDFE of 50 kcal mol⁻¹ [27]. While exceptionally weak, this bond it is still far too strong to serve as an effective H-atom donor to many common organic π-systems such as those depicted in Figure 1b.

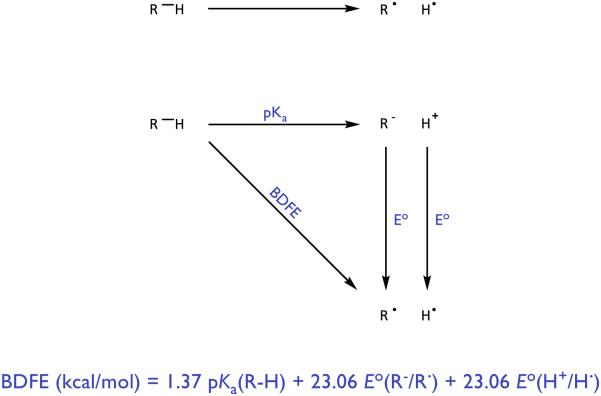
In light of these limitations, it is interesting to consider how one might rationally design new HAT catalysts to target specific organic functional groups. Classically, the homolytic strengths of covalent bonds are analyzed using a simple thermodynamic cycle popularized by Bordwell [28]. In this scheme, the bond dissociation free energy (BDFE) is defined as the energy required to heterolytically break the bond (represented as a pK_a value) summed together with the energies required to oxidize the resulting anion to a neutral radical and reduce the remaining proton to H•. As such, this formalism would suggest that to create a molecular H-atom donor with a weaker R-H bond, one must either increase the Brønsted acidity of the donor, make its conjugate base more reducing, or some combination thereof. Unfortunately, within any single molecule these two key physical properties – the pK_a and the oxidation potential of the conjugate base – are interdependent and inversely correlated. The energetic benefits of making a donor more acidic will be largely compensated for by a concomitant loss in the reducing ability. Analogous difficulties arise in the design of new oxidative HAT reagents, wherein any increase in basicity of an H-atom acceptor will be compensated in part by a correlated decrease in oxidizing power. This leveling effect suggests that rational design of more powerful molecular H-atom donors and acceptors through variation of these parameters is likely to be challenging.

However, Mayer has pointed out that this method for conceptualizing covalent bond strengths suggests a thermodynamic equivalency between direct HAT, in which the transferring proton and electron originate in the same chemical bond, and a multisite PCET mechanism wherein the proton and electron travelling to the acceptor originate from site-separated and independent donors – a Brønsted acid and a one-electron reductant (Figure 3) [29]. While no bond is formally homolyzed in such a process, summing the pK_a and redox potential values in a similar fashion provides an ‘effective’ bond strength, which quantitatively reflects the capacity of any given acid/reductant combination to function jointly as a hydrogen atom donor. Significantly, in this PCET manifold the pK_a of the proton donor and the potential of the reductant may be varied independently. This in turn allows the effective BDFE of any given acid/reductant (or oxidant/base) pair to be varied over an arbitrarily wide range of energies. While not all bases are compatible with all oxidants [30], the use of excited state redox partners as PCET components tends to allow for greater flexibility with respect to which bases may be used [31]. The same principle applies for combinations of acids and reductants. This formalism provides a straightforward means to identify acid/reductant combinations with effective bond strengths far weaker (<20 kcal/mol) than those found for any known molecular H• donor catalysts. Similarly, thermochemical arguments can be constructed for combinations of bases and oxidants that act in unison as thermodynamically potent hydrogen atom abstractors, with effective BDFEs in excess of 110 kcal/mol. In principle, this remarkable energetic range can enable the rational identification of catalyst systems that are thermodynamically competent to effect homolytic activation of many common organic functional groups that are currently inaccessible using traditional HAT technologies. Even if PCET to a substrate is endergonic, several synthetic examples highlight that even highly endergonic PCET events can be coupled with secondary chemical reactions in catalysis [31-32].

Figure 3.

A square scheme for ‘effective’ BDFEs as popularized by Mayer [29] along with example bond strengths available by the joint action of select bases/oxidants and acids/reductants respectively. Asterisks denote ET from an excited state except for Cp*, which refers to pentamethylcyclopentadiene. Abbreviations: bpy = 2,2’-bipyridine, bpz = 2,2’-bipyrazine, ppy = 2-phenylpyridinato-C², dF(CF₃)ppy = 2-(2,4-difluorophenyl)-5-(trifluoromethyl)pyridinato-C², DMAP = 4-dimethylamino pyridine, PTSA = p-toluenesulfonic acid.

In addition to enabling access to more powerful HAT reagents, the preferences for site selectivity in multisite PCET reactions are expected to be orthogonal to those of many traditional HAT catalysts. Selectivity in HAT processes is generally a function of bond strength differential, with the weakest bonds in the substrate being oxidized most rapidly [33]. In fact, such relationships are often presented as evidence for radical-based mechanisms of bond cleavage. In contrast, the site-selectivity of multisite PCET mechanisms is dictated by specific hydrogen bonding interactions [6]. In physical descriptions of PCET reactivity, significant emphasis is placed on the length scales of the transfer reactions. While electrons tunnel readily over large distances (>10 Å), heavier protons can only travel over relatively small distances (1–2 Å). Consequently, pre-association by hydrogen bonding is a characteristic feature of concerted multisite PCET activation as it defines the proton transfer reaction coordinate and confines it to an appropriate length scale. As typical C-H bonds are poor hydrogen bond donors, separated base/oxidant catalyst systems should, in principle, be able to activate stronger O-H and N-H bonds of polar H-bond donors selectively. Similarly, concerted PCET activation of ketones and other polar π bonds should be possible in preference to the activation of olefins, despite a large thermodynamic bias for the latter pathway.

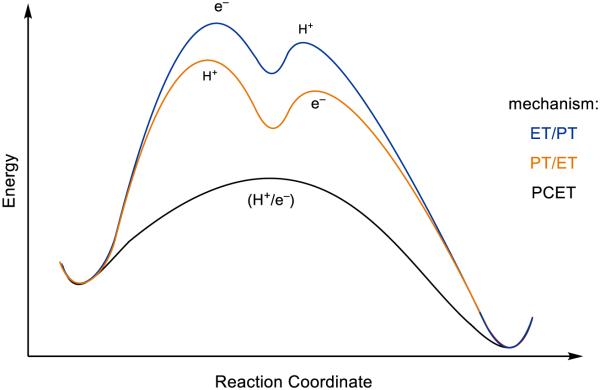
Lastly, in addition to the these thermodynamic advantages, concerted PCET processes often exhibit rates that are significantly faster than the constituent electron transfer (ET) or proton transfer (PT) steps in isolation (Figure 4). This observation follows from the fact that PCET kinetics, like those of ET and HAT, are functions of the reaction’s thermodynamic driving force [34-36]. The products formed directly in the concerted pathway are necessarily lower in energy than the intermediates formed in the competing stepwise pathways. This thermodynamic bias is manifested kinetically, enabling facile charge transfer to occur with catalyst potentials that are far less energetic than the thermodynamic potentials of their substrates. These kinetic advantages are well precedented in a large number of molecular systems and are thought to underlie the pervasive use of concerted PCET mechanisms in biological redox catalysis.

Figure 4.

A sample reaction coordinate demonstrating the diminished barriers for concerted PCET relative to stepwise ET/PT or PT/ET. [32]

In light of these advantages, PCET has significant potential to expand the scope of homolytic bond activation catalysis in organic synthesis, and enable the direct generation of valuable radical intermediates directly from their native functional group precursors [37]. In support of this hypothesis, the remaining sections of this chapter are devoted to mechanistic studies and relevant synthetic examples of PCET segmented by functional groups.

Metal-Oxo Complexes for C-H Bond Oxidation

Among the most synthetically important PCET reactions are the oxidations of C-H bonds by metal-oxo complexes. However, prior to a full discussion of metal-oxo PCET reactions, it is important to comment in more detail on the distinctions between HAT and PCET. Meyer has proposed a definition for HAT that is limited to reactions in which “the transferring electron and proton come from the same bond” [5,38-39]. Mayer has noted a number of problems associated with this definition that are especially pertinent in the reactions of metal-oxo complexes [29]. Specifically, Mayer cites compound I in cytochrome P450 enzymes where the metal oxo (Fe=O) group accepts a proton at oxygen while the electron is transferred into a ligand-centered orbital of the porphyrin radical cation [40]. He further elaborates that a forward abstraction step could be accurately defined as a HAT step, as the proton and electron come from the C-H bond, but not its microscopic reverse, where the proton comes from the O-H bond and the electron comes from a ligand-centered orbital. Accordingly, he suggests HAT to be more broadly defined as “concerted transfer of [a proton] and [an electron] from a single donor to a single acceptor.” While this definition suggests that classical HAT is a specific subset of concerted PCET reactions, subtleties between the two elementary steps preclude these terms from being truly interchangeable (or, in many cases, from being readily distinguished) [39,41-42]. In light of these problems in both terminology and identification, we present examples pertinent to PCET-type mechanisms and have adopted the nomenclature presented by the original authors. We defer judgment regarding the aptness and accuracy of these classifications to the reader.

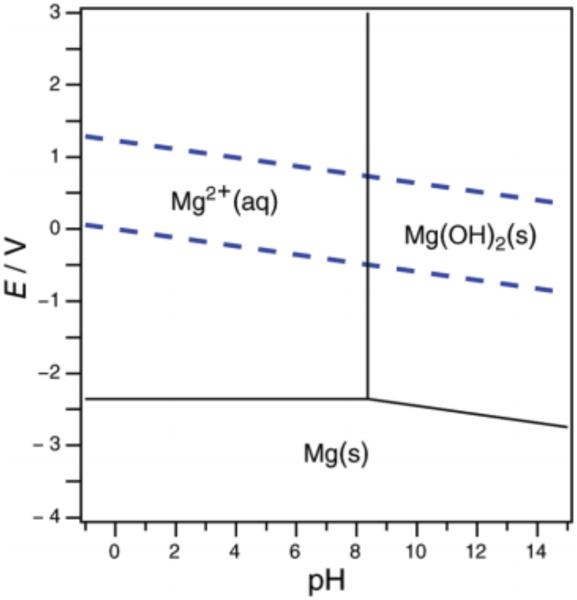
In his doctoral thesis in 1945, Pourbaix established the use of “potential-pH diagrams” – now referred to as Pourbaix diagrams – to predict the equilibrium state of a given element and its ions in aqueous solution (Figure 5) [44]. Since that time, Pourbaix diagrams for many elements have been developed for their utility in assessing the thermodynamic viability of certain processes, especially corrosion [45]. Crossing a line on the diagram represents changes in the dominant species in situ; such boundaries are dependent on both the pH and the potential and (if the potential is reversible) can be outlined using the following form of the Nernst equation [29]:

$$E=E^0-\frac{RT}{nF}ln\frac{\left[{\text{H}}_m{\text{A}}^{(n-m)-}\right]}{\left[\text{A}\right]}-\frac{RT}{F}\frac{m}{n}\text{pH}$$

Figure 5.

A sample Pourbaix diagram of magnesium in water; the dashed blue lines represent the potentials at which water is oxidized (top line) and reduced (bottom line). Reprinted with permission from [43]. Copyright 2012 American Chemical Society.

In the above equations, m represents the number of protons transferred, n refers to the number of electrons transferred, R is the ideal gas constant, F is Faraday’s constant, and T is the temperature. At a constant, standard temperature of 298 K, the value (RT/F) is 59 mV and is constant. As the pH changes, the slope ΔE/ΔpH reflects the ratio of protons to electrons (m/n) transferred in a single step: a horizontal line (m = 0) indicates no proton transfer occurs, vertical lines (n ~ 0) imply no involvement of electron transfer, and diagonal lines indicate both protons and electrons transfer for a net loss of protons and electrons in some ratio m/n. For example, the net loss of a hydrogen atom (i.e., one proton and one electron) proceeds with m/n = 1. An important note, however, is that a Pourbaix diagram only provides thermochemical information for a PCET event and does not distinguish between stepwise or concerted processes: further mechanistic analysis is required to distinguish the operative mechanisms. In addition, for aqueous solutions such diagrams are limited to potential/pH regimes in which water is stable. Nevertheless, boundaries of thermochemical viability are valuable to the synthetic chemist seeking to choose reagents to affect a particular PCET process.

The idea that both the pH and applied voltage affects the stability of metal oxo, hydroxo, and aquo species has proven influential over time. Based on these diagrams, the community has come to understand the influence of both the substrate pK_a and the potential associated with its (de)protonated form on the overall bond strength of a species and how these may be leveraged to tune said bond strengths. For a metal oxo, the O-H bond strength inherent to a metal oxo is determined by both its basicity and its oxidizing power. As further examples will demonstrate, the basicity is oftentimes the dominant contributor to the bond strength of this species. The importance of oxo basicity was highlighted by Green and Gray in their seminal studies of chloroperoxidase, which identified that chloroperoxidase compound II (CPO-II) must have a minimum aqueous pK_a of ~ 8.2 [22]. The basicity implies this species is protonated at physiological pH; these authors credit remarkable unusually high basicity to the binding of an axial thiolate ligand. In a later study, Green concluded that the ferryl forms of P540_BM3 and P450_cam were protonated at physiological pH using a combination of Mössbauer spectroscopy and density functional calculations [46]. Where iron-heme complexes such as Horseradish peroxidase C (and its associated Compounds I and II) are poorly oxidizing (approximately 1.08 V at pH = 6.5) [47], these enzymes are among a small set of enzymes capable of cleaving strong C-H bonds [48]. The bond strengths of these species are thought to be a direct function of the oxo basicity; where the thiolate decreases the oxidation potential of the iron center, it concomitantly increases the basicity of the oxo such that the O-H bond strength is strong despite a lack of oxidative driving force. Moreover, the axial ligation of the metal oxo in iron heme proteins has been demonstrated to have a profound effect on the pK_a of the Fe^IV oxo form of the enzyme [49] as well as the Fe-O bond strength observed in model systems [50].

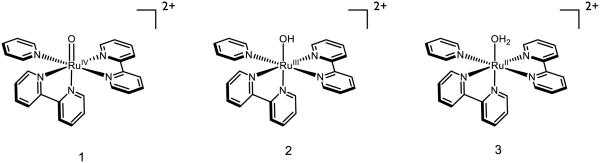
More braodly, discrete metal-oxo complexes have garnered intense interest because of their stability, tunability, and utility as model systems for the study of metalloproteins. In 1978, Meyer disclosed the ruthenium-oxo species 1, and demonstrated its acid-dependent redox transformations to form 2 and 3 (Figure 6) [51]. Where 3 has a pK_a of 10.8 in aqueous 0.33 M NaSO₄, a sharp decrease in pK_a to 0.85 in 1 M HClO₄/LiClO₄ solution is observed upon one-electron oxidation to [Ru^IIIOH₂]³⁺. Above pH = 2, the corresponding potentials between Ru^IV/Ru^III and Ru^III/Ru^II are observed to change by 59 mV per pH unit, indicative of a one-proton one-electron process. Based on thermochemical values furnished by Meyer, Mayer estimated that the bond strengths for the O-H bonds in 3 and 2 are approximately 82 and 85 kcal mol⁻¹ respectively [29,52-53]. Accordingly, concerted PCET between 1 and 3 to form two equivalents of 2 has been documented [54]. Comproportionation of these species is demonstrated to be first order in both 1 and 3, and the associated barriers associated with initial proton or electron transfer are demonstrated to be too high to correspond to the experimentally measured activation barrier, consistent with a concerted process. In addition, the redox step is demonstrated to have a solvent KIE of 16.1, a clear indicator that O-H bond cleavage of water is involved in the rate-determining step. While also documented to participate in stoichiometric oxygen-atom transfer to triphenyl phosphine [55] and dimethyl sulfide [56], 1 and 2 have been demonstrated to oxidize hydroquinone through both concerted and stepwise PCET mechanisms depending on the nature of the aqueous environment [39]. Evidence for proton movement concomitant to the redox step is supported by H₂O/D₂O KIEs for these reactions, which are 28.7 and 9.3 for abstraction by 1 and 2 respectively, with the difference in magnitude attributed to differences in both the hybridization of oxygen and the hydrogen bond distances [5]. These complexes may also cleave the O-H bonds of hydrogen peroxide by PCET [57-58] (reclassified from HAT [5]) with similarly large solvent KIEs. In one example, in which aniline is proposed to be oxidized to phenyl nitrene or its associated nitrenium ion, complex 1 is demonstrated to accept one proton and two electrons in a single elementary step [59]. Under the disclosed conditions this intermediate is captured either by water to form the corresponding hydroxylamine or by another equivalent of aniline to form the corresponding hydrazine, both of which undergo further (non-PCET) oxidations. Evidence for nitrene (or nitrenium) involvement is provided by a significant ArNH₂/ArND₂ KIE of 15.5 for aniline and 10.2 for p-toluidine, no direct oxo transfer of the metal oxo as determined by ¹⁸O isotopic labeling, sensitivity of the product distribution between hydroxylamine and hydrazine products (but not the rate law) on the concentration of water, initial formation of 3 rather than 2 in these oxidations, and a negative correlation on the rate of aniline oxidation against the Hammett parameter σ⁺.

Figure 6.

Ruthenium species reported by Meyer [51]

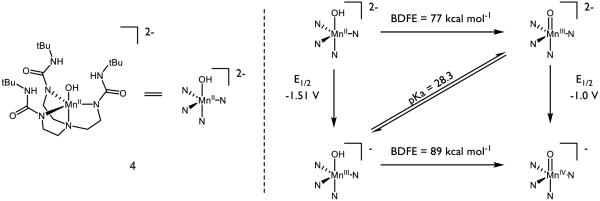
Manganese-oxo complexes have also been designed for PCET and HAT reactions, and have been studied extensively in the context of the special role of manganese oxo clusters in the oxygen evolving complex of photosystem II [60-63]. Borovik has disclosed a compound with the backbone structure 4, which features an unusual non-bridging terminal hydroxo ligand, and has measured its pK_a and redox properties (Figure 7) [64-66]. In a preliminary study of 4 and its isomers, the Mn^IV oxo was observed to abstract the hydrogen atom from TEMPO-H, cyclohexadiene, dihydroanthracene, 1,2-diphenyl hydrazine, and 2,4,6-tri-tert-butyl phenol. However, the oxo was incapable of abstracting a hydrogen atom from triphenylmethane, diphenyl methane, ethyl benzene, or 2,3-dimethyl-2-butene. Further study indicated the BDFE to be 89 kcal mol⁻¹ [67], which is in agreement to the O-H BDFE of non-heme manganese terminal oxo complex prepared by Stack [68-69]. The bond strength in the Mn^IV oxo form is driven by the high basicity of the oxygen, which is akin to that of methoxide (methanol pK_a ~ 29.0 in DMSO [70]). Investigation of C-H abstraction from dihydroanthracene (DHA) using the Mn^III and Mn^IV oxo forms of the complex revealed two competing mechanisms based on the oxidation state of the metal [67]. Citing a large entropic barrier (ΔS^‡ = −49 kcal mol⁻¹) and a primary KIE of 6.8, the Mn^IV oxo is suspected to abstract the C-H bond by a PCET event. Initial proton or electron transfer is indicated to be highly unfavorable. On the other hand, the Mn^III oxo boasts a much smaller entropic barrier (ΔS^‡ = −15 kcal mol⁻¹) and primary KIE (2.6). The cited pK_a of 28 matches well with that of DHA (30 in DMSO [71]), suggesting a stepwise PT-ET mechanism for HAT. Together, these divergent mechanisms demonstrate the sensitivity of PCET on the thermodynamics of the oxo species in question. Recent work by Borovik on analogous complexes has demonstrated that oxidation of the [Mn^III hydroxo]⁻ species to the neutral Mn^IV hydroxo further increases the BDFE to 95 kcal mol⁻¹ [72]. In the presence of an external reductant such as diphenyl hydrazine or hydrazine, Borovik has reported the catalytic reduction of oxygen to water using a slightly modified version of 4 [73]. Study of 4 highlights key thermodynamic contributors to overall bond strength and the sensitivity of the mechanism of net HAT on such parameters and is exemplary of metal oxos of this class.

Figure 7.

Borovik’s Manganese Complexes for HAT Reactions. All potentials are measured in DMSO and referenced to the Fc/Fc⁺ couple [64-66]

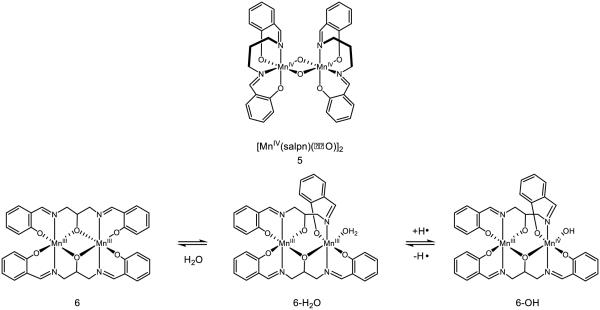
Binuclear manganese complexes featuring bridging oxo ligands are also capable of engaging in PCET/HAT reactivity (Figure 8). Complex 5 has been extensively studied by Pecoraro, who has reported a pK_a of 13.4 (MeCN), the protonated redox potential of 0.42 V v. NHE, and a BDFE of 77 kcal mol⁻¹ for the D(O-H) bond of the corresponding hydroxo-bridged species [74-75]. PCET in this case is accompanied by conversion of one bridging oxo to a hydroxo and reduction of one of the Mn centers to Mn^III. The value provided is consistent with the observation that 2,4,6-tri-tert-butyl phenol (OH BDFE = 82 kcal mol⁻¹) undergoes PCET with this complex, but not phenol (O-H BDFE = 88 kcal mol⁻¹). The pK_a of the oxo bridges in 5 are sensitive to the oxidation state of the manganese sites and have been predicted to drop approximately 10.5 pK_a units upon oxidation of a Mn center [76]. When a modified salpn ligand, which creates a bridging oxo species by virtue of a tethered alkoxide, is used to form binuclear manganese complex 6, the molecule is known to reversibly bind water and engage in HAT reactivity [77]. The strength of the O-H bond in 6-H₂O is measured to be 85 kcal mol⁻¹; upon initial oxidation (0.54 V in 16 M H₂O/MeCN vs. NHE), the bond strength is increased to 89 kcal mol⁻¹. These bond strengths are noticeably stronger than those of bridging hydroxo ligands, demonstrating the sensitivity of the O-H bond strength on both the binding mode of water (i.e. bridging or terminal) as well as the ligand framework on the metal center.

Figure 8.

Complexes with bridging oxo ligands known to engage in HAT reactivity [74-75]

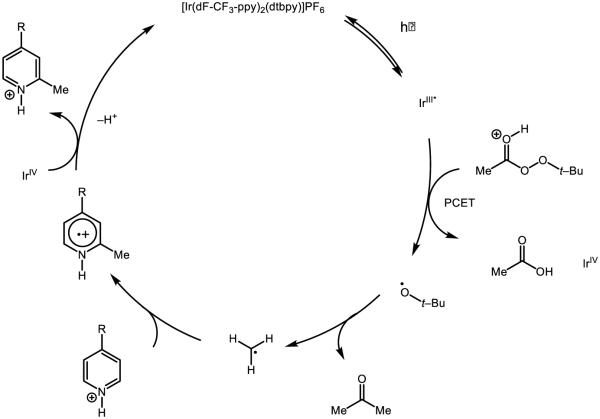
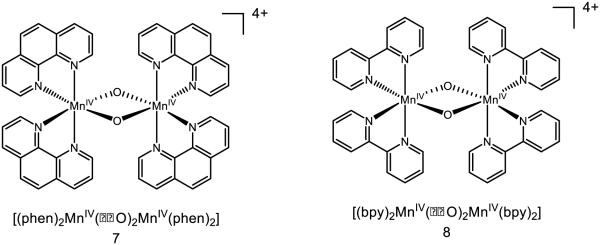
Mayer identified that species 7 was capable of oxidizing toluene by an initial hydride abstraction, with concomitant proton transfer to the oxo and two electron transfers to the manganese centers [78]. Based on the thermochemistry of interconversion between isomers, it is evident that 7 lacks the oxidizing power (0.95 V in MeCN v. Fc/Fc⁺) to oxidize toluene (2.08 V in MeCN v. Fc/Fc⁺) and initial electron transfer is too endergonic to proceed, eliminating mechanisms, which rely on an initial ET event. Upon two-electron reduction of 7 to the Mn^III dimer, the pK_a of the bridging oxo is ~15 in MeCN, which also suggests 7 is not nearly basic enough to deprotonate toluene. The authors observe that nitrotoluene is unreactive with 7 under their conditions and notice that diphenymethane reacts one-hundred times faster than toluene; taken together, they cite these data as strong evidence for a highly electron deficient transition state and accordingly argue against an initial HAT event. The measured hydride affinity of the complex is provided to be 122 kcal mol⁻¹ by the authors. The mechanism of activation by these complexes is highly substrate dependent and may proceed by initial HAT, electron transfer, or hydride transfer [79]. On the other hand, prior reduction of this species to the Mn^IV-Mn^III allows for HAT reactivity: (phen)₂Mn(μ-O)₂Mn(phen)₂]³⁺ may undergo two HAT events to form the bridged hydroxo species (phen)₂Mn(μ-OH)₂Mn(phen)₂]³⁺. Based on thermochemical data, addition of the first hydrogen atom to the bis-oxo species has an O-H BDFE of 79 kcal mol⁻¹, where addition of the second hydrogen atom to form the bis-hydroxo species has an O-H BDFE of 75 kcal mol⁻¹ [80]. While these complexes are thought to engage substrates such as dihydroanthracene by HAT, a Pourbaix diagram of the (bpy) variant 8 demonstrates a pH-dependent potential corresponding to a one-proton, one-electron transfer event [81]. Under the proper circumstances, it is possible 8 may be able to react by a PCET mechanism.

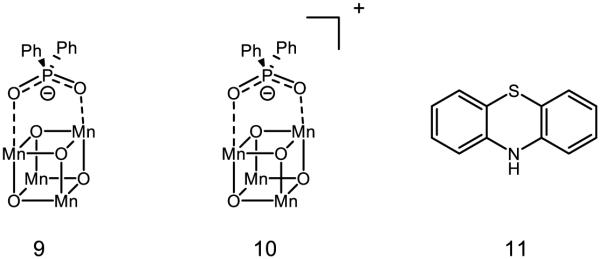
Moving to further-bridged species, Dismukes has reported the synthesis and kinetics of PCET for “cubane” type species 9 and 10 [82]. 9 is thought to feature two Mn^III and two Mn^IV sites, and 10 to have one Mn^III and three Mn^IV sites. Movement between these oxidation states comes with reactive consequence: 9 is thought to undergo PCET with pzH 11 to form the pz radical, where 10 is observed to undergo hydride transfer with 11 (net one proton two electron PCET) to form the pz cation [83]. The original assessment of the hydroxo species was based on the capacity for 9 to engage para-cyanophenol in PCET, giving a lower limit of the O-H BDFE as ~94 kcal mol⁻¹; inclusion of the potential necessary to move from 9 to 10 furnishes an approximate hydride affinity of ~127 kcal mol⁻¹ [84]. Important to note is that 9 does not engage the anion pz⁻ in redox activity, strongly implying that electron transfer between these complexes must be accompanied by proton transfer. In addition, the pKa of protonated 9 (pK_a < 3) is not basic enough to deprotonate pzH (pK_a = 22) [85]. The bond strength of 9 is among the strongest reported for a bridging oxo species.

Iron-oxo species are also documented to undergo HAT and PCET reactions (Figure 11). In particular, complex 12, reported by Que, Nam, and Münck in 2004, has garnered a great deal of attention for its reactivity, as it is capable of abstracting the C-H bond from cyclohexane (BDE = 99 kcal mol⁻¹) at room temperature [86]. While no mechanism is posed in the initial disclosure, the authors note a large KIE for abstraction from ethyl benzene (k_H/k_D = 30) at ambient temperature that parallels those observed for other systems known to engage in hydrogen atom abstraction [87-88]. Moreover, a correlation between the hydrocarbon BDE and the rate of the reaction strongly indicates an initial C-H abstraction event [89-90]. Fukuzumi and Nam further studied this complex for its capacity to undergo both HAT as well as acid-assisted PCET [91]. The rate constant for oxidation of hexamethylbenzene was found to be three orders of magnitude higher in the presence of HClO₄ (57 M⁻¹ s⁻¹) than without (5.1 × 10⁻² M⁻¹ s⁻¹); the authors posit a change in mechanism from HAT to a stepwise PCET event in which the protonated iron-oxo first oxidizes hexamethylbenzene followed by deprotonation. Protonation of the oxo is found to shift the potential of 12 by 0.92 V [92]. Complex 13, prepared from a two-electron oxidation of the Fe(III) analogue and reported in 2009 by Que and Münck, has also demonstrated a remarkable affinity for hydrogen atoms [93]. The first oxidation potential of this complex is provided as 1.50 V v. Fc/Fc⁺ in MeCN and is thereby strongly oxidizing. In comparison to 12, which has a potential of 0.9 v. Fc/Fc⁺ in MeCN [94], 13 abstracts the hydrogen atom from cyclohexane 10²-10³ times more rapidly.

Figure 11.

Various Non-Heme Iron Oxo Complexes for C-H Abstraction

The authors noticed no C-H/C-D isotope effect for the reaction of 13 with methanol and tert-butanol, but saw a KIE (k_H/k_D = 1.4) for the O-H/O-D bond, suggesting that the stronger O-H bond is activated preferentially over the weaker C-H bonds. In addition, the authors observed the formation of both acetone and 2-methylpropene upon the oxidation of tert-butanol. Upon comparison of rate constants (which have been normalized to account for the amount of hydrogens available for abstraction), tert-butanol reacts 50 times faster than cyclohexane. The authors propose a proton-coupled electron transfer event is responsible for the observed selectivity; this complex represents a rare case in which O-H bonds may be homolyzed preferentially to C-H bonds. In further study, 13 was shown to oxidize water to the hydroxyl radical by PCET [95]. Under pseudo-first-order conditions, conversion of 13 to its one-electron reduced state was found to have a second-order dependence on the concentration of water, in stark contrast to the first-order dependence observed for aliphatic hydrocarbons and alcohols. Based on the thermoneutral oxidation of water (2.13 V v. NHE in MeCN under neutral conditions [96]) by 13 (2.14 V v. NHE in MeCN under neutral conditions) and the rate dependence, the authors propose a proton-coupled electron transfer event in which water serves as a base. While the mechanism for O-H bond cleavage of alcohols and water is not well understood in these instances, the capacity to cleave a stronger O-H bond in the presence of much weaker C-H bonds is a tremendous advance in metal-oxo chemistry and represents an exciting avenue for chemoselective substrate activation.

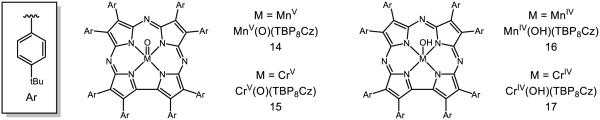
Heme mimics have also been a fruitful area of research for metal-oxo reactivity (Figure 13). Goldberg has reported the synthesis of metal complexes featuring the corrolazine framework, which serves as a porphyrin-like donor ligand for the study of high valent transition metals [97-98]. The manganese (14) and chromium (15) variants of these complexes can be synthesized and even isolated by benchtop chromatography [99]. Based on the capacity of 14 to abstract the oxygen-bound H atom from 2,4,6-tri-tert-butyl phenol but not the methyl-bound H atom from hexamethylbenzene, the Mn^IVO-H bond in 16 is estimated to be between 80 and 83 kcal mol⁻¹; likewise, the capacity of 15 to abstract from TEMPO-H but not from xanthene places the O-H bond in 17 between 67 and 73 kcal mol⁻¹. In the presence of dimethyl ferrocene (E_1/2 = −0.24 V v. Fc/Fc⁺ in MeCN) and acetic acid (pK_a = 23.5 in MeCN), which together have an effective BDFE of 82 (cf. Figure 3, [29]), 14 may be converted to 16 in a multisite PCET process. In the absence of either reductant or acid, no 16 is observed, demonstrating the necessity of both components to forge the O-H bond and the accuracy of the bracketed BDFE. The pK_a of 16 is estimated to be approximately 22, which is thought to contribute most of the energy to the effective O-H BDFE of 16 given the low potential of the Mn^IV/Mn^V couple (−0.05 V v. SCE) [100-101]. Moreover, the basicity of 14 is largely credited for the discrepancy between the O-H bond strengths of 16 and 17 given the small difference in M^V/M^IV potential of Mn and Cr (ΔE = −100 mV, where chromium features a more positive potential; ca. 2.3 kcal mol⁻¹ difference).

Figure 13.

Porphyrinoids 14 and 15 and their reduced counterparts 16 and 17 [97-98]

The HAT and PCET capabilities of 14 have been extensively studied. Work by Fukuzumi and Goldberg has demonstrated that 14 will engage acridinium species in hydride transfer and two-electron reduction by ferrocene derivatives in the presence of proton donors [102]. The strength of the added proton donor correlated to the rate of reduction, suggesting a proton-coupled mechanism for the formal reduction of 14. Hydride transfer is not thought to be concerted, instead proceeding first by an initial PCET event to transfer an H-atom followed by electron transfer. The addition of anionic ligands to bind the unoccupied axial site of 14 was found to have a profound impact on the rate of HAT [103]. Compared to the rate of HAT from 9,10-dihydroanthracene to 14 in the absence of external anion donors, addition of F⁻ and CN⁻ were found to increase the reaction rate by factors of 2,100 and 16,000 respectively. DFT calculations of the bond strengths of these complexes suggest that the basicity of the oxo species is principally responsible for the large increase in the O-H BDFE. In the presence of light, oxygen, and acid, hexamethylbenzene may be oxidized to the corresponding alcohol (18 turnovers) and aldehyde (9 turnovers) respectively, demonstrating the potential for catalytic HAT using these scaffolds [104].

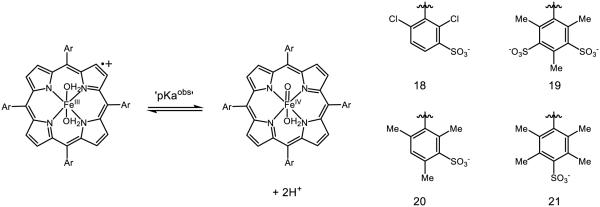
Non-heme porphyrin complexes such as 18 – 21 have also been synthesized by Groves (Figure 14) [105]. Unique about these systems is the existence of a proton-coupled hydrogen atom transfer equilibrium, which may be thought of as a formal two-proton, one-electron transfer step. Because HAT in this instance is proton-coupled, the authors define a metric for the bond dissociation energy, D(OH₂) which accounts for both hydrogen-atom abstraction as well as protonation of the oxo-species that can be described using the following, modified Bordwell equation [106]:

$$D\left(O{H}_2\right)=23.06E_{por}^{\prime }+1.37\left[2\left(p{K_A}^{obs}\right)\right]-1.37\text{pH}+57$$

Figure 14.

Iron-porphyrin complexes synthesized by Groves. [105]

For 19, the pK_a ^obs is found to be 5.5, and the potential E’ = 1.06 v. NHE, furnishing a final D(OH₂) of 90-93 kcal mol⁻¹. When HAT is not coupled with proton transfer, the conventional O-H BDFE is calculated to be 87 kcal mol⁻¹ using the canonical Bordwell equation; this species accordingly has a pK_a ~ 7. Where prior examples cite the basicity of the oxo as a direct contributor to the O-H BDFE, complexes 18-21 present a unique situation in which a second, concomitant protonation increases the driving force for hydrogen atom abstraction from a given substrate. Accordingly, C-H abstraction from xanthene demonstrates KIEs not only for the C-H/D bonds in xanthene (k_H/D = 1.80), but also for the solvent D₂O/H₂O (k_H/D = 2.2), demonstrating the reliance on HAT and proton-transfer in the rate-determining step. While unconventional (or underappreciated) for metal-oxo species, two-proton one-electron transfer events have been previously documented in optical excitation of hydrogen bonded dyes by Meyer [107] and is predicted to play a role in proton transport by Chen and Liu [108]. In addition, many analogous manganese oxo porphyrins have recently been documented by Groves to catalyze aliphatic C-H fluorination [109], azidation [110], and chlorination [111], as well as pH-dependent conversion of chlorite to chlorine dioxide [112-113].

Metal oxos are among the most dynamic, well-studied examples of PCET and continue to attract the attention of the community at large. The oxo basicity and oxidative power of the metal contribute significantly to the BDFEs involved in PCET processes, which is further influenced by the coordination geometry of the oxo as well as the ancillary ligation on the metal center. The development of catalytic protocols utilizing such species bears much promise for synthetic chemists for mild substrate modification.

Phenols

Phenols are perhaps the organic functional group whose PCET reactivity has been explored most extensively. The redox activity of the phenolic amino acid tyrosine is known to play an important role in many biological redox processes. As noted by Svistunenko [114], some of the earliest examples of tyrosyl radicals documented in proteins include the bacteriophage T4-induced ribonucleotide reductase by Sjöberg in 1982 [115], Photosystem II by Babcock and Barry in 1988 [116], and prostaglandin endoperoxide synthase-2 by Hoganson and Babcock in 1994 [117]. Since these seminal discoveries, the role of tyrosyl radicals in proteins has been subject to intense study, both in califying their role in catalysis as well as documenting further examples.

The first evidence for concerted PCET activation of phenols in non-enzymtic systems was provided by Linschitz, studying the quenching kinetics of C₆₀ and tetracene fluorescence by hydroquinone in the presence of variously substituted pyridines [118]. The authors identified strong correlations between the rate of quenching and the pK_a of the corresponding pyridinium species, with higher pK_a’s trending with an increased rate of reaction. In addition, voltammetric studies of solutions containing both phenol and pyridine exhibited a new and irreversible anodic wave occurring at more positive potentials than for the phenol alone, consistent with a PCET process. In further studies, the relevant intermediates (i.e., the C₆₀ radical anion, the phenoxyl radical, and the pyridinium salt) of the PCET step in benzonitrile (PhCN) were observed by flash photolysis with 4-hydroxyanisole in the presence of 7,8-benzoquinoline [119] and 1-naphthol in the presence of collidine [120].

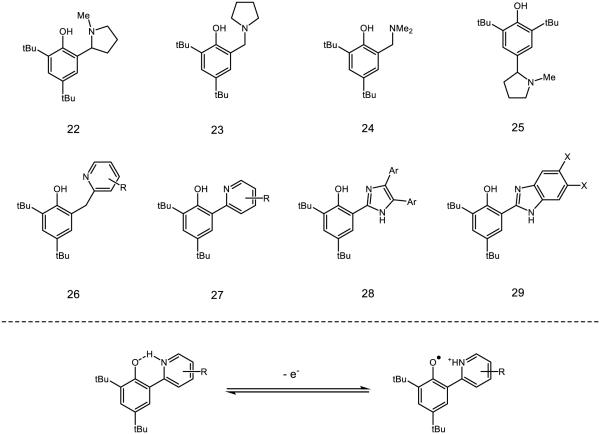
These observations have sparked significant mechanistic interest in the underpinnings of PCET in phenol O-H homolysis, with particular emphasis placed on the role of hydrogen-bonding. Several model systems containing intramolecular hydrogen bonds have been developed (Figure 15). Matsumura and colleagues synthesized compounds 22-25, of which 22 demonstrates a reversible oxidation potential (E_1/2 = 757 mV v. Ag/AgCl reference) and a UV-Vis spectra characteristic of phenoxyl radicals [121]. Compounds 23 and 24 show partially reversible CV traces and have similar potentials, whereas 25 demonstrates an irreversible redox couple. The persistence of the phenoxyl derived from 22 is attributed to stabilization of the radical by an intramolecular hydrogen bond. Savéant has attributed partial reversibility of the CV traces of closely related compounds to instability at low scan rates, as the current response for voltammograms with scan rates of 5 V/s were found to be completely reversible [122]. In certain circumstances, phenoxyl radicals are preferentially stabilized by hydrogen bonding relative to the parent phenol, resulting in decreased O-H BDFEs and longer radical lifetimes [123]. In these instances, the phenoxyl radical may serve to increase the acidity of additional O-H or N-H bonds present in the molecule or serve as direct hydrogen-bond acceptors.

Figure 15.

Phenol model systems capable of intramolecular hydrogen boding synthesized by Matsumura (22-25) and Mayer (26-29) as model systems for the study of PCET in biological contexts. Variation of the amine donor allows for deep interrogation of hydrogen bonding on PCET processes.

Along with measures of stability, Mayer has examined correlations between the rates of phenol PCET and various intramolecular hydrogen bonding parameters with pyridyl and imidazoyl bases of type 26-29 [124-125]. In pyridyl-substituted compounds such as 26 and 27, the rate constant for PCET is found to vary linearly with the thermodynamic driving force (ΔG_PCET). Important to note, however, is that the rate of oxidation of various analogues of 26 can be impacted by changing the driving force as a function of pyridyl substitution or the identity of the oxidant, which implies a constant intrinsic reaction barrier λ. In addition, variation of the pyridyl substitution has a minimal impact on the rate of PCET. However, when the pyridine base is conjugated with the phenol (as in 27) both ΔG_PCET and λ vary as a function of pyridyl substitution, with electron-withdrawing R-groups demonstrating slower rates relative to electron-donating groups. It is worth noting the pK_a’s of the corresponding pyridinums associated with scaffolds 26 and 27 show a positive correlation with the –OH ¹H NMR resonance and a negative correlation with the both the O-N bond distance and the potential of the substrate. For the oxidations of imidazole-type systems 28 and 29, a similar rate dependence on ΔG_PCET was also observed. Moving from electron-rich to electron-poor substituents on the aryl or −X groups was found to have a monotonic effect on the driving force and consequentially little impact on the overall rate of PCET. As the identity of the base is changed – from imidazoles, pyridines, aliphatic amine bases, or other motifs – the rate of PCET is dependent on not only the driving force, but also λ as well as the associated probabilities for tunneling. [126-127].

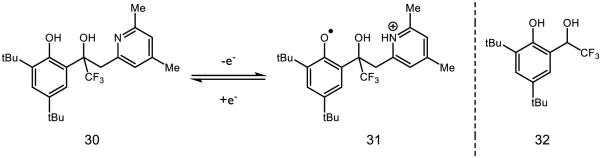
Hydrogen bonding to phenols may also serve as template for long-range proton transfer (Figure 16), providing a mechanism for proton transport across relatively large distances. Savéant has prepared polyol 30, which upon electrochemical oxidation converts to 31 in a single elementary step with a reversible potential [128]. The stability of 31 is such, in fact, that upon bulk electrolysis the authors can observe it by UV-Vis spectroscopy and cite a change in the pyridine bands of the IR spectra of 30 as evidence for proton transfer from the phenol to the pyridyl species. Alternatively, for the substrate lacking the pyridine terminus (32) voltammetric experiments demonstrated that the oxidation is irreversible. These experiments elucidate not only the role for hydrogen bonding in proton transfer, but also corroborate work by Thomas demonstrating increased stability of hydrogen-bound phenoxyl radicals [129]. Proton movement in PCET processes is limited to short (i.e., hydrogen-bonding contact) distances [130]; however, hydrogen-bonding networks are frequently used as “proton wires” [131] to accomplish long-range proton transfer and are well documented in GFP [132], ferredoxin I of Azotobacter vinelandii [133], cytochrome c oxidase [134], and numerous other proteins [135]. In a notable example, a hydrogen-bonding network between Tyr122 and Cys439 in ribonucleotide reductase (RNR) allows for a net proton transfer over > 30 Å [136]. Over longer distances this process may be stepwise, but in carbonic anhydrase PT is calculated to be concerted over a distance as long as 8 Å [137]. Hammarström demonstrated that the presence of an internal hydrogen accelerates concerted PCET relative to reactions with the same driving force without an internal hydrogen bond [138]; it has also been suggested that hydrogen bonding intrinsically lowers the reorganization energy by virtue of weakening the O-H force constant [139-140].

Figure 16.

A mechanistic example of a hydrogen-bond relay, capable of transferring a proton to the pyridyl nitrogen while simultaneously removing a proton from the phenoxyl oxygen.

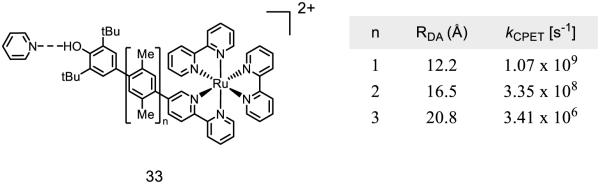
Along with the distances associated with proton transfer, the distance-dependence of electron transfer on PCET reactions of phenols has also been of considerable interest. To study the effect of distance on the rates of phenol oxidation, Wenger and coworkers synthesized a series of heteroleptic ruthenium polypyridine complexes where the distance from the metal to the distal phenol was varied as a function of the the number of xylene spacers incorporated into the bpy ligand (Figure 17) [141]. While the electron transfer rates decrease with increasing distance, long range electron transfer with an exogenous pyridine base still proceeds with rate constants greater than 10⁶ s⁻¹ when the donor-acceptor difference is ~20 Å. Long-range electron transfers from phenols involved in enzymatic PCET processes have been documented for photosystem II (ca. ~10 Å) [10], the R1 subunit of RNR (~7 Å) [11], and prostaglandin-H synthase-2 (~ 7 Å) [142] among others [143].

Figure 17.

Wenger’s model polypyridyl system with spacers, Ru-O distances, and corresponding rates of concerted PCET [141].

In biological settings, spatial separation between redox-active sites may be a consequence of mitigating back electron transfer when excited states are involved. In a particularly dramatic example from Photosystem II, electron transfer between a Tyr_Z/His190 pair (Y_z) and P680⁺ proceeds with a forward rate constant ~ 10⁷ s⁻¹, with back-electron transfer between P680⁺ and Q_A^•− proceeding at ~10³ s⁻¹ [144]. In the forward reaction, Meyer has noted that the necessity of His190 in water oxidation [145-147] provides strong evidence for the necessity of proton movement in oxidation of Yz [144]. Sluggish back electron transfer can be attributed to the both long distance involved (17-18 Å) as well as the high driving force (−1.4 eV); the thermodynamic favorability causes back electron transfer to occur in the Marcus-inverted region and the distance of electron transfer further slows this charge recombination process.

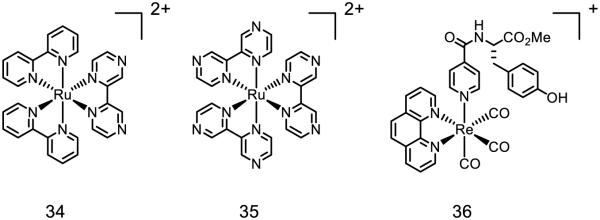
Similar ruthenium complexes have also been modified in numerous ways to study phenol oxidation via PCET with respect to factors other than distance (Figure 18) [148]. Upon irradiation with visible light, these complexes become stronger oxidants and reductants, concomitant with a MLCT event, wherein a metal-centered electron is transferred into a ligand-based anti bonding orbital [149], further increasing the driving force (and thereby the rate) of PCET. Reductive quenching of the excited states of [Ru(bpy)₂(bpz)]²⁺ 34 [150] and [Ru(bpz)₃]²⁺ 35 [151] by phenols has been identified by Meyer and Wenger, with the unbound nitrogen on the bpz ligand serving as the basic site for the reaction. Using 35 as the oxidant, the effect of electron rich and electron poor substituents on the phenol component was thoroughly examined: Wenger calculated the ligand-phenol association constant (K_A) for a number of para-substituted phenols ranging from 1478 M⁻¹ (R = OMe) to 5 M⁻¹ (R = CN). While the rate constants for PCET of the protiated phenols do not appreciably differ (R = OMe 1.87 × 10⁶ s⁻¹ and R = CN 1.73 * 10⁶ s⁻¹) as a function of substituent, virtually no KIE was observed for R = OMe (k_H/k_D = 1.03) while a significant KIE was observed for R = CN (k_H/k_D = 10.18). In addition, the driving force of each PCET event differs by merely 0.07 eV. On the basis of KIEs the authors suggest an ET-PT event for R = OMe and a concerted PCET event for R = CN, demonstrating how subtle differences in substrate-complex association may have a dramatic effect on the mechanism of charge transfer. In another related example, the rhenium-complex 36 synthesized by Nocera, featuring a tyrosine-like ligand directly appended to the metal center, is documented to form the phenoxyl radical in the presence of exogenous pyridine or imidazole with rate constants of 4.1 × 10⁵ s⁻¹ and 4.8 × 10⁶ s⁻¹ for pyridine and imidazole respectively [152]. The equilibrium constant for hydrogen bonding was measured as 16 M⁻¹ and 157 M⁻¹ for pyridine and imidazole respectively, suggesting that hydrogen bonding is still crucial for the proton-transfer event in these systems. The role of hydrogen bonding on the rate of PCET, as exemplified by these two case studies, is complicated and highly variable pending choice of hydrogen bond partner.

Figure 18.

Various Ruthenium complexes used to induce oxidative PCET, as well as a Rhenium complex featuring an unconjugated phenol ligand which readily forms the phenoxyl in the presence of base [148]

In addition to kinetic and spectroscopic methods, electrochemical methods have also proven useful in examination of phenol PCET given the precise control over pH and applied potential. Such techniques can provide not only kinetic data, but also useful thermodynamic data as demonstrated by the Pourbaix diagram for phenol generated by Savéant (Figure 19) [153]. The slope of the Pourbaix diagram demonstrates the PCET event to form the phenoxyl radical in the concerted PCET regime is a one-proton one-electron event; where Pourbaix diagrams alone do not shed light on the concerted nature of the oxidation process, the authors were able to fit the experimental data to detailed kinetic models and demonstrate the concerted PCET is the most rapid and thereby predominant mechanism of phenol oxidation. The authors also needed to employ low concentrations of phenols and high scan rates to mitigate deleterious phenoxyl dimerization. Unbuffered water proved necessary to observe dominant concerted PCET: in the presence of phosphate buffer, i.e. HPO₄²⁻, the reaction is driven to a predominant stepwise, proton-first PCET event. Otherwise, water serves as a proton acceptor in a concerted PCET process. Direct rate constants (uncorrected from double layer effects) for concerted PCET were derived as 25 ± 5 and 10 ± 2 cm s⁻¹ for protiated and deuterated phenol respectively, demonstrating a significant KIE of ~2.5.

Figure 19.

A Pourbaix diagram for phenol oxidation in water with concentration regimes for favored concerted proton coupled electron transfer (CPET), proton-first stepwise PCET (PET), or electron-first stepwise PCET (EPT). Figure reprinted with permission from Proc. Nat. Acad. Sci. [153].

Electrochemical techniques can provide exquisite information with relatively simple experiments, even for more complex systems. A recent report by Tommos has demonstrated the applicability of such electrochemical analyses to assess the role of PCET (concerted or otherwise) in the model protein α₃Y using a Pourbaix diagram (Figure 20) [154-155]. In this system, the tyrosine residue is positioned inside a protein matrix in a desolvated and well-structured environment. Voltammetric study of its oxidation displays a reversible square-wave and differential pulse voltammogram under basic conditions. The tyrosine residue in question exhibits a potential of 0.910 and 1.070 against NHE at pH 8.5 and 5.5 respectively [156]. Based on expected rate constants for side reactions associated with square-wave voltammetry [157-158], the authors initially suspected the radical species in question must have a lifetime of at least 30 ms: in collaboration with Hammarström, transient absorption spectroscopy has placed the half-life somewhere between 2 and 10 seconds [159]. Decay of this signal was observed to follow second-order kinetics by intramolecular coupling, suggesting dimerization of the protein. Observation of an emission spectrum consistent with dityrosine and the long lifetime are cited as further evidence of this process. Such a model system provides a thermochemical estimate for the properties of tyrosine residues otherwise buried in hydrophobic pockets, with a model system that allows for excellent characterization of this species.

Figure 20.

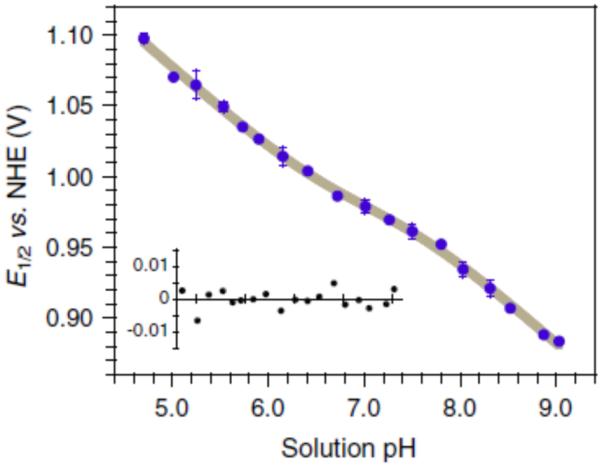
A Pourbaix diagram for reversible oxidation of a tyrosine residue in the α₃Y protein; the gray line is a non-linear regression featuring a slope of 59 ± 5 mV. Reprinted with permission from Figure reprinted with permission from Proc. Nat. Acad. Sci. [154].

Phenol PCET, more than any other substrate class for these reactions, provides insight into the role of hydrogen bonding. The judicious design of model systems affords examination of thermodynamic, kinetics, and exploration of Marcus-related reorganization energies. The lessons learned from studies of phenols serve an excellent primer on important design motifs for the future design of PCET reactions; in addition, the work provided has provided some evidence to the machinery of life required during enzymatic redox catalysis.

Indoles

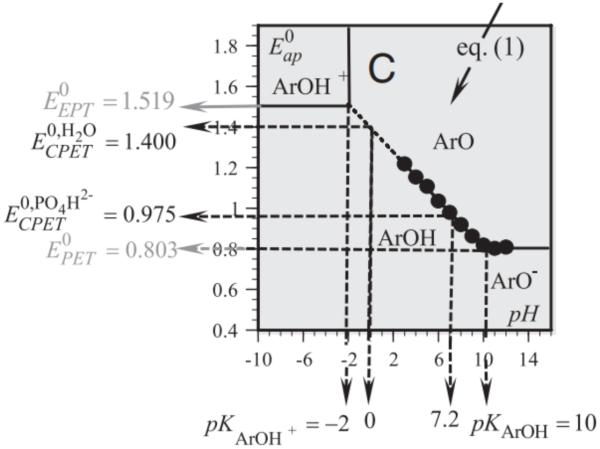
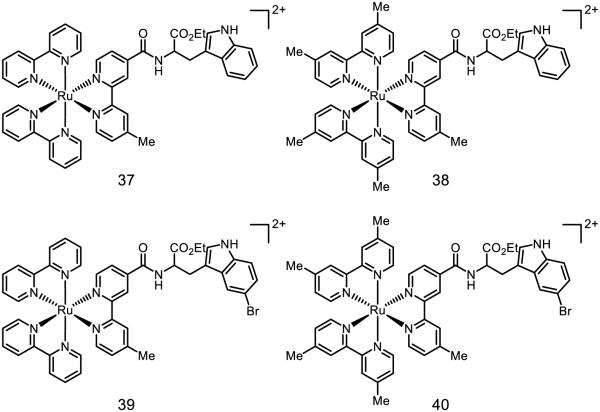
Indoles, ubiquitous in redox-active proteins, also serve as important biological charge carriers. In many instances, PCET is necessary to facilitate otherwise endergonic ET steps for charge transfer in biological contexts. Of note, however, are the thermodynamics of such processes: indole is 0.25 V easier to oxidize than phenol and features an N-H bond that is ~3 kcal mol⁻¹ stronger than the phenol O-H bond. Accordingly, Mayer has noted that phenols are far more likely to undergo concerted PCET, whereas indole activation typically proceeds through the radical cation in a stepwise fashion [29]. Documented evidence of concerted PCET activations of the indole N-H bond is relatively scarce. In 2011, Hammarström studied the viability PCET of tryptophan with water as a proton acceptor, tethered to a ruthenium photocatalyst (Figure 21) [160]. Both 37 and 39 undergo stepwise ETPT below pH = 10; only above pH = 10 do these reactions occur by concerted PCET. Compounds 38 and 40, however, show a constant pH dependence. These studies have been repeated in bimolecular fashion with free indole and an unbound Ru(bpy)₃²⁺ or Ru(dmb)₃²⁺ oxidant [161]. Even without a molecular tether, which causes the oxidant and indole to travel as a single molecular entity, these reactions are kinetically competent to engage in concerted PCET as well as ET/PT mechanisms. With the weaker oxidant Ru(dmb)₃²⁺, the ethyl ester of tryptophan is demonstrated to undergo concerted PCET regardless of pH: use of the stronger oxidant Ru(bpy)₃²⁺ only results in concerted PCET at pH values greater than 6. Concurrently, Meyer reported that N-acetyl-tryptophan could undergo concerted PCET with hydroxide as a base with Os(bpy)₃³⁺ as the oxidant in water [162]. Hydroxide is uniquely effective in this respect, as the use of other bases (2-amino-2-(hydroxymethyl)propane-1,3-diol, monobasic phosphate, or dibasic phosphate) did not result in concerted PCET. The sensitivity of concerted PCET and ET/PT mechanisms in aqueous conditions – to the oxidant employed, the role of hydroxide, and other contributors – demonstrates the subtle interplay between facile oxidation of the indole moiety and the importance of N-H activation by proton acceptors.

Figure 21.

Ruthenium complexes synthesized by Hammarström for studies of indole PCET [160]

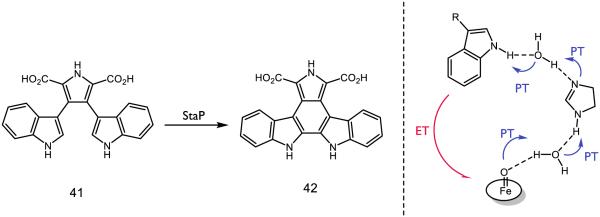
One recently proposed example of concerted PCET in a biological context is the unusual intramolecular aryl-aryl coupling of chromopyrrolic acid 41 (CPA) in route to staurosporine catalyzed by cytochrome P450 StaP (Figure 22). In an extensive computational study, Shaik and colleagues predicted that an initial PCET event through a hydrogen-bonding triad involving two water molecules and a histidine residue could serve as a proton shuttle from the substrate to the iron-oxo moiety [16]. The necessity of the water-histidine-water triad was analyzed using two changes: using a modified version of 41 where the hydrogen at the 7-position is chlorinated as well as modifying the protein such that the His₂₅₀ residue was mutated into phenylalanine or alanine. In the prior case, substitution of chlorine was found to expel water from the active site for steric considerations and resulted in significantly decreased activity for the aryl-aryl coupling. In the absence of histidine, enzyme function decreases to 25% for alanine and 72% for phenylalanine. A computational analysis attributed this reactivity to a water diad serving as a hydrogen-bonding chain from the indole to the iron-oxo. The substrate is thought to react as the dianion, which is anchored into the active site by a number of short hydrogen bonds to the carboxylate moieties [163]. His250 is conserved across P450 StaP as well as relatives RebP and AtmP, suggesting the importance of PCET in the construction of indolocarbazole cores by these enzymes [164-165].

Figure 22.

Oxidation of CPA (41) by StaP P450 Cpd1 into a precursor (42) to staurosporine with a schematic for the PCET activation step proposed by Shaik [16].

The majority of PCET reactions to indoles in biology proceed in a stepwise fashion through the indole radical cation. However, even if a proton cannot transfer (i.e., move from one atom to another) in the same step, movement in the relative position of a proton within a hydrogen-bonding interface is documented to influence the rate of electron transfer in PCET [167-171]. Provided an appropriate hydrogen-bond acceptor is present, the potentials of indoles can be attenuated. Nordlund and Eklund have identified a triad of residues in ribonucleotide reductase (RNR), Trp48, Asp237, and His118 which are highly conserved across various species (Figure 23) [143,172-173]. It is thought this network modulates the potential of the indole moiety, presumably by stabilizing the radical cation through hydrogen bonding [174]. Moreover, His118 in this triad is directly coordinated to the Fe1 center. When a water molecule binds to Fe1, it enables Tyr122 to engage in HAT and abstract a hydrogen atom from said water; Siegbahn has presented computational evidence that suggests this process proceeds in a single step to ultimately form the Trp48 radical cation [136,175]. The Trp48, Asp237, and His118 catalytic triad may also enable this reactivity. While Trp48 in this instance serves as a hydrogen-bond donor, study of tryptophan-centered radicals in RNR by EPR and ENDOR spectroscopies by Lendzian and Lassmann indicates two neutral tryptophan moieties, one of which (Trp111 [176]) is a hydrogen bond acceptor and posit hydrogen bond donation by nearby E204 [177]. Given the prominence of tryptophan residues thought to engage in electron transfer in RNR and the documentation of long-range PCET in these complexes [11], redox-modulation through the agency of hydrogen bonds provides a plausible mechanism for charge transfer.

Figure 23.

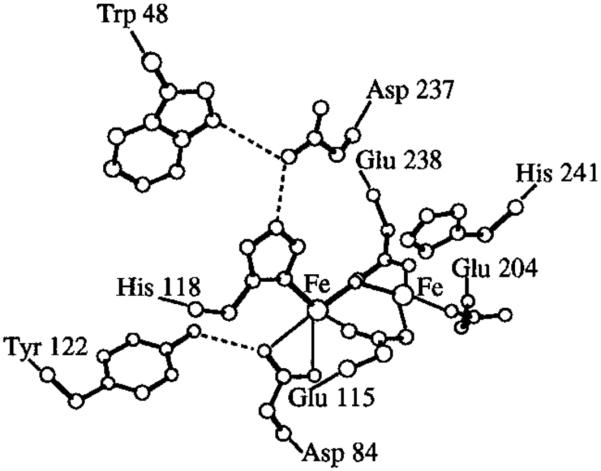
A highly conserved hydrogen bonding triad Trp48, Asp237, and His118 [166] in Ribonucleotide Reductase (RNR). Adapted with permission from [136]. Copyright 1998 American Chemical Society.

Further examples of tryptophan residues involved in charge transfer in proteins come from DNA photolyase and azurin (Figure 24). In the former, Brettel has demonstrated that FAD initiates oxidation of Trp382, which engages in a hole-hopping oxidation of Trp359 and finally Trp306, which deprotonates to yield the neutral tryptophan radical [1,178-179]. For the oxidation of the terminal Trp306 found in E. coli photolyase, Schelvis and coworkers have demonstrated the electron transfer proceeds by concerted PCET below pH = 6.5, but otherwise undergoes stepwise PCET via an initial electron transfer [180]. Moreover, charge recombination between FADH• and Trp306 is pH dependent, slowing down at increased pH [181-182], presumably in accord with this mechanistic switch. In azurin, tryptophan residues have been demonstrated by Gray and coworkers to greatly accelerate electron transfer by enabling electron “hopping” between amino acid residues [183]. Where tunneling over 19 Å is slow, tryptophan-mediated transfer is more rapid by approximately two orders of magnitude. In tyrosine-depleted mutants of azurin (AzC), two tryptophan-centered radicals have been observed by ultrahigh field EPR [184] attributed to neutral tryptophan radicals Trp108 and Trp48. Based on ²H ENDOR experiments, Stoll and Britt determine that Trp108 is hydrogen bound and Trp48 exists as an unbound radical species. Trp48 is nestled in a hydrophobic pocket of the protein and thought to be important in long-range charge transfer in azurin [185]. In further studies, Trp48 has proven necessary for redox activity in azurin mutants [186] and shows significant fluorescence quenching in the presence of copper [187], further demonstrating the profound effect of protonation state on tryptophan-mediated charge transfer. The properties of indoles and their capacity to engage in both concerted and stepwise PCET afford these species great flexibility as electron-shuttle residues in redox-active proteins; model systems allow for close examination of the subtleties pertinent to both concerted and stepwise PCET pathways and their consequences.

Figure 24.

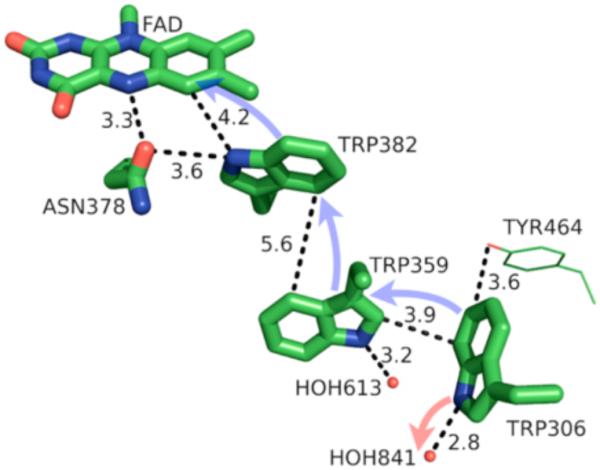
A model of the PCET pathway from DNA photolyase. Reproduced with permission from [1]. Copyright 2014 American Chemical Society. This article may be accessed online at the following URL: http://pubs.acs.org/doi/pdf/10.1021/cr4006654

Thiols

Thiols are classical HAT agents in free radical chemistry, and recently their ability to participate in multisite PCET chemistry has also been explored. Meyer has studied the potential for PCET to the cysteine (or N-acetyl cysteine) S-H bond using [Os(bpy)₃]³⁺ as a stoichiometric oxidant and various buffer conditions (Figure 25) [188]. Through kinetic modeling, the authors conclude that (along with other pathways) cysteine can be activated by multisite, concerted PCET in the presence of the appropriate buffers, which include AcO⁻ and H₂PO₄⁻. When tested with buffer conditions relevant to biological reactions, the authors conclude this pathway is likely dominant given the relative acidity of the S-H proton as well as the high concentration of buffer. The influence of buffer effects on the oxidation of glutathione by [IrCl₆]²⁻ had been previously documented by Alvarez, who found that the observed rate constant for oxidation trended with an increase in the pK_a of various buffers (including citrate and phosphate) when pH = pK_a [189]. Moreover, the rate of the reaction is also accelerated as a function of the concentration of phosphate buffer at constant pH’s of 5.0 or 7.0, suggesting some dependence on the buffer ion itself.

Figure 25.

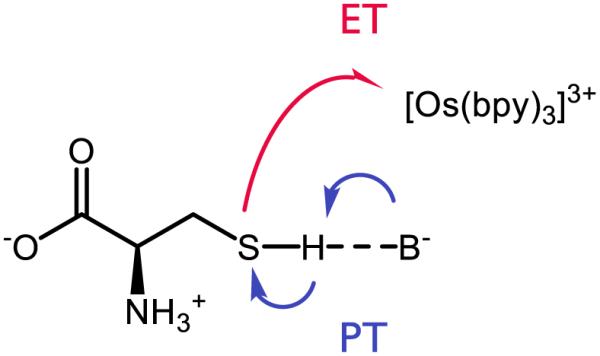
MS-EPT of cysteine by base and [Os(bpy)₃]³⁺ [188]

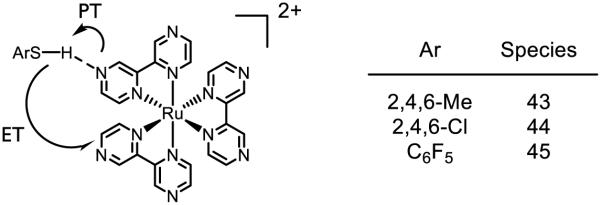
In analogy to phenol oxidations (see discussion above), Wenger has demonstrated that thiophenol may also undergo oxidative PCET upon treatment with photoexcited [Ru(bpz)₃]²⁺ (Figure 26) [190]. In this case the substituents on the thiophenol were found to have a profound effect on the mechanism of S-H bond activation. For thiol 43, no KIE is observed upon luminescence decay of the photocatalyst excited state, suggesting the quenching event is not accompanied bv a significant degree of proton motion. In contrast, 44 and 45 show KIEs of 1.6 and 1.5 respectively, indicating that proton motion is likely involved in excited state quenching. This trend is consistent with the PhSH/PhSH^•+ potentials for 43-45: compared to the Ru^II/Ru^I potential (0.92 V against Fc/Fc⁺ [151]), 43 has a potential close enough to undergo straight electron transfer (0.95 V against Fc/Fc⁺), whereas 44 (1.7 V against Fc/Fc⁺) and 45 (>2.0 V against Fc/Fc⁺) would require a much stronger oxidant to proceed by stepwise ET/PT. Based on the aqueous pK_a data, the pK_a of protonated [Ru(bpz)₃]²⁺ (2.3) is much lower than that of 44 (4.8) and marginally lower than that of 45; the authors acknowledge these trends may not hold for acetonitrile solution (where the relevant acidities have not been determined) and ultimately conclude the marginal pK_a difference between the catalyst and thiols is not enough to clearly distinguish between PT/ET and concerted PCET.

Figure 26.

PCET of thiophenol by [Ru(bpz)₃]²⁺ [190]

In synthetic contexts, thiyl radicals are known to engage in a number of useful reactions [191-198], including C-H bond abstraction [197,199-203]. Recently, MacMillan has demonstrated the capacity of catalytically generated thiyl radicals to cleave the C-H bond of benzylic ethers for radical coupling reactions (Figure 27) to form diaryl methanols (a) [204] or β-amino ethers (b) [205]. The light source is either a Blue LED or a Compact fluorescent lamp (CFL), as designated above. In both reactions, a wide variety of arene components and ether substitutions are tolerated to furnish a diverse set of products and only a catalytic amount of methyl thioglycolate is necessary to affect the desired C-H HAT event. In the formation of diaryl ethers (Figure 27, (a)), phosphate serves as the base, whereas the β-amino ether protocol (Figure 27, (b)) employs acetate. In the latter case, Stern-Volmer quenching studies were employed to elucidate the nature of thiyl generation. The excited state of the photocatalyst was found to be incapable of oxidizing the catalyst thiol in the absence of base, but inclusion of acetate resulted in quenching of the excited state. While sequential ET/PT may be ruled out based on these results, the similarity in pK_a’s between methyl thioglycolate (13 in DMSO [206]) and acetate (acetic acid pK_a ~ 12.6 in DMSO [207]) do not permit further classification of this activation into concerted PCET or stepwise PT/ET activation. Nevertheless, the use of PCET to generate a synthetically versatile radical under mild catalytic conditions presents an exciting new avenue for C-H bond functionalization chemistry.

Figure 27.

Recent benzylic C-H activations reported by MacMillan [204-205]

Amides

Recently our group has developed concerted PCET-based methods for the activation of amide N-H bonds to form neutral amidyl radicals. Long recognized as valuable synthons for C-N bond formation [203,208-213], these intermediates have not enjoyed widespread application in synthesis because of the inability to access these intermediates directly from native amide N-H bond precursors. The most common methods of amidyl generation typically require N-functionalized amides or the use of strong stoichiometric oxidants to effectively furnish the radical species. Few methods for catalytic amidyl generation have been reported [214]. We suspected that PCET could provide an amenable solution to producing neutral amidyls under mild catalytic conditions directly by activation of the amide N-H bond.

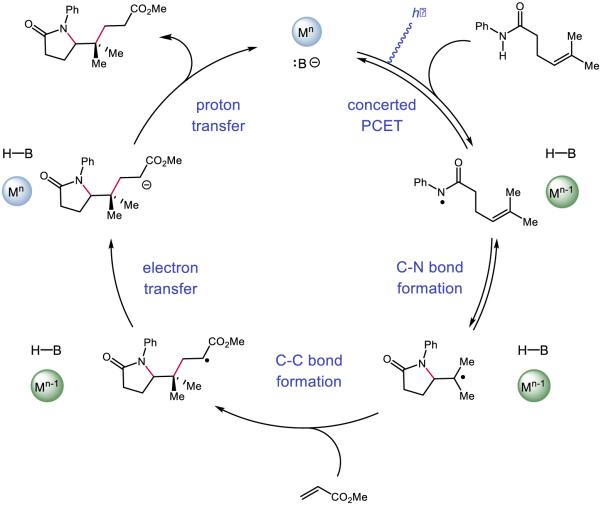
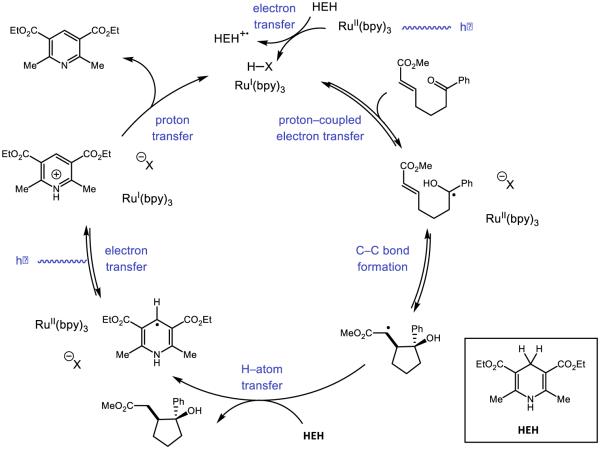
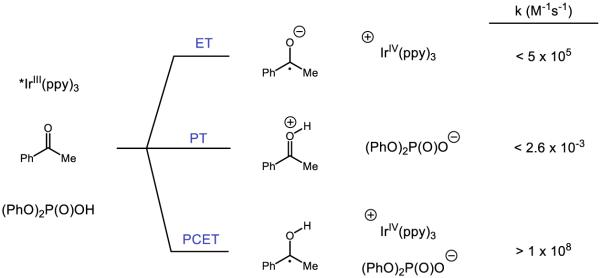
Our initial efforts focused on developing a PCET-based protocol for olefin carboamidation (Figure 28) [31]. In this process, PCET activation of N-aryl amide N-H bonds using an Ir-based visible-light photoredox catalyst as the oxidant and a weak Brønsted base would furnish reactive amidyls that could undergo intramolecular addition to a proximal olefin. Following C-N bond formation, the nascent carbon-centered radical could react with an acrylate species to form an α-carbonyl radical. Turnover of the catalysts could be achieved by one-electron reduction of this electrophilic radical to its corresponding enolate by the reduced form of the photocatalyst, followed by subsequent protonation by the conjugate acid of the catalytic base. Using Mayer’s effective BDFE formalism [29], we identified a number of combinations of photocatalysts and bases which could furnish the desired carboamidation product. However, the highest yielding combination was found to be the tetrabutylammonium salt of dibutyl phosphate Bu₄N⁺ (BuO)₂PO₂⁻ and [Ir{dF(CF₃)ppy}₂(bpy)]PF₆. The reaction is demonstrated to have a broad substrate scope, tolerating electron-rich and electron-deficient arenes, as well as a number of arene substitution patterns. Various olefin substitutions are tolerated, including tetrasubstituted olefins and, as are substrates which lead to fused rings and spirocyclic products. Lastly, various electron-deficient olefins other than acrylates may be employed as trapping reagents, including vinyl pyridine, acrylonitrile, acrolein, and α,β-unsaturated ketones.

Figure 28.

The proposed catalytic cycle [215] for our disclosed carboamidation protocol. Reprinted with permission from [31]. Copyright 2013 American Chemical Society.

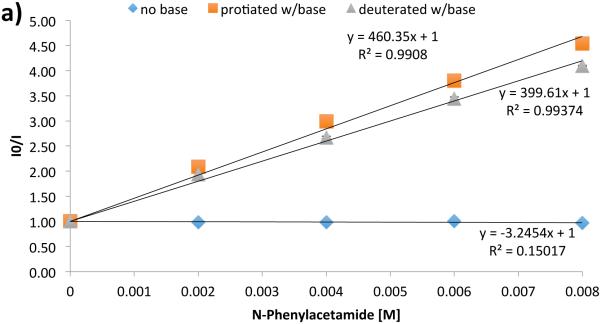
In an effort to address the role of PCET in the initial N-H activation step, we turned to luminescence quenching experiments using acetanilide as a model substrate in acetonitrile solvent (Figure 29). In the absence of base, the photocatalyst luminescence is not affected by the presence of the amide: this is consistent with the observation that the excited state potential of the catalyst (*E_1/2 = 1.0 V vs. Fc/Fc⁺ in MeCN) is not competent to oxidize acetanilide (*E_1/2 = 1.2 V vs. Fc/Fc⁺ in MeCN). With the inclusion of a constant quantity of phosphate base, however, variation of the amide concentration leads to efficient and linear quenching of the Ir excited state. An analogous experiment with a constant concentration of acetanilide and varied phosphate demonstrates first-order concentration dependence on the phosphate as well. Given the difference in pK_a between the phosphate and the substrate (Δ pK_a ~ 20) and the short excited-state lifetime of the catalyst (2.3 μs in MeCN at RT [216]), it is unlikely activation proceeds through stepwise PT/ET. Lastly, independent quenching experiments with N-protiated and N-deuterated acetanilide demonstrated a KIE of 1.15; such small KIEs have been demonstrated to be consistent with proton-involvement in multisite PCET processes [46,217-221]^. Taken together, our mechanistic data are most consistent with amide activation proceeding through concerted PCET.

Figure 29.

Luminescence quenching data evidence for amide N-H activation by PCET. a) Analysis of photocatalyst excited state quenching as a function of the concentration of protiated acetanilide in the presence and absence of base, as well as quenching as a function of concentration of deuterated acetanilide in the presence of base. b) Quenching as a function of base concentration in the presence and absence of acetanilide. Reprinted with permission from [31]. Copyright 2013 American Chemical Society.

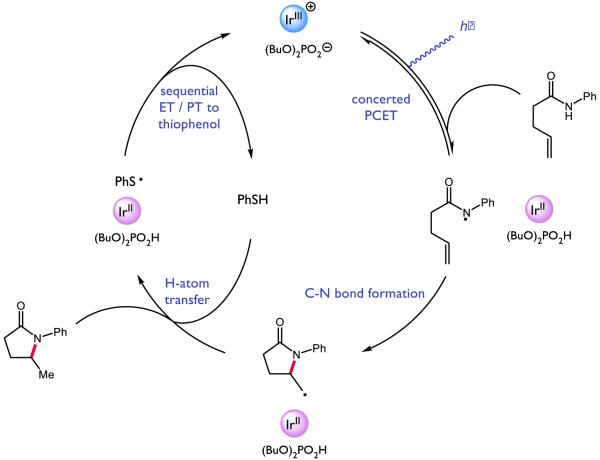
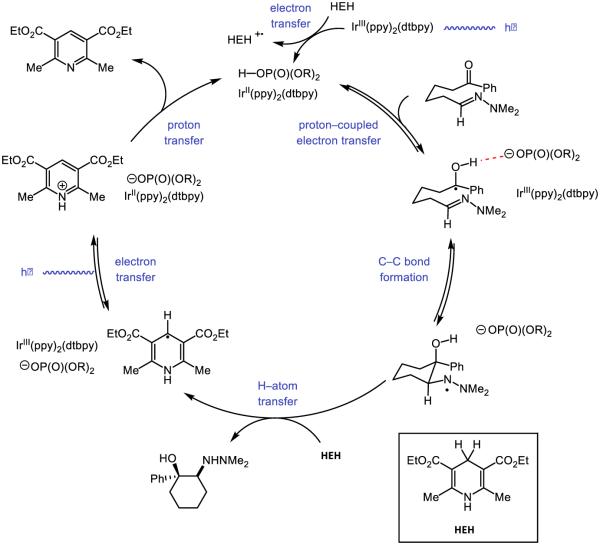
Looking to expand on these results and develop further olefin amidofunctionalization reactions, we questioned if we could identify a suitable hydrogen-atom donor reagent capable of furnishing a hydroamidation product, as illustrated in Figure 30 [222]. Based on this catalytic cycle, we anticipated such a donor would ideally enable facile HAT to the cyclized radical alkyl species, as wel as a R•/R⁻ redox couple suitable to oxidize the reduced state of the photocatalyst, resulting in the formation of an anion basic enough to deprotonate the phosphoric acid generated during the initial PCET event. Electing to retain our successful combination of photocatalyst and oxidant, we screened a number of potential hydrogen-atom donors and ultimately identified thiophenol as a competent HAT catalyst capable of furnishing the desired hydroamidation product in high yield. Compared to our carboamidation conditions, the hydroamidation protocol demonstrated an even broader substrate scope, capable of addition to terminal olefins and competent to form more exotic ring-fused species.

Figure 30.

Proposed catalytic cycle for PCET-enabled hydroamidation [222]

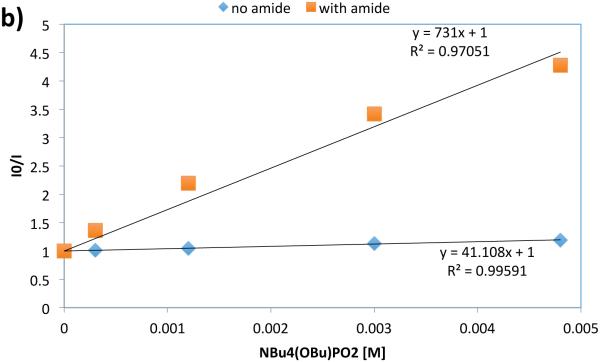
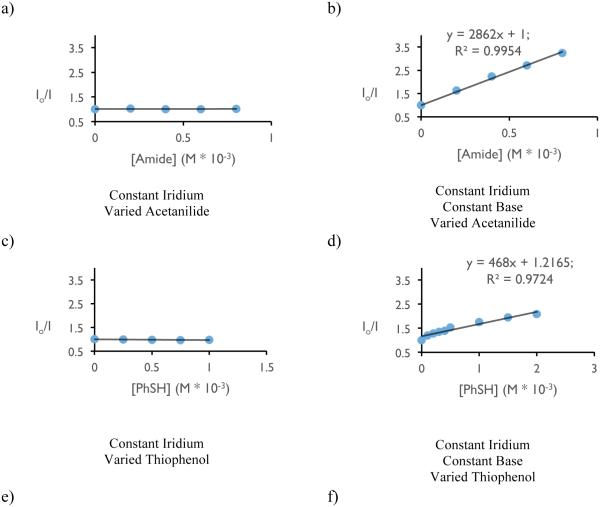
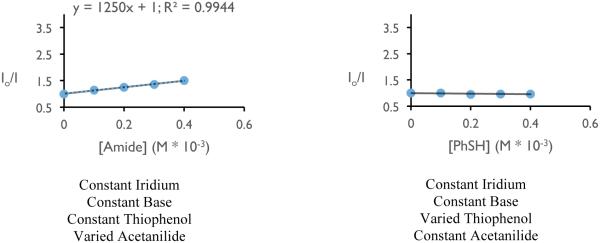
With respect to the proposed mechanism, the success of thiophenol as a catalytic hydrogen atom donor was surprising; not only are thiophenols observed to undergo multisite PCET reactivity as outlined in the previous section, but the large difference in bond strengths between thiophenol and the N-aryl amide (ΔBDFE ~ 20 kcal mol⁻¹) would suggest preferential activation of the weaker S-H bond. To elucidate the underlying kinetic selection between N-H and S-H activation, we undertook another set of luminescence quenching studies with acetanilide and thiophenol as our model substrates using DCM as solvent (Figure 31). Consistent with the observations in our carboamidation protocol, photocatalyst emission in DCM was unaffected by amide alone and demonstrated first-order dependence in the presence of a catalytically-relevant concentration of the phosphate base with K_SV = 2860 M⁻¹ (Figure 31 (a) and (b)). Analogously, concentration-dependent quenching with thiophenol was only observed in the presence of base (Figure 31 (c) and (d)), albeit with a smaller K_SV (480 M⁻¹). In a final set of experiments, increasing the concentration of acetanilide in the presence of constant concentrations of base and thiophenol was found to quench the excited state of the photocatalyst in a concentration dependent manner (Figure 31, (e)), albeit with a diminished K_SV (1250 M⁻¹) relative to quenching in the absence of thiophenol. When this experiment is inverted such that the concentration of thiophenol is varied in the presence of constant concentrations of base and amide (Figure 31, (f)), the luminescence intensity was found not to vary as a function of increasing thiophenol concentration.

Figure 31.

Luminescence quenching data for mechanistic studies to elucidate the selectivity for amide activation in the presence of thiophenol (vide infra). Figures reprinted with permission from [222]. Copyright 2015 American Chemical Society. This article may be accessed online at the following URL: http://pubs.acs.org/doi/pdf/10.1021/jacs.5b09671

The rate constants from Stern-Volmer analysis of excited-state quenching in the presence of base for acetamide (2860 M⁻¹) and thiophenol (480 M⁻¹) lie within an order of magnitude, suggesting that the observed kinetic bias for amide N-H activation does not correspond simply to difference in the quenching rate constant as demonstrated by Figure 31 (f). In PCET reactivity, pre-equilibrium hydrogen bonding is required to associate the proton donor and acceptor in solution prior to the electron transfer step. Accordingly, we hypothesized that the observed selectivity might be the result of a stronger affinity for phosphate hydrogen bonding to the N-H bond relative to the S-H bond. This hypothesis is consistent with all of the data presented in Figure 31 and corroborated by DFT calculations, which suggest the phosphate-amide hydrogen bond is stronger than the phosphate-thiophenol hydrogen bond by 5.2 kcal mol⁻¹. Such selectivity further highlights the importance of hydrogen bonding in concerted PCET and may serve as a design principle for future synthetic reactions invoking PCET activation of stronger bonds in the presence of weaker bonds.

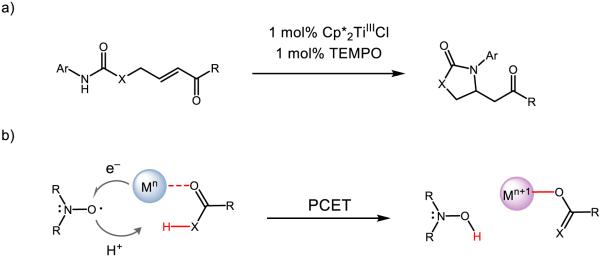
The concept of coupled proton and electron movement can be used not only to cleave strong amide N-H bonds by the joint action of a base and oxidant, but can also serve to weaken the amide N-H bond such that it can be activated by a weak H-atom abstractor. Exploiting the concept of bond-weakening upon coordination to redox-active metals [223-232], our lab demonstrated that a redox-active titanium catalyst Cp*₂Ti^IIICl and a weak hydrogen atom acceptor TEMPO enable intramolecular additions of amides to Michael acceptors (Figure 32) [223]. The substrate scope allows for N-H activation of amides, carbamates, thiolcarbamates, and ureas bearing phenyl or electron-rich arenes in uniformly high yield. Upon coordination to the titanium catalyst, the strength of the amide N-H bond is predicted to decrease from ~99 kcal mol⁻¹ to ~66 kcal mol⁻¹ based on DFT calculations. Related N-aryl carbamates were predicted to experience enhanced bond-weakening of up to 39 kcal mol⁻¹. Formal HAT to TEMPO is thought to proceed as a concerted PCET event, where the proton originates from the N-H bond and the titanium(III) species provides the necessary electron, resulting in the formation of a closed-shell aza-enolate species in the absence of an identifiable base. As a testament to the mildness of these base-free conditions, an acrylate featuring a base-labile FMOC group was maintained in this reaction; repeating this reaction under standard basic conditions resulted in quantitative deprotection of the ester.

Figure 32.

Amide activation via bond-weakening PCET to nitroxyl species. Adapted with permission from [233]. Copyright 2015 American Chemical Society.

It is known that Cp₂Ti^IIICl and TEMPO form a bond of approximately 25 kcal mol⁻¹; in light of this, we were unable to observe any conjugate amination at elevated temperatures using these two catalysts or the known complex Cp₂Ti^IVCl-OTEMP [234-236]. Our DFT calculations estimate the strength of the Cp*₂Ti^IVCl-OTEMP bond to be 23 kcal mol⁻¹ weaker than that of the Cp₂Ti^IVCl-OTEMP complex, putting an approximate value of this BDFE at 2 kcal mol⁻¹. This finding is consistent with the observed room temperature EPR spectra of a 1:1 mixture of Cp*₂Ti^IIICl and TEMPO (Figure 33), which demonstrates a signal consistent with both titanium- and oxyl-centered radical species present together in solution. Simulations of the individual EPR spectra for each component overlay with the experimentally-observed mixed spectra, indicating weak (if any) bonding between these species in solution. Destabilization of the Ti-O bond is credited to the increased steric bulk of the cyclopentadienyl ligand, which would encounter significant steric repulsion with TEMPO upon binding. In this way, this system can be thought of as an intriguing one-electron parallel to traditional frustrated Lewis pair chemistry in which the steric bulk of both the Lewis acid and the Lewis base prevent undesired association between the two, yet allow for joint substrate activation. Together, these three synthetic examples demonstrate the power of PCET in two two different synthetic contexts to activate strong amide N-H bonds and generate synthetically useful amidyl and aza-enolate intermediates.

Figure 33.

EPR spectra and simulations for Cp*₂Ti^IIICl, TEMPO, and a 1:1 mixture in MeCN. Adapted with permission from [223]. Copyright 2015 American Chemical Society.

Quinones

The ability of Brønsted acids to modulate the redox properties of quinones has long been recognized and has been the subject of extensive study [237-241]. Selected examples relevant to synthetic applications are discussed below. A seminal report in 1989 from Fukuzumi and coworkers demonstrated the ability of Brønsted acids to catalyze electron–transfer between various ferrocene derivatives and simple quinones [242]. Ferrocene is known to undergo oxidation by strong organic oxidants such as 2,3–dicholoro–5,6–dicyano–p–benzoquione, and 7,7,8,8–tetracyano–p–quinodimethane; no reaction occurs with weaker oxidants such as p–benzoquinone. However, the addition of HClO₄ was shown to catalyze efficient electron transfer between 1,1’–dimethylferrocene and p–benzoquinone to afford dihydroquinone and 1,1’–dimethylferrocenium. By plotting the concentration of 1,1’–dimethylferrocenium ion versus the ratio of benzoquinone to 1,1’–dimethylferrocene, the stoichiometry for the reduction was experimentally determined to be 2:1 with respect to ferrocene to benzoquinone (Figure 34). Moreover, kinetic experiments showed the rate of reduction increases as HClO₄ concentration increases. Analogous experiments employing cis–[Et₂Co(bpy)₂]⁺ as the one–electron reductant exhibited the same rate dependence on [HClO₄], consistent with a PCET process.

Figure 34.

Perchloric acid promted quinone reduction by ferrocene derivatives. Reproduced from [242] with permission of the Royal Society of Chemistry.

Later Fukuzumi studied the mechanism of p–benzoquinone reductions by NADH analogues [243-244]. Kinetic experiments again revealed an increase in the rate of reduction of p–benzoquinone (Q) and analogues as a function of increasing HClO₄ concentration. Additionally, independent kinetic runs using protiated and deuterated 10–methylacridine (AcrH₂ or ArcD₂) revealed primary KIEs for a variety of p–benzoquinone derivatives (Figure 35). These kinetic observations are consistent with three possible mechanisms: rate-limiting, acid-catalyzed hydride transfer from AcrH₂, proton transfer from AcrH₂^•+ to semiquinone radical, or hydrogen atom transfer from AcrH₂^*+ to semiquinone radical. An observed correlation between E_o(QH^•/QH₂) vs k_H/k_D led the authors to conclude that reversible electron transfer followed by rate limiting hydrogen–atom transfer between AcrH₂^•+ and the neutral semiquinone radical (QH^•) is the most likely reaction pathway (Figure 36).

Figure 35.

KIEs for various benzoquinone reductions by 10-methylacridine [243]

Figure 36.

Plot of the primary kinetic isotope effects for the acid-catalysed rate constant k’_H/k’_D vs. E_o (QH• / QH₂) in the reduction of p-benzoquinone derivatives by AcrH₂ and AcrD₂ in H₂O-EtOH (5:1 v/v) at 298 K. Reproduced from [244] with permission of the Royal Society of Chemistry.

Fukuzumi reported a detailed mechanistic study of quinone reduction catalyzed by protonated amino acids [245]. Kinetic experiments, EPR spectroscopy and cyclic voltammetry were employed to illustrate the role protonated histidine plays in mediating electron transfer between NADH analog 9,10–dihydro–10–methylacridine (AcrH₂) and 1–(p–tolylsulfinyl)–2,5–benzoquinone (TolSQ). Cyclic voltammetry experiments demonstrate a 0.55 V positive shift in the one–electron reduction potential of TolSQ in the presence of 5.0 × 10⁻² M of protonated histidine. This change in the reduction potential was attributed to the stabilizing effect of hydrogen bonding interactions between protonated histidine and TolSQ radical anion, which was observed by EPR spectroscopy (Figure 37).

Figure 37.

EPR spectra of semiquinone radical – protonated histidine interactions. Reprinted with permission from [245]. Copyright 2008 American Chemical Society.

The ability of Brønsted acids to increase the oxidizing power of benzoquinone derivatives was further investigated by Rathore in the context of the Scholl reaction [246]. Arene substrates with oxidation potentials as high as +1.7 V vs SCE were readily oxidized by dichlorodicyano–p– benzoquinone (E_red = +0.60 V vs SCE) in the presence of methane sulfonic acid (Figure 38). However, no reaction was observed in the absence of acid.

Figure 38.

MsOH-promoted arene oxidation [246]

Recently, Jacobsen and Nocera investigated the ability of various hydrogen–bond donors to affect the rates and thermodynamics of quinone reductions [247]. Energetically favorable associations between hydrogen bond donors and quinone radical anions provide the additional thermodynamic driving force necessary to enable otherwise endergonic electron transfers, as quantified by the following expression:

$$\Delta G_{net}=\Delta G_{ET}+\Delta G_{association}$$

This study is particularly notable in being the first to study these effects in electron-deficient quinones. Prior work has focused on comparatively electron-rich quinones, which are more Lewis basic and thereby provide a higher association energy, resulting in a larger ΔE_1/2. In this work, the authors sought to quantify the activation of more electron deficient quinones that have oxidation potentials closer to those of synthetically relevant functional groups. In particular, a variety of hydrogen bond donors were prepared to evaluate their ability to promote the reduction of ortho–chloranil (Figure 39). To evaluate the ability of the H-bond donors to promote quinone reduction, the authors experimentally determined the association constants for binding between the hydrogen bond donors and both the oxidized and reduced forms of ortho– chloranil, K_Q and K_Q•– respectively, using cyclic voltammetry experiments and the following equation derived from the Nernst relation:

$$\Delta E_{1∕2}=0.059V\text{log}\frac{1+K_{Q•-}\left[HBD\right]}{1+K_Q\left[HBD\right]}$$

Figure 39.

Quinone reduction promoted by hydrogen-bond donors [247]

Fitting the current response for each individual H-bond donor revealed the stoichiometry of binding to be 2:1 for the monocationic and neutral catalysts, and 1:1 for the bisamidinium catalyst. To further support this proposed mechanism, additional kinetic studies revealed a second order dependence on the rate of quinone reduction with monocationic catalysts, and a first order dependence on the rate of reduction using the biscationic amidinium salt.

After studying the mechanism by which hydrogen bond donors catalyze electron transfer, the authors developed a novel oxidative lactonization reaction to demonstrate the synthetic utility of hydrogen–bond coupled electron transfer (Figure 40). Importantly, this work extends the current understanding of how hydrogen bonding can promote electron transfer events in synthetic contexts, even in the absence of a formal proton transfer event.

Figure 40.

Hydrogen bond-coupled electron transfer promoted oxidative lactonization [247]

Ketones and Carbonyl Derivatives

In pioneering work in the mid 1980’s, Fukuzumi and coworkers identified that strong Brønsted acids can catalyze electron transfer reactions between outer-sphere reductants and acetophenone derivatives [242]. Specifically, they demonstrated that while the excited state of [Ru(bpy)₃]²⁺ cannot donate an electron to acetophenone derivatives directly in acetonitrile [248], addition of 0.1M HClO₄ led to efficient charge transfer. Through the use of luminescence quenching assays, the authors were able to quantify a positive shift in the one-electron reduction potential of ketones in the presence of HClO₄ and the corresponding rates of acid-catalyzed ET.

Acetophenone derivatives containing electron donating groups possess E_1/2^red values significantly more negative than the excited state of [Ru(bpy)₂]⁺³. As a consequence, electron transfer does not occur in the absence of HClO₄. However, upon inclusion of 0.1 M HClO₄ electron transfer proceeds rapidly (Figure 41). The authors speculate that protonation of the ketyl radical anion is stabilizing, thereby providing additional thermodynamic driving force which is observed as an increase in k_ET. For acetophenone derivatives bearing electron withdrawing substituitents (meta or para nitro) no increase in k_ET was observed upon inlcusion of HClO₄. The authors postulate that electron withdrawing groups decrease the basicity of the ketyl radical anion to such a degree that protonation by HClO₄ is not favorable.

Figure 41.

Perchloric acid catalyzed ET from photoexcited Ru(bpy)₃²⁺ to acetophenone derivatives. ΔE_red corresponds to the positive shift in the one-electron reduction potential observed in the presence of perchloric acid relative to the one-electron reduction potential observed in the absence of perchloric acid. [242]

To study the mechanism by which HClO₄ catalyzes electron transfer, the kinetic order in acid was measured by performing a series of Stern–Volmer luminescence quenching experiments at various concentrations of HClO₄. These experiments revealed a linear relationship between k_et and [HClO₄] (Figure 42) showing electron transfer from [Ru*(bpy)₃]²⁺ is first order in acid. In this work, the authors proposed a stepwise ET/PT mechanism in which protonation of the ketyl radical anion provides additional thermodynamic driving force which causes an increase in k_ET. This work predated the wide-spread acceptance of concerted proton–coupled electron transfer as an elementary step, however these seminal observations provided the conceptual framework for PCET to be applied further in contemporary synthetic chemistry.

Figure 42.

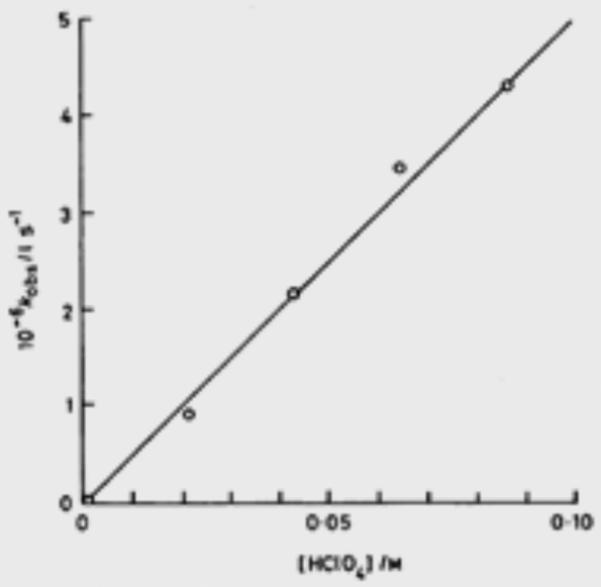
k_ET v. [HClO₄] for electron transfer between Ru(bpy)₃²⁺ and acetophenone. Reproduced from [242] with permission of the Royal Society of Chemistry.

The Fukuzumi group later investigated the mechanism of reduction of α–haloketones using NADH model compounds [249-250]. This non–enzymatic model system was developed to investigate the role of Brønsted acids in enzymatic ketone reductions. The use of an acid-stable NADH analogue enabled the authors to study the reaction both in the presence and absence of HClO₄. By comparing these results to kinetic experiments employing classical outer–sphere reductants, the authors were able to demonstrate that ketone reduction by NADH model compounds proceeds through an initial Brønsted acid-promoted electron transfer step. To investigate the mechanism of ketone reduction, kinetic data was obtained for a series of α–haloketone reductions by an acid-stable NADH analog 10–methylacridan (AcrH₂) with HClO₄ in acetonitrile (Figure 43). Additionally, the rate of electron transfer from classical one–electron reductants such as Fe(MeC₅H₄)₂ and [Ru*(bpy)₃]²⁺ was measured for the same series of ketones. Comparing the two sets of rate data allowed the authors to draw conclusions about the mechanism of acid catalyzed ketone reduction by NADH analogues. While no reduction was observed in the absence of acid with any reductant, a linear correlation between the rate of electron transfer k_et was observed with increasing HClO₄ concentration with Fe(MeC₅H₄)₂ as well as [Ru*(bpy)₃]²⁺. Additionally, a linear correlation was observed between the rate constant (log k_obs) for the reduction of α–haloketone by AcrH₂, and the rate constants (log k_et) for electron transfers from Fe(MeC₅H₄)₂ and [Ru*(bpy)₃]²⁺. On the basis of these findings, the authors suggest that the first step in acid-catalyzed ketone reductions by NADH model compounds involves initial electron transfer to an activated ketone substrate.

Figure 43.

α-haloketone reduction with NADH model compound versus dimethyl ferrocene [249-250]

Despite this correlation, different product distributions were observed when the reduction is run with AcrH₂ versus Fe(MeC₅H₄)₂ (Figure 43). This observation can be rationalized by considering the subsequent steps of the reduction mechanism (Figure 44). The 1,2 reduction product forms as a result of hydrogen–atom transfer from the AcrH₂ radical cation to yield the α–halohydrin product. Since this pathway is unavailable for the outersphere one–electron reductants, only the dehalogenated acetophenones are observed.

Figure 44.

Mechanistic rationale for product distribution employing different reductants

Unactivated aldehydes and ketones do not undergo reduction by NADH analogues readily, however in the presence of HClO₄ and acetonitrile compounds are rapidly reduced to the corresponding alcohols (Figure 45) [251]. First the authors measured the rate of reduction (k_obs) of acetaldehyde and related compounds by AcrH₂ in the presence of HClO₄. Next, the rate of electron transfer (k_et) from [Ru*(bpy)₃]²⁺ to the same series of carbonyl compounds was measured by Stern–Volmer luminescence quenching experiments. A plot of log k_obs vs log k_et again revealed a linear relationship, suggesting that acid catalyzed electron transfer may play an important role in the reductions of aldehydes and ketones by NADH analogs such AcrH₂ as well (Figure 45). In these papers, the authors propose a stepwise mechanism in which electron transfer first occurs to generate a radical anion, which is rapidly protonated by acid. However, in light of more recent advances, mechanisms involving stepwise PT–ET, or concerted proton–coupled electron transfer should also be considered. In particular. given the pK_a of HClO₄ (−0.7 in MeCN) relative to a typical ketone (pK_a = −0.1 for acetophenone in MeCN) the possibility of electron transfer to a protio–oxocarbenium ion cannot be easily discounted.

Figure 45.

Non-enzymatic acetaldehyde reduction. Adapted from [251] with permission of The Royal Society of Chemistry.

In an analogous set of experiments, this model system was again used by the Fukuzumi group to investigate the mechanism of flavin reduction [252]. NADH and flavins are coenzymes which play an essential role in many biological redox processes, including the reduction of dioxygen in respiration. In this work the authors investigate the acid catalyzed reduction of flavin analogues by both NADH model 10–methyl–9,10–dihydroacridine (AcrH₂), and cis–dialkylcobalt(III) complexes. Kinetics experiments were performed to study the mechanism by which flavin reduction occurs. These experiments revealed an increase in k_obs associated with an increase in [HClO₄] for both AcrH₂ as well as the outer sphere reductants cis–[Me₂Co(bpy)₂]⁺ and cis–[Et₂Co(bpy)₂]⁺. From the obtained rate data, the authors calculated a positive shift in the one–electron reduction potential as a function of increasing [HClO₄], further demonstrating the ability of acid to catalyze electron transfers.

Building upon these early observations that Brønsted acids can play a significant role in catalyzing electron transfers, Yoon and coworkers reported an acid-catalyzed reductive cyclization of enones in the context of visible light photoredox catalysis (Figure 46) [253]. The Yoon lab had previously demonstrated the ability of Lewis acid salts to activate similar systems [254-255], however different products were formed based on the method of enone activation. Specifically, it was proposed that Lewis acid activation affords a radical anion intermediate, whereas Brønsted acid activation results in a neutral radical. These distinct radical intermediates are known to have different reaction chemistries, and this difference was proposed to be the origin of the differing product distributions.

Figure 46.

Brønsted acid promoted reductive cyclization.

The authors propose the Brønsted acid-catalyzed mechanism (Figure 47) which begins by reductive quenching of [Ru*(bpy)₃]²⁺ by a sacrificial reductant, such as iPr₂NEt to afford the more reducing [Ru(bpy)₃]⁺. Next, electron transfer occurs from [Ru(bpy)₃]⁺ to a proto–oxocarbenium ion to afford a neutral radical intermediate. Carbon–carbon bond formation occurs through a 5–exo–trig cyclization to afford an α–carbonyl radical. It was proposed the cyclized radical could be reduced either through HAT from the radical cation of iPr₂NEt or sequential electron transfer from the photoredox catalyst, followed by protonation of the enolate. However, considering the large difference in pK_a between formic acid (pK_a ~ 23 in MeCN) and typical ketones (−0.1 acetophenone in MeCN) protio–oxocarbenium formation may be less favorable than activation through hydrogen bonding. The authors demonstrated the utility of this protocol in 24 examples with yields ranging from 60 – 95% and including both aryl and alkyl enones, and demonstrated the use of stoichiometric Brønsted acids to facilitate electron transfer to substrates with reduction potentials previously inaccessible using common photoredox catalysts.

Figure 47.

Plausible mechanism for reductive enone coupling. Adapted from [253] with permission of The Royal Society of Chemistry.

In 2013, our lab demonstrated the feasibility of concerted proton–coupled electron transfer as a mechanism of substrate activation in the development of a catalytic ketyl–olefin coupling protocol [32]. The thermodynamics associated with ketone reduction make them particularly well suited for activation by concerted PCET. The strongly negative reduction potentials (E^1/2red = −2.48 V vs Fc for acetophenone) and poor basicity (pK_a in MeCN = −0.1 for acetophenone) of typical ketones require extremely reducing or acidic conditions for activation by either sequential transfer pathway. However, we anticipated that through a concerted PCET mechanism, ketyl formation could be viable using suitable combinations of Brønsted acids and one-electron reductants with values far removed from those required for either sequential transfer pathway. Furthermore, we postulated a concerted PCET mechanism would benefit from decreased kinetic barriers relative to mechanisms involving stepwise transfer associated with the generation of high-energy charged species along the reaction coordinate.

Notably, the ability for a given pair of Brønsted acid and one–electron reductant to jointly activate ketones through concerted PCET could be predicted using the effective BDFE formalism outlined by Mayer [29]. As outlined in the introduction, the equation in Figure 48 enables an energy value thermodynamically equivalent to a BDFE to be calculated for a given acid–reductant combination. This effective BDFE value formally represents the strength of the X–H bond that may be formed from a given acid–reductant combination in a thermoneutral process. We expected combinations of acids and reductants with effective BDFEs significantly higher than the ketyl radical O–H bond (BDFE = 26 kcal/mol) would not possess sufficient thermodynamic driving force to enable ketyl formation via PCET (Figure 48, entries 1–4). However, when the combination of acid and reductant furnish an effective BDFE at or below the threshold required for ketyl formation, PCET activation will be favorable and substrate 41 will rapidly cyclize to give products 42 and 43 (Figure 48, entries 5–10).

Figure 48.

Evaluation of acid/reductant pairs for PCET. Reprinted with permission from [32]. Copyright 2013 American Chemical Society.

After establishing conditions required for ketyl formation, we proposed the following mechanism for the catalytic ketyl–olefin coupling (Figure 49). The intermediate ketyl radicals would undergo 5–exo–trig cyclization with pendant olefins to form a new carbon–carbon bond and afford an α-carbonyl radical. These radicals can be subsequently reduced by hydrogen–atom transfer from Hantzsch ester to afford the cyclized products. Electron transfer from the oxidized HEH to the excited state of [Ru(bpy)₃]²⁺, followed by proton transfer to phosphate will regenerate both Brønsted acid and photoredox catalyst and close the catalytic cycle.

Figure 49.

Plausible mechanism for ketyl-olefin cyclization. Reprinted with permission from [32]. Copyright 2013 American Chemical Society.

To determine whether substrate activation occurs through concerted PCET or a sequential transfer pathway, luminescence quenching studies were conducted using acetophenone as a model substrate together with diphenyl phosphoric acid and an excited state reductant, Ir*(ppy)₃. Notably, no quenching of the Ir excited state was observed in solutions of acetophenone or diphenyl phosphoric acid individually. However admixtures of these two reagents led to efficient quenching that exhibited a first order kinetic dependence on the concentration of each component. Additionally a deuterium kinetic isotope effect (k_H/k_D) of 1.22 ± 0.02 was observed when these luminescence quenching experiments were run using either the protiated or deuterated form of diphenyl phosphoric acid. Taken together, these experiments are inconsistent with rate-limiting ET activation. Similarly, rate-limiting proton transfer was ruled out on energetic grounds, as the difference in pK_a between diphenyl phosphoric acid (pK_a = 13, MeCN) and acetophenone (pK_a = −0.1, MeCN) corresponds to a free energy difference of 18 kcal/mol. Taking this unfavorable free energy change as the minimum kinetic barrier for proton transfer, rate of proton transfer cannot exceed 2.6 × 10⁻³ M⁻¹ s⁻¹. This process is thus much too slow to be competitive with luminescent decay of the catalyst excited state, which has a lifetime of 1.9 μs. As both stepwise pathways can be ruled out, these results are most consistent with a concerted PCET mechanism of ketone activation.

Building on these results, we next questioned whether a chiral Brønsted acid could be used to serve as a handle for asymmetric induction in photoredox catalysis [256]. A key challenge would be to identify conditions in which a hydrogen–bonding interaction between a neutral ketyl intermediate and the conjugate base of achiral Brønsted acid catalyst are maintained throughout subsequent bond forming events. We demonstrated the feasibility of this proposal in the successful development of a catalytic asymmetric aza–pinacol coupling promoted by reductive proton–coupled electron transfer. Chiral phosphoric acid catalysts were employed with Ir-based visible light photoredox catalysts to jointly activate ketones to form neutral ketyl radicals. These free radical intermediates remain associated with the chiral phosphate through a stabilizing hydrogen–bonding interaction throughout carbon–carbon bond formation to afford vicinal amino–alcohols in high yield and enantioselectivities.

We propose the reaction may proceed by the following mechanism (Figure 51). First, reductive quenching of the Ir^III(ppy)₂(dtbpy) excited state by Hantzsch ester will afford the more reducing Ir^II(ppy)₂(dtbpy). PCET would then occur to a hydrogen bond complex between substrate and chiral phosphoric acid to afford the neutral ketyl radical. This neutral ketyl radical would remain associated with the chiral phosphate throughout the subsequent carbon–carbon bond formation to afford a cyclized hydrazyl radical. HAT from Hantzsch ester would afford the closed–shell product. Electron transfer followed by proton transfer will again regenerate both catalysts and close the catalytic cycle.

Figure 51.

Proposed mechanism for asymmetric aza-pinacol coupling. Reprinted with permission from [256]. Copyright 2013 American Chemical Society.

Catalyst and reaction parameter optimization led to the identification of 2 mol% [Ir(ppy)₂(dtbpy)](PF6), 10 mol% (R–R)–2,2’–TPS–binol phosphoric acid and Hantzsch ester as the stoichiometric reductant in dioxane solvent as the optimal conditions. The reaction afforded a variety of cyclized vicinal amino–alcohols in high yields and enantioselectivities. Density functional calculations demonstrate neutral ketyl radicals are excellent hydrogen bond donors and can engage in highly stabilizing hydrogen bonding interactions with phosphate anions (Figure 12). Consistent with this view, we observed that high enantioselectivity was maintained even in polar solvents with relatively high dielectric constants (81% ee in MeCN, 88% ee in DME). This reaction first demonstrated the ability of hydrogen bonding in a PCET event to serve as a platform for asymmetric induction in photoredox-catalyzed free radical transformations.

Figure 12.

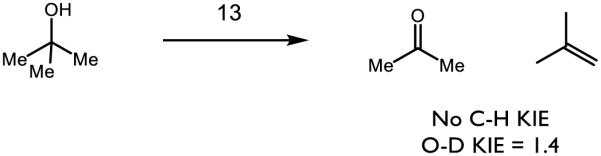
Products and C-H/D and O-H/D KIEs for Oxidation of tert-butanol by 13 [93]

In 2015 Rueping and coworkers described the reductive homodimerization of carbonyls catalyzed by Brønsted acids [257]. The authors employ iridium and ruthenium-based visible light photoredox catalysts and NBu₃ as a stoichiometric reductant to form ketyl radical intermediates which rapidly dimerize to form symmetrical pinacol products. The authors note that electron transfer between the excited state of [Ir(dF(CF₃)(ppy)]₂(dtbpy)PF₆ (E_1/2^red = −1.69 V vs Fc) and acetophenone (E_1/2^red = −2.48 V vs Fc) is significantly endergonic. As such, they propose the reduction is catalyzed by trace Brønsted acid formed from the oxidation of NBu₃. To probe this hypothesis the authors investigated the effect of acidic and basic additives on the homodimerization of acetophenone (Figure 53). The observation that basic additives inhibit the reaction and additional acids promote the reaction is consistent with PCET as the mechanism of substrate activation in these reductive homodimerizations. The reaction was shown to be efficient for the reductive homocoupling of a variety of diverse benzaldehyde and acetophenone derivatives providing pinacol products in high yield. Additionally the methodology was successfully applied to imines to afford vicinal diamines in good to excellent yields.

Figure 53.

Reductive homocoupling of ketones promoted by Brønsted acids [257]

With respect to PCET coupling of imine derivatives, Sigman has reported the synthesis of piperazines by the reductive coupling of bisimines with a combination of Brønsted acids and elemental manganese as a one–electron reductant (Scheme 54) [258]. The authors found that the success of the reaction correlated with the acidity of the Brønsted acid additive, consistent with a PCET process. The high diastereoselectivity of this transformation was a noteworthy compared to other previously reported imine dimerizations. A radical–radical coupling mechanism was proposed to account for the observed diastereocontrol. While it is possible that the reaction proceeds through radical addition to a second equivalent of imine followed by subsequent reduction, we defer to the mechanism put forward by the authors.

Related to the ketones examples shown above, in 2014 DiRocco and coworkers reported the late stage functionalization of biologically active small molecules using Brønsted acids and photoredox catalysts to activate peresters (Figure 55) [259]. The presence of trifluoroacetic acid enables one–electron reduction of tert–butyl peracetate and biscyclopropanecarbonyl peroxide by visible light photoredox catalysts. This proton-coupled reduction event initiates a series of bond fragmentations, which afford methyl or cyclopropyl radicals. These radical species then undergo efficient Minisci-type additions to heteroaromatic compounds to enable late stage diversification of drugs and drug candidates (Figure 56). As peresters have reduction potentials ~1 V endergonic relative to the redox catalyst employed, the authors suggest that Brønsted acid additives catalyze the reduction via concerted PCET.

Figure 55.

Late stage diversification enabled by PCET

Figure 56.

Proposed mechanism of perester reduction

Concluding Remarks

We believe that the examples and discussion above highlight the potential of PCET processes for applications for organic synthesis. Together with the large body of biological, organic, and inorganic mechanistic studies and limited synthetic examples, we are optimistic that PCET will continue to develop as a general mode of organic substrate activation and provide solutions to longstanding challenges in homolytic bond activation catalysis and the associated reaction chemistry of the resulting radicals.

Figure 2.

A square scheme for the determination of BDFEs as popularized by Bordwell [28]

Figure 9.

Bridging manganese oxo species with phen and bpy ligands

Figure 10.

“Cubane” complexes 9 and 10 introduced by Dismukes, as well as phenothiazine (pzH) 11. Note that each face is thought to bind one molecule of phosphate: these are omitted for structural clarity.

Figure 50.

Summary of mechanistic data supporting PCET reactivity

Figure 52.

Computational estimate of ketyl-phosphate hydrogen bond strength. Reprinted with permission from [256]. Copyright 2013 American Chemical Society.

Figure 54.

Reductive coupling of bisimines [258]