A Novel Cross-Frequency Coupling Detection Method Using the Generalized Morse Wavelets

Abstract

Background

Cross-frequency coupling (CFC) occurs when non-identical frequency components entrain one another. A ubiquitous example from neuroscience is low frequency phase to high frequency amplitude coupling in electrophysiological signals. Seminal work by Canolty revealed CFC in human ECoG data. Established methods band-pass the data into component frequencies then convert the band-passed signals into the analytic representation, from which we infer the instantaneous amplitude and phase of each component. Though powerful, such methods resolve signals with respect to time and frequency without addressing the multiresolution problem.

New Method

We build upon the ground-breaking work of Canolty and others and derive a wavelet-based CFC detection algorithm that efficiently searches a range of frequencies using a sequence of filters with optimal trade-off between time and frequency resolution. We validate our method using simulated data and analyze CFC within and between the primary motor cortex and dorsal striatum of rats under ketamine-xylazine anesthesia.

Results

Our method detects the correct CFC in simulated data and reveals CFC between frequency bands that were previously shown to participate in corticostriatal effective connectivity.

Comparison with Existing Methods

Other CFC detection methods address the need to increase bandwidth when analyzing high frequency components but none to date permit rigorous bandwidth selection with no a priori knowledge of underlying CFC. Our method is thus particularly useful for exploratory studies.

Conclusions

The method developed here permits rigorous and efficient exploration of a hypothesis space and is particularly useful when the frequencies participating in CFC are unknown.

Graphical abstract

1. Introduction

1.1. Cross-Frequency Coupling and Conventional Estimation Methods

Cross-frequency coupling (CFC), defined as correlated activity across distinct frequency bands, is a recently discovered neural correlate of multiple cognitive and behavioral states (Canolty et al., 2006; Canolty and Knight, 2010). CFC has been observed in intra-cranial recordings from epileptic patients (Fitzgerald et al., 2013), the basal ganglia of patients undergoing DBS (Cohen et al., 2009), EEG data recorded from schizophrenia patients during auditory steady state response (Spencer et al., 2009) and rats engaged in reward seeking behavior (Tort et al., 2008). Given the ubiquity of CFC, this phenomenon has become a topic of intense investigation in recent years. While the functional significance of CFC is not fully understood, it likely plays a role in perceptual binding as well as in intra-structural and cross-structural neuronal synchronization in the brain.

Canolty et al. first proposed to study CFC using a sequence of standard linear least squared (LLS) band-pass filters followed by converting the signal x_t to the form x_t,analytic = x_t + iH(x_t) where i is the imaginary unit and H(f) is the Hilbert transform of the enclosed function. The Hilbert transform is the convolution of a function with the kernel (πt)⁻¹. In practice, the analytic representation is obtained by Fourier transforming the signal, setting all frequencies above the Nyquist frequency to zero, and inverse Fourier transforming the resulting function. The analytic signal gives both the instananeous amplitude and phase of the signal at a given time; by extracting these values from band passed data we obtain the amplitude and phase - the modulus and angle of x_t,analytic - of the frequency components under analysis. Binning the amplitude values by phase and computing a modified version of the Kullback-Leibler divergence between the obtained distribution and the uniform distribution yields the modulation index (MI). The MI measures the degree of phase-amplitude synchronization across frequency bands. Statistical significance is determined via permutation techniques.

1.2. The Multiresolution Problem and Motivation for a Wavelet-Based Approach

We build upon Canolty's approach and develop a novel method of CFC detection using the generalized Morse Wavelets (GMWs). Resolving instantaneous amplitude and phase requires one to analyze a signal with respect to both time and frequency simultaneously. By the uncertainty principle, it is not possible to resolve a signal with simultaneous arbitrary precision in both domains. Canolty's method does not provide a principled manner in which to vary the frequency range of the band-pass filters in order to obviate this issue. Furthermore, it is preferable to use a narrow band filter for low frequency components and a broader filter for high frequency components. This increases the chance that the low frequency signal consists of smoothly varying sinusoidal components in order to avoid phase slips, while the high frequency signal is obtained with a sufficiently broad filter to ensure the side bands arising from cross-frequency influence are not excluded (See Aru et al. (2014) for a detailed discussion). Fortunately, the wavelet transform applies narrow-band filters to low frequency components and increasingly broad-band filters as the peak frequency of the impulse response function increases.

The wavelet transform was developed in part to overcome the multiresolution problem and naturally partitions time-frequency space such that the trade-off between temporal and spectral resolution is constant across all bands. We use the term “multiresolution” to refer to the problem of partitioning a univariate signal over a multivariate space when constant resolution across all degrees of freedom is unavailable; this use of the term should not be confused with the multiresolution approach to constructing wavelet bases (see chapter 5 of Daubechies (1992)). We consider the GMWs over the Morlet wavelet since, while the Morlet wavelets are commonly used and their construction is relatively intuitive, we believe the GMWs are preferable for phase analysis. Though the Morlet wavelets are in theory strictly analytic - that is they have vanishing support for non-positive frequencies - in reality they exhibit leakage onto the negative frequency axis under certain paramaterizations that increase time resolution at the cost of frequency resolution (Lilly and Olhede, 2009). Due to this property, use of the Morlet wavelets risks aliasing. The GMWs, in contrast, are strictly analytic across their parameter regime.

Here, we explore the behavior of the GMWs as the band-pass filters used to generate the MI. We validate our method using both simulated and empirical data. Our method gives rise to an efficient and parsimonious means to scan multiple frequency bands for CFC without prior knowledge of whether and where CFC will occur. We conclude with a discussion of the comparative strengths and weaknesses of our approach and recommendations regarding best practices when applying the method.

2. Materials and Methods

2.1. Animals and Electrophysiology

All procedures followed NIH guidelines regarding use of animals in research and were approved by the Institutional Animal Care and Use Committee (Assurance Number A4049-01)

Surgery and electrophysiology techniques are described in detail elsewhere (Nakhnikian et al., 2014). Briefly, we recorded local field potentials in the primary motor cortex (M1) and dorsal striatum (dStr) of 4 male Sprague-Dawley rats under ketamine/xylazine anesthesia. Signals were sampled at 1 kHz and downsampled to 240 Hz offline using an in-house interpolation algorithm. Power line noise at 60 Hz was reduced using a multitaper method (Mitra and Pesaran, 1999). Data gathered under anesthesia were divided into 5 s epochs separated by 2 s buffers to reduce serial correlations among consecutive epochs. Epochs contaminated with obvious artifacts, as well as those recorded from animals exhibiting incomplete anesthesia (as indicated by any response to a paw pinch or whisker flick) were discarded. In our final analysis, we used 252 5 s trials.

2.2. Data Analysis

To assess CFC within and between M1 and dStr, we applied our CFC detection algorithm (see section 3) to the data set described above. We extracted phase and amplitude information for all frequencies from 1 to 80 Hz by convolving each trial with the 0th GMW. Instantaneous phase and amplitude data were extracted for each bandpassed signal. We constructed phase to amplitude histograms for all pair-wise combinations of frequencies and computed the modulation index for each pair. For all analyses, we set γ = 3 and β = 6 (see section 3.2). Analysis was carried out using the open-source Jlab package developed by Lilly (2016) (available online: http://www.jmlilly.net/software.html) and in-house code. Jlab uses a spacing parameter, D, to determine the amount of overlap in Fourier between consecutive wavelets. We set D to Lilly's recommended value of 4. We compared results for multiple values of D and found them to be almost identical (data not shown).

3. Theory and Computation

3.1. Conventional CFC Estimation

The standard flow of computation to estimate CFC is as follows.

1. Extract the frequency bands of interest using a LLS filter. Reverse filter to reduce phase distortions.

2. Transform the band passed data sets to Fourier space and set all values corresponding to negative frequencies equal to zero.

3. Inverse Fourier transform the resulting function to obtain the analytic representation.

4. Extract amplitude and phase values from the analytic representation. Bin the amplitudes by phase and average the resulting histograms over multiple trials to obtain an ensemble estimate of phase-amplitude coupling.

5. Estimate the normalized entropy of the phase-amplitude distribution to get the MI. Specifically, we define the MI as (H_max – H_obt)/H_max, where H_obt is the entropy of the obtained distribution and H_max is the maximum entropy (the logarithm of the number of bins).

Useful illustrations of the steps involved in CFC computation are provided in the supplements to Tort et al. (2008).

As noted above, the LLS filter approach does not account for the multiresolution problem in a rigorous manner. Furthermore, our wavelet approach is more parsimonious as it requires fewer steps. First, it is not necessary to reverse filter using the GMWs, which are acausal filters since there is zero phase lag when implementing the transformation digitally - analytic wavelets are conjugate-symmetric in the time domain hence their Fourier transform is purely real. By the convolution theorem, convolving the wavelet with a signal amounts to multiplying the signal's Fourier transform by a real-valued sequence; hence, only the amplitude is altered, with zero phase distortion. Second, the wavelet transform naturally returns a complex valued time-series and obviates the need to convert the signal to its analytic representation following the Fourier transform.

3.2. The Generalized Morse Wavelets

The GMWs are described in detail elsewhere (Olhede and Walden, 2002). Briefly, the GMWs are a set of eigenvectors corresponding to the following time frequency localization operator P_DC,β,γ under certain parameterizations of D. Daubechies and Paul (1988) showed that the domain over which the operator can be completely characterized is (in terms of t and f):

$$D_{C,\beta ,\gamma }=\{(t,f)\in R^2:{\left(\frac{t}{C_2}\right)}^2{\left(\frac{C_1}{|2\pi f|}\right)}^{2\gamma -2}+{\left(\frac{C_1}{|2\pi f|}\right)}^{2\gamma }+1\le 2C{\left(\frac{C_1}{|2\pi f|}\right)}^{\gamma }\},$$

where C₁ and C₂ are parameters defined by Olhede and Walden (2002). For particular parameter choices, P_DC,β,γ admits a complete orthonormal eigenbasis. For example, when D corresponds to a disc in time-frequency space, the eigenfunctions are equal to the scaled Hermite functions. Olhede and Walden (2002) extend this analysis to affine time-scale space and show 1) the resulting eigenfunctions are equal to the class of GMWs and 2) the GMWs outperform the Hermite functions in energy concentration except for the special cases for which γ = 1.

Ordering the GMWs by k=0,1,…n (where λ₀ is the principal eigenvalue) we have the following definition of the k_th GMW in the frequency domain:

$${\psi }_{k;\beta ,\gamma }^{+}(f)=\sqrt{2}H(f)A_{k;\beta ,\gamma }{(2\pi f)}^{\beta }{e}^{-{(2\pi f)}^{\gamma }}{L}_k^c(2(2\pi f)\gamma ),$$ (1)

where H(f) is the Heaviside step function, which sends the negative frequency components to zero, “A” and “c” are parameters defined in Brittain et al. (2007) and Olhede and Walden (2002) and $L_k^c(\ast )$ is the Laguerre polynomial:

$$L_k^c(x)=\sum _{m=0}^k{(-1)}^m\frac{\mathrm{\Gamma }(k+c+1)}{\mathrm{\Gamma }(c+m+1)\mathrm{\Gamma }(k-m+1)}\frac{x^m}{m!}$$

Γ(*) is the gamma function. ${\psi }_{k;\beta ,\gamma }^{+}$ is the analytic GMW, that is ψ⁺ is zero for all f < 0. The analytic wavelet is appropriate for real-valued functions. For signals that are complex in the time domain, both the analytic and anti-analytic wavelet - ${\psi }_{k;\beta ,\gamma }^{-}(t)=\overline{{\psi }_{k;\beta ,\gamma }^{+}(t)}$ or equivalently ${\psi }_{k;\beta ,\gamma }^{-}(f)={\psi }_{k;\beta ,\gamma }^{+}(-f)$ (where *¯ denotes complex conjugation) - are required to analyze the signal. As we are only concerned with real-valued signals we consider the analytic GMWs from here onward. The time-domain representation of the wavelet transformed signal is easily obtained utilizing Eq. 1 and the convolution theorem. Importantly, P_DC,β,γ is self-adjoint and, assuming D is bounded, P is compact; hence, by the Hilbert-Schmidt theorem the eigenbasis of P is orthonormal and complete. The orthogonality of the wavelets decorrelates the spectral estimators derived from any two eigenfunctions corresponding to non-identical eigenvalues and allows us to treat the convolution of a signal with any GMW as an independent estimate of the signal's energy. Here we consider only the 0th GWM, which corresponds to the largest eigenvalue of P and has optimal energy concentration properties. Note that when assessing power and coherence, the GMWs can be used in an analogous manner to Thomson's multitaper method (Thomson, 1982) and provide a smoothing method in time frequency space that does not require the use of overlapping data segments (see Brittain et al. (2007) for details on generating smoothed spectrograms using the GMWs). Though higher order wavelets are not considered here, they are useful for researchers interested in smoothed spectral estimators in time-frequency space. A representative GMW, corresponding to the principal eigenvalue of P_DC,β,γ is shown in both the time and frequency domains in Fig. 1.

Figure 1.

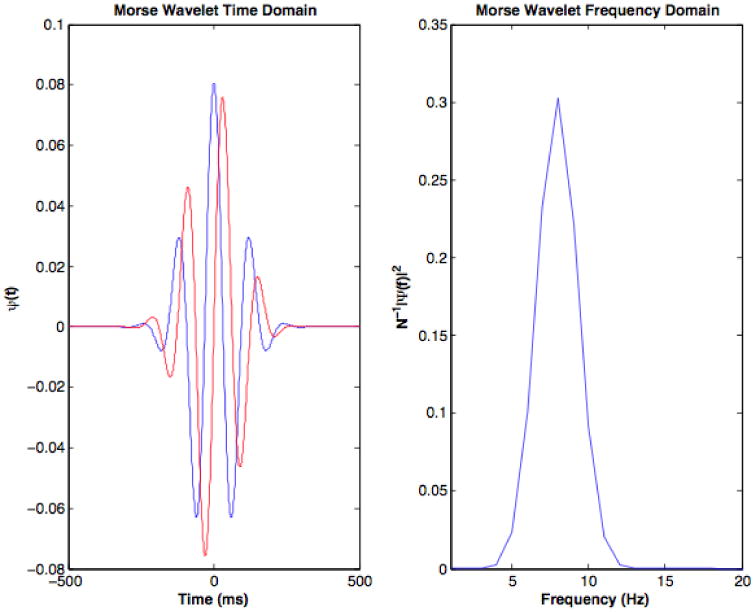
A 0th order GMW in the time (left) and frequency (right) domains. In the time domain, blue and red curves indicate, respectively, the real and imaginary parts of the wavelet.

3.3. Estimating CFC from the GWMs

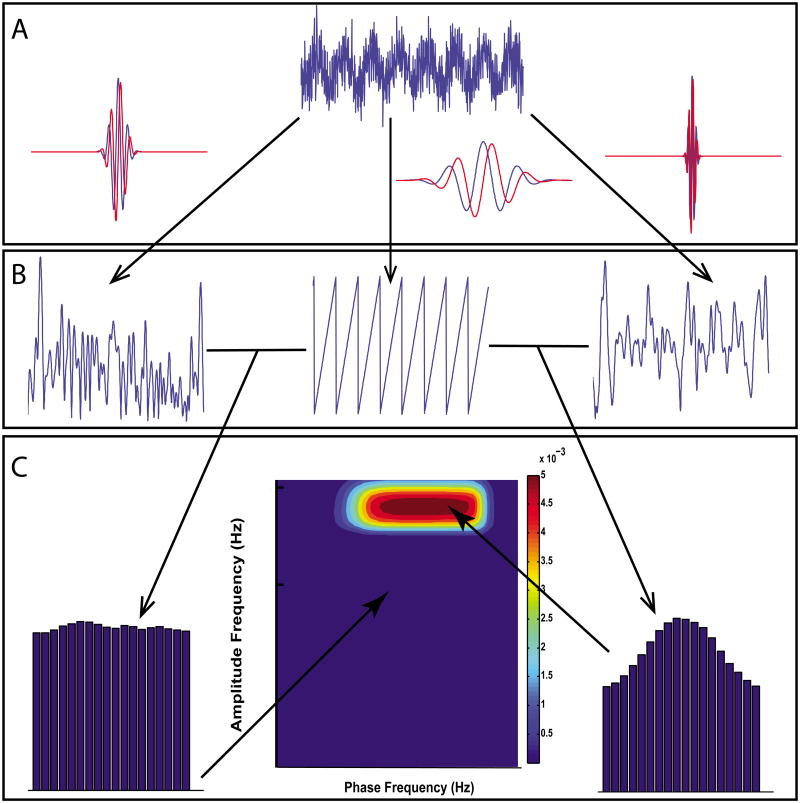
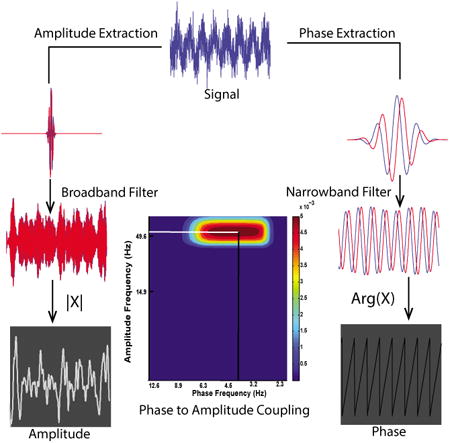
Estimating CFC from the GMWs follows naturally from the fact that the wavelet transform of a signal (in the time domain) assigns an amplitude and phase value to each time point, as does the analytic representation. Moreover, as each scaled wavelet acts as a band-pass filter, we are able to convert the signal to an analytic representation and filter it in a single step. Note that “scale” is inversely related to oscillatory frequency since larger scales produce broader wavelets in time space. Broadening or shortening the wavelet increases or decreases the wavelength, respectively, without altering the number of complete cycles. The software used in this analysis takes a user-defined upper and lower frequency, creates a logarithmically spaced frequency vector, and scales the wavelets such that the peak of the wavelet's Fourier transform occurs at the frequency of interest. Once we have the wavelet transforms across all frequencies under analysis, we proceed to construct the MI per Canolty's method. A visual flow of computation is provided in Fig. 2.

Figure 2.

Scanning multiple frequency bands for CFC using the GMWs. The simulated signal displayed at the top exhibits cross-frequency modulation from 4 Hz to 50 Hz. The signal is separated into component frequencies via the wavelet transform (A), where blue and red curves indicate, respectively, the real and imaginary parts of the wavelet. In B we show extraction of amplitude (first and third trace) or phase information (middle trace) from 3 bands with central frequencies - from left to right - of 15 Hz, 4 Hz, and 50 Hz. The 4 Hz component is converted to a phase series and the 15 Hz and 50 Hz components to amplitude series. Combining amplitude and phase information into a normalized histogram and computing the MI corresponding to each frequency combination measures CFC for each phase/amplitude pair.

3.4. Validation of the Method

To confirm that our method correctly detects CFC when present, we applied the algorithm to a simulated signal with known phase to amplitude coupling between the theta and gamma bands. We used simulated data generated using the methods of Tort et al. (2010). Briefly, CFC between two frequencies of interest is governed by a single parameter, χ ∈ [0, 1], that is inversely proportional to the magnitude of CFC. This method allows the end user both to control the magnitude of CFC and to produce either unimodal or multimodal coupling. Multimodal coupling occurs when the phase-amplitude histogram exhibits more than one peak over the phase range [0,2π], that is the modulation of the carrier wave is distributed across multiple phases of the modulator.

The technical details of the model are given in the appendix to Tort et al. (2010). The model developed by Tort and colleagues allows the end user to generate both unimodal and multimodal coupling. Using this model, we examined the behavior of our method over a range of coupling strengths, and tested its sensitivity to multimodal interactions. Note that Tort et al. provide two approaches to modeling CFC. One uses only element wise multiplication of the carrier signal by a time-varying amplitude governed by χ and the modulator frequency. The simulated amplitude envelope is given by:

$$A_{f_A}(t)={\overline{A}}_{f_A}\frac{(1-\chi )\mathit{sin}(2\pi f_{P}t)+1+\chi }{2},$$ (2)

and the simulated signal by:

$$x(t)=A_{f_A}(t)\mathit{sin}(2\pi f_{A}t)+{\overline{A}}_{f_P}\mathit{sin}(2\pi f_{P}t)+W(t)$$

where Ā_fA and Ā_fP are constants that determine, respectively, the maximum amplitude of the carrier and modulator components (for all simulations we set these to 1). W(t) is Gaussian white noise.

The second, which is used to model multimodal coupling, uses a mixture of Gaussian functions g(f_pt), where

$$g(f_{p}t)=\frac{\mathrm{\Phi }[s(f_{p}t)]-\mathit{min}[\mathrm{\Phi }(s)]}{\mathit{max}[\mathrm{\Phi }(s)]-\mathit{min}[\mathrm{\Phi }(s)]},$$

and the amplitude envelope is given by:

$$A_{f_A}(t)={\overline{A}}_{f_A}[(1-\chi )g(f_{p}t)+\chi ].$$

g(f_pt) is a normalized Gaussian function and Φ is a standard Gaussian distribution. For all simulations, we set the variance of Φ to 1, although one can modify the variance across simulations if desired (Tort et al., 2010). Finally, s is a sawtooth function oscillating at f_p Hz. Multimodal coupling is generated by mixing Gaussian functions that are identical except for variations in the phase lag of s. We implemented the model developed by Tort and colleagues to generate multiple simulated “trials” with a random phase lag added to the modulator and carrier component of each pseudo-trial. This approach allows us to treat each pseudo-trial as a separate realization of the same underlying stochastic process.

We also modeled non-stationary coupling by replacing the sine function in Eq. 2 with an order α chirp, c(x) = sin(2πf_Pt^α), to explore the behavior of the GMW MI when the modulation is non-constant over time. This is of particular interest here since an advantage of wavelets is their utility in resolving time-localized variations in signals.

3.5. Determining Statistical Significance

To determine statistical significance for each phase-amplitude pairing, we permuted the phase and amplitude information across trials following the approach of Tort et al. (2008). We permuted the phase and amplitude information 200 times. For each randomization the phase information obtained from the ith trial is randomly matched with the amplitude data from the jth trial, where i and j are pseudorandom integers. This procedure retains the global statistical properties of the data while disrupting the phase-amplitude concordance and generating a sequence of MIs expected under the null hypothesis that phase-amplitude coupling is due to chance. To obtain p values for each phase-amplitude pair we converted the corresponding vector of random MI values to an empirical cumulative distribution function and then found p values based on the non-randomized MI's location in the cumulative distribution of the randomized MIs.

To control for multiple comparisons we applied false discovery rate (FDR). Instead of modifying the critical p value for all tests based on the number of comparisons, the FDR approach controls the proportion of incorrectly rejected true null hypotheses (Benjamini and Hochberg, 1995). A free parameter determines the maximum percentage (e.g. 5%) of true null hypotheses that are incorrectly rejected. We applied the Benjamini-Yekutieli algorithm (Benjamini and Yekutieli, 2001) using code written by David M. Groppe available on the Mathworks file exchange. We validated this approach using simulated data. Furthermore, this method detects significant CFC between frequency bands already shown to participate in effective corticostriatal connectivity in a previous study (Nakhnikian et al., 2014).

4. Results

4.1. General Observations

Our method reliably detects CFC in a simulated signal and our permutation algorithm detects CFC above chance when phase-amplitude coupling occurs and incorrectly rejects less than 5% of true null hypotheses when there is zero coupling and the critical FDR value is 0.05. Furthermore, we show that cross-frequency coupling occurs between two frequency bands that account for significant and near-significant Granger causality between M1 and dStr based on prior analysis of these data. Power spectral densities of signals recorded in M1 and dStr showed a peak at 2 Hz (see Nakhnikian et al. (2014) for representative power spectra and coherence plots). The presence of a peak at the phase frequency is a requisite condition for reliable CFC analysis (Aru et al., 2014). A previous analysis of these data using bootstrapping and multiwavelet methods revealed consistency of the spectral estimates among trials and animals (Nakhnikian et al., 2014).

4.2. Results from Simulated Data

We showed that our algorithm reliably reconstructs the known CFC in a simulated data set. We set the modulator frequency to 4 Hz and the carrier frequency to 50 Hz. This selection ensures that the results are not confounded by harmonic interactions between the phase and amplitude components.

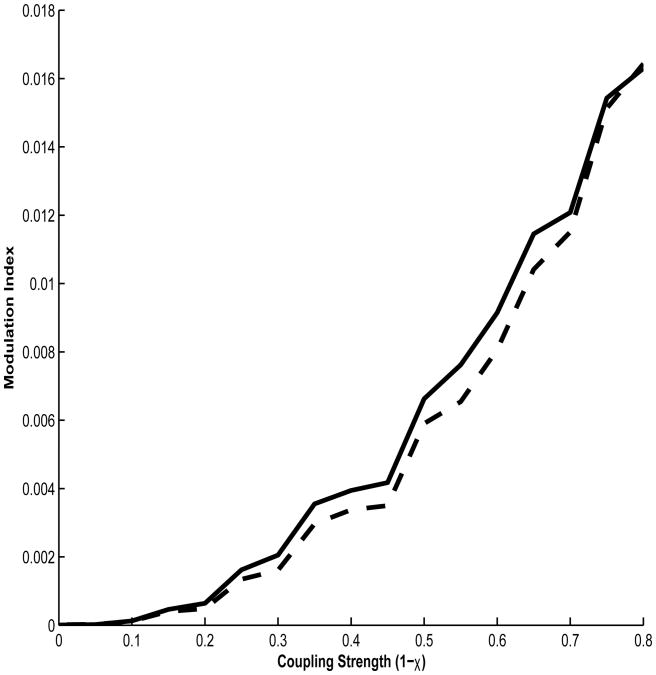
We tested our method's sensitivity to CFC, when present, by varying χ from 0.5 to 1 and computing the MI using both the GMW and Tort methods. We found excellent agreement between the MIs obtained from these methods over this range of the coupling parameter (Fig. 3).

Figure 3.

MIs between a simulated modulator and carrier frequency generated using both the GMW (solid line) and Tort methods (dashed line) across varying values of the coupling parameter χ, which is inversely proportionate to modulation strength. Note the agreement between these methods.

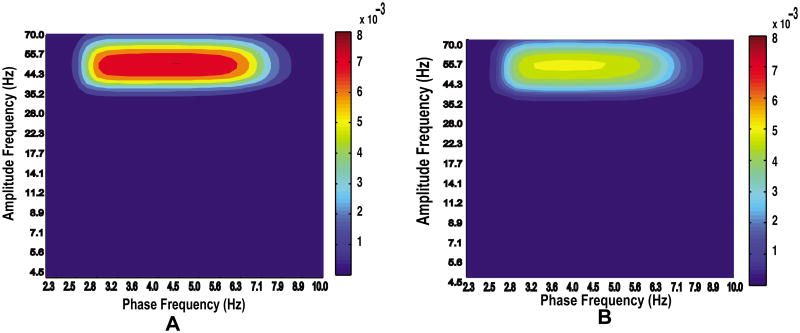
We then generated comodulograms from simulated signals exhibiting unimodal and bimodal coupling (Fig. 4). Our results show that the GMW MI, like the Tort MI, is sensitive to multimodal coupling.

Figure 4.

Comodulograms generated from data exhibiting unimodal (A) and bimodal (B) coupling. Note that, in agreement with previous results reported by Tort et al. (2010), CFC is reduced for bimodal coupling when the value of χ is the same for both simulations.

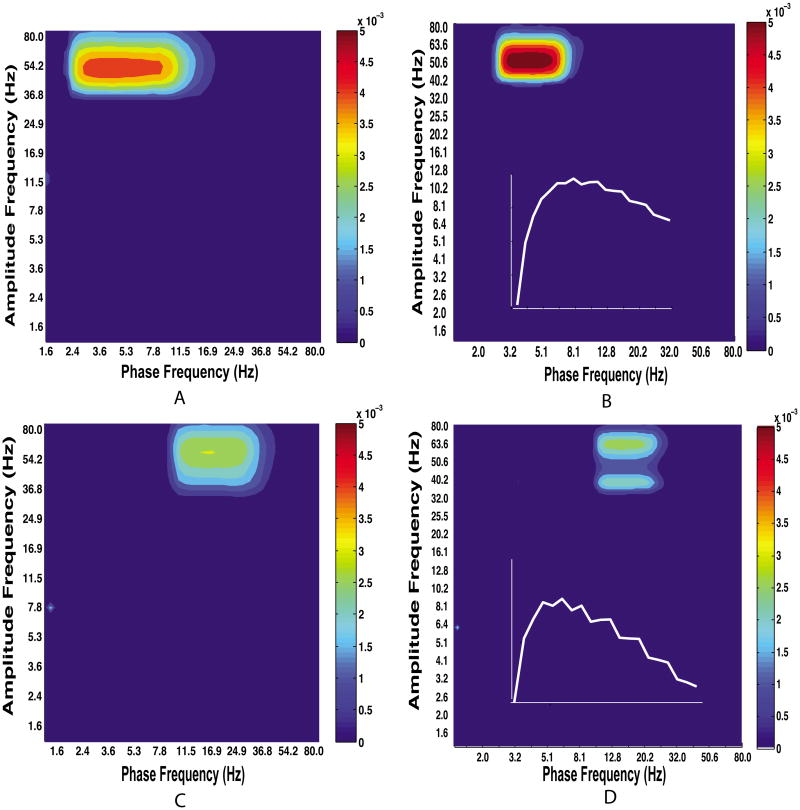
To demonstrate the influence of β on the GMW estimation of CFC we estimated the CFC between the known modulator and carrier signal in simulated data obtained with varying values of β (Fig. 5). Note that the effect of changing β depends upon the frequencies participating in CFC, at least for this particular model.

Figure 5.

The effect of β on simulated cross-frequency coupling. Row 1 shows two comodulograms with equal coupling strength from 4 to 50 Hz with β = 2 (A) and β = 6 (B). Note that the results are generally similar for different values of β in the first row; this is the case for low frequency modulators. Row 2 shows the effect of increasing β when CFC involves a higher modulator frequency. Here, increasing β from 2 (C) to 6 (D) creates splits in the peak of the comodulogram, likely due to increased spectral resolution resulting in partitioning of the carrier frequency and side-bands into distinct frequencies. Note that the frequency axes are non-identical for different panels because changing the value of β changes the frequency resolution of the corresponding wavelet. Insets in the second column show the peak MI obtained for different values of coupling strength with 4 Hz modulator and 50 Hz carrier. The curve for χ = 0.5 is shown in C and the one for χ = 0.07 in D.

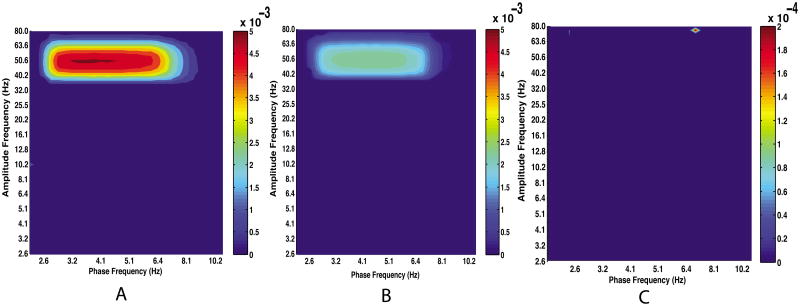
To show that the FDR approach correctly accepts all but a tolerable proportion (e.g. 0.05) of null hypotheses when no MIs are above chance, we compared three simulations with varying coupling strengths, including one in which there is no CFC (Fig. 6). When CFC is not present, the FDR method incorrectly rejects fewer than 5% of all null hypotheses.

Figure 6.

Comodulograms generated from simulated data with, from left to right, strong coupling, weak coupling, and no coupling. FDR control was applied to determine MIs above chance with correction for multiple comparisons. MIs below change are set to zero. Note that the FDR algorithm returns some “significant” MIs even when no coupling is present (MIs “above chance” when CFC is absent are circled in red in panel C). The proportion of incorrectly rejected true null hypothesis is approximately 0.01-0.03 across different simulations with no CFC, a tolerable false discovery rate. Because the FDR returns some false positives in general, it is necessary to inspect the data to ensure that the signals' power spectral densities support the hypothesis that CFC is present (See Fig. 7). Panel C is displayed on a different color scale so that the false positive values are visible.

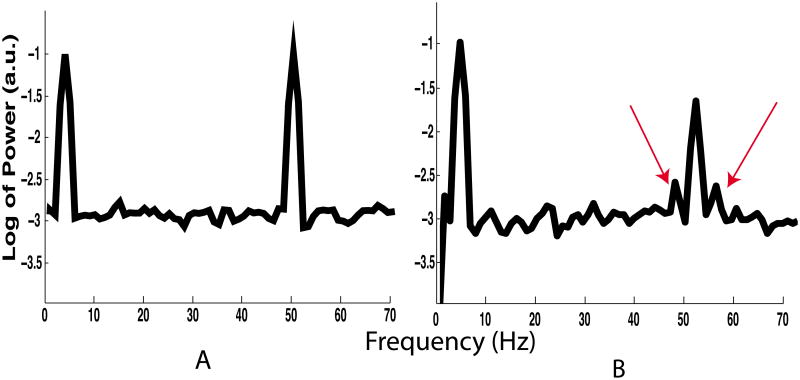
Note that significant modulation indices are not alone sufficient for the presence of CFC since there will almost surely be some false positives for any given analysis. With that in mind, we recommend inspecting the power spectral density of each signal to ensure that there is a clear peak at the putative modulator frequency. Furthermore, when the signal-to-noise level permits, it is advisable to inspect the frequency regime near the putative carrier frequency to ensure for side-bands arising from cross-frequency interactions (Fig. 7).

Figure 7.

Power spectral densities generated using simulated data in which CFC is absent (A) and present (B). Arrows in B indicate side-bands arising from CFC. The 4 Hz component modulates the 50 Hz component in B. The spectrum in Fig. 7 A was generated using the same simulated data analyzed to produce Fig. 6 C. Note that, although some MIs are above chance according to the permutation with FDR correction method, the power spectra corresponding to non-zero coupling do not show a clear modulator peak, nor side bands around the putative carrier frequency.

Finally, we tested the robustness of our method when non-stationary CFC is present in the system. We explored a variety of non-stationary modulators for which the chirp order varied from 1 to 3. To control for the effects of modulator frequency and band-width, we repeated the analysis with modulator frequencies ranging from 4 to 8 Hz and band-widths of the filter used to obtained amplitude components (for the Tort MI) from 4 to 20 Hz; the GMW MI is more accurate for high order chirps regardless of the analysis parameters. We used a chirp with a starting frequency of 8 Hz and a carrier signal at 53 Hz. We found that our method is more accurate in detecting the coupling present in this system. Though both methods return inaccurate results for chirp orders greater than 3 the Tort MI fails to detect the known CFC for low values of the chirp order whereas the GMW MI is accurate, given this particular model, for values up to and including 3. Representative results for a quadratic chirp are shown in Fig. 8. Importantly, we obtained superior results when β = 2, which is expected since the GMWs obtain better time resolution at low values of β. Our method is less accurate in detecting non-stationary CFC when β = 6. We address this issue in more detail in the discussion.

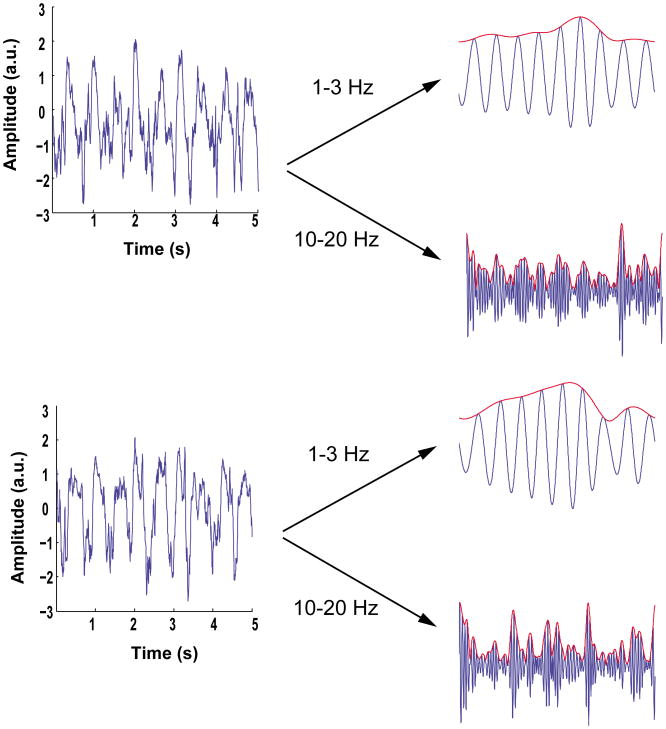
Figure 8.

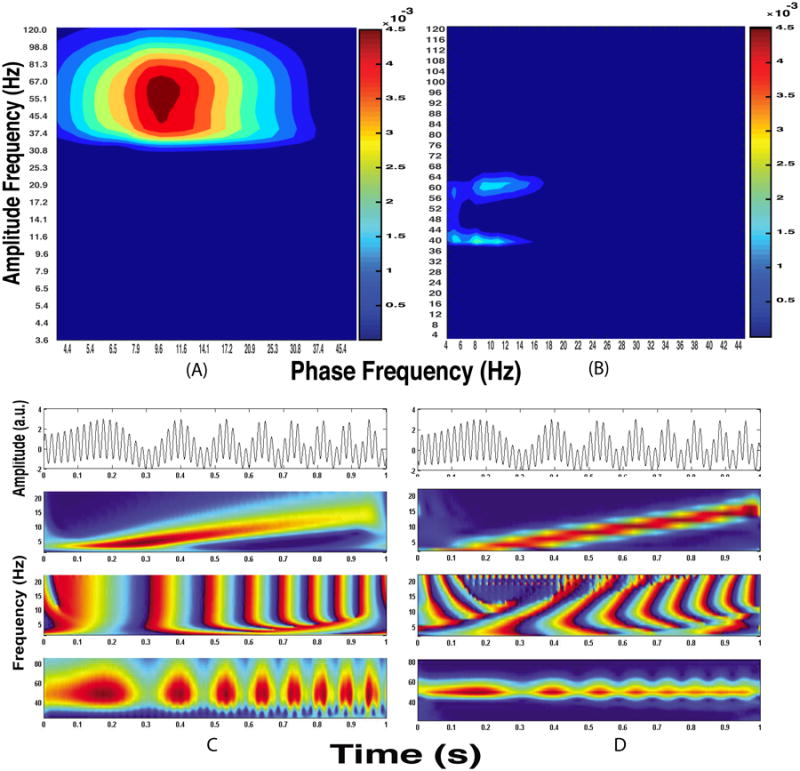
A comparison of CFC analysis of a non-stationary signal using the GMWs (left column) and Hilbert Transform (right column) approaches. The signal was generated by coupling the 53 Hz amplitude to the phase of a quadratic chirp with a starting frequency of 8 Hz and injecting unit amplitude Gaussian white noise. The upper row shows chance-corrected comodulograms generated using the GMW (A) and Tort (B) MIs. Note that the frequency axes are non-identical for different comodulograms because the GMW method using logarithmic frequency spacing, whereas the Tort method uses linearly spaced frequencies. The entries in the lower row shows, from top to bottom, representative 1 s epochs of the signal and time-frequency representations of low frequency energy, low frequency phase, and high frequency energy derived using the GMWs with γ = 3, β = 2 (C) and Hilbert transform (D). For clarity, we show noise-free signals in C and D.

4.3. Results from Empirical Data

We found CFC between the 1-2 Hz phase component and the 10-15 Hz amplitude component. Representative single-trial traces and corresponding wavelet filtered data are shown in Fig. 9 and the comodulograms in Fig. 10. This effect was present within and between signals recorded in both M1 and dStr. In a previous analysis of these data (Nakhniian et al., 2014) we showed that the 1-2 Hz component of the co8rtical and striatal LFPs accounts for a significant portion of spectral Granger causality between these signals and that Granger causality at the 10-15 Hz component approached significance.

Figure 9.

Representative 5 s epochs of LFP data recorded from M1 (top row) and dStr (bottom row) with wavelet transformed data (blue) and the corresponding amplitude envelope (red) in the right column. The bandwidths of the wavelets are beside the corresponding arrows.

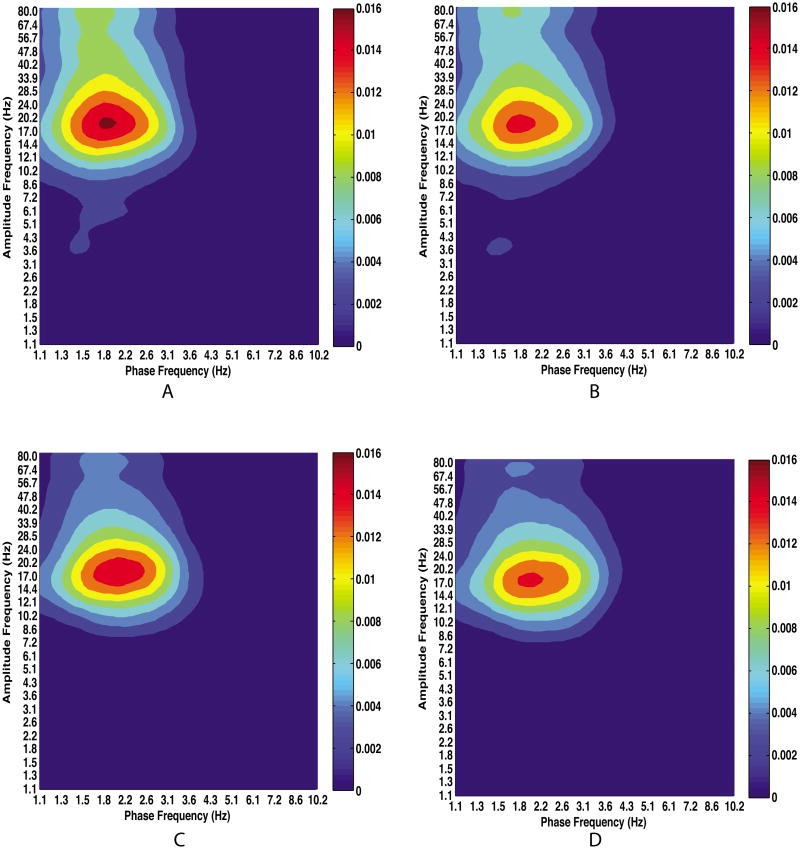
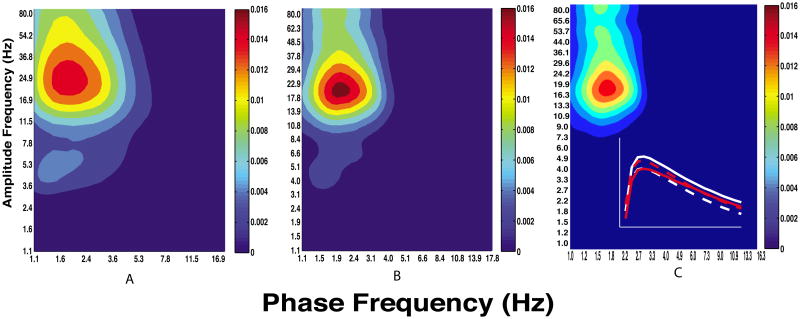
Figure 10.

Comodulograms showing CFC between all pairs of structures during anesthesia. Plots show corticocortical (A), corticostriatal (B), striatocortical (C), and striatostriatal (D) coupling. Note that CFC is strongest in frequency bands involved in striatocortical functional and effective connectivity reported elsewhere (Nakhnikian et al., 2014). All non-zero values are above chance at the 0.05 significance level.

In addition to our analysis of corticostriatal CFC, we analyzed the effect of varying β on the empirical results using intracortical CFC as a representative data set. Changing β affects the frequency resolution and shape of the comodulogram but does not substantially change the modulator/carrier pair returned by our analysis. The peak MI obtained from these data exhibits the same variation with different values of β as do simulated data (Fig. 11 inset). Note that since our results include only a low frequency modulator we are not able to explore the effects of variations of β on the MIs for high frequency modulators using biological data.

Figure 11.

The effect of varying β on empirical data. Here we show the same comodulogram, displaying intracortical CFC for β values of 2, 5 and 8 (left to right). Frequency axes are non-identical for different comodulograms since high values of β produce increased spectral resolution. Also note that though the shape of the comodulgram changes for different values of β each shows a similar overall pattern: delta phase to high alpha/beta amplitude coupling. The inset in the third panel shows peak CFC across different values of β for corticocortical (solid white) corticostriatal (solid red) striatostriatal (dashed white) and striatocortical (dashed red)

Finally, we analyzed the M1 LFPs using a method developed by Pittman-Polletta et al. (2014) that is also designed to address some of the problems of established CFC analysis. Briefly, the method of Pittman-Polletta et al. uses adaptive signal decompositions to extract fast and slow components from a signal. We found significant corticocortical CFC using this approach that generally agrees with the results produced using the GMW approach (Fig. 12). Note that Pittman-Polletta et al.'s algorithm returns a slightly lower modulator frequency and an broader range of carrier frequencies; however, both methods detect the same overall pattern, with the phase of the delta components modulating the amplitude of the beta bands. See the discussion for more details regarding this method.

Figure 12.

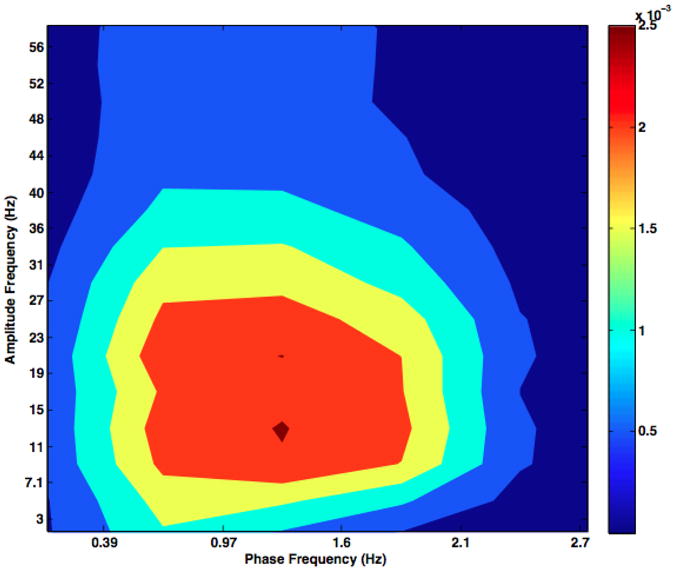
Intra-structural CFC in M1 quantified using the method of Pittman-Polletta and colleagues. The results obtained using this method are non-identical to ours,though the both show CFC between the delta phase and beta amplitude of the coritical signal. Note that the frequency axes on comodulograms differ between those generated using the GMW and those generated with the Pittman-Polletta method because these methods do not identically partition frequency space.

5. Discussion

5.1. Overview

Our algorithm reliably detects simulated CFC. We have also demonstrated the utility of our method by applying it to data gathered at both a cortical and extra-cortical site in anesthetized rats. We conclude with possible applications of our method, theoretical considerations and pitfalls of which the end user should be aware, and a discussion of remaining problems in CFC detection and future avenues of research.

5.2. Implications of Empirical Results

Once we demonstrated that our method reliably estimates the known CFC in simulated data, we applied it to data gathered in rats under ketamine-xylazine anesthesia and showed that, in keeping with previous work (Thompson et al., 2014), NMDA-antagonist induced anesthesia is accompanied by CFC. In particular Thompson et al. report significant CFC within cortex when rats are under isoflurane, but not dexmedetomidine, anesthesia. It is important to note that there are substantial differences between these studies. In particular we analyze different structures, use different anesthetics, and found a modulator frequency that is twice that of the infraslow frequency reported by Thompson and colleagues; nevertheless, the presence of intracortical CFC under NDMA antagonist-induced anesthesia in both studies is worth considering. Thompson et al. suggest that isoflurane might produce CFC via the well-established tonic bursting induced in thalamic neurons by NMDA-antagonists. As both isoflurane and ketamine belong to this category, our results along with those of Thompson et al. provide converging evidence that CFC is a neural correlate of anesthesia induced by attenuated NMDA receptor activation. It is possible that both ours and Thompson's results reflect an epiphenomenal correlate of anesthesia that emerges from a primary effect of the drug, specifically increased thalamic bursting, which generates network wide-oscillations giving rise to CFC with no functional significance. Alternatively, CFC might play a role in maintaining anesthesia. Testing this hypothesis will require assessing CFC in animals at varying levels of anesthesia. The issue would be further clarified by stimulating the thalamus in an anesthetized rat to disrupt tonic bursting. If such a manipulation has an effect on both the CFC we report here, as well as the animal's response to the drug, it would suggest that CFC in this circuit is functionally related to anesthesia. Such studies would provide useful data as the mechanisms of anesthetic are still poorly understood.

We note that, though there is some variation in the CFC reported both within and between MI and dStr, the effect is largely symmetric; maximum CFC values are within a comparable range for all analyses, and the participating frequencies are the same. In previous work, we not only showed that theta and alpha oscillations contribute to the causality spectrum between M1 and dStr of anesthetized rats, we also show that this effect is asymmetric (Nakhnikian et al., 2014). Though we previously reported asymmetric connectivity between M1 and dStr, while here reporting symmetric CFC, there is no reason to expect that CFC between these bands would also be asymmetric as Granger causality and CFC are fundamentally different metrics. Unlike Granger causality, CFC is not an effective connectivity measure since it quantifies correlated activity and not directed influence. Furthermore, Granger causality by construction cannot detect interactions across distinct frequencies. In spite of the fundamental differences between Granger causality and CFC analysis, it is noteworthy that the theta and alpha bands participate in anesthesia-induced cortiostriatal coactivation as measured by these two distinct metrics.

5.3. Advantages of our method and potential applications

The wavelet approach we develop here overcomes the multiresolution problem inherent in any time-frequency analysis that employs a fixed bandwidth across all spectral regimes of interest. Other researchers have proposed a bandwidth varying approach to CFC analysis that has distinct strengths and weaknesses relative to ours (Berman et al., 2012). The method of Berman et al. rigorously accounts for the effect of the modulator frequency on the location of the side bands surrounding the carrier frequency. Using Berman's method, the bandwidth of the amplitude filter is given by f_c ± f_m, where f_c is the carrier (amplitude) frequency and f_m is the the modulator (phase) frequency. An advantage of Berman's method is that it minimizes the probability of type-II error by ensuring that existing CFC is not undetected due to a filter that is too narrow to capture the side bands. This advantage comes at the cost of inconsistent time-frequency resolution; moreover, Berman's method requires a priori knowledge of the modulator and carrier frequency, which is not always available. Our method is thus suitable for exploratory experiments and, in concert with method such as those of Berman et al., could be used to search for converging evidence of CFC using different analytic techniques that complement one another's strengths and weaknesses.

Our method also requires fewer computational steps than most existing CFC detection algorithms. Note that, unlike LLS filters, the GMWs admit closed form expressions for any given paramaterization and frequency range of interest. Thus, there is no need to fit a model to each trial in order to construct the filter. Furthermore, using a computational implementation of an analytic wavelet transform we are able to produce a zero-phase lag convolution, obviating the need to reverse filter the data. Finally, the GMWs return a complex valued analytic signal from which we can infer the instantaneous amplitude hence there is no need to analyze the signal's Hilbert transform.

5.4. Pitfalls and Limitations of the Method

Our method has a number of substantial advantages over established CFC detection algorithms; however, it is not without limitations and we present this method to complement, rather than replace, existing analysis methods. Here we discuss the limits of our method and provide recommendations regarding best practices given the behavior of the GMWs.

Parameter choice is critical when constructing the family of wavelets to be used in CFC detection. We recommend setting γ to 3 and leaving it unaltered as the GMWs achieve optimal energy localization in time-frequency space when γ = 3 (Lilly and Olhede, 2009).

β is the critical parameter and must be chosen with care. Note that certain results in the analysis of the GMWs depend on the restriction β > (γ – 1)/2 (Olhede and Walden, 2002). See Lilly and Olhede (2009) for a thorough discussion of the effects of various parameter choices on the GMWs. The practical result of increasing β is that the wavelet transform obtains better frequency resolution at the cost of reduced temporal resolution. As there does not exist, to our knowledge, a rigorous theoretical justification for a particular choice of β, we suggest exploring the behavior of the MI over the parameter space of β and avoid regimes over which the MIs returned by the algorithm vary substantially. Furthermore, as noted in the results, optimal value of β depends upon the particulars of the data. Data containing high modulator frequencies may be susceptible to spurious separation of peaks in the comodulograms for higher values of β, although we cannot say whether this is the case for empirical as well as simulated data. In particular, we recommend a number of preliminary steps prior to applying our method. First, inspect the power spectra for multiple low frequency peaks that could suggest more than one modulator is present in the signal. Second, inspect time-frequency plots of the data for evidence that multiple carrier signals are present. Third, inspect the spectrograms for evidence that the modulator frequency is stationary -such information is not available from the power spectra. If multiple, stationary components are present in the data, we recommend setting β to a relatively high value to increase spectral resolution. If there is evidence that the modulator itself is non-stationary we recommend lower values of β to increase temporal resolution.

A major caveat regarding this method is that it necessarily imposes a broad band-pass on higher frequencies. This is an unavoidable consequence of the logarithmic spacing the wavelet transform imposes on frequency space and without varying the band width across frequencies we would violate the uncertainty principle. Though broad-band filters should be applied to high frequency components in order to capture the side bands, our method does not allow the end user to specify a particular bandwidth such that the filter captures only the central frequency and side-bands (the location of the side bands varies depending on the frequency of the modulator). Such flexible bandwidth selection is not possible if we wish to maintain consistent resolution across all frequencies.

Note that broad band-pass filtering has risks when using the analytic representation to extract time-varying phase and amplitude information. Incorporating a wide range of frequencies - both those arising from signal and noise components - might return a mixture of more than one oscillatory function varying with time. This is a concern if multiple spectral peaks occur between the upper and lower bounds of the filter. Mixing of different time-varying functions violates the assumptions underlying Gabor's solution to the problem of resolving instantaneous frequency in band-passed noisy data. The technical reasons for this behavior are discussed elsewhere (Bedrosian, 1962; Boashash, 1992) and also addressed briefly by Aru et al. (2014).

It is important to note that the wavelet transform imposes narrow band filtering on low frequency components, which generally account for the modulator frequency. We strongly advise, however, that if the phase of high frequency components is of interest our method should be applied conservatively and used in tandem with a constant band-pass analysis method. Converging evidence between results returned by our method and those returned by other methods would mutually obviate the shortcomings of each.

Finally, ours is not the only available CFC detection method that addresses the limitations of conventional CFC analysis. For example, Pittman-Polletta et al. (2014) provide a creative approach to CFC detection using the Hilbert-Huang transform (HHT); see the results section for a representative comodulogram generated with this method. The HHT is an iterative process, operating entirely in the time-domain, that decomposes a signal into oscillator-like “intrinsic mode functions” (IMFs). The HHT is sensitive to both non-stationary and nonlinear dynamics. Moreover, in contrast to the Fourier transform, the HHT decomposes the signal according to its characteristic time scales instead of projecting the data onto a predefined space. The only major drawback of the HHT is that it lacks an analytic form and hence the underlying theory is less easily characterized than that of the Fourier and wavelet transforms. It is, nevertheless, a powerful tool. In keeping with our view that converging evidence is critical to CFC analysis given the state of the field, we recommend this method as well as our own for researchers interested in exploratory analyses.

6. Conclusions

We have developed a novel CFC detection method that partly overcomes the problem of bandwidth selection. We validate this method using simulated data in which the phase and amplitude components involved in CFC are known a priori. Applying this method to data gathered in anesthetized rats yielded new results that dovetail with previous work (Thompson et al., 2014; Nakhnikian et al., 2014). Our method is well-suited for exploratory analysis and analysis of large data sets.

Highlights.

We develop a wavelet based cross-frequency coupling detection method

This analysis produces consistent time-frequency resolution

We select a wavelet with zero-phase distortion

We analyze corticostriatal interactions in anesthetized rats