Abstract
This work proposes a novel approach for motion-robust diffusion-weighted (DW) brain MRI reconstruction through tracking temporal head motion using slice-to-volume registration. The slice-level motion is estimated through a filtering approach that allows tracking the head motion during the scan and correcting for out-of-plane inconsistency in the acquired images. Diffusion-sensitized image slices are registered to a base volume sequentially over time in the acquisition order where an outlier-robust Kalman filter, coupled with slice-to-volume registration, estimates head motion parameters. Diffusion gradient directions are corrected for the aligned DWI slices based on the computed rotation parameters and the diffusion tensors are directly estimated from the corrected data at each voxel using weighted linear least squares. The method was evaluated in DWI scans of adult volunteers who deliberately moved during scans as well as clinical DWI of 28 neonates and children with different types of motion. Experimental results showed marked improvements in DWI reconstruction using the proposed method compared to the state-of-the-art DWI analysis based on volume-to-volume registration. This approach can be readily used to retrieve information from motion-corrupted DW imaging data.
Index Terms: Diffusion-weighted MRI, motion tracking, motion-robust MRI, outlier-robust kalman filter, slice registration
I. Introduction
Magnetic resonance imaging (MRI) is a relatively slow imaging technique because of the nature of its acquisition, which relies on exciting the spins of atoms and recording their relaxation times within a spatial encoding scheme. Nonetheless, it is one of the most compelling imaging modalities that has enabled advanced in-vivo analysis of brain activity and neuronal microstructure using techniques such as functional MRI and diffusion-weighted (DW)-MRI. These advanced imaging techniques require relatively long acquisitions that are, consequently, very susceptible to the subject's motion. When possible, subjects and patients are asked to stay still during MRI scans, but motion is inevitable [1], [2].
Extensive research has been carried out on motion-robust sequences and motion correction techniques in MRI; e.g., reviews in [2]–[4]; however, the use of motion compensation techniques is limited by the type and amount of motion that can be compensated for [5], [6], the dependency on the scanner platform and the need for pulse sequence modifications [7]–[11], and/or difficult setup [12]–[18]. Current MRI practice is still based on prevention of motion. In newborns, young children, and patients with limited cooperation, this commonly requires full sedation or general anesthesia, which is time consuming, costly, and is associated with significant risks.
In this paper we seek an approach that does not require prospective planning, pulse sequence modification, or an active or passive motion tracking sensor; but corrects motion at the slice level and aims at extracting as much reliable information as possible from motion-corrupted DWI data. While state-of-the-art DWI analysis is based on volume rejection and volume-to-volume registration for motion correction ([1] and [19] for reviews and comparison), our approach relies on slice-level registration-based motion tracking to compensate for fast and large motion leading to an effective use of imaging data.
Slice-to-volume registration was previously used for motion correction in functional MRI analysis [20], [21] and motion-robust fetal brain MRI [22]–[31], but is not routinely used for motion-robust DWI reconstruction because of technical challenges. Image registration is an ill-posed problem without a guaranteed optimal solution. Slice-to-volume registration is further challenging due to the limited information available in the 2D slice to estimate the 3D mapping to a reference volume, which may also be challenging to obtain or reconstruct for a moving subject. Often, for the registration to be successful, the slice has to be in close proximity to its corresponding spatial location in the coordinates of the 3D image. Previous works have thus used multistage registration schemes to initialize slice-to-volume transformations [26], [27], or parametric models to estimate relative slice positions [25].
We introduce the notion of slice-level registration-based motion tracking in this paper. A number of key features distinguish our proposed method from the current commonly-used motion correction techniques in brain DWI reconstruction. First, we correct motion at the slice-level rather than at the volume level. This gives us higher temporal resolution needed for motion tracking and enables dealing with fast motion. Second, we reinforce slice-to-volume registration by coupling it with a state-space model of motion dynamics. This novel formulation makes the registration robust to noise and image artifacts boosting its accuracy for large motion. Third, we use an outlier-robust Kalman filtering approach to improve the robustness of the technique to registration failures, inaccuracies, and motion-corrupted scans. With these developments, we achieved a purely computational technique that can recover useful information from previously intractable motion-corrupted DWI scans.
The paper follows with a description of the methods in Section II. Section III presents the details of our algorithm for motion-robust DWI reconstruction. The evaluation materials and experimental results are presented in Sections IV and V, respectively. A discussion is followed in Section VI, and the paper concludes in Section VII.
II. Methods
A. Motion Tracking
Our goal is to capture dynamics of subject's motion through slice-level image registration. Each image slice has a time stamp k, which shows the sequence of its acquisition among all t slices. A natural choice to model dynamics of motion is a state-space model. Assuming a finite sequence of observations y1, …, yt, generated by a corresponding sequence of hidden states x1, …, xt that represent the motion, the goal is to estimate the states x ∈ ℜd of a discrete-time dynamic process, which is governed by a stochastic equation as
| (1) |
with a measurement y ∈ ℜm that is
| (2) |
where ωk and νk are process and measurement noise/disturbances and represent uncertainty in the modeling of motion dynamics and measurements, respectively. H in (1) defines motion dynamics relating the states at the previous time step k − 1 to the states at the current step k in the absence of process noise. IS in (2) is a nonlinear function that relates states xk to the measurement yk. In other words, IS(xk) is the image slice corresponding to yk in the coordinates of the base 3D image, i.e., IV. The observation yk can be considered as a vector of gray-scale intensities of the image slice acquired at time step k or any other information extracted from the image reflecting the motion effects. Without loss of generality and since our focus will be on head motion in this study, we assume a 6-parameter rigid 3D transformation here, i.e., d = 6 and x is represented by [θx, θy, θz, tx, ty, tz]T; where t = [tx, ty, tz]T is the vector of translation parameters along x, y and z axes, and θ = [θx, θy, θz] is the vector of Euler rotation parameters about these axes [32].
Using the representation of motion dynamics and measurements in (1) and (2), various linear and nonlinear state estimation techniques can be employed to obtain head motion states based on image slice information over time. We integrated state estimation with slice-to-volume image registration to achieve image-based motion tracking using variants of Kalman filter (KF) for state estimation. Thus, the motion dynamics in (1) can be modeled as
| (3) |
where any change in the states from the previous time step is due to some random movement of the patient modeled by ωk−1. Given that yk in (2) is a vector of gray-scale intensities of the acquired image slice, the output model of IS(xk) will be highly nonlinear. Nonlinear state estimation methods are not as widely available as their linear counterparts and are often difficult to implement and robustly tune the parameters. Hence, we separate the nonlinear output model from the filtering process and rewrite (2) as
| (4) |
in which f(IS(p), yk) is a similarity metric between the image slice acquired at time step k, i.e., yk (image measurement vector), and the corresponding slice in the base 3D volume that is rigidly transformed with parameters p (i.e., IS(p)). Therefore, we first register the base 3D volume to the slice acquired at time step k, and use the resulted Euler transformation parameters (zk) as the measurement vector for the Kalman filtering process to estimate motion parameters. In this formulation, νk represents uncertainties in the estimation of the rigid head motion parameters based on slice-to-volume registration.
There are two main advantages in filter-based inter-slice motion estimation using (3) and (4). First, we initialize slice-to-volume registration at time step k based on the states estimated at time step k − 1, i.e., x̂k − 1. Considering that the time step between slice acquisitions is about 100 ms, which is relatively fast compared to the scale of subject movements, the initialization puts each slice in a very close proximity to the corresponding spatial locations of the 3D image volume. This increases the success rate of the registration algorithm and enables slice-level registration-based motion tracking. Second, we employ an outlier-robust Kalman filter (ORKF) [33] for motion estimation, which accounts for noisy measurements caused by motion-corrupted slices and registration failures. Noisy measurements may occur when fast subject motion results in through-plane motion artifacts or when slice-to-volume registration fails in the boundary of the imaged anatomy due to the lack of sufficient image features.
Similar to the classical Kalman filter, ORKF assumes that the process noise has a Gaussian distribution with a fixed covariance matrix Q (i.e., ωk ~ 𝒩 (0, Q)); but unlike Kalman filter, that assumes measurements are also corrupted by additive white Gaussian noise with a fixed covariance matrix R (i.e.,νk ~ 𝒩 (0, R)), ORKF allows more flexible modeling of uncertainties in measurements in which the noise level may vary over time or the noise may have heavier tail than the Gaussian distribution. The covariance of the measurement noise is therefore not fixed a priori and changes based on the sequential observations over time. The distribution of the measurement noise can be defined as
| (5) |
in which Sk is the covariance of the measurement noise at time step k, sampled from a probability distribution as [33]
| (6) |
where 𝒲 (Λ, s) denotes a Wishart distribution [34] with a d × d precision matrix Λ ⊱ 0 and s > d − 1 degrees of freedom. The prior mean of 𝒲 (Λ, s) is sΛ where s quantifies the concentration of the distribution around its mean. With the definition of the measurement noise model in (5) and (6), the state estimation problem for motion tracking will be robust to outliers. To further strengthen the algorithm, as will be explained in Section III, we identify motion-corrupted slices using an outlier detection strategy and exclude them from motion estimation and DWI analysis.
Algorithm 1.
Pseudo-code of the ORKF-based motion estimation for each slice. is the a priori estimate of the states at time step k given knowledge of the process prior to that time, x̂k is the a posteriori estimate of the states at time step k given measurement zk. and Pk are a priori and a posteriori estimates of the error covariance, respectively. Kk is the Kalman gain. Q and R are the covariance of the process and measurement noise, respectively.
| Input: IV, yk, x̂k−1 | ||
| Output: x̂k | ||
| 1: | slice-to-volume registration: | |
| 2: | ; p0 = x̂k−1 | |
| 3: | predict states: | |
| 4: | ||
| 5: | ||
| 6: | repeat | |
| 7: | update noise: | |
| 8: | δ = zk − x̂k | |
| 9: | Λk = (sR + δδT + Pk)/(s + l) | |
| 10: | update states: | |
| 11: | ||
| 12: | ||
| 13: | ||
| 14: | until converged | |
| 15: | return x̂k | |
Algorithm 1 shows an implementation of the outlier-robust slice-level registration-based motion estimation in pseudo-code. Each slice in the acquisition order is first registered to the reference volume to compute zk. The registration is initialized based on the estimated motion in the previous time step, i.e., x̂k − 1. Then, motion states are computed in an iterative algorithm to compute x̂k based on zk. The process of motion estimation using the explained algorithm is applied in two stages on b = 0 and diffusion-sensitized images (b ≠ 0), separately. First, we apply motion estimation to b = 0 images to reconstruct a motion-free isotropic 3D base image shown by B̃0. In the second stage, we use the reconstructed base b = 0 image (B̃0) as the reference volume for motion tracking, where it is registered to the diffusion-sensitized image slices.
B. Image Reconstruction
Estimated motion parameters for each diffusion-sensitized image slice allow us to bring all DWI data to the same coordinates and perform further analysis. Although more complex models of the diffusion signal could be considered to benefit from motion correction, for the sake of simplicity and to focus on the effect of motion correction, we consider reconstruction of the diffusion tensor matrix based on the Stejskal-Tanner (ST) equation [35]. Having a base B̃0 image and Nb≠0 diffusion-sensitized volumes, a diffusion tensor can be estimated at any point of the regular grid in B̃0 by solving ST equation as
| (7) |
where B̃0,regular is the intensity at the regular grid location in B̃0, and Bi,regular is the corresponding intensity at the ith diffusion-sensitized image; gi = [gix, giy, giz] represents the ith diffusion gradient direction in the B̃0 coordinates and b is an imaging sequence dependent constant, which specifies the diffusion sensitivity. Furthermore, D is a 3 × 3 symmetric positive definite matrix representing a diffusion tensor expressed in B̃0 coordinates with elements that are then rearranged in a parameter vector γ = [Dxx, Dxy, Dxz, Dyy, Dyz, Dzz].
Given n ≥ 6 diffusion-sensitized images with noncollinear gradient directions and a constant b-value, diffusion tensors can be estimated by minimizing an objective function as [36]
| (8) |
where n = Nb≠0, and
| (9) |
is an n × 6 design matrix. Moreover, αis are weights for different gradient directions in the objective function. Koay et al. [36] and Salvador et al. [37] proposed to use the observed diffusion weighted signals as weights in the computation of diffusion tensors using a weighted linear least square (WLLS) method. Similarly, we put αi = Bi,regular in (8). By definition of the design matrix (9), the diffusion tensor matrix (D) is not guaranteed to be positive definite, although it is symmetric. A typical solution is to use the Cholesky factorization to define D = UTU where U is an upper triangular matrix with non-zero diagonal elements [36]. Estimating elements of U would guarantee a positive definite D.
In order to compute diffusion tensors using (8), image intensities of the diffusion-sensitized images at the regular grid locations identical to those of the B̃0 image are required. In our case, however, due to motion correction, diffusion-sensitized image intensities are available at some irregularly sampled points in the 3D space of the imaged anatomy. A naive approach to estimate diffusion tensors from these motion-corrected DWI slices is to use scattered data interpolation to reconstruct each predefined diffusion gradient image on a common regular grid and then estimate the tensors based on these images using (8).
This approach has two main limitations: first, due to motion and motion-corrupted slices, sufficient data samples may not be available in a small neighborhood around all of the regular grid points, thus a large neighborhood window size (5 × 5 × 5 or larger) may be needed to compute intensity values at regular grid locations. However, a large neighborhood window size blurs out the reconstructed gradient images and reduces the accuracy of the final diffusion tensor estimation. Smaller neighborhood window in volumes with motion-corrupted slices or using image points of the corrupted slices would produce image artifacts in the reconstructed isotropic 3D image. Second, this approach does not allow compensating for the effect of subject motion on the diffusion gradient directions.
To mitigate these limitations, we eliminate scattered data interpolation in the space of predefined diffusion directions and directly reconstruct diffusion tensors at regular grid points using data from motion-corrected irregular point locations. To this end, we form a data structure of motion-corrected point locations and their properties around any regular grid point in a local neighborhood. Each data point in the data structure is characterized by its position in the B̃0 coordinates, a gray-scale value, b value and a vector of diffusion gradient directions.
Gradient directions recorded in diffusion-sensitized images are in the scanner coordinates. In order to compute the gradient directions in the B̃0 coordinates in (7), not only the orientation of the acquired image with respect to the scanner coordinates has to be considered, but also the estimated rotation for each slice with respect to the B̃0 coordinates from the motion estimation step has to be applied. Let us assume that R0 is the rotation matrix obtained from the image volume orientation and Rm is the rotation matrix estimated for each slice through the slice-to-volume registration-based motion tracking. Then, the diffusion gradient direction for each slice in the B̃0 coordinates, i.e., gi in (7), is calculated as
| (10) |
where g0i is the vector of the ith predefined gradient direction in the scanner coordinates.
Then, similar to (8), given n ≥ 6 diffusion-sensitized points with noncollinear gradient directions, diffusion tensors are computed by minimizing the following objective function
| (11) |
where αi = Bi,irregular, Bi,irregular is the observed diffusion-sensitized signal (gray-scale value) at any motion-corrected point location, and B̃0,irregular is the corresponding non-diffusion weighted signal, which is interpolated from the B̃0 image at that irregular point location. Finally, wi is a weighting factor that is computed as
| (12) |
where ri is the distance between the ith point and the center of the grid point computed in the slice space to account for the slice profile. σ is the standard deviation of a bell-shaped Gaussian function, and n is the total number of points in the neighborhood. The weights (wis) balance the contribution of multiple observed points based on their distance to the location where the tensor is computed.
Algorithm Design and Implementation
The slice-level registration-based motion tracking explained in the previous section is a generic motion correction method, which can be used for processing any set of sequentially acquired 2D MR images (structural, functional or diffusion MRI) from a dynamically moving subject. Our focus in this study has been on DW brain MRI, which involves relatively long duration scans with varying contrast that makes it particularly challenging for such an image registration-based approach.
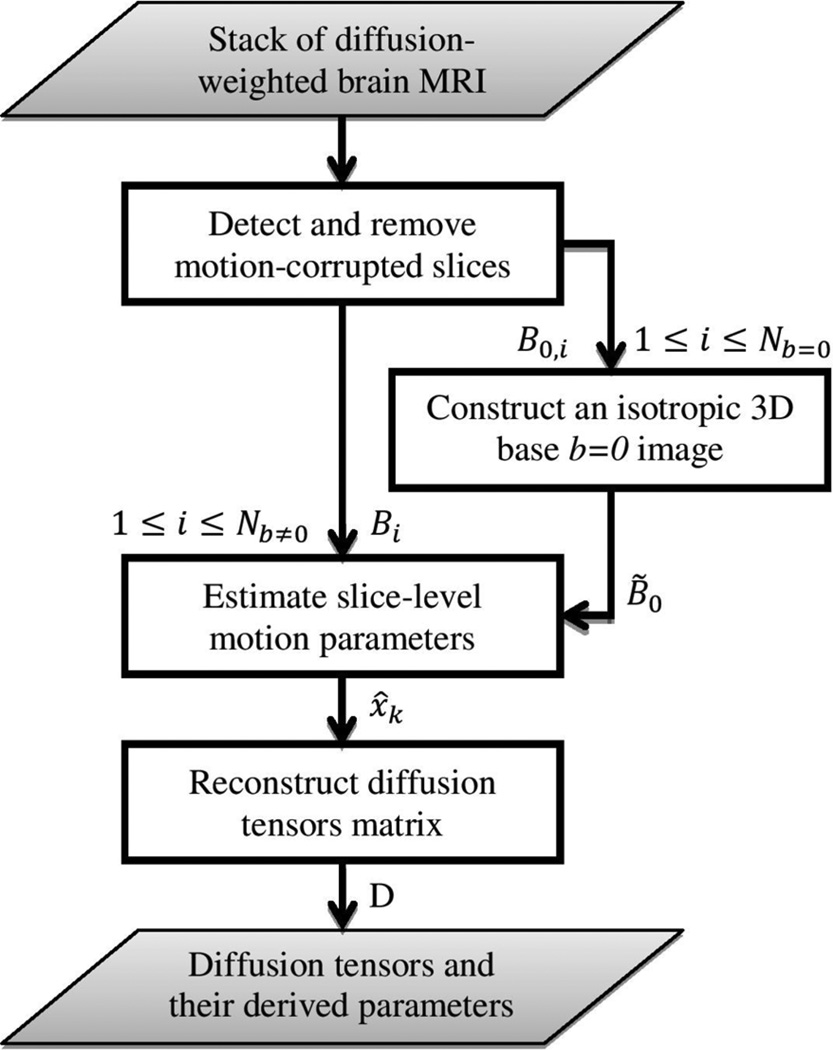
The flowchart of our motion-robust DW brain MRI reconstruction technique is shown in Fig. 1. Given a set of DW brain MRI volumes, first, slices corrupted by through-plane motion were automatically detected using image features. These motion-corrupted slices were excluded from motion estimation and DTI reconstruction. Then, an isotropic 3D image was reconstructed from multiple b = 0 images. The proposed filtering-based motion estimation method was used to correct for the slice-level motion in all b = 0 images and to reconstruct a 3D base image (i.e., B̃0) which is a weighted average of all b = 0 images. In the next step, temporal head motion was estimated using the approach proposed in Section II-A through registering all diffusion-sensitized image slices to the reconstructed B̃0 image. Finally, diffusion tensors were computed in the B̃0 coordinates using image information from all gradient directions. In the following subsections these steps are explained in detail.
Figure 1.
Flowchart of the motion-robust diffusion-weighted brain MRI reconstruction using slice-level registration-based motion tracking.
C. Identification of Motion-Corrupted Slices
In routine image slice acquisitions, diffusion-weighted slices are obtained in an interleaved order to avoid slice cross-talk and spin history artifacts. In an interleaved acquisition adjacent slices are obtained at different time points and patient's head motion results in corruption of image slices independently. In this scheme, artifacts caused by motion can be identified in the out-of-plane views of an image volume in which motion-corrupted slices appear as severe intensity discontinuity along the slice-select direction. In order to automatically identify these slices, we used image features based on inter-slice intensity discontinuity (ISID) [38], computed using a morphological closing filter along the slice-select direction.
Assuming a 3D image, I, with m slices and the image after applying the morphological closing, Ic, the difference image can be expressed as Ĩ = Ic − I. Having the difference image Ĩ,.we used the median and mean intensity of slices, i.e., Ĩk, 0 ≤ k ≤ m − 1, to detect motion-corrupted slices. An image slice was considered a corrupted image if the median intensity in the difference image was greater than zero, i.e., median(Ĩk) > 0 or the mean slice intensity in the difference image was detected as an outlier among mean intensities of all slices. The interquartile rule (IQR) for outliers [39] was used to detect motion-corrupted slices based on the mean slice intensity in the difference image. Volumes with more than 15% corrupted slices were excluded from the analysis.
D. Constructing an Isotropic 3D b = 0 Image
Multiple b = 0 images are often acquired along with diffusion-sensitized images. We reconstruct a base image namely B̃0 in an isotropic regular 3D grid from multiple b = 0 images through an iterative process.
The first b = 0 volume or a b = 0 with least amount of motion is chosen as the reference image at the beginning and is registered to slices in all other b = 0 image volumes using the explained outlier-robust motion estimation method. Then, an isotropic 3D image is reconstructed in the coordinates of the selected b = 0 image using image information of all b = 0 images. This initial reconstructed b = 0 image may not have high quality because of suboptimal motion estimation due to an imperfect initial reference image for registration; therefore, the reconstructed image is used as a new reference for the next iteration of slice-level registration-based motion tracking. Our experiments on various image data sets showed that the algorithm converges after 2–3 iterations and a high-quality B̃0 image is obtained that is used as a reference image in the registration-based motion tracking of all b ≠ 0 images. The image intensity at the center of the regular grid points of the B̃0 image is computed based on all (n) irregular points around the center grid in a 3 × 3 × 3 neighborhood using
| (13) |
where wi is a distance weight based on a Gaussian kernel centered at the regular grid point, computed using (12), where ri determines the distance between the ith point and the center grid point. For the experiments in this study, we set σ = 0.5.
E. Motion Estimation and Reconstruction
The reconstructed B̃0 image was then used as a reference volume to bring all diffusion-sensitized images b ≠ 0 to the same coordinates and calculate diffusion tensors. This was achieved through the techniques explained in Section II. For all practical purposes slice-to-volume registration (SVR) was performed through registering the reference volume to the image slice and inverting the transformation. Estimated motion parameters for each slice were stored for the reconstruction of diffusion tensors in the next step. Similar to the motion estimation in b = 0 images, slices corrupted by through-plane motion were automatically detected and rejected. Motion parameters corresponding to the time step of any motion-corrupted slice were considered equal to those of the previous time step.
All steps of the proposed technique were implemented in C++ using the Insight Toolkit (ITK) [40]. We also used the Computational Radiology Laboratory Toolkit (CRKit) for diffusion MRI analysis, tractography, and the evaluation and visualization of results. For the registration of diffusion-weighted images, we used Mattes mutual information intensity-based image similarity metric [41], a versor type rigid 3D transformation and a gradient-descent approach for optimization.
III. Materials
A. Subjects and Scanning Protocols
For the experiments of this paper we used two sets of DWI data. First, we acquired images from healthy adult volunteers with and without motion. Each image set had 30 gradient directions (Nb≠0 = 30) with 6 b = 0 images distributed in between them (Nb=0 = 6). We obtained one set of DW images while the volunteer kept still during the scan. We used these images as ground truth or gold standard (GS) to evaluate motion correction and tensor estimation techniques. Then, the volunteer was asked to move during the scan. We acquired 2–3 sets of DW images from each volunteer having different motion scenarios (slow vs fast, large vs small motion) including making head rotations up to 30°. In total, 9 sets of DW images with motion were obtained from four volunteers (1–1 to 4–2 in Table III, Table IV and Table VI).
TABLE III.
NRMSE Between the Gold Standard b = 0 Image and the Reconstructed 3D B̃0 Image Using MT-SVR, VVR, and Orig in Nine Volunteer Experiments. The Difference Between MT-SVR and VVR/Orig is Statistically Significant (p < 0.001 in a Paired-Sample t-Test With α = 0.05)
| experiment | MT-SVR | VVR | Orig |
|---|---|---|---|
| 1-1 | 0.0163 | 0.0321 | 0.0373 |
| 1–2 | 0.0177 | 0.0303 | 0.0413 |
| 2-1 | 0.0185 | 0.0350 | 0.0327 |
| 2-2 | 0.0212 | 0.0576 | 0.0546 |
| 2–3 | 0.0198 | 0.0450 | 0.0324 |
| 3-1 | 0.0076 | 0.0209 | 0.0203 |
| 3-2 | 0.0093 | 0.0162 | 0.0113 |
| 4-1 | 0.0290 | 0.0403 | 0.0467 |
| 4-2 | 0.0249 | 0.0368 | 0.0391 |
| mean±SD | 0.0182±0.0067 | 0.0348±0.0123 | 0.0351±0.0131 |
TABLE IV.
Average FA Values in CC, ALIC, and Ventricles in Nine Experiments. Imaging Data Were Obtained From Four Adult Volunteers. The Difference Between MT-SVR and VVR/Orig is Statistically Significant (p < 0.002 in a Paired-Sample t-test With α = 0.05). The Best Values are Highlighted in Bold
| CC (the higher the better) | ALIC (the higher the better) | ventricles (the lower the better) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| experiment | GS | MT-SVR | VVR | Orig | GS | MT-SVR | VVR | Orig | GS | MT-SVR | WR | Orig |
| 1-1 | 0.7048 | 0.5947 | 0.4554 | 0.4095 | 0.5448 | 0.5152 | 0.3966 | 0.2772 | 0.0931 | 0.1023 | 0.1761 | 0.1740 |
| 1–2 | 0.5817 | 0.4200 | 0.3959 | 0.5053 | 0.3366 | 0.2668 | 0.0997 | 0.1850 | 0.1587 | |||
| 2-1 | 0.7722 | 0.6488 | 0.6261 | 0.6535 | 0.5486 | 0.4874 | 0.4772 | 0.4571 | 0.0849 | 0.0808 | 0.0984 | 0.1088 |
| 2-2 | 0.6602 | 0.5421 | 0.3040 | 0.4819 | 0.4068 | 0.3344 | 0.0889 | 0.1201 | 0.1451 | |||
| 2–3 | 0.6645 | 0.5753 | 0.4239 | 0.4967 | 0.4722 | 0.3902 | 0.1004 | 0.1260 | 0.1471 | |||
| 3-1 | 0.6682 | 0.5254 | 0.4817 | 0.4439 | 0.5486 | 0.4892 | 0.3849 | 0.2551 | 0.0874 | 0.1126 | 0.1629 | 0.1318 |
| 3-2 | 0.5363 | 0.5012 | 0.4168 | 0.4882 | 0.3874 | 0.2976 | 0.1203 | 0.1427 | 0.1351 | |||
| 4-1 | 0.7875 | 0.6401 | 0.4893 | 0.4801 | 0.5152 | 0.4779 | 0.4612 | 0.3958 | 0.0761 | 0.0952 | 0.1440 | 0.1928 |
| 4-1 | 0.6551 | 0.4625 | 0.4874 | 0.5072 | 0.3766 | 0.3170 | 0.0932 | 0.1405 | 0.1587 | |||
| mean | 0.7375 | 0.6119 | 0.5060 | 0.4461 | 0.5428 | 0.4943 | 0.4111 | 0.3323 | 0.0853 | 0.0993 | 0.1440 | 0.1502 |
| SD | 0.0475 | 0.0511 | 0.0608 | 0.0890 | 0.0067 | 0.0118 | 0.0457 | 0.0647 | 0.0058 | 0.0112 | 0.0259 | 0.0232 |
TABLE VI.
DSC Metric Between Tract Density Images in Nine Volunteer Experiments. The Difference Between MT-SVR and VVR/Orig is Statistically Significant (p < 0.001 in a Paired-Sample t-Test With α = 0.05)
| CC | ALIC/PLIC | |||||
|---|---|---|---|---|---|---|
| experiment | MT-SVR | VVR | Orig | MT-SVR | WR | Orig |
| 1-1 | 0.7486 | 0.5363 | 0.5133 | 0.7674 | 0.5391 | 0.5570 |
| 1-2 | 0.7526 | 0.4716 | 0.4773 | 0.7530 | 0.4972 | 0.5015 |
| 2-1 | 0.7644 | 0.6608 | 0.6905 | 0.7734 | 0.7016 | 0.6968 |
| 2-2 | 0.7645 | 0.5312 | 0.4450 | 0.7588 | 0.5510 | 0.4979 |
| 2-3 | 0.7434 | 0.6038 | 0.5471 | 0.7490 | 0.6365 | 0.5733 |
| 3-1 | 0.6713 | 0.6119 | 0.5787 | 0.6744 | 0.5925 | 0.5364 |
| 3-2 | 0.7080 | 0.6289 | 0.5932 | 0.6769 | 0.6427 | 0.5467 |
| 4-1 | 0.6685 | 0.4953 | 0.5000 | 0.6640 | 0.5029 | 0.5092 |
| 4-1 | 0.7538 | 0.5362 | 0.5112 | 0.7144 | 0.5323 | 0.5421 |
| mean SD |
0.7306 | 0.5640 | 0.5396 | 0.7257 | 0.5773 | 0.5512 |
| 0.0360 | 0.0609 | 0.0692 | 0.0413 | 0.0663 | 0.0569 | |
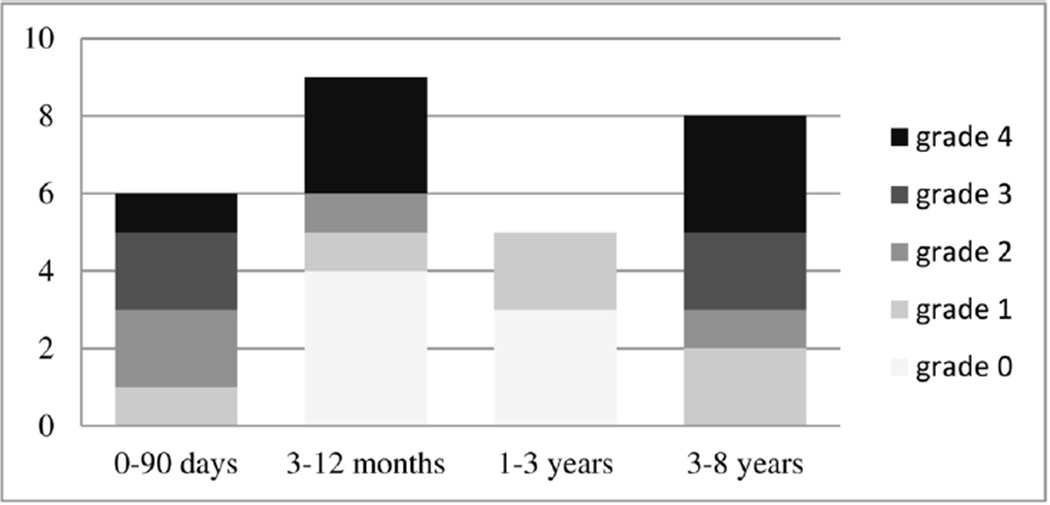
Second, we retrospectively applied our motion correction technique to 28 sets of clinical DWI scans acquired from children and neonates. Each image set had 30 gradient directions (Nb≠0 = 30) with 5–8 b = 0 images distributed in between them. As shown in Fig. 2, these subjects were selected from different age groups (1-day to 8-years old). We also assigned a grade (0–4) to all subjects based on the amount of motion they had during scan. These motion grades are defined in Table I. Among our patient population we chose several cases at different age ranges with different types and amounts of motion to test the performance of the proposed method in various conditions. Access to this data and retrospective analysis of de-identified data were approved by the institutional review board committee.
Figure 2.
Number of clinical MR-DWI scans of children and neonates analyzed in this study per age group with their motion grades.
TABLE I.
Definition of Motion Grades in DWI of Children and Neonates
| motion grade | definition |
|---|---|
| grade 0 | not any noticeable motion |
| grade 1 | small slow/fast motion in a few volumes |
| grade 2 | small/medium slow/fast motion in a few volumes |
| grade 3 | small/medium/large slow/fast motion in a few volumes |
| grade 4 | small/medium/large slow/fast motion in many volumes |
Diffusion weighted imaging was performed on 3 Tesla Trio or Skyra Siemens scanners (Siemens Healthcare, Erlangen, Germany), with a 32 channel head coil, b = 1000 s/mm2, TR/TE = 9000–13200/88 ms, flip angle of 90 degrees, slice thickness of 2 mm, matrix size of 128 × 128, and variable field-of-view depending on the head size, between 176 to 256 mm.
B. Evaluation Methods
1) Slice-Level Registration Accuracy
We designed an experiment to evaluate the accuracy of the slice-level registration-based motion tracking technique. To this end, we acquired a set of DW images with 30 gradient directions from a volunteer. The volunteer was asked to stay still during the scan. Then, from these scans, we synthesized DWI images with motion using parameters obtained from an electromagnetic motion tracking sensor attached to the volunteer's head in another experiment. The volunteer made slow and fast frequent movements and tracker data was recorded every 100 ms, corresponding to one DWI slice acquisition.
All slices of the scan with synthetic motion were registered to the b = 0 image volume of the original motion-free image set using different approaches: In the first experiment, each slice was registered independently (independent-SVR). The SVR in this case was initialized using parameters obtained from registering the whole volume of each diffusion-sensitized image to the b = 0 image volume. In the second experiment, image slices were registered sequentially in the acquisition order (sequential-SVR). The SVR in this case was initialized using parameters obtained from the registration at the previous time step. In the last experiment, we used the proposed motion estimation of this paper to register diffusion-sensitized image slices to the b = 0 image volume. The proposed method not only accounts for the acquisition order of the image slices, but also uses outlier-robust Kalman filter to estimate motion parameters using Algorithm 1 in Section II-A. We refer to this method as MT-SVR for motion-tracking slice-to-volume registration.
It should be noted that this is the only experiment in this paper that we simulated motion in the images in order to compare estimated parameters to those of the actual motion in the images. This experiment has mainly been done to show the importance of outlier-robust filtering in slice-level registration-based motion tracking.
2) Performance Evaluation and Comparison
We evaluated the performance of the proposed method (MT-SVR) using various metrics and compared to those of volume-to-volume registration (VVR), as well as the original images without motion correction (Orig). Motion-corrupted slices were identified and isotropic 3D base b = 0 images were reconstructed using the methods discussed in Section III. These were applied identically to MT-SVR, VVR, and Orig, therefore, the only difference was the technique used for registration.
We computed and compared fractional anisotropy (FA) and mean diffusivity (MD) [42] in four regions-of-interest (ROIs) including the corpus callosum (CC), anterior and posterior limb of the internal capsule (ALIC and PLIC) and the ventricles. High FA values (close to 1) are expected in CC, ALIC, and PLIC regions and very low FA (close to zero) in the ventricles. Uncompensated motion would result in unexpected FA changes in these regions, i.e., decreased FA in CC, ALIC, and PLIC, and increased FA in the ventricles.
For the volunteer subject experiments, since we had motion-free image sets (the stationary gold standard), we evaluated the performance of MT-SVR compared to VVR and Orig based on four dissimilarity metrics. These metrics [43] include
| (14) |
| (15) |
| (16) |
| (17) |
where nx is the number of voxels in the ROI, Di and D̃i are 3×3 tensor matrices in the reconstructed DTI and the gold standard image, respectively. ΔFA and ΔMD compute the root mean squared differences (RMSD) between FAs and MDs, respectively. Δdir computes the angle between the principal eigenvectors in the tensors (e1,i and ẽ1,i); and ΔFro is computed based on the Frobenius norm of the difference tensor.
We also computed tracts that passed through the ROIs and compared the results of MT-SVR with those of VVR and Orig. For the imaging data obtained from volunteer subjects, we also computed the Dice similarity coefficient (DSC) [44] between tract density images in the GS imaging data and those obtained from different motion correction techniques. To compute the DSC metric, we binarized the tract density images by labeling any voxel with at least one passing tract (tract density greater than zero) as 1 and the remaining voxels as 0.
IV. Results
A. Identification of Motion-Corrupted Slices
Using the criteria explained in Section III-A for the detection and exclusion of motion-corrupted slices, the sensitivity and specificity of the employed technique was 80.5% and 98.5%, respectively. These numbers were computed over a set of 2520 DW image slices (36 volumes in total) among which 126 slices were visually identified as corrupted by motion. The criteria was conservative enough to include most of the intact images in the DTI reconstruction excluding 80.5% of the corrupted slices; however, parameters of the corrupted-slice detection algorithm can be tuned depending on the amount of motion and the available imaging data for DTI analysis.
B. Slice-Level Registration Accuracy
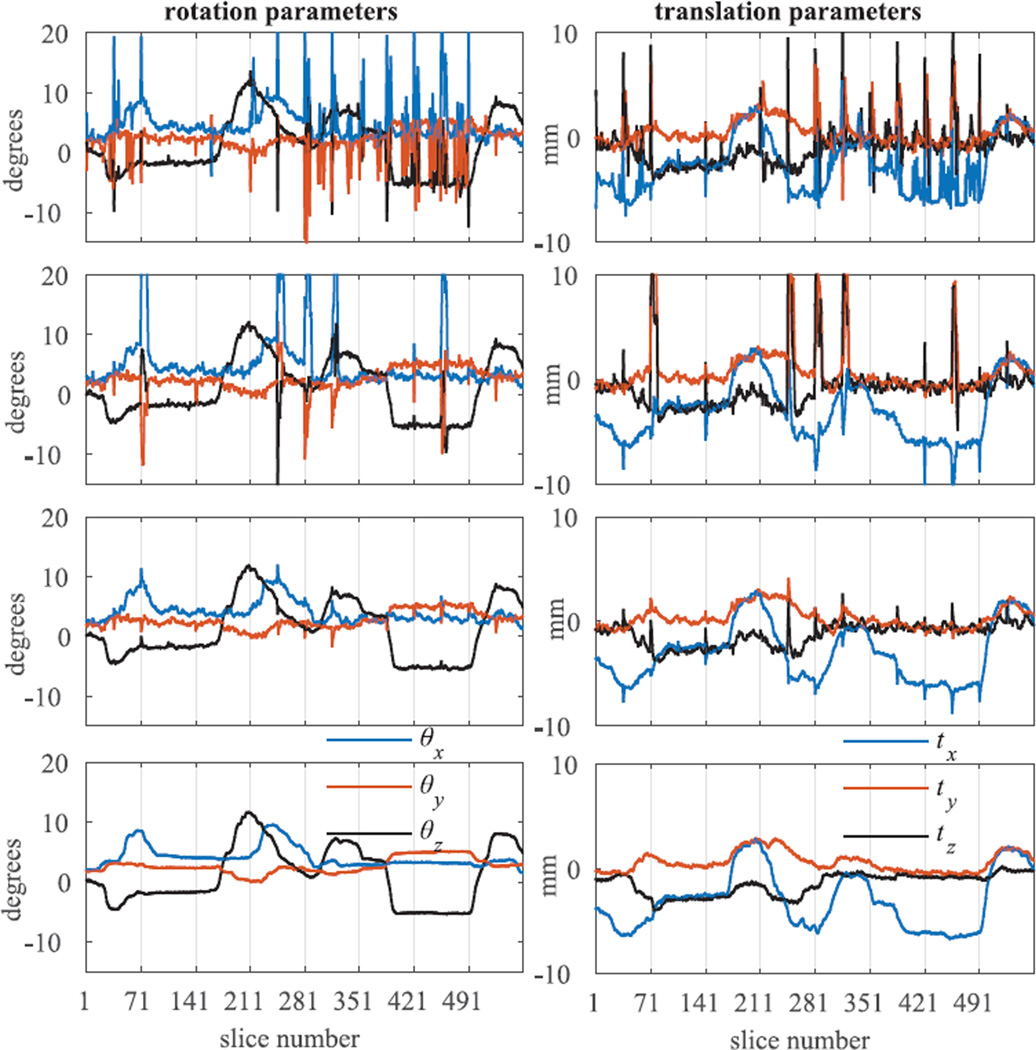
The effectiveness of the proposed method (MT-SVR) in estimating head motion parameters over time is shown in Fig. 3. Estimated rotation and translation parameters using different SVR approaches are depicted in this figure and compared to the parameters obtained from the electromagnetic tracker system. In this figure, each volume has 70 slices (interleaved acquisition). For better representation, estimated motion parameters for only first 8 volumes out of 36 image volumes have been shown in Fig. 3. Average of the mean and standard deviation (SD) of the error in the estimated rotation and translation parameters over 2520 consecutive image slices have also been shown and compared in Table II.
Figure 3.
Comparison of the rotation and translation parameters estimated using different SVR methods. From top to bottom: independent-SVR, sequential-SVR, MT-SVR, and actual parameters recorded from the electromagnetic motion tracking sensor.
TABLE II.
Average of the Mean and Standard-Deviation (SD) of Error in the Estimated Rotation and Translation Parameters Using Different SVR Methods. MT-SVR Shows the Best Performance. The Best Values are Highlighted in Bold
| parameters | MT-SVR | sequential-SVR | independent-SVR |
|---|---|---|---|
| rotation (deg) | 0.27±0.26 | 0.76±2.31 | 1.18±2.82 |
| translation (mm) | 0.30±0.30 | 0.63±1.56 | 0.64±1.18 |
Both Fig. 3 and Table II show that MT-SVR outperforms both independent- and sequential-SVR methods. Although sequential SVR performs better than independent SVR in most slices, its performance degrades especially at slices close to the bottom and top of the brain, where image slices have less information to guide registration as compared to the mid-brain slices. As shown in the first and the second row of Fig. 3, it takes longer (more temporal image slices) for the sequential-SVR to recover from mis-registration and track real motion parameters than the independent-SVR. Our other experimental results showed that this issue intensifies with the fast and large head motions and as a result sequential-SVR fails completely to track head motion. In this experiment through-plane motion was not simulated (there was no motion-corrupted image slices); but both independent and sequential-SVR methods can fail in case slices are corrupted by motion and heavy-tailed noise. Estimated motion parameters in this case may significantly deviate from the true motion parameters. On the other hand, MT-SVR shows very robust performance in the presence of registration failure and motion-corrupted slices. Therefore, in the remaining experiments of this paper, we only evaluated the performance of the MT-SVR in the slice-level motion correction and compared it to the VVR and Orig.
C. Constructing Isotropic Base b = 0 Image
We compared the normalized root mean squared error (NRMSE) between the gold standard b = 0 image and the reconstructed B̃0 images using all three methods (MT-SVR, VVR, and Orig) in Table III. These results, given for each volunteer subject experiment, show that our proposed method (MT-SVR) outperforms VVR and Orig.
D. DTI in Volunteer Subjects
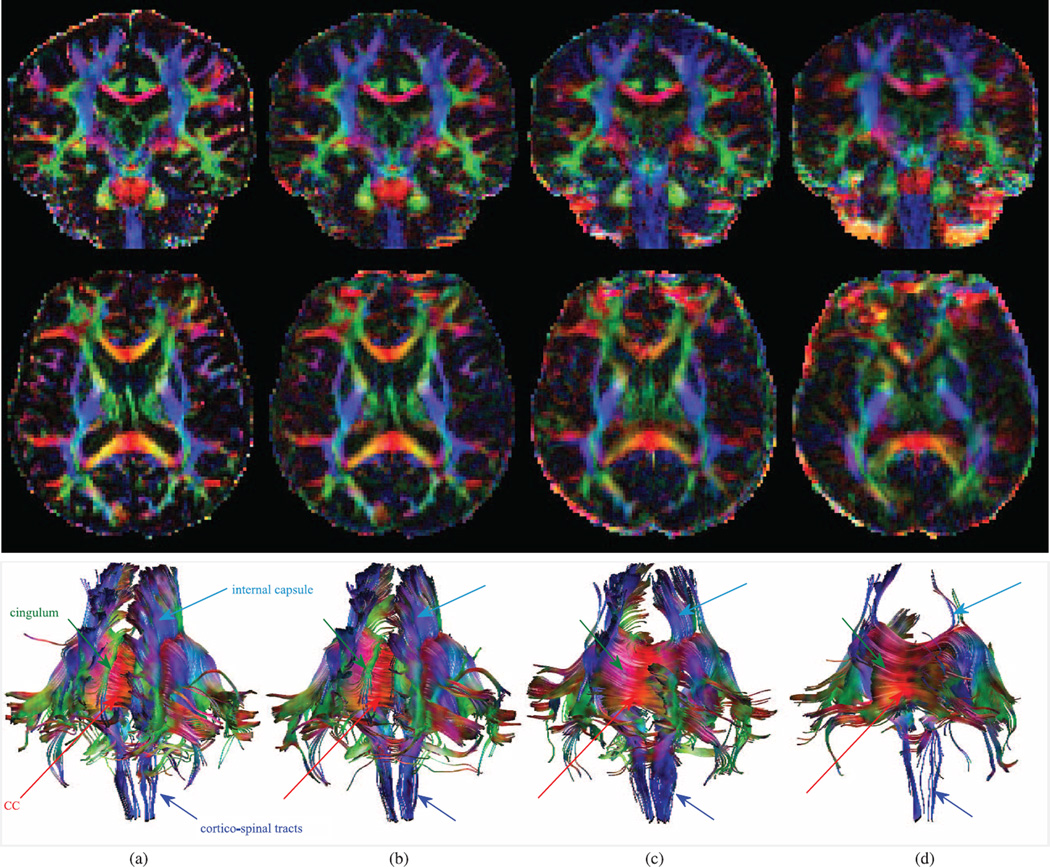
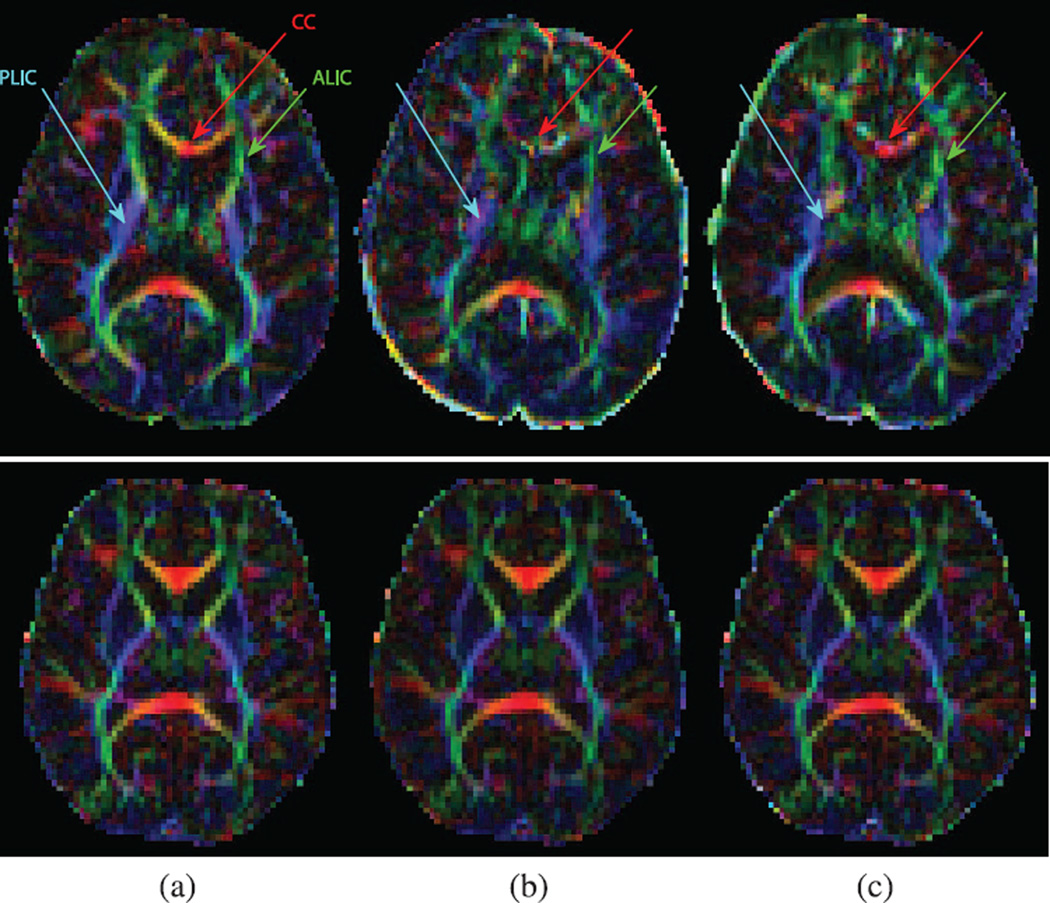
Two orthogonal views of the color-coded FA and the computed tracts passing the CC ROI using different motion correction approaches are shown in Figs. 4(b)–4(d) and compared to those of the gold standard image (a). Both color-coded FA and tractography results show that MT-SVR outperforms VVR and Orig. For quantitative evaluation, we computed average FA in CC, ALIC, and ventricles and compared the values to those of the GS in Table IV. Estimated FA values using MT-SVR are closer to the GS values than values estimated using VVR and Orig. Also, it is worth noting that the difference between estimated FA values in different motion experiments of the same subjects are smaller in MT-SVR than in VVR and Orig, which indicates better test-retest reliability.
Figure 4.
Color-coded FA and tractography results comparison in a volunteer subject (2–2). Coronal (top) and transverse (middle) planes along with tracts passing CC. Cingulum tracts are completely missing in VVR and Orig. The FA and tracts obtained from MT-SVR are much more similar to those of the GS compared to the ones obtained from VVR and Orig. (a) gold standard (GS) (b) MT-SVR (c) VVR (d) Orig.
The mean and SD of ΔFA, ΔDir, ΔFro and ΔMD dissimilarity metrics in all volunteer imaging data are given in Table V. Moreover, the DSC metric between tract densities in the GS and the estimated tract densities using the MT-SVR, VVR, and Orig are given in Table VI. The DSC values in this table were computed based on the tracts passing the CC and ALIC/PLIC ROIs. The DSC value in MT-SVR is higher than VVR and Orig, which indicates that MT-SVR performed best in estimating white-matter tracts.
TABLE V.
Mean and SD of ΔFA, ΔDir, ΔFro (×l0−3) and ΔMD(×10−3) in the CC, ALIC, PLIC and Ventricles in Nine Volunteer Experiments. The Difference Between MT-SVR and VVR/Orig is Statistically Significant (p < 0.05 in a Paired-Sample t-Test With α = 0.05). The Best Values are Highlighted in Bold
| CC | ALIC | PLIC | ventricles | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| metric | MT-SVR | VVR | Orig | MT-SVR | VVR | Orig | MT-SVR | VVR | original | MT-SVR | VVR | Orig | |
| ΔFA | mean SD |
0.1791 | 0.3066 | 0.3569 | 0.1206 | 0.2382 | 0.2785 | 0.0649 | 0.1694 | 0.1190 | 0.0590 | 0.1026 | 0.0996 |
| 0.0281 | 0.0648 | 0.0815 | 0.0292 | 0.0412 | 0.0539 | 0.0062 | 0.0537 | 0.0249 | 0.0590 | 0.1026 | 0.0996 | ||
| ΔDir | mean SD |
0.2188 | 0.3923 | 0.5552 | 0.3503 | 0.5533 | 0.7386 | 0.0264 | 0.1013 | 0.0569 | 0.7664 | 0.8271 | 0.8429 |
| 0.0940 | 0.1413 | 0.1594 | 0.0569 | 0.0865 | 0.1463 | 0.0145 | 0.0672 | 0.0296 | 0.0459 | 0.0616 | 0.0451 | ||
| ΔFro | mean SD |
0.6444 | 1.0152 | 1.1028 | 0.2793 | 0.5113 | 0.6013 | 0.1997 | 0.4051 | 0.3338 | 0.6466 | 1.2802 | 1.3278 |
| 0.1250 | 0.1698 | 0.4543 | 0.0297 | 0.0743 | 0.0922 | 0.0100 | 0.0905 | 0.0574 | 0.1168 | 0.2630 | 0.2708 | ||
| ΔMD | mean SD |
0.3255 | 0.4840 | 0.5079 | 0.0954 | 0.1324 | 0.1849 | 0.0592 | 0.0789 | 0.0710 | 0.3018 | 0.6742 | 0.6954 |
| 0.0574 | 0.1065 | 0.2690 | 0.0063 | 0.0332 | 0.0457 | 0.0080 | 0.0173 | 0.0107 | 0.0824 | 0.1618 | 0.1752 | ||
Finally, we note the effect of motion on images and FA values. Motion results in blurring artifacts in color FA (Fig. 4). Consequently, uncompensated motion results in reduced FA in fiber-rich tract regions like CC and ALIC/PLIC (where high FAs are expected), and results in increased FA in ventricles (where very low FA values are expected). These effects can be observed in the images as well as in Table IV.
E. DTI in Neonates and Children
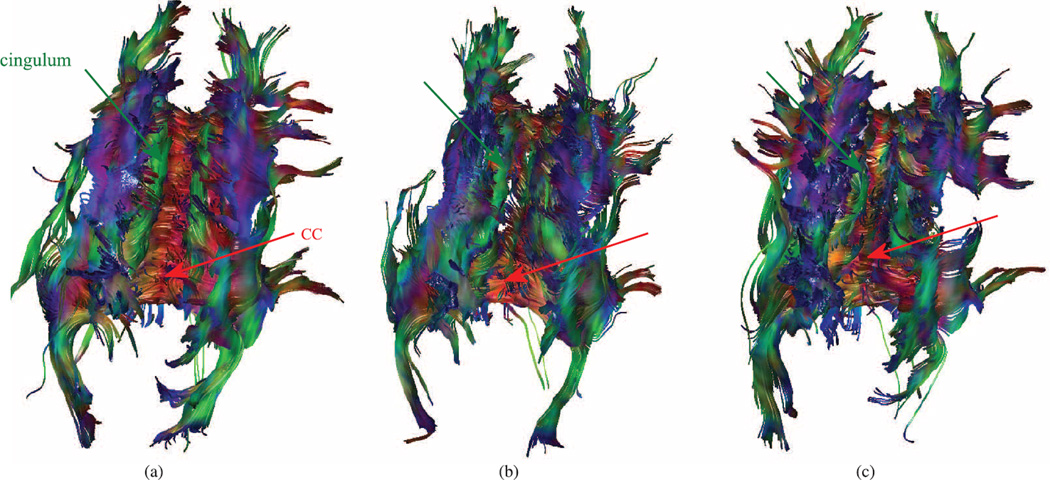
We applied MT-SVR to all 28 subjects and compared the results with VVR and Orig. Transverse planes of the color-coded FA in two cases (different ages and motion grades) are shown in Fig. 5. This figure is a representative of all results showing that our proposed method (MT-SVR) did not degrade DWI of the subjects without noticeable motion, but significantly improved the analysis of cases with motion. A marked improvement over VVR-based motion correction was also observed. Fig. 6 shows the estimated tracts passing through a relatively big ROI around the CC in a 5-year old subject with motion grade 4. This figure shows much better delineation of corpus callosum, internal capsule, superior longitudinal fasciculus, and cingulum tracts using MT-SVR (a) compared to VVR (b) and Orig (c).
Figure 5.
Transverse views of the color-coded FA in children and newborns. Top: a 6-years old, motion grade 4; bottom: a 1-day old, motion grade 0. These images indicate much better delineation of the CC, ALIC, and PLIC regions due to motion-robust reconstruction (top image), as well as a consistent performance in the absence of noticeable motion (bottom image). (a) MT-SVR (b) VVR (c) Orig.
Figure 6.
Estimated tracts passing the CC ROI calculated from DWI of a 5-years old child who moved significantly during the acquisition. These images indicate much better delineation of all major pathways including the CC and cingulum tracts using MT-SVR compared to VVR and Orig. (a) MT-SVR (b) VVR (c) Orig.
We also computed FA values in different ROIs and compared the results to those of the VVR and Orig in Table VII. We divided subjects to different assigned motion grades and provided mean and SD of the FA in all ROIs. Higher FA values in CC, ALIC and PLIC indicate better alignment of the estimated fibers in these fiber-rich zones. In contrast, lower FA values are expected in ventricles. It can be concluded from Table VII that MT-SVR improved FA values in CC, ALIC, PLIC, and ventricles in subjects with motion grades higher than 0 and out-performed VVR. In subjects with motion grade 0, FA values slightly decreased in CC and ALIC/PLIC and slightly increased in the ventricles after motion correction using both MT-SVR and VVR but the differences were insignificant. This is mostly due to the smoothing effect of the applied image interpolation in motion correction techniques.
TABLE VII.
Average FA Values in CC, ALIC, PLIC and Ventricles in Children and Newborns. ns is the Number of Subjects per Motion Grade
| ns | motion grade |
CC | ALIC | PLIC | ventricles | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MT-SVR | VVR | Orig | MT-SVR | VVR | Orig | MT-SVR | WR | Orig | MT-SVR | WR | Orig | |||
| 7 | 4 | mean SD |
0.5798 | 0.5455 | 0.4824 | 0.4220 | 0.3519 | 0.3471 | 0.6153 | 0.5334 | 0.5695 | 0.0875 | 0.0975 | 0.1091 |
| 0.1481 | 0.1578 | 0.1403 | 0.0753 | 0.0969 | 0.0646 | 0.0910 | 0.1407 | 0.0897 | 0.0179 | 0.0199 | 0.0371 | |||
| 4 | 3 | mean SD |
0.6319 | 0.5971 | 0.5714 | 0.3955 | 0.3668 | 0.3538 | 0.5631 | 0.5675 | 0.5539 | 0.0935 | 0.0959 | 0.1002 |
| 0.1199 | 0.1183 | 0.1323 | 0.0977 | 0.0985 | 0.1285 | 0.0651 | 0.0579 | 0.0696 | 0.0175 | 0.0192 | 0.0233 | |||
| 4 | 2 | mean SD |
0.5244 | 0.5132 | 0.5019 | 0.3578 | 0.3415 | 0.3507 | 0.5733 | 0.5587 | 0.5697 | 0.0846 | 0.0900 | 0.0974 |
| 0.1683 | 0.1648 | 0.1640 | 0.1103 | 0.1228 | 0.1173 | 0.0766 | 0.0841 | 0.0718 | 0.0259 | 0.0254 | 0.0269 | |||
| 6 | 1 | mean SD |
0.6928 | 0.6870 | 0.6895 | 0.4523 | 0.4386 | 0.4474 | 0.6671 | 0.6586 | 0.6675 | 0.0786 | 0.0789 | 0.0805 |
| 0.0489 | 0.0515 | 0.0558 | 0.0762 | 0.0823 | 0.0793 | 0.0423 | 0.0465 | 0.0439 | 0.0073 | 0.0114 | 0.0060 | |||
| 7 | 0 | mean SD |
0.6641 | 0.6637 | 0.6741 | 0.4416 | 0.4429 | 0.4492 | 0.6589 | 0.6591 | 0.6628 | 0.0687 | 0.0693 | 0.0680 |
| 0.0804 | 0.0835 | 0.0790 | 0.0444 | 0.0448 | 0.0465 | 0.0631 | 0.0642 | 0.0638 | 0.0098 | 0.0124 | 0.0102 | |||
| 28 | 0-4 | mean SD |
0.6246 | 0.6081 | 0.5901 | 0.4204 | 0.3939 | 0.3956 | 0.6238 | 0.6001 | 0.6116 | 0.0813 | 0.0851 | 0.0897 |
| 0.1305 | 0.1371 | 0.1464 | 0.0850 | 0.0990 | 0.0983 | 0.0807 | 0.1051 | 0.0858 | 0.0181 | 0.0210 | 0.0285 | |||
V. Discussion
The problem of subject motion in MRI has been considered as a complex problem with partial solutions [4]. A variety of techniques have been investigated and evaluated [3]. Prospective techniques such as PACE [6] and its extensions based on free induction decay (FID) navigators [9] have been specifically designed for fMRI and DWI; but these techniques work at a volume-level correction basis, and therefore, are relatively slow and cannot effectively deal with large, fast and continuous motion. Retrospective motion correction through volume-to-volume registration is also an important routine part of all fMRI and DWI processing pipelines [1], [19], [45].
Slice-to-volume registration was previously used for motion correction in functional MRI [20], [21] and motion-robust fetal MRI reconstruction [22]–[31]. In particular, Oubel et al. [28] presented a method for slice-level motion correction and reconstruction of fetal DW-MRI data in which a group-wise registration and a dual spatio-angular interpolation technique was employed. Here we have developed and presented a novel robust slice-to-volume registration technique that incorporates a dynamic model of head motion. While our application, model, and assumptions are different here from the previous work addressing the fetal MRI problem, a direct comparison would be fair in the future when the technique is adapted and applied to fetal DW-MRI.
The novel algorithm, proposed in this paper, outperforms volume-to-volume registration which is the current commonly-used approach in DW-MRI analysis pipelines. The proposed method allows better handling of DWI data due to head motion tracking, motion correction, and filtering at the slice-level. The use of an outlier-robust Kalman filter enables capturing the dynamics of motion through registration-based motion tracking at a rate close to 10 Hz. Our experiments show that this approach can effectively retrieve DTI data from DWI scans corrupted by fast and large motion at ranges close to 15 mm and 20 degrees.
Kalman filter (KF), which has been the subject of extensive research and applications since its introduction in 1960 [46], has been widely used for tracking objects from video or time series of images. For linear dynamical systems with Gaussian noise, KF provides optimal estimates yielding the smallest expected mean-square-error [47]. Nonlinear extensions of KF, the extended KF and the unscented KF [48], are considered the de facto standards in nonlinear state estimation. Its performance, however, significantly degrades in the presence of non-Gaussian noise like heavy-tailed disturbances and outlying measurements. The outlier-robust Kalman filter, utilized here to mitigate the effect of anomalous registration measurements in estimating and tracking head motion, is a discrete-time model for processing sequential data in the presence of outliers, non-Gaussian, and heavy-tailed noise in measurements [33]. It is evident from Fig. 3 and Table II that this filtering scheme is a crucial part of our method to reinforce slice-to-volume registration for motion tracking.
We also developed a technique to directly reconstruct tensors from motion-corrected DWI data in Section II. We adjusted diffusion gradient directions based on estimated motion parameters and used a modified WLLS approach to estimate tensors. It has been shown that WLLS with well-defined weights provides more accurate estimate of the diffusion tensors compared to unweighted linear least squares (LLS) estimation [36], [37], [49]. A constrained weighted linear least squared (CWLLS) objective function was used to compute diffusion tensors as given in (8) and (11). Since the variance of a log-transformed DW signal depends on the signal itself, using the observed DW signal as weights in CWLLS method could correct for the distortion induced by the logarithmic transformation [49]. Therefore, we used the square of voxel intensities in diffusion-sensitized images as weights in CWLLS function in (11), i.e., αi = Bi,irregular. Another advantage of the CWLLS with DW signal intensity-based weights over LLS is its inherent ability to mitigate the effect of signal loss in motion-corrupted slices. Through-plane motion results in signal loss and appears as low intensity in motion-corrupted slices. The CWLLS method in (11) gives smaller weights to the image data obtained from motion-corrupted slices compared to LLS. Our results confirmed this hypothesis.
With these developments we have achieved a computational motion-robust DWI reconstruction technique that is capable of restoring DTI information from severely motion-corrupted DWI scans. We reported retrospective application of this technique to previously acquired clinical data. With optimized implementation on sufficiently powerful hardware it would be possible to use this algorithm for prospective motion tracking and retrospective reconstruction. The advantage of prospective motion tracking is that in case of severe motion, it would be possible to adaptively acquire more data in the required diffusion directions to maintain a desired signal-to-noise ratio (SNR). Without prospective implementation we will be limited to the available data, which in case of severe continuous motion may not provide sufficient SNR. Future work also involves the integration of this motion correction scheme with multi-compartment models of the diffusion signal [43], [50]. The reconstruction part of the algorithm may be further improved by incorporating more realistic physical models of DWI acquisition [51].
Diffusion-weighted echo-planar imaging data are affected in different ways by several sources of distortion including artifacts caused by B0 and B1 field inhomogeneity that are particularly significant at higher magnetic fields, as well as eddy currents that may distort images in complex ways. All these distortions should be minimized in DWI acquisition and compensated in the analysis based on physics-driven models of distortion [52], [53], especially in the presence of motion [21], [28], [54]–[56]. In this study we focused on tracking and correcting the head motion and did not consider or correct for distortions. An important direction of future work, therefore, is to correct the effect of geometric and intensity distortions due to eddy currents and B0 and B1 field inhomogeneities.
VI. Conclusion
We have developed a novel technique for slice-level motion estimation and correction in MRI. This technique employs a filtering method to track subject's head motion during scans based on registering acquired slices to a base volume over time. Experimental results on DWI sequences showed that the technique was successful in robustly estimating head motion, rejecting motion-corrupted slices, filtering motion-corrupted data, and reconstructing diffusion tensors. Through effective processing of imaging data, this technique outperforms the state-of-the-art DWI motion correction based on volume-to-volume registration; and can readily be used for retrospective analysis of motion-corrupted DWI scans. The technique is platform-independent in the sense that it can be used for retrospective motion-correction of DWI data obtained using different scanners and does not require a specific vendor platform, hardware setup, pulse sequence modification or prospective planning. Experimental results showed that the proposed technique can deal with slow and fast motions across some extremes; so, depending on the goals and the imaging protocols, it may palliate the need for sedation or anesthesia, or repeated scans in newborns, young children, and patients with limited cooperation, and can significantly simplify, improve, and promote research using MRI in these populations.
Acknowledgments
This work was supported by the National Institutes of Health grants R01EB018988, R01EB019483, R01 NS079788, U01 NS082320, U54NS092090, Intel(C) IPCC and a faculty career development award from the Office of Faculty Development at Boston Children’s Hospital to A. Gholipour. B. Scherrer was also supported by Boston Children’s Hospital TRP Pilot Grant and Boston Children’s Hospital K-To-R Award. The Developmental Synaptopathies Consortium (U54 NS092090) is part of the NCATS Rare Diseases Clinical Research Network (RDCRN). RDCRN is an initiative of the Office of Rare Diseases Research (ORDR), NCATS, funded through collaboration between NCATS, NIMH, NINDS, and NICHD
Footnotes
Color versions of one or more of the figures in this paper are available online at http://ieeexplore.ieee.org.
Contributor Information
Bahram Marami, Email: bahram.marami@childrens.harvard.edu, Department of Radiology, Boston Children's Hospital, and Harvard Medical School, Boston, MA 02115 USA.
Benoit Scherrer, Department of Radiology, Boston Children's Hospital, and Harvard Medical School, Boston, MA 02115 USA.
Onur Afacan, Department of Radiology, Boston Children's Hospital, and Harvard Medical School, Boston, MA 02115 USA.
Burak Erem, Department of Radiology, Boston Children's Hospital, and Harvard Medical School, Boston, MA 02115 USA.
Simon K. Warfield, Department of Radiology, Boston Children's Hospital, and Harvard Medical School, Boston, MA 02115 USA
Ali Gholipour, Department of Radiology, Boston Children's Hospital, and Harvard Medical School, Boston, MA 02115 USA.
References
- 1.Elhabian S, et al. Subject-motion correction in HARDI acquisitions: Choices and consequences. Front. Neurol. 2014;5 doi: 10.3389/fneur.2014.00240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Malamateniou C, et al. Motion-compensation techniques in neonatal and fetal MR imaging. Am. J. Neuroradiol. 2013;34(6):1124–1136. doi: 10.3174/ajnr.A3128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Maclaren J, Herbst M, Speck O, Zaitsev M. Prospective motion correction in brain imaging: A review. Magn. Reson. Med. 2013;69(3):621–636. doi: 10.1002/mrm.24314. [DOI] [PubMed] [Google Scholar]
- 4.Zaitsev M, Maclaren J, Herbst M. Motion artifacts in MRI: A complex problem with many partial solutions. J. Magn. Reson. Imag. 2015 doi: 10.1002/jmri.24850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Pipe JG, et al. Motion correction with PROPELLER MRI: Application to head motion and free-breathing cardiac imaging. Magn. Reson. Med. 1999;42(5):963–969. doi: 10.1002/(sici)1522-2594(199911)42:5<963::aid-mrm17>3.0.co;2-l. [DOI] [PubMed] [Google Scholar]
- 6.Thesen S, Heid O, Mueller E, Schad LR. Prospective acquisition correction for head motion with image-based tracking for real-time fMRI. Magn. Reson. Med. 2000;44(3):457–465. doi: 10.1002/1522-2594(200009)44:3<457::aid-mrm17>3.0.co;2-r. [DOI] [PubMed] [Google Scholar]
- 7.Maclaren J, et al. Navigator accuracy requirements for prospective motion correction. Magn. Reson. Med. 2010;63(1):162–170. doi: 10.1002/mrm.22191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.White N, et al. PROMO: Real-time prospective motion correction in MRI using image-based tracking. Magn. Reson. Med. 2010;63(1):91–105. doi: 10.1002/mrm.22176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kober T, Gruetter R, Krueger G. Prospective and retrospective motion correction in diffusion magnetic resonance imaging of the human brain. Neuroimage. 2012;59(1):389–398. doi: 10.1016/j.neuroimage.2011.07.004. [DOI] [PubMed] [Google Scholar]
- 10.Skare S, Hartwig A, Mårtensson M, Avventi E, Engström M. Properties of a 2D fat navigator for prospective image domain correction of nodding motion in brain MRI. Magn. Reson. Med. 2015;73(3):1110–1119. doi: 10.1002/mrm.25234. [DOI] [PubMed] [Google Scholar]
- 11.Gallichan D, Marques JP, Gruetter R. Retrospective correction of involuntary microscopic head movement using highly accelerated fat image navigators (3D Fatnavs) at 7T. Magn. Reson. Med. 2015 doi: 10.1002/mrm.25670. [DOI] [PubMed] [Google Scholar]
- 12.Qin L, et al. Prospective head-movement correction for high-resolution MRI using an in-bore optical tracking system. Magn. Reson. Med. 2009;62(4):924–934. doi: 10.1002/mrm.22076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ooi MB, Krueger S, Thomas WJ, Swaminathan SV, Brown TR. Prospective real-time correction for arbitrary head motion using active markers. Magn. Reson. Med. 2009;62(4):943–954. doi: 10.1002/mrm.22082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Aksoy M, et al. Real-time optical motion correction for diffusion tensor imaging. Magn. Reson. Med. 2011;66(2):366–378. doi: 10.1002/mrm.22787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gholipour A, Polak M, Van der Kouwe A, Nevo E, Warfield SK. Motion-robust MRI through real-time motion tracking and retrospective super-resolution volume reconstruction. Proc. IEEE Eng. Med. Bio. Soc. 2011:5722–5725. doi: 10.1109/IEMBS.2011.6091385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Sengupta S, Tadanki S, Gore JC, Welch EB. Prospective real-time head motion correction using inductively coupled wireless NMR probes. Magn. Reson. Med. 2014;72(4):971–985. doi: 10.1002/mrm.25001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Haeberlin M, et al. Real-time motion correction using gradient tones and head-mounted NMR field probes. Magn. Reson. Med. 2014 doi: 10.1002/mrm.25432. [DOI] [PubMed] [Google Scholar]
- 18.Todd N, Josephs O, Callaghan M, Lutti A, Weiskopf N. Prospective motion correction of 3D echo-planar imaging data for functional MRI using optical tracking. NeuroImage. 2015;113:1–12. doi: 10.1016/j.neuroimage.2015.03.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kreilkamp BA, Zacà D, Papinutto N, Jovicich J. Retrospective head motion correction approaches for diffusion tensor imaging: Effects of preprocessing choices on biases and reproducibility of scalar diffusion metrics. J. Magn. Reson. Imag. 2015 doi: 10.1002/jmri.24965. [DOI] [PubMed] [Google Scholar]
- 20.Kim B, Boes J, Bland P, Chenevert T, Meyer CR. Motion correction in fMRI via registration of individual slices into an anatomical volume. Magn. Reson. Med. 1999;41(5):964–972. doi: 10.1002/(sici)1522-2594(199905)41:5<964::aid-mrm16>3.0.co;2-d. [DOI] [PubMed] [Google Scholar]
- 21.Kim B, Yeo DT, Bhagalia R. Comprehensive mathematical simulation of functional magnetic resonance imaging time series including motion-related image distortion and spin saturation effect. Magn. Reson. Imag. 2008;26(2):147–159. doi: 10.1016/j.mri.2007.05.007. [DOI] [PubMed] [Google Scholar]
- 22.Rousseau F, et al. Registration-based approach for reconstruction of high-resolution in utero fetal MR brain images. Acad. Radiol. 2006;13(9):1072–1081. doi: 10.1016/j.acra.2006.05.003. [DOI] [PubMed] [Google Scholar]
- 23.Jiang S, et al. MRI of moving subjects using multislice snapshot images with volume reconstruction (SVR): Application to fetal, neonatal, and adult brain studies. IEEE Trans. Med. Imag. 2007 Jul;26(7):967–980. doi: 10.1109/TMI.2007.895456. [DOI] [PubMed] [Google Scholar]
- 24.Jiang S, et al. Diffusion tensor imaging (DTI) of the brain in moving subjects: Application to in-utero fetal and ex-utero studies. Magn. Reson. Med. 2009;62(3):645–655. doi: 10.1002/mrm.22032. [DOI] [PubMed] [Google Scholar]
- 25.Kim K, et al. Intersection based motion correction of multislice MRI for 3-D in utero fetal brain image formation. IEEE Trans. Med. Imag. 2010 Jan;29(1):146–158. doi: 10.1109/TMI.2009.2030679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Gholipour A, Estroff J, Warfield SK. Robust super-resolution volume reconstruction from slice acquisitions: application to fetal brain MRI. IEEE Trans. Med. Imag. 2010 Oct;29(10):1739–1758. doi: 10.1109/TMI.2010.2051680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kuklisova-Murgasova M, Quaghebeur G, Rutherford MA, Hajnal JV, Schnabel JA. Reconstruction of fetal brain MRI with intensity matching and complete outlier removal. Med. Imag. Anal. 2012;16(8):1550–1564. doi: 10.1016/j.media.2012.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Oubel E, Koob M, Studholme C, Dietemann J-L, Rousseau F. Reconstruction of scattered data in fetal diffusion MRI. Med. Imag. Anal. 2012;16(1):28–37. doi: 10.1016/j.media.2011.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Fogtmann M, et al. A unified approach to diffusion direction sensitive slice registration and 3-D DTI reconstruction from moving fetal brain anatomy. IEEE Trans. Med. Imag. 2014 Feb;33(2):272–289. doi: 10.1109/TMI.2013.2284014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ferrazzi G, et al. Resting state fMRI in the moving fetus: a robust framework for motion, bias field and spin history correction. NeuroImage. 2014;101:555–568. doi: 10.1016/j.neuroimage.2014.06.074. [DOI] [PubMed] [Google Scholar]
- 31.Kainz B, et al. Fast volume reconstruction from motion corrupted stacks of 2d slices. IEEE Trans. Med. Imag. 2015 Sep;34(9):1901–1913. doi: 10.1109/TMI.2015.2415453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Sciavicco L, Siciliano B, et al. Modelling and Control of Robot Manipulators. New York: Springer Sci. Business Media; 2012. [Google Scholar]
- 33.Agamennoni G, et al. Approximate inference in state-space models with heavy-tailed noise. IEEE Trans. Signal Process. 2012 Oct60(10):5024–5037. [Google Scholar]
- 34.Dawid AP. Some matrix-variate distribution theory: Notational considerations and a bayesian application. Biometrika. 1981;68(1):265–274. [Google Scholar]
- 35.Stejskal E, Tanner J. Spin diffusion measurements: Spin echoes in the presence of a time-dependent field gradient. J. Chem. Phys. 1965;42(1):288–292. [Google Scholar]
- 36.Koay CG, Chang L-C, Carew JD, Pierpaoli C, Basser PJ. A unifying theoretical and algorithmic framework for least squares methods of estimation in diffusion tensor imaging. J. Magn. Reson. 2006;182(1):115–125. doi: 10.1016/j.jmr.2006.06.020. [DOI] [PubMed] [Google Scholar]
- 37.Salvador R, et al. Formal characterization and extension of the linearized diffusion tensor model. Hum. Brain Mapp. 2005;24(2):144–155. doi: 10.1002/hbm.20076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Li Y, et al. Image corruption detection in diffusion tensor imaging for post-processing and real-time monitoring. PLOS ONE. 2013;8(10) doi: 10.1371/journal.pone.0049764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Miller I, Freund JE, Johnson RA, et al. Probability and Statistics for Engineers. Vol. 1110. Englewood Cliffs, NJ: Prentice-Hall; 1965. [Google Scholar]
- 40.Johnson HJ, McCormick M, Ibáñez L, Consortium TIS. The ITK Software Guide. 3rd. Clifton Park, NY: Kitware; 2013. [Google Scholar]
- 41.Mattes D, Haynor DR, Vesselle H, Lewellen TK, Eubank W. PET-CT image registration in the chest using free-form deformations. IEEE Trans. Med. Imag. 2003 Jan;22(1):120–128. doi: 10.1109/TMI.2003.809072. [DOI] [PubMed] [Google Scholar]
- 42.Vos SB, Jones DK, Jeurissen B, Viergever MA, Leemans A. The influence of complex white matter architecture on the mean diffusivity in diffusion tensor MRI of the human brain. Neuroimage. 2012;59(3):2208–2216. doi: 10.1016/j.neuroimage.2011.09.086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Taquet M, et al. A mathematical framework for the registration and analysis of multi-fascicle models for population studies of the brain microstructure. IEEE Trans. Med. Imag. 2014 Feb;33(2):504–517. doi: 10.1109/TMI.2013.2289381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Dice LR. Measures of the amount of ecologic association between species. Ecology. 1945;26(3):297–302. [Google Scholar]
- 45.Ben-Amitay S, Jones DK, Assaf Y. Motion correction and registration of high b-value diffusion weighted images. Magn. Reson. Med. 2012;67(6):1694–1702. doi: 10.1002/mrm.23186. [DOI] [PubMed] [Google Scholar]
- 46.Kalman RE. A new approach to linear filtering and prediction problems. J. Fluid Eng. 1960;82(1):35–45. [Google Scholar]
- 47.Morris JM. The kalman filter: A robust estimator for some classes of linear quadratic problems. IEEE Trans. Inf. Theory. 1976 Sep22(5):526–534. [Google Scholar]
- 48.Julier SJ, Uhlmann JK. Unscented filtering and nonlinear estimation. Proc. IEEE. 2004 Mar92(3):401–422. [Google Scholar]
- 49.Veraart J, Sijbers J, Sunaert S, Leemans A, Jeurissen B. Weighted linear least squares estimation of diffusion MRI parameters: Strengths, limitations, and pitfalls. Neuroimage. 2013:335–346. doi: 10.1016/j.neuroimage.2013.05.028. [DOI] [PubMed] [Google Scholar]
- 50.Scherrer B, et al. Characterizing brain tissue by assessment of the distribution of anisotropic microstructural environments in diffusion-compartment imaging (DIAMOND) Magn. Reson. Med. 2015 doi: 10.1002/mrm.25912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Scherrer B, et al. Information Processing in Medical Imaging. New York: Springer; 2015. Accelerated high spatial resolution diffusion-weighted imaging; pp. 69–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Jezzard P, Balaban RS. Correction for geometric distortion in echo planar images from b0 field variations. Magn. Reson. Med. 1995;34(1):65–73. doi: 10.1002/mrm.1910340111. [DOI] [PubMed] [Google Scholar]
- 53.Andersson JL, Skare S. A model-based method for retrospective correction of geometric distortions in diffusion-weighted EPI. Neuroimage. 2002;16(1):177–199. doi: 10.1006/nimg.2001.1039. [DOI] [PubMed] [Google Scholar]
- 54.Rohde G, Barnett A, Basser P, Marenco S, Pierpaoli C. Comprehensive approach for correction of motion and distortion in diffusion-weighted MRI. Magn. Reson. Med. 2004;51(1):103–114. doi: 10.1002/mrm.10677. [DOI] [PubMed] [Google Scholar]
- 55.Sutton BP, Noll DC, Fessler JA. Dynamic field map estimation using a spiral-in/spiral-out acquisition. Magn. Reson. Med. 2004;51(6):1194–1204. doi: 10.1002/mrm.20079. [DOI] [PubMed] [Google Scholar]
- 56.Mohammadi S, Möller HE, Kugel H, Müller DK, Deppe M. Correcting eddy current and motion effects by affine whole-brain registrations: Evaluation of three-dimensional distortions and comparison with slicewise correction. Magn. Reson. Med. 2010;64(4):1047–1056. doi: 10.1002/mrm.22501. [DOI] [PubMed] [Google Scholar]