Abstract

Herein, a systematic study of [L2Fe2S2]n model complexes (where L = bis(benzimidazolato) and n = 2-, 3-, 4-) has been carried out using iron and sulfur K-edge X-ray absorption (XAS) and iron Kβ and valence-to-core X-ray emission spectroscopies (XES). These data are used as a test set to evaluate the relative strengths and weaknesses of X-ray core level spectroscopies in assessing redox changes in iron–sulfur clusters. The results are correlated to density functional theory (DFT) calculations of the spectra in order to further support the quantitative information that can be extracted from the experimental data. It is demonstrated that due to canceling effects of covalency and spin state, the information that can be extracted from Fe Kβ XES mainlines is limited. However, a careful analysis of the Fe K-edge XAS data shows that localized valence vs delocalized valence species may be differentiated on the basis of the pre-edge and K-edge energies. These findings are then applied to existing literature Fe K-edge XAS data on the iron protein, P-cluster, and FeMoco sites of nitrogenase. The ability to assess the extent of delocalization in the iron protein vs the P-cluster is highlighted. In addition, possible charge states for FeMoco on the basis of Fe K-edge XAS data are discussed. This study provides an important reference for future X-ray spectroscopic studies of iron–sulfur clusters.
Short abstract
A systematic study of [L2Fe2S2]n model complexes (where n = 2-, 3-, 4-) has been performed using Fe and S K-edge X-ray absorption (XAS) and Fe Kβ and valence-to-core X-ray emission spectroscopies (XES). It is shown that the Fe K-edge XAS data may be used to obtain insight into the extent of valence delocalization. The implications of these results for the evaluation of the electronic structure of iron−sulfur active sites are highlighted.
A. Introduction
Iron–sulfur clusters play essential roles in countless biological processes ranging from electron transfer to catalysis. In metalloproteins the active sites range from the simple single iron, Fe(SR)4 active sites found in rubredoxins, to Fe2S2 and Fe4S4 clusters involved in electron transfer,1 to the complex Fe8S7 and MoFe7S9C sites found in the P-cluster and FeMoco, respectively, of the nitrogenase enzymes.2−6 Examination of the large family of iron–sulfur proteins clearly suggests that nature evolves structural complexity in order to enable diverse functionality.7−10 While Fe2S2 and Fe4S4 clusters are most often involved in electron transfer processes, the complex FeMoco active site of nitrogenase is capable of cleaving the N≡N triple bond of dinitrogen.11 In the iron–sulfur sites optimized for electron transfer, the FeS cores typically shuttle between only two different oxidation states. In contrast, in the FeMoco site of nitrogenase, the active site must accept eight electrons from the P-cluster before N2 is fully reduced to two molecules of ammonia. It is generally accepted that the resting (E0) state of FeMoco must accept three or four electrons from the P-cluster before N2 can bind,12 implying that the iron atoms are reduced by three or four electrons (potentially stored in the form of metal hydrides13,14) before any of these reducing equivalents are used to cleave N2. Ideally, one would like to understand the electronic structure of the cluster that is capable of enabling this remarkable chemistry. However, the oxidation states of the iron atoms in FeMoco and the total charge of the cluster remain a source of controversy.15−17
Interestingly, despite numerous Fe K-edge X-ray absorption spectroscopy (XAS) studies on nitrogenase, the average oxidation state of the iron atoms in the FeMoco cluster has not been assigned on the basis of XAS data.18−21 In contrast, in studies of the Fe4S4 iron protein (the native reductase of nitrogenase22) and the Fe8S7 P-cluster,23 Fe K-edge XAS data have been used to assign and discuss average oxidation states. Musgrave et al. observed systematic edge shifts (0.4 to 0.9 eV) on going from the [Fe4S4]2+ to [Fe4S4]1+ to the super-reduced [Fe4S4]0 cluster of the nitrogenase iron protein, showing that a change in oxidation state of only one of the four iron atoms was observable at the Fe (and S) K-edge.22 In contrast, the two-electron oxidation of the P-cluster (corresponding to oxidation of 25% of the iron atoms) resulted in no observable shift in the Fe K-rising edge.23 To our knowledge, the reasons for these seeming discrepancies have yet to be explained in the literature. To this end, understanding the factors that result in the presence (or absence) of an experimentally observable shift in the rising edge energy requires further investigation. This knowledge is essential in enabling the quantitative assessment of the electronic structure of iron–sulfur clusters by X-ray spectroscopy.
In this context, we were interested in evaluating the relative strengths and weaknesses of X-ray core level spectroscopies in assessing redox changes in iron–sulfur clusters. It is here that studies on synthetic iron–sulfur clusters play an essential role.4,24−30 In order to quantitatively evaluate the changes that occur in both X-ray absorption and X-ray emission (XES) spectra upon oxidation/reduction, we have undertaken a systematic study of a series of Fe2S2 complexes (Figure 1), for which the diferric ([L2Fe2S2]2–), mixed-valent ([L2Fe2S2]3–), and diferrous ([L2Fe2S2]4–) forms have all been reported within the same ligand framework.28−30 This series, first reported by one of our groups, is one of only two model systems for which all three redox states can be isolated.27−30 As these complexes have been previously characterized by a combination of XRD, Mössbauer, and SQUID measurements (Table 1), they form a rigorous test set for the sensitivity of XAS and XES methods to one-electron redox events at the iron. Herein, the Fe K-edge XAS, S K-edge XAS, and Fe Kβ and valence-to-core (VtC) XES data for the complete series of [L2Fe2S2]n (n = 2-, 3-, 4-) complexes are reported. The experimental results are correlated to density functional theory (DFT) calculations. The strengths and weaknesses of each experimental approach for evaluating oxidation state changes in FeS clusters are discussed. The Fe2S2 model study results are then compared to published data on the iron protein,22 the all-ferrous P-cluster,22 and the resting state of FeMoco.18 It is shown that these data may be used to obtain insight into the extent of delocalization in iron–sulfur clusters and may help narrow the possible charge state assignments in FeMoco. The implications of these results for the evaluation of FeS electronic structure by X-ray spectroscopic methods are discussed.
Figure 1.
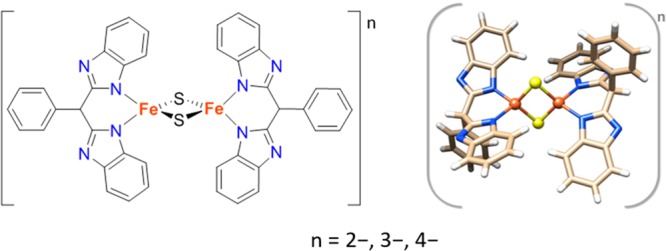
Schematic view (left) and structural representation (right) of [L2Fe2S2]n compounds, where n = 2-, 3-, 4- corresponds to diferric, mixed-valent, and diferrous forms, respectively, and L = bis(benzimidazolato). Color code: yellow - sulfur; orange - iron; blue - nitrogen; light brown - carbon; white - hydrogen.28−30
Table 1. Oxidation State, Spin State, and Structural Data for Fe2S2 Clusters Described in This Work.
| compounda | iron oxidation states | total spin | d(Fe···Fe) [Å] | d(Fe···S) [Å] | d(Fe···N) [Å] |
|---|---|---|---|---|---|
| [L2Fe2S2](NEt4)2 | FeIII:FeIII | 0 | 2.70 | 2.19/2.21 | 1.98/1.99 |
| [L2Fe2S2](NEt4)3 | FeII:FeIII | 1/2 | 2.73 | 2.23/2.24 | 2.06/2.07 |
| [L2Fe2S2](NEt4)4 | FeII:FeII | 0 | 2.75 | 2.26/2.27 | 2.11/2.12 |
L = bis(benzimidazolato).
B. Materials and Methods
B.1. Sample Preparation
[L2Fe2S2](NEt4)2, [L2Fe2S2](NEt4)3, and [L2Fe2S2](NEt4)4 (where L = bis(benzimidazolato)) were synthesized according to published procedures.28−30 All the samples used in this work consisted of solids, and in the case of the Fe K-edge XAS experiments they were diluted in boron nitride to a calculated absorbance of approximately 1. The powder samples were finely ground together with BN and pressed in aluminum sample holders of 1 mm path length, which were then sealed with 38 μm thick adhesive Kapton tape. As the samples are air-sensitive, the preparation was done in an inert atmosphere using nitrogen or argon gloveboxes. The diferrous compound is also known to be temperature sensitive, so special care was taken during its handling: all materials used in the preparation of the sample (tweezers, spatulas, pestle and mortar, sample holder, etc.) were kept in the glovebox freezer at −40 °C for at least 10 min. Grinding and mixing with BN were done gently in an agate mortar and for short periods of time (not more than 2 min), after which the sample container was moved to the freezer for another minimum of 10 min in order to prevent an increase in temperature. This process was repeated until sample homogeneity was achieved; then the diferrous sample was loaded in the Al holders using a similar procedure to that used for the other compounds. After the sample holders were loaded they were immediately taken out of the glovebox, frozen in liquid nitrogen, and kept at this temperature until the measurements.
A similar procedure used in the preparation of the samples for the XAS experiments was applied for the XES experiments; however the samples were utilized neat (i.e., without dilution in BN). This was done in order to maximize the already weak signal in the VtC region and is justified because the excitation was done at a fixed energy well above the edge; therefore, self-absorption effects are not expected to distort the spectra.
The samples used in the S K-edge XAS measurements were also manipulated inside gloveboxes, following the same procedure of diluting them in BN and finely grinding with the help of a pestle and mortar. A mixture of about 50% in mass of BN was used, mainly to minimize self-absorption effects and to increase the total sample volume. The same protocol of using cold tools and avoiding long manipulation times was used in the case of the diferrous sample, as noted above. The homogeneous powdered samples were then dispersed as thinly as possible over sulfur/chlorine-free Kapton (diferrous sample) or carbon tape (diferric and mixed-valent samples) supported on Al sample holders. The sample holders were finally covered with polypropylene (diferrous sample) or Mylar (diferric and mixed-valent samples tape) having 6.4 and 3.6 μm thickness, respectively.
B.2. Data Collection and Processing
B.2.1. Iron K-Edge X-ray Absorption
Iron K-edge XAS measurements were performed at the beamline 7–3 located at the Stanford Synchrotron Radiation Lightsource facility, operated at 3 GeV, with an electron beam current of 350 mA. A fully tuned double-crystal monochromator (DCM) equipped with a Si(220) crystal pair was used to select the energy of the incoming X-rays with an energy resolution (ΔE/E) of about 10–4. A Rh-coated mirror with a cutoff of 9.5 keV was used to reject higher harmonics. The X-ray beam was unfocused, having a size of approximately 1 × 10 mm2 (vertical × horizontal). The samples were kept at approximately 10 K by using a continuous-flow liquid helium cryostat (Oxford Instruments CF1208). The energy of the incident beam was calibrated by measuring the XAS spectrum of an iron foil and setting the first inflection point to 7111.2 eV. A total of four consecutive scans were averaged together for each sample to improve the signal-to-noise (S/N) ratio. XAS data were measured in both transmission (using a N2 gas filled ionization chamber) and total fluorescence yield (TFY, using a Lytle detector31,32) modes; however the TFY data presented a better S/N ratio. Therefore, only TFY-detected Fe K-edge XAS data are presented in this work. No significant self-absorption effects were observed. No signs of radiation-induced changes or photoreduction were observed during the course of the measurements. The first and last scans overlap, as can be seen in Figure S1 in the SI, attesting to sample integrity. Since the diferrous compound was the least stable, an additional measurement was made on the decay product. As can be seen in Figure S2 (in the SI), the spectrum of this decay sample has no resemblance to any of those of the intact compounds. Background subtraction and normalization were performed using the ATHENA package.33 A first-order polynomial was subtracted from the pre-edge region, while in the post-edge region a second-order polynomial was used to account for the background.
B.2.2. Sulfur K-Edge X-ray Absorption
Sulfur XAS measurements were performed at both the Stanford Synchrotron Radiation Lightsource (SSRL) and at the Brazilian Synchrotron Light Laboratory (LNLS), at beamlines 4-3 and SXS, respectively. The SSRL storage ring operated at 3 GeV ring energy and 350 mA electron beam current, whereas the LNLS storage ring operated at 1.37 GeV and 250 mA. Beamline 4-3 uses radiation from a 20-pole, 2 T wiggler, delivering about 1012 photons/s at the sample position in a spot of 2 × 12 mm2 (vertical × horizontal). A Ni-coated Si mirror was used to collimate the beam vertically, and a DCM equipped with Si(111) crystals was used to select the energy with an energy resolution (ΔE/E) of 10–4. Only the diferrous compound was measured at beamline 4-3 of SSRL. During the measurements the sample was maintained inside a plastic compartment filled with helium and subjected to a constant cold He flow via a cryostream system. The estimated temperature at the sample was ∼50 K, and a Lytle detector31,32 was used to record the S K-edge data in TFY mode. A total of nine consecutive scans were averaged. The energy calibration was done based on the S K-edge XAS spectrum of Na2S2O3·5H2O by setting the position of the lowest energy feature to 2472.02 eV. The diferric and mixed-valent samples were measured at beamline SXS at LNLS. This beamline uses radiation from a bending magnet, and its DCM is equipped with several crystal pairs (beryl (1010), YB66 (400), InSb (111), and Si (111)), allowing X-ray energies to be obtained in the range from 0.9 keV up to 5.5 keV.34 The reported S K-edge XAS data from the SXS beamline were recorded using InSb(111) crystals in the DCM, and a Ni-coated Si mirror with toroidal bending was used to focus the X-ray beam to a spot size of approximately 1 × 4 mm2 (vertical × horizontal) at the sample position. The photon flux was estimated to be on the order of 1010 photons/s. The data from SXS were collected in TFY mode using a one-element Amptek XR100 silicon drift detector (SDD) with an integrating window of about 150 eV centered around the sulfur Kα emission line (2307.8 eV). During the course of these measurements the samples were maintained at a pressure smaller than 10–2 mbar by a differential pumping system and at ambient temperature. The energy calibration was performed using two reference compounds: the position of the L3 edge of a Mo foil was set to 2520 eV and the position of the first lower energy feature of the S K-edge spectrum of Na2S2O3·5H2O to 2472.02 eV. A total of 8–11 scans were averaged to compose the signal reported here. The data averaging, background subtraction, and normalization were performed using the ATHENA package,33 similarly to that done for the Fe K-edge XAS data.
B.2.3. Iron Kβ X-ray Emission
Iron Kβ XES measurements were performed at beamline 6-2 of the SSRL synchrotron. The source of X-rays at beamline 6-2 is a 56-pole, 0.9 T wiggler, which delivers about 1013 photons/s at the sample position. A Rh-coated Si mirror is used to vertically collimate the beam, and a cylindrically bent Si mirror, also Rh-coated, is used to focus, resulting in a beam spot at the sample of about 0.1 × 0.5 mm2 (vertical × horizontal). The incident energy was set to 7800 eV using a liquid nitrogen cooled DCM equipped with Si(111) crystals. The XES spectra were recorded using the multicrystal spectrometer installed at the 6-2 beamline operating in Johansson geometry. Five spherically bent Ge(620) crystal analyzers (100 mm diameter, 1 m radius of curvature) aligned on intersecting Rowland circles were used to select the iron Kβ emission energy, which was detected by a Vortex SDD. Further details on this spectrometer are given in ref (35). The samples were maintained below 50 K using an Oxford CF1208 continuous-flow liquid helium cryostat. Signal attenuation in the air path sample–analyzers–detector was minimized by placing a helium-filled bag in this path. The iron XES data were recorded in the range from 7020 eV up to 7130 eV to cover the Kβ1,3 mainline (7020 to 7080 eV) and the VtC region (7080 to 7130 eV). The energy stepping and integration time was varied in these two regions to increase the data quality and optimize data collection time. Around the Kβ mainline an energy step size of 0.2 eV was used, and in the VtC region the step size was 0.15 eV. A limit of X-ray exposure time before radiation-induced changes were observed was systematically established for each sample. The data were collected such that each illuminated spot was used during two consecutive scans, after which the sample was moved and a fresh spot was chosen. At least 10 successive scans for each compound were averaged in order to improve the data quality. The emitted spectra were calibrated by using the spectrum of Fe2O3 as a reference with the maximum of the Kβ1,3 line at 7060.6 eV and the Kβ2,5 at 7107.2 eV.36 The Fe Kβ XES data were normalized by setting the integrated area under the spectra to 1000 units.
B.3. Computational Details
All DFT calculations were performed using the ORCA Quantum Chemistry Package version 3.0.3.37 Calculations used both geometries from the published crystal structures,28,29 with DFT-optimized positions of the hydrogen atoms as well as fully optimized structures on the broken-symmetry (BS) surfaces (see below). All geometry optimizations used the GGA functional BP86.38,39 Scalar relativistic effects were accounted for using the zeroth-order regular approximation for relativistic effects (ZORA),40 and scalar relativistically recontracted versions of the all-electron def2-TZVP basis sets were employed.41,42
The conductor-like screening model (COSMO) in an infinite dielectric constant43 and DFT-D3BJ44,45 were utilized for charge compensation and dispersion corrections, respectively.
Broken-symmetry solutions (for both single-point calculations and geometry optimizations) of MS = 0 or MS = 1/2 were found by first converging the ferromagnetic solution and then flipping the spin on one iron atom and reconverging to the antiferromagnetic broken-symmetry solution.
Single-point calculations were performed with both the B3LYP hybrid functional44,45 and the range-separated hybrid CAM-B3LYP.46 Both def2-TZVP and ma-def2-TZVPP (more polarization functions and diffuse functions47) basis sets were used. The RIJCOSX approximation was used to speed up all hybrid DFT calculations.48,49 The molecular orbital analysis in the Results section used unrestricted natural orbitals (UNOs) and quasi-restricted orbitals (QRDs).50
Time-dependent DFT (TDDFT) calculations for XAS of Fe and S K-edge pre-edge were performed using previously reported protocols.51−53 The donor orbitals for XAS calculations were chosen as 1s for both Fe and S centers, and virtual orbitals were selected as acceptor orbitals. The number of roots was limited to 50 with a focus on an accurate prediction of the XAS pre-edge transitions. Constant energy shifts of 22.53 and 40.68 eV were applied for the calculated Fe and S XAS spectra, respectively. Broadenings of 2.0 and 1.5 eV (FWHM) modeled by a Gaussian function were applied to the calculated Fe and S K-edge transitions, respectively, in order to facilitate comparison with experiment. XES calculations were performed using the one-electron approach as previously described36 and using the BP86 functional in order to be consistent with previously published results.36,54 We note, however, that similar trends were observed using the B3LYP functional. For all Fe XES-calculated spectra a broadening of 2 eV and a constant energy shift of 54.3 eV was applied.
Full multiple scattering XANES calculations were carried out using FEFF 9.6 code.55,56 XANES calculations were carried out using both the crystallographic and DFT geometry optimized coordinates (as provided in the SI). The presented plots are based on the optimized geometries. In all cases a Hedin–Lundqvist potential was utilized. The many-body reduction factor (S02) was set to 1.0. The default core-hole broadening was utilized for spectral plots, with no additional experimental broadening.
C. Results
C.1. Experimental Results
C.1.1. Fe K-Edge XAS
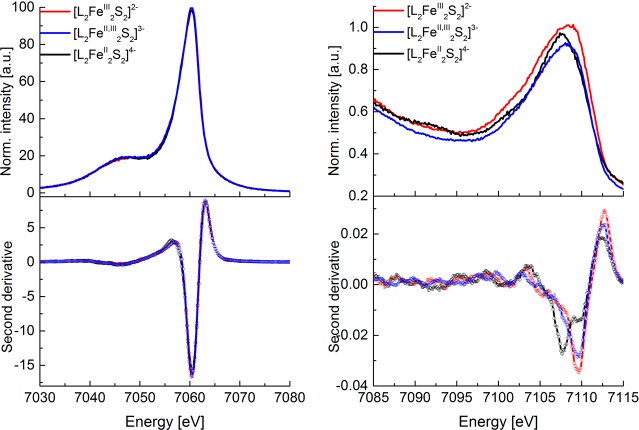
Figure 2 shows a comparison of the normalized Fe K-edge XAS spectra for [L2Fe2S2]2–, [L2Fe2S2]3–, and [L2Fe2S2]4– (top), together with the corresponding first (middle) and second derivatives (bottom). There are two characteristic features in XAS spectra: the rising edge (at ∼7120 eV) and the lower energy lying pre-edge (at ∼7113 eV). Note that all reported rising edge and pre-edge energy positions are based on the maxima of the first- and minima of the second-derivative spectra, respectively. The energy position of the rising edge corresponds to a 1s to 4p transition (with possible imposed charge transfer shakedown transitions)57,58 and is generally used as an indicator of the oxidation state of an element assuming a similar ligand environment.59 On the basis of literature studies a decrease of ∼1–2 eV in the rising edge position is generally attributed to a one-electron reduction.60,61 In the present data, a shift of ∼1.2 eV in the rising edge position is observed on going from the diferric [L2Fe2S2]2– to the diferrous [L2Fe2S2]4–, consistent with complete reduction of the cluster. On this basis, one would expect that the rising edge for the mixed-valent [L2Fe2S2]3–species should appear between that of the [L2Fe2S2]2– and [L2Fe2S2]4–. In contrast, the spectra of [L2Fe2S2]3– and [L2Fe2S2]4– are effectively superimposable in the ∼7115–7119 eV region of the rising edge. This observation highlights the fact that caution must be exercised in using the rising edges as an isolated measure of oxidation state.62,63 We do note, however, that there is a systematic decrease in the intensity of the white line feature at ∼7125 eV upon successive oxidations. Similar trends have been noted in previous Fe K-edge studies,22,60 although to our knowledge the origins of these changes are not yet understood. Both of these observations will be evaluated in greater detail in the subsequent sections.
Figure 2.

Normalized Fe X-ray absorption spectra (XAS) of the diferric (red), mixed-valent (blue), and diferrous (black) Fe2S2 clusters (top), together with corresponding first-derivative (middle) and second-derivative spectra (bottom).
Despite the similarities of the [L2Fe2S2]3– and [L2Fe2S2]4– species in the rising edge region, all three complexes are clearly distinct in the pre-edge region (see also Figure 6 (top) for an expansion of the pre-edge region). The less intense pre-edge feature originates from a quadrupole allowed Fe 1s to 3d transition, which gains intensity through 3d–4p mixing in the local Td symmetry.61 As shown in Figure 2 (top), both the pre-edge energies and intensities show systematic changes across the series. The pre-edge decreases in intensity on going from the [L2Fe2S2]2– to [L2Fe2S2]3– to the [L2Fe2S2]4– complex. This decrease in intensity is consistent with a decrease in the number of holes in the 3d shell, as well as a decrease in covalently mediated 3d–4p mixing. Similarly the pre-edges shift down in energy upon reduction, with the diferric species appearing at highest energy (7113.0 eV) and the diferrous at lowest energy (7112.4 eV). Interestingly, as most clearly shown in the second derivative, the mixed-valent species is composed of two resolvable pre-edge features, a lower energy feature at ∼7112.1 eV and a higher energy feature at 7113.0 eV (Figure 2, bottom, and Figure S3 in the SI). This finding emphasizes the localized nature of the mixed-valent species and indicates that the pre-edge region is effectively composed of “local” ferrous and ferric contributions. We note that similar arguments could also apply in the rising edge region. However, resolved “Fe2+” and “Fe3+” shakedown and/or rising edge features are not observed. The consequences of a trapped valence Fe2+/Fe3+ vs a fully delocalized “Fe2.5+” on the rising edge energy is addressed in more detail in the Computational Details and Discussion sections.
Figure 6.

Experimental (left) and calculated (right) spectra of diferric (red), mixed-valent (blue), and diferrous (black) Fe2S2 clusters: Fe XAS (top), S XAS (middle), Fe XES VtC (bottom). Computational details are provided in section B.3.
C.1.2. S K-Edge XAS
S K-edge XAS spectra of the series of Fe2S2 clusters are shown in Figure 3 (top). The edge represents a dipole-allowed S 1s to 4p transition. The shift in the edge position across the series reflects the changes in charge donation of the bridging sulfides to the Fe.64−67 The more covalent the Fe–S interaction (i.e., the shorter the Fe–S bonds, Table 1), the more “oxidized” the sulfur will appear based on its rising edge energy. Hence, the diferric form has the highest energy rising edge position (2474.5 eV), while for the mixed-valent and diferrous forms the positions are respectively lower (2473.9 and 2473.3 eV). If one assumes that the 4p levels approximate the continuum, then these shifts largely reflect changes in the S 1s ionization energy.
Figure 3.

Normalized S K-edge X-ray absorption spectra (XAS) of diferric (red), mixed-valent (blue), and diferrous (black) Fe2S2 clusters (top), together with corresponding first- (middle) and second-derivative spectra. Both first- and second-derivative spectra were smoothed using the second-order polynomial Savitzky–Golay algorithm in order to obtain better peak definition.
To lower energy, a pre-edge feature appears that formally corresponds to an S 1s to 3p transition, which gains intensity due to mixing of the filled ligand orbitals with the Fe 3d-based orbitals, imparting increasing S 3p hole character as a function of metal–ligand covalency. Therefore, the diferric form has the highest intensity pre-edge, consistent with the largest number of d-holes and the greatest Fe–S covalency.67 Upon successive reductions, the pre-edge decreases in intensity, reflecting a decrease in Fe–S covalency and in the number of d-holes. This is verified by computational studies (vide infra). The energy positions of the pre-edges for the diferric, mixed-valent, and diferric species series vary from 2470.1 to 2470.0 to 2470.4 eV. At first glance, there is no apparent pattern. However, as these pre-edge energies reflect the S 1s to Fe 3d transitions, the changes in S 1s ionization energy (as reflected by the rising edge energy) must be taken into account.
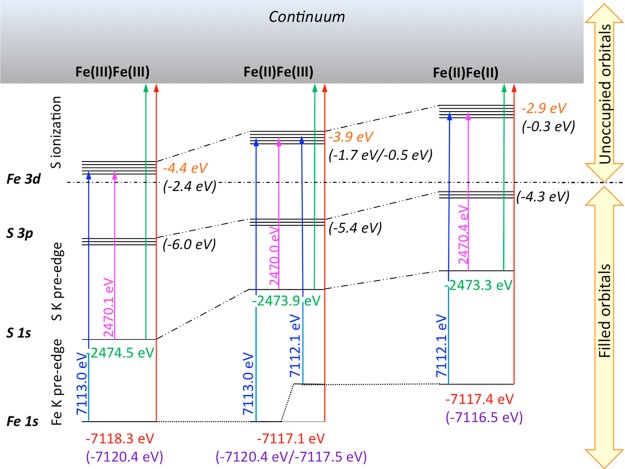
As shown in Figure 4, by using the S 1s edge energy, together with the S and Fe K-edge pre-edge transition energies, the relative energetic positions of the unoccupied 3d manifold for this series can be determined. Specifically, the S K-edge pre-edge energy is used to determine the sulfur 1s to Fe 3d transition energy for the entire series. We note that the pre-edge transition energy corresponds to the S 1s to LUMO transitions, i.e., transitions to the unoccupied Fe 3d orbitals. For simplicity Figure 4 depicts the average energy of all unoccupied Fe 3d orbitals. We note that the occupied Fe 3d orbitals are at lower energy than the filled S 3p orbitals (due to an inverted energy level scheme).68 Hence, for clarity, the occupied 3d orbitals are not depicted in Figure 4, as they are not probed in an XAS measurement.69 Assuming that the S K-edge approximates the continuum, the S rising edge inflection point is used to correct for the relative differences in 1s ionization energy. Comparison to the Fe 1s to 3d transition energies then allows for the relative shifts in the Fe 1s core energies to be assessed. In the Computational Details section a similar correlation is made based on theory.
Figure 4.
Relative energies of the Fe 1s, S 1s, S 3p, and Fe 3d levels based on the Fe K- and S K-edge pre-edge and edge XAS transition energies. The arrows show the experimental energy for 1s to LUMO transitions for each model complex (written in pink for S and blue for Fe); the ionization energies (based on rising edge inflections) are written in red for Fe and green for S and marked with arrows. Calculated Fe 1s orbital energies (based on broken symmetry DFT calculations) are written in purple in parentheses. Together these results provide the average energies for the filled S 3p and empty antibonding Fe 3d molecular orbitals. The values derived from experiment are shown in orange italics, and the values from theory (based on broken symmetry DFT calculations) are given in black italics in parentheses.
On the basis of the present combined results of experimental X-ray spectra, we are able to quantify the relative d-manifold shifts in this series and observe a destabilization from −4.4 to −3.9 to −2.9 eV upon going from the diferric to the mixed-valent to the diferrous. We note that the values in parentheses in Figure 4 are derived from ground state DFT orbital energies and are discussed further in the Computational Details section. This indicates that while the difference between the diferrous and mixed-valent is not very pronounced at the Fe K-edge, there are nonetheless measurable changes in the d-manifold energies, which translate into observable shifts from the S K-edge XAS. The lack of change at the Fe K-edge likely derives from a canceling effect due to shifts in the Fe 1s core levels, which do not contribute to the S K-edge. This highlights the important complementary information that the S K-edge provides for assessing the electronic structure in FeS clusters.
C.1.3. Fe Kβ XES
Fe Kβ XES mainline and valence-to-core region spectra of all three Fe2S2 compounds are shown in Figure 5 (top). The more intense and lower in energy so-called Kβ mainline spectra (Figure 5, top left) arise from the fluorescence occurring after Fe 3p electrons refill the Fe 1s core-hole.70 Due to the 3p–3d exchange, this feature is split into two peaks: the Kβ1,3 and Kβ′. To higher energy, the so-called VtC XES (Figure 5, top right) features arise from transitions from filled ligand np/ns orbitals to the metal 1s core-hole (Kβ2,5/Kβ″ features), which gain intensity though Fe np mixing into filled valence orbitals.36,71,72
Figure 5.
Fe X-ray emission spectra (XES) of diferric (red), mixed-valent (blue), and diferrous (black) Fe2S2 clusters: mainline (top left) and second-derivative spectra (bottom left; smoothed with second-order Savitzky–Golay algorithm); valence-to-core (top right) and second-derivative spectra (bottom right). Derivative spectra were smoothed using the second-order polynomial Savitzky–Golay algorithm in order to obtain better peak definition.
Despite the changes in Fe oxidation states in the Fe2S2 compounds, the energies and shapes of the mainlines for all three forms are superimposable within the experimental resolution. This observation appears to contradict standard interpretations of the Kβ mainline, where it is generally assumed that the decreasing spin state (in this case upon reduction of Fe3+ to Fe2+) should decrease the 3p–3d exchange coupling and thus decrease the splitting of the Kβ1,3 and Kβ′.73,74 The fact that the mainlines are superimposable indicates that the decrease in spin state is exactly canceled by a decrease in covalency. This is consistent with recent studies by Pollock et al.75 and serves as a cautionary note against using Kβ mainlines as an isolated probe of spin state.76,77
While the Fe Kβ mainlines of this series are effectively superimposable, to higher energy in the VtC XES region, clear changes are observable (Figure 5, top right). The diferric species has the most intense VtC region, consistent with shorter, more covalent bonds. As seen in second derivatives (Figure 5 bottom, right), the diferric and mixed-valent species have similar valence-to-core maxima at approximately 7109.7 eV, while the diferrous maximum appears to lower energy (at approximately 7107.7 eV). Here it is of interest to note that the energetic trends are opposite of what was observed at the Fe K-edge XAS, where the diferrous and mixed-valent are energetically very similar. This suggests that for the mixed-valent and diferrous complexes, the shifts in the Fe 1s core energies are largely compensated by shifts in the ligand valence orbital energies. In contrast, in the diferrous species, this is not the case. These trends are graphically shown in Figure 4. These results highlight the complementarity of using both XAS and XES to probe the electronic structure of FeS complexes.
D. Calculations
In order to obtain more quantitative insights into and interpretation of the experimental data, the XAS and XES spectra were calculated using TDDFT and ground-state DFT protocols, respectively. Calculations were performed on geometry-optimized structures on the BS antiferromagnetic solution (coordinates provided in the SI and Figure S5). The resulting electronic structures were consistent with antiferromagnetically coupled d5:d5, d6:d5, and d6:d6 ground states for the diferric, mixed-valent, and diferrous complexes, respectively. In all cases, the ground states are highly covalent, with the dominant bonding contribution coming from the bridging sulfides. Besides “standard” TDDFT approaches for calculating the Fe K-edge pre-edge region,52 we also explored the use of range-separated hybrid DFT methods as a means to better model the long-range potential and thus to calculate further into the rising edge.
Further, in addition to the TDDFT calculations, we performed multiple scattering (MS)-based calculations of the Fe K-edge XANES spectra, using both the crystal structures and the DFT-optimized structures. While the strength of DFT calculations is generally in simulating the lower energy transitions to low-lying molecular orbitals localized on the photoabsorber, MS-based approaches are better able to capture the full XANES region. In the context of the present study, we were particularly interested in capturing the changes that occur in the white line intensity at ∼7125 eV upon successive oxidations. These results are discussed in detail in the section Multiple Scattering Calculations of the Fe K-Edge XANES.
Comparisons of the experimental and calculated spectra are shown in Figure 6. The Fe K-edge pre-edges (top), S K-edge pre-edges (middle), and VtC XES (bottom) spectra are all well modeled by the calculations, with the general trends in both energies and intensities being reasonably reproduced. The largest outlier is the diferrous complex, for which the calculated Fe K-edge pre-edge and Fe VtC XES are somewhat too low in energy, whereas the corresponding S K-edge pre-edge is slightly too high in energy. These trends are consistent with previous observations that for highly ionic species the Fe orbital energies are more destabilized than for those complexes with a lower total charge.51
Importantly, the calculations are able to quantitatively capture many of the empirical trends observed in the experimental data. Namely, the Fe K-edge pre-edge intensities largely correlate with the number of d-holes in the system. As the complex is reduced, the number of d-holes decreases, the covalency decreases, and the Fe K-edge pre-edge is reduced in both energy and intensity. Quantitatively, the oscillator strength for the dipole-allowed transitions in the pre-edge region decreases from 3.9 au to 2.8 au to 2.2. au on going from the diferric to the mixed-valent to the diferrous. At the S K-edge one similarly observes a reduction in intensity upon complex reduction. This reflects the decrease in covalency of the Fe–S bonds and its manifestation in a decrease in the S 3p character over the unoccupied Fe 3d orbitals. This is reflected in a decrease in the total S 1s to 3p oscillator strength in the pre-edge region, which decreases from 182 au to 132 au to 76 au upon successive reductions. As noted above, the S K-edge pre-edge energy trend is reversed relative to the trend at the Fe K-edge pre-edge, due to the fact that the Fe 3d manifold has become destabilized with respect to the sulfur 1s core, which is faithfully reproduced by the calculations. This is an important finding, as it illustrates the utility of using the S K-edge as a complementary probe of Fe oxidation state.
The previously discussed contributions of covalency and orbital energetics are also reproduced in the VtC XES calculations. The calculations show that the Kβ2,5 emission has strong contributions arising from transitions from the filled S 3p orbitals to the Fe 1s core-hole. The allowed intensity derives from the mixing of Fe np character into the filled ligand orbitals. Minor contributions from the filled N 2p’s are observed for all of the investigated complexes. As has been noted previously, the weak Kβ″ features, while predicted by calculations, are often not observable in the experimental data.54,78
In order to derive a more holistic picture of the changes that occur upon reduction, we have used the experimental pre-edge and edge transition energies (further supported by calculations) to derive a simple energy level scheme for this series of complexes, as described above and displayed in Figure 4. The relative energies of the Fe 1s, S 1s, S 3p, and Fe 3d manifolds for the diferric, mixed-valent, and diferrous complexes, as derived from the broken symmetry DFT calculations, are shown in parentheses in Figure 4. Full details of the individual MO orbital energies are provided in Tables S1–S3. The reported d-manifold energies in Figure 4 correspond to the average of the LUMO energies (for the diferrous and diferric complexes). In the case of the mixed-valent species the average energy is reported for each iron site separately. We note that this separation is not readily feasible from the experimental data due to the relatively low resolution of the data. As expected, the diferric complex has the most stabilized core and valence orbital energies. Due to the localized nature of the mixed-valent species, two different Fe 1s core level energies are observed both experimentally (based on the pre-edge) and computationally. This observation may explain the lack of an energy shift in the Fe K-edge rising edge position, as it suggests that the edge should be composed of “localized” Fe2+ and Fe3+ features and not a simple averaged “Fe2.5+” spectrum (Figure S4 in the SI). The relative differences for class III delocalized vs valence-trapped Fe dimers are addressed in more detail in the section that follows.
We note that Figure 4 also highlights the ability to use multiple edges in order to extract the relative energies of the 3d manifold. Here the changes in the electronic structure are clearly manifest in the destabilization of the average 3d manifold energy from −2.4 eV to −1.1 eV (an average of −1.7 and −0.5 eV) to −0.3 eV on going from the diferric to mixed-valent to diferrous. This schematic provides a quantitative analysis of many of the empirical trends discussed above. While there are discrepancies between the values derived from experiment vs theory in Figure 4, the trends are generally in good agreement. We note that some of these discrepancies may derive from the fact that relaxation due to the presence of an Fe 1s or S 1s core will contribute to the observed experimental energies, and the contribution of the core-hole is not captured in these calculations.
Calculation of Rising Edges
An important observation that was made for the Fe K-edge XAS data for the present series of iron–sulfur complexes is that the rising edge does not shift on going from the diferrous to the mixed-valent complex. Similar observations were recently reported by Driess and co-workers27 for an analogous series of complexes, suggesting that this trend may be generalizable.
While the TDDFT calculations presented in the preceding section generally do a good job of reproducing the pre-edge region, the calculations are known to break down in the edge region due to failure of the utilized DFT functionals to properly model the long-range potential. In order to address this shortcoming, we have also calculated the Fe K-edge XAS spectra utilizing the range-separated hybrid functional CAM-B3LYP, which should better model the long-range potential and thus capture the rising edge. At the same time we also increased the basis set to the diffuse ma-def2-TZVPP.41,42 The results of these calculations are shown in Figure 7. In order to test our hypothesis that the iron atoms in the mixed-valent complexes may be behaving as localized “Fe2+” and “Fe3+” sites, we tested both the fully delocalized high-spin solution with ferromagnetically (F) coupled iron atoms and the broken symmetry solution with antiferromagnetically (AF) coupled iron atoms for all three complexes. More details on the geometric and electronic structure of the F and AF solution are provided in the SI (Figures S5 and S6). The spin density plots in Figure S6 and their corresponding Mulliken spin populations are in complete agreement with a trapped valence ground state for the AF solution and a fully delocalized ground state for the F solution.
Figure 7.

TD-DFT calculations (CAM-B3LYP/ma-def2-TZVPP) of the Fe K-edge XAS using a range-separated hybrid functional to model the rising edge features. AF corresponds to the antiferromagnetically coupled broken symmetry solution. F corresponds to the ferromagnetically coupled high-spin solution.
Figure 7 displays all AF coupled solutions as solid lines and the F coupled solutions as dashed lines. Interestingly, the experimentally observed trends in the rising edge energy are reproduced only for the AF series. In this series, the calculated rising edges are effectively the same for the diferrous and mixed-valent complex, while the diferric appears to higher energy. In contrast, inspection of the F series shows a systematic increase in the edge energy upon increasing oxidation state. While subtle changes are observed for the diferrous and diferric species upon changing from the F to AF solution, the most dramatic changes occur for the mixed-valent complex. The calculated rising edges for the mixed-valent complex nicely highlight the fact that the mixed-valent complex behaves as a localized “Fe2+” and “Fe3+” site at the AF limit, while in the F limit it behaves as an “Fe2.5+” species with a higher energy rising edge, as illustrated in Figure 8. This suggests that the rising edge position may serve as a marker for the extent of delocalization.
Figure 8.
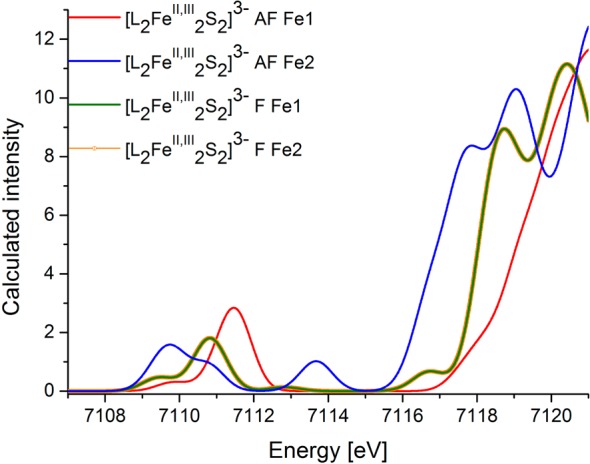
TD-DFT calculations (CAM-B3LYP/ma-def2-TZVPP) of the Fe K-edge XAS spectra for the mixed-valent compound, deconvoluted for each individual iron atom (Fe1, Fe2). AF corresponds to the antiferromagnetically coupled broken symmetry solution. F corresponds to the ferromagnetically coupled high-spin solution.
In addition to the changes in the rising edge region, interesting changes are also observed in the Fe K-edge pre-edge region for all three complexes as the coupling is changed from AF to F. Notably the intensity-weighted average energy (or the first moment) of the pre-edge decreases for the F solutions. This is consistent with the greater stabilization of the d-manifold upon increasing the total spin. Again, we note that the largest changes are observed for the mixed-valent species. Here not only the energy but also the ratio of the peak intensities has changed. We note that the calculated AF solution is in far better agreement with the experimental data, where the second derivative over the pre-edge region (Figure 2 bottom) clearly shows two peaks in an ∼2:3 intensity ratio. In the AF case the two peaks largely reflect the stabilized 1s to 3d alpha transitions of the Fe(II) at lowest energy and the Fe(III) beta transitions to higher energy. The pre-edge intensity dominantly derives from transitions to the t2 set of d orbitals, for which symmetry-mediated Fe d–p mixing is allowed. In the case of the ferromagnetic solution, the complete t2 set of orbitals now appears at approximately the same energy (as all transitions are to the empty beta 3d orbitals), giving rise to the more intense pre-edge peak at ∼7112.5 eV, with the less intense lower energy (7111.3 eV) feature corresponding to quadrupole-allowed transitions into the e-set of orbitals. This emphasizes that the shape and energy distribution in the pre-edge region may also be used to assess the extent of delocalization. This hypothesis however awaits further experimental validation, as to our knowledge no Fe K-edge XAS data on an S = 9/2 Fe2S2 cluster are presently available. Thus far, a ferromagnetically coupled ground state in an Fe2S2 cluster has been observed only in a mutant form of Clostridium pasteurianum ferredoxins,79 for which XAS data are not available. One can, however, draw comparisons to the existing Fe K-edge XAS data on Fe4S4 clusters, which are composed of fully delocalized Fe2S2 subunits. This is addressed further in the Discussion section.
Multiple Scattering Calculations of the Fe K-Edge XANES
In the preceding section, it was shown that a TD-DFT approach in combination with a range-separated hybrid functional can reasonably reproduce the Fe K-edge rising energy trends. This requires a relatively high computational overhead (due to the need to calculate more than 500 roots), but allows for a computationally assisted interpretation of the XAS data to be extended by ∼10 eV above the pre-edge. This approach, however, still fails to model the complete XANES region. For this reason, we also utilized a multiple-scattering-based approach, as implemented in the FEFF code, to model the Fe K-edge XANES spectra. The results of these calculations are presented in Figure 9 (top, left) and illustrate that the general trends in the rising edge features are also generally well reproduced in a multiple-scattering-based approach. However, the changes that were observed in the white line region (i.e., the decrease in intensity at ∼7125 eV upon oxidation) are unfortunately not reproduced by this approach.
Figure 9.
FEFF-calculated XANES spectra for the diferric (red), mixed-valent (blue), and diferrous (black) complexes (top left) and Fe K-edge XAS experimental data (top right). Comparison of the calculated XANES spectra for each Fe in the mixed-valent AF (antiferromagnetically coupled broken symmetry solution; bottom left) and F cases (ferromagnetically coupled high-spin solution; bottom right).
It is also of interest to explore to what extent the multiple-scattering-based calculations are sensitive to the use of the F or AF mixed-valent structures of [L2Fe2S2]3–. These structures together with the relevant metrical parameters are provided in Figure S5 in the SI. Figure 9 (bottom, left) displays the FEFF calculations for the two structurally inequivalent iron atoms that arise in the AF solution. Here (as was also seen in the TDDFT calculations), the two iron atoms are also spectroscopically inequivalent, with the “more oxidized” Fe appearing ∼0.2 eV to higher energy. In contrast, for the structurally identical iron atoms in the F solution the multiple scattering calculations result in fully superimposable spectra (Figure 9, bottom, right). We note, however, that the changes between the F and AF solutions using multiple-scattering calculations are much smaller than the changes observed using TDDFT, where a shift of ∼0.9 eV was observed upon going from the AF to F solution. This suggests that while the changes in structural parameters account for the general trends, additional electronic structural input is required for more quantitative agreement.
E. Discussion
Herein, a systematic X-ray spectroscopic study of diferric, mixed-valent, and diferrous Fe2S2 model complexes is presented. We have demonstrated that a unified picture of the electronic structure can be obtained through the parallel analysis of Fe and S K-edge XAS and Fe Kβ XES spectra. However, several cautionary notes have emerged from the present study. Namely, (1) Fe K-edge rising edges do not necessarily shift upon one-electron reduction and (2) canceling effects in spin state changes and covalency may result in superimposable Fe Kβ mainlines for iron–sulfur complexes in different redox states. The latter is particularly important, as it serves as a cautionary note for using Kβ mainlines as an isolated measure of electronic structure. However, oxidation state information may still be extracted in the case of the Fe K-edge data by careful comparison with complementary S K-edge and Fe VtC XES data. This observation allows one to utilize X-ray spectroscopic data for a more detailed electronic structural description. The quantitative information that can be obtained from these data is further supported by DFT calculations of the Fe and S K-edges and Fe VtC XES data. By combining the information from multiple spectroscopic measurements, we have shown that the shifts in the redox-active molecular orbitals in Fe2S2 model complexes can be quantified.
Further, through a detailed analysis of the Fe K-edge data, together with computations, we have assessed the reason for an absence of an Fe K-edge edge shift on going from the diferrous complex to the mixed-valent complex. In the case of a trapped valence complex (S = 1/2), as is the case in the present series, localized “Fe2+” and “Fe3+” edge transitions are observed, resulting in a low-energy “Fe2+” feature that overlaps with the diferrous spectrum. In contrast, we have shown computationally that a fully delocalized mixed-valent complex (S = 9/2) will have a rising edge that is intermediate between the diferrous and the diferric analogues, i.e., an “Fe2.5+” transition energy. We have also observed that there is a systematic decrease in the intensity of the white line feature of iron–sulfur clusters upon successive oxidations. In light of these observations, it is of interest to reevaluate some of the seeming discrepancies in the existing literature.
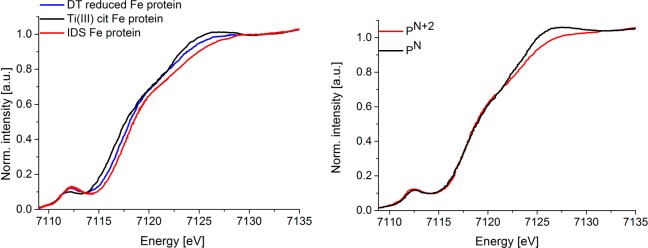
As noted in the Introduction, previous studies of Musgrave and co-workers indicated that oxidation of one out of four iron atoms was observable in the Fe4S4 site of the nitrogenase iron protein22 (Figure 10 left), while oxidation of two out of eight iron atoms in the P-cluster22 resulted in no observable shift in the Fe K-edge rising edge (Figure 10 right). The present analysis provides an explanation for these observations. Namely, the [Fe4S4]2+ cluster of the iron protein has fully delocalized mixed-valent “Fe2.5+” pairs.80 In contrast, the two-electron-oxidized P-cluster has contributions from both localized Fe2+–Fe3+ and delocalized Fe2.5+ dimer configurations.81 Hence edge shifts may be expected in the former case, but not in the latter.
Figure 10.
Normalized Fe X-ray absorption spectra (XAS) of (left) sodium dithionate reduced Fe protein [Fe4S4]+ (blue), Ti(III) citrate reduced Fe protein [Fe4S4]0 (black), and indigo disulfonate oxidized Fe protein [Fe4S4]2+ (red)22 and (right) all-ferrous P-cluster (PN black) and two-electron-oxidized P-cluster (PN+2 red) (left) [copyright (1998) Society of Biological Inorganic Chemistry].23
Interestingly, for both the iron protein and the P-cluster, as well as the present series of complexes, a systematic decrease in the white line intensity (at ∼7125 eV) is always observed upon oxidation. Unfortunately, neither DFT nor multiple-scattering-based approaches are presently able to reproduce this trend. It does indicate, however, that the white line intensity may be used as an empirical fingerprint for changes in oxidation state in iron–sulfur clusters.
In this context, it is of interest to compare the Fe K-edge data for the P-cluster, FeMoco, and the MoFe protein (containing both FeMoco and the P-cluster), as shown in Figure 11. We note that the FeMoco spectrum was based on subtraction of the protein-bound P-cluster from MoFe protein. Hence, it represents the resting S = 3/2 FeMoco bound to MoFe protein. One notes three major spectral trends when comparing the Fe K-edge XAS data of the all-ferrous P-cluster to that of resting FeMoco: (1) FeMoco shows a significant decrease in the white line intensity at ∼7125 eV relative to the P-cluster, (2) FeMoco has increased pre-edge intensity, and (3) the rising edge energies of FeMoco and the P-cluster are superimposable. Currently, the proposed iron oxidation state distributions in the MoFe7S9C cluster are Mo(III):6Fe(III):1Fe(II) ([MoFe7S9C]1+), Mo(III):4Fe(III):3Fe(II) ([MoFe7S9C]1–), or Mo(III):2Fe(III):5Fe(II) ([MoFe7S9C]3–). The trends in the white line appear to disfavor the last possibility. This also appears consistent with recent spatially resolved anomalous dispersion (SpReAD) studies by Spatzal et al., which favor a Mo(III):4Fe(III):3Fe(II) assignment.82 We emphasize, however, that the SpReAD data indicate only that three irons appear “more reduced” than the other four, and the possibility that this reflects contributions from mixed-valent iron sites cannot be ruled out. On the basis of the results presented here, however, the lack of a shift in the rising edge on going from the P-cluster to FeMoco could be rationalized if FeMoco is composed of localized Fe2+–Fe3+ sites as opposed to delocalized Fe2.5+ dimer configurations. This, however contradicts theoretical interpretations of the electronic structure, which favor the presence of valence delocalized mixed-valent pairs.15,83,84 Additionally, one must exercise caution, as the contribution of the interstitial carbon atom to overall edge shape (including the pre-edge, rising edge, and white line intensity) is not known. A more quantitative analysis of the FeMoco oxidation state distribution will be the focus of future studies.
Figure 11.
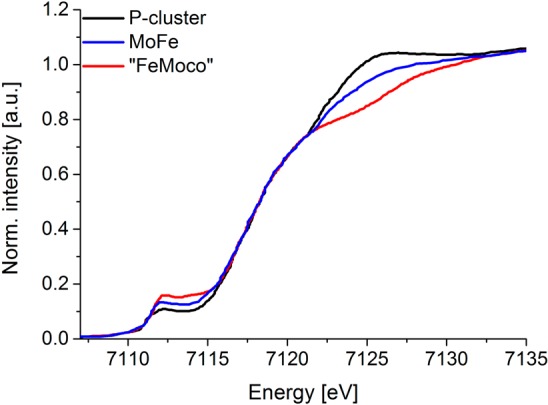
Normalized Fe X-ray absorption spectra (XAS) of protein-bound FeMo cofactor of nitrogenase (red; based on subtraction of protein-bound P-cluster from MoFe), MoFe protein (blue), and protein-bound P-cluster (black)18 [copyright (2006) National Academy of Sciences, USA].
In summary, we have presented Fe K-, S K-edge XAS and Fe Kβ XES data on a series of Fe2S2 complexes, which span three redox levels. We have shown that through parallel analysis of the experimental data, together with calculations, a detailed picture of the electronic structure emerges. In addition, we have shown that using Kβ XES mainlines and Fe K-edges XAS as “fingerprints” for oxidation states must be treated with caution. However, through detailed analysis of the Fe K-edge data, together with other experimental and computational analysis, insight into the extent of cluster delocalization may be obtained. These observations have been utilized to assess existing literature Fe K-edge XAS data on the iron protein, P-cluster, and FeMoco sites of nitrogenase. We have shown that these data support fully delocalized mixed-valent iron pairs in the iron protein, while in the P-cluster localized trapped valence Fe2+–Fe3+ pairs also contribute to the spectra. Finally, this analysis has been applied to the FeMoco active site and motivates the need for more detailed and quantitative studies of the Fe K-edge data. The present study serves as an important reference for future X-ray spectroscopic studies of iron–sulfur clusters, as well as other highly covalent transition metal clusters.
Acknowledgments
J.K.K., A.W.H., R.B., F.A.L., and S.D. thank the Max Planck Society for funding. S.D. acknowledges funding from the European Research Council under the European Union’s Seventh Framework Programme (FP/2007-2013)/ERC Grant Agreement No. 615414. F.M., A.A., and C.E.S. gratefully acknowledge funding from the Deutsche Forschungsgemeinschaft (IRTG 1422: Metal Sites in Biomolecules: Structures, Regulation and Mechanisms). A.A. also thanks the Cusanuswerk for a Ph.D. fellowship. R.B. acknowledges support from the Icelandic Research Fund, Grant No. 141218051. Use of the Stanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, is supported by the U.S. Department of Energy, Office of Basic Energy Sciences, under Contract No. DE-AC02-76SF00515. The SSRL Structural Molecular Biology Program is supported by the DOE Office of Biological and Environmental Research and by the National Institutes of Health, National Institute of General Medical Sciences (including P41GM103393). The contents of this publication are solely the responsibility of the authors and do not necessarily represent the official views of NIGMS or NIH. The authors thank CNPEM-LNLS for granting beamtime and the SXS beamline staff for the support during the experiments.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.inorgchem.6b00295.
(PDF)
Author Present Address
⊥ Science Institute, University of Iceland, Dunhagi 3, IS-107 Reykjavik, Iceland.
Author Present Address
∥ Centro Nacional de Pesquisa em Energia e Materiais, Brazilian Synchrotron Light Laboratory–LNLS, CP 6192, 13084-971 Campinas, SP, Brazil.
The authors declare no competing financial interest.
Supplementary Material
References
- Colbert C. L.; Couture M. M. J.; Eltis L. D.; Bolin J. T. Structure 2000, 8, 1267. 10.1016/S0969-2126(00)00536-0. [DOI] [PubMed] [Google Scholar]
- Lovenberg W.; Sobel B. E. Proc. Natl. Acad. Sci. U. S. A. 1965, 54, 193. 10.1073/pnas.54.1.193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howard J. B.; Rees D. C. Chem. Rev. 1996, 96, 2965. 10.1021/cr9500545. [DOI] [PubMed] [Google Scholar]
- Lee S. C.; Lo W.; Holm R. H. Chem. Rev. 2014, 114, 3579. 10.1021/cr4004067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seefeldt L. C.; Hoffman B. M.; Dean D. R. Annu. Rev. Biochem. 2009, 78, 701. 10.1146/annurev.biochem.78.070907.103812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ribbe M. W.; Hu Y. L.; Hodgson K. O.; Hedman B. Chem. Rev. 2014, 114, 4063. 10.1021/cr400463x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beinert H.; Holm R. H.; Münck E. Science 1997, 277, 653. 10.1126/science.277.5326.653. [DOI] [PubMed] [Google Scholar]
- Fontecave M. Nat. Chem. Biol. 2006, 2, 171. 10.1038/nchembio0406-171. [DOI] [PubMed] [Google Scholar]
- Johnson D. C.; Dean D. R.; Smith A. D.; Johnson M. K. Annu. Rev. Biochem. 2005, 74, 247. 10.1146/annurev.biochem.74.082803.133518. [DOI] [PubMed] [Google Scholar]
- Mettert E. L.; Kiley P. J. Biochim. Biophys. Acta, Mol. Cell Res. 2015, 1853, 1284. 10.1016/j.bbamcr.2014.11.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rees D. C.; Howard J. B. Curr. Opin. Chem. Biol. 2000, 4, 559. 10.1016/S1367-5931(00)00132-0. [DOI] [PubMed] [Google Scholar]
- Thorneley R. N. F.; Lowe D. J. J. Biol. Inorg. Chem. 1996, 1, 576. 10.1007/s007750050095. [DOI] [Google Scholar]
- Hoffman B. M.; Lukoyanov D.; Yang Z. Y.; Dean D. R.; Seefeldt L. C. Chem. Rev. 2014, 114, 4041. 10.1021/cr400641x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lukoyanov D.; Pelmenschikov V. M. N.; Laryukhin M.; Yang T. C.; Noodleman L.; Dean D. R.; Case D. A.; Seefeldt L. C.; Hoffman B. M.; Yang Z. Y.; Khadka N.; Dean D. R.; Seefeldt L. C.; Hoffman B. M. J. Am. Chem. Soc. 2015, 137, 3610. 10.1021/jacs.5b00103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bjornsson R.; Lima F. A.; Spatzal T.; Weyhermüller T.; Glatzel P.; Bill E.; Einsle O.; Neese F.; DeBeer S. Chem. Sci. 2014, 5, 3096. 10.1039/C4SC00337C. [DOI] [Google Scholar]
- Bjornsson R.; Neese F.; Schrock R. R.; Einsle O.; DeBeer S. J. Biol. Inorg. Chem. 2015, 20, 447. 10.1007/s00775-014-1230-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris T. V.; Szilagyi R. K. Inorg. Chem. 2011, 50, 4811. 10.1021/ic102446n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corbett M. C.; Hu Y. L.; Fay A. W.; Ribbe M. W.; Hedman B.; Hodgson K. O. Proc. Natl. Acad. Sci. U. S. A. 2006, 103, 1238. 10.1073/pnas.0507853103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corbett M. C.; Hu Y. L.; Naderi F.; Ribbe M. W.; Hedman B.; Hodgson K. O. J. Biol. Chem. 2004, 279, 28276. 10.1074/jbc.M403156200. [DOI] [PubMed] [Google Scholar]
- Fay A. W.; Blank M. A.; Lee C. C.; Hu Y. L.; Hodgson K. O.; Hedman B.; Ribbe M. W. J. Am. Chem. Soc. 2010, 132, 12612. 10.1021/ja1019657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fay A. W.; Blank M. A.; Lee C. C.; Hu Y. L.; Hodgson K. O.; Hedman B.; Ribbe M. W. Angew. Chem., Int. Ed. 2011, 50, 7787. 10.1002/anie.201102724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Musgrave K. B.; Angove H. C.; Burgess B. K.; Hedman B.; Hodgson K. O. J. Am. Chem. Soc. 1998, 120, 5325. 10.1021/ja980598z. [DOI] [Google Scholar]
- Musgrave K. B.; Liu H. I.; Ma L.; Burgess B. K.; Watt G.; Hedman B.; Hodgson K. O. J. Biol. Inorg. Chem. 1998, 3, 344. 10.1007/s007750050243. [DOI] [Google Scholar]
- Fitzpatrick J.; Kalyvas H.; Filipovic M. R.; Ivanovic-Burmazovic I.; MacDonald J. C.; Shearer J.; Kim E. J. Am. Chem. Soc. 2014, 136, 7229. 10.1021/ja5024207. [DOI] [PubMed] [Google Scholar]
- Saouma C. T.; Kaminsky W.; Mayer J. M. J. Am. Chem. Soc. 2012, 134, 7293. 10.1021/ja3019324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X. D.; Zhang W.; Duncan J. S.; Lee S. C. Inorg. Chem. 2012, 51, 12891. 10.1021/ic301868m. [DOI] [PubMed] [Google Scholar]
- Yao S. M. F.; Lindenmaier N.; Rudolph R.; Blom B.; Adelhardt M.; Sutter J.; Mebs S.; Haumann M.; Meyer K.; Kaupp M.; Driess M. Angew. Chem., Int. Ed. 2015, 54, 12506. 10.1002/anie.201506788. [DOI] [PubMed] [Google Scholar]
- Albers A.; Bayer T.; Demeshko S.; Dechert S.; Meyer F. Chem. - Eur. J. 2013, 19, 10101. 10.1002/chem.201301760. [DOI] [PubMed] [Google Scholar]
- Albers A.; Demeshko S.; Dechert S.; Bill E.; Bothe E.; Meyer F. Angew. Chem., Int. Ed. 2011, 50, 9191. 10.1002/anie.201100727. [DOI] [PubMed] [Google Scholar]
- Albers A.; Demeshko S.; Proepper K.; Dechert S.; Bill E.; Meyer F. J. Am. Chem. Soc. 2013, 135, 1704. 10.1021/ja311563y. [DOI] [PubMed] [Google Scholar]
- Stern E. A.; Heald S. M. Rev. Sci. Instrum. 1979, 50, 1579. 10.1063/1.1135763. [DOI] [PubMed] [Google Scholar]
- Lytle F. W.; Greegor R. B.; Sandstrom D. R.; Marques E. C.; Wong J.; Spiro C. L.; Huffman G. P.; Huggins F. E. Nucl. Instrum. Methods Phys. Res., Sect. A 1984, 226, 542. 10.1016/0168-9002(84)90077-9. [DOI] [Google Scholar]
- Ravel B.; Newville M. J. Synchrotron Radiat. 2005, 12, 537. 10.1107/S0909049505012719. [DOI] [PubMed] [Google Scholar]
- Tolentino H.; Compagnon-Cailhol V.; Vicentin F. C.; Abbate M. J. Synchrotron Radiat. 1998, 5, 539. 10.1107/S0909049597016087. [DOI] [PubMed] [Google Scholar]
- Sokaras D.; Weng T. C.; Nordlund D.; Alonso-Mori R.; Velikov P.; Wenger D.; Garachtchenko A.; George M.; Borzenets V.; Johnson B.; Rabedeau T.; Bergmann U. Rev. Sci. Instrum. 2013, 84, 053102. 10.1063/1.4803669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee N.; Petrenko T.; Bergmann U.; Neese F.; DeBeer S. J. Am. Chem. Soc. 2010, 132, 9715. 10.1021/ja101281e. [DOI] [PubMed] [Google Scholar]
- Neese F. WIREs Comput. Mol. Sci. 2012, 2, 73. 10.1002/wcms.81. [DOI] [Google Scholar]
- Becke A. D. Phys. Rev. A: At., Mol., Opt. Phys. 1988, 38, 3098. 10.1103/PhysRevA.38.3098. [DOI] [PubMed] [Google Scholar]
- Perdew J. P. Phys. Rev. B: Condens. Matter Mater. Phys. 1986, 33, 8822. 10.1103/PhysRevB.33.8822. [DOI] [PubMed] [Google Scholar]
- van Wüllen C. J. Chem. Phys. 1998, 109, 392. 10.1063/1.476576. [DOI] [Google Scholar]
- Pantazis D. A.; Chen X. Y.; Landis C. R.; Neese F. J. Chem. Theory Comput. 2008, 4, 908. 10.1021/ct800047t. [DOI] [PubMed] [Google Scholar]
- Weigend F.; Ahlrichs R. Phys. Chem. Chem. Phys. 2005, 7, 3297. 10.1039/b508541a. [DOI] [PubMed] [Google Scholar]
- Klamt A.; Schüürmann G. J. Chem. Soc., Perkin Trans. 2 1993, 799. 10.1039/P29930000799. [DOI] [Google Scholar]
- Grimme S.; Antony J.; Ehrlich S.; Krieg H.. J. Chem. Phys. 2010, 132, 154104. 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
- Grimme S.; Ehrlich S.; Goerigk L. J. Comput. Chem. 2011, 32, 1456. 10.1002/jcc.21759. [DOI] [PubMed] [Google Scholar]
- Yanai T.; Tew D. P.; Handy N. C. Chem. Phys. Lett. 2004, 393, 51. 10.1016/j.cplett.2004.06.011. [DOI] [Google Scholar]
- Zheng J. J.; Xu X. F.; Truhlar D. G. Theor. Chem. Acc. 2011, 128, 295. 10.1007/s00214-010-0846-z. [DOI] [Google Scholar]
- Izsák R.; Neese F. J. Chem. Phys. 2011, 135, 144105. 10.1063/1.3646921. [DOI] [PubMed] [Google Scholar]
- Neese F.; Wennmohs F.; Hansen A.; Becker U. Chem. Phys. 2009, 356, 98. 10.1016/j.chemphys.2008.10.036. [DOI] [Google Scholar]
- Neese F. J. Am. Chem. Soc. 2006, 128, 10213. 10.1021/ja061798a. [DOI] [PubMed] [Google Scholar]
- DeBeer George S.; Petrenko T.; Neese F. J. Phys. Chem. A 2008, 112, 12936. 10.1021/jp803174m. [DOI] [PubMed] [Google Scholar]
- Chandrasekaran P.; Stieber S. C. E.; Collins T. J.; Que L.; Neese F.; DeBeer S. Dalton Trans. 2011, 40, 11070. 10.1039/c1dt11331c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeBeer George S.; Neese F. Inorg. Chem. 2010, 49, 1849. 10.1021/ic902202s. [DOI] [PubMed] [Google Scholar]
- Beckwith M. A.; Roemelt M.; Collomb M. N.; DuBoc C.; Weng T. C.; Bergmann U.; Glatzel P.; Neese F.; DeBeer S. Inorg. Chem. 2011, 50, 8397. 10.1021/ic200970t. [DOI] [PubMed] [Google Scholar]
- Rehr J. J.; Kas J. J.; Prange M. R.; Sorini A. P.; Campbell L. W.; Vila F. D. AIP Conf. Proc. 2006, 882, 85. 10.1063/1.2644437. [DOI] [Google Scholar]
- Rehr J. J.; Kas J. J.; Vila F. D.; Prange M. P.; Jorissen K. Phys. Chem. Chem. Phys. 2010, 12, 5503. 10.1039/b926434e. [DOI] [PubMed] [Google Scholar]
- Bair R. A.; Goddard W. A. III Phys. Rev. B: Condens. Matter Mater. Phys. 1980, 22, 2767. 10.1103/PhysRevB.22.2767. [DOI] [Google Scholar]
- Kau L. S.; Spira-Solomon D. J.; Penner-Hahn J. E.; Hodgson K. O.; Solomon E. I. J. Am. Chem. Soc. 1987, 109, 6433. 10.1021/ja00255a032. [DOI] [Google Scholar]
- DeBeer S. Methods Mol. Biol. 2011, 766, 165. 10.1007/978-1-61779-194-9_11. [DOI] [PubMed] [Google Scholar]
- Kowalska J.; DeBeer S. Biochim. Biophys. Acta, Mol. Cell Res. 2015, 1853, 1406. 10.1016/j.bbamcr.2014.11.027. [DOI] [PubMed] [Google Scholar]
- Westre T. E.; Kennepohl P.; DeWitt J. G.; Hedman B.; Hodgson K. O.; Solomon E. I. J. Am. Chem. Soc. 1997, 119, 6297. 10.1021/ja964352a. [DOI] [Google Scholar]
- Tomson N. C.; Williams K. D.; Dai X. L.; Sproules S.; DeBeer S.; Warren T. H.; Wieghardt K. Chem. Sci. 2015, 6, 2474. 10.1039/C4SC03294B. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walroth R. C.; Uebler J. W. H.; Lancaster K. M. Chem. Commun. 2015, 51, 9864. 10.1039/C5CC01827G. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glaser T.; Hedman B.; Hodgson K. O.; Solomon E. I. Acc. Chem. Res. 2000, 33, 859. 10.1021/ar990125c. [DOI] [PubMed] [Google Scholar]
- Glaser T.; Rose K.; Shadle S. E.; Hedman B.; Hodgson K. O.; Solomon E. I. J. Am. Chem. Soc. 2001, 123, 442. 10.1021/ja002183v. [DOI] [PubMed] [Google Scholar]
- Rose K.; Shadle S. E.; Glaser T.; de Vries S.; Cherepanov A.; Canters G. W.; Hedman B.; Hodgson K. O.; Solomon E. I. J. Am. Chem. Soc. 1999, 121, 2353. 10.1021/ja983455l. [DOI] [Google Scholar]
- Anxolabehere-Mallart E.; Glaser T.; Frank P.; Aliverti A.; Zanetti G.; Hedman B.; Hodgson K. O.; Solomon E. I. J. Am. Chem. Soc. 2001, 123, 5444. 10.1021/ja010472t. [DOI] [PubMed] [Google Scholar]
- Noodleman L.; Peng C. Y.; Case D. A.; Mouesca J. M. Coord. Chem. Rev. 1995, 144, 199. 10.1016/0010-8545(95)07011-L. [DOI] [Google Scholar]
- Solomon E. I.; Hedman B.; Hodgson K. O.; Dey A.; Szilagyi R. K. Coord. Chem. Rev. 2005, 249, 97. 10.1016/j.ccr.2004.03.020. [DOI] [Google Scholar]
- Glatzel P.; Juhin A. In Local Structural Characterisation; John Wiley & Sons, Ltd: Chichester, UK, 2013; p 89. [Google Scholar]
- Pollock C. J.; DeBeer S. Acc. Chem. Res. 2015, 48, 2967. 10.1021/acs.accounts.5b00309. [DOI] [PubMed] [Google Scholar]
- Smolentsev G.; Soldatov A. V.; Messinger J.; Merz K.; Weyhermüller T.; Bergmann U.; Pushkar Y.; Yano J.; Yachandra V. K.; Glatzel P. J. Am. Chem. Soc. 2009, 131, 13161. 10.1021/ja808526m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glatzel P.; Bergmann U. Coord. Chem. Rev. 2005, 249, 65. 10.1016/j.ccr.2004.04.011. [DOI] [Google Scholar]
- Vankó G.; Neisius T.; Molnar G.; Renz F.; Karpati S.; Shukla A.; de Groot F. M. F. J. Phys. Chem. B 2006, 110, 11647. 10.1021/jp0615961. [DOI] [PubMed] [Google Scholar]
- Pollock C. J.; Delgado-Jaime M. U.; Atanasov M.; Neese F.; DeBeer S. J. Am. Chem. Soc. 2014, 136, 9453. 10.1021/ja504182n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hugenbruch S.; Shafaat H. S.; Krämer T.; Delgado-Jaime M. U.; Weber K.; Neese F.; Lubitz W.; DeBeer S. Phys. Chem. Chem. Phys. 2016, 10.1039/C5CP07293J. [DOI] [PubMed] [Google Scholar]
- Vankó G.; Bordage A.; Pápai M.; Haldrup K.; Glatzel P.; March A. M.; Doumy G.; Britz A.; Galler A.; Assefa T.; Cabaret D.; Juhin A.; van Driel T. B.; Kjær K. S.; Dohn A.; Møller K. B.; Lemke H. T.; Gallo E.; Rovezzi M.; Németh Z.; Rozsályi E.; Rozgonyi T.; Uhlig J.; Sundström V.; Nielsen M. M.; Young L.; Southworth S. H.; Bressler C.; Gawelda W. J. Phys. Chem. C 2015, 119, 5888. 10.1021/acs.jpcc.5b00557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chandrasekaran P.; Chiang K. P.; Nordlund D.; Bergmann U.; Holland P. L.; DeBeer S. Inorg. Chem. 2013, 52, 6286. 10.1021/ic3021723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crouse B. R.; Meyer J.; Johnson M. K. J. Am. Chem. Soc. 1995, 117, 9612. 10.1021/ja00142a049. [DOI] [Google Scholar]
- Noodleman L.; Lovell T.; Liu T. Q.; Himo F.; Torres R. A. Curr. Opin. Chem. Biol. 2002, 6, 259. 10.1016/S1367-5931(02)00309-5. [DOI] [PubMed] [Google Scholar]
- Mouesca J. M.; Noodleman L.; Case D. A. Inorg. Chem. 1994, 33, 4819. 10.1021/ic00100a004. [DOI] [Google Scholar]
- Spatzal T. S. J.; Burger E.-M.; Sippel D.; Zhang L.; Andradem S. L. A.; Rees D. C.; Einsle O. Nat. Commun. 2016, 7, 10902. 10.1038/ncomms10902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lukoyanov D. P. V.; Maeser N.; Laryukhin M.; Yang T. C.; Noodleman L.; Dean D. R.; Case D. A.; Seefeldt L. C.; Hoffman B. M. Inorg. Chem. 2007, 46, 11437. 10.1021/ic7018814. [DOI] [PubMed] [Google Scholar]
- Lovell T. T.; Liu T. T.; Case D. A.; Noodleman L. J. Am. Chem. Soc. 2003, 125, 8377. 10.1021/ja0301572. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.