Comparative Effectiveness Research Using Observational Data: Active Comparators to Emulate Target Trials with Inactive Comparators

Abstract

Introduction:

Because a comparison of noninitiators and initiators of treatment may be hopelessly confounded, guidelines for the conduct of observational research often recommend using an “active” comparator group consisting of people who initiate a treatment other than the medication of interest. In this paper, we discuss the conditions under which this approach is valid if the goal is to emulate a trial with an inactive comparator.

Identification of Effects:

We provide conditions under which a target trial in a subpopulation can be validly emulated from observational data, using an active comparator that is known or believed to be inactive for the outcome of interest. The average treatment effect in the population as a whole is not identified, but under certain conditions this approach can be used to emulate a trial in the subset of individuals who were treated with the treatment of interest, in the subset of individuals who were treated with the treatment of interest but not with the comparator, or in the subset of individuals who were treated with both the treatment of interest and the active comparator.

The Plausibility of the Comparability Conditions:

We discuss whether the required conditions can be expected to hold in pharmacoepidemiologic research, with a particular focus on whether the conditions are plausible in situations where the standard analysis fails due to unmeasured confounding by access to health care or health seeking behaviors.

Discussion:

The conditions discussed in this paper may at best be approximately true. Investigators using active comparator designs to emulate trials with inactive comparators should exercise caution.

Introduction

Randomized trials to evaluate the effectiveness or safety of an active treatment can be classified into two groups: trials that compare the treatment of interest with an active treatment that is a clinical alternative to the treatment of interest (head-to-head trials), and trials that compare the treatment of interest with an inactive comparator such as usual care without treatment. Observational data are often used to try to emulate both types of randomized trials. Head-to-head trials may be emulated by comparing individuals initiating the treatment of interest versus initiating the active comparator.1 Trials with inactive comparators may be emulated by comparing individuals initiating versus not initiating the active treatment.2

While all trial emulations using observational data are subject to bias, emulating trials with inactive comparators is especially challenging because people who initiate treatment may be different from noninitiators in ways that are difficult to assess: access to healthcare; health-seeking behaviors; and time since and accuracy of the measurement of confounders, outcome, and comorbidities. As a result, the observational estimates may be biased by unmeasured confounding and differential mismeasurement of key variables.3 This bias is of particular concern in studies that rely on administrative data.4,5

A proposal to reduce these biases in observational research is the use of active comparators even when the goal of the research is to emulate a trial with inactive comparators.6 To do so, investigators often choose an active comparator that is thought to be inactive for the outcome under consideration and therefore not a clinical alternative to the treatment of interest. It has been argued that using such active comparators may mitigate bias because initiators of the treatment of interest and of the active comparator are expected to have a similar health status7 and use of the health care system,8 and comparable quality of information. The idea is similar to that of “negative exposure controls.”9,10

The use of active comparators has been endorsed in several guidelines for the conduct of observational research, including the GRACE principles,3 Agency for Healthcare Research and Quality (AHRQ)’s “Protocol for Observational Comparative Effectiveness Research,”4 Patient-Centered Outcomes Research Institute (PCORI)’s “Standards for Causal Inference in Analyses of Observational Studies,”5 and the United States Food and Drug Administration (FDA)’s “Best practices for conducting and reporting pharmacoepidemiologic safety studies.”11 Table 1 summarizes several published examples of observational studies that used active comparators to emulate trials with inactive comparators.

Table 1.

Examples of Observational Studies that Use Active Comparators to Emulate Randomized Trials with Inactive Comparators

STUDY	TREATMENT GROUP	COMPARATOR GROUP	OUTCOME
Glynn et al. (2001)14	Initiators of several classes of cardiac drugs	Initiators of glaucoma drugs	Death
Glynn et al. (2006)15	Initiators of lipid-lowering medications	Initiators of any other medications who do not use lipid-lowering medications	Death
Solomon et al. (2006)8	Initiators of NSAIDS/Coxibs	Initiators of glaucoma/hypothyroidism therapy who do not take NSAIDs/Coxibs	Hospital admission for myocardial infarction or stroke
Schneeweiss et al. (2007)16	Initiators of statins who do not use glaucoma therapy	Initiators of glaucoma therapy who do not use statins	Death
Setoguchi (2007)17	Initiators of statins who do not use glaucoma therapy	Initiators of glaucoma therapy who do not use statins	Lung, breast, and colorectal cancer

However, these guidelines do not describe the method in detail. For example, none of these documents explicitly differentiate between the use of active comparators to emulate head-to-head trials or to emulate trials with inactive comparators. In addition, they do not provide a precise definition of the causal effect that is to be estimated when active comparators are used, and therefore cannot characterize the conditions that are necessary in order to identify this causal effect. Finally, the guidelines specify neither whether the treatment group should exclude individuals who also take the comparator drug nor whether the analysis should be restricted to individuals with indications for both active treatments. As a result, different versions of active comparator approaches exist (see Table 1).

In this paper, we consider several possible designs of observational studies that use active comparators to emulate trials with inactive comparators. We characterize the causal effect that is targeted by each design and the comparability assumptions under which the design-specific causal effects are identified from the data. Since we are interested in identification and not inference we shall ignore sampling variability by supposing the study population is sufficiently large that sampling variability can be ignored.

Example and Notation

As a running example, we will consider a target trial whose goal is to compare usual care plus initiation of statin therapy (A=1) versus usual care without initiation of statin therapy (A =0) on the five-year risk of coronary heart disease Y (1: yes, 0: no) in some well-defined study population in a large database. We sometimes use “treated” as shorthand for “initiated treatment with statins.”

Let the counterfactuals Y^a=1 and Y^a=0 denote the outcome of interest Y when treated and not treated with statins respectively. A subject’s observed outcome Y is equal to Y^a=1 if the subject initiated statin treatment; otherwise Y is equal to Y^a=0. We first consider two causal effects that are often of interest.

First, the average treatment effect (ATE) in the entire study population is defined as E[Y^a=1] – E[Y^a=0], i.e., the difference between the five-year risk of coronary heart disease had everyone undergone usual care plus initiation of statin therapy and the five-year risk of coronary heart disease had everyone undergone usual care alone. Second, the average treatment effect in the treated subpopulation—the effect of treatment in the treated (ETT)—is defined as E[Y^a=1 |A=1] – E[Y^a=0 |A=1], which equals E[Y |A=1 – E[Y^a=0 |A=1] by consistency.

As discussed above, the observational risk difference between statin initiators and noninitiators, E[Y|A=1] – E[Y|A=0], may be biased for both the ATE and the ETT. The bias may persist even if the observational contrast were computed within levels of the measured confounders L available in the database, i.e., E[Y|A=1,L=l] – E[Y|A=0,L=l], owing to within stratum confounding by unmeasured factors and measurement error of the measured covariates. For notational simplicity, in this paper we often suppress L=l from the conditioning event, but consider that all observational contrasts are calculated in a subset of the population L=l.

Let B denote the active comparator drug so that subjects with B=1 initiate the active comparator and subjects with B=0 do not. In our example, we take B to be an active therapy for glaucoma that is inactive for our outcome coronary heart disease. Subjects who have yet to initiate either treatment before the start of follow-up can be divided into four subsets: initiators of A but not B, initiators of B but not A, initiators of both A and B, and initiators of neither A nor B. Note that if A and B are alternative therapies for the same illness, then it may be that there exist no subjects initiating A and B at once. Since we are considering the case in which A and B do not treat the same condition, we assume there do exist simultaneous initiators.

We define the start of follow-up as the first day a subject initiates either treatment A or treatment B. On that day, we classify subjects as having initiated A only, B only, or both. Subjects who never initiate either treatment are not included in our analyses. In practice, too few people may initiate both treatments on the same day. Therefore we might elect to define joint initiators as those who start both treatments within a short period of, say, two months. Because some subjects may develop the outcome of interest during those two months, this definition of joint initiation would necessitate the use of special techniques like those described by Cain et al. (2010),12 which are beyond the scope of this paper.

Identification of Effects in Initiators of A

Consider three observational contrasts to estimate the ETT:

• Contrast 1: E[Y|A=1] – E[Y|A=0, B=1]

• Contrast 2: E[Y|A=1, B=0] – E[Y|A=0, B=1]

• Contrast 3: E[Y|A=1, B=1] – E[Y|A=0, B=1]

All three contrasts use as comparator the mean outcome in the subset of initiators of B that do not initiate A. This quantity is compared with the mean outcome in all initiators of A (contrast 1), in initiators of A who do not initiate B (design 2), and initiators of both A and B (contrast 3).

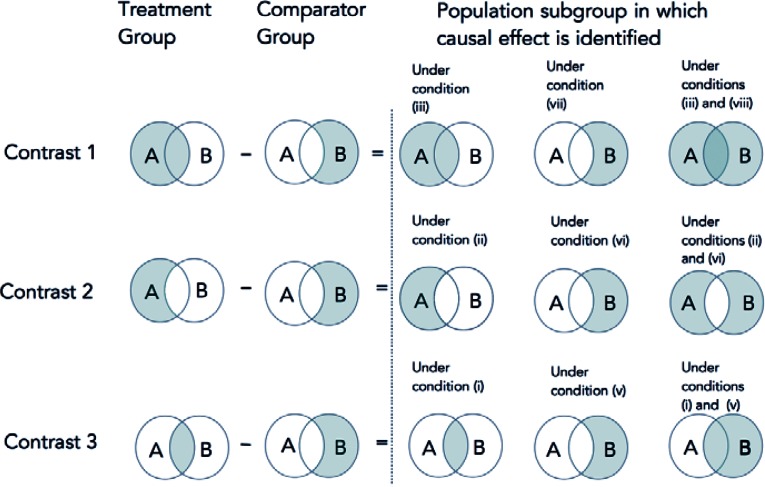
Under comparability conditions described below, each contrast identifies the average causal effect of A=1 versus A=0 in a particular subset of the treated (with A) subpopulation: the entire treated subpopulation (contrast 1), the subset of treated subpopulation who do not initiate B (contrast 2), and the subset of the treated subpopulation who initiate B (contrast 3). Figure 1 represents the groups that are compared and the causal effects that are identified.

Figure 1.

Three Observational Contrasts and the Population Subgroup in Which the Effect Is Identified under Several Conditions

Note: A is the treatment of interest, B is the active comparator.

Consider the four comparability conditions:

1. p₁₁=p₀₁

2. p₁₀=p₀₁

3. p₁₀=p₀₁=p₁₁

4. p₁₀=p₀₁=p₁₁ =p₀₀

where p_ab ≡ E[Y^a=0|A=a,B=b]. For example, p₀₁ is the mean of Y^a=0 among subjects who initiate B but do not initiate A. We now show that some of these conditions identity the subpopulation causal effects described earlier.

The Effect of A Among Initiators of A and B

Condition (i) states that among initiators of B, those initiating A have the same mean of Y^a=0 as those not initiating A. Under condition (i), contrast 3 E[Y|A=1, B=1] – E[Y|A=0, B=1] identifies the ETT among initiators of the comparator drug B=1, E[Y^a=1–Y^a=0|A=1, B=1]. In our example, this is the average causal effect of statins versus no statins among subjects who initiated both statins and glaucoma therapy.

Lemma 1: If p₁₁=p₀₁ then E[Y|A=1, B=1] – E[Y|A=0, B=1]= E[Y^a=1–Y^a=0|A=1, B=1]

Proof:

E[Y|A=1, B=1]	= E[Ya=1|A=1, B=1]	by consistency
E[Y|A=0, B=1]	= E[Ya=0|A=0, B=1]	by consistency
	= E[Ya=0|A=1, B=1]	by (i)

The Effect of A Among Initiators of A but not B

Condition (ii) states that subjects initiating B but not A have the same mean of Y^a=0 as those initiating A but not B. Under condition (ii), contrast 2 identifies the ETT among noninitiators of B, E[Y^a=1–Y^a=0|A=1, B=0]. In our example, this is the average causal effect of statins versus no statins among initiators of statins who did not initiate glaucoma therapy.

Lemma 2: If p₁₀=p₀₁ then E[Y|A=1, B=0] – E[Y|A=0, B=1]= E[Y^a=1–Y^a=0|A=1, B=0].

Proof:

E[Y|A=1, B=0]	= E[Ya=1|A=1, B=0]	by consistency
E[Y|A=0, B=1]	= E[Ya=0|A=0, B=1]	by consistency
	= E[Ya=0|A=1, B=0]	by (ii)

Lemma 2 is due to Rosenbaum (2006).6,13

The Effect of A among All Initiators of A

Under condition (iii), contrast 1 identifies the effect of treatment in all those treated with A, E[Y^a=1–Y^a=0|A=1]. In our example, this is the average causal effect of statins versus no statins among all initiators of statins.

Lemma 3: If p₁₀=p₀₁=p₁₁ then not only are the results of Lemma 1 and 2 true but in addition E[Y|A=1] – E[Y|A=0, B=1]= E[Y^a=1–Y^a=0|A=1]

Proof:

Condition (iii) implies that conditions (i) and (ii) hold. It thus suffices to prove the results under conditions (i) and (ii). Note that the converse also holds, i.e., (iii) is implied by (i) and (ii) jointly.

E[Y|A=1]	= E[Ya=1 | A=1]	by consistency
E[Y|A=0, B=1]	= E[Ya=0 | A=0, B=1]	by consistency
	= E[Ya=0 | A=1, B=1]	by (i)
	= E[Ya=0 | A=1, B=0]	by (ii)
	It follows that E[Y|A=0, B=1] = E[Ya=0 | A=1]

If the even stronger condition (iv) holds, the simple contrast E[Y|A=1] – E[Y|A=0] identifies the effect of treatment in those treated with A. Thus, if condition (iv) holds we would not need to collect data on B to identify the ETT. However, condition (iv) is generally implausible as discussed below and in the Introduction.

Lemma 4: If p₁₀=p₀₁=p₁₁ =p₀₀ then E[Y|A=1] – E[Y|A=0] = E[Y^a=1–Y^a=0|A=1]

Proof:

E[Y|A=1]	= E[Ya=1 | A=1]	by consistency
E[Y|A=0]	= E[Ya=0 | A=0]	by consistency
	= E[Ya=0 | A=1]	by (iv)

Identification of Effects in Noninitiators of A

Heretofore we have considered comparability conditions that equate the mean of Y^a=0 in different subgroups and proved that under these conditions we can identify the ETT in various subsets of initiators of A. In this section we consider additional comparability conditions that equate the mean of Y^a=1 rather than Y^a=0 in different subgroups. Figure 1 represents the groups that are compared and the causal effects that are identified.

• v. q₁₁=q₀₁

• vi. q₁₀=q₀₁

• vii. q₁₀=q₀₁=q₁₁

• viii. q₁₀=q₀₁=q₁₁ = q₀₀

where we define q_ab ≡ E[Y^a=1|A=a, B=b]

Conditions (v)–(viii) differ from (i)–(iv) only in that Y^a=0 is replaced by Y^a=1. Like condition (iv), condition (viii) assumes that subjects with A=0, B=0 are comparable with the other subjects, which is implausible in the setting considered here. Hence we do not discuss condition (viii) further.

When any of the other conditions holds, we can identify the effect of A in initiators of B who did not initiate A, E[Y^a=1–Y^a=0|A=0, B=1]. In our example, this is the average causal effect of statins versus no statins among subjects who initiated glaucoma therapy but not statins. Specifically, this effect is identified under condition (v) using contrast 3, under condition (vi) using contrast 2, and under condition (vii) using contrast 1. The proofs follow.

Lemma 5: If q₁₁=q₀₁ then E[Y|A=1, B=1] – E[Y|A=0, B=1]= E[Y^a=1–Y^a=0|A=0, B=1]

E[Y|A=1, B=1]	= E[Ya=1|A=1, B=1]	by consistency
	= E[Ya=1| A=0, B=1]	by (v)
E[Y|A=0, B=1]	= E[Ya=0|A=0, B=1]	by consistency

Lemma 6: If q₁₀=q₀₁ then E[Y|A=1, B=0] – E[Y|A=0, B=1]= E[Y^a=1–Y^a=0|A=0, B=1]:

E[Y|A=1, B=0]	= E[Ya=1|A=1, B=0]	by consistency
	= E[Ya=1|A=0, B=1]	by (vi)
E[Y|A=0, B=1]	= E[Ya=0|A=0, B=1]	by consistency

Lemma 7: If q₁₀=q₀₁=q₁₁ then E[Y|A=1] – E[Y|A=0, B=1]= E[Y^a=1–Y^a=0|A=0, B=1]:

E[Y|A=1]	= E[Ya=1| A=1]	by consistency
	= E[Ya=1| A=1, B=0] * Pr[B=0 |A=1] + E[Ya=1| A=1, B=1] * Pr[B=1 |A=1]
		by law of total probability
	= E[Ya=1| A=0, B=1] * Pr[B=0 |A=1] + E[Ya=1| A=0, B=1] * Pr[B=1 |A=1]
		by (v) and (vi), which are implied by (vii)
	= E[Ya=1| A=0, B=1]
E[Y|A=0, B=1]	= E[Ya=0| A=0, B=1]	by consistency

Thus if any one of the conditions (v), (vi), or (vii) hold, E[Y^a=1–Y^a=0|A=0, B=1] is identified and is the only causal contrast identified. Therefore, comparability conditions with respect to Y^a=1 identify fewer causal contrasts than comparability conditions with respect to Y^a=0.

However condition (vii) has an important property that none of the other conditions (i)–(vi) possess. Since condition (vii) implies both conditions (v) and (vi), it follows from above that when (vii) holds E[Y^a=1–Y^a=0|A=0, B=1] is identified by the contrasts of all three designs. Thus when (vii) holds we can conclude that E[Y|A=1]=E[Y|A=1, B=0]= E[Y|A=1, B=1]. These equalities are equivalent to the statement that Y and B are independent conditional on A=1. Hence we can empirically test whether condition (vii) holds by testing whether Y and B are independent given A=1 (within levels of L). If an α-level test of this conditional independence rejects, then we can also reject the null hypothesis that condition (vii) holds at level α.

We now consider comparability conditions with respect to both Y^a=1 and Y^a=0. Since it would be unusual to find two groups that have identical means for one of the two treatment counterfactuals but not the other, these comparability conditions may be the most relevant. It is straightforward to check that the combination of the above results for comparability conditions with respect to Y^a=0 and Y^a=1 implies the following:

• If both conditions (i) and (v) hold, then contrast 3 identifies E[Y^a=1–Y^a=0| B=1].

• If both conditions (ii) and (vi) hold, then contrast 2 identifies E[Y^a=1–Y^a=0| A+B=1] where A+B=1 denotes the set of subject who initiated A or B but not both. See Rosenbaum (2006).

• If both conditions (iii) and (vii) hold, then contrast 1 identifies E[Y^a=1–Y^a=0|A+B≠0], the effect of treatment in all subjects who initiated either A or B or both.

(See Figure 1.)

The Plausibility of the Comparability Conditions

As discussed above, conditions (i)–(vi) can neither be empirically verified nor refuted, and condition (vii) cannot be empirically verified. We should only adopt the conditions that are plausible a priori. We now discuss the plausibility of the conditions in various settings.

Setting 1: When the Comparator B Has a Direct Effect

When the comparator B has a direct effect on the outcome, conditions (ii), (iii), (iv), (vi), (vii), and (viii) are not expected to hold. This should not be surprising, as the absence of a direct effect of the comparator on the outcome is the essential intuition behind most active comparator designs.

To proceed we need some further definitions. Let Ya, b be a subject’s outcome under treatment values A=a and B=b. The comparator B has no direct effect on Y if Y^a = Y^a, b=0 = Y^a, b=1 for every subject. Note that, by consistency, Y^a, b=1 = Y^a for initiators of B, and Y^a, b=0 = Y^a for noninitiators of B.

We now show that condition (ii) is implausible if B has a direct effect. When fully written out, the condition p₁₀=p₀₁ becomes E[Y^a=0, b=1|A=0, B=1] = E[Y^a=0, b=0|A=1, B=0]. Since the counterfactuals Y^a=0, b=1 and Y^a=0, b=0 differ when B has a direct effect, there is no a priori reason to expect that the mean of Y^a=0, b=1 in the subgroup A=0, B=1 equals that of Ya=0, b=0 in the subgroup A=1, B=0. As conditions (iii) and (iv) hold only if condition (ii) does, they too are implausible if B has a direct effect. An exactly analogous argument can be made for condition (vi), and by extension, for (vii) and (viii). Henceforth, we will assume B has no direct effect. In our example, this means that we assume that glaucoma therapy B has no direct effect on heart disease.

Setting 2: When Indications of the Comparator B Are Associated with the Outcome

Our observational contrasts need to be adjusted for risk factors that serve as indications for initiation of A. In our example this means we must include in L joint risk factors for heart disease and statin initiation such as LDL cholesterol. But do we need to adjust for indications for the initiation of B? In our example, do we need to adjust for (the presence of) glaucoma G, an indication necessary for initiation of glaucoma therapy B?

Suppose glaucoma is highly correlated with Y^a=0, for example, because glaucoma is a proxy for unmeasured risk factors for cardiovascular disease. Then the distribution of Y^a=0 will differ between subjects with B=0 and B=1. That is, even if B has no direct effect on Y, we still need to adjust for an indication (glaucoma) for initiation of B if, within levels of the other covariates in L, glaucoma G is associated with the outcome among initiators of A. It follows that condition (ii) would not be expected to hold and thus neither would (iii) and (iv). Analogous arguments can be made for (vi), (vii), and (viii).

However, we cannot always adjust for glaucoma because adjustment can result in nonpositivity. To see why, we make the only slightly exaggerated assumption that all subjects with incident glaucoma G=1 initiate glaucoma therapy B but no subject without incident glaucoma initiates B. Then contrast 2 is undefined because all subjects with B=1 have glaucoma and all subjects with B=0 do not; contrast 3 naturally adjusts for glaucoma since all subjects with B=1 have glaucoma; contrast 1 is equivalent to contrast 3 in the stratum with glaucoma, but undefined in the stratum without glaucoma because all subjects with B=1 have glaucoma.

It follows that for all contrasts other than 3, if adjustment for glaucoma is required to control confounding, then initiators of glaucoma drugs cannot be used as active comparators. Therefore in the following sections we restrict consideration to the setting in which glaucoma is independent of Y^a=0 in initiators of A, so no adjustment for glaucoma is needed.

Setting 3: When Indications of the Comparator B Are Not Associated with the Outcome

Conditions (iv) and (viii) cannot generally be assumed to hold because they imply that subjects who initiated neither treatment A nor treatment B are comparable with those who did. As discussed in the Introduction, this is implausible, an observation that indeed motivated the need for active comparators. We therefore proceed to describe situations where one or more of the weaker conditions (iii), (ii), or (i) holds, but (iv) does not. In such settings, an active comparators design may be required. We discuss these situations in terms of conditions (i) through (iii), but point out that analogous logic will hold for conditions (v) through (vii).

Condition (iii) would hold if there were two indistinguishable groups of subjects in the population with different means of Y^a=0 (i.e., two groups that on average have different cardiac risks), and hence noncomparable. All Group 1 (𝒢₁) members refrain from initiating either statins or glaucoma therapy, whereas comparability condition (iv) holds in Group 2 (𝒢₂). Therefore, all subjects who initiated either A or B would be in 𝒢₂ while those who initiated neither would be an indistinguishable mixture of groups 𝒢₁ and 𝒢₂. As an example, we might suppose all subjects with health-seeking behaviors were in group 𝒢₂ and those without were in group 𝒢₁. However, since covariates such as health-seeking behavior are not truly binary, and since sicker individuals will tend seek health care preferentially, it is implausible that the division into such groups will ever hold precisely.

An alternative way to think about this setting is in terms of a mechanistic treatment choice model as discussed by Rosenbaum (2006) using ideas introduced by Tversky and Sattath (1979). In these models, a subject first decides whether to refrain from all treatment or not. The probability of refraining can depend on Y^a=0. Having decided to take a treatment, the decision about whether to take A, B, or both does not further depend on Y^a=0. If treatment is assigned by such a model, condition (iii) will hold.

Condition (ii) but not (iii) would hold if in the above mechanistic treatment model the subject first decides whether to take 0, 1, or 2 treatments with the decision depending on Y^a=0, and in the event that he decides to take 1 proceeds to choose among A and B with a probability that does not depend on Y^a=0. As discussed by Rosenbaum, this scenario might be plausible if A and B were alternative therapies prescribed for the same indication. However, this model—and the corresponding model for condition (iii)—becomes less plausible when, as in this paper, the indication for treatment with the comparator B (e.g., glaucoma therapy) differs from that for active treatment A (statins).

The requirements for condition (i) are less restrictive. This condition would hold if among initiators of B, initiators and noninitiators of A are exchangeable with respect to the outcome Y, i.e., if Y^a=0 ∐ A | B=1. This condition will be true under the following scenario: Suppose that initiators and noninitiators of statins are not exchangeable because of differences in health care access (an unmeasured variable). If all initiators of glaucoma therapy have access to health care, then, in the subset of initiators of B, initiators and noninitiators of A do not differ with respect to health care access. Therefore, conditional on prognostic factors other than health care access, comparability condition (i) would hold among initiators of B even if health care access remains unmeasured. Note that whether or not B has a direct effect on Y has no bearing on the plausibility of condition (i).

Note that all independence assumptions in this paper are defined in terms of counterfactual variables that are specific for each outcome Y under consideration. It is often the case that a comparator will be independent of one outcome, but not another. Therefore, the active comparator has to be chosen specifically in the context of subject-matter knowledge about the relationship between the comparator and the outcome under study, and justifications for using an active comparator B for one outcome Y do not readily transfer to using the same comparator for a different outcome. For these reasons, in any design that uses active comparators in observational data, it will be difficult to analyze multiple outcomes within the same study.

Discussion

Investigators should think carefully about what effects they are estimating when using “active comparators” to emulate a target trial of treatment versus no treatment. In this paper, we have provided the conditions under which such a trial can be validly emulated using a comparator group that consists of initiators of an active treatment that is inactive for the outcome of interest.

We have discussed eight conditions that allow the identification of different causal effects. In most settings, conditions (i) and (v) will be the most plausible assumptions (because they do not rely on the assumption that the comparator treatment has no effect on the outcome), but an approach based on conditions (i) and (v) will reduce sample size considerably and will restrict the interpretation of the estimated effect to the small subset of the population who share characteristics with those subjects who initiated treatment B in the observational data.

Conditions (ii) and (vi), (iii) and (vii), and (iv) and (viii) will be difficult to justify in most settings. Conditions (ii) and (v) are weaker than conditions (iii) and (vii), and therefore less likely to be violated, but conditions (iii) and (vii) identify potentially more relevant causal effects. Of conditions that do not assume exchangeability of those who initiate neither treatment A nor B, i.e., conditions (i)–(iii) and (v)–(vii), only condition (vii) is subject to an empirical test from the study data. Thus other informal ways of testing these comparability conditions are needed.

With the possible exception of conditions (i) and (v), the best that could be hoped for is that some of these conditions would be approximately true. Perhaps the best way to test whether these conditions hold approximately would be to obtain observational data containing all relevant covariates including access to health care and health-seeking behavior, and see whether an analysis that strips the dataset of these variables is able to use the methods proposed in this paper to obtain approximately the same results as the standard analysis for estimating the causal effect in the corresponding subgroup based on all the covariate data.