The Multimorbidity Index: A Tool for Assessing the Prognosis of Patients from Their History of Illness

Abstract

Background:

The Multimorbidity (MM) Index predicts the prognosis of patients from their diagnostic history. In contrast to existing approaches with broad diagnostic categories, it treats each diagnosis as a separate independent variable using individual International Classification of Disease, Revision 9 (ICD-9) codes.

Objective:

This paper describes the MM Index, reviews the published data on its accuracy, and provides procedures for implementing the Index within electronic health record (EHR) systems. Methods: The MM Index was tested on various patient populations by using data from the United States Department of Veterans Affairs data warehouse and claims data within the Healthcare Cost and Utilization Project of the Agency for Health Care Research and Quality.

Results:

In cross-validated studies, the MM Index outperformed prognostic indices based on physiological markers, such as CD4 cell counts in HIV/AIDS, HbAlc levels in diabetes, ejection fractions in heart failure, or the 13 physiological markers commonly used for patients in intensive care units. When predicting the prognosis of nursing home patients by using the cross-validated area under a receiver operating characteristic (ROC) curve, the MM Index was 15 percent outperformed the Quan variant of the Charlson Index, 27 percent more accurate than the Deyo variant of the Charlson Index, and 22 percent more accurate than the von Walraven variant of the Elixhauser Index. For patients in intensive care units, the MM Index was 13 percent outperformed the cross-validated area under ROC associated with Elixhauser’s categories. The MM Index also demonstrated greater accuracy than a number of commercially available measures of illness severity; including a fivefold greater accuracy than the All Patient Refined Diagnosis-Related Groups and a threefold greater accuracy than All Payer Severity-Adjusted Diagnosis-Related Groups.

Conclusion:

The MM Index is statistically more accurate than many existing measures of prognosis. The magnitude of improvement is large and may lead to a clinically meaningful difference in patient care. Given the large improvements in accuracy, the use of the MM Index for policy and comparative effectiveness analysis is recommended.

Introduction

Prognostic information has many meaningful uses. Patients and clinicians can use it to plan for end of life decisions, such as setting treatment priorities. Policy analysts can use it to evaluate the comparative effectiveness of various treatment options. Administrators can also use it to anticipate patients’ acuity and nursing needs. All of these uses presuppose that an accurate measure of prognosis exists. In this paper, we describe and report on the accuracy of the Multimorbidity (MM) Index. Alemi and colleagues1–6 developed the MM Index to account for the prognosis of patients with multiple diagnoses.

Several other investigators have also proposed methods for predicting a prognosis from patients’ diagnoses. Charlson and colleagues were among the first group of investigators to do so.7 These authors developed an index that predicted mortality from 22 broad disease categories, including one category for all heart diseases, another for AIDS, and still another for all cancers. Deyo et al.,8 Romano et al.,9 Manitoba et al.,10 and D’Hoores et al.11 attempted to improve on the initial Charlson Index by modifying the broad categories and dropping or adding new categories. Elixhauser and colleagues12 continued these modifications by creating a list of 30 broad categories of comorbidities, and van Walraven et al. organized these categories into an index.13

In contrast to existing approaches, the MM Index does not classify diagnoses into broad disease categories. Instead, it scores the underlying disease. In existing methods, diagnoses with widely varying hazard ratios are scored the same because they fall in the same disease category. For example, consider the variation in mortality among the 28 diagnoses in the “secondary malignancies” category that are used in variants of the Elixhauser Index. In a recent study of the prognosis of heart failure patients,14 patients who also had a “secondary malignant neoplasm of brain and spinal cord” had an odds ratio of mortality equal to 17.28. In comparison, those who had another variant of a secondary malignancy (i.e., a “secondary neuroendocrine tumor of distant lymph nodes”) only had an odds ratio of mortality equal to 2.43. This example illustrates that the same category, secondary malignancies, includes diagnoses that have a nearly ninefold difference in mortality, and that grouping all secondary malignancies into one category overly simplifies the differences within this category. One would anticipate that the accuracy of prognostication could be improved by considering the 28 types of secondary malignancies separately rather than together as one category, which is a feature of the MM Index.

In this paper, we review the design of the MM Index, compare its performance to other prognostic indices, and describe how the index can be used within an electronic health record (EHR). The paper also includes code for constructing the MM Index in different data sets or for incorporating the method into EHRs.

Derivation of the Multimorbidity Index

The key feature of the MM Index is that it is built from thousands of diagnoses, without classifying these diagnoses into categories. In order to effectively model the relationship between thousands of diagnoses and mortality, the MM Index uses the Naive Bayes data mining model. In this approach, one assumes that the impact of each disease on mortality is independent from other diseases. This assumption is also made in traditional statistical approaches that use linear logistic regression. Even though the assumption is obviously false, numerous studies have shown that the Naive Bayes produces predictions that are as accurate as more complicated models that assume interactions among diseases.15–26 In this approach, the overall probability of mortality is calculated as follows:

$$\text{Patient}\text{'}\text{s}\hspace{0.17em}\hspace{0.17em}\text{MM}\hspace{0.17em}\text{score}\hspace{0.17em}\prod _{\begin{array}{l}\mathit{Patient}\text{'}s\\ \mathit{Diagnoses}\end{array}}{\text{L}}_{\text{Diagnosis}}$$

where L_Diagnosis indicates the likelihood ratio associated with the diagnostic code in the training data set.

The likelihood associated with each diagnosis is calculated using the following formula from the portion of the data set aside for training of the model:

$${\text{L}}_{\text{Diagnosis}}=\frac{\mathit{Prevalenc}\hspace{0.17em}\mathit{of}\hspace{0.17em}\mathit{diagnosis}\hspace{0.17em}\mathit{among}\hspace{0.17em}\mathit{patients}}{\mathit{Prevalenc}\hspace{0.17em}\mathit{of}\hspace{0.17em}\mathit{diagnosis}\hspace{0.17em}\mathit{among}\hspace{0.17em}\mathit{alive}\hspace{0.17em}\mathit{patients}}=\frac{\text{p}\left(\text{Dx}|\text{Dead}\right)}{\text{p}\left(\text{Dx}|\text{Alive}\right)}.$$

The likelihood ratio associated with each diagnosis can be interpreted as the number of times the diagnosis increases the odds of mortality. A likelihood ratio of 2 indicates that the diagnosis doubles the risk of mortality, while a likelihood ratio of 0.5 indicates that the odds of mortality is reduced by half.

These likelihood ratios were estimated from data within the United States Department of Veterans Affairs (Veterans Affairs) medical records and are publicly available for heart failure1 and for nursing home patients.2 To facilitate the estimation of these ratios for other populations, the Standard Query Language (SQL) code that we had used is provided in the Appendix A.

One problem with the method used to estimate the likelihood ratios is that it is affected by co-occurring diagnoses. Thus, hypertension may receive higher likelihood of mortality if it tends to occur with more serious diseases such as heart failure or shock. Procedures to remove confounding are available in several published papers.27 We recommend the use of Stratified Covariate Balancing (see R Package StratifiedBalancing) in removing confounding as this approach is not parametric and can be done within EHRs using SQL.31 Applying methods of removing confounding to the estimation of survival of patients with co-occurring diagnoses remains an active area of research.

Sample Size Needed to Construct the MM Index

To derive the MM Index, it is important to recognize that a large number of parameters are estimated. There are in excess of 14,000 International Classification of Diseases (ICD) codes, and within most populations 3,000–5,000 unique diagnoses occur. This means that approximately 3,000–5,000 parameters must be estimated. There are a number of ways to estimate the sample size that would be needed for such a large number of determinations. Some investigators have suggested that the power of the investigation depends on the ratio of the number of subjects to the number of variables, using heuristics such as 10 times32,33,34 or 20 times35 the number of subjects compared to the number of variables in the model (i.e., in order to estimate 5,000 parameters, 100,000 subjects would be needed). In most of the analyses reported here, the total sample size exceeds 30 times the number of variables, suggesting the estimated model has sufficient power to detect the needed parameters.

Others posit that the most important consideration is the accuracy of local estimates, such as the likelihood ratio associated with each diagnosis.36,37 To calculate those likelihood ratios, a sample size formula for a two-sample t-test can be applied to calculate the required sample size for one diagnosis. In multivariate analysis, the impact of a single diagnosis is evaluated within the context of many others. In these situations, a correction factor associated with the percent of variation explained by the covariates is added to inflate the variance and improve the power.38,39 In selecting one of these two approaches, one may consider the intended use of the study findings. If an overall index score is of interest, then heuristics that use the ratio of the number of subjects to the number of estimates may be most appropriate. However, if individual likelihood ratios associated with each of the respective diagnoses are of concern, then a more localized estimation of the individual likelihood ratios is needed.

Use of MM Index

Many investigators and clinicians may wish to estimate the probability of mortality at different time intervals (e.g., 6 months, 12 months, or 5 years). By using prior odds of mortality, one can transform the MM Index to estimate the probability of mortality within a specific period. According to the Bayes formula, the posterior odds of mortality are calculated as follows:

$$\begin{array}{l}\mathit{Posterior}\hspace{0.17em}\mathit{odds}\hspace{0.17em}=\hspace{0.17em}\mathit{Prior}\hspace{0.17em}\mathit{odds}*\mathit{MM}\hspace{0.17em}\mathit{Index}\\ \mathit{Probability}\hspace{0.17em}\mathit{of}\hspace{0.17em}\mathit{Mortality}=\frac{\mathit{Posterior}\hspace{0.17em}\mathit{Odds}}{1+\mathit{Posterior}\hspace{0.17em}\mathit{Odds}}\end{array}$$

Adjustments for Diseases with No Mortality or Mortality in All Cases

Many common diseases are associated with no patient mortality, and there are also rare diseases where every patient dies. In both of these situations, a likelihood ratio cannot be calculated. In these circumstances, Alemi40,41 proposed using the following formulas:

$${\text{L}}_{\text{Diagnosis}}=\{\begin{array}{ll}\mathit{if}\hspace{0.17em}\mathit{all}\hspace{0.17em}\mathit{survive}\hfill & 1/\left(n+1\right)\hfill \\ \mathit{if}\hspace{0.17em}\mathit{none}\hspace{0.17em}\mathit{survive}\hfill & n+1\hfill \end{array}$$

where n indicates the number of patients with the diagnosis.

Other adjustments have been reported in the literature, including adding a fraction of a case to either the denominator or the numerator to avoid division by zero. The adjustment used here has the advantage that it is proportional to the number of patients with the diagnosis (i.e., a higher likelihood ratio is assigned when all patients die from diseases that are more frequent). For example, if all 100 patients with a disease died, then the assigned likelihood ratio is 101. This assigned likelihood ratio (i.e., 11) is higher than if all 10 patients with a disease had died.

Adjustment for Rare Diseases

Although the MM Index is derived from a large data repository, there are several diagnoses that are rare and have insufficient observations to estimate a likelihood ratio. In a minority of cases (e.g., when a patient presented with a diagnosis that was not seen in at least 29 cases in the training set), then the likelihood ratio associated with a broader diagnostic category is used to score the patient. A typical International Classification of Disease, Revision 9 (ICD-9) diagnosis is represented as a five-digit number consisting of three initial digits, a period, and two additional digits. The first three digits represent a disease category. Each additional digit after the period represents further refinements. If the patient’s diagnosis is rare, then one could use the likelihood ratio for a broader category of the diagnosis that repeats more often (e.g., by dropping the last digit in the diagnosis code). Appendix A includes the SQL code that can be used to estimate the likelihood ratios associated with three-, four-, and five-digit codes from data in EHRs.

Adjustment for the International Classification of Diseases, Revision 10 (ICD-10)

To date, the MM Index has been evaluated using diagnoses coded with ICD-9. In the International Classification of Diseases, Revision 10 (ICD-10), a sixth digit was added to further clarify the disease categories. The procedures described in this paper and the computer code provided in Appendix A can be used to estimate the prognosis of each code within ICD-10. Because ICD-10 has tenfold more codes than ICD-9, reliable estimates for this version cannot be made until tenfold larger data are available. Even when the data are available, many disease codes in ICD-10 are unlikely to occur with sufficient frequency so that the prognosis for these codes can be estimated reliably. When ICD-10 codes cannot be estimated reliably, investigators should combine data and rely on higher order codes in ICD-9, using the procedures explained earlier for estimating rare diseases. If ICD-10 codes can be estimated reliably, then these codes should be used instead of ICD-9. By using this method, the best description of the patient would be used. When the estimate is not available, a less precise description would be used.

Multidimensional Variant of the MM Index

Because MM Index scores each diagnosis, this leads to a model with thousands of independent variables. Since clinicians have a difficult time tracking thousands of variables, a solution is needed that would allow the scoring of each diagnosis but would classify the respective diagnoses into a smaller set of dimensions that are easier to manage. Similarly, when evaluating the comparative effectiveness of treatments, there is a need to have sub-indices that indicate the relative severity of different diseases within body systems. The propensity scoring then adjusts for risks introduced by the different body systems and not just the overall mortality risk. The Multidimensional Multiple Morbidity (MMM) Index was created to address this scenario by breaking the overall MM Index into distinct subcategories. A modeling technique used for this purpose is the Multiattribute Utility model. The first application of utility theory to prognosis modeling can be traced to the work of Gustafson and colleagues.42 Later applications have included testing of preferential independence assumptions of additive or multiplicative utility models.43 In this approach, each attribute describes a set of comorbidities, typically within the same body system. The overall MMM score is then organized using the following formulas:

$$\mathit{MMM}=1-\prod _i\left(1=k_i{U}_i\right)$$

where:

• U_i is the maximum relative severity of disease in the i^th category of disease. These scores are scaled to range from 0 to 1, with 1 indicating the score for the worst disease in the category. These scores are made proportional to the hazard rate associated with each disease and are estimated from the data.

• k_i is the largest probability of mortality associated with the unconfounded impact of diseases within the i^th category.

Table 1 shows examples of how the MMM Index is organized from a progression in three body systems. Three body systems are shown in Table 1, and more are available through the first author.44 The columns in the table show the various body systems (e.g., diseases in the circulatory system). Each row in Table 1 corresponds to a particular level of severity. An example for the circulatory system is “1st [hospitalization for] 459.2, Ruptured Abdominal Aortic Aneurysm.” It is assigned a score of 0.4, while “2^nd [hospitalization for] 785.51, Cardiogenic Shock” is assigned a score of 1. These scores illustrate the relative severity within the category of Circulatory System. In essence, the utility scores list the diagnoses within the system (from relatively benign to the most serious) in the order of their hazard rate. This parameter k is the maximum unconfounded probability of mortality within each body system. In this scoring of the body system, each disease is initially rated based on its associated utility score. Then within each body system, the disease with the highest score is selected. Finally, an overall score is calculated by using the MMM formula.

Table 1.

Example Body Systems in the Multidimensional Multiple Morbidity Index

UTILITY SCORE	CIRCULATORY SYSTEM	DIGESTIVE SYSTEM	ENDOCRINE, NUTRITION, METABOLIC SYSTEM
0.0	1st 941.1, Erythema due to 1st degree Burn Not Otherwise Specified	1st 997.4 Retained Cholelithiasis Following Cholecystectomy	1st 244, Benign Neoplasm Pituitary
0.1	2nd 941 Burn of Face, Head, and Neck	1st 151.1, Perforation of Intestine	1st 783.3, Vitamin A Deficiency Not Otherwise Specified
0.2	1st 996.02, Lower Extremity Embolism	1st 151.3, Malignant Neoplasm Stomach NOS
0.3	1st 428.2, Acute pericarditis in Diseases Classified Elsewhere	1st 197.4, Malignant Neoplasm Abdomen	1st 194.9, Malignant Neoplasm Endocrine Not Otherwise Specified
0.4	1st 459.2, Ruptured Abdominal Aortic Aneurysm	1st 197.6, Secondary Malignant Neoplasm Peritoneum	4th 262, Other Severe Malnutrition
0.5	2nd 425.7, Metabolic Cardiomyopathy	3rd 197.8, Secondary Malignant Neoplasm Peritoneum
0.6	1st 785.5, Shock Not Otherwise Specified
0.7	3rd 427.5, Cardiac Arrest	6th 151.9, Malignant Neoplasm Stomach Not Otherwise Specified	1st 198.7, Second Malig Neo Adrenal
0.8
0.9	8th 428.23, Acute On Chronic Systolic Heart Failure
1.0	2nd 785.51, Cardiogenic Shock	1st 529.8, Epistaxis	2nd 198.7, Second Malig Neo Adrenal

Note: Repeated hospitalizations for the same diagnosis are scored separately.

Accuracy of the MM Index Compared to Physiological Markers

The health care literature is replete with studies that report the use of physiological markers as prognostic indicators. In this section, the performance of the MM Index is compared to select physiological markers. Alemi and colleagues examined the prognosis of patients with HIV/AIDS by using an MM Index45 in 1999 and found that the index was more predictive of patients’ survival than an index developed from an average of physiological indicators, such as CD4 T lymphocytes counts. Subsequent analyses by other investigators also demonstrated that the index was accurate in predicting HIV/AIDS prognosis for patients who died in six months and who were eligible for hospice care.46 This early attempt at constructing an MM Index did not take into account all diagnoses and was limited to specific diagnoses that followed a diagnosis of HIV/AIDS.

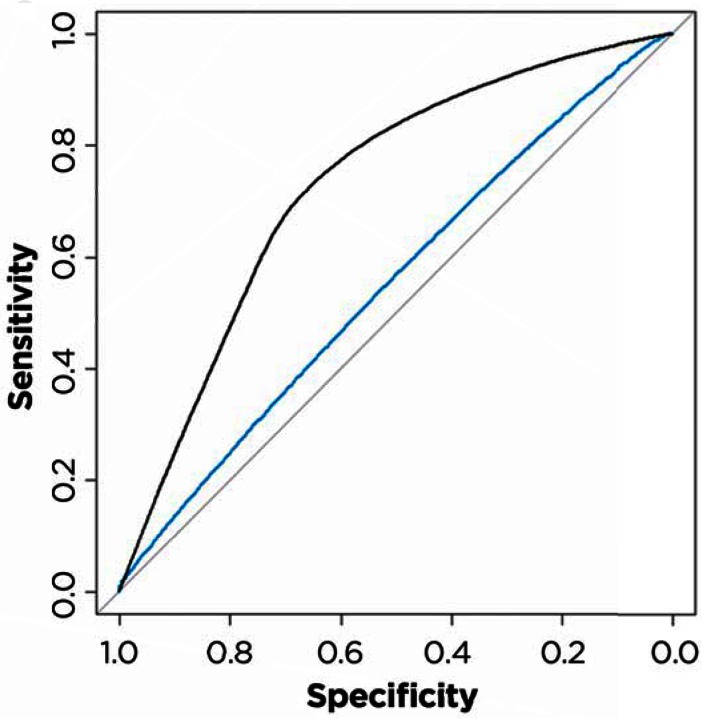
In 2013, a comprehensive MM Index was used to predict 12-month mortality for diabetes patients.47 This Index correctly predicted the mortality of 89.9 percent of cases. In as yet unpublished data,48 the performance of the diabetes MM Index was compared to the accuracy of Hemoglobin A1c levels for 468,867 diabetic patients. A number of investigators have shown how tight control of, or high levels of, Hemoglobin A1c might affect prognosis.49,50,51,52,53 Figure 1 shows that the sensitivity and specificity of the MM Index was superior to prognostic indicators based on HbA1c levels alone. The area under an ROC curve for predicting 6-month mortality for HbA1c levels was 0.652; in contrast the ROC for the MM Index was 0.812. The MM Index was therefore 1.25 times more accurate than the widely used HbA1c levels.

Figure 1.

Comparison of MM Index and HbA1C in Predicting 12-Month Mortality

In 2015, the MM Index was used to predict the 6-month mortality of 140,699 nursing home residents.54 The cross-validated accuracy of the MM Index was compared to a common measure of daily functional activity, the Barthel Index.55,56 The cross-validated ROC for the MM Index was 0.838. In contrast, the cross-validated ROC for the Barthel Index was 0.692.

Also in 2015, the MM Index was compared to the ejection fraction for 602,050 unique heart failure patients across 130 Veterans Affairs medical centers.57 The cross-validated ROC for the MM Index was 0.784. In contrast, the cross-validated ROC for the ejection fraction was only 0.533, which was barely above a random chance event. Ejection fraction was not predictive of long-term mortality rates.

In a study of patients in intensive care, we compared the accuracy of the MM Index to 13 physiological markers.58 These markers included the following: (1) sodium, (2) blood urea nitrogen, (3) creatinine, (4) glucose, (5) albumin, (6) bilirubin, (7) white blood cell count, (8) hematocrit, (9) PaO2, (10) PaCO2, (11) pH, (12) eGFR, and (13) lactic acid. We examined the 6-month and 12-month mortality of 442,692 unique patients seen in 87 Medical Intensive Care Units of Veterans Affairs Medical Centers between 2003 and 2013. The MM Index, relying solely on diagnostic codes, yielded an ROC of 0.84. In contrast, the logistic regression based on the combined impact of 13 physiological markers yielded a ROC of 0.65. These studies collectively show that the MM Index is more accurate in predicting 6-month or 12-month mortality compared to select physiological makers.

Accuracy of MM Indices Compared to Other Diagnoses-Based Indices

This section compares the MM Index and its variants to the Charlson Index and other diagnoses-based indices. In 2002, the MMM Index was used to predict mortality from childhood diseases.59 The source of data was the 2006 Kid’s Inpatient Database of the Healthcare Cost and Utilization Project of the Agency for Healthcare Research and Quality. This database contained data on pediatric (children 20 years of age and younger) discharges from 3,739 community, nonrehabilitation hospitals in 38 states. A total of 3,131,324 unweighted discharges were available. The accuracy of the MMM Index was compared to All Patient Refined Diagnosis-Related Groups,60 the All Payer Severity-adjusted Diagnosis-Related Groups,61 and a simple count of diagnoses.62 The MMM Index explained 32 percent of the variation in mortality, as measured by percent of deviance explained in mortality. It was fivefold more accurate than All Patient Refined Diagnosis-Related Groups and threefold more accurate than All Payer Severity-adjusted Diagnosis-Related Groups. This study demonstrated that prognostic information can be significantly improved by scoring each diagnosis separately.

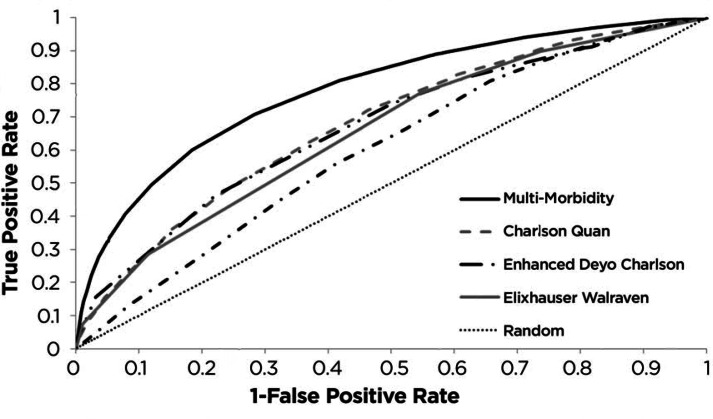
In 2015, the MM Index was directly compared to the Charlson and Elixhauser variants by predicting the 6-month mortality of heart failure patients.63 In this study, the prognosis of 602,050 unique heart failure patients across 130 Veterans Affairs medical centers was studied. The MM Index had a cross-validated ROC of 0.784. The MM Index was more accurate than the Quan variant of the Charlson Index,64 with an ROC of 0.656. It was also more accurate than the enhanced65 Deyo variant66 of the Charlson Index, with an ROC of 0.677. It was more accurate than the von Walraven variant of the Elixhauser Index,67 with an ROC of 0.639. It was also more accurate than chronological age with an ROC of 0.649, illustrating the importance of illness over age. Figure 2 compares the performance of these indices against each other. In all of these comparisons, not only was the cross-validated improvement in accuracy achieved by the MM Index statistically significant, but the magnitude of the improvement was large enough to potentially explain away small or medium treatment effects.

Figure 2.

MM Index and Variants of the Charlson Index

In the study of intensive care patients (discussed above in the comparison of the MM Index to physiological markers), we also compared the performance of the MM Index to comorbidity categories within the Elixhauser list, immunosuppressant medication use, and age. The study reported the 6-month and 12-month mortality of 442,692 unique intensive care patients. The MM Index relied on 5,695 diagnoses codes. The cross-validated ROC for the MM Index was 0.84. In contrast, the ROC for immunosuppressant medication use was 0.59; for age it was 0.60; for Elixhauser comorbidities it was 0.69; and for all combined variables (including physiological markers) it was 0.80. As in previous studies, these differences were all cross-validated and statistically significant. The fact that the MM Index, which scores each diagnosis, was more accurate than the Elixhauser’s categories of comorbidities suggests that grouping diagnoses into broad diagnostic categories reduces the accuracy of predictions.

Methods for Using the MM Index

To illustrate the application of the MM Index to specific cases, we use a case from a recent analysis of the prognosis of nursing home residents. The resident was 81 years old with 10 diagnoses during the last hospital admission (see Table 1). The likelihood ratio of each diagnosis was looked up in the online Table from the George Mason University Dataverse.68 For one diagnosis, “chronic airway obstruction, not COPD, and not elsewhere classified,” the table does not provide any information and therefore this diagnosis was ignored and scored with a likelihood ratio of 1. The MM score, the product of all likelihood ratios, was calculated as 45.07. In this database, the prior odds of mortality for this population was 0.16. The prior odds was multiplied by the product of the likelihood ratios to obtain the posterior odds. The posterior odds can be expressed as a probability by dividing the posterior odds by one plus the odds. This patient’s diagnoses has resulted in a probability of 0.88 for dying in the next six months. The likelihood ratios in Table 1 can also be used to explain the prediction. Likelihood ratios above 1 indicate diagnoses that increased the odds of mortality. Based on these data, the main reason for the high estimate of mortality pertained to the following: (1) lung cancer, (2) anorexia, and (3) cachexia. Each more than doubled the risk of mortality. Kidney disease also contributed to the high probability of mortality, but to a lesser extent.

The following example can also demonstrate how the MMM variant of the MM Index can be used. A patient presents with the worst disease in the circulatory system (i.e., second hospitalization for cardiogenic shock) and has two diseases within the digestive system (i.e., first hospitalization with perforation of intestine and first hospitalization for malignant neoplasm of stomach, not otherwise specified). For simplicity, assume that this patient has no other diseases within other body systems. The maximum progression within circulatory disease is 1, and the maximum progression within digestive diseases is 0.2 (the maximum of 0.1 and 0.2). For all other categories, there is no progression and they are scored 0. The overall probability of death for the patient is then calculated as follows:

$$\mathit{MMM}=1-\left(1-1.0\times 0.74\right)\left(1-0.20\times 0.81\right)=0.78$$

Note that in this method of scoring, any diagnosis with elevated risk, no matter how benign, always increases the probability of mortality.

Derivation of the MM Index from Data in an Electronic Health Record (EHR)

To facilitate the use of the MM Index in different EHR systems, Appendix A contains an SQL code that will facilitate the estimation of the parameters of the Index for a specific cohort of patients within a data warehouse. While we have experience with ICD-9 codes, a similar SQL can be run for ICD-10, thereby allowing the EHR to adjust for changes in the coding procedures. In addition, a similar SQL code can be run for procedures, exposure to medications, and categorized physiological measures, as well as decades of age, thereby allowing the prognostic index to reflect more than diagnoses.

Conclusion

This paper reviews the recent methodological research on the performance and application of the MM Index. One finding of this review was that MM Index had higher ROC than various physiological measures of prognosis, including ejection fraction for heart failure, HbA1c levels for diabetic patients, and 13 physiological measures for patients in intensive care units. Clinicians may prefer relying on physiological measures for any of the following reasons:

1. Many are concerned with coding errors in reporting patient diagnoses.69 However, given the accuracy of the results reported in this paper, coding errors are not extensive enough to significantly reduce the accuracy of diagnosis-based indices.

2. Some clinicians are concerned with reports that diagnoses in administrative data are less accurate than physiological markers when predicting prognosis, e.g., Brinkman et al.70 These studies do not contradict the data presented in this paper. These studies compare the accuracy of broad categories of diagnoses and not individual diagnoses. As reviewed, when diagnoses are not grouped into broad categories, the results are radically different and worse than when each diagnosis is scored.

3. Some clinicians prefer to use physiological markers because they often use these markers in patient management. Clearly, abnormal physiological markers raise the chances of mortality, but physiological markers are often transient and return to normal with good care. There is no reason to believe that these variations affect long-term mortality six months later.

A major conclusion of this paper was that MM Index is more accurate than existing diagnosis-based indices, such as variants of Charlson and Elixhauser indices. To the best of our knowledge, the MM Index is the first index that scores each disease separately rather than grouping similar diagnostic codes into broad categories. The observed improved accuracy of the MM Index may be due to this feature of its scoring.

The comprehensive inclusion of thousands of comorbidities in the MM Index makes its use within clinical settings more difficult. To address use in clinical settings, the paper also described the MMM variant of the MM Index. The MMM variant still scores each disease but classifies these diseases by body system after scoring and selects the maximum (worst) score within each body system. This organization of diagnoses in various body systems allows clinicians to think through the prognosis of their patients more intuitively and without access to a computer. The MMM Index is also helpful for conducting a propensity-matched comparative effectiveness study, where cases and controls must have similar scores across different body systems. Matching on scores ranges in the body systems may be more practical than matching on separate diagnoses within the body system.

Use of the MM Index is more practical now that many clinics have access to EHRs. These computers have access to the patients’ diagnostic history, can score patient’s prognosis, and can explain the top two or three reasons for the predicted prognosis. Then, the use of MM Index in a clinical setting will be akin to use of any laboratory test, where the results are available but details of how the results were obtained are masked.

The Appendix to this paper (as well as CIELO repository) provides an SQL code that can be used to estimate the parameters of the MM Index from data within warehouses or EHR systems. This code allows investigators to estimate the parameters of the MM Index for the population that they are working with. It can also be easily incorporated into the design and operations of an EHR.

There are a number of ways that the MM Index can be further improved, including the examination of interaction among diseases and removal of confounding in estimates of likelihood ratios. In addition, the MM Index may be improved if medications, physiological markers, or procedures were used to predict prognosis.

The use of the MM Index, as well as other prognostic indices, is fraught with difficulties when personalizing data for one patient. The MM Index reflects average probabilities associated with a disease. No patient is the average patient, since patients are likely to experience a combination of comorbidities that may radically differ from the average patient.

Furthermore, a discussion of mortality with patients may be understood differently if it is framed in terms of survival as opposed to mortality. Probabilities may be misunderstood, and patients may prefer to know expected survival days as opposed to the probability of mortality in six months. Obviously, any discussion of prognosis with patients requires empathetic communication on the part of clinicians. These and other limitations continue to frustrate efforts to make data on prognostic information available to patients and their families. Additional research is needed to clarify how to best communicate prognostic information to individual patients.

The MM and MMM Indices can be used easily in policy analysis, decision support, and program evaluation. In these uses, the index enables assessment of comparative effectiveness of treatment. Because these indices are more accurate than existing comprehensive diagnosis-based indices, we recommend their use despite the complexity of the underlying scoring procedures.

Table 2.

Calculation of the MM Index from Diagnoses of an 81-Year-Old Resident

DESCRIPTION OF DIAGNOSIS	LIKELIHOOD RATIO
(1) Malignant neoplasm of upper lobe, bronchus, or lobe	3.18
(2) Other specified chronic ischemic heart disease	1.41
(3) Abdominal aneurysm without mention of rupture	1.04
(4) Peripheral vascular disease, unspecified	0.96
(5) Chronic airway obstruction, not COPD, and not elsewhere classified	Not Found
(6) Chronic kidney disease, stage IV (severe)	1.45
(7) Secondary hyperparathyroidism of renal origin	1.03
(8) Anorexia	2.16
(9) Nausea and vomiting	1.02
(10) Cachexia	3.06
STEPS IN CALCULATION	RESULTS
MM Index (product of all likelihood ratios)	45.07
Prior odds for all residents	0.16
Posterior odds for this case (prior odds times MM Index)	7.21
Probability of Mortality (posterior odds divided by 1 plus posterior odds)	0.88

Appendix A.

The SQL code for the derivation of parameters of the Multimorbidity (MM) Index is provided below. Similar SQL code is also available for measurement of episodes of illness.71 Because the source of data may include millions of records, the code is written in steps, with each step generating a temporary or a permanent file that is used in subsequent steps. In this fashion, if for some reason the server operations are interrupted, intermediary results are still available and one can start the analysis from the point of the interruption and not from the beginning.

In the first step, we select 80 percent of the cases for calculations of the likelihood ratios and set aside the remaining cases for validation purposes:

In the second set of steps, we calculate the length of service to a patient. This information is used to exclude patients who are not deceased but have no visit after a certain date for at least one year. These patients are likely to have changed providers and may be receiving care outside of Veterans Administration.

In the third step, the likelihood ratios are estimated from the data within the database.