Detecting Gene-Environment Interactions for a Quantitative Trait in a Genome-Wide Association Study

Abstract

A genome-wide association study (GWAS) typically is focused on detecting marginal genetic effects. However, many complex traits are likely to be the result of the interplay of genes and environmental factors. These SNPs may have a weak marginal effect and thus unlikely to be detected from a scan of marginal effects, but may be detectable in a gene-environment (G×E) interaction analysis. However, a genome-wide interaction scan (GWIS) using a standard test of G×E interaction is known to have low power, particularly when one corrects for testing multiple SNPs. Two 2-step methods for GWIS have been previously proposed, aimed at improving efficiency by prioritizing SNPs most likely to be involved in a G×E interaction using a screening step. For a quantitative trait, these include a method that screens on marginal effects [Kooperberg and Leblanc, 2008] and a method that screens on variance heterogeneity by genotype [Paré et al., 2010] In this paper, we show that the Paré et al. approach has an inflated false-positive rate in the presence of an environmental marginal effect, and we propose an alternative that remains valid. We also propose a novel 2-step approach that combines the two screening approaches, and provide simulations demonstrating that the new method can outperform other GWIS approaches. Application of this method to a G × Hispanic-ethnicity scan for childhood lung function reveals a SNP near the MARCO locus that was not identified by previous marginal-effect scans.

Introduction

Genome-wide association studies (GWAS) have been conducted for years as a tool for identifying genetic susceptibility loci that are associated with complex traits. Several hundred trait-related loci for many human diseases and quantitative traits have been discovered through the scans of marginal genetic effects [Hindorff et al., 2015]. However, there remains a significant amount of heritability left unexplained for many traits after accounting for the SNPs that have been identified. This missing heritability is not likely to be explained by additional marginal-effect loci that might be detectable even with larger sample sizes [Maher, 2008]. A number of alternative explanations for this “missing” heritability have been discussed [Manolio et al., 2009]. One possible reason is that many complex traits are likely to be the result of the interplay of genes and environmental factors, such that a given trait-related locus may be important only for a subgroup of the population defined by some environmental factor. The presence of gene-environment (G×E) interaction may produce a weak marginal genetic effect that is unlikely to be detected using a standard genome-wide scan. In fact, an interaction with opposite genetic effects in different subgroups (qualitative interaction) could produce virtually no marginal genetic effect. Testing for G×E interactions in genome-wide association studies is a promising approach to find novel genes that could be missed from the primary scans of marginal effect. Identifying G×E interaction is considered one possible key to better understanding the genetic architecture of complex traits [Manolio and Collins, 2007; Zuk et al., 2012], and incorporating G×E interactions into trait prediction models is a primary goal of the President's Precision Medicine Initiative (http://www.nih.gov/news/health/sep2015/od-17.htm).

The traditional analysis of G×E interaction is based on an exhaustive scan for interaction with each SNP using a regression framework – linear regression for a quantitative outcome and logistic regression for a dichotomous outcome. In the context of dichotomous outcome this approach has been shown to have poor power and several 2-step approaches have been developed to improve efficiency in the context of case-control sampling [Murcray et al., 2009, 2011; Kooperberg and LeBlanc, 2008; Hsu et al., 2012; Gauderman et al, 2013]. For a quantitative trait, power for the traditional approach is also poor and 2-step alternatives have been proposed. Kooperberg and LeBlanc [Kooperberg and Leblanc, 2008] proposed screening SNPs based on their marginal effect, followed by testing of G×E interaction in Step 2 for only those SNPs that pass a 0.05 significance threshold in the screen. Pare et al. [Paré et al., 2010] developed an alternative procedure, with screening in Step 1 based on a test of variance heterogeneity across SNP genotypes. However, as we show in this paper, the Pare et al. approach does not preserve the overall Type I error, except in limited circumstances. In this paper, we develop a solution to this problem that recovers a valid 2-step method using variance heterogeneity screening. We also propose a new 2-step approach that combines both marginal and variance-heterogeneity information in a single screening test. We use simulations to compare the Type I error and power of these various approaches across a wide range of underlying models. We also apply these methods to a GWIS of childhood lung function.

Materials and Methods

Let Y be a quantitative phenotype. We define E to be an exposure variable, it can be an environmental variable (e.g. air pollution), personal exposure (e.g. smoking), or other personal characteristic (e.g. sex). We further assume that M SNPs have been genotyped on each of the N study individuals, with G₁, G₂, ..., G_M denoting the genotypes at the M loci. We let q_A to be the minor allele frequency (MAF) of allele A for the quantitative trait locus (QTL). In the following sections we describe several different approaches that can be used to analyze these data.

Marginal (YG) test

A standard GWAS is conducted by testing the null hypothesis β_G=0 for each of the M SNPs using a linear regression model of the form

$$Y={\beta }_0+{\beta }_{G}G+\epsilon$$ (1)

Adjustment covariates to control for potential confounders are typically included in the model. A correction [Dudbridge and Gusnanto, 2008] is applied to the p-value (p_G) to preserve the family-wise error rate (FWER). In the presence of an environmental factor (E) and a G×E interaction, β_G is a weighted average of the corresponding genetic effect in each environmental group, hence the use of the term ‘marginal’ to describe this effect. The same magnitude of β_G can result from different underlying patterns of G×E interaction.

Interaction test (G×E)

In a follow-up to the primary marginal scan, one can test for G×E interaction using the model

$$Y={\beta }_0+{\beta }_{G}G+{\beta }_{E}E+{\beta }_{GE}G\times E+\epsilon$$ (2)

based on testing the null hypothesis β_GE=0 for each of the M SNPs. Let p_G×E denote the p-value for the test of G×E interaction. A correction is also needed to preserve the FWER.

Two-Step test with screening on marginal G (YG|G×E)

In the pursuit of gene-gene (G×G) interactions, Kooperberg and Leblanc [Kooperberg and Leblanc, 2008] developed a 2-step approach that screens SNPs by genetic marginal effects at Step-1 significance level α₁. They proposed to formally test for G×G interactions for the subset m ≤ M SNPs that pass the Step-1 screen, with a Bonferroni-corrected significance level α/m to preserve the FWER. This approach is based on the observation that most variants involved in the interactions are also likely to display some non-zero (although possibly weak) marginal effect on the phenotype. An analogous screening on marginal effects can also be applied for G×E analysis. We explore the power of this strategy for G×E interactions by screening M SNPs in the first step by genetic marginal effects (model 1). One can use either subset testing [Kooperberg and Leblanc, 2008] or an alternative weighted hypothesis testing [Ionita-Laza et al., 2007] in Step 2 (model 2). These two hypothesis testing approaches are described in more detail below.

Two-Step test with screening on variance heterogeneity (Var|G×E)

An alternative 2-step approach can be constructed by screening for variance heterogeneity across genotypic groups [Paré et al., 2010]. The rationale is that if the effect of a QTL differs depending on an environmental factor, the variability of the quantitative trait among individuals carrying the risk allele will also be different from the variability among non-carriers. Paré et al. [Paré et al., 2010] proposed to use Levene's test [Levene H, 1960] for homogeneity of variance across genotypic groups at the screening step for all M SNPs, and then only test for G×E interactions for a subset of SNPs that pass the screening step using model 2. They showed that the power of this procedure can be higher than the power of the standard G×E analysis depending on the magnitude of the main effect of the interacting factor E, where the main effect is defined as the effect of E when G=0. However, we show that the correlation between the variance estimator and the G×E interaction estimator is dependent on the marginal effect of E and this correlation will only be equal to zero when no marginal effect of E exists (Details shown in Supplemental material). In other words, the Step-1 Levene's test, which is based on comparing variances across G, is correlated with the Step-2 test of G×E in the presence of a marginal effect of E. This correlation violates the basic premise of 2-step testing procedures that requires independence of Steps 1 and 2 for validity [Murcray et al., 2009]. The result, as we will show in our simulation studies, is that the Paré et al. approach can produce an unacceptably high false-positive rate.

Two-Step test with a screening on residual variance heterogeneity (rVar|G×E)

As we show in the Supplemental materials, the correlation between Levene's test and the G×E interaction test can be eliminated if the marginal effect of E is removed. Moreover, removing the marginal effect of E will not affect the magnitude of G×E interaction (Supplemental materials, Fig. S1). Based on these two observations, we propose a revised 2-step approach to using variance heterogeneity as follows:

Step-0

Given a quantitative trait Y, fit the linear regression model:

$$Y_i={\alpha }_0+{\alpha }_E{E}_i+{\tau }_i$$ (3)

Where i=1,...,N for N individuals in the sample.

Step-1

Given K groups defined by genotype, test the null hypothesis of equality of variance, H₀: σ₁= σ₂=... σ_K, where σ_k is the standard deviation of τ within the k^th subgroup (k=1,...,K, e.g. K=3 for an additive model, K=2 for a dominant model), using Levene's test defined as:

$$W=\frac{(N-K)\sum _{k=1}^K{N}_k{(Z_{k•}-Z_{••})}^2}{(K-1)\sum _{k=1}^K\sum _{j=1}^{N_k}{(Z_{kj}-Z_{•})}^2}$$ (4)

Where N is the total sample size, Z_kj=|τ_kj– τ_k•| where τ_kj is the residual of the regression in (3) for j^th observation in k^th subgroup, and τ_k• is the mean or median of k^th subgroup. Z_k• is the mean of Z_kj for k^th subgroup, and Z_•• is the mean of all Z_kj. Note that Equation 4 defined Levene's test of variance heterogeneity applied to the residuals τ instead of the original trait Y. The p-value is defined as:

$${\mathrm{P}}_{\mathrm{rVar}}=\mathrm{Pr}(F_{(K-1,N-K)}>W)$$ (5)

Where F is the F-distribution with K–1 and N–K degrees of freedom.

Step-2

Considering results of the Step-1 screen, test the null hypothesis H₀: β_GE=0 using model 2.

The use of residuals removes the marginal E effect and thus eliminates the correlation between the Levene's test and the test of G×E interaction. This leads to a 2-step procedure that preserves the FWER, as we show by simulation. One can use either subset testing or weighted hypothesis testing in Step 2 (see below).

Joint Two-Step test with screening based on both YG and rVar (Joint|G×E)

So far we have seen three pieces of information that can be utilized in the search for G×E interactions: the G×E interaction effect, the marginal G effect, and variance heterogeneity across G. The standard test uses only the G×E interaction effect, Kooperberg and Leblanc [Kooperberg and Leblanc, 2008] use the marginal effect of G to screen and G×E to test, and our modification of Paré et al [Paré et al., 2010] utilizes residual variance heterogeneity to screen and G×E to test. We propose a novel 2-step approach that uses all three of these sources of available information, as follows:

Step-0

Remove the marginal E effect and collect residuals from model 3, as described for the rVar|G×E approach above.

Step-1

Combine the P-value (P_G) from marginal G scan and P-value (P_rVar) from test of variance heterogeneity using Fisher's method [Fisher RA, 1932]:

$$T_{jo\mathrm{int}}=-2[\ln \left({\mathrm{P}}_G\right)+\ln \left({\mathrm{P}}_{\mathrm{rVar}}\right)]$$ (6)

Note that the test of marginal G effect is independent of the test of variance heterogeneity across G (Supplemental materials). T_joint therefore follows a chi-squared distribution with 4 degrees of freedom under the joint null H₀: σ₁= σ₂=... σ_k and β_G=0.

Step-2

Considering results of the Step-1 screen, test the null hypothesis H₀: β_GE=0 using model 2.

The G×E interaction estimator is uncorrelated with both the residual variance per genotype (Supplemental materials) and with the marginal G estimator [Dai et al., 2012], and so the joint test in Step-1 is uncorrelated with the Step-2 interaction test. One can either use subset testing or weighted hypothesis testing in Step 2 (see below).

Hypothesis Testing Approaches in Step 2

For a 2-step approach, it is important to have an efficient testing scheme in Step 2 to make the best use of the information from Step 1. Previously developed 2-step methods have described both subset testing and hypothesis testing for Step 2 [Gauderman et al., 2013; Hsu et al., 2012]. In subset testing, a step-1 significance threshold α₁ is pre-specified. At the screening step, SNPs with a step-1 p-value less than α₁ will be passed into the Step 2 and only that subset of SNPs passed into Step 2 will be formally tested for G×E interaction. A Bonferroni correction for the number of SNPs tested in Step 2 will be utilized. Simulation studies suggest that the power of this 2-step approach depends strongly on the choice of α₁ (Gauderman et al, 2013). A larger value of α₁ will increase the chance of passing a true trait-related SNP into Step 2, but at the expense of also passing more null markers leading to a larger penalty for multiple testing. A lower value of α₁ will produce a smaller subset of SNPs tested in Step 2 and less-severe multiple testing burden, but at the possible cost of screening out a truly associated SNP.

Instead of specifying a significance threshold α₁ to screen out SNPs, Ionita-Laza et al. [Ionita-Laza et al., 2007] proposed a weighted hypothesis testing scheme. At the screening step, all M SNPs are ordered by their step-1 p-values. At Step 2, the M SNPs are assigned with different weights to the significance level based on their rankings in Step 1. Specifically, an initial bin size B is pre-specified and the B most significant SNPs based on step-1 P-values are tested at significance level α/2B , the next 2B SNPs are tested at significance level α/[2²(2B)], the next 4B SNPs will be tested at significance level α/[2³(2²B)], etc.The weighted testing schema follows the intuition that SNPs with strong step-1 evidence are more likely to be truly involved in a G×E interaction, and thus should be ‘rewarded’ with a less stringent significance threshold than the standard Bonferroni correction. However, this approach ‘punishes’ those SNPs with lower step-1 rankings by requiring a stricter significance threshold than the standard Bonferroni.

Simulation Study

We use simulation to evaluate Type I error rates and compare power of all methods discussed above. We consider two scenarios for the data generating model. In scenario 1, Y is a function of a marginal effect of G (the QTL), a marginal effect of E₁ and an interaction effect between G and E₁ as follows:

$$Y={\beta }_0+{\beta }_G(G-{\mu }_G)+{\beta }_{E_1}(E_1-{\mu }_{E_1})+{\beta }_{G{E}_1}(G-{\mu }_G)\times (E_1-{\mu }_{E_1})+\epsilon$$ (7)

Here we assume μ_G and μ_E1 are the population means of the covariates G and E₁. For example, if G is coded according to a dominant model (G = 1 for AA or Aa genotype, and G=0 for aa genotype), then μ_G=q_A(2–q_A). For simplicity, we assume E₁ is a binary indicator of exposure, so that μ_E1=P_E1, is the population prevalence of exposure.

In scenario 2, we assume Y is related to two uncorrelated exposures E₁ and E₂, according a model that includes marginal effects and two G×E interactions as follows:

$$Y={\beta }_0+{\beta }_G(G-{\mu }_G)+{\beta }_{E_1}(E_1-{\mu }_{E_1})+{\beta }_{G{E}_1}(G-{\mu }_G)\times (E_1-{\mu }_{E_1})+{\beta }_{E_2}(E_2-{\mu }_{E_2})+{\beta }_{G{E}_2}(G-{\mu }_G)\times (E_2-{\mu }_{E_2})+\epsilon$$ (8)

Similarly, μ_E2 is the population mean of E₂ and the components in model 8 are pairwise uncorrelated due to the centering of each variable on its respective mean. The variance of Y conditional on G can be written as:

$$Var(Y\mid G)=Var[{\beta }_0+{\beta }_G(G-{\mu }_G)+{\beta }_{E1}(E_1-{\mu }_{E1})+{\beta }_{GE1}(G-{\mu }_G)\times (E_1-{\mu }_{E1})+{\beta }_{E2}(E_1-{\mu }_{E2})+{\beta }_{GE2}(G-{\mu }_G)\times (E_2-{\mu }_{E2})+\epsilon ]={[{\beta }_{E1}+{\beta }_{GE1}(G-{\mu }_G)]}^2{P}_{E1}(1-P_{E1})+{[{\beta }_{E2}+{\beta }_{GE2}(G-{\mu }_G)]}^2{P}_{E2}(1-P_{E2})+{\sigma }^2$$ (9)

In this model, β_G is the marginal effect of G, β_E1 and β_E2 are marginal effects of E₁ and E₂ respectively, β_GE1 and β_GE2 are the two interaction effects, and ε is assumed to have a normal distribution with mean 0 and variance σ². The expression for the variance and interpretations of the parameters are similar for the simpler model in scenario 1. Note that in scenario 2, although the true model includes E₂ and G×E₂, we assume that the focus is still only on G×E₁ interaction, and that data for E₂ are not part of the available data, to mimic the typical scenario in a GWIS that we only have limited data on environment. For both scenarios, we specify a ‘base’ model that includes a QTL with q_A=0.1635 and a dominant model so that 30% carry at least one A allele. The exposure variables E₁ and E₂ were both assumed to be binary variables with P_E1= P_E2=0.3. Without loss of generality, we assumed the total variance of Y to be 1.0 and used the strategy proposed by Gauderman [Gauderman, 2003] to partition the variance. Specifically, the proportion of the total variance of Y explained by the marginal effect of G (QTL) was defined as R²_G=β²_GVar(G–μ_G) where Var(G–μ_G)=Var(G)=q_A(2–q_A)(1–q_A)². Similarly, the proportion of the total variance of Y explained by the marginal effect of E₁ was defined as R²_E1=β²_E1Var(E₁–μ_E1) where Var(E₁–μ_E1)=Var(E₁)=P_E1(1– P_E1). The quantity R²_GE1= β²_GE1Var[(G–μ_G)(E₁–μ_E1)] gives the proportion of total variance explained by the interaction effect between G and E₁, where Var[(G–μ_G)(E₁–μ_E1)]=2P_E1(1– P_E1)q_A(2–q_A)(1–q_A)². The analogous quantities R²_E2=β²_E2Var(E₂–μ_E2) and R²_GE2= β²_GE2Var[(G–μ_G)(E₂–μ_E2)] denote the proportion of variance explained by the marginal effects of E₂ and G×E₂ interaction, respectively. The error ε was assumed to have a normal distribution with mean 0 and variance σ²=1 – (R²_G+ R²_E1+ R²_GE1) for scenario 1 and σ²=1 – (R²_G+ R²_E1+ R²_GE1+ R²_E2+ R²_GE2) for scenario 2. For scenario 1, our base model has a modest interaction effect with no effect of G when E=0 and no effect of E when G=0, and with marginal G and E effect sizes of R²_G= R²_E1=0.17% and interaction effect size R²_GE1=0.4%. For scenario 2, we used the same settings as for Scenario 1, but add a marginal effect of E₂ (R²_E2=2%) and an interaction effect between G and E₂ (R²_GE2=2%). In all simulations we generated 1,000 replicate data sets per simulation. For all of the 2-step approaches, we adopted weighted hypothesis testing and assumed the initial bin size of B=5.

Type 1 Error

We evaluated the Type I error rate for both scenarios 1 and 2. We defined non-QTL (null) SNPs as those have neither marginal G nor G×E₁ effect. We performed multiple simulations varying the magnitude of R²_E1 from 0 to 4% by 2%. For scenario 2, one SNP was generated to have G×E₂ interaction effect (but no marginal G and G×E effect) and R²_E2 and R²_GE2 were fixed at 2%. We also considered an alternative model in which 10 loci had a marginal (but no G×E₁ or G×E₂) effect on the trait, with R²_G for those 10 loci randomly sampled from a uniform distribution in the range 0.17%-0.43%. In each replicated data set, we simulated 10,000 null SNPs with 6,000 study individuals. For each of the SNPs we randomly sampled an allele frequency from a uniform distribution in the range 0.1 – 0.4. The Type I error rate for each procedure was estimated as the proportion of replicates in which at least one of the 10,000 non-QTL SNPs was declared statistically significant at a FWER of α=0.05.

Power Comparison

To estimate power, we simulated 1,000 replicate datasets, each including 1 million SNPs and 6,000 study subjects. One SNP was designated as the QTL, first generated according to the base model and then using alternative models to examine sensitivity of the power comparisons. We performed GWIS using all the methods described above. The marginal effect of E₁ is expected to affect neither the power to detect the marginal G effect nor the power to detect G×E₁ interaction. Moreover, since the marginal effect of E₁ needs to be removed in the rVar|G×E and Joint|G×E methods, the magnitude of β_E1 is also expected not to affect the power of the test of variance heterogeneity. Thus, we kept R²_E1 fixed at 0.17% for all scenarios. We varied R²_G from 0 to 0.425% by 0.085%. These settings yielded a wide range of interaction models, including both quantitative (effects of G in same direction depending on E₁) and qualitative (effects of G in opposite directions depending on E₁) interaction models (Table S1 in Supplemental materials). We also performed multiple simulations varying R²_GE1 from 0.10% to 0.85%. In scenario 2, we performed additional simulations varying the magnitudes of R²_E2 in the interval [0, 10%], and R²_GE2 in the interval [0, 5%]. To further explore the robustness of our power comparisons, we also considered alternative models with different QTL minor allele frequency (q_A) and exposure prevalence (P_E1 and P_E2). The power for each method was estimated as the proportion of replicates in which the QTL was declared as statistically significant at a FWER of α=0.05. For each model, we also estimated the power to detect the marginal effect of the QTL, to quantify the chance that the QTL would be identified by the primary G-only scan.

Lung Function Analysis

Forced expiratory volume in the first second (FEV₁) is a widely used measure to evaluate pulmonary function. Prior GWAS scans have identified several loci that have marginal G association with FEV₁ [Hancock et al., 2009]. We hypothesize that heritability for FEV₁ can be different across ethnic groups for three possible reasons: 1) there is a difference in allele frequency across groups, but the same effect of the QTL on the trait in all groups, 2) the allele frequency is similar across groups but the QTL effect varies by group, 3) both the allele frequency and QTL effect vary across groups. In the first situation, a standard marginal G scan should provide the best power, while situations 2 and 3 should show evidence of G × Ethnicity interaction. For example, a QTL could have no effect on FEV₁ in a non-Hispanic White population but serve as an important contributor to the explained heritability for a Hispanic White population.

In an attempt to identify additional loci for FEV₁, we performed a genome-wide scan for G × Hispanic-ethnicity interaction using data from the Children's Health Study (CHS). The CHS is an ongoing cohort study investigating both genetic and environmental effect on asthma risk [McConnell et al., 2006] and lung function development [Gauderman et al., 2015] in children from 16 southern California communities. FEV₁ was measured for each child by trained technicians and was log-transformed to satisfy assumptions of the linear regression model. The GWAS was based on a nested Case-Control sample of 1,249 asthmatic and 1,751 nonasthmatic children selected from the Hispanic White (HW) and non-Hispanic White (NHW) participants in the CHS cohorts. Ethnicity was self-reported by parents on the CHS baseline questionnaire. For our G × Hispanic-ethnicity analysis of FEV₁, we focused on participants that had a lung function measurement in 9^th grade (average 15 years of age), which included a total of 1,728 children (684 HW, 1,044 NHW). Genome-wide genotyping was conducted using the Illumina Human Hap 550 or Human610Quad Bead Chip microarrays at the USC Genomic Center. After quality control, 506,788 SNPs were included in the GWIS analysis. The model included adjustment for sex, age, body-mass index (BMI), BMI squared, log transformed height (log height), log height squared, community and estimated individual global ancestry (adjustment for population substructure). We applied all the methods described in this paper. Both subset testing with α₁=0.1 and weighted hypothesis testing with initial bin size of 5 were used for each of the 2-step approaches.

Results

Simulation Study

Type 1 Error

Both Table 1 and Table S2 (Supplemental materials) show that when there is no marginal effect of E₁ (R²_E1), all the methods maintain the correct test size. However, the Type 1 error rate of the Var|G×E approach (Paré et al.) is inflated to unacceptable levels as the marginal effect of E₁ increased. The standard G×E test, and the YG|G×E, rVar|G×E and Joint|G×E 2-step methods achieve the nominal Type 1 error rate, whether or not there is a marginal effect of E₁. The Type I error rates are similar for all methods under either scenario 1 or 2.

Table 1.

Type 1 error rates for tests of G×E₁ interaction when non-QTL SNPs have neither marginal G effect nor G×E₁ interaction effect

		R2E1
Method		0.00	0.02	0.04
Exhaustive
G×E
	Scenario 1	0.046	0.046	0.048
	Scenario 2	0.042	0.043	0.043
2-step
Var|G×E
	Scenario 1	0.049	0.159	0.264
	Scenario 2	0.048	0.134	0.218
YG|G×E
	Scenario 1	0.054	0.054	0.054
	Scenario 2	0.047	0.048	0.047
rVar|G×E
	Scenario 1	0.053	0.053	0.050
	Scenario 2	0.048	0.049	0.047
Joint|G×E
	Scenario 1	0.053	0.053	0.048
	Scenario 2	0.040	0.041	0.041

Scenario 1 involves E₁ only.

Scenario 2 involves E₁ and E₂ with R²_E2 and R²_GE2 fixed at 2%.

Each estimate of Type 1 error is based on the proportion of 1,000 replicate data sets for which the indicated procedure identified at least one statistically significant result among 10,000 non-QTL SNPs, with Type 1 error rate set to be 0.05.

Weighted hypothesis testing is used for 2-step approaches.

Significantly inflated Type 1 error is indicated in bold

Power Comparison

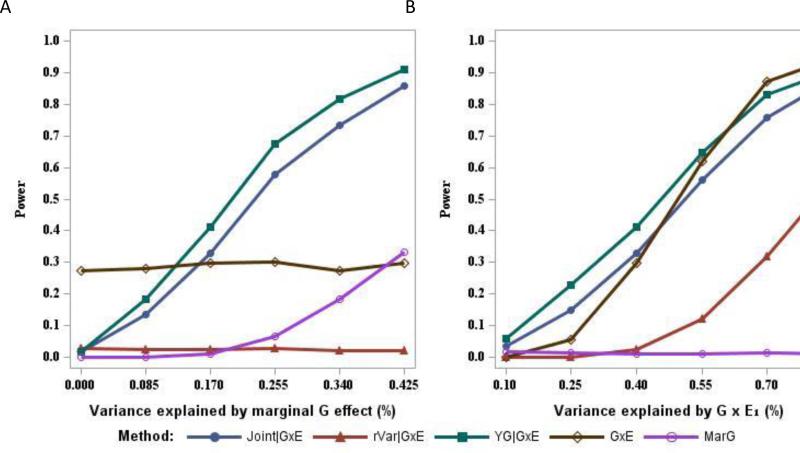
Figure 1 shows the results when G×E₁ is the only interaction contributing to the heritability of Y(scenario 1). The power to detect an interaction of magnitude R²_GE1=0.4% with 6,000 individuals is quite low (30%) using the standard G×E analysis (Fig. 1A). The rVar|G×E method is the least powerful method (2%) under this scenario, almost always failing to detect the QTL. Power for these two methods was nearly independent of the size of the marginal G effect (R²_G). On the other hand, power for those methods that utilize marginal G information in the screen (YG|G×E and Joint|G×E) depend strongly on the size of R²_G. The YG|G×E method is the most powerful method when there is a small to moderate marginal genetic effect and is always more powerful than the Joint|G×E method.

Figure 1.

Power to detect G×E₁ interaction in the presence of one interaction effect, with 6,000 individuals. (A) Power is presented across a range of magnitudes for the marginal genetic effect (R²_G) with R²_GE1=0.4%. (B) Power is presented across a range of magnitudes for G×E₁ interaction (R²_GE1) with R²_G=0.17%.

Holding the marginal G effect constant at R²_G=0.17%, power for all the procedures increases as the magnitude of the interaction effect increases (Fig. 1B), as we would expect. The rVar|G×E method again performs poorly in this situation. The YG|G×E method still provides greater power than the Joint|G×E method across all the magnitudes of R²_GE1 considered, with a gain of power in the range 2%-9%.

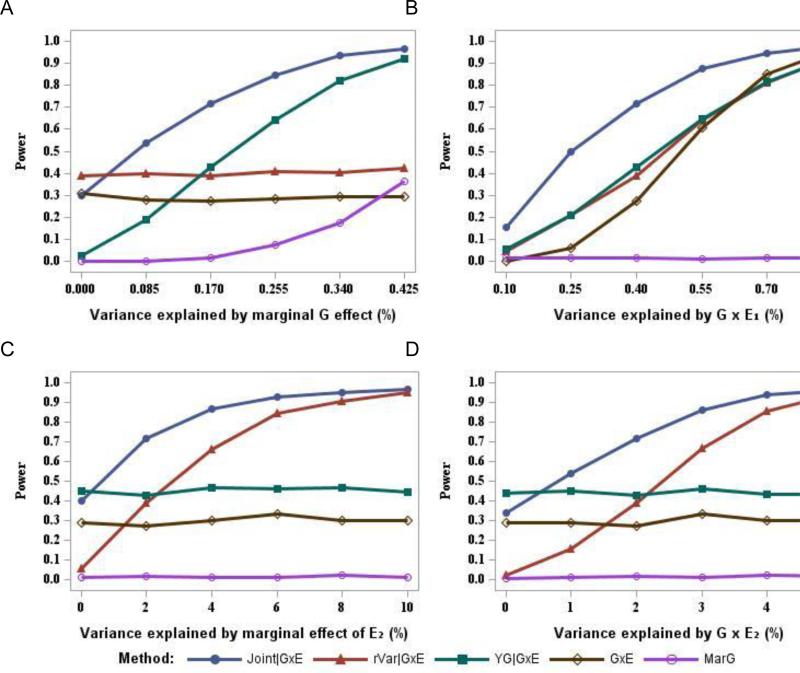
Figure 2 presents the power to detect G×E₁ when two G×E interactions (G×E₁ and G×E₂) contributing to the heritability of Y (Scenario 2). Unlike the results for scenario 1, the rVar|G×E method provides higher power (by about 10%) than the standard G×E scan across a range of marginal G effect sizes (Fig. 2A). The Joint|G×E method is more powerful than the YG|G×E method across all the sizes of R²_G evaluated, with a gain of power from 4% to 27% (Fig. 2A). Note that when the magnitude of marginal genetic effect is small (R²_G=0.085%), the power for YG|G×E method is about 9% lower than the standard G×E scan, while the Joint|G×E method provides power that is 26% higher than the standard G×E scan.

Figure 2.

Power to detect G×E₁ interaction in the presence of two interaction effects, with 6,000 individuals. (A) Power is presented across a range of magnitudes for the marginal genetic effect (R²_G) with R²_GE1=0.4%, R²_E2= R²_GE2=2%. (B) Power is presented across a range of magnitudes for G×E₁ interaction (R²_GE1) with R²_G=0.17%, R²_E2= R²_GE2=2%. (C) Power is presented across a range of magnitudes for the marginal effect of E₂ (R²_E2) with R²_G=0.17%, R²_GE1=0.4%, R²_GE2=2%. (D) Power is presented across a range of magnitudes for G×E₂ interaction (R²_GE2) with R²_G=0.17%, R²_GE1=0.4%, R²_E2=2%.

As shown in Fig 2B, the standard G×E scan has the least power when the size of R²_GE1 is small to moderate, in the range of 0.1%-0.55%. The power for rVar|G×E and YG|G×E is about the same across the sizes of R²_GE1 evaluated. The Joint|G×E method again provides most power across all the sizes of R²_GE1 evaluated. When R²_GE1=0.7%, power for the standard G×E scan is about 4% higher than both YG|G×E and rVar|G×E, while Joint|G×E still provides about 9% higher power than the standard G×E scan.

Power for YG|G×E and standard G×E scan is independent of the size of R²_E2 (Fig. 2C). On the other hand, power of the 2-step methods that utilize variance heterogeneity information in their screening step (rVar|G×E and Joint|G×E) depends strongly on the magnitude of R²_E2. When R²_E2=0, there is little heterogeneity in variance across genotype and as a result, rVar|G×E performs poorly, with power 6% compared to 30% for the standard G×E scan. The Joint|G×E and rVar|G×E methods begin to outperform YG|G×E and the standard G×E scan when R²_E2>0, with a gain in power increasing with the magnitude of R²_E2.

Similar trends are observed across a range of different values for R²_GE2 (Fig. 2D). When there is no G×E₂ interaction (R²_GE2=0), the rVar|G×E method has almost no power to detect the QTL (2%). The Joint|G×E method provides a power slightly greater than the standard G×E scan but less than the YG|G×E. The power for the two 2-step approaches that utilize variance heterogeneity information in their screening step increases as the magnitude of the R²_GE2 increases. The Joint|G×E method again is the most powerful method when R²_GE2≥1%.

The power for the 2-step approaches that utilize the variance heterogeneity information also depends on the magnitude of q_A for the QTL (Supplemental materials, Fig. S2A). Note that the proportions of variance explained by each component (G, E₁, E₂, G×E₁ and G×E₂) are fixed under the base model (See ‘Simulation Study’ for details). The power for the Joint|G×E and rVar|G×E drops as the magnitude of the minor allele frequency q_A increases. The Joint|G×E method remains as the most powerful across the range of q_A evaluated (0.01-0.25). The power of all the methods is independent of the size of P_E1 and P_E2 (Supplemental materials, Figs. S2B, S2C).

For the 2-step methods, all of the above results are based on weighted hypothesis testing. We also examined the power using subset testing, considering a range of step-1 significance threshold (α₁). We explored the power varying the model settings around the base model. Table S3 (Supplemental materials) shows that the power of Joint|G×E using subset testing depends strongly on the choice of α₁ and the optimal magnitude of α₁ varies across the underlying models. When the information (marginal G association or residual variance heterogeneity) used in the screening step is weak, for example, when any of R²_G, R²_E2 or R²_GE2 is set to be 0, the highest power for subset testing occurs with a loose step-1 threshold (α₁=0.05 or 0.01) and is higher than the power for the weighted testing. However, when any of R²_G, R²_E2 or R²_GE2 has a relatively large value, a strict step-1 threshold (α₁=0.0001) leads to the highest power for the subset testing and no choice of α₁ for a subset testing leads to as much power as can be achieved using weighted hypothesis testing.

Lung Function Analysis

In our analysis of G × Hispanicity interaction for FEV₁, the marginal G scan does not identify any SNPs with genome-wide significant P-values after Bonferroni correction (Supplemental materials, Fig. S3). Note that the test of variance heterogeneity is not specific to the G×E interaction tested in step-2 and variance heterogeneity could also be induced by biological mechanisms other than interactions (Takeuchi et al., 2011). As a result, we observed inflation of Levene's test statistic in the step-1 QQ plot for the rVar|G×E method. As shown in the Manhattan plots of Figure S4 (Supplemental materials), one SNP was identified by the standard G×E test and the rVar|G×E and Joint|G×E 2-step approaches. This SNP is rs1439945 with MAF=0.16 in the Hispanic White (HW) sample, MAF=0.14 in non-Hispanic White (NHW) sample, and MAF= 0.15 for the combined sample. The SNP is located on chromosome 2 near the MARCO gene, with Step-1 screening P-value 5.4 × 10⁻² for Joint|G×E, 1.8 × 10⁻² for rVar|G×E and Step-2 testing P-value 6.4 × 10⁻⁸ (Table 2).

Table 2.

Top 10 SNPs from Joint|G×E analysis of 506,788 SNPs for G × Hispanic-ethnicity interaction of FEV₁ in the Children's Health Study

SNP	CHR	Location	Nearest Gene	Step-1 P-value	Step-2 P-value	Significance Threshold
rs1439945	2	119535662	MARCO	5.4 × 10−2	6.4 × 10−8	8.0 × 10−7
rs12338838	9	218848	DOCK8	2.5 × 10−2	1.8 × 10−6	8.0 × 10−7
rs296513	1	199173096	MROH3P	4.7 × 10−2	1.3 × 10−5	8.0 × 10−7
rs4478805	13	115405425	TSPAN2	8.6 × 10−2	5.0 × 10−5	8.0 × 10−7
rs6063141	6	45779866	SULF2	5.8 × 10−2	6.0 × 10−5	8.0 × 10−7
rs6933322	12	53099317	GCM1	2.8 × 10−2	7.0 × 10−5	8.0 × 10−7
rs10173517	12	230737937	SP110	7.3 × 10−2	7.4 × 10−5	8.0 × 10−7
rs2146390	12	98040506	DNTT	7.4 × 10−2	8.6 × 10−5	8.0 × 10−7
rs11237700	15	78437535	TENM4	5.4 × 10−2	8.8 × 10−5	8.0 × 10−7
rs6780603	2	34222683	LOC101928114	4.8 × 10−2	1.0 × 10−4	8.0 × 10−7
rs12296349	9	99835504	ANO4	6.3 × 10−3	1.1 × 10−4	8.0 × 10−7

The MARCO gene has been found to be associated with susceptibility to pulmonary tuberculosis in a Chinese Han population (Ma et al., 2011) and in a Gambian population (Bowdish et al., 2013). This locus exhibits a qualitative interaction (Supplemental materials, Fig. S5), with a 130.3 milliliters decrease in FEV₁ per allele for Hispanic whites and a 83.0 milliliters increase in FEV₁ per allele for non-Hispanic whites. Note that this SNP was identified by subset testing with α₁=0.1 and would not have been found using the weighted hypothesis testing. The marginal effect of this SNP is weak (β_G = −0.004, P-value=0.53), and as shown in Table S3 (Supplemental materials), subset testing with a liberal screening threshold provides the highest power in this situation. This locus has not been previously identified in marginal G scans of FEV₁.

Discussion

As demonstrated by simulation, the previously proposed 2-step G×E method that screens on variance heterogeneity [Paré et al., 2010] has inflated Type 1 error in presence of a marginal E effect. In this paper, we proposed an alternative that uses variance heterogeneity and preserves the Type 1 error rate whether or not there is a marginal effect of E. We also proposed a novel 2-step method that utilizes both variance heterogeneity and the marginal G effect in a joint screening test. However, when only one G×E interaction is involved in the underlying trait model, our simulations demonstrated that neither the variance heterogeneity nor the joint approach lead to increased power to detect G×E interaction compared to the standard test of G×E interaction. However, these two new methods can provide greater power than the standard test across a wide range of models when the trait depends on two (or more) G×E interactions. When only one interaction with a modest effect size is involved in the development of Y (scenario 1), the variance of Y conditional on G only depends on G×E₁ interaction effect β_GE1 and marginal effect of E₁ β_E1 (See equation 9). The magnitude of variance heterogeneity across G also depends on β_E1 and β_GE1 if β_GE1≠0. When β_E1 is removed, as required in the 2-step approaches that utilize the test of variance heterogeneity in their screening step (Joint|G×E and rVar|G×E), the magnitude of variance heterogeneity is reduced which makes the screening steps of those methods have very limited power to pass the true QTL to the testing step. As a result, power of the 2-step approaches that utilize the test of residual variance heterogeneity will be diminished due to sacrificing degrees of freedom for utilizing an inefficient source of information. The YG|G×E method is generally the most powerful method in the presence of one interaction. The YG|G×E method can outperform the standard G×E test when even a small marginal G effect is present, with increasing gains in power as the marginal G effect increases (Figure 1).

When two interactions (G×E₁ and G×E₂) are involved in the development of Y (scenario 2), the test of variance heterogeneity begins to play a part and the rVar|G×E method can provide higher power than the standard G×E test (Fig. 2). That is because when β_E1 is removed, the magnitude of variance heterogeneity across G still depends on β_GE1, β_E2 and β_GE2. If the sizes of β_E2 and β_GE2 are large enough, then the magnitude of variance heterogeneity remains an efficient source of information even when the size of β_GE1 is small. As demonstrated by simulation, the rVar|G×E method can outperform YG|G×E method when the size of marginal G effect is small. When interactions induce both a marginal G effect and variance heterogeneity across G, the Joint|G×E method can prioritize SNPs for step-2 testing more efficiently than either the YG|G×E or rVar|G×E method. Note that in this paper E₁ and E₂ are simulated to be independent. It would be of interest to evaluate our new methods in the presence of different relationships between E₁ and E₂ (positively correlated and negatively correlated), which could be a subject of a future paper.

Note that the 2-step approaches for a case-control sample [Murcray et al., 2009, 2011; 2008; Hsu et al., 2012; Gauderman et al, 2013] are all based on the observation that there is an induced correlation between environment and genetic (E-G) in the combined case-control sample due to the over ascertainment of cases from the source population in the presence of G×E interaction (e.g., Unmatched case-control with 1 control per case). However, in a scan for quantitative trait loci (QTLs), we typically draw a random sample from the source population without regard for phenotype, and thus there is no induced E-G correlation in the sample. Consequently, unlike the case-control sample, screening on the E-G correlation cannot provide us with information on potential G×E interaction. The previously proposed joint/hybird approaches [Murcray et al., 2009, 2011; 2008; Hsu et al., 2012; Gauderman et al, 2013] are all in the context of a disease trait. In this paper, we adopt the idea of combining useful information in the screening step that was developed for disease traits in the development of a quantitative trait. To our knowledge, ours is the first paper to propose a joint screening test for a quantitative trait.

Using these novel approaches applied to the CHS, we identified evidence of G × Hispanic-ethnicity interaction for SNP rs1439945 at genomewide significance. In our analysis of G × Hispanic-ethnicity for FEV₁ in the CHS, we identified the SNP rs1439945 at genomewide significance using both the rVar|G×E and Joint|G×E methods. This SNP has not been detected in previous marginal GWAS scans. Based on our simulations, finding this locus using the rVar|G×E and Joint|G×E approaches may suggest that this SNP also interacts with additional factors other than Hispanic-ethnicity to affect lung function. For example, previous studies in the CHS have shown that FEV₁ in children is affected by many factors, including air pollution [Gauderman et al., 2004], the oxidative stress gene GSTM1 [Gilliland et al., 2002], and in-utero tobacco smoke [Breton et al., 2009]. The power to detect interaction of the rs1439945 SNP with Hispanic-ethnicity by either the rVar|G×E or Joint|G×E approach would be increased if it also interacts with one of these additional factors, or some other factor, to affect lung function. Further interpretation of our finding will require additional study, including replication in other samples.

While we described our methods in the context of a binary environmental factor, we note that the “E” can be replaced by a continuous variable, or a pre-specified candidate gene. The Levene's test of variance heterogeneity can also be extended to imputed data (Supplemental materials). We have developed computationally efficient G×E analysis software (G×EScan, available at http://biostats.usc.edu/software) that implements all the methods described in this paper. G×EScan also implements a comprehensive collection of G×E analysis methods for a case-control sample [Gauderman et al, 2013].

It is widely accepted that the etiology of many complex traits involves not only genetic and environmental factors but also interactions between the two as well as G × G interactions. In this paper, we described two new methods for detecting interactions for a quantitative trait in a genomewide setting. Both methods use a novel test of variance heterogeneity that does not depend on the size of marginal G effect. These two new methods, Joint|G×E and rVar|G×E, have the potential to identify novel SNPs that have been missed from primary GWAS scans.