Modelling effects on grid cells of sensory input during self‐motion

Abstract

The neural coding of spatial location for memory function may involve grid cells in the medial entorhinal cortex, but the mechanism of generating the spatial responses of grid cells remains unclear. This review describes some current theories and experimental data concerning the role of sensory input in generating the regular spatial firing patterns of grid cells, and changes in grid cell firing fields with movement of environmental barriers. As described here, the influence of visual features on spatial firing could involve either computations of self‐motion based on optic flow, or computations of absolute position based on the angle and distance of static visual cues. Due to anatomical selectivity of retinotopic processing, the sensory features on the walls of an environment may have a stronger effect on ventral grid cells that have wider spaced firing fields, whereas the sensory features on the ground plane may influence the firing of dorsal grid cells with narrower spacing between firing fields. These sensory influences could contribute to the potential functional role of grid cells in guiding goal‐directed navigation.

Abbreviations

GABA

gamma‐aminobutyric acid

mEC

medial entorhinal cortex

Modelling the sensory influences on spatial firing of entorhinal neurons

The behaviour of many different mammalian species requires the accurate coding of spatial location in the environment, ranging from the foraging behaviour of rodents to the social interactions of humans. Research in rodents and humans indicates that the neural mechanisms for coding of space appear to include neuronal spiking activity of place cells in the hippocampus (O'Keefe & Dostrovsky, 1971; O'Keefe, 1976; O'Keefe & Nadel, 1978) and grid cells in the medial entorhinal cortex (mEC) (Fyhn et al. 2004; Hafting et al. 2005; Moser & Moser, 2008; Jacobs et al. 2013). Place cells fire when an animal visits specific individual spatial locations in an environment, while grid cells in the mEC fire during visits to a regular array of locations that fall on the vertices of a hexagonal grid across an environment. These neuronal populations are clearly not the only mechanism of spatial localization, as humans with medial temporal lobe damage, such as the patient known as H.M., can find their way around familiar environments (Scoville & Milner, 1957; Milner et al. 1968). Similarly, rats with hippocampal lesions are not impaired in the use of reference memory to avoid unrewarded arms in an eight‐arm radial maze (Olton et al. 1979, 1986) and can still navigate to a specific location, though their learning is much slower (Morris et al. 1982). However, these structures appear important for rapidly encoding new spatial locations in unfamiliar, novel environments (Olton et al. 1979, 1986; Morris et al. 1982), and hence their accurate updating on the basis of sensory features appears to be essential to memory‐guided behaviour in new environments.

This review will focus on models of the role of sensory input during self‐motion in determining the firing properties of grid cells. This will draw on extensive experimental data showing the response of neurons in entorhinal cortex to manipulations of sensory features in the environment. On a broad scale, location can be computed in either relative or absolute coordinates. Absolute coordinates would index Cartesian coordinates for location relative to the same origin (0, 0) on multiple visits to an environment. In contrast, relative coordinates would update location based on some arbitrary starting coordinate. For example, the relative coordinate shift of (2, 3) on different visits would be the same for the transition from a first absolute starting location (1, 2) to (3, 5) and for the transition from a second absolute starting location (5, 11) to (7, 14). Absolute location can be coded by reference to the static distance and angle of sensory features (such as visual or auditory stimuli). Relative location can be computed based on sensory features from self‐motion (including both proprioceptive feedback and motor efference copy concerning generated movements, as well as moving sensory features such as optic flow or whisker input). The terms absolute and relative location will be discussed repeatedly in this review, and we will also refer to static sensory features, moving sensory features, proprioceptive feedback and efference copy of self‐motion.

Relative location from proprioceptive and efference copy of self‐motion signals

Many early models of grid cells focused on path integration from the running velocity of the animal (the speed and direction of movement) based on the integration of the motor output. These early models did not directly address the computation of speed and movement direction. Instead, these models usually assumed that these properties can be computed from proprioceptive feedback or efference copy of self‐motion signals from motor command centres, but as reviewed here they could also be computed from moving sensory features.

Input about running velocity was used to drive the majority of models of grid cells using attractor dynamics (Fuhs & Touretzky, 2006; McNaughton et al. 2006; Guanella et al. 2007; Burak & Fiete, 2009; Giocomo et al. 2011; Pastoll et al. 2013). These models generate the grid cell firing pattern across a wide population of neurons, and then shift the current location coded by the population based on velocity input provided by structured connectivity of conjunctive grid‐by‐head‐direction cells (McNaughton et al. 2006; Burak & Fiete, 2009). In these models, the population pattern of grid cell firing is driven by circularly symmetric excitatory or inhibitory recurrent synapses. This results in a major strength of these models in accounting for experimental data on shared orientation and spacing of firing fields (Sargolini et al. 2006; Stensola et al. 2012), and the quantal nature of grid cell spacing in different modules (Barry et al. 2007; Stensola et al. 2012). These models are also supported by recent data supporting circular symmetry of synaptic interactions between grid cells (Heys et al. 2014). The use of velocity input in these attractor models means that most existing simulations of these models compute relative location. However, these models could be modified to compute absolute location based on direct associations between specific patterns of sensory feature input indicating position and specific subpopulations of neurons within the population as done in a recent model (Bush & Burgess, 2014).

Velocity input was also used as input in a class of grid cell models using oscillatory interference (Burgess et al. 2005, 2007; Blair et al. 2008; Burgess, 2008; Hasselmo, 2008; Welday et al. 2011). In these models, individual grid cells are driven by input from multiple velocity‐controlled oscillators that change frequency based on current speed and the current movement direction relative to the preferred direction angle of individual oscillators. These oscillatory interference models effectively simulate the theta rhythmic firing of grid cells (Hafting et al. 2008; Jeewajee et al. 2008; Brandon et al. 2011; Koenig et al. 2011; Stensola et al. 2012), and the changes in rhythmic firing frequency based on running speed and the spacing between firing fields (Jeewajee et al. 2008; Stensola et al. 2012).

Because these oscillatory interference models arose from models of theta phase precession in the hippocampus (O'Keefe & Recce, 1993; Skaggs et al. 1996; Lengyel et al. 2003), these models effectively account for the theta phase precession of grid cells (Hafting et al. 2008; Climer et al. 2013; Eggink et al. 2014) and the prominent theta in the local field potential of entorhinal cortex (Mitchell & Ranck, 1980; Mitchell et al. 1982; Alonso & Garcia‐Austt, 1987; Jeffery et al. 1995). Models related to oscillatory interference (Hasselmo & Shay, 2014) can also address theta cycle skipping in the medial septum (King et al. 1998; Varga et al. 2008) and mEC (Jeffery et al. 1995; Deshmukh et al. 2010; Brandon et al. 2013) and firing of different populations on opposite phases of theta (Mizuseki et al. 2009; Newman & Hasselmo, 2014). Attractor models have only simulated phase precession during one‐dimensional movement (Navratilova et al. 2012).

Oscillatory interference can be successfully merged with attractor dynamics (Bush & Burgess, 2014). Such a merger accounts for data showing depolarizations in grid cell firing fields without changes in envelopes of theta oscillations (Domnisoru et al. 2013; Schmidt‐Hieber & Hausser, 2013). Oscillatory interference models can compute absolute location either through sensory input to drive a subpopulation of cells (Bush & Burgess, 2014), or by updating oscillation phase using visual features (Burgess, 2008). Variants of these models generate the periodicity in the firing of grid cells using ring oscillators (Blair et al. 2008, 2014; Welday et al. 2011) or using wave inputs (Hasselmo & Brandon, 2012; Hasselmo, 2014; Hasselmo & Shay, 2014).

An additional class of models uses self‐organization of feedforward signals from place cells (Kropff & Treves, 2008; Mhatre et al. 2010; Si et al. 2012) providing coding of absolute location in grid cells that depends upon place cell firing. As an alternative, some attractor models use global input to entorhinal cortex from place cells in hippocampus to account for the loss of grid cell firing during inactivation of the hippocampus (Bonnevie et al. 2013).

The focus of many models on path integration with a self‐motion signal was partly due to data showing that grid cells continue to show regular firing fields in darkness (Hafting et al. 2005), suggesting that they do not require visual sensory input. However, studies have not analysed the dependence of grid cells on other sensory input such as somatosensory input from whisking or auditory localization input. The question remains whether path integration based on proprioceptive feedback and efference copy of motor signals for self‐motion can generate grid cells in isolation from other sensory influences. Studies in absolute darkness should be combined with the use of sound attenuation chambers and clipping of whiskers to remove these components of sensory input so that the animal must solely rely on proprioceptive, efference copy and vestibular self‐motion signals.

Head direction dominates over movement direction

As noted above, the self‐motion signal could come from either internal signals (proprioceptive feedback or efference copy) or from sensory input. The use of a proprioceptive self‐motion signal must assume that the grid cells in mEC have access to proprioceptive feedback or efference copy coding both translational speed and movement direction to create a velocity signal. As noted above, the use of velocity input is present in most published attractor dynamic models (Fuhs & Touretzky, 2006; McNaughton et al. 2006; Guanella et al. 2007; Burak & Fiete, 2009; Bonnevie et al. 2013; Couey et al. 2013; Pastoll et al. 2013) as well as oscillatory interference models (Burgess et al. 2007; Blair et al. 2008; Burgess, 2008; Hasselmo, 2008; Zilli & Hasselmo, 2010). Thus, these models use input of both speed and movement direction.

The requirement of a speed signal is supported by data showing examples of linear and saturating exponential relationships of firing rate to running speed in recordings from hippocampus and mEC (O'Keefe et al. 1998; Wills et al. 2012; Kemere et al. 2013; Kropff et al. 2015; Hinman JR, Brandon MP, Chapman GW, Climer JR & Hasselmo ME, submitted). The important role of speed in these models is further supported by data on changes in the frequency of spiking in the medial septum (King et al. 1998) or theta frequency field potentials in hippocampus during changes in running speed (Hinman et al. 2011). This indicates a potentially important role of the input from the medial septum to the hippocampus. It is possible that the impairments of spatial memory caused by inactivation of the medial septum (Chrobak et al. 1989) are due to loss of a speed signal input from medial septum. This is further supported by data showing the loss of spatial periodicity of grid cells when network theta rhythm oscillations are reduced by inactivation of the medial septum (Brandon et al. 2011; Koenig et al. 2011). It is not yet clear which cell population underlies this effect, as the medial septum inactivation in those previous studies (Brandon et al. 2011; Koenig et al. 2011) would involve simultaneous inactivation of cholinergic, GABAergic and glutamatergic neurons. Recent data show that phasic optogenetic activation at theta frequency of glutamatergic neurons in the medial septum triggers running by mice at speeds regulated by the frequency of optogenetic stimulation (Fuhrmann et al. 2015). These data on coding of translational speed by the medial septum support models using translational speed as a component of a velocity signal for grid cell generation.

However, the requirement of models for movement direction is more problematic, despite the fact that many papers cite head direction responses of mEC as the evidence for a movement direction signal. Head direction cells are one of the most dramatic neural responses to spatial dimensions found in the brain. Head direction cells were initially discovered in the dorsal presubiculum (Ranck, 1984; Taube et al. 1990 a,b) and subsequently described in the anterior thalamus (Taube, 1995) and mEC (Sargolini et al. 2006). Head direction cells clearly depend upon input from the vestibular system coding angular velocity (the turning speed of the head), but also show dependence upon visual cues (Taube et al. 1996; Taube & Bassett, 2003). Many attractor models use grid‐by‐head‐direction cells to shift the grid cell population activity during movement (McNaughton et al. 2006; Burak & Fiete, 2009; Couey et al. 2013), and equate head direction with movement direction.

However, an analysis of behavioural data shows that the head direction signal does not match movement direction (Fig. 1 A). Because of this, when behavioural data on head direction is used as input to attractor models or oscillatory interference models in place of a behavioural movement direction signal, the models do not generate accurate grid cell firing (Raudies et al. 2015) as shown in Fig. 1 E and F. This occurs because the integration of velocity in those models is distorted by the use of head direction instead of movement direction. Further analysis of experimental data on the firing properties of a large population of medial entorhinal neurons during periods when head direction does not match movement direction shows little evidence for neurons coding a movement direction signal (Raudies et al. 2015). In the data, numerous neurons clearly code head direction alone, but only a few neurons code both head direction and movement direction and no neurons respond on the basis of movement direction alone (Fig. 1 C and D). One possibility is that the movement direction signal is present in other regions and may drive the mechanisms of the firing of grid cells in other networks such as the pre‐ or parasubiculum (Boccara et al. 2010) without being evident in medial entorhinal cortex. As an alternative hypothesis, this stronger coding of head direction and relative lack of a movement direction signal suggests that a self‐motion signal might rely less on internal signals of movement direction and instead may depend on a representation of the head direction for coding sensory input. The coding of the head direction angle would allow the computation of the absolute angle of visual, auditory and somatosensory input because these sensory inputs are initially detected in terms of their angle relative to coordinates centred on current head direction.

Figure 1. Analysis of single cell recording data from entorhinal cortex for head direction (HD) and movement direction (MD) along with a model simulation of grid cells using HD or MD as input .

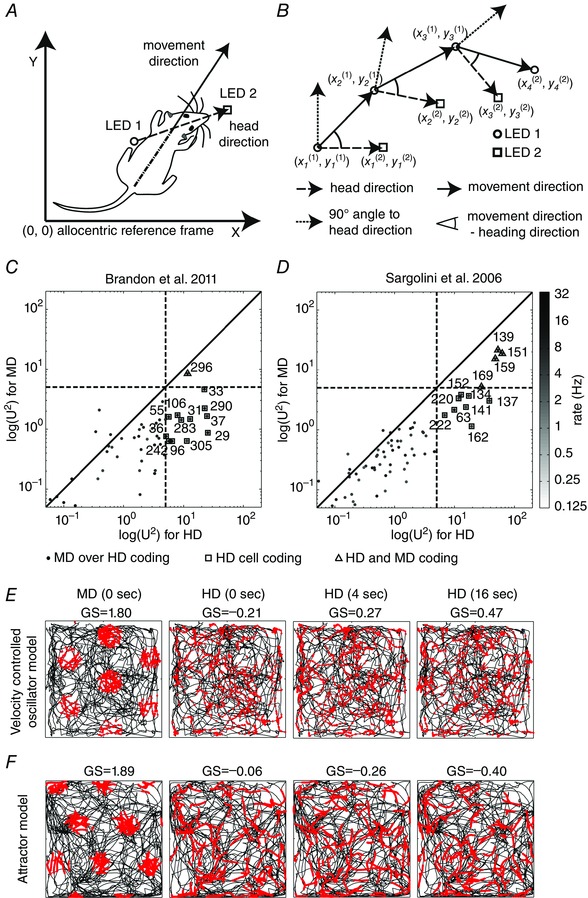
A, we infer the head direction through the orientation given by the two LEDs, 1 and 2, and the movement direction taking the temporal advancement of the mid‐point between LED 1 and 2. B, a sketched sequence for the temporal succession of the positional sample points of LED 1 and 2 to illustrate the definition of HD, MD and the angular difference between HD and MD. C, the Watson U² for the population of 305 cells from the Hasselmo laboratory. D, the Watson U² for the population of 453 cells from the Moser laboratory. Plotted points of the Watson U ² for MD tuning versus Watson U² for HD tuning are from the same cell. Axes are log‐scaled as are the grey values that represent the firing rate of each cell in hertz. Cells whose Watson U² pair is below the diagonal primarily encode HD, whereas those above the diagonal primarily encode MD. The distribution of cells is predominantly biased toward statistical encoding of HD rather than MD. Numbers denote cell indices. Dashed lines mark the threshold of 5 for the U²s that we used to categorize HD and MD cells. Plotted squares around points indicate HD coding and plotted triangles around points indicate combined HD and MD coding. E, simulations of the velocity controlled oscillator (VCO) model (top row) and attractor model (bottom row) with MD or HD as directional input. The speed input was that of the measured trajectory. Different panels show the simulated cell firing for the HD or MD while integrating over a 0, 4 or 16 s time window. Whenever HD is provided as input no grid cell firing appears (last three columns in E and F). In contrast, the direct input of MD (0 s time window) produces grid cell firing (first column in E and F). Adapted from Raudies et al. (2015).

Optic flow can drive grid cells and boundary vector cells

The dominant coding of head direction by cells in the mEC supports the importance of sensory input in coding of grid cells. The influence of sensory input on grid cells has not been explicitly discussed as extensively as path integration based on proprioceptive self‐motion. However, a modelling study showed how optic flow of visual features could be used to compute a velocity signal to drive grid cell models using attractor dynamics or oscillatory interference (Raudies et al. 2012). This model used template matching of optic flow to estimate velocity, and then used the estimated velocity to compute the relative location in a grid cell model (Fig. 2 D). Note that this model did not compute absolute location.

Figure 2. Modelled firing patterns of simulated grid cells and boundary vector cells using optic flow as input .

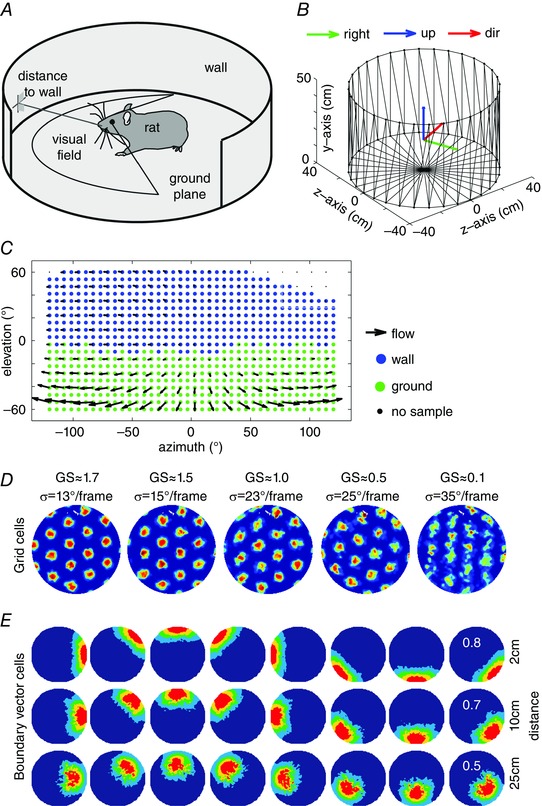
A, a rat in a circular box with a depiction of its distance to the wall. B, simulated box environment for boundary vector cells. The coordinate system (red, blue and green arrows) indicates the initial position and orientation of the simulated visual field of the rat. C, an optic flow field for a spherical camera with its segmentation into ground plane (green dots) and wall (blue dots). This optic flow field is used to estimate the linear and rotational velocity of the rat as well as the distance of the wall in ego‐centric space and the orientation of the wall in allo‐centric space. Adapted from Raudies & Hasselmo (2012). D, simulated grid cell firing using the oscillatory interference model while superimposing independent, additive Gaussian noise onto the optic flow components with a standard deviation σ of 13, 15, 23, 25 and 35 deg frame⁻¹. The simulated grid cell firing vanishes above a standard deviation of σ ≈ 23 deg frame⁻¹. The simulation uses the trajectory ‘Hafting_Fig2C_Trial1’ from Hafting et al. (2005). The box has a diameter of 100 cm with a 15 cm annulus added to provide visual features beyond the limits of locomotion. Adapted from (Raudies et al. 2012). E, the rate map of our model for boundary vector cells when estimating distance and direction of walls from optic flow. The box has a diameter of 79 cm and the height of the wall is 50 cm.

As shown in Fig. 2, optic flow can also be used as sensory input to model the generation of boundary cells (Raudies & Hasselmo, 2012). Boundary cells in mEC and subiculum show robust spiking responses dependent on the distance and angle of environmental boundaries (Burgess et al. 2000; Barry et al. 2006; Savelli et al. 2008; Solstad et al. 2008; Lever et al. 2009). For example, they might respond when an environmental boundary is to the north of an animal at a specific distance. In an important theoretical model, these boundary cells were predicted (Burgess et al. 2000; Hartley et al. 2000) based on the response of place cells to manipulations of environmental barriers (O'Keefe & Burgess, 1996). For example, if the east–west distance between boundaries of an environment is expanded, then the size of a place field may expand in the east–west dimension, or the cell may split into two firing fields. These properties of place cells were modelled using boundary vector cells with properties that were extensively analysed in computational work (Burgess et al. 2000; Hartley et al. 2000).

The explicit predictions of these models were then supported by the later experimental discovery of these cells (Barry et al. 2006; Savelli et al. 2008; Solstad et al. 2008; Lever et al. 2009). Boundary cells allow for analysing the absolute distance and angle of environmental boundaries from the current position of an animal. As shown in Fig. 2 A–C, optic flow was used to model the firing of boundary cells (Fig. 2 E) through detection of a discontinuity in the optic flow at the border between a wall and the ground plane of the environment (Raudies & Hasselmo, 2012). Note that though this model uses optic flow, because it detects the distance and angle of a boundary, it is computing absolute location in the environment and could be used to drive the absolute location of grid cell firing or place cell firing, as proposed in the initial models of boundary vector cells (Burgess et al. 2000; Hartley et al. 2000).

Absolute location from static sensory features

Experimental data on grid cells indicate the influence of sensory input on their firing properties. For example, grid cells fire in the same spatial location in a specific experimental environment even after the animal has been removed from the room and returned to the room (Hafting et al. 2005; Fyhn et al. 2007), indicating that grid cells not only track location relative to the initial position, but are able to reinstate the appropriate location activity based on sensory cues when reintroduced to a previously visited environment. The sensory cues regulating the location of grid cell firing include visual cues in the environment. Rotation of the position of a white cue card on the wall of an environment between recording sessions will cause grid cells to rotate according to the rotation of the cue card (Hafting et al. 2005). In addition, shifting the position of the walls of the environment between sessions causes compression or expansion of the spacing and size of grid cell firing fields temporarily (Barry et al. 2007). After adaptation to the alteration in the environment the grid cell firing fields return to their previous hexagonal firing pattern. Further experimental studies showed that this shift in the position of the walls affects grid cells with large spacing between firing fields more so than cells with small spacing (Stensola et al. 2012).

These effects of boundary movement could partly be due to close somatosensory interactions with the boundaries, as the firing accuracy of grid cells depends upon the recency of interaction with boundaries in the environment (Hardcastle et al. 2015). A recent model has shown that the influence of boundary cells could alter the positioning of grid cell firing fields based on different shapes of environments (Krupic et al. 2014), correctly predicting that an environment with trapezoid walls would have distorted firing field location as supported by recent data from grid cells (Krupic et al. 2015).

As shown in Fig. 3, recent modelling work has shown that differential sensitivity to boundary movement could arise from differences in the nature of simulated location computation by different grid cell modules (Raudies & Hasselmo, 2015). The term module refers to populations of grid cells that have been shown to share firing field properties such as orientation and spacing between fields (Barry et al. 2007; Stensola et al. 2012). Modelling shows that modules sensitive to static visual features on the walls of the environment (Fig. 3 A–F) would be particularly sensitive to the shift of the visual features with wall movement (Raudies & Hasselmo, 2015), as shown in experimental data (Barry et al. 2007; Stensola et al. 2012). In contrast, modelling shows that modules responding to visual features on the ground plane near the rat would be less sensitive to wall movement (Fig. 3 G–I), particularly if the firing location is driven by integration of a moving feature signal from the ground plane near the rat (Raudies & Hasselmo, 2015). This could explain the lack of compression of firing fields for grid cells with smaller spacing (Stensola et al. 2012). Cells with smaller spacing between firing fields tend to occur in more dorsal anatomical locations that might be more sensitive to the ventral visual field.

Figure 3. A model of compression effects that occur in grid cells from modules that map to the ventral visual field but not in grid cells from modules that map to the dorsal visual field .

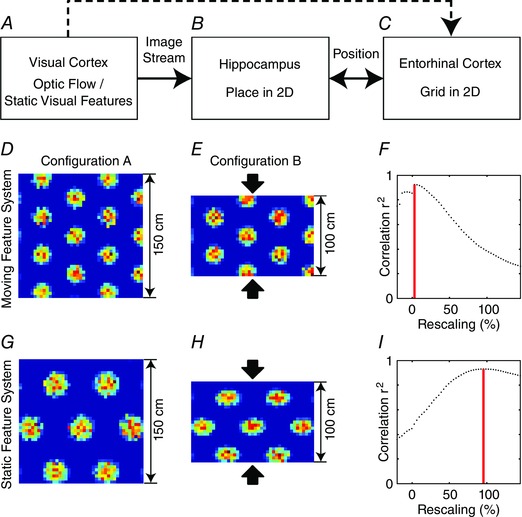
A, the visual cortex processes optic flow and visual features. Optic flow is strongly present on the ground plane in the ventral visual field whereas distal visual features in the dorsal visual field make good landmarks. B, via multiple processing stages, optic flow and visual features influence hippocampal activity, giving rise to a place‐specific firing in a 2D environment. C, in the entorhinal cortex this 2D place information is translated into the firing of grid cells. Our model has two modules, one that estimates location from optic flow on the ground plane and one that estimates location from static visual features on the walls through triangulation. The anatomical projections from visual cortex to entorhinal cortex are not currently used in our model as shown by the dashed line. D, E, G and H, in configuration A the box is square (D and G) and in configuration B the box is rectangular (E and H) after pushing two opponent walls closer together (when the rat is outside of the box). For the moving feature system responding to the ground plane in the ventral visual field this compression of walls left the firing pattern of a simulated dorsal entorhinal cell unchanged (see D vs. E), while for the static feature system responding to distal features in the dorsal visual field this led to a compression of the firing pattern of a simulated ventral entorhinal cell (see G vs. H). F, for the firing pattern of the simulated dorsal entorhinal cell correlation values for different compressions of B relative to A, there is a peak correlation at ∼3.1% compression. I, for the firing pattern of the simulated ventral entorhinal cell, correlation values peak at ∼95.5% (or about 50 cm) compression of B relative to A.

The selective effect on individual modules suggests differences in the anatomical pathways of visual feature processing reaching different portions of mEC. In the rodent visual system, some regions (e.g. area AM) respond more strongly to grating stimuli with high temporal frequency (movement) and low spatial frequency, other regions (e.g. area PM) respond more to low temporal frequency (more static stimuli) with higher spatial frequency, and yet other regions respond to a mixture (area LM) (Andermann et al. 2011; Wang et al. 2011, 2012; Glickfeld et al. 2014). These responses might indicate differential processing in the rodent similar to the distinction between the ‘where’ and ‘what’ pathways described extensively for the dorsal and ventral streams of the primate cortex (Ungerleider & Mishkin, 1982). Note that the primate extrastriate visual cortex contains regions that explicitly respond to the self‐motion indicated by optic flow (Rodman & Albright, 1987; Graziano et al. 1994; Duffy & Wurtz, 1995). These pathways might correspond to differential visual processing inputs, with optic flow signals entering the dorsal mEC versus the landmark signals entering the ventral mEC. Alternately, these might reflect the differential influence of input from different portions of the visual field, with dorsal mEC responding to features on the ground plane whereas ventral mEC responds to features on distal walls.

Computing location from full visual images

The model described above simulated differential effects on grid cell firing field spacing used the relative angle of pre‐defined visual features, but there are also models that have addressed the use of more detailed visual images in driving spatial responses of grid cells. For example, a paper used a ray‐tracing algorithm to create images of a rat environment to drive the firing responses of oriented Gabor filters that could drive an attractor model of grid cells (Sheynikhovich et al. 2009). This explicit simulation of visual input is rare, but other models assume that sensory input can provide a position signal to periodically correct the firing location of grid cells (Burgess et al. 2007; Pastoll et al. 2013; Bush & Burgess, 2014) or use slow feature extraction to drive grid cells (Franzius et al. 2007). Recent work in our laboratory addresses the mechanism for generating a position signal from visual input based on previous robotics work by Michael Milford (Milford, 2008; Milford & Wyeth, 2008, 2010; Milford et al. 2010; Chen et al. 2014). The effectiveness of the visual input depends upon an appropriate Gaussian tuning width for detection of visual features that allows generalization between adjacent locations without overgeneralizing. In a recent model shown in Fig. 4 (F. Raudies and M. E. Hasselmo, unpublished), this position signal was used as input to different models of grid cells, and the sensitivity of the models to external position noise was evaluated. A similar analysis of sensitivity to external position noise was evaluated recently (Towse et al. 2014).

Figure 4. The simulation of grid cells using a wave model that is driven by the position signal that in turn is retrieved from visual views .

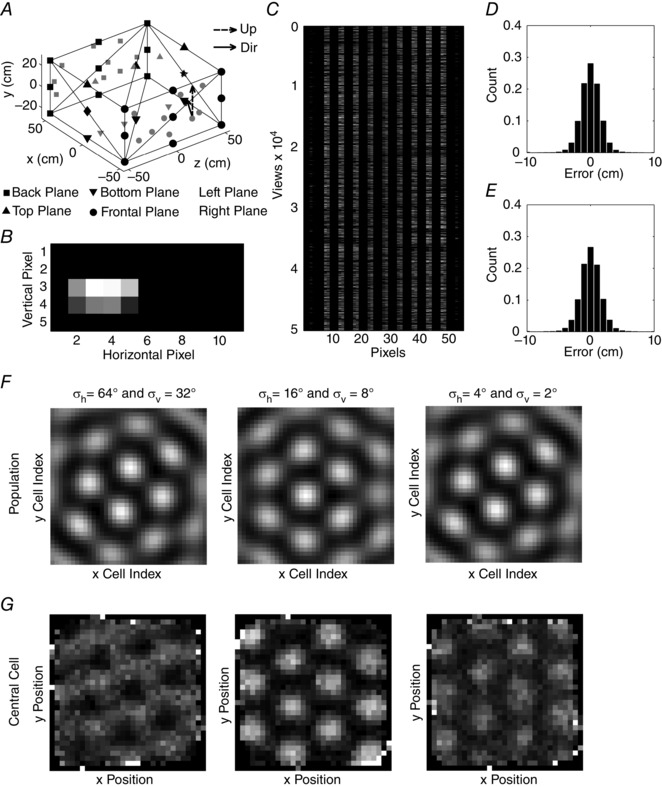
A, enclosure used in the simulation with ground (downward triangle), side walls (square, circle, diamond and star symbols), and ceiling (upward triangle) – in the actual simulation the lines were not present. Black symbols show the positions of features before random displacement on their associated surface (i.e. ground, walls or ceiling). Scattered features are drawn as grey symbols. All features were identical for the actual generation of an image. B, exemplar image for the camera position indicated in A by the direction (Dir) vector and upward vector (Up). Bright regions indicate the overlay of 2D Gaussian blobs generated by features. C, stored images for 50,000 sample points and 11 pixel × 5 pixel or 55 total pixel values. Grey values for pixels in the image are flattened along the vertical dimension. D, position errors for retrieval in the horizontal direction are fitted by a normal distribution with zero mean and a standard deviation of 2.79 cm. E, position errors in the vertical direction are fitted by a normal distribution with zero mean and a standard deviation of 3.10 cm. F, population responses and firing pattern of the central cell for images generated by 2D Gaussians with σ_h = 64° and σ_v = 32° (fist column), σ_h = 16° and σ_v = 8° (second column), and σ_h = 4° and σ_v = 2° (third column). The population response at a single time step in F shows that the wave model always generates a hexagonal grid pattern at individual time steps. Bright encodes a high activation and dark a low activation of cells. G, firing patterns of the central cell in the population were recorded over 50,000 sample steps. This shows how accurately the population activity is shifted over time by the estimate of position based on visual input, in order to allow a single cell to fire like a grid cell during the full trajectory. Bright indicates a high firing rate and dark indicates a low firing rate. The GSs are −0.37, 1.91 and 0.93 for the first, second and third column, respectively, indicating best performance with the intermediate Gaussian widths that allow best generalization of visual images over nearby positions.

Note that the external position noise used in the model in Fig. 4 and the Towse paper differs from most previous noise evaluations in grid cell models, in that external noise rather than internal noise and position noise rather than velocity noise were used. Internal noise causes problems for oscillatory interference models (Burgess et al. 2007; Zilli et al. 2009), but can be overcome by attractor dynamics (Burak & Fiete, 2009; Bush & Burgess, 2014). In contrast, both attractor dynamic models and oscillatory interference models have difficulty in overcoming the external noise in a velocity signal because attractor dynamics overcome the noise of internal dynamics but not the noise on an input signal. The problem of external noise is somewhat less severe when the noise affects a position signal based on sensory input rather than a velocity signal from self‐motion because the integration of a velocity signal by the model results in integration of the noise over time, whereas noise on a position signal is not integrated. In the simulations shown here, visual input is used to create a position signal that is provided as input to models of grid cells. Noise is then added to this position signal to determine its impact on different grid cell models.

In the model shown in Fig. 4 (Raudies and Hasselmo, unpublished model), the generation of synthesized rat trajectories provides the position signals for our renderer that generates images for each position. Such memorized images are then used to retrieve position through normalized cross‐correlation, which in turn is fed into our proposed wave model. This wave model resembles previous oscillatory interference models (Burgess et al. 2007) and ring oscillator models (Blair et al. 2008). The wave model generates grid cell firing across a population with waves representing medial septal input that are summed to compute grid cell firing (Hasselmo & Brandon, 2012; Hasselmo & Shay, 2014). Feedback from the grid cells to the wave input results in self‐organization that selectively strengthens input from sets of waves with specific head direction orientations at 60 degree intervals. In a separate analysis performed for comparison with the wave model, the position signal is temporally differentiated to define a velocity signal that is then fed into an attractor model or oscillatory interference model. Our results present properties of the wave model and compare our wave model using position input from visual stimuli to the attractor model or oscillatory interference model using self‐motion velocity input. The use of position input based on visual stimuli can tolerate more noise than the use of self‐motion velocity input even when equating the signal‐to‐noise ratio of the noise in the velocity with the noise in the position signal.

Models of goal‐directed navigation using grid cells and place cells

Behavioural data indicate that humans and animals do not need the hippocampus and entorhinal cortex to navigate in a familiar environment. The mechanisms of navigation in highly familiar environments appears to depend upon neocortical regions such as the parietal cortex (Byrne et al. 2007). However, entorhinal cortex and hippocampus may be essential for the formation of spatial representations and goal‐directed navigation within novel environments (Milford et al. 2010; Erdem et al. 2015), to allow behaviours such as forward planning of trajectories to goal locations (Erdem & Hasselmo, 2012, 2014; Erdem et al. 2015). In these models, the current head direction can be used to trigger forward replay of a trajectory through the environment, to allow for the selection of a trajectory that will overlap with a desired goal location. In this framework, the coding of visual stimuli (Milford et al. 2010) allows for the correction of position errors that could distort goal‐directed navigation (Erdem et al. 2015). A similar framework can be used to model episodic memory (Hasselmo, 2009, 2012), in which specific locations and head direction along a spatiotemporal trajectory can be associated with sensory input features via modifications of synaptic connections. During replay or recollection, a retrieval cue activating a specific segment of the trajectory can trigger retrieval of other segments and the associated sensory input features. Models of this type could address the physiological data on replay of previously encoded sequences of place cells observed in behaving rats (Johnson & Redish, 2007; Mehta, 2007; Davidson et al. 2009; Jadhav et al. 2012).

Additional information

Competing interests

The authors have no conflict of interest.

Author contributions

M.H. and F.R. conceived simulation projects, F.R. designed and performed the simulations, and J.H. interpreted physiological data. All authors have approved the final version of the manuscript and agree to be accountable for all aspects of the work. All persons designated as authors qualify for authorship, and all those who qualify for authorship are listed.

Funding

Research supported by NIMH R01 MH60013, NIMH R01 MH61492, NSF EAGER PHY 1444389 and the Office of Naval Research MURI grant N00014‐10‐1‐0936.

Biographies

Florian Raudies obtained his PhD in Computer Science (summa cum laude) from the University of Ulm, Germany, working with Prof. Heiko Neumann. He worked as a post‐doctoral fellow and Research Assistant Professor at Boston University in the Department of Psychological and Brain Sciences and the Centre for Computational Neuroscience and Neural Technology before taking his current position as a Research Engineer at Hewlett Packard Labs.

James R. Hinman obtained his PhD in Psychology from the University of Connecticut working with Prof. James Chrobak and is currently a post‐doctoral fellow at Boston University.

Michael E. Hasselmo is a Professor in the Department of Psychological and Brain Sciences and the Director of the Center for Systems Neuroscience at Boston University. He is principal investigator on two NIMH R01 grants and an ONR MURI award.