Abstract
The inwardly rectifying potassium current (IK1) and the fast inward sodium current (INa) are reciprocally modulated in mammalian ventricular myocytes. An increase in the expression of channels responsible for one of these two currents results in a corresponding increase in expression of the other. These currents are critical in the propagation of action potentials (AP) during the normal functioning of the heart. This study identifies a physiological role for IK1–INa reciprocal modulation in ventricular fiber activation thresholds and conduction. Simulations of action potentials in single cells and propagating APs in cardiac fibers were carried out using an existing model of electrical activity in cardiac ventricular myocytes. The conductances, GK1, of the inwardly rectifying potassium current, and GNa, of the fast inward sodium current were modified independently and in tandem to simulate reciprocal modulation. In single cells, independent modulation of GK1 alone resulted in changes in activation thresholds that were qualitatively similar to those for reciprocal GK1–GNa modulation and unlike those due to independent modulation of GNa alone, indicating that GK1 determines the cellular activation threshold. On the other hand, the variations in conduction velocity in cardiac cell fibers were similar for independent GNa modulation and for tandem changes in GK1–GNa, suggesting that GNa is primarily responsible for setting tissue AP conduction velocity. Conduction velocity dependence on GK1–GNa is significantly affected by the intercellular gap junction conductance. While the effects on the passive fiber space constant due to changes in both GK1 and the intercellular gap junction conductance, Ggj, were in line with linear cable theory predictions, both conductances had surprisingly large effects on fiber activation thresholds. Independent modulation of GK1 rendered cardiac fibers inexcitable at higher levels of GK1 whereas tandem GK1–GNa changes allowed fibers to remain excitable at high GK1 values. Reciprocal modulation of the inwardly rectifying potassium current and the fast inward sodium current may have a functional role in allowing cardiac tissue to remain excitable when IK1 is upregulated.
Keywords: reciprocal modulation, cardiac cells, mathematical model
Introduction
The inwardly rectifying potassium current (IK1) sets the resting membrane potential of atrial and ventricular cardiac myocytes while the fast inward sodium current (INa) determines the rate of depolarization and speed of propagating action potentials (APs) in tissue. These two currents have opposing effects on cardiac excitability: increasing the conductance, GK1, of IK1 is thought to decrease excitability by raising the threshold needed to initiate an AP while increasing the conductance, GNa, of INa is believed to increase excitability mainly by facilitating depolarization. The conductance values of ionic currents reflect the number of functional channels in the cell membrane and, therefore, alterations in conductances represent long-term changes that occur in cardiac cells and tissue. The term “reciprocal modulation” refers to the recent finding (Milstein et al., 2012) in mammalian heart cells that upregulation of channel density of one current (IK1 or INa) results in a parallel upregulation of the other current. One question that arises from the data of Milstein et al. (2012) is why heart cells would have such a regulatory mechanism: does reciprocal modulation have a role in cardiac excitability? Milstein et al. discuss the importance of reciprocal modulation in potentially fatal cardiac rhythm disturbances but such a function would be unfavorable to an organism. A cardioprotective role for reciprocal modulation would provide an evolutionary advantage and, therefore, a teleological reason for the existence of this important biological phenomenon. While a number of modeling studies have examined the effect of changes in individual conductances in heart cells, the effect of tandem changes in IK1 and INa have not yet been fully explored. The central hypothesis of this study is that the reciprocal modulation of IK1 and INa discovered by Milstein et al. (2012) is a mechanism that cardiac cells use to regulate excitability.
Cardiac ion channels are organized and targeted to specific cellular locations by numerous cardiac-specific membrane and structural proteins (Balse et al., 2012). Kucera et al. (2002) showed that Nav 1.5 (also referred to as “rH1” in rat cells) channels, responsible for much of the fast inward sodium current in mammalian ventricular myocytes, co-localize at cardiac cell intercalated disks (ID) with Connexin-43 (Cx43), the molecule primarily responsible for the intercellular gap junction current, Igj, in ventricular tissue. Cx43 is linked biochemically to ZO-1, the zona occludens-1 protein found in intercalated disks, and was shown by Barker et al. (2002) to be regulated by ZO-1. Ankyrin-G, which is also expressed in cardiac cell intercalated disks (Mohler et al., 2004), plays a role in anchoring Nav1.5 (Lowe et al., 2008) at IDs. Milstein et al. (2012) showed that Kir2.1, which is responsible for IK1 in ventricular cells, and Nav1.5 channels interact functionally within a macromolecular complex involving the SAP97 scaffolding protein localized to cardiac gap junctions; the Kir2.1–Nav1.5 interaction was referred to as “reciprocal modulation” by Milstein et al. (2012) because experimental interventions that increase the channel density of one current were found to increase the other. Their data (Milstein et al., 2012, Figures 1, 2) showed no significant changes in channel gating or voltage dependence and while they did see hyperpolarizing shifts in both sodium channel activation and inactivation in one case (Milstein et al. Figure 4), it is likely that the larger shift in the voltage dependence of inactivation will result in an overall reduced excitability due to changes in Nav1.5 gating. The primary effect of reciprocal modulation appears to be that of parallel changes in channel densities. These results suggest some amount of cooperativity between IK1, INa, and Igj. Recently, Varghese et al. (2015) showed, using a combination of simulations and experiments, that the mode of action of therapeutic doses of class I antiarrhythmic agents can be understood by analyzing the three currents involved in initiating cardiac APs: IK1, INa, and Igj. This paper focuses on the changes in excitability due to independent and reciprocal modulation of the IK1–INa conductances.
Figure 1.
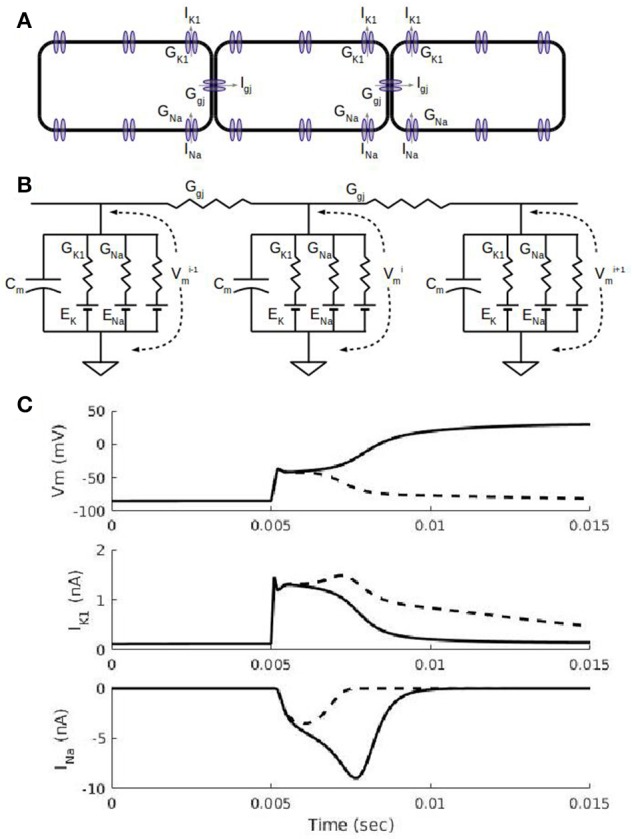
Action potential propagation in a cardiac fiber. (A) Schematic view of three cells in a fiber. In addition to a number of sodium, potassium, and calcium currents in the cell membrane, each cell has non-selective gap junction channels that allow currents to flow down the fiber. The gap junction current, Igj, allows a depolarized cell to drive electrical activity in a neighboring cell. (B). Equivalent circuit representation of the three cells in (A). Each cell has a capacitance associated with the cell membrane and ionic currents represented by a conductance and a battery for the Nernst potential for the corresponding ion. The inward rectifier potassium current, IK1, current has a non-linear conductance (see Methods) with a maximal conductance, GK1, and its reversal potential is the potassium Nernst potential, EK. The fast sodium current, INa, has a time-dependent conductance with the maximal conductance, GNa, and its reversal potential is the sodium Nernst potential, ENa. (C) Simulations showing cell membrane potential, Vm, and ion channel currents, IK1 and INa, for a subthreshold stimulus (dashed curves) and suprathreshold stimulus (solid curves). Results shown are for the 5th cell in a fiber of 100 cells with 0.2 ms-duration current stimuli administered at the 5 ms mark to the first 4 cells. A subthreshold stimulus brings Vm to about −60 mV after which Vm declines (dashed curve) back to its resting membrane potential of about −90 mV; the IK1 waveform due to a subthreshold stimulus is larger than the suprathreshold case (solid curve) because the subthreshold Vms are more negative and thus less inward rectified. INa is partially activated (dashed curve) for a subthreshold stimulus and fully activated (solid curve) for the suprathreshold stimulus; the fully activated INa is what triggers the full depolarization of Vm to about +20 Mv.
Figure 2.
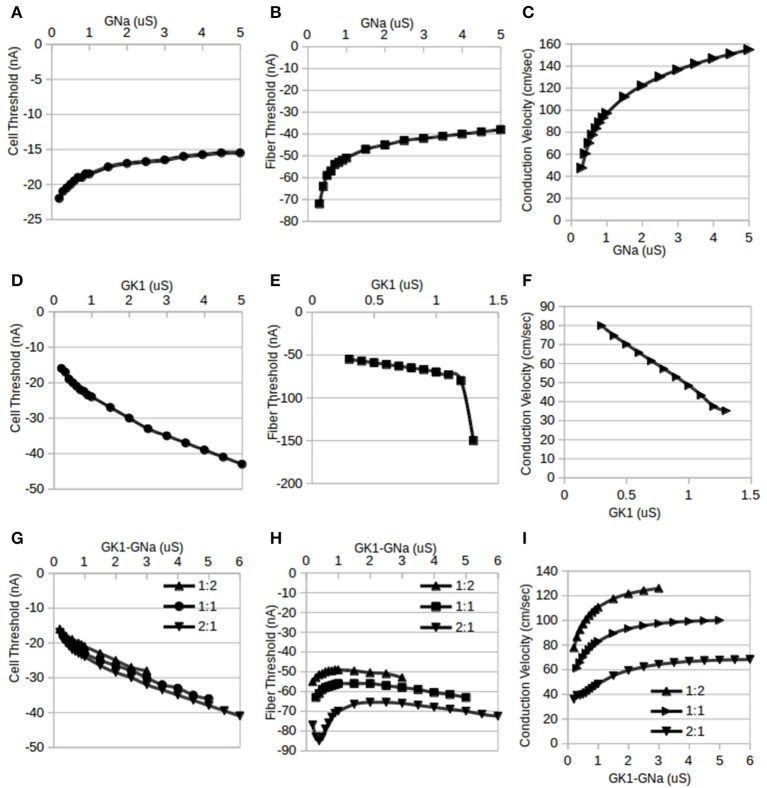
Independent and reciprocal modulation of IK1 and INa in single cells and fibers. By standard convention, inward (depolarizing) stimulus currents are negative. (A). Changes in single cell threshold due to independent modulation of GNa. These results indicate that as GNa is increased, the magnitude of the threshold is lowered. GK1 was held at its default value of 0.5 μS. (B) Fiber threshold was also lowered as GNa was increased. GK1 was held at 0.5 μS and Ggj was held at 10 μS. (C) Fiber conduction velocity increased as GNa was increased (same conditions as B). (D) Changes in single cell threshold due to independent modulation of GK1: as GK1 is increased, the magnitude of the threshold is raised. GNa was held at 0.5 μS. (E) Fiber threshold was raised as GK1 was increased. For values of GK1 larger than 1.3 μS, the fiber was inexcitable. GNa was held at its default value of 0.5 μS and Ggj was held at 10 μS. (F) Fiber conduction velocity decreased as GK1 was increased (same conditions as D). (G) Changes in single cell threshold due to reciprocal modulation of GK1 and GNa. Cell threshold increased monotonically with the tandem changes in GK1:GNa. Three different ratios for GK1:GNa were used: 1:2, 1:1, and 2:1; the X-axis shows the GK1 values, the corresponding GNa value depends on the ratio used. (H) Fiber threshold changes due to reciprocal modulation of GK1 and GNa. Three different ratios for GK1:GNa were used (1:2, 1:1, and 2:1) while Ggj was held at 10 μS. The X-axis shows the GK1 values, the corresponding GNa value depends on the ratio used. (I) Fiber conduction velocity increased with reciprocal modulation of GK1 and GNa (same conditions as D). The X-axis shows the GK1 values, the corresponding GNa value depends on the ratio used.
The dynamics of IK1 & INa are key to understanding cardiac action potential propagation characteristics. Figure 1A shows a schematic view of three neighboring cells in a fiber with IK1, INa, and Igj channels shown in the cell membrane. Although there are numerous other channels in cardiac cells which are included in the simulations in this paper, they are set to their default parameter values and are not of particular interest in this paper. An equivalent circuit diagram for the three cells is shown in Figure 1B with linear resistors modeling intercellular gap junction connexin channels. Figure 1C shows two short simulations of changes in the cell membrane voltage (Vm), IK1, and INa in one cell in a fiber due to 0.2 ms duration stimuli applied at the 5 ms point: one simulation shows the result of a suprathreshold stimulus (solid curves) and the other is for a subthreshold (dashed curves) one. At cardiac resting potentials (around −85 mV, first 5 ms of top trace in Figure 1C), the cell membrane voltage, Vm, is close to the reversal potential for potassium, EK, and even though Kir2 channels (responsible for IK1) are open at these potentials, the lack of driving force for potassium ions results in IK1 being close to 0 as can be seen in the first 5 ms of the middle traces in Figure 1C. An inward current due to an external current stimulus (as was used in simulations in Figure 1C) or current from neighboring cells through gap junction Cx43 channels will depolarize the cell, increasing the driving force for potassium ions and causing an outward flow of potassium which will tend to repolarize the cell. The dashed curves in Figure 1C show the result of a subthreshold stimulus: Vm returns to the resting potential, IK1 is large and INa is only partially activated. The solid curves in Figure 1C show the result of a suprathreshold stimulus: when the stimulus is sufficient to depolarize the cell to about −60 mV, the inward (negative) INa through Nav1.5 channels can be fully activated (solid curve, bottom trace of Figure 1C), causing further depolarization. Cell depolarization above −40 mV inactivates INa, making it decrease in magnitude. Meanwhile, the inward rectification property of Kir2 channels will result in IK1 decreasing with additional depolarization above −50 mV. Ventricular cells typically reach a maximum potential of about 20 mV at which point, both IK1 and INa are minimal due, respectively, to inward rectification and inactivation. Depolarization of one cell in a fiber results in current (Igj in Figure 1A) flowing downstream through Connexin43 (Cx43) channels to a neighboring cell, causing the same sequence of events as described above in the neighbor cell and in this way causing the AP front to propagate through the fiber. The relation between the simulations used in this paper and predictions from linear and non-linear cable theory is summarized in the Appendix.
Recent studies have shown evidence for spatial localization of Nav1.5, Kir2.1, and Cx43 channels at the intercalated disks (IDs) in cardiac myocytes using both immunofluorescence and computational modeling. Kucera et al. (2002) showed that Nav1.5 channels co-localize with Cx43 in IDs and their simulations, which included a model of the intercellular cleft space, suggested that such co-localization may have a protective role under conditions of greatly reduced coupling. Simulations of ephaptic coupling by Mori et al. (2008) have also generalized the cable model and shown how this mechanism may play a role under conditions of reduced gap junction coupling. The experimental and modeling results of Veeraraghavan et al. (2016) also suggest a role for Nav1.5 and Kir2.1 in intercellular communication through an ephaptic coupling mechanism in addition to gap junctions, myocyte geometry, and tissue architecture; by comparing a “uniform” model where ion channels are uniformly distributed with a “polarized” model where ion channels are spatially localized, it was shown that the polarized model was able to better explain anisotropic conduction patterns. Wei et al. (2016) also used an ephaptic coupling model to study anisotropic phenomena under conditions of reduced gap junction coupling. While ephaptic coupling could play a role in reciprocal modulation under conditions of reduced gap junction coupling, in order to simplify computations, it was not used here as the majority of the simulations involved high gap junction conductance values. The most practical approach for investigating reciprocal modulation appears to be monodomain simulations of cardiac fibers to construct hypotheses that may be tested in vitro in the future. This study examines the effects of independent modulation of GK1 & GNa and reciprocal GK1–GNa modulation on single-cell thresholds, fiber current thresholds, fiber conduction velocities and fiber space constants along with effects of changes in fiber Ggj.
Methods
A number of cardiac cell models are currently available and could be used to study reciprocal modulation. The guinea-pig ventricular myocyte model of Noble et al. (1998) was used here for simulations of single cells and one-dimensional cardiac fiber for a number of reasons: first, it is a well-established model of cells at physiological temperatures (37°C) that has been found to reproduce experimental data from isolated cells and cardiac fibers (Varghese et al., 2015). Secondly, it has the convenient feature that the INa and IK1 conductances were already the same: 0.5 μS and thus required no scaling or baseline adjustments for the study of reciprocal modulation. Other models were found to have very different values for GK1 and GNa and while they could be scaled by single channel conductance (which are roughly the same for Kir2.1 homotetramers and Nav1.5), most other models have baseline parameters that yield very different channel densities for Kir2.1 and Nav1.5. Third, the guinea-pig ventricular myocyte has an action potential morphology that is closer to those in larger mammals and may make it easier to apply the results of guinea-pig studies to cardiac excitability in humans.
Each cardiac cell involves a set of 22 simultaneous non-linear differential equations listed in the aforementioned references. For the sake of brevity, the full set of equations are not shown but a few key currents are discussed here. The inward rectifier current, IK1, was modeled using the formulation:
where [K]o is the external potassium concentration and EK is the Nernst reversal potential for potassium, the other parameters are listed in the aforementioned references. The fast inward current, INa: involves two differential equations for the kinetics of activation (m) and inactivation (h). The default value for both GK1 and GNa was 0.5 μS (micro Siemens); the default value of the intercellular gap junction coupling conductance, Ggj, was set to 10 μS in order to obtain a baseline conduction velocity of 70 cm/s. Fibers had uniform parameter values: there were no spatial variation in parameters. The standard notation of outward currents having positive sign is used throughout this paper: a negative current value indicates that the current is an inward one.
The gap junction coupling currents flowing into the i-th cell (see Figures 1A,B) are:
These gap junction currents are combined with the cell capacitance current and the total ion channel current in cell i to arrive at the differential equation involving the cell membrane potential for each cell:
Boundary conditions at both ends were Neumann or “no-flux” or “sealed end” boundary conditions. Thus, a chain of 100 cells in a fiber is, in essence, a system of 2200 differential equations that are solved simultaneously using standard numerical ordinary differential equation methods. The Matlab (Mathworks, Natick, MA, USA) variable-order variable-step size stiff differential equation solver ode15s with a default absolute tolerance of 1e-6 was used to compute numerical solutions.
Stimulus current thresholds were computed separately for each specified set of parameters. Single cells were stimulated at 1 Hz intervals using 0.2 ms duration square pulses whose magnitudes were increased in 0.5 nA increments until an action potential was successfully elicited by two consecutive pulses. The threshold for a fiber was computed by stimulating the first four cells in a 100 cell chain at 1 Hz intervals using 0.2 ms duration square pulses of increasing magnitude until two consecutive stable propagating APs were seen. The short pulse duration was selected so that there would be minimal effect on sodium activation and inactivation (the fast sodium current peaks in <1 ms and inactivates about as quickly). In addition, this stimulus duration is practical in patch-clamp and tissue experiments (Varghese et al., 2015). Conduction velocity simulations involved triggering a propagating AP with a current stimulus (in four cells at one end of the fiber) that was, by convention, 1.5 times the threshold to avoid artifacts due to propagation delays. By symmetry (Rall, 1977; Crawford et al., 1991), stimulating one end with sealed end boundary conditions is equivalent to stimulating in the middle of a fiber that is twice as long. Conduction velocities were measured by dividing the difference in the activation times at the 75th and 25th cells in the fiber by the distance in order to avoid end effects such as slower initiation of waves at the stimulus end and wave speed-up at the distal end due to the sealed-end boundary condition. The length, Lc, of each cell was 74 μm. Fiber space constants were computed using long-duration subthreshold stimulus pulses administered at one end of the chain. These 100 ms pulses were long enough in time duration for the fiber to reach steady state and large enough in pulse magnitude (within 10% below the threshold) to allow accurate fitting to an exponential function. As in Noujaim et al. (2007) and Seidel et al. (2010), the voltages of the cells at the end of the pulse were fitted to a single exponential decay function. The Matlab lsqcurvefit least squares method was used to determine the rate of spatial decay, i.e., the space constant, as a multiple of cell lengths.
Results
The results of this study show how excitability in single cardiac cells and fibers changes as ionic current conductances were modified. Parameter sweeps were conducted in two main ways: one was independent modulation where only a single conductance (either GK1 or GNa) was changed and the other was reciprocal modulation where both, GK1 & GNa, were modified in tandem. Figure 2 summarizes the results of modifying GK1 & GNa independently (Figures 2A–F) and reciprocally (Figures 2G–I) in single cells (Figures 2A,D,G) and fibers (Figures 2B,C,E,F,H,I). Figure 3 shows the effects of reciprocal modulation for a parameter sweep of Ggj values and Figure 4 shows the results of independent (Figure 4A) and reciprocal (Figure 4B) modulation and Ggj changes on fiber space constant.
Figure 3.
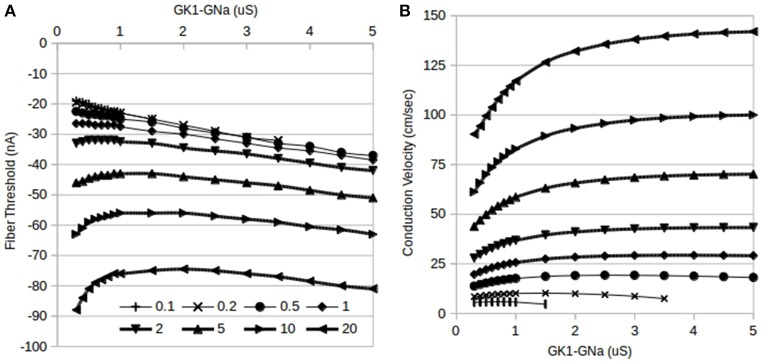
Effects of reciprocal modulation of IK1 and INa and changes in gap junction conductance, Ggj, on fiber thresholds. (A) Changes in fiber threshold due to reciprocal modulation of GK1–GNa (1:1 ratio). At any particular value of GK1–GNa, increasing Ggj raises the threshold for initiating a propagating action potential. The curves for Ggj = 0.1 and 0.2 μS (top two curves) overlap considerably. Magnitudes of current thresholds increase monotonically with increasing GK1–GNa for Ggj = 0.1–1 μS while higher values of Ggj result in biphasic dependence. (B) Changes in fiber conduction velocity due to reciprocal modulation of GK1–GNa. At any particular value of GK1–GNa, increasing Ggj increases the conduction velocity of propagating action potentials. Markers are the same as panel A: top curve is for Ggj = 20 μS.
Figure 4.
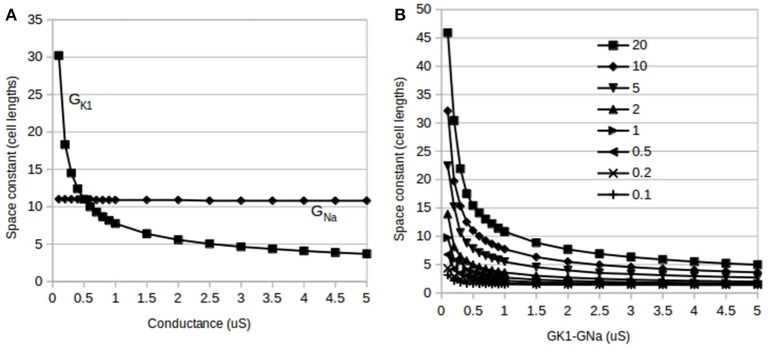
Effects of independent and reciprocal modulation of IK1 and INa and changes in gap junction conductance, Ggj, on fiber space constant. (A) Changes in fiber space constant due to independent modulation of GK1 and GNa: the space constant is insensitive to changes in GNa alone (GK1 held at 0.5 μS–flat line) but is very sensitive to alterations in GK1 (GNa held at 0.5 μS–curve). (B) Changes in fiber space constant due to reciprocal modulation of GK1–GNa (1:1 ratio). Each curve is for a different value of Ggj from 0.1 to 20 μS.
Single cell threshold
Cells were stimulated using a 0.2 ms duration square pulse. At the default value of GK1 = GNa = 0.5 μS, the computed single cell threshold was approximately −19 nA, matching observations in patch-clamp experiments with isolated guinea-pig cardiac ventricular myocytes using the same square pulse duration (Varghese et al., 2015). As shown in Figure 2A, holding the conductance, GK1, of the IK1 current at the default value of 0.5 μS and increasing GNa from 0.2 to 5 μS, we see, as expected, that higher values of GNa lowers the magnitude of the inward current needed to trigger an action potential (AP). Figure 2D shows that with GNa held at its default value of 0.5 μS and GK1 varied from 0.3 to 5 μS, the magnitude of the threshold is raised monotonically by increasing GK1. Values of GK1 lower than 0.3 μS resulted in action potential durations (APD) >1 s and were, therefore, not considered while values higher than 5 μS resulted in extremely short APDs, on the order of ms and were not considered realistic. Baseline observations showing that independent increments in GNa lowers the threshold while increments in GK1 raises it agree with expectations: since INa is an excitatory current and IK1 inhibits APs, increasing GNa would be expected to make it easier to APs while increasing GK1 has the opposite effect. This poses the question of which trend will be seen with reciprocal modulation when GK1 and GNa are both incremented in tandem: will one current dominate or will they neutralize each other?
Figure 2G shows the effect of reciprocal modulation on single cell thresholds: even though the actual magnitude of IK1 is lower than that of INa, it is GK1 that primarily determines the threshold for cellular activation. In the competition between the opposing conductances, GK1 and GNa, it is GK1 that “wins.” While Milstein et al. (2012) did have quantitative data on reciprocal modulation, they did not predict a particular ratio for the changes in GK1 and GNa. Simulations using GK1:GNa stoichiometries other than 1:1 reciprocal modulation, such as 2:1 and 1:2 (Figure 2G; the x-axis shows the GK1 values, the corresponding GNa value depends on the ratio used) reveal that the overall trends were qualitatively very similar to that seen for 1:1 reciprocal modulation: increasing GK1 and GNa in tandem raises the threshold for activation.
Fiber threshold
Chains of 100 coupled (Ggj = 10 μS) cells were stimulated using 0.2 ms square pulses applied to four cells at one end of the fiber. Figure 1C shows the cell Vm, IK1, and INa for the 5th cell in the fiber for two such simulations: one for a subthreshold stimulus and one for a suprathreshold stimulus. While similar results would be expected for the dependence of the thresholds in single cells and fibers, simulation results show some important differences. Figure 2B shows the trend in stimulus threshold in a fiber as the GK1 of each cell was held at the default value of 0.5 μS and GNa was increased from 0.2 to 5 μS. As in the case of single cells (Figure 2A), we see that an increase in GNa lowers the magnitude of the threshold required to initiate a propagating AP; as expected, larger current stimuli are needed to initiate APs in fibers vs. single cells.
Figure 2E shows that with GNa held at its default value of 0.5 μS while GK1 is increased from 0.3 μS, the magnitude of the threshold is raised monotonically by increasing GK1. As with single cells, the fiber does not allow the use of values of GK1 below 0.3 μS since the APD of each cell exceeds 1 s. A crucial difference between the single cell case and the fiber is that at values of GK1 above 1.2 μS, the fiber threshold increases dramatically to the point where the fiber is rendered inexcitable for GK1 > 1.3 μS.
Unlike the results of independent modulation of GK1, reciprocal modulation of GK1 and GNa results (Figure 2H; the x-axis shows the GK1 values, the corresponding GNa value depends on the ratio used) in the fiber remaining excitable for a significantly larger range of parameter values. Furthermore, the shapes of the curves in Figure 2H are qualitatively different from those for single cells (Figure 2G). Rather than the monotonically increasing or decreasing curves seen in Figures 2A,B,D,E,G, the fiber threshold is more complicated: a biphasic dependence on GK1/GNa is seen for 1:1 and 1:2 stoichiometries while the results for 2:1 reciprocal modulation show a triphasic dependence. Thus, we cannot say that GK1 alone determines the fiber threshold. The interaction of the three currents, IK1, INa, and Igj, with reciprocal modulation reveal behavior that is more complicated than predictions either from single cells or from independent modulation. These results in Figures 2E,H suggest that cells with larger GK1 become inexcitable unless accompanied by some increase in GNa. One interpretation may be that reciprocal modulation of the two opposing currents allows the threshold to stay within a tighter set of limits while also allowing ventricular tissue to remain excitable.
Conduction velocity
The conduction velocities of propagating action potentials in fibers were studied under conditions of independent modulation (Figures 2C,F) and reciprocal modulation (Figure 2I; the x-axis shows the GK1 values, the corresponding GNa value depends on the ratio used). It would be expected that GK1 would decrease excitability and, thus, conduction velocities as well while GNa would have the opposite effect and that was precisely what was observed in simulation results. Figure 2C shows that, as predicted by non-linear cable theory (see Appendix), conduction velocity increases with independent modulation of GNa from 0.3 to 5 μS while GK1 was held at its default value of 0.5 μS. Figure 2F shows that conduction velocity decreases as GK1 is increased from 0.2 to 1.3 μS while GNa was held at 0.5 μS. As explained above, independent modulation of GK1 results in inexcitable tissue for values of GK1 above 1.3 μS. One remaining question is which of the two opposing currents will determine conduction velocity changes for the case of reciprocal modulation. Figure 2I shows that for all three stoichiometries, 1:1, 2:1, and 1:2, conduction velocities increase with tandem increases (the x-axis shows the GK1 values, the corresponding GNa value depends on the ratio used) in GK1:GNa, which is to say that it is GNa that primarily determines conduction velocity.
Gap junction conductance changes
While the above results establish the main features of changes in excitability due to reciprocal modulation of IK1-INa, a third current, Igj, is also involved in determining excitability in cardiac tissue. In order to elucidate the effects of changes in cell coupling, the dependence of reciprocal modulation was studied as the gap junction conductance, Ggj, was varied from 0.1 to 20 μS and the results are summarized in Figure 3. At low values of Ggj (0.1 and 0.2 μS), only a limited range of tandem changes in GK1–GNa are possible as a result of inexcitability setting in in the fiber for larger values of GK1. These limited ranges are difficult to see in the plots of fiber thresholds vs. GK1–GNa values in Figure 3A since there is considerable overlap of curves for Ggj = 0.1–0.3 μS; these ranges can, however, be seen in Figure 3B which shows the effects of GK1–GNa reciprocal modulation on conduction velocity: the bottom-most curves are for the lowest values of Ggj.
As Ggj is increased, in addition to the threshold being raised, the shapes of the threshold vs. GK1–GNa curves change from monotonically increasing (top four curves in Figure 3A) for Ggj <1 μS to a biphasic dependence for Ggj > 0.5 μS (bottom four curves in Figure 3A).
In general, conduction velocity increases as Ggj is increased at any given value of GK1–GNa (Figure 3B). On the other hand, the shape of the conduction velocity vs. GK1–GNa curves has the opposite trend: for lower Ggj values from 0.1 to 0.5 μS, there is a biphasic dependence (lower 3 curves in Figure 3B) on GK1–GNa values and this switches to monotonically increasing dependence for higher values of Ggj.
Changes in fiber space constant
Unlike short-duration pulses that minimally affect the fast sodium current as used above, longer duration pulses do allow fibers to reach threshold and conduct APs even with large GK1 values. Subthreshold long duration pulses allow fibers to approach steady state conditions and were used to estimate the fiber space constant, λ, in a manner similar to that used by Noujaim et al. (2007) and Seidel et al. (2010). As would be expected from long-duration pulses, we see in Figure 4A that the space constant was insensitive to changes in GNa (flat line). Figure 4A also shows that compared to GNa, the space constant is very sensitive to changes in GK1 and appears to have a dependence as predicted by linear cable theory. Figure 4B shows the results of reciprocal modulation of GK1–GNa at different values of Ggj: these curves are very similar in form to independent modulation of GK1 (Figure 4A) indicating that without activation of INa, λ is primarily dependent on GK1. Although the results of reciprocal modulation should be identical to independent modulation of GK1 alone, for the sake of consistency, these calculations did use reciprocal modulation. Finally, λ increases with increasing Ggj, and does appear to have the predicted dependence as well.
Discussion
This paper examined the functional effects of reciprocal modulation of IK1–INa on electrophysiological characteristics of single cardiac cells and cardiac fibers using an established model of ventricular cells with the goal of determining a teleological reason for the existence of reciprocal modulation. An important finding was the loss of excitability seen with independent modulation of GK1 in ventricular fibers (Figure 2E). While the single cell threshold does increase with GK1 (Figuer 2D), the effect on the fiber threshold is much more dramatic than would be expected from the cell results. It appears that the combination of electrotonic effects and increases in GK1 has a cumulative effect of raising cellular thresholds and decreasing the space constant (Figure 4A) as was also shown by Noujaim et al. (2007, see their supplement). Large IK1 channel densities lower the excitability of ventricular tissue to the point where fibers become inexcitable in response to short-duration stimuli. This was not predicted by linear cable theory and these results show an important physiological role for reciprocal modulation in ventricular myocytes. Reciprocal modulation would guarantee a commensurate increase in INa channels thereby preserving cardiac fiber excitability.
The results of simulations of independent modulation of GK1 and reciprocal modulation of GK1–GNa appears to suggest a paradoxical effect for IK1 upregulation: although IK1 by itself would be expected to lower excitability and therefore lower conduction velocity as was shown in Figure 2F, reciprocal modulation results in a parallel upregulation of INa which is predicted by non-linear cable theory to increase conduction velocity (see Appendix) which was confirmed in this study by independent modulation of GNa in Figure 2C. So which effect dominates? The results of the reciprocal modulation simulations here predict that the GNa effect dominates (Figure 2I): upregulation of GK1 is predicted to increase conduction velocity. It turns out that this prediction has already been confirmed: Noujaim et al. (2007), Sekar et al. (2007), and Sekar et al. (2009) found that Kir2.1 upregulation increases conduction velocity. However, their explanation was that Kir2.1 upregulation hyperpolarizes the cell resting membrane potential, thereby increasing sodium channel availability. Figure 2F shows that increasing GK1 alone actually decreases conduction velocity and this is in agreement with the experimental results of (Veeraraghavan and Poelzing, 2008) and Veeraraghavan et al. (2016) and with data on reduction of conduction velocity by pinacidil activation of IK−ATP. With the discovery of reciprocal modulation (Milstein et al., 2012), we can see that IK1 upregulation induces a parallel upregulation of INa which is the root cause of the increase in conduction velocity. Indeed, Figure 2C shows that independent modulation of GNa has the type of pronounced effect on conduction velocity that is predicted by non-linear cable theory and we see in Figure 2I that with reciprocal modulation of GK1 and GNa, the GNa effect on conduction velocity dominates. This suggests a reinterpretation of the data in Noujaim et al. (2007), Sekar et al. (2007), Sekar et al. (2009) which were based on 4–6 day cultured cells which have been shown to have greatly reduced IK1 (Mitcheson et al., 1996; Christé, 1999). The conduction velocity increases can be understood to be caused by the large and “hidden” upregulation of INa alone; it is not necessary to resort to the sodium channel availability argument which is unlikely to be valid in cells in vivo.
The concept of a fiber space constant is based on linear cable theory and is used to estimate the spatial effect of stimuli and propagating waves. Assuming the ionic current has a linear conductance, we can estimate the length of fiber that will be excited by a local subthreshold stimulus. Cardiac fibers are not continuous cables with linear membrane conductances; they have discontinuous intercellular conductance changes at gap junctions. Furthermore, they have numerous non-linear and time-dependent currents and even the relatively “simple” IK1 has a non-linear dependence on voltage (see Methods). Although these caveats preclude a direct application of linear cable theory to compute space constants, the cable theory prediction of the space constant, λ, being proportional to . appears to hold. A more accurate analysis of the effects on λ, is likely to require subcellular discretization as used by Seidel et al. (2010). The decrease in λ with increasing GK1 explains the loss of excitability seen at higher GK1 values: an increasing in GK1 from the default value of 0.5–1.5 μS halves the value of λ (Figure 4A). The sharp drop in λ with GK1 makes it more difficult to bring enough cells to threshold to trigger a propagating AP. While the liminal length has been shown to be proportional to for simplified non-near cae models (Jack et al., 1975) the results of this study imply that the liminal length appears to increase much more dramatically with GK1 than the predictions of simplified models. The predicted dependence of the liminal length on the ratio of GK1 to GNa does explain why reciprocal modulation preserves excitability since tandem changes in these two conductances would leave both their ratio and, therefore, the liminal length intact.
Non-linear cable theory using simplified models (Jack et al., 1975) predicted that conduction velocity, θ, will be proportional the square-root of both GNa and Ggj: θ ∝ . Similar results were also obtained by Shaw and Rudy (1997, Figures 4, 6) and Veeraraghavan et al. (2016, Figure 7) using different non-linear ionic models and our results are qualitatively consistent with these earlier studies. While Veeraraghavan et al. (2016) also showed that a potassium conductance had a qualitatively similar effect on transverse conduction velocity to that seen here, this conductance had biphasic effect on longitudinal conduction velocity; however, their potassium channel was of the delayed rectifier type and may explain the differences between their results and those in this paper.
Limitations of this study: For one-dimensional or planar AP propagation, the monodomain model used here is generally considered sufficient for the study of cardiac AP propagation while two-dimensional and anisotropic AP propagation may require bidomain models. Mori et al. (2008) showed that the resistance of the intercellular cleft space has a significant effect on AP propagation via ephaptic coupling when gap junction conductance is reduced. These mechanisms were not employed here (also see Dhein et al., 2014) but it is possible, as indicated by the results of Veeraraghavan et al. (2016), that the co-localization of Nav1.5 and Kir2.1 in intercalated disks may have important modulatory effects on currents in the intercellular cleft space which may involve another role for reciprocal modulation. The results of Kucera et al. (2002) and Wei et al. (2016) suggest that computation models that incorporate spatial subcellular localization of ion channels may be useful in explaining phenomena in anisotropic tissue and at the extremes of high GK1, low GNa, and very low or very high Ggj. While cardiac cells have spatial variations in channel densities such as pools of Nav channels and calcium fluxes at T-tubules, each cell in cardiac tissue has been shown experimentally (Bu et al., 2009) to be roughly isopotential suggesting that the monodomain cell isopotential model used here is a reasonable one. Such approximations of isopotential intracellular conditions have also been used in ephaptic coupling simulations (Wei et al., 2016).
Cardiac cells assemble ion channel subunits composed of homomeric and heteromeric alpha subunits and heteromeric alpha-beta subunits in endoplasmic reticula and subsequently insert these channels at targeted locations in the cell membrane such as intercalated disks or t-tubules using structural proteins such as SAP97, Ankyrin-G, syntrophin, and dystrophin (Balse et al., 2012). Reciprocal modulation appears to be one way control the densities of IK1 and INa channels. Although the exact mechanism of reciprocal modulation and the exact stoichiometry of IK1–INa channels is unknown at this time, our results show that reciprocal modulation allows better control over excitability in ventricular tissue. Furthermore, it is likely that Ggj or gap junction channel density is also probably controlled by analogous cell trafficking and assembly mechanisms to control conduction velocities in ventricular tissue. Cardiac ventricular conduction velocities are usually in the range from 30 to 100 cm/s and the results shown in Figure 3B suggest that GK1, GNa, and Ggj have to stay within a limited and coordinated range of values to accomplish target speeds. Biological data show that these three channel types are co-localized in IDs suggesting the possibility of cooperative behavior between Kir2.1, Nav1.5, and Connexin43 channel proteins.
Lastly, this study yields a second apparently paradoxical result that could be a testable hypothesis. Just as IK1 upregulation through reciprocal modulation can be understood to enhance conduction velocity, overexpression of Nav1.5 in cardiac cells will appear to have the counter-intuitive effect of raising the threshold for activation: this is due to the fact that through reciprocal modulation, Nav1.5 upregulation will cause a parallel upregulation of Kir2.1 and, at least in isolated cells (Figure 2G), the IK1 effect on threshold is predicted to dominate, thus increasing the cell stimulus threshold. The predicted effect of IK1–INa upregulation on fiber thresholds is more complicated as seen in Figure 2H but nevertheless can be tested in vitro. Cardiac cells have evolved a number of mechanisms to keep relative ion channel densities within certain ranges. It is logical that two opposing currents such as IK1 and INa would have to be “balanced” in some way for cells to function properly. Reciprocal modulation may be just one of many such control mechanisms for cardiac excitability.
Author contribution
AV conceived the experiments, carried them out and wrote the manuscript.
Conflict of interest statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary material
The Supplementary Material for this article can be found online at: http://journal.frontiersin.org/article/10.3389/fphys.2016.00542/full#supplementary-material
References
- Balse E., Steele D. F., Abriel H., Coulombe A., Fedida D., Hatem S. N. (2012). Dynamic of ion channel expression at the plasma membrane of cardiomyocytes. Physiol. Rev. 92, 1317–1358. 10.1152/physrev.00041.2011 [DOI] [PubMed] [Google Scholar]
- Barker R. J., Price R. L., Gourdie R. G. (2002). Increased association of ZO-1 with connexin43 during remodeling of cardiac gap junctions. Circ. Res. 90, 317–332. 10.1161/hh0302.104471 [DOI] [PubMed] [Google Scholar]
- Bu G., Adams H., Berbari E. J., Rubart M. (2009). Uniform action potential repolarization within the sarcolemma of in situ ventricular cardiomyocytes. Biophys. J. 96, 2532–2546. 10.1016/j.bpj.2008.12.3896 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christé G. (1999). Localization of K+ channels in the tubules of cardiomyocytes as suggested by the parallel decay of membrane capacitance, IK1 and IKATP during culture and by delayed IK1 response to barium. J. Mol. Cell. Cardiol. 31, 2207–2213. 10.1006/jmcc.1999.1034 [DOI] [PubMed] [Google Scholar]
- Crawford J. D., Golubitsky M., Gomes M. G. M., Knobloch E., Stewart I. N. (1991). Boundary conditions as symmetry constraints, in Singularity Theory and its Applications: Warwick 1989, Part II: Singularities, Bifurcations and Dynamics, ed Roberts M. (Berlin: Springer; ), 63–79. [Google Scholar]
- Dhein S., Seidel T., Salameh A., Jozwiak J., Hagen A., Kostelka M., et al. (2014). Remodeling of cardiac passive electrical properties and susceptibility to ventricular and atrial arrhythmias. Front. Physiol. 5:424. 10.3389/fphys.2014.00424 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fozzard H. A., Schoenberg M. (1972). Strength-duration curves in cardiac Purkinje fibres: effects of liminal length and charge distribution. J. Physiol. 226, 593–618. 10.1113/jphysiol.1972.sp009999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hunter P. J., McNaughton P. A., Noble D. (1975). Analytical models of propagation in excitable cells. Prog. Biophys. Mol. Biol. 30, 99–144. 10.1016/0079-6107(76)90007-9 [DOI] [PubMed] [Google Scholar]
- Jack J. J. B., Noble D., Tsien R. W. (1975). Electric Current Flow in Excitable Cells. Oxford: Clarendon Press. [Google Scholar]
- Joyner R. W. (1982). Effects of the discrete pattern of electrical coupling on propagation through an electrical syncytium. Circ Res. 50, 192–200. 10.1161/01.RES.50.2.192 [DOI] [PubMed] [Google Scholar]
- Keener J. P. (1991). The effects of discrete gap junction coupling on propagation in myocardium. J. Theor. Biol. 148, 49–82. 10.1016/S0022-5193(05)80465-5 [DOI] [PubMed] [Google Scholar]
- Kucera J. P., Rohr S., Rudy Y. (2002). Localization of sodium channels in intercalated disks modulates cardiac conduction. Circ. Res. 91, 1176–1182. 10.1161/01.RES.0000046237.54156.0A [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lowe J. S., Palygin O., Bhasin N., Hund T. J., Boyden P. A., Shibata E., et al. (2008). Voltage-gated Nav channel targeting in the heart requires an ankyrin-G dependent cellular pathway. J. Cell Biol. 180, 173–186. 10.1083/jcb.200710107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milstein M. L., Musaa H., Balbuenaa D. P., Anumonwoa J. M. B., Auerbach D. S., Furspan P. B., et al. (2012). Dynamic reciprocity of sodium and potassium channel expression in a macromolecular complex controls cardiac excitability and arrhythmia. Proc. Natl. Acad. Sci. U.S.A. 109, E2134–E2143. 10.1073/pnas.1109370109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitcheson J. S., Hancox J. C., Levi A. J. (1996). Action potentials, ion channel currents and transverse tubule density in adult rabbit ventricular myocytes maintained for 6 days in cell culture. Pflugers Arch. 431, 814–827. 10.1007/s004240050073 [DOI] [PubMed] [Google Scholar]
- Mohler P. J., Splawski I., Napolitano C., Bottelli G., Sharpe L., Timothy K., et al. (2004). A cardiac arrhythmia syndrome caused by loss of ankyrin-B function. Proc. Natl. Acad. Sci. U.S.A. 101, 9137–9142. 10.1073/pnas.0402546101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mori Y., Fishman G. I., Peskin C. S. (2008). Ephaptic conduction in a cardiac strand model with 3D electrodiffusion. Proc. Natl. Acad. Sci. U.S.A. 105, 6463–6468. 10.1073/pnas.0801089105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noble D. (1972). The relation of Rushton's ‘liminal length’ for excitation to the resting and active conductances of excitable cells. J. Physiol. 226, 573–591. 10.1113/jphysiol.1972.sp009998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noble D., Varghese A., Kohl P., Noble P. (1998). Improved guinea-pig ventricular cell model incorporating a diadic space, IKr and IKs, and length- and tension-dependent processes. Can. J. Cardiol. 14, 123–134. [PubMed] [Google Scholar]
- Noujaim S. F., Pandit S. V., Berenfeld O., Vikstrom K., Cerrone M., Mironov S., et al. (2007). Up-regulation of the inward rectifier K+ current (IK1) in the mouse heart accelerates and stabilizes rotors. J. Physiol. 578, 315–326. 10.1113/jphysiol.2006.121475 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rall W. (1977). Core conductor theory and cable properties of neurons, in Handbook of Physiology–Section I: The Nervous System, ed Kandel E. R. (Baltimore, MD: Williams & Wilkins; ), 39–98. [Google Scholar]
- Rushton W. A. H. (1937). Initiation of the Propagated Disturbance. Proc. R. Soc. B 124, 210–243. 10.1098/rspb.1937.0083 [DOI] [Google Scholar]
- Seidel T., Salameh A., Dhein S. (2010). A simulation study of cellular hypertrophy and connexin lateralization in cardiac tissue. Biophys. J. 99, 2821–2830. 10.1016/j.bpj.2010.09.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sekar R. B., Kizana E., Cho H. C., Molitoris J. M., Hesketh G. G., Eaton B. P., et al. (2009). IK1 heterogeneity affects genesis and stability of spiral waves in cardiac myocyte monolayers. Circ. Res. 104, 355–364. 10.1161/CIRCRESAHA.108.178335 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sekar R. B., Kizana E., Smith R. R., Barth A. S., Zhang Y., Marbán E., et al. (2007). Lentiviral vector-mediated expression of GFP or Kir2.1 alters the electrophysiology of neonatal rat ventricular myocytes without inducing cytotoxicity. Am. J. Physiol. Heart Circ. Physiol. 293, H2757–H2770. 10.1152/ajpheart.00477.2007 [DOI] [PubMed] [Google Scholar]
- Shaw R. M., Rudy Y. (1997). Ionic mechanisms of propagation in cardiac tissue. Roles of the sodium and L-type calcium currents during reduced excitability and decreased gap junction coupling. Circ. Res. 81, 727–741. 10.1161/01.RES.81.5.727 [DOI] [PubMed] [Google Scholar]
- Varghese A., Spindler A. J., Paterson D., Noble D. (2015). Rate-dependent activation failure in isolated cardiac cells and tissue due to Na+ channel block. Am. J. Physiol. Heart Circ. Physiol. 309, H1753–H1763. 10.1152/ajpheart.00805.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veeraraghavan R., Lin J., Keener J. P., Gourdie R., Poelzing S. (2016). Potassium channels in the Cx43 gap junction perinexus modulate ephaptic coupling: an experimental and modeling study. Pflugers Arch. 468, 1651–1661. 10.1007/s00424-016-1861-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veeraraghavan R., Poelzing S. (2008). Mechanisms underlying increased right ventricular conduction sensitivity to flecainide challenge. Cardiovasc. Res. 77, 749–756. 10.1093/cvr/cvm090 [DOI] [PubMed] [Google Scholar]
- Wei N., Mori Y., Tolkacheva E. G. (2016). The dual effect of ephaptic coupling on cardiac conduction with heterogeneous expression of connexin 43. J. Theor. Biol. 397, 103–114. 10.1016/j.jtbi.2016.02.029 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.