Network sampling coverage II: The effect of non-random missing data on network measurement

Abstract

Missing data is an important, but often ignored, aspect of a network study. Measurement validity is affected by missing data, but the level of bias can be difficult to gauge. Here, we describe the effect of missing data on network measurement across widely different circumstances. In Part I of this study (Smith and Moody, 2013), we explored the effect of measurement bias due to randomly missing nodes. Here, we drop the assumption that data are missing at random: what happens to estimates of key network statistics when central nodes are more/less likely to be missing? We answer this question using a wide range of empirical networks and network measures. We find that bias is worse when more central nodes are missing. With respect to network measures, Bonacich centrality is highly sensitive to the loss of central nodes, while closeness centrality is not; distance and bicomponent size are more affected than triad summary measures and behavioral homophily is more robust than degree-homophily. With respect to types of networks, larger, directed networks tend to be more robust, but the relation is weak. We end the paper with a practical application, showing how researchers can use our results (translated into a publically available java application) to gauge the bias in their own data.

1. Introduction

Network data are often incomplete, especially when collected through traditional means, such as surveys. Conventional logic suggested that even small amounts of missing data were unacceptable, since network measures are dependent on the connections between all actors in a network and missing even a few nodes could badly bias the estimates of distance, cohesion or other structural measures. Recent work has challenged that assumption, showing that many network measures can be well-estimated with incomplete information (Borgatti et al., 2006; Smith and Moody, 2013). This does not mean that measurement concerns can be ignored (for example, see Marsden, 1993; Brewer and Webster, 2000; Marin and Hampton, 2007; Eagle and Proeschold-Bell, 2015), only that missing data itself does not necessarily invalidate a network study. Still, we are only beginning to understand the practical consequences of missing data for network studies (e.g. Kossinets, 2006; Wang et al., 2012). How much missing data is too much? And should our tolerance for missing data vary by network type, measure of interest and type of missing data (Frantz et al., 2009)? Are there circumstances when missing 30% of the network is acceptable, but others when missing 10% is not?

This paper is the second part of a series on missing network data (Smith and Moody, 2013), with the overall goal of providing straightforward, practical guidance for researchers collecting and analyzing network data.¹ Network scholars have long been concerned with measurement error; for example, asking how different collection strategies invite different threats to validity (Marsden, 1990; Butts, 2003; Marsden, 2005). Here we focus on the types of settings – archetypically surveys² – where node-missingness is common (e.g. McFarland et al., 2014; Patacchini and Zenou, 2016). We thus focus on measurement issues most likely to cause problems in such settings (for example, see Laumann et al., 1983; Strully, 2014 for a discussion of the boundary problem; see also Smith and Faris, 2015; Hipp et al., 2015 for a discussion related specifically to longitudinal network data). Node missingness may be less of a concern when dealing with automated data, such as sensor, cell phone or online data (Bliss et al., 2014; González-Bailón et al., 2014), though these also have peculiar issues of their own, such as distinguishing between ‘real’ and ‘fake’ nodes in an online network (see Wang et al., 2012).

Our primary question is what happens to network measures when central actors are more (or less) likely to be missing? This is particularly pressing for researchers administrating network surveys in schools, organizations and other medium-sized, bounded settings (Valente et al., 2003; Moore et al., 2004; Steglich et al., 2012). Certain actors may be disproportionally absent the day of the survey or particularly unwilling to take part in the study, and it is important to know how such a practical, common problem will affect one's analysis (see Kreager et al., 2015). We condition missingness on centrality for two reasons: first, centrality nicely captures the kinds of structural problems common in this sort of data collection. In adolescent populations, for example, peripheral nodes are likely to be absent from school and thus not in the survey (resulting in a negative correlation between centrality and missingness); while in organizational or elite networks very central nodes might be too busy to participate (resulting in a positive correlation between centrality and missingness). While other characteristics might also drive missingness (cluster membership or attributes not associated with centrality), centrality provides a general bias that likely maps onto data collection difficulty. Second, many of the structural features we care to measure are built on sequences of paths in networks, in much the same way that centrality is, and thus centrality-biased missingness likely produces the extreme case for how missingness affects network metrics.

To provide general guidelines across research settings, we must consider more than the amount of missing data. One must also consider the nature of the missing data, the network of interest and the measure of interest, as well as the complex dependencies between these factors. Missing network data thus require a holistic view and our results offer a toolset to help make that view possible. By looking at a wide range of networks, measures and types of missing data, we can offer recommendations and best practices for applied network practitioners (see Silk et al., 2015, who call for just such an analysis). Even better, a researcher faced with a particular set of circumstances (network type, type of missing data, amount of missing data) might use our results to estimate the bias for their measure of interest.

We begin with a short background on missing data and network measurement. We then describe our empirical networks, measures and network sampling scheme. Our approach mirrors prior work in this area, removing nodes from the network, recalculating the measures of interest, and then comparing the resulting value to the true value. We describe results based on the type of missing data across four types of network measures: centrality, centralization, topology and homophily.

2. Prior work

Our papers add to the expanding literature on missing network data (Galaskiewicz, 1991; Costenbader and Valente, 2003; Borgatti et al., 2006; Smith and Moody, 2013). The majority of past work has relied, as we do, on Monte-Carlo simulations to evaluate the robustness of network measures to missing data. Simulation offers an alternative to analytical approaches, which are often intractable for most network measures (although see the past work of Frank, 1971; Granovetter, 1976). Past studies have generally followed the same basic setup: identify a set of networks and measures of interest; calculate the measures of interest on the selected networks; (randomly) generate missingness by removing nodes (or links) from the full network; calculate the measures of interest on the distorted networks; compare the statistics from the incomplete networks to the true value (Kossinets, 2006; Wang et al., 2012). The experimental question is simple: how does bias correlate with different types or levels of missing data?

Many of the missing at random studies have focused exclusively on centrality measures (Johnson et al., 1989; Galaskiewicz, 1991; Costenbader and Valente, 2003; Borgatti et al., 2006). Predictably, centrality scores become less accurate as more nodes are removed, but less obvious is their relative robustness. For instance, Borgatti et al. (2006) found a correlation of .7 between the true values and the sampled values for closeness centrality even in networks with 50% of the nodes missing and the correlation is higher for in-degree. Costenbader and Valente (2003) found a correlation of .9 with 50% of the nodes missing (for in-degree).

Some recent work moves beyond centrality. Part I of this study offers one of the more comprehensive analysis of nodes missing at random (see also Kossinets, 2006; Huisman, 2009; Wang et al., 2012; Žnidaršič et al., 2012; González-Bailón et al., 2014). Most topological measures decreased in accuracy with more missing data, but the rate of deterioration varies widely across measures and networks (see Kossinets, 2006 as well). Distance and triad summary metrics exhibited greater bias than transitivity or group metrics, while measures of behavioral homophily were quite robust to missing data, especially in larger, more concentrated networks.

We follow this standard Monte Carlo design, but without assuming missing-at-random removal, similar to Huisman (2009) and Fitzhugh and Butts (2010), as well as work done in the robustness/attack literature (Albert et al., 2000; Carley et al., 2002). For example, Fitzhugh and Butts (2010) explore the effect of missing central nodes on the robustness of a network in an emergency setting. A large literature in physics and computer science asks a related question of how vulnerable a network is to random, compared to targeted, node removal (Gallos et al., 2005; Yehezkel and Cohen, 2012). Most studies find that networks with skewed degree distributions are robust to random node removal but quite vulnerable to targeted attacks (e.g. Albert et al., 2000). Huisman (2009) falls more directly in the missing data tradition, asking how measurement bias is affected by missing certain types of nodes.

Our goal is to make these studies more general and provide practical reference points for researchers faced with missing network data. To do so, we need variation across the many network domains that researchers study. We study a dozen different networks drawn from a wide variety of empirical domains, examine network metrics ranging from individual centrality scores to the aggregate block structure, and allow missingness to range from a minor inconvenience weakly associated with centrality to high levels strongly associated with centrality.

Unfortunately, such generality comes at the cost of parsimony: the multiple conditions generate detailed results that can obscure general patterns. While we want to include this detail so that individual researchers can compare their work to the cases in our study that closely resemble their own, we also want to provide an overview of the general trends. As such, we provide 3 ways of summarizing the results for each class of network measures, organized by the dozen empirical networks. First, the most practical summaries are found in the “target bias tables.” These are analogous to power-calculation tables and express the maximum amount of missing data that could be observed and still maintain a score within a target bias range (for example, to maintain at least a .9 correlation with the true value, see Table 2). The non-parametric version of this table is captured in the corresponding appendix figures providing response curves for each scenario, showing graphically the level of bias by the level of missingness for each type of missing data. Second, we step back from the detail and provide a regression-based summary of the general effect of the scenario attributes (network size, type of missingness and so forth) on the overall level of bias observed. This gives one a sense of the marginal effects of particular case features. Finally, we ask about the interactive nature of these factors and cluster our scenarios into common bias classes.³ To help ease use, we also provide a simple web-based calculator that translates these results into a predicted bias level under user-specified scenarios.

Table 2.

Maximum percent missing to retain target correlation of .9 with true score, node removal defined by in-degree.

Network	Correlation with centrality	In-degree	Out-degree	Total degree	Bonacich power	Closeness	Betweenness
Interlock	−.75	30	30	30	34	14	17
	.75	15	15	15	12	4	9
Prison	−.75	29	22	24	21	14	16
	.75	25	12	15	10	7	8
Sorority	−.75	23	27	22	17	20	6
	.75	18	18	15	9	12	4
6th graders	−.75	47	41	42	36	50	24
	.75	35	31	30	18	40	18
Coauthor	−.75	a	a	a	a	4	36
	.75	28	28	28	19	1	13
Prosper	−.75	34	30	28	27	20	12
	.75	27	20	20	14	14	8
Co-citation	−.75	a	a	a	a	17	38
	.75	39	39	39	33	6	21
Elites	−.75	a	29	a	a	17	31
	.75	61	10	41	14	10	13
HS 13	−.75	46	28	37	38	22	18
	.75	36	19	26	19	18	14
BioTech	−.75	a	a	a	a	2	60
	.75	35	35	35	18	1	20
HS 24	−.75	43	31	37	40	27	19
	.75	33	21	25	18	20	14
CSprings	−.75	a	a	a	65	2	48
	.75	43	43	43	22	1	16
Mean (Std Dev)	−.75	50.2 (18.8)	43.2 (20.3)	47.5 (20.6)	46.5 (21)	17.4 (13)	27.1 (15.9)
	.75	32.9 (12.1)	24.2 (10.8)	27.7 (10.2)	17.2 (6.4)	11.2 (11.2)	13.2 (5.2)

^aCases where percent missing is above 70, our observed maximum. In these cases, 70 is used to calculate overall means. The maximum percent missing was calculated based on a quadratic fit to the data.

3. Data

We examine the effects of missing data across a dozen empirical networks. We select networks with highly variable characteristics to cover a wide range of likely empirical contexts, although we limit the analysis to networks with less than a 1000 nodes. Medium to small sized networks are sensitive to missing data and the most conducive to additional data collection efforts, making them particularly relevant to study missing data (i.e. one could collect more data if the bias was considered too high). The networks represent a variety of substantive settings, including many of the most commonly studied network types – school/friendship, organizational, and citation networks. The networks are the same as in Part I of this study.⁴ They include: “data on elites (corporate interlocks: “Mizruchi Interlock” and “River City Elite”), young youth networks (“Gest 6th graders”, “Prosper s220”),⁵ adolescent and young adult networks (“Sorority Friendship”, “High School (p.13 and p.24)”), the Gagnon prison network (MacRae, 1960), science networks (a portion of the sociological abstracts collaboration graph and the Social Networks article co-citation graph, the biotechnology exchange network) and epidemiological networks (Colorado Springs HIV risk network – Morris and Rothenberg, 2011)⁶” (quoted from Smith and Moody, 2013). See Fig. 1 for plots and summary statistics.

Figure 1.

Networks Used for Sampling Simulation

4. Network measures

We explore the effect of missing data on four common types of network measures: centrality, centralization, topology and homophily and present the empirical values for each network in Table 1.

Table 1.

Sample network descriptive statistics.

	Inter-lock	Prison	Sorority	6th grade	Co-author	Prosper	Co-citation	Elite	HS 13	Bio-tech	HS24	HIV risk
Directed?	No	Yes	Yes	Yes	No	Yes	No	Yes	Yes	No	Yes	No
Centrality
In-degree	3.02 (1.93)	2.72 (2.02)	2.89 (1.75)	8.86 (5.26)	6.16 (5.98)	3.83 (2.69)	9.32 (10.62)	2.39 (7.59)	6.06 (4.42)	3.85 (4.99)	5.71 (3.96)	6.05 (8.12)
Out-degree	3.02 (1.93)	2.72 (1.48)	2.89 (1.85)	8.86 (4.67)	6.16 (5.98)	3.83 (2.36)	9.32 (10.62)	2.39 (1.63)	6.06 (2.90)	3.85 (4.99)	5.71 (2.99)	6.05 (8.12)
Symmetric degree	3.02 (1.93)	5.43 (2.73)	5.78 (2.88)	17.7 (7.73)	6.16 (5.98)	7.65 (3.85)	9.32 (10.62)	4.78 (7.83)	12.1 (6.04)	3.85 (4.99)	11.43 (5.84)	6.05 (8.12)
Closeness	.36 (.08)	.18 (.08)	.15 (.09)	.35 (.12)	.32 (.06)	.18 (.09)	.38 (.09)	.03 (.02)	.22 (.05)	.26 (.04)	.2 (.06)	.25 (.04)
Betweenness	.06 (.07)	.03 (.05)	.04 (.05)	.01 (.02)	.02 (.06)	.02 (.03)	.01 (.02)	0 (0)	.01 (.01)	.01 (.02)	.01 (.01)	0 (.02)
Bonacich power	.82 (.58)	.86 (.52)	.86 (.51)	.9 (.43)	.58 (.82)	.82 (.57)	.63 (.78)	.64 (.77)	.83 (.55)	.6 (.8)	.83 (.56)	.57 (.82)
Centralization
In-degree	.10	.08	.06	.14	.19	.08	.26	.29	.04	.07	.03	.09
Out-degree	.10	.08	.06	.15	.19	.02	.26	.03	.01	.07	.01	.09
Symmetric degree	.10	.06	.05	.08	.19	.05	.26	.15	.03	.07	.02	.09
Closeness	.27	.12	.17	.16	.35	.11	.48	.06	.08	.36	.08	.28
Betweenness	.20	.17	.16	.06	.37	.16	.12	.01	.05	.24	.03	.17
Bonacich power	.20	.18	.14	.13	.26	.16	.22	.41	.13	.29	.12	.23
Topology
Component size	43	67	72	147	148	155	162	250	556	571	619	908
Bicomponent size	27	62	59	145	75	147	118	195	545	336	605	517
Distance	.36	.18	.15	.35	.32	.18	.38	.03	.22	.26	.2	.25
Transitivity	.11	.28	.36	.29	.63	.29	.44	.17	.22	.02	.22	.32
TauRC	−.91	2.35	4.65	17.75	17.65	7.22	−27.36	163.6	23.66	−91.61	22.91	−104.22
Homophily
In-degree	−.07	.02	.03	.1	.31	−.01	.03	−.29	.05	−.13	.13	−.13
Out-degree	−.07	−.13	−.03	−.08	.31	−.06	.03	0	.14	−.13	.16	−.13
High attribute	.75	.75	.77	.88	.78	.82	.84	.79	.93	.75	.8	.77
Low attribute	.36	.39	.37	.35	.38	.37	.35	.39	.37	.38	.38	.4

Standard deviations are in parentheses.

4.1. Centrality

We include in-degree, out-degree, total degree, closeness, betweenness and Bonacich centrality. The networks are treated as symmetric for Bonacich centrality, and we define beta as .75 times the largest eigenvalue. Closeness centrality is calculated from the inverse distance matrix, where disconnected nodes have a value of 0 and directly connected nodes have a value of 1. We use the inverse distance matrix to avoid summations over undefined values (a problem when all pairs of people cannot reach one another).

4.2. Centralization

Centralization captures the inequality in the distribution of centrality, and we have a centralization score corresponding to each centrality measure. Note that centralization is a graph-level statistic while centrality is an individual level score. We examine both the standard Freeman (1979) deviation scores and, since these prove somewhat unstable, the simpler standard deviation of individual centrality.

4.3. Topology

We use six topological measures, ranging in scale from macro structure to local clustering. The first two are global measures of connectivity: percent in the largest component and percent in the largest bicomponent. A component is a set of nodes connected by at least one path. The fraction in the largest component captures a minimal measure of system connectivity. The largest bicomponent is the maximal set of people connected by at least two independent paths, and is a stronger indicator of network cohesion (Moody and White, 2003). For our main results, we divide size in the largest bicomponent by total network size. We also present a set of alternative results in the appendix (see Table A3), where bicomponent size is scaled by component size.

Our third topological measure captures global structure by measuring the mean inverse distance (i.e. “closeness”) between pairs of nodes. In networks with low average distance, all nodes are close to each other, and have values approaching 1, while networks with high average distance will have values that trend toward 0 (not close). Our fourth measure, transitivity, reflects local clustering; or the tendency for a “friend of a friend to be a friend.” We use the transitivity ratio, defined as the relative number of two-step paths that also have a direct path.

Our fifth measure, the tau statistic, is a summary of the triad distribution and describes both micro and macro properties (Wasserman and Faust, 1994). At the micro level, the triad census reflects hierarchy, clustering and other local tie formation processes. At the macro level, the triad census can be used to describe the group structure of a network (Johnsen, 1985, 1986). We use the tau statistic developed by Holland and Leinhardt (1976) to characterize the triad distribution (see also Wasserman, 1977). The tau statistic is used to test configurations of triads against known macro-structural models, based on necessary structural constraints implicit in the macrostructure (Johnsen, 1985, 1986) and can generally be used as ways to evaluate hierarchical orderings of clusters. The tau statistic is a weighted sum of the triad distribution conditioned on the dyad distribution. Larger tau values indicate that a particular weighting scheme fits the data relatively well. Here we use the ranked-cluster (RC) weighting scheme. The specific ranked-cluster formulation represents a hierarchical ordering of cliques with multiple parallel ranks, such that cliques on the same level are not connected while cliques at different levels are asymmetrically connected.⁷ A network following a ranked-cluster triad distribution will be hierarchically arranged: with ordered asymmetric nominations between well-defined groups. We are not particularly concerned if this weighting scheme is the best fit for all networks, rather, we only care how this summary of the triad distribution becomes less accurate as missing data increases.

Our final topological measure is positional: we blockmodel each network, partitioning the full network into a simpler set of equivalence blocks (White et al., 1976), placing nodes together if they have a similar pattern of ties. We can use the rand statistic (Rand, 1971) to compare the observed full-data partition to that observed under the missing data conditions. The unadjusted rand statistic captures the proportion of pairs in one partition that are grouped together in a second partition. We fix the observed partition using a depth = 3 CONCOR solution for all networks and compare a similar partition to the incomplete networks.⁸

4.4. Homophily

Homophily is an organizing principle of many social systems (McPherson et al., 2001; Smith et al., 2014). Homophily captures the tendency for similar people to be socially connected at a higher rate than dissimilar people. Past substantive work on homophily has examined behaviors, such as smoking and drinking, and demographic characteristics, such as race and education (e.g. Haynie, 2001; Goodreau et al., 2009; Schaefer et al., 2012). We measure homophily as the edgewise correlation for an attribute and here focus on two attributes: node degree and behavior. Thus, our homophily measures are at the network level: the correlation between connected nodes on degree or behavior.

We measure assortative degree mixing by the edgewise correlation on degree. Nodes with high degree are more likely to be connected to others with high degree when there is strong assortative mixing. The correlation is negative when high degree nodes are disproportionately connected to low degree nodes. We present results for both out-degree and in-degree.

Since there exists no comparable behavioral measure across all of our networks (as there is no naturally occurring characteristic that is common to all of the networks in question), we construct a behavioral measure with known properties, using the Friedkin (1990) peer influence model. We begin by randomly seeding the network with values drawn from a uniform distribution and then apply a peer-influence model to the network, updating the values for each node by the average of their peers, until the desired level of homophily is achieved. We test two levels, a low setting (edgewise correlation of .35) and a high setting (correlation of .75). These constructed attributes are fixed and then used across all missing data distortion scenarios. The advantage of this model is that it captures the pure structural foundation of behavior homophily that would be generated by a known peer influence process, independent of particularistic context or selection processes, allowing an assessment of missing data on peer influence.⁹

5. Network sampling and bias

Our design answers two main questions: what is the effect of increasing missing data on measurement bias? And what is the effect of removing more or less central nodes from the network? The sampling process follows the standard in this literature: for each network, we remove a portion of the nodes and calculate the measures of interest on the reconstructed network. The removed nodes are not present in the reconstructed network, even if a sampled respondent nominates them. This follows a listwise deletion procedure common in this sort of Monte Carlo experiment (see also Galaskiewicz, 1991; Costenbader and Valente, 2003; Borgatti et al., 2006). We then compare the observed statistic in the incomplete networks to the known, empirically true measure, repeating this process 1000 times for each missingness level: 1%, 2%, 5%, 10%, 15%, 20%, 25%, 30%, 40%, 50%, 60%, 70%.

Since centrality is an individual level score, we use the correlation between nodes' true centrality score and the score observed in the distorted network (with missing data) to summarize the effect of missingness. That is, we calculate the centrality of the nodes in the full non-perturbed network, calculate it again with the nodes removed, and correlate these two vectors. A high correlation means that nodes are ranked similarly in the true network and the network with missing data. The higher the correlation, the greater is the reliability of the incomplete network data (see Costenbader and Valente, 2003 for a similar approach).

We use a standardized bias score for all graph-level measures – including centralization, topology and homophily. We define bias as:

$$\frac{(\text{True}-\text{observed})}{\text{True}}$$

A bias score shows how much the observed score (under the given missing data scheme) differs from the true value and gives us a proportionate distance from the true value. The difference is relative to the true empirical value, making the bias scores comparable across networks and statistics. Bias scores can be negative (over-estimates) or positive (under-estimates), but we use the absolute value of the bias scores in our analysis to make them comparable across all measures and networks (save for the appendix figures). Note that this measure is different from a traditional measure of bias that would compare the true value to the mean over all sampled values.

Instead of simple random missingness, here we remove nodes proportional to their centrality. We implement this selection by making the probability of being selected as a missing node a weighted average of centrality and random noise. The results will approach random missingness as we put less weight on the centrality portion, as follows:

$$p_i=\frac{b\ast {\text{centrality}}_i+(1-|b|)}{\mathit{\text{sign}}(b)\ast u(0,1)}$$

$$\mathit{w}=\frac{(\mathit{p}-min(\mathit{p}))}{(max(\mathit{p})-min(\mathit{p}))}$$

$${\text{prob}}_i=\frac{w_i}{\sum \mathit{w}}$$

where b is the scalar we set experimentally, centrality_i is the centrality score of person i, u(0,1) is a random draw from a uniform distribution ranging from 0 to 1 and prob_i is the probability that person i is selected as a missing case.

We experimentally set four levels of the correlation between centrality and missingness: −.75 (strong negative correlation), where people with high centrality are much less likely to be missing; −.25 (weak negative correlation), where people with high centrality are slightly less likely to be missing; .25 (weak positive correlation), where people with high centrality are slightly more likely to be missing; and .75 (strong positive correlation), where people with high centrality are much more likely to be missing. Our analysis includes results for each correlation value for two centrality types: in-degree and closeness. Thus, for each measure and level of missing data, there are 96 different scenarios: 12 networks × 4 correlation settings (−.75, −.25, .25, .75) × 2 types of degree definitions (in-degree and closeness). Note that not all of the tables and figures will include results for both definitions of missing nodes (in-degree and closeness) as the results are often quite similar.¹⁰

Nodes on the outskirts of the network are more likely to be missing when there is a negative correlation between centrality and missingness. This mimics situations where peripheral members of a community are difficult to study, as is common in school networks (peripheral members are more likely to be absent). When the correlation is positive, central nodes are more likely to be missing, mimicking situations where active nodes might have scheduling difficulties (such as public officials in elite networks), or cases where ties represent hidden populations (such as links to known criminals or terrorists-Everton, 2012). Note that the positive correlation results provide a conservative estimate on the effects of missing data, since it is difficult to capture many network features accurately if the most “important” nodes are missing: a measure is quite robust to missing data if the error is low even when the most central nodes are removed. The effect of missing high degree nodes may, however, be dependent on the features of the network, such as centralization: missing high degree nodes may matter less when all actors have similar scores. Similarly, the effect of missing high degree nodes may depend on the distribution of the measure of interest. This is why we include such a wide variety of networks in our analysis.

We use the positive and negative correlation results to produce upper and lower bounds of missing data bias. Our goal is to provide researchers with a practical sense of the bias likely observed in their own data. As such, a researcher who can estimate the approximate level of missingness and make reasonable assumptions about the correlation of missingness to centrality can use our results to identify bounds on bias in their own work. A researcher without information on the missing data can still gauge the range of possible bias. We offer a detailed example in the conclusion; we have also developed an online calculator to perform all of the necessary calculations (link provided after review).

6. Presentation outline

We first present target bias tables, akin to a statistical power-analysis for missing data. For centrality, the table presents the percent missing that would yield a target correlation of .9 between the true and observed score for each network and measure.¹¹ We also include analogous tables for centralization, topology and homophily for a target absolute value bias of .25. The presented tables only include results where node removal is defined by in-degree (for the sake of simplicity) but the closeness results are very similar.

We next regress bias on the amount of missing data. Thus, we predict bias (using the absolute value) for each scenario as a function of percent missing: bias = b₀ + b₁ (%missing/10). The resulting slope coefficients, b₁, represent the expected increase in bias for a 10% increase in the number of nodes removed. We use b₁ as a summary measure, showing how quickly bias increases as missing data increases. For centrality, we define bias as 1 minus the correlation between the true and observed centrality scores.

To provide a general overview of the results, we use regression models to summarize how bias varies across measures, networks and types of missing data (including the correlation with centrality and the node removal type, in-degree or closeness). We run separate HLM models for each network measure, using the bias slopes described above as the dependent variable.¹² Larger coefficients imply more bias, indicating that bias increases at a faster rate as missing data increases. Our main independent variables are the four correlation with centrality settings (−.75 through .75) and the node removal type (in-degree (1) or closeness (0)) and their interaction term. The remaining predictors capture network properties that may be related to measurement bias: network size, type (directed = 1; undirected = 0) and concentration (measured as the standard deviation of in-degree). For each network property, we include a main effect and an interaction between the correlation and centrality. For example, larger networks may have less bias than smaller networks (the main effect) and may be less affected by missing central nodes (the interaction).

Finally, we use cluster analysis to identify patterns in the results across networks. For each of the four broad categories of network statistics (centrality, centralization, topology and homophily), we partition our scenarios into clusters based on the pattern of bias (using the absolute value of bias) across different levels of missing data which allows us to compare missingness effect profiles. A case here is defined by the combination of network, missing data type and measure (e.g. Interlock network, .75 correlation with in-degree; Bonacich centrality). We include all missing data scenarios in the clustering analysis, including both node removal definitions, closeness and in-degree. Each case will have 12 different bias values to cluster (one for each level of missing data), and thus cases with similar bias profiles are placed in the same cluster.¹³ We then summarize which types of networks, measures, and missing data fall into each cluster.

There are thus three tables for each set of measures: a target bias table, showing how much data one can miss and still retain high confidence; a regression table, showing what network and missing data features are correlated with bias; and a cluster table, showing how different factors combine to create high/low bias measurement.

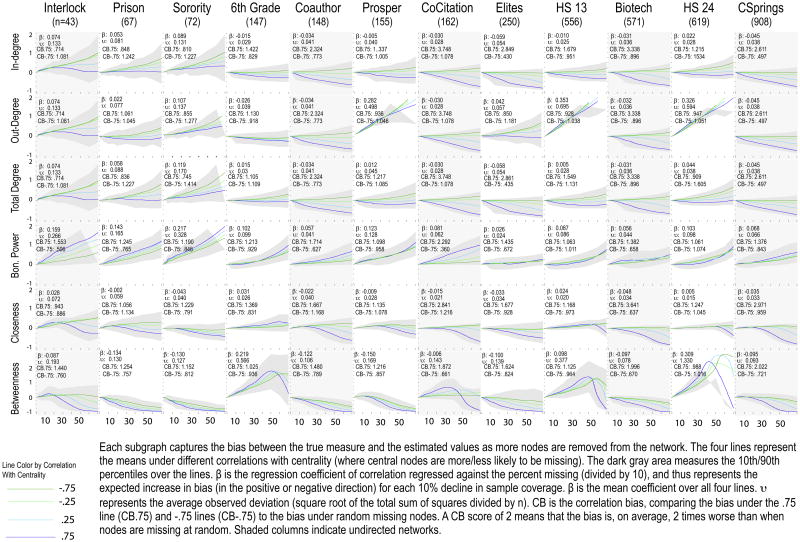
In addition to these tables, we include a detailed graphical presentation of the results in Appendix. We present curves for centrality, centralization, topology and homophily (for simplicity, we only present the results where node removal is defined by in-degree). Each subplot in the figures represents a network/measure combination with bias on the y-axis and the level of missing data on the x-axis. The subplots contain one curve for each of the four correlation levels. The light gray area around the curves provides the upper and lower bounds. We also include a set of summary statistics. For each subplot, we include the mean bias slope across the four curves (here allowing for negative and positive bias values) and the mean average deviation from the true value (υ). The correlation bias captures the differences across the centrality correlation settings. The correlation bias, CB, is the ratio of total bias in a given curve to the total bias under random missing data. For example, the Interlock network on in-degree has a value of 1.56 when missingness is strongly correlated with centrality (.75). This means that the bias is 1.56 times worse when central nodes are missing compared to nodes missing at random.

7. Results

7.1. Centrality

Table 2 presents the target bias results for centrality, giving estimates for each network and measure under strong positive and strong negative correlation conditions. It is clear from Table 2 that the effect of missing data is worse when more central nodes are more likely to be missing. The correlation between nodes' true centrality and the measure obtained after nodes are removed is lower when more central nodes are removed. For example, for the Interlock network, a researcher missing low-degree nodes could miss up to 30% of the network and maintain a .9 correlation for total degree, but could only miss 15% if the missing nodes are high-degree. Fig. A1 shows a clear decline in accuracy as missing data increases (overall negative curve), but higher absolute bias when more central nodes are missing. For in-degree, the positive correlation line has 2.3 times more bias (on average) than random missing data, while the negative correlation lines has 1.3 times less bias than random missing data.

Closeness and betweenness centrality have higher levels of bias than the degree measures, while Bonacich power centrality appears most sensitive to missing high degree nodes. On average, one can miss up to 46.5% of the data and maintain a .9 correlation (between nodes' true degree and their degree after nodes have been removed) if low in-degree nodes are more likely to be missing, but only 17.2% if high in-degree nodes are more likely to be missing.

Table 3 summarizes the relationship between network characteristics and sensitivity to missing central nodes. The models regress the bias slopes – the summary measure of the relation between bias and amount of missing data – on the level of correlation with centrality. These models also include interactions between the correlation with centrality and node removal type (in-degree or closeness), size, directionality, and in-degree standard deviation (centralization) of each network. The models suggest that large, directed networks are less affected by missing high degree nodes (based on the strong negative coefficients for Correlation with Centrality*Directed and Correlation with Centrality*Log of Size across the models).

Table 3.

Centrality bias regression: beta coefficients from closeness and in-degree simulations.

Variables	Model 1	Model 2	Model 3	Model 4	Model 5	Model 6
	In-degree	Out-degree	Total degree	Bon. power	Closeness	Betweeness
Intercept	.09***	.074***	.091***	.09***	.058**	.085***
	(.01)	(.02)	(.01)	(.01)	(.02)	(.02)
Correlation with centrality	.036***	.026*	.035***	.04***	.058***	.012
	(.01)	(.01)	(.01)	(.01)	(.01)	(.02)
Correlation type (0 = closeness 1 = in-degree)	.004***	.005***	.005***	.009***	.005***	.004***
	(.001)	(.001)	(.001)	(.002)	(.001)	(.001)
Correlation with Centrality*Correlation type	.009***	.021***	.016***	.028***	.013***	.008***
	(.002)	(.002)	(.002)	(.004)	(.003)	(.002)
Directed	−.004	.02**	.005	.005	.013	.022***
	(.004)	(.01)	(.005)	(.003)	(.01)	(.01)
Correlation with Centrality*Directed	−.013***	−.012**	−.01**	−.019***	−.019***	−.005
	(.003)	(.004)	(.003)	(.004)	(.004)	(.01)
Log of Size	−.006*	−.006	−.006*	−.005**	.001	−.002
	(.002)	(.004)	(.002)	(.001)	(.004)	(.003)
Correlation with Centrality*Log of Size	−.003*	−.004	−.004*	−.002	−.006**	.001
	(.002)	(.002)	(.002)	(.002)	(.002)	(.003)
In-degree Std. Dev.	−.005***	−.003	−.005***	−.005***	−.003	−.004**
	(.001)	(.001)	(.001)	(.001)	(.002)	(.001)
Correlation with Centrality*In-degree Std. Dev.	−2e−04	.001	−1e−04	−2e−04	−3e−04	−1e−04
	(.001)	(.001)	(.001)	(.001)	(.001)	(.001)
N	96	96	96	96	96	96
Networks	12	12	12	12	12	12

Note: The regression uses the betas slopes from each line as the dependent variable. The betas represent the expected drop in correlation (between the empirical and the observed) for a 10% increase in the amount of missing data. Larger numbers mean larger bias with more missing data. The correlation with centrality takes four values: −.75, −.25, .25, and .75.

We provide a summary of the clustering results in Table 4, which capture the factors associated with similar missingness response profiles. The table is organized by the bias response profile (first column). Within each type, we examine network type (defined as small, medium, large), missing data correlation, and measure.¹⁴ The cluster analysis suggested 5 large clusters, arranged from low to high bias. The first two clusters represent situations with consistently low bias. For example, the median bias at 30% missing is only .08 for cluster 2. A researcher is likely to find such low bias in scenarios involving a large or medium network, where missingness is negatively correlated with centrality (in-degree or closeness). The third and fourth clusters represent cases with medium bias response curves. These represent scenarios involving small networks, missingness negatively correlated with centrality and degree-based outcome measures. The highest bias cluster (with median bias of .30 at 30% missing) generally includes any scenario involving measures of closeness or small networks for measures of betweenness and Bonacich power, with missing data positively associated with centrality.

Table 4.

Cluster analysis summary, centrality measures.

Note: This table summarizes the results of our clustering analysis. Bias is on the y-axis of the plots and percent missing is on the x-axis. Each case (network, measure, missing data type) was placed into a cluster based on the pattern of bias across different levels of missing data. We then summarized what types of networks, measures and missing data went into each cluster. Note that this table only includes results for the strong positive and strong missing data types. A positive correlation means central nodes are more likely to be missing.

Table 4 clearly shows how different factors combine to increase or decrease bias; for example, while larger networks tend to have lower bias than smaller networks (see Table 3, Log of Size), a large network will still have significant bias when measuring betweenness centrality when missing high degree nodes. Similarly, missing low centrality nodes does not guarantee low bias, although, on average, the bias is lower. For example, scenarios involving small networks and in-degree centrality would yield medium bias, even if the missing nodes tend to have low centrality.

7.2. Centralization

Tables 5 and 6 present the main results for centralization. Centralization is a graph-level statistic calculated from the individual-level centrality scores. We have one centralization measure for each of our six centrality measures. We focus on the standard deviation of centrality as our measure of centralization because the traditional Freeman centralization score offers inconsistent, difficult to interpret results (we present these for completeness in Fig. A2 and Tables A1–A2).

Table 5.

Maximum percent missing to remain under target bias of .25: centralization, node removal defined by in-degree.

Network	Correlation with centrality	In-degree	Out-degree	Total degree	Bonacich power	Closeness	Betweenness
Interlock	−.75	48	48	48	a	10	15
	.75	20	20	20	38	8	12
Prison	−.75	45	60	57	62	a	10
	.75	24	31	25	40	24	6
Sorority	−.75	55	50	59	52	a	6
	.75	28	30	31	35	24	4
6th graders	−.75	35	34	37	65	a	32
	.75	21	25	22	57	67	42
Coauthor	−.75	42	42	42	a	5	12
	.75	12	12	12	a	1	9
Prosper	−.75	40	42	44	a	52	17
	.75	23	27	25	63	27	14
Co-citation	−.75	42	42	42	a	13	15
	.75	11	11	11	a	22	22
Elites	−.75	33	48	34	a	68	13
	.75	11	20	11	a	23	6
HS 13	−.75	35	43	39	a	a	38
	.75	21	27	22	a	51	43
BioTech	−.75	37	37	37	a	5	15
	.75	12	12	12	a	1	11
HS 24	−.75	38	43	42	a	a	37
	.75	21	26	22	a	45	44
CSprings	−.75	33	33	33	a	5	15
	.75	13	13	13	a	1	11
Mean (Std Dev)	−.75	40.2 (6.6)	43.5 (7.4)	42.8 (8.3)	67.4 (5.5)	42.3 (31.1)	18.8 (10.7)
	.75	18.1 (5.9)	21.2 (7.5)	18.8 (6.8)	60.2 (14.2)	24.5 (21)	18.7 (15.4)

^aCases where percent missing is above 70, our observed maximum. In these cases, 70 is used to calculate overall means. The maximum percent missing was calculated based on a quadratic fit to the data. Note that centralization is measured as the standard deviation of the centrality scores.

Table 6.

Centralization bias regression: beta coefficients from closeness and in-degree simulations.

Variables	Model 1	Model 2	Model 3	Model 4	Model 5	Model 6
	In-degree	Out-degree	Total degree	Bon. power	Closeness	Betweeness
Intercept	.058***	.067***	.056***	.07***	.098***	.186***
	(.01)	(.01)	(.01)	(.01)	(.02)	(.03)
Correlation with centrality	.04***	.04***	.042***	.042***	−.087**	−4e−04
	(.01)	(.01)	(.01)	(.01)	(.03)	(.01)
Correlation type (0 = closeness 1 = in-degree)	.004***	.004***	.004***	.002**	.002	.003***
	(.001)	(.001)	(.001)	(.001)	(.003)	(.001)
Correlation with Centrality*Correlation type	.01***	.011***	.011***	.001	.021***	.002
	(.001)	(.001)	(.001)	(.001)	(.01)	(.001)
Directed	−.001	−.016***	−.005	.013*	−.036***	−.019
	(.004)	(.004)	(.004)	(.01)	(.01)	(.01)
Correlation with Centrality*Directed	−.016***	−.019***	−.016***	−.003	.107***	−.008
	(.002)	(.003)	(.003)	(.004)	(.01)	(.004)
Log of Size	.003	.002	.003	−.007*	−.003	−.008
	(.002)	(.002)	(.002)	(.003)	(.005)	(.01)
Correlation with Centrality*Log of Size	−.003**	−.003*	−.003*	−.005*	−1e−04	.003
	(.001)	(.002)	(.001)	(.002)	(.01)	(.002)
In-degree Std. Dev.	.003***	.001	.003***	−.003**	−4e−04	−.001
	(.001)	(.001)	(.001)	(.001)	(.002)	(.003)
Correlation with Centrality*In-degree Std. Dev.	.001*	.001*	.001	−.001	−.001	−.001
	(0)	(.001)	(.001)	(.001)	(.002)	(.001)
N	96	96	96	96	96	96
Networks	12	12	12	12	12	12

Note: The regression uses the beta slopes from each line as the dependent variable. The direction of the bias is ignored when calculating the regressions. The betas represent the expected increase in bias for a 10% increase in the amount of missing data. Larger numbers mean larger bias with more missing data. The correlation with centrality takes four values: −.75, −.25, .25, and .75. Note that centralization is measured as the standard deviation of the centrality scores.

Across all measures, bias is worse when central nodes are more likely to be missing, and smallest when less central nodes are more likely to be missing. The top end of the degree distribution is truncated when more central nodes are removed; the standard deviation is thus underestimated, leading to a downward bias. For example, for in-degree centralization, one can miss up to 40% of the network and retain a bias of .25 when less central nodes are missing, but one can only have 18% missing if central nodes are missing. In general, removing central nodes has stronger effects on degree centralization and weaker effects on betweenness centralization.¹⁵ Betweenness does, however, have the highest overall bias. On average, one can only miss 19% of the network and still retain a bias under .25, even when central nodes are less likely to be missing. It is difficult to estimate betweenness centralization with substantial missing data as the measure depends on the structure of the entire network, making it particularly dependent on missing nodes.

Table 6 presents our bias regression results. The degree-based measures offer the clearest story, where larger, directed networks are less affected by missing central nodes, evidenced by the negative coefficients in Models 1–3 for Correlation with Centrality*Directed and Correlation with Centrality*Log of Size.

Table 7 presents a summary of our clustering results. The best fitting model yields 5 broad clusters, arranged from low to high bias. The two lowest bias clusters (with mean bias of .02 and .07 under 30% missing) include Bonacich centrality for large and medium networks and closeness for directed networks. Note that for closeness centralization it was necessary to divide directed and undirected networks, as undirected networks have considerably higher bias (see the main effect for Directed in Model 5, Table 6). The middle bias cluster includes the degree-based measures. The highest bias cluster, with a median bias of .68 when missing 30% of the data, includes undirected networks when one is measuring closeness. A researcher is also likely to have high bias if they are measuring betweenness centralization.

Table 7.

Cluster analysis summary, centralization.

Note: This table summarizes the results of our clustering analysis. Bias is on the y-axis of the plots and percent missing is on the x-axis. Each case (network, measure, missing datatype) was placed into a cluster based on the pattern of bias across different levels of missing data. We then summarized what types of networks, measures and missing data went into each cluster. Note that this table only includes results for the strong positive and strong missing data types. A positive correlation means central nodes are more likely to be missing.

Thus, it seems that the measure itself strongly determines the level of bias for centralization. Closeness and betweenness centralization tend to be in the high bias clusters while Bonacich power and the degree measures tend to be in the low and middle bias clusters, although, here too, we find exceptions. Bonacich centralization has low bias for large and medium networks, but medium to high bias when the network is small. Similarly, a researcher could have low or high bias when measuring closeness centralization, depending on whether the network is directed or undirected.

7.3. Topology

We present the topology results in Table 8 and Fig. A3. Overall, we see the same pattern as before: the negative bias caused by increasing missing data is exaggerated when central nodes are more likely to be missing (high positive correlation). For example, bicomponent size in the Interlock network has 1.5 times more bias than random missing data when central nodes are most likely to be removed, while removing low centrality nodes has 2 times lower bias than expected with nodes missing at random. The results are qualitatively similar for percent in the largest component and distance. Measures of connectivity have higher bias when more central nodes are removed because the paths that generate cohesion tend to flow through central nodes, so removing them creates systematically lower cohesion.

Table 8.

Maximum percent missing to remain under target bias of .25: topology, node removal defined by in-degree.

Network	Correlation with centrality	Component size	Bicomponent size	Distance	Transitivity	TauRC	CONCOR
Interlock	−.75	a	44	56	32	5	a
	.75	14	10	14	1	3	42
Prison	−.75	62	31	40	47	17	a
	.75	30	16	12	35	8	60
Sorority	−.75	54	34	38	57	17	a
	.75	30	17	14	42	15	60
6th graders	−.75	a	a	a	a	18	a
	.75	a	67	49	a	15	a
Coauthor	−.75	45	34	40	a	25	a
	.75	12	10	12	49	9	44
Prosper	−.75	61	43	30	a	20	a
	.75	42	32	16	53	12	a
Co-citation	−.75	a	a	a	a	15	a
	.75	18	23	20	41	13	53
Elites	−.75	69	36	59	58	21	a
	.75	6	12	10	21	8	27
HS 13	−.75	a	69	45	a	20	a
	.75	57	52	29	68	13	a
BioTech	−.75	52	38	37	37	22	a
	.75	9	14	11	12	9	32
HS 24	−.75	a	66	45	a	20	a
	.75	56	49	27	65	13	a
CSprings	−.75	50	31	36	a	21	a
	.75	7	11	10	59	9	35
Mean (Std Dev)	−.75	61.9 (9.4)	47.2 (16.5)	47.2 (13.4)	60.1 (14.1)	18.4 (5)	70(0)
	.75	29.2 (22.2)	26.1 (19.5)	18.7 (11.5)	43 (22.4)	10.6 (3.5)	52.8 (16.2)

^aCases where percent missing is above 70, our observed maximum. In these cases, 70 is used to calculate overall means. The maximum percent missing was calculated based on a quadratic fit to the data.

We find similar, but smaller, effects for tau statistic and CONCOR (i.e. blockmodels). CONCOR, as in Part I of this study, is not greatly affected by missing data and this does not change much when more central nodes are missing. The tau statistic is greatly affected by missing data (with strongly negative slopes in Fig. A3), but the nature of the missing nodes is less consequential than with connectivity or cohesion measures. For example, for the Sorority network, a researcher could miss up to 17% of the network and retain a bias under .25 when less central nodes are missing and 15% when more central nodes are missing; the analogous numbers are 54 and 30% for component size. Transitivity is quite robust to missing data under random node removal, where central nodes are neither more nor less likely to be missing, and we see higher bias than in Part I of this study. Transitivity also tends to have lower bias than the tau statistic, distance or bicomponent size. See Table 8.

Table 9 shows how the effect of missing central nodes varies by network type and measure. For most measures, directed networks are more robust to missing high centrality nodes. We can see this as the coefficient for Correlation with Centrality*Directed is negative and significant in Models 1 –4 and 6 in Table 9. For bicomponent size and distance (and possibly component size), networks with higher in-degree standard deviation have lower overall bias but are more affected by missing central nodes (see the negative coefficient for the main effect for in-degree standard deviation and the positive coefficient for Correlation with Centrality*in-degree standard deviation in Models 2 and 3). Concentrated networks are prone to poor estimates when central nodes are removed because their structure is (more) dependent on the high degree nodes.

Table 9.

Topology bias regression: beta coefficients from closeness and in-degree simulations.

Variables	Model 1	Model 2	Model 3	Model 4	Model 5	Model 6
	Component size	Bicomponent size	Distance	Transitivity	TauRC	CONCOR
Intercept	.134**	.154*	.025	.274***	.153***	.025***
	(.05)	(.06)	(.02)	(.08)	(.02)	(.01)
Correlation with Centrality	.07**	.051***	.069***	.185***	.014	.023***
	(.03)	(.01)	(.01)	(.06)	(.02)	(.01)
Correlation type (0 = closeness 1 = in-degree)	.016***	.008***	.01***	.009***	.004*	.003***
	(.004)	(.002)	(.002)	(.002)	(.002)	(.001)
Correlation with Centrality*Correlation type	.043***	.009**	.011**	.014***	.012***	.007***
	(.01)	(.003)	(.004)	(.004)	(.003)	(.001)
Directed	−.039*	−.026	−.024**	−.069*	−.011	−.005
	(.02)	(.02)	(.01)	(.03)	(.01)	(.003)
Correlation with Centrality*Directed	−.026**	−.022***	−.019***	−.049*	−.011	−.012***
	(.01)	(.01)	(.004)	(.02)	(.01)	(.003)
Log of Size	−.008	−.006	.019***	−.023	−.005	4e−04
	(.01)	(.01)	(.004)	(.02)	(.005)	(.002)
Correlation with Centrality*Log of Size	−.007	−.004	−.005*	−.018	.002	−.002
	(.01)	(.003)	(.002)	(.01)	(.003)	(.001)
In-degree Std. Dev.	−.001	−.004	−.006***	−.012	3e−04	−1e−04
	(.004)	(.01)	(.002)	(.01)	(.002)	(.001)
Correlation with Centrality*In-degree Std. Dev.	.002	.003*	.002*	−.007	−.002	−4e−04
	(.002)	(.001)	(.001)	(.004)	(.001)	(.001)
N	96	96	96	96	96	96
Networks	12	12	12	12	12	12

Note: The regression uses the beta slopes from each line as the dependent variable. The direction of the bias is ignored when calculating the regressions. The betas represent the expected increase in bias for a 10% increase in the amount of missing data. Larger numbers mean larger bias with more missing data. The correlation with centrality takes four values: −.75, −.25, .25, and .75.

We present our clustering results in Table 10, where we found 6 broad clusters. The first two clusters have very low bias for almost all levels of missing data. The low bias clusters include CONCOR (i.e. blockmodeling) for all networks and missing data correlation. We also see transitivity for large and medium sized networks, as well as component size – but here only for large/medium networks under favorable missing data conditions (i.e., missing low degree nodes). Component size is more affected by missing high degree nodes, and thus the positive correlation cases are found in the high bias clusters.

Table 10.

Cluster analysis summary, topology.

Note: This table summarizes the results of our clustering analysis. Bias is on the y-axis of the plots and percent missing is on the x-axis. Each case (network, measure, missing data type) was placed into a cluster based on the pattern of bias across different levels of missing data. We then summarized what types of networks, measures and missing data went into each cluster. Note that this table only includes results for the strong positive and strong missing data types. A positive correlation means central nodes are more likely to be missing.

The fourth cluster captures cases of medium bias, with a median bias of 28% at 30% missing (and higher bias at all levels of missing data than the lower bias clusters). This cluster is more heterogeneous and we see complex combinations of measure, network type and missing data. For example, a researcher with a large network and missing high centrality nodes would have medium bias when trying to measure distance and bicomponent size. In contrast, a researcher with the same missing data conditions (missing high centrality nodes) but a small network would face similar bias measuring transitivity, component size or distance.

Finally, the two high bias clusters contain the tau statistic (as well as bicomponent size for small networks when missing high centrality nodes). A researcher with any size network trying to measure the tau statistic is likely to face high bias, at least compared to other topology measures. This holds for all missing data types, as missing high centrality nodes has only a weak effect on the bias for the tau statistic.

7.4. Homophily

We examine homophily first for degree and then for (simulated) behavior. Table 11 presents the target bias scores. Looking at the out-degree and in-degree columns, we see highly variable levels of sensitivity. In many cases, missing more than 1 % of the network will exceed a target bias of .25. This suggests the difficulty of estimating degree homophily when missing high or low degree nodes (see also Fig. A4).¹⁶ In general, however, it is still the case that missing high degree nodes is worse than missing low degree nodes. For in-degree homophily, one can miss (on average) 23% of the network and retain a bias under .25 when less central nodes are missing, but only 11% if more central nodes are missing. High in-degree nodes are relatively rare. It is thus difficult to measure degree mixing if the high in-degree nodes are missing, as the measure is driven by the propensity for high degree nodes to be connected.

Table 11.

Maximum percent missing to remain under target bias of .25: homophily, node removal defined by in-degree.

Network	Correlation with centrality	In-degree	Out-degree	High behavioral	Low behavioral
Interlock	−.75	3	3	35	26
	.75	1	1	38	25
Prison	−.75	1	16	a	31
	.75	1	15	a	25
Sorority	−.75	1	1	a	46
	.75	1	1	a	37
6th graders	−.75	27	21	a	62
	.75	20	16	a	55
Coauthor	−.75	44	44	a	37
	.75	14	14	a	20
Prosper	−.75	1	7	a	52
	.75	1	1	a	45
Co-citation	−.75	1	1	a	42
	.75	1	1	a	23
Elites	−.75	58	1	27	55
	.75	12	1	27	40
HS 13	−.75	23	54	a	a
	.75	18	44	a	a
BioTech	−.75	54	54	61	68
	.75	1	1	63	43
HS 24	−.75	51	59	a	a
	.75	27	40	a	a
CSprings	−.75	45	45	a	a
	.75	5	5	a	61
Mean (Std Dev)	−.75	23.1 (24.1)	22.7 (24.3)	62.8 (15.1)	52.4 (16)
	.75	11.4 (10.7)	16.9 (18.7)	63.2 (14.7)	42.8 (18)

^aCases where percent missing is above 70, our observed maximum. In these cases, 70 is used to calculate overall means. The maximum percent missing was calculated based on a quadratic fit to the data.

The behavioral homophily scores offer a very different picture. The estimates are still worse when more central nodes are missing but here the overall bias is low and the effect of missing central nodes is weak. For example, one can miss a large portion of the Colorado Springs network and still accurately measure low behavioral homophily. One can miss up to 61% of the network and still retain a bias under .25 when more central nodes are missing and 70% if less central nodes are missing; compare that to 5% and 45% for in-degree homophily on the same network.¹⁷

Table 12 presents our bias regression results. Directed networks have lower bias and are less affected by missing more central nodes for low behavioral homophily (see the negative coefficients in Model 4 for Directed and Correlation with Centrality*Directed). Larger networks still generally have lower overall bias, evidenced by the negative, significant coefficients for Log of Size in Models 2 and 4.

Table 12.

Homophily bias regression: beta coefficients from closeness and in-degree simulations.

Variables	Model 1	Model 2	Model 3	Model 4
	In-degree	Out-degreea	High behavioral	Low behavioral
Intercept	2.276*	1.516**	.111*	.234***
	(.92)	(.53)	(.05)	(.02)
Correlation with centrality	.87*	.628*	.001	.08***
	(.43)	(.29)	(.01)	(.02)
Correlation type (0 = closeness1 = in-degree)	.168***	.107***	5e−04	.005**
	(.04)	(.03)	(.001)	(.002)
Correlation with Centrality*Correlation type	.391***	.219***	.005***	.009**
	(.07)	(.06)	(.001)	(.003)
Directed	.151	−.074	−.02	−.033***
	(.35)	(.23)	(.02)	(.01)
Correlation with Centrality*Directed	−.001	−.118	−.002	−.029***
	(.16)	(.13)	(.004)	(.01)
Log of Size	−.326	−.253*	−.013	−.029***
	(.19)	(.11)	(.01)	(.004)
Correlation with Centrality*Log of Size	−.145	−.112	4e−04	−.009*
	(.09)	(.06)	(.002)	(.005)
In-degree Std. Dev.	−.03	.033	−.001	−.002
	(.07)	(.05)	(.004)	(.001)
Correlation with Centrality*In-degree Std. Dev.	−.001	.022	−.001	−.001
	(.03)	(.03)	(.001)	(.002)
N	96	88	96	96
Networks	12	11	12	12

Note: The regression uses the beta slopes from each line as the dependent variable. The direction of the bias is ignored when calculating the regressions. The betas represent the expected increase in bias for a 10% increase in the amount of missing data. Larger numbers mean larger bias with more missing data. The correlation with centrality takes four values: −.75, −.25, .25, and .75.

^aRC Elite network removed from regression as it is an extreme outlier.

The cluster results for homophily in Table 13 suggest a simple 3 cluster solution. The first cluster has low bias and includes the behavioral homophily scores for all network sizes and missing data correlations. The second cluster has higher bias overall (e.g., a median bias of .26 with 30% missing) and includes in-degree and out-degree homophily for large and medium sized networks.¹⁸ Finally, the high bias cluster includes small networks for in-degree and out-degree homophily. The cluster analysis thus reinforces the picture that we have already seen: that behavioral measures appear less sensitive to missing data than degree measures.

Table 13.

Cluster analysis summary, homophily measures.

Note: This table summarizes the results of our clustering analysis. Bias is on the y-axis of the plots and percent missing is on the x-axis. Each case (network, measure, missing data type) was placed into a cluster based on the pattern of bias across different levels of missing data. We then summarized what types of networks, measures and missing data went into each cluster. Note that this table only includes results for the strong positive and strong missing data types. A positive correlation means central nodes are more likely to be missing.

8. Conclusion

Missing data is a complication faced by many network scholars, as traditional measures assume full coverage of a well-bounded population (Laumann et al., 1983; Wasserman and Faust, 1994). It is thus important to know how missing data biases commonly used network measures. Unfortunately, this is a rather difficult task at present. There are few concrete guidelines for dealing with missing network data and the effect of missing data depends on a number of factors: the amount of missing data; the nature of the missing data; the measure of interest; and the characteristics of the network in question. This paper tries to expand our understanding of missing data effects on network measurement by exploring the effect of missing data across networks, measures, and missing data scenarios.

As with similar studies, estimates are always worse with more missing data. Most measures have the greatest bias when more central nodes are missing and the least when peripheral nodes are missing, but this is far from the full story. Some measures are particularly affected by missing central nodes (e.g. Bonacich power centrality, bicomponent size) while others are not (behavioral homophily and tau statistic). The results also vary systematically by the network of interest. Larger, directed networks are generally less affected by missing central nodes, but this too varies across measures.

How do these results compare to past findings on the effect of missing-at-random data on network estimates? There are, in general, important differences, as some measures are robust to missing data only under favorable conditions, while others are more uniformly robust. For example, for centrality, degree and Bonacich Power centrality are robust to missing-at-random data. In contrast, when more central nodes are missing, only the degree measures are not greatly affected by missing data. Here, Bonacich Power centrality has high bias scores, similar to closeness and betweenness (which have high bias in both missing data cases). This is the case as Bonacich Power is particularly susceptible to missing central nodes. There are similar patterns with the topology measures. For example, under missing-at-random data, transitivity, component size and CONCOR (blockmodeling) are robust to missing nodes, while distance and the tau statistic are not. When more central nodes are missing, component size and bicomponent size join distance and the tau statistic in the list of less robust measures. In contrast, when less central nodes are missing, only the tau statistic suffers badly under conditions of missing data.

The overriding lesson here is a simple one: it is not enough to know the level of missing data to determine the level of bias. Different collection strategies are required for different measures, networks, and types/levels of missing data. It is the combination of these factors that determine how good or bad an estimate is likely to be. The results are thus complex but systematic. We know the basic factors that contribute to measurement bias. The difficulty is putting these factors together to estimate the bias in a particular research setting. We have tried to make this difficult problem easier by producing summary tables based on our cluster analysis. Those tables present the type of bias likely to arise from combinations of size, measurement and missing data type. Our results will make it easier to gauge bias in a research setting, but we would also call for more work on generative models of missing data, including model-based inference for missing data within the ERGM framework (Handcock and Gile, 2010; Koskinen et al., 2013). In that way, we may move beyond empirical regularities to a model of a network with missing data.

Practically, how would one use our results to assess bias in one's own network?

First, a researcher could look up the situation that most closely matches their particular case in the summary (cluster analysis) tables. Alternatively, one could use the regression models to estimate the level of bias in their network (based on the estimates in Tables 3, 6, 9 and 12). The output of the models is the expected bias, given the network characteristics, measure of interest, type of missing data and level of missing data. To make this simpler, we developed a web calculator to facilitate these calculations; a researcher will only have to input the conditions appropriate for their study, and the tool will calculate the expected bias level.

As a demonstration, consider a setting similar to the Sorority network where we are interested in measuring in-degree under conditions of missing data (assume 19% is missing). The first step in assessing bias is to characterize the network itself. For example, we can start by determining the total size of the network (the number of present and missing nodes). This would, practically speaking, come from the initial roster that was used to collect the network data in the first place. In our case, we know that the total network size is 72. We also know whether the network is directed. We can also estimate the centralization of the network, measured as the standard deviation of in-degree. In the simplest case, we can use our observed score (from the network with missing data). In our case, the observed standard deviation of in-degree (on the network with missing data) is 1.46. Of course, this measure of standard deviation is biased, so a better estimate would take the estimated standard deviation and try to adjust the value based on the expected level of bias, but we use 1.46 for the sake simplicity.

The second step is to characterize the missing data in our network. In our example, we know that the network size is 72 and that there are 14 missing students, making the proportion missing .194. By using nominations from respondents (those people who filled out the survey) to non-respondents we can estimate the in-degree of the missing nodes. For this example, the mean in-degree of the missing nodes is 3.21 while the mean in-degree of the present nodes is 2.10. We thus know that missing nodes have higher degree than present nodes. There is a positive correlation between degree and missingness. To get reasonable bounds, we calculate bias under both strong (.75) and weak (.25) conditions.

We can take those inputs (network characteristics and missing data properties) and use them to calculate the predicted bias for our measure of interest, in-degree. We demonstrate the calculation using our web calculator (we have included images of the java applet in Appendix). One first selects the network type: one must designate if the network resembles a network in this study, and, if so, which one.¹⁹ For our estimate here, we assume that we do not know which network best matches our network and simply designate it as uncharacterized. We next select whether the calculation should use the in-degree or closeness formulas. We opt for the in-degree calculations. The remaining inputs are values we already calculated: the size of the network (72), percentage of missing data (19.44), in-degree standard deviation (1.46) and directed (True). The final input is the correlation between centrality and the presence of nodes in the network. In this case, we calculate expected bias where nodes are very likely to be missing (corresponding to a .75 correlation) and likely to be missing (corresponding to a .25 correlation) (Fig. A5).

Looking at the in-degree results, we see that the expected bias is .138 under strong positive correlation and .12 under a weak positive correlation.²⁰ We thus expect the correlation between true and estimated in-degree to be biased between 12 and 14% (so that the correlation will be between 86 and 88%).

In the end, a researcher has three options in the face of missing data: do nothing (if the estimated bias is small), collect more data (if the estimated bias is large) or impute the missing edges and nodes (if the estimated bias is too large and it is infeasible to collect more data). This paper offers a means of estimating the bias in a given context. One can take that estimate and decide on the proper course of action. We have not, however, considered the validity, or payoff, of different imputation approaches. It is this question that we turn to next. The final part of the project will consider different options for dealing with missing data. We will ask how competing imputation methods fare across networks, measures and types of missing data. The overall goal is to provide a comprehensive, practical guide for all researchers grappling with incomplete network data.

Highlights.

• We examine the effect of missing more/less central nodes on network measurement.

• We look at measures of centrality, topology, homophily and centralization.

• Measurement bias is generally worse when central nodes are missing.

• The effect of missing central nodes varies by measure and network type.

• Researchers can estimate bias in their own network using our web-based calculator.

Appendix

Fig. A1.

Centrality score robustness by network, centrality score and missingness level: probability of node removal defined by in-degree.

Fig. A2.

Centralization score robustness by network, centrality score and missingness level: probability of node removal defined by in-degree.

Fig. A3.

Topology score robustness by network, centrality score and missingness level: probability of node removal defined by in-degree.

Fig. A4.

Homophily score robustness by network, centrality score and missingness level: probability of node removal defined by in-degree.

Fig. A5.

Example using java applet to calculate predicted bias central nodes very likely to be missing and central nodes likely to be missing.

Table A1.

Maximum percent missing to remain under target bias of .25: traditional centralization, node removal defined by in-degree.

Network	Correlation with centrality	In-degree	Out-degree	Total degree	Bonacich power	Closeness	Betweenness
Interlock	−.75	21	21	21	34	29	25
	.75	22	22	22	9	19	13
Prison	−.75	34	38	34	28	29	19
	.75	48	25	40	15	35	9
Sorority	−.75	22	29	19	12	a	13
	.75	28	35	29	8	36	7
6th graders	−.75	a	a	57	39	a	11
	.75	35	41	a	36	48	8
Coauthor	−.75	65	65	65	a	52	30
	.75	16	16	16	34	40	13
Prosper	−.75	55	10	47	23	a	27
	.75	34	8	32	22	56	16
Co-citation	−.75	a	a	a	a	a	50
	.75	25	25	25	18	45	10
Elites	−.75	a	40	a	a	a	21
	.75	13	60	13	a	35	8
HS 13	−.75	a	9	56	38	68	13
	.75	35	7	32	41	a	9
BioTech	−.75	a	a	a	57	a	49
	.75	21	21	21	24	30	14
HS 24	−.75	47	11	40	35	a	10
	.75	a	8	a	40	63	7
CSprings	−.75	a	a	a	48	a	55
	.75	17	17	17	29	39	21
Mean (Std Dev)	−.75	52.6 (19.3)	29.6 (22.2)	51.6 (19.2)	43.7 (19.5)	61.5 (16)	26.9 (16.1)
	.75	37.6 (17.7)	26.3 (20.3)	32.2 (19.2)	28.8 (17.2)	43 (14.4)	11.2 (4.3)

^aCases where percent missing is above 70, our observed maximum. In these cases, 70 is used to calculate overall means. The maximum percent missing was calculated based on a quadratic fit to the data.

Table A2.

Traditional centralization bias regression: beta coefficients from closeness and in-degree simulations.

Variables	Model 1	Model 2	Model 3	Model 4	Model 5	Model 6
	In-degree	Out-degree	Total degree	Bon. power	Closeness	Betweeness
Intercept	.15***	−.194	.157***	.263***	.076***	−.046
	(.03)	(.18)	(.04)	(.06)	(.01)	(.13)
Correlation with Centrality	−.103***	−.042	−.107***	.149***	−.055	.13
	(.03)	(.04)	(.03)	(.03)	(.03)	(.08)
Correlation type (0 = closeness 1 = in-degree)	.003	1e–04	.004	.005***	.006*	.004
	(.003)	(.003)	(.003)	(.001)	(.002)	(.002)
Correlation with Centrality*Correlation type	.014**	−.01	.009	.002	.015***	.011*
	(.005)	(.01)	(.005)	(.003)	(.004)	(.004)
Directed	−.016	.076	−.013	.004	−.015**	.077
	(.01)	(.07)	(.01)	(.02)	(.005)	(.05)
Correlation with Centrality*Directed	−.002	−.024	−.011	−.024*	−.008	−.065*
	(.01)	(.02)	(.01)	(.01)	(.01)	(.03)
Log of Size	−.014*	.07	−.015	−.023*	−.005	.031
	(.006)	(.04)	(.01)	(.01)	(.002)	(.03)
Correlation with Centrality*Log of Size	.011	.004	.011	−.022***	.01	−.017
	(.01)	(.01)	(.01)	(.01)	(.01)	(.02)
In-degree Std. Dev.	−.003	−.02	−.003	−.01*	−.002	−.006
	(.002)	(.01)	(.003)	(.005)	(.001)	(.01)
Correlation with Centrality*In-degree Std. Dev.	.008***	.007	.009***	.002	.002	.001
	(.002)	(.003)	(.003)	(.002)	(.002)	(.01)
N	96	96	96	96	96	96
Networks	12	12	12	12	12	12

Note: The regression uses the betas from each line as the dependent variable. The direction of the bias is ignored when calculating the regressions. The betas represent the expected drop in correlation (between the empirical and the observed) for a 10% increase in the amount of missing data. Smaller numbers (or more negative) mean larger bias with more missing data. The correlation with centrality takes four values: −.75, −.25, .25, and .75.

Table A3.

Maximum percent missing to remain under target bias of .25: Alternative measures of bicomponent size and ConCorr.

Network	Correlation with centrality	Bicomponent size (divided by size)	Bicomponent size (divided by component size)	ConCorr: depth set to 3	ConCorr: depths allowed to vary
Interlock	−.75	44	60	a	a
	.75	10	12	42	36
Prison	−.75	31	41	a	a
	.75	16	15	60	a
Sorority	−.75	34	45	a	a
	.75	17	19	60	54
6th graders	−.75	a	a	a	a
	.75	67	64	a	a
Coauthor	−.75	34	57	a	a
	.75	10	11	44	32
Prosper	−.75	43	53	a	a
	.75	32	32	a	a
Co-citation	−.75	a	a	a	a
	.75	23	20	53	38
Elites	−.75	36	53	a	a
	.75	12	4	27	10
HS 13	−.75	69	a	a	a
	.75	52	50	a	a
BioTech	−.75	38	a	a	a
	.75	14	10	32	22
HS 24	−.75	66	a	a	a
	.75	49	49	a	68
CSprings	−.75	31	54	a	a
	.75	11	8	35	30
Mean (Std Dev)	−.75	47.2 (16.5)	59.4 (10.6)	70 (0)	70 (0)
	.75	26.1 (19.5)	24.5 (19.7)	52.8 (16.2)	47.5 (22)

^aCases where percent missing is above 70, our observed maximum. In these cases, 70 is used to calculate overall means. The maximum percent missing was calculated based on a quadratic fit to the data.