Approximating the Little Grothendieck Problem over the Orthogonal and Unitary Groups

Abstract

The little Grothendieck problem consists of maximizing Σ_ij C_ijx_ix_j for a positive semidef-inite matrix C, over binary variables x_i ∈ {±1}. In this paper we focus on a natural generalization of this problem, the little Grothendieck problem over the orthogonal group. Given C ∈ ℝ^dn × ^dn a positive semidefinite matrix, the objective is to maximize ${\displaystyle {\sum }_{\mathit{ij}}\text{tr}}\left(C_{\mathit{ij}}^T{O}_i{O}_j^T\right)$ restricting O_i to take values in the group of orthogonal matrices ${\mathcal{O}}_d$, where C_ij denotes the (ij)-th d × d block of C.

We propose an approximation algorithm, which we refer to as Orthogonal-Cut, to solve the little Grothendieck problem over the group of orthogonal matrices ${\mathcal{O}}_d$ and show a constant approximation ratio. Our method is based on semidefinite programming. For a given d ≥ 1, we show a constant approximation ratio of α_ℝ(d)², where α_ℝ(d) is the expected average singular value of a d × d matrix with random Gaussian $\mathcal{N}\left(0,\frac{1}{d}\right)$ i.i.d. entries. For d = 1 we recover the known α_ℝ(1)² = 2/π approximation guarantee for the classical little Grothendieck problem. Our algorithm and analysis naturally extends to the complex valued case also providing a constant approximation ratio for the analogous little Grothendieck problem over the Unitary Group ${\mathcal{U}}_d$.

Orthogonal-Cut also serves as an approximation algorithm for several applications, including the Procrustes problem where it improves over the best previously known approximation ratio of $\frac{1}{2\sqrt{2}}$. The little Grothendieck problem falls under the larger class of problems approximated by a recent algorithm proposed in the context of the non-commutative Grothendieck inequality. Nonetheless, our approach is simpler and provides better approximation with matching integrality gaps.

Finally, we also provide an improved approximation algorithm for the more general little Grothendieck problem over the orthogonal (or unitary) group with rank constraints, recovering, when d = 1, the sharp, known ratios.

1 Introduction

The little Grothendieck problem [AN04] in combinatorial optimization is written as

$$\underset{x_i\in \{\pm 1\}}{max}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{C}_{\mathit{ij}}{x}_i{x}_j}},$$ (1)

where C is a n × n positive semidefinite matrix real matrix.

Problem (1) is known to be NP-hard. In fact, if C is a Laplacian matrix of a graph then (1) is equivalent to the Max-Cut problem. In a seminal paper in the context of the Max-Cut problem, Goemans and Williamson [GW95] provide a semidefinite relaxation for (1):

$$\underset{m\in \mathbb{N}}{\sup }\underset{\underset{{\Vert X_i\Vert }^2=1}{X_i\in {ℝ}^m}}{max}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{C}_{\mathit{ij}}{X}_i^T{X}_j}}.$$ (2)

It is clear that in (2), one can take m = n. Furthermore, (2) is equivalent to a semidefinite program and can be solved, to arbitrary precision, in polynomial time [VB96]. In the same paper [GW95] it is shown that a simple rounding technique is guaranteed to produce a solution whose objective value is, in expectation, at least a multiplicative factor $\frac{2}{\pi }{min}_{0\le \theta \le \pi }\frac{\theta }{1-\cos \theta }\approx 0.878$ of the optimum.

A few years later, Nesterov [Nes98] showed an approximation ratio of $\frac{2}{\mathrm{\pi }}$ for the general case of an arbitrary positive semidefinite C ⪰ 0 using the same relaxation as [GW95]. This implies, in particular, that the value of (1) can never be smaller than $\frac{2}{\mathrm{\pi }}$ times the value of (2). Interestingly, such an inequality was already known from the influential work of Grothendieck on norms of tensor products of Banach spaces [Gro96] (see [Pis11] for a survey on this).

Several more applications have since been found for the Grothendieck problem (and variants), and its semidefinite relaxation. Alon and Naor [AN04] showed applications to estimating the cut-norm of a matrix; Ben-Tal and Nemirovski [BTN02] showed applications to control theory; Briet, Buhrman, and Toner [BBT11] explored connections with quantum non-locality. For many more applications, see for example [AMMN05] (and references therein).

In this paper, we focus on a natural generalization of problem (1), the little Grothendieck problem over the orthogonal group, where the variables are now elements of the orthogonal group ${\mathcal{O}}_d$, instead of {±1}. More precisely, given C ∈ ℝ^dn × ^dn a positive semidefinite matrix, we consider the problem

$$\underset{O_1,\dots ,O_n\in {\mathcal{O}}_d}{max}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\text{tr}(C_{\mathit{ij}}^T{O}_i{O}_j^T)}},$$ (3)

where C_ij denotes the (i, j)-th d × d block of C, and ${\mathcal{O}}_d$ is the group of d × d orthogonal matrices (i.e., $O\in {\mathcal{O}}_d$ if and only if OO^T = O^T O = I_d×d).

We will also consider the unitary group variant, where the variables are now elements of the unitary group ${\mathcal{U}}_d$ (i.e., $U\in {\mathcal{U}}_d$ if and only if UU^H = U^H U = I_d×d). More precisely, given C ∈ ℂ^dn×dn a complex valued positive semidefinite matrix, we consider the problem

$$\underset{U_1,\dots ,U_n\in {\mathcal{U}}_d}{max}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\text{tr}}}\left(C_{\mathit{ij}}^H{U}_i{U}_j^H\right).$$ (4)

Since C is Hermitian positive semidefinite, the value of the objective function in (4) is always real. Note also that when d = 1, (3) reduces to (1). Also, since ${\mathcal{U}}_1$ is the multiplicative group of the complex numbers with unit norm, (4) recovers the classical complex case of the little Grothendieck problem. In fact, the work of Nesterov was extended [SZY07] to the complex plane (corresponding to ${\mathcal{U}}_1$, or equivalently, the special orthogonal group $S{\mathcal{O}}_2$) with an approximation ratio of $\frac{\mathrm{\pi }}{4}$ for C ⪰ 0. As we will see later, the analysis of our algorithm shares many ideas with the proofs of both [Nes98] and [SZY07] and recovers both results.

As we will see in Section 2, several problems can be written in the forms (3) and (4), such as the Procrustes problem [Sch66, Nem07, So11] and Global Registration [CKS15]. Moreover, the approximation ratio we obtain for (3) and (4) translates into the same approximation ratio for these applications, improving over the best previously known approximation ratio of $\frac{1}{2\sqrt{2}}$ in the real case and $\frac{1}{2}$ in the complex case, given by [NRV13] for these problems.

Problem (3) belongs to a wider class of problems considered by Nemirovski [Nem07] called QO-OC (Quadratic Optimization under Orthogonality Constraints), which itself is a subclass of QC-QP (Quadratically Constrainted Quadratic Programs). Please refer to Section 2 for a more detailed comparison with the results of Nemirovski [Nem07]. More recently, Naor et al. [NRV13] proposed an efficient rounding scheme for the non commutative Grothendieck inequality that provides an approximation algorithm for a vast set of problems involving orthogonality constraints, including problems of the form of (3) and (4). We refer to Section 1.2 for a comparison between this approach and ours.

Similarly to (2) we formulate a semidefinite relaxation we name the Orthogonal-Cut SDP:

$$\underset{m\in \mathbb{N}}{\sup }\underset{\underset{X_i\in {ℝ}^{d\times m}}{X_i{X}_i^T=I_{d\times d}}}{max}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\text{tr}(C_{\mathit{ij}}^T{X}_i{X}_i^T)}}.$$ (5)

Analogously, in the unitary case, we consider the relaxation

$$\underset{m\in \mathbb{N}}{\sup }\underset{\underset{Y_i\in {ℂ}^{d\times m}}{Y_i{Y_i}^H=I_{d\times d}}}{max}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\text{tr}(C_{\mathit{ij}}^H{Y}_i{Y}_j^H)}}.$$ (6)

Since C is Hermitian positive semidefinite, the value of the objective function in (6) is guaranteed to be real. Note also that we can take m = dn as the Gram matrix ${[X_i{X}_j^T]}_{i,j}$ does not have a rank constraint for this value of m. In fact, both problems (5) and (6) are equivalent to the semidefinite program

$$\underset{\underset{G_{\mathit{ii}}=I_{d\times d},G\underset{\_}{\succ }0}{G\in {\mathbb{K}}^{dn\times dn}}}{max}\text{tr}(CG),$$ (7)

for $\mathbb{K}$ respectively ℝ and ℂ, which are generally known to be computationally tractable¹ [VB96, Nes04, AHO98]. At first glance, one could think of problem (5) as having d²n variables and that we would have to take m = d²n for (5) to be tractable (in fact, this is the size of the SDP considered by Nemirovski [Nem07]). The savings in size (corresponding to number of variables) of our proposed SDP relaxation come from the group structure of ${\mathcal{O}}_d$ (or ${\mathcal{U}}_d$).

One of the main contributions of this paper is showing that Algorithm 3 (Section 1.1) gives a constant factor approximation to (3), and its unitary analog (4), with an optimal approximation ratio for our relaxation (Section 6). It consists of a simple generalization of the rounding in [GW95] applied to (5), or (4).

Theorem 1

Let C ⪰ 0 and real. Let $V_1,\dots ,V_n\in {\mathcal{O}}_d$ be the (random) output of the orthogonal version of Algorithm 3. Then

$$\mathbb{E}\left[{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\text{tr}(C_{\mathit{ij}}^T{V}_i{V}_j^T)}}\right]\ge {\alpha }_{ℝ}{\left(d\right)}^2\underset{O_1,\dots ,O_n\in {\mathcal{O}}_d}{max}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\text{tr}\left(C_{\mathit{ij}}^T{O}_i{O}_j^T\right)}},$$

where α_ℝ(d) is the constant defined below.

Analogously, in the unitary case, if $W_1,\dots ,W_n\in {\mathcal{U}}_d$ are the (random) output of the unitary version of Algorithm 3, then for C ⪰ 0 and complex,

$$\mathbb{E}\left[{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\text{tr}(C_{\mathit{ij}}^H{W}_i{W}_j^H)}}\right]\ge {\alpha }_{ℂ}{\left(d\right)}^2\underset{U_1,\dots ,U_n\in {\mathcal{U}}_d}{max}{\displaystyle \sum _{i=1}^N{\displaystyle \sum _{j=1}^n\text{tr}(C_{\mathit{ij}}^H{U}_i{U}_j^H)}},$$

where α_ℂ(d) is defined below.

Definition 2

Let G_ℝ ∈ ℝ^d×d and G_ℂ ∈ ℂ^d×d be, respectively, a Gaussian random matrix with i.i.d real valued entries $\mathcal{N}\left(0,d^{-1}\right)$ and a Gaussian random matrix with i.i.d complex valued entries $\mathcal{N}\left(0,d^{-1}\right)$. We define

$${\alpha }_{ℝ}(d):=\mathrm{𝔼}\left[\frac{1}{d}{\displaystyle \sum _{j=1}^d{\sigma }_j(G_{ℝ})}\right]\mathit{and}{\alpha }_{ℂ}(d):=𝔼\left[\frac{1}{d}{\displaystyle \sum _{j=1}^d{\sigma }_j(G_{ℂ})}\right],$$

where σ_j(G) is the jth singular value of G.

Although we do not have a complete understanding of the behavior of α_ℝ(d) and α_ℂ(d) as functions of d, we can, for each d separately, compute a closed form expression (see Section 4). For d = 1 we recover the sharp ${\alpha }_{ℝ}{\left(1\right)}^2=\frac{2}{\mathrm{\pi }}$ and ${\alpha }_{ℂ}{\left(1\right)}^2=\frac{\mathrm{\pi }}{4}$ results of, respectively, Nesterov [Nes98] and So et al. [SZY07]. One can also show that ${\lim }_{d\to \infty }{\alpha }_{\mathbb{K}}{\left(d\right)}^2={\left(\frac{8}{3\mathrm{\pi }}\right)}^2$, for both $\mathbb{K}=ℝ$ and $\mathbb{K}=ℂ$. Curiously,

$${\alpha }_{ℝ}{\left(1\right)}^2=\frac{2}{\mathrm{\pi }}<{\left(\frac{8}{3\mathrm{\pi }}\right)}^2<\frac{\mathrm{\pi }}{4}={\alpha }_{ℂ}{\left(1\right)}^2.$$

Our computations strongly suggest that α_ℝ(d) is monotonically increasing while its complex analog α_ℂ(d) is monotonically decreasing. We find the fact that the approximation ratio seems to get, as the dimension increases, better in the real case and worse in the complex case quite intriguing. One might naively think that the problem for a specific d can be formulated as a degenerate problem for a larger d, however this does not seem to be true, as evidenced by the fact that ${\alpha }_{ℝ}^2(d)$ is increasing. Another interesting point is that α_ℝ(2) ≠ α_ℂ(1) which suggests that the little Grothendieck problem over ${\mathcal{O}}_2$ is quite different from the analog in ${\mathcal{U}}_1$ (which is isomorphic to $S{\mathcal{O}}_2$). Unfortunately, we were unable to provide a proof for the monotonicity of ${\alpha }_{\mathbb{K}}(d)$ (Conjecture 8). Nevertheless, we can show lower bounds for both ${\alpha }_{ℝ}^2(d)$ and ${\alpha }_{ℂ}^2(d)$ that have the right asymptotics (see Section 4). In particular, we can show that our approximation ratios are uniformly bounded below by the approximation ratio given in [NRV13].

In some applications, such as the Common Lines problem [SS11] (see Section 5), one is interested in a more general version of (3) where the variables take values in the Stiefel manifold ${\mathcal{O}}_{(d,r)}$, the set of matrices O ∈ ℝ^d×r such that OO^T = I_d×d. This motivates considering a generalized version of (3) formulated as, for r ≥ d,

$$\underset{O_1,\dots ,O_n\in {\mathcal{O}}_{(d,r)}}{max}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\text{tr}(C_{\mathit{ij}}^T{O}_i{O}_j^T)}},$$ (8)

for C ⪰ 0. The special case d = 1 was formulated and studied in [BBT11] and [BFV10] in the context of quantum non-locality and quantum XOR games. Note that in the special case r = nd, (8) reduces to (5) and is equivalent to a semidefinite program.

We propose an adaption of Algorithm 3, Algorithm 9, and show an approximation ratio of α_ℝ(d, r)², where α_ℝ(d, r) is also defined as the average singular value of a Gaussian matrix (see Section 5). For d = 1 we recover the sharp results of Briet el al. [BFV10] giving a simple interpretation for the approximation ratios, as α(1, r) is simply the mean of a normalized chi-distribution with r degrees of freedom. As before, the techniques are easily extended to the complex valued case.

In order to understand the optimality of the approximation ratios α_ℝ(d)² and α_ℂ(d)² we provide an integrality gap for the relaxations (5) and (6) that matches these ratios, showing that they are tight. Our construction of an instance having this gap is an adaption of the classical construction for the d = 1 case (see, e.g., [AN04]). As it will become clear later (see Section 6), there is an extra difficulty in the d > 1 orthogonal case which can be dealt with using the Lowner-Heinz Theorem on operator convexity (see Theorem 13 and the notes [Car09]).

Besides the monotonicity of ${\alpha }_{\mathbb{K}}^2(d)$ (Conjecture 8), there are several interesting questions raised from this work, including the hardness of approximation of the problems considered in this paper (see Section 7 for a discussion on these and other directions for future work).

Organization of the paper

The paper is organized as follows. In Section 1.1 below we present the approximation algorithm for (3) and (4). In Section 1.2, we compare our results with the ones in [NRV13]. We then describe a few applications in Section 2 and show the analysis for the approximation ratio guarantee in Section 3. In Section 4 we analyze the value of the approximation ratio constants. Section 5 is devoted to a more general, rank constrained, version of (4). We give an integrality gap for our relaxation in Section 6 and discuss open problems and future work in Section 7. Finally, we present supporting technical results in the Appendix.

1.1 Algorithm

We now present the (randomized) approximation algorithm we propose to solve (3) and (4).

Algorithm 3

Compute X₁, …, X_n ∈ ℝ^d×nd (or Y₁, …, Y_n ∈ ℂ^d×nd) a solution to (5) (or (6)). Let R be a nd × d Gaussian random matrix whose entries are real (or complex) i.i.d. $\mathcal{N}(0,\frac{1}{d})$. The approximate solution for (3) (or (4)) is now computed as

$$V_i=\mathcal{P}(X_{i}R),$$

where $\mathcal{P}(X)=\arg {min}_{Z\in {\mathcal{O}}_d}{\Vert Z-X\Vert }_F(or\mathcal{P}(Y)=\arg {min}_{Z\in {\mathcal{U}}_d}{\Vert Z-Y\Vert }_F)$, for any X ∈ ℝ^d×d (or Y ∈ ℂ^d×d) and ${\Vert X\Vert }_F=\sqrt{\text{tr}(X{X}^T)}({\Vert Y\Vert }_F=\sqrt{\mathrm{tr}(Y{Y}^H)})$ is the Frobenius norm.

Note that (5) and (6) can be solved with arbitrary precision in polynomial time [VB96] as they are equivalent to a semidefinite program (followed by a Cholesky decomposition) with a, respectively real and complex valued, matrix variable of size dn × dn, and d²n linear constraints. In fact, this semidefinite program has a very similar structure to the classical Max-Cut SDP. This may allow one to adapt specific methods designed to solve the Max-Cut SDP such as, for example, the row-by-row method [WGS12] (see Section 2.4 of [Ban15]).

Moreover, given X a d × d matrix (real or complex), the polar component $\mathcal{P}(X)$ is the orthogonal (or unitary) matrix part of the polar decomposition, that can be easily computed via the singular value decomposition of X = UΣV^H as $\mathcal{P}(X)=U{V}^H$ (see [FH55, Kel75, Hig86]), rendering Algorithm 3 efficient. The polar component $\mathcal{P}(X)=U{V}^H$ is the analog in high dimensions of the sign in ${\mathcal{O}}_1$ and the angle in ${\mathcal{U}}_1$ and can also be written as $\mathcal{P}(X)=X{\left(X^{H}X\right)}^{-\frac{1}{2}}$.

1.2 Relation to non-commutative Grothendieck inequality

The approximation algorithm proposed in [NRV13] can also be used to approximate problems (3) and (4). In fact, the method in [NRV13] deals with problems of the form

$$\underset{X,Y\in {\mathcal{O}}_N}{\sup }{\displaystyle \sum _{pqkl}{M}_{pqkl}{X}_{pq}{Y}_{kl}},$$ (9)

where M is a N × N × N × N real valued 4-tensor.

Problem (3) can be encoded in the form of (9) by taking N = dn and having the d × d block of M, obtained by having the first two indices range from (i − 1)d + 1 to id and the last two from (j − 1)d + 1 to jd, equal to C_ij, and the rest of the tensor equal to zero [NRV13]. More explicitly, the nonzero entries of M are given by M_{(i−1)d+r,(i−1)d+r,(j−1)d+s,(j−1)d+s} = [C_ij]_rs, for each i, j and r, s = 1, …, d. Since C is positive semidefinite, the supremum in (9) is attained at a pair (X, Y) such that X = Y.

In order to describe the relaxation one needs to first define the space of vector-valued orthogonal matrices ${\mathcal{O}}_N(m)=\{X\in {ℝ}^{N\times N\times m}:X{X}^T=X^{T}X=I_{N\times N}\}$ where XX^T and X^TX are N × N matrices defined as ${(X{X}^T)}_{pq}={\displaystyle {\sum }_{k=1}^N{\displaystyle {\sum }_{r=1}^m{X}_{pkr}{X}_{qkr}}}$ and ${(X^{T}X)}_{pq}={\displaystyle {\sum }_{k=1}^N{\displaystyle {\sum }_{r=1}^m{X}_{kpr}{X}_{kqr}}}$.

The relaxation proposed in [NRV13] (which is equivalent to our relaxation when M is specified as above) is given by

$$\underset{m\in \mathbb{N}}{\sup }\underset{U,V\in {\mathcal{O}}_N(m)}{\sup }{\displaystyle \sum _{pqkl}{M}_{pqkl}{U}_{pq}{V}_{kl}},$$ (10)

and there exists a rounding procedure [NRV13] that achieves an approximation ratio of $\frac{1}{2\sqrt{2}}$. Analogously, in the unitary case, the relaxation is essentially the same and the approximation ratio is $\frac{1}{2}$. We can show (see Section 4) that the approximation ratios we obtain are larger than these for all d ≥ 1. Interestingly, the approximation ratio of $\frac{1}{2}$, for the complex case in [NRV13], is tight in the full generality of the problem considered in [NRV13], nevertheless α_ℂ(d)² is larger than this for all dimensions d.

Note also that to approximate (3) with this approach one needs to have N = dn in (10). This means that a naïve implementation of this relaxation would result in a semidefinite program with a matrix variable of size d²n² × d²n², while our approach is based on semidefinite programs with matrix variables of size dn × dn. It is however conceivable that when restricted to problems of the type of (3), the SDP relaxation (10) may enjoy certain symmetries or other properties that facilitate its solution.

2 Applications

Problem (3) can describe several problems of interest. As examples, we describe below how it encodes a complementary version of the orthogonal Procrustes problem and the problem of Global Registration over Euclidean Transforms. Later, in Section 5, we briefly discuss yet another problem, the Common Lines problem, that is encoded by a more general rank constrained version of (3).

2.1 Orthogonal Procrustes

Given n point clouds in ℝ^d of k points each, the orthogonal Procrustes problem [Sch66] consists of finding n orthogonal transformations that best simultaneously align the point clouds. If the points are represented as the columns of matrices A₁, …, A_n, where A_i ∈ ℝ^d×k then the orthogonal Procrustes problem consists of solving

$$\underset{O_1,\dots ,O_n\in {\mathcal{O}}_d}{min}{\displaystyle \sum _{i,j=1}^n{\Vert O_i^T{A}_i-O_j^T{A}_j\Vert }_F^2}.$$ (11)

Since ${\Vert O_i^T{A}_i-O_j^T{A}_j\Vert }_F^2={\Vert A_i\Vert }_F^2+{\Vert A_j\Vert }_F^2-2\text{tr}\left({(A_i{A}_j^T)}^T{O}_i{O}_j^T\right)$, (11) has the same solution as the complementary version of the problem

$$\underset{O_1,\dots ,O_n\in {\mathcal{O}}_d}{max}{\displaystyle \sum _{i,j=1}^n\text{tr}({(A_i{A}_j^T)}^T{O}_i{O}_j^T)}.$$ (12)

Since C ∈ ℝ^dn×dn given by $C_{\mathit{ij}}=A_i{A}_j^T$ is positive semidefinite, problem (12) is encoded by (3) and Algorithm 3 provides a solution with an approximation ratio guaranteed (Theorem 1) to be at least α_ℝ(d)².

The algorithm proposed in Naor et al. [NRV13] gives an approximation ratio of $\frac{1}{2\sqrt{2}}$, smaller than α_ℝ(d)², for (12). As discussed above, the approach in [NRV13] is based on a semidefinite relaxation with a matrix variable of size d²n² × d²n² instead of dn × dn as in (5) (see Section 1.2 for more details).

Nemirovski [Nem07] proposed a different semidefinite relaxation (with a matrix variable of size d²n × d²n instead of dn × dn as in (5)) for the orthogonal Procrustes problem. In fact, his algorithm approximates the slightly different problem

$$\underset{O_1,\dots ,O_n\in {\mathcal{O}}_d}{max}{\displaystyle \sum _{i\ne j}\text{tr}\left({\left(A_i{A}_j^T\right)}^T{O}_i{O}_j^T\right)},$$ (13)

which is an additive constant (independent of O₁, …, O_n) smaller than (12). The best known approximation ratio for this semidefinite relaxation, due to So [So11], is $\mathcal{O}\left(\frac{1}{\log (n+k+d)}\right)$. Although an approximation to (13) would technically be stronger than an approximation to (12), the two quantities are essentially the same provided that the point clouds are indeed perturbations of orthogonal transformations of the same original point cloud, as is the case in most applications (see [NRV13] for a more thorough discussion on the differences between formulations (12) and (13)).

Another important instance of this problem is when the transformations are elements of $S{\mathcal{O}}_2$ (the special orthogonal group of dimension 2, corresponding to rotations of the plane). Since $S{\mathcal{O}}_2$ is isomorphic to ${\mathcal{U}}_1$ we can encode it as an instance of problem (4), in this case we recover the previously known optimal approximation ratio of $\frac{\mathrm{\pi }}{4}$ [SZY07].

Note that, since all instances of problem (3) can be written as an instance of orthogonal Procrustes, the integrality gap we show (Theorem 14) guarantees that our approximation ratio is optimal for the natural semidefinite relaxation we consider for the problem.

2.2 Global Registration over Euclidean Transforms

The problem of global registration over Euclidean rigid motions is an extension of orthogonal Procrustes. In global registration, one is required to estimate the positions x₁, …, x_k of k points in ℝ^d and the unknown rigid transforms of n local coordinate systems given (perhaps noisy) measurements of the local coordinates of each point in some (though not necessarily all) of the local coordinate systems. The problem differs from orthogonal Procrustes in two aspects: First, for each local coordinate system, we need to estimate not only an orthogonal transformation but also a translation in ℝ^d. Second, each point may appear in only a subset of the coordinate systems. Despite those differences, it is shown in [CKS15] that global registration can also be reduced to the form (3) with a matrix C that is positive semidefinite.

More precisely, denoting by P_i the subset of points that belong to the i-th local coordinate system (i = 1 … n), and given the local coordinates

$$x_j^{(i)}=O_i^T(x_l-t_i)+{\xi }_{il}$$

of point x_l ∈ P_i (where O_i denotes an unknown orthogonal transformation, t_i an unknown translation and ξ_il a noise term). The goal is to estimate the global coordinates x_l. The idea is to minimize the function

$$\varphi ={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{l\in P_i}{\Vert x_l-\left(O_i{x}_l^{(i)}+t_i\right)\Vert }^2}},$$

over x_l, t_i ∈ ℝ^d, $O_i\in {\mathcal{O}}_d$. It is not difficult to see that the optimal $x_l^{\star }$ and $t_i^{\star }$ can be written in terms of O₁, …, O_n. Substituting them back into ε, the authors in [CKS15] reduce the previous optimization to solving

$$\underset{O_i\in {\mathcal{O}}_d}{max}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\text{tr}\left({\left[B{L}^{†}{B}^T\right]}_{\mathit{ij}}{O}_i{O}_j^T\right)}},$$ (14)

where L is a certain (n + k) × (n + k) Laplacian matrix, L^† is its pseudo inverse, and B is a (dn) × (n + k) matrix (see [CKS15]). This means that BL^†B^T ⪰ 0, and (14) is of the form of (3).

3 Analysis of the approximation algorithm

In this Section we prove Theorem 1. As (5) and (6) are relaxations of, respectively, problem (3) and problem (4) their maximums are necessarily at least as large as the ones of, respectively, (3) and (4). This means that Theorem 1 is a direct consequence of the following theorem.

Theorem 4

Let C ⪰ 0 and real. Let X₁, …, X_n be a feasible solution to (5). Let $V_1,\dots ,V_n\in {\mathcal{O}}_d$ be the output of the (random) rounding procedure described in Algorithm 3. Then

$$\mathrm{𝔼}\left[{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\text{tr}(C_{\mathit{ij}}^T{V}_i{V}_j^T)}}\right]\ge {\alpha }_{ℝ}{(d)}^2{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\text{tr}(C_{\mathit{ij}}^T{X}_i{X}_j^T)}},$$

where α_ℝ(d) is the constant in Definition 2. Analogously, if C ⪰ 0 and complex and Y₁, …, Y_n is a feasible solution of (6) and $W_1,\dots ,W_n\in {\mathcal{U}}_d$ the output of the (random) rounding procedure described in Algorithm 3. Then

$$\mathbb{E}\left[{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\text{tr}(C_{\mathit{ij}}^H{W}_i{W}_j^H)}}\right]\ge {\alpha }_{ℂ}{(d)}^2{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\text{tr}(C_{\mathit{ij}}^T{Y}_i{Y}_j^H)}},$$

where α_ℂ(d) is the constant in Definition 2.

In Section 6 we show that these ratios are optimal (Theorem 14).

Before proving Theorem 4 we present a sketch of the proof for the case d = 1 (and real). The argument is known as the Rietz method (See [AN04])²:

Let X₁, …, X_n ∈ ℝ^1×n be a feasible solution to (5), meaning that $X_i{X}_i^T=1$. Let R ∈ ℝ^n×1 be a random matrix with i.i.d. standard Gaussian entries. Our objective is to compare $\mathbb{E}[{\displaystyle {\sum }_{i,j}^n{C}_{\mathit{ij}}\text{sign}(X_{i}R)\text{sign}(X_{j}R)}]$ with ${\displaystyle {\sum }_{i,j}^n{C}_{\mathit{ij}}{X}_i{X}_j^T}$. The main observation is that although $\mathbb{E}[\text{sign}(X_{i}R)\text{sign}(X_{j}R)]$ is not a linear function of $X_i{X}_j^T$, the expectation $\mathbb{E}[\text{sign}(X_{i}R)X_{j}R]$ is. In fact $\mathbb{E}[\text{sign}(X_{i}R)X_{j}R]={\alpha }_{ℝ}(1)X_i{X}_j^T=\sqrt{\frac{2}{\mathrm{\pi }}}{X}_i{X}_j^T$ — which follows readily by thinking of X_i and X_j as vectors in the two dimensional plane that they span. We use this fact (together with the positiveness of C) to show our result. The idea is to build the matrix S ⪰ 0,

$$S_{\mathit{ij}}=\left(X_{i}R-\sqrt{\frac{\mathrm{\pi }}{2}}\text{sign}(X_{i}R)\right)\left(X_{j}R-\sqrt{\frac{\mathrm{\pi }}{2}}\text{sign}(X_{j}R)\right).$$

Since both C and S are PSD, tr(CS) ≥ 0, which means that

$$0\le \mathbb{E}\left[{\displaystyle \sum _{\mathit{ij}}{C}_{\mathit{ij}}(X_{i}R-\sqrt{\frac{\mathrm{\pi }}{2}}\text{sign}(X_{i}R))(X_{j}R-\sqrt{\frac{\mathrm{\pi }}{2}}\text{sign}(X_{j}R))}\right].$$

Combining this with the observation above and the fact that $\mathbb{E}[X_{i}R{X}_{j}R]=X_i{X}_j^T$, we have

$$\mathbb{E}{\displaystyle \sum _{i,j}^n{C}_{\mathit{ij}}\text{sign}(X_{i}R)\text{sign}(X_{j}R)\ge \frac{2}{\mathrm{\pi }}{\displaystyle \sum _{i,j}^n{C}_{\mathit{ij}}{X}_i{X}_j^T}}.$$

Proof

[of Theorem 4] For the sake of brevity we restrict the presentation of the proof to the real case. Nevertheless, it is easy to see that all the arguments trivially adapt to the complex case by, essentially, replacing all transposes with Hermitian adjoints and α_ℝ(d) with α_ℂ(d).

Let R ∈ ℝ^nd×d be a Gaussian random matrix with i.i.d entries $\mathcal{N}(0,\frac{1}{d})$. We want to provide a lower bound for

$$\mathbb{E}\left[{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\text{tr}(C_{\mathit{ij}}^T{V}_i{V}_j^T)}}\right]=\mathbb{E}\left[{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\text{tr}(C_{\mathit{ij}}^T\mathcal{P}(U_{i}R)\mathcal{P}{(U_{j}R)}^T)}}\right].$$

Similarly to the d = 1 case, one of the main ingredients of the proof is the fact given by the lemma below.

Lemma 5

Let r ≥ d. Let M, N ∈ ℝ^d×nd such that MM^T = NN^T = I_d×d. Let R ∈ ℝ^nd×d be a Gaussian random matrix with real valued i.i.d entries $\mathcal{N}(0,\frac{1}{d})$. Then

$$\mathbb{E}[\mathcal{P}\left(MR\right){\left(NR\right)}^T]=\mathbb{E}[\left(MR\right)\mathcal{P}{\left(NR\right)}^T]={\alpha }_{ℝ}(d)M{N}^T,$$

where α_ℝ(d) is constant in Definition 2.

Analogously, if M, N ∈ ℂ^d×nd such that MM^H = NN^H = I_d×d, and R ∈ ℂ^nd×r is a Gaussian random matrix with complex valued i.i.d entries $\mathcal{N}(0,\frac{1}{d})$, then

$$\mathbb{E}[\mathcal{P}\left(MR\right){\left(NR\right)}^H]=\mathbb{E}[\left(MR\right)\mathcal{P}{\left(NR\right)}^H]={\alpha }_{ℂ}(d)M{N}^H,$$

where α_ℂ(d) is constant in Definition 2.

Before proving Lemma 5 we use it to finish the proof of Theorem 4.

Just as above, we define the positive semidefinite matrix S ∈ ℝ^dn×dn whose (i, j)-th block is given by

$$S_{\mathit{ij}}=(U_{i}R-{\alpha }_{ℝ}{(d)}^{-1}\mathcal{P}(U_{i}R)){(U_{j}R-{\alpha }_{ℝ}{(d)}^{-1}\mathcal{P}(U_{j}R))}^T$$

We have $\mathbb{E}{S}_{\mathit{ij}}$ =

$$\begin{array}{l}=\mathbb{E}[U_{i}R{(U_{j}R)}^T-{\alpha }_{ℝ}{(d)}^{-1}\mathcal{P}(U_{i}R){(U_{j}R)}^T-{\alpha }_{ℝ}{(d)}^{-1}{U}_{i}R\mathcal{P}{(U_{j}R)}^T+{\alpha }_{ℝ}{(d)}^{-2}\mathcal{P}(U_{i}R)\mathcal{P}{(U_{j}R)}^T]\\ =U_i\mathbb{E}[R{R}^T]U_j^T-{\alpha }_{ℝ}{(d)}^{-1}\mathbb{E}[\mathcal{P}(U_{i}R){(U_{j}R)}^T]-{\alpha }_{ℝ}{(d)}^{-1}\mathbb{E}[U_{i}R\mathcal{P}{(U_{j}R)}^T]+{\alpha }_{ℝ}{(d)}^{-2}\mathbb{E}[V_i{V}_j^T]\\ =U_i{U}_j^T-U_i{U}_j^T-U_i{U}_j^T+{\alpha }_{ℝ}{(d)}^{-2}\mathbb{E}[V_i{V}_j^T]\\ ={\alpha }_{ℝ}{(d)}^{-2}\mathbb{E}[V_i{V}_j^T]-U_i{U}_j^T.\end{array}$$

By construction S ⪰ 0. Since C ⪰ 0, tr(CS) ≥ 0, which means that

$$0\le \mathbb{E}[\text{tr}(CS)]=\text{tr}(C\mathbb{E}[S])={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\text{tr}(C_{\mathit{ij}}^T({\alpha }_{ℝ}{(d)}^{-2}\mathbb{E}[V_i{V}_j^T]-U_i{U}_j^T))}}.$$

Thus,

$$\mathbb{E}\left[{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\text{tr}(C_{\mathit{ij}}^T{V}_i{V}_j^T)}}\right]\ge {\alpha }_{ℝ}{(d)}^2{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\text{tr}(C_{\mathit{ij}}^T{U}_i{U}_j^T)}}.$$

      □

We now present and prove an auxiliary lemma, needed for the proof of Lemma 5.

Lemma 6

Let G be a d × d Gaussian random matrix with real valued i.i.d. $\mathcal{N}(0,\frac{1}{d})$ entries and let α_ℝ(d) as defined in Definition 2. Then,

$$\mathbb{E}(\mathcal{P}(G)G^T)=\mathbb{E}(G\mathcal{P}{(G)}^T)={\alpha }_{ℝ}(d)I_{d\times d}.$$

Furthermore, if G is a d × d Gaussian random matrix with complex valued i.i.d. $\mathcal{N}(0,\frac{1}{d})$ entries and α_ℂ(d) the analogous constant (Definition 2), then

$$\mathbb{E}(\mathcal{P}(G)G^H)=\mathbb{E}(G\mathcal{P}{(G)}^H)={\alpha }_{ℂ}(d)I_{d\times d}.$$

Proof

We restrict the presentation to the real case. All the arguments are equivalent to the complex case, replacing all transposes with Hermitian adjoints and α_ℝ(d) with α_ℂ(d).

Let G = UΣV^T be the singular value decomposition of G. Since GG^T = UΣ²U^T is a Wishart matrix, it is well known that its eigenvalues and eigenvectors are independent and U is distributed according to the Haar measure in ${\mathcal{O}}_d$ (see e.g. Lemma 2.6 in [TV04]). To resolve ambiguities, we consider Σ ordered such that Σ₁₁ ≥ Σ₂₂ ≥ … ≥ Σ_dd.

Let $Y=\mathcal{P}(G)G^T$. Since

$$\mathcal{P}(G)=\mathcal{P}(U\sum V^T)=U{I}_{d\times d}{V}^T,$$

we have

$$Y=\mathcal{P}\left(U\sum V^T\right){\left(U\sum V^T\right)}^T=U{I}_{d\times d}{V}^{T}V\sum U^T=U\sum U^T.$$

Note that $G\mathcal{P}{\left(G\right)}^T=U\sum U^T=Y$.

Denoting u₁, …, u_d the rows of U, since U is distributed according to the Haar measure, we have that u_j and −u_j have the same distribution conditioned on Σ and u_i, for any i ≠ j. This implies that if i ≠ j, $Y_{\mathit{ij}}=u_i\sum u_j^T$ is a symmetric random variable, and so $\mathbb{E}{Y}_{\mathit{ij}}=0$. Also, u_i ~ u_j implies that Y_ii ~ Y_jj. This means that $\mathbb{E}Y=c{I}_{d\times d}$ for some constant c. To obtain c,

$$c=c\frac{1}{d}\text{tr}\left(I_{d\times d}\right)=\frac{1}{d}\mathbb{E}\text{tr}(Y)=\frac{1}{d}\mathbb{E}\text{tr}(U\sum U^T)=\frac{1}{d}\mathbb{E}{\displaystyle \sum _{k=1}^n{\sigma }_k(G)={\alpha }_{ℝ}(d)},$$

which shows the lemma.

Proof

[of Lemma 5] We restrict the presentation of proof to the real case. Nevertheless, as before, all the arguments trivially adapt to the complex case by, essentially, replacing all transposes with Hermitian adjoints and α_ℝ(d) with α_ℂ(d).

Let A = [M^T N^T] ∈ ℝ^dn×2d and A = QB be the QR decomposition of A with Q ∈ ℝ^nd×nd an orthogonal matrix and B ∈ ℝ^nd×2d upper triangular with non-negative diagonal entries; note that only the first 2d rows of B are nonzero. We can write

$$Q^{T}A=B=\left[\begin{array}{cc}{B}_{11}& B_{12}\\ 0_d& B_{22}\\ 0_d& 0_d\\ ⋮& ⋮\\ 0_d& 0_d\end{array}\right]\in {ℝ}^{dn\times 2d},$$

where B₁₁ ∈ ℝ^d×d and B₂₂ ∈ ℝ^d×d are upper triangular matrices with non-negative diagonal entries. Since

${(Q^T{M}^T)}_{11}^T{(Q^T{M}^T)}_{11}={(Q^T{M}^T)}^T(Q^T{M}^T)=MQ{Q}^T{M}^T=M{I}_{nd\times nd}{M}^T=M{M}^T=I_{d\times d},$

B₁₁ = (Q^TM^T)₁₁ is an orthogonal matrix, which together with the non-negativity of the diagonal entries (and the fact that B₁₁ is upper-triangular) forces B₁₁ to be B₁₁ = I_d×d.

Since R is a Gaussian matrix and Q is an orthogonal matrix, QR ~ R which implies

$$\mathbb{E}[\mathcal{P}(\mathit{MR}){(\mathit{NR})}^T]=\mathbb{E}[\mathcal{P}(\mathit{MQR}){(\mathit{NQR})}^T].$$

Since $MQ=[B_{11}^T,0_{d\times d},\cdots ,0_{d\times d}]=[I_{d\times d},0_{d\times d},\cdots ,0_{d\times d}]$ and $NQ=[B_{12}^T,B_{22}^T,0_{d\times d},\cdots ,0_{d\times d}]$,

$$\mathbb{E}[\mathcal{P}(MR){(NR)}^T]=\mathbb{E}[\mathcal{P}(R_1){(B_{12}^T{R}_1+B_{22}^T{R}_2)}^T],$$

where R₁ and R₂ are the first two d × d blocks of R. Since these blocks are independent, the second term vanishes and we have

$\mathbb{E}[\mathcal{P}(MR){(NR)}^T]=\mathbb{E}[\mathcal{P}(R_1)R_1^T]B_{12}.$

The Lemma now follows from using Lemma 6 to obtain $\mathbb{E}[\mathcal{P}(R_1)R_1^T]={\alpha }_{ℝ}(d)I_{d\times d}$ and noting that B₁₂ = (Q^TM^T) (Q^TN^T) = MN^T.

The same argument, with Q’B’ the QR decomposition of A’ = [N^TM^T] ∈ ℝ^dn×2d instead, shows

$$\mathbb{E}[(MR)\mathcal{P}{(NR)}^T]=\mathbb{E}[R_1\mathcal{P}{(R_1)}^T]M{N}^T={\alpha }_{ℝ}(d)M{N}^T.$$

       □

4 The approximation ratios α_ℝ(d)² and α_ℂ(d)²

The approximation ratio we obtain (Theorem 1) for Algorithm 3 is given, in the orthogonal case, by α_ℝ(d)² and, in the unitary case, by α_ℂ(d)². α_ℝ(d) and α_ℂ(d) are defined as the average singular value of a d × d Gaussian matrix G with, respectively real and complex valued, i.i.d $\mathcal{N}(0,\frac{1}{d})$ entries. These singular values correspond to the square root of the eigenvalues of a Wishart matrix W = GG^T, which are well-studied objects (see, e.g., [She01] or [CD11]).

For d = 1, this corresponds to the expected value of the absolute value of standard Gaussian (real or complex) random variable. Hence,

$${\alpha }_{ℝ}(1)=\sqrt{\frac{2}{\mathrm{\pi }}}\text{and}{\alpha }_{ℂ}(1)=\sqrt{\frac{\mathrm{\pi }}{4}},$$

meaning that, for d = 1, we recover the approximation ratio of $\frac{2}{\mathrm{\pi }}$, of Nesterov [Nes98] for the real case, and the approximation ratio of $\frac{\mathrm{\pi }}{4}$ of So et al. [SZY07] in the complex case.

For any d ≥ 1, the marginal distribution of an eigenvalue of the Wishart matrix W = GG^T is known [LV11, CD11, Lev12] (see Section B). Denoting by $p_d^{(\mathbb{K})}$ the marginal distribution for $\mathbb{K}=ℝ$ and $\mathbb{K}=ℂ$, we have

$${\alpha }_{\mathbb{K}}(d)=\frac{1}{d^{1/2}}{\displaystyle {\int }_0^{\infty }{x}^{1/2}}{p}_d^{(\mathbb{K})}(x)dx.$$ (15)

In the complex valued case, $p_d^{(ℂ)}(x)$ can be written in terms of Laguerre polynomials [CD11, Lev12] and α_ℂ(d) is given by

$${\alpha }_{ℂ}(d)=d^{-3/2}{\displaystyle \sum _{n=0}^{d-1}{\displaystyle {\int }_0^{\infty }{x}^{1/2}}{e}^{-x}{L}_n{\left(x\right)}^{2}dx},$$ (16)

Where L_n(x) is the nth Laguerre polynomial. In Section B we give a lower bound to (16). The real case is more involved [LV11], nevertheless we are able to provide a lower bound for α_ℝ(d) as well.

Theorem 7

Consider α_ℝ(d) and α_ℂ(d) as defined in (2). The following holds,

$${\alpha }_{ℂ}(d)\ge \frac{8}{3\mathrm{\pi }}-\frac{5.05}{d}\mathrm{and}{\alpha }_{ℝ}(d)\ge \frac{8}{3\mathrm{\pi }}-\frac{9.07}{d}.$$

Proof

These bounds are a direct consequence of Lemmas 20 and 21.

One can easily evaluate ${\lim }_{d\to \infty }{\alpha }_{\mathbb{K}}(d)$ (without using Theorem 7) by noting that the distribution of the eigenvalues of the Wishart matrix we are interested in, as d → ∞, converges in probability to the Marchenko-Pastur distribution [She01] with density

$$\text{mp}(x)=\frac{1}{2\mathrm{\pi }x}\sqrt{x(4-x)}{1}_{[0,4]},$$

for both $\mathbb{K}=ℝ$ and $\mathbb{K}=ℂ$. This immediately gives,

$$\underset{d\to \infty }{\lim }{\alpha }_{\mathbb{K}}(d)={\displaystyle {\int }_0^4\sqrt{x}\frac{1}{2\mathrm{\pi }x}\sqrt{x(4-x)}dx=\frac{8}{3\mathrm{\pi }}}.$$

We note that one could also obtain lower bounds for ${\alpha }_{\mathbb{K}}^2(d)$ from results on the rate of convergence to mp(x) [GT11]. However this approach seems to not provide bounds with explicit constants and to not be as sharp as the approach taken in Theorem 7.

For any d, the exact value of ${\alpha }_{\mathbb{K}}(d)$ can be computed, by (15), using Mathematica (See table below). Figure 1 plots these values for d = 1, …, 44. We also plot the bounds for the real and complex case obtained in Theorem 7, and the approximation ratios obtained in [NRV13], for comparison.

Figure 1.

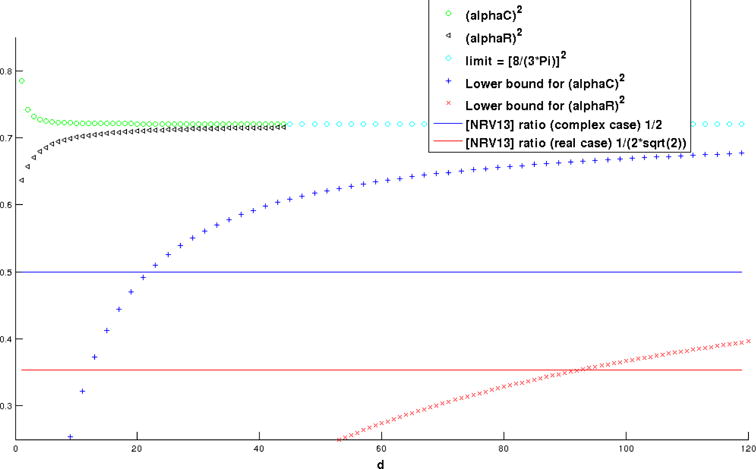
Plot showing the computed values of ${\alpha }_{\mathbb{K}}{\left(d\right)}^2$, for d ≤ 44, the limit of ${\alpha }_{\mathbb{K}}{\left(d\right)}^2$ as d → ∞, the lower bound for ${\alpha }_{\mathbb{K}}{\left(d\right)}^2$ given by Theorem 7 as function of d, and the approximation ratio of $\frac{1}{2\sqrt{2}}$ and $\frac{1}{2}$ obtained in [NRV13].

d	αℝ(d)	αℂ(d)	αℝ(d) ≈	αℝ(d)2 ≈	αℂ(d) ≈	αℂ(d)2 ≈
1	$\sqrt{\frac{2}{\mathrm{\pi }}}$	$\frac{\sqrt{\mathrm{\pi }}}{2}$	0.7979	0.6366	0.8862	0.7854
2	$\frac{2\sqrt{2}-1}{4}\sqrt{\mathrm{\pi }}$	$\frac{11\sqrt{\frac{\mathrm{\pi }}{2}}}{16}$	0.8102	0.6564	0.8617	0.7424
3	$\frac{2\sqrt{2}+3\mathrm{\pi }}{6\sqrt{3\mathrm{\pi }}}$	$\frac{107\sqrt{\frac{\mathrm{\pi }}{3}}}{128}$	0.8188	0.6704	0.8554	0.7312
∞	$\frac{8}{3\mathrm{\pi }}$	$\frac{8}{3\mathrm{\pi }}$	0.8488	0.7205	0.8488	0.7205

The following conjecture is suggested by our analysis and numerical computations.

Conjecture 8

Let α_ℝ(d) and α_ℂ(d) be the average singular value of a d × d matrix with random i.i.d., respectively real valued and complex valued, $\mathcal{N}(0,\frac{1}{d})$ entries (see Definition 2). Then, for all d ≥ 1,

$${\alpha }_{ℂ}(d+1)\le {\alpha }_{ℂ}(d)\mathrm{and}{\alpha }_{ℝ}(d+1)\ge {\alpha }_{ℝ}(d),$$

5 The little Grothendieck problem over the Stiefel manifold

In this section we focus on a generalization of (3), the little Grothendieck problem over the Stiefel manifold ${\mathcal{O}}_{(d,r)}$, the set of matrices O ∈ ℝ^d×r such that OO^T = I_d×d. In this exposition we will restrict ourselves to the real valued case but it is easy to see that the ideas in this Section easily adapt to the complex valued case.

We consider the problem

$$\underset{O_1,\dots ,O_n\in {\mathcal{O}}_{(d,r)}}{max}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\text{tr}(C_{\mathit{ij}}^T{O}_i{O}_j^T)}},$$ (17)

for C ⪰ 0. The special case d = 1 was formulated and studied in [BBT11] and [BFV10] in the context of quantum non-locality and quantum XOR games.

Note that, for r = d, problem (17) reduces to (3) and, for r = nd, it reduces to the tractable relaxation (5). As a solution to (3) can be transformed, via zero padding, into a solution to (17) with the same objective function value, Algorithm 3 automatically provides an approximation ratio for (17), however we want to understand how this approximation ratio can be improved using the extra freedom (in particular, in the case r = nd, the approximation ratio is trivially 1). Below we show an adaptation of Algorithm 3, based on the same relaxation (5), for problem (17) and show an improved approximation ratio.

Algorithm 9

Compute X₁, …, X_n ∈ ℝ^d×nd a solution to (5). Let R be and × r Gaussian random matrix whose entries are real i.i.d. $\mathcal{N}(0,\frac{1}{r})$. The approximate solution for (17) is now computed as

$$V_i={\mathcal{P}}_{(d,r)}(X_{i}R),$$

where ${\mathcal{P}}_{(d,r)}(X)=\arg {min}_{Z\in {\mathcal{O}}_{(d,r)}}{\Vert Z-X\Vert }_F$, for any X ∈ ℝ^d×r, is a generalization of the polar component to the Stiefel manifold ${\mathcal{O}}_{(d,r)}$.

Below we show an approximation ratio for Algorithm 9.

Theorem 10

Let C ⪰ 0. Let $V_1,\dots ,V_n\in {\mathcal{O}}_{(d,r)}$ be the (random) output of Algorithm 9. Then,

$$\mathbb{E}\left[{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\text{tr}(C_{\mathit{ij}}^T{V}_i{V}_j^T)}}\right]\ge {\alpha }_{ℝ}{(d,r)}^2\underset{O_1,\dots ,O_n\in {\mathcal{O}}_{(d,r)}}{max}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\text{tr}(C_{\mathit{ij}}^T{O}_i{O}_j^T)}},$$

where α_ℝ(d, r) is the defined below (Definition 11).

Definition 11

Let r ≥ d and G ∈ ℝ^d×r be a Gaussian random matrix with i.i.d real entri $\mathcal{N}\left(0,\frac{1}{r}\right)$. We define

$${\alpha }_{ℝ}(d,r):=\mathbb{E}\left[\frac{1}{d}{\displaystyle \sum _{j=1}^d{\sigma }_j(G)}\right],$$

where σ_j(G) is the jth singular value of G.

We investigate the limiting behavior of α_ℝ(d, r) as r → ∞ and as r, d → ∞ at a proporitional rate in Section 6.2.

The proof of Theorem 10 follows the same line of reasoning as that of Theorem 1 (and Theorem 4). We do not provide the proof in full, but state and prove Lemmas 17 and 18 in the Appendix, which are the analogous, to this setting, of Lemmas 6 and 5.

Besides the applications, for d = 1, described in [BBT11] and [BFV10], Problem (17) is also motivated by an application in molecule imaging, the common lines problem.

5.1 The common lines problem

The common lines problem arises in three-dimensional structure determination of biological molecules using Cryo-Electron Microscopy [SS11], and can be formulated as follows. Consider n rotation matrices $O_1,\dots ,O_n\in S{\mathcal{O}}_3$. The three columns of each rotation matrix form a orthonormal basis to ℝ³. In particular, the first two columns of each rotation matrix span a two-dimensional subspace (a plane) in ℝ³. We assume that no two planes are parallel. Every pair of planes intersect at a line, called the common-line of intersection. Let b_ij ∈ ℝ³ be a unit vector that points in the direction of the common-line between the planes corresponding to O_i and O_j. Hence, there exist unit vectors c_ij and c_ji with vanishing third component (i.e., c_ij = (x_ij, y_ij, 0)^T) such that O_ic_ij = O_jc_ji = b_ij. The common lines problem consists of estimating the rotation matrices O₁, …, O_n from (perhaps noisy) measurements of the unit vectors c_ij and c_ji. The least-squares formulation of this problem is equivalent to

$$\underset{O_1,\dots ,O_n\in S{\mathcal{O}}_3}{max}{\displaystyle \sum _{i,j=1}^n\text{tr}(c_{\mathit{ji}}{c}_{\mathit{ij}}^T{O}_i^T{O}_j)}$$ (18)

However, since c_ij has zero in the third coordinate, the common-line equations O_ic_ij = O_jc_ji do not involve the third columns of the rotation matrices. The optimization problem (18) is therefore equivalent to

$$\underset{{\stackrel{\sim }{O}}_1^T,\dots ,{\stackrel{\sim }{O}}_n^T\in {\mathcal{O}}_{(2,3)}}{max}{\displaystyle \sum _{i,j=1}^n\text{tr}(\mathrm{\Pi }(c_{\mathit{ji}})\mathrm{\Pi }{(c_{\mathit{ij}})}^T{\stackrel{\sim }{O}}_i^T{\stackrel{\sim }{O}}_j)},$$ (19)

where Π: ℝ³ → ℝ² is a projection discarding the third component (i.e., Π(x, y, z) = (x, y)) and ${\stackrel{\sim }{O}}_i^T\in {\mathcal{O}}_{(2,3)}$. The coefficient matrix in (19), C_ij = Π(c_ij)Π(c_ji)^T, is not positive semidefinite. However, one can add a diagonal matrix with large enough values to it in order to make it PSD. Although this does not affect the solution of (19) it does increase its function value by a constant, meaning that the approximation ratio obtained in Theorem 10 does not directly translate into an approximation ratio for Problem (19); see Section 7 for a discussion on extending the results to the non positive semidefinite case.

5.2 The approximation ratio α_ℝ(d, r)²

In this Section we attempt to understand the behavior of α_ℝ(d, r)², the approximation ratio obtained for Algorithm 9. Recall that α_ℝ(d, r) is defined as the average singular value of G ∈ ℝ^d×r, a Gaussian random matrix with i.i.d. entries $\mathcal{N}\left(0,\frac{1}{r}\right)$.

For d = 1 this simply corresponds to the average length of a Gaussian vector in ℝ^r with i.i.d. entries $\mathcal{N}\left(0,\frac{1}{r}\right)$. This means that α_ℝ(1, r) is the mean of a normalized chi-distribution,

$${\alpha }_{ℝ}\left(1,r\right)=\sqrt{\frac{2}{r}}\frac{\mathrm{\Gamma }\left(\frac{r+1}{2}\right)}{\mathrm{\Gamma }\left(\frac{r}{2}\right)}.$$

In fact, this corresponds to the results of Briet el al [BFV10], which are known to be sharp [BFV10].

For d > 1 we do not completely understand the behavior of α_ℝ(d, r), nevertheless it is easy to provide a lower bound for it by a function approaching 1 as r → ∞.

Proposition 12

Consider α_ℝ(d, r) as in Definition 11. Then,

$${\alpha }_{ℝ}\left(d,r\right)\ge 1-\sqrt{\frac{d}{r}}.$$ (20)

Proof

Gordon’s theorem for Gaussian matrices (see Theorem 5.32 in [Ver12]) gives us

$$\mathbb{E}{s}_{min}\left(G\right)\ge 1-\sqrt{\frac{d}{r}},$$

where s_min(G) is the smallest singular value. The bound follows immediately from noting that the average singular value is larger than the expected value of the smallest singular value.

As we are bounding α_ℝ(d, r) by the expected value of the smallest singular value of a Gaussian matrix, we do not expect (20) to be tight. In fact, for d = 1, the stronger ${\alpha }_{ℝ}(1,r)\ge 1-\mathcal{O}\left(\frac{1}{r}\right)$ bound holds [BFV10].

Similarly to α_ℝ(d), we can describe the behavior of α_ℝ(d, r) in the limit as d → ∞ and $\frac{r}{d}\to \rho$. More precisely, the singular values of G correspond to the square root of the eigenvalues of the Wishart matrix [CD11] $G{G}^T~W_d\left(\frac{1}{r},r\right)$. Let us set r = ρd, for ρ ≥ 1. The distribution of the eigenvalues of a Wishart matrix $W_d\left(\frac{1}{\rho d},d\right)$, as d → ∞ are known to converge to the Marchenko Pastur distribution (see [CD11]) given by

$$d\nu (x)=\frac{1}{2\mathrm{\pi }}\frac{\sqrt{({(1+\sqrt{\lambda })}^2-x)(x-{(1-\sqrt{\lambda })}^2)}}{\lambda x}{1}_{[{(1-\sqrt{\lambda })}^2,{(1+\sqrt{\lambda })}^2]}dx,$$

where $\mathrm{\lambda }=\frac{1}{\rho }$.

Hence, we can define ε(ρ) as

$$\varphi (\rho ):=\underset{d\to \infty }{\lim }{\alpha }_{ℝ}(d,\rho d)={\displaystyle {\int }_{{\left(1-\sqrt{\frac{1}{\rho }}\right)}^2}^{{\left(1+\sqrt{\frac{1}{\rho }}\right)}^2}\sqrt{x}\frac{1}{2\pi }\frac{\sqrt{({\left(1+\sqrt{\frac{1}{\rho }}\right)}^2-x)(x-{\left(1-\sqrt{\frac{1}{\rho }}\right)}^2)}}{\frac{1}{\rho }x}}dx.$$

Although we do not provide a closed form solution for ε(ρ) the integral can be easily computed numerically and we plot it below. It shows how the approximation ratio improves as ρ increases.

6 Integrality Gap

In this section we provide an integrality gap for relaxation (5) that matches our approximation ratio α_ℝ(d)². For the sake of the exposition we will restrict ourselves to the real case, but it is not difficult to see that all the arguments can be adapted to the complex case.

Our construction is an adaption of the classical construction for the d = 1 case (see, e.g., [AN04]). As it will become clear below, there is an extra difficulty in the d > 1 orthogonal case. In fact, the bound on the integrality gap of (5) given by this construction is ${\alpha }_{ℝ}^{\ast }{\left(d\right)}^2$, defined as

$${\alpha }_{ℝ}^{\ast }(d)=\underset{\underset{{\Vert D\Vert }_F^2=d,D\underset{\_}{\succ }0}{D\text{diagonal}}}{max}\mathbb{E}\frac{1}{d}{\displaystyle \sum _{i=1}^d{\sigma }_i(GD)},$$ (21)

where G is a Gaussian matrix with i.i.d. real entries $\mathcal{N}\left(0,\frac{1}{d}\right)$.

Fortunately, using the notion of operator concavity of a function and the Lowner-Heinz Theorem [Car09], we are able to show the following theorem.

Theorem 13

Let d ≥ 1. Also, let α_ℝ(d) be as defined in Definition 2 and ${\alpha }_{ℝ}^{\ast }\left(d\right)$ as defined in (21). Then,

$${\alpha }_{ℝ}^{\ast }(d)={\alpha }_{ℝ}(d).$$

Proof

We want to show that

$$\underset{\underset{\underset{D\underset{\_}{\succ }0}{{\Vert D\Vert }_F^2=d}}{D\text{diagonal}}}{max}\mathbb{E}{\displaystyle \sum _{i=1}{\sigma }_i(GD)=\mathbb{E}{\displaystyle \sum _{i=1}{\sigma }_i(G)}},$$

where G is a d × d matrix with i.i.d. entries $\mathcal{N}\left(0,\frac{1}{d}\right)$. By taking V = D², and recalling the definition of singular value, we obtain the following claim (which immediately implies Theorem 13)

Claim 6.1

$$\underset{\underset{\underset{V\underset{\_}{\succ }0}{\text{tr}(V)=d}}{V\mathit{diagonal}}}{max}\mathbb{E}\text{ tr}\left[{(GV{G}^T)}^{\frac{1}{2}}\right]=\mathbb{E}\text{ tr}\left[{(G{G}^T)}^{\frac{1}{2}}\right].$$

Proof

We will proceed by contradiction, suppose (6.1) does not hold. Since the optimization space is compact and the function continuous it must have a maximum that is attained by a certain V ≠ I_d×d. Out of all maximizers V, let V^(*) be the one with smallest possible Frobenius norm. The idea will be to use concavity arguments to build an optimal V^(card) with smaller Frobenius norm, arriving at a contradiction and hence showing the theorem.

Since V^(*) is optimal we have

$$\mathbb{E}\text{ tr}\left[{\left(G{V}^{(\ast )}{G}^T\right)}^{\frac{1}{2}}\right]={\alpha }_{ℝ}^{\ast }(d).$$

Furthermore, since V^(*) ≠ I_d×d, it must have two different diagonal elements. Let V^(**) be a matrix obtained by swapping, in V^(*), two of its non-equal diagonal elements. Clearly, ‖V^(**)‖_F = ‖V^(*)‖_F and, because of the rotation invariance of the Gaussian, it is easy to see that

$$\mathbb{E}\text{ tr}\left[{\left(G{V}^{(\ast \ast )}{G}^T\right)}^{\frac{1}{2}}\right]={\alpha }_{ℝ}^{\ast }(d).$$

Since V^(*) ⪰ 0, these two matrices are not multiples of each other and so

$$V^{(\text{card})}=\frac{V^{(\ast )}+V^{(\ast \ast )}}{2},$$

has a strictly smaller Frobenius norm than V^(*). It is also clear that V^(card) is a feasible solution. We conclude the proof by showing

$$\mathbb{E}\text{ tr}\left[{\left(G{V}^{(\text{card})}{G}^T\right)}^{\frac{1}{2}}\right]\ge \frac{1}{2}\left(\mathbb{E}\text{ tr}\left[{\left(G{V}^{(\ast )}{G}^T\right)}^{\frac{1}{2}}\right]+\mathbb{E}\text{ tr}\left[{\left(G{V}^{(\ast \ast )}{G}^T\right)}^{\frac{1}{2}}\right]\right)={\alpha }_{ℝ}^{\ast }(d).$$ (22)

By linearity of expectation and construction of V^(card), (22) is equivalent to

$$\mathbb{E}\left[\text{tr}\right[{\left(\frac{G{V}^{(\ast )}{G}^T+G{V}^{(\ast \ast )}{G}^T}{2}\right)}^{\frac{1}{2}}]-\frac{1}{2}\left(\text{tr}\right[{\left(G{V}^{(\ast )}{G}^T\right)}^{\frac{1}{2}}]+\text{tr}\left[{\left(G{V}^{(\ast \ast )}{G}^T\right)}^{\frac{1}{2}}\right]\left)\right]\ge 0.$$

This inequality follows from the stronger statement: Given two d × d matrices A ⪰ 0 and B ⪰ 0, the following holds

$${\left(\frac{A+B}{2}\right)}^{\frac{1}{2}}-\frac{A^{\frac{1}{2}}+B^{\frac{1}{2}}}{2}\underset{\_}{\succ }0.$$ (23)

Finally, (23) follows from the Lowner-Heinz Theorem, which states that the square root function is operator concave (See these lecture notes [Car09] for a very nice introduction to these inequalities).

Theorem 13 guarantees the optimality of the approximation ratio obtained in Section 3. In fact, we show the theorem below.

Theorem 14

For any d ≥ 1 and any ɛ > 0, there exists n for which there exists C ∈ ℝ^dn×dn such that C ⪰ 0, and

$$\frac{\underset{O_1,\dots ,O_n\in {\mathcal{O}}_d}{max}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\text{tr}(C_{\mathit{ij}}^T{O}_i{O}_j^T)}}}{\underset{\underset{X_i\in {ℝ}^{d\times dn}}{X_i{X}_i^T=I_{d\times d}}}{max}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\text{tr}(C_{\mathit{ij}}^T{X}_i{X}_j^T)}}}\le {\alpha }_{ℝ}{(d)}^2+\epsilon .$$ (24)

We will construct C randomly and show that it satisfies (24) with positive probability. Given p an integer we consider n i.i.d. matrix random variables V_k, with k = 1, …, n, where each V_k is a d × dp Gaussian matrix whose entries are $\mathcal{N}\left(0,\frac{1}{dp}\right)$. We then define C as the random matrix with d × d blocks $C_{\mathit{ij}}=\frac{1}{n^2}{V}_i{V}_j^T$. The idea now is to understand the typical behavior of both

$$w_r=\underset{\underset{X_i\in {ℝ}^{d\times dn}}{X_i{X}_i^T=I_{d\times d}}}{max}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\text{tr}(C_{\mathit{ij}}^T{X}_i{X}_j^T)}}\text{ and }{w}_c=\underset{O_1,\dots ,O_n\in {\mathcal{O}}_d}{max}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\text{tr}(C_{\mathit{ij}}^T{O}_i{O}_j^T)}}.$$

For w_c, we can rewrite

$$w_c=\underset{O_1,\dots ,O_n\in {\mathcal{O}}_d}{max}\frac{1}{n^2}{\displaystyle \sum _{i,j}\text{tr}({(V_i{V}_j^T)}^T{O}_i{O}_j^T)}=\underset{O_1,\dots ,O_n\in {\mathcal{O}}_d}{max}{\Vert \frac{1}{n}{\displaystyle \sum _{i=1}^n{O}_i^T{V}_i}\Vert }_F^2.$$

If

$$\mathcal{D}=\frac{\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{O}_i^T}{V}_i}{{\Vert \frac{1}{n}{\displaystyle {\sum }_{i=1}^n{O}_i^T{V}_i}\Vert }_F}$$

then $\sqrt{w_c}={\displaystyle {\sum }_{i=1}^n\text{tr}({max}_{O_i\in {\mathcal{O}}_d}{O}_i^T{V}_i{\mathcal{D}}^T)}={\displaystyle {\sum }_{i=1}^n\text{tr}(\mathcal{P}{(V_i{\mathcal{D}}^T)}^T{V}_i{\mathcal{D}}^T)}$. The idea is that, given a fixed (direction unit frobenius-norm matrix) $\mathcal{D}$, ${\displaystyle {\sum }_{i=1}^n\text{tr}(\mathcal{P}{(V_i{\mathcal{D}}^T)}^T{V}_i{\mathcal{D}}^T)}$ converges to the expected value of one of the summands and, by an ε-net argument (since the dimension of the space where $\mathcal{D}$ is depends only on d and p and the number of summands is n which can be made much larger than d and p) we can argue that the sum is close, for all $\mathcal{D}’\mathrm{s}$ simultaneously, to that expectation. It is not hard to see that we can assume that $\mathcal{D}=\frac{1}{\sqrt{d}}[D0]$ where D is diagonal and non-negative d × d matrix with ${\Vert D\Vert }_F^2=d$. In that case (see (21)),

$$\mathbb{E}\text{ tr}(\mathcal{P}{(V_i{\mathcal{D}}^T)}^T{V}_i{\mathcal{D}}^T)=\mathbb{E}\frac{1}{\sqrt{pd}}{\displaystyle \sum _{k=1}^d{\sigma }_k(GD)\le \sqrt{\frac{d}{p}}}{\alpha }_{ℝ}^{\ast }(d),$$

where G is a Gaussian matrix with i.i.d. real entries $\mathcal{N}\left(0,\frac{1}{d}\right)$. This, together with Theorem 13, gives $\mathbb{E}\text{ tr}(\mathcal{P}{(V_i{\mathcal{D}}^T)}^T{V}_i{\mathcal{D}}^T)\le \sqrt{\frac{d}{p}}{\alpha }_{ℝ}(d)$. All of this is made precise in the following lemma

Lemma 15

For any d and ɛ > 0 there exists p₀ and n₀ such that, for any p > p₀ and n > n₀,

$$\underset{O_1,\dots ,O_n\in {\mathcal{O}}_d}{max}{\Vert \frac{1}{n}{\displaystyle \sum _{i=1}^n{O}_i^T{V}_i}\Vert }_F^2\le \frac{d}{p}{\alpha }_{ℝ}{\left(d\right)}^2+\epsilon ,$$

with probability strictly larger than 1/2.

Proof

Let us define

$$A(V):=\underset{O_1,\dots ,O_n\in {\mathcal{O}}_d}{max}{\Vert \frac{1}{n}{\displaystyle \sum _{i=1}^n{O}_i^T{V}_i}\Vert }_F.$$

We have

$$\begin{array}{l}A(V)=\underset{D\in {ℝ}^{d\times pd}:{\Vert D\Vert }_F=1}{max}\underset{O_1,\dots ,O_n\in O(d)}{max}\text{tr}\left(\frac{1}{n}{\displaystyle \sum _{i=1}^n{O}_i^T{V}_i{D}^T}\right)\\ =\underset{D\in {ℝ}^{d\times pd}:{\Vert D\Vert }_F=1}{max}\frac{1}{n}{\displaystyle \sum _{i=1}^n\underset{O_i\in O(d)}{max}}\text{tr}(O_i^T{V}_i{D}^T)\\ =\underset{D\in {ℝ}^{d\times pd}:{\Vert D\Vert }_F=1}{max}\frac{1}{n}{\displaystyle \sum _{i=1}^n\text{tr}\left(\mathcal{P}{(V_i{D}^T)}^T{V}_i{D}^T\right)}.\end{array}$$

For D with ‖D‖_F = 1, we define

$$A_D(V)=\frac{1}{n}{\displaystyle \sum _{i=1}^n\text{tr}\left(\mathcal{P}{\left(V_i{D}^T\right)}^T{V}_i{D}^T\right)}.$$

We proceed by understanding the behavior of A_D(V) for a specific D.

Let $D=U_L\left[\sum 0\right]U_R^T$, where Σ is a d × d non-negative diagonal matrix, be the singular value decomposition of D. For each i = 1, …, n, we have (using rotation invariance of the Gaussian distribution):

$$\begin{array}{l}\text{tr}\left(\mathcal{P}{\left(V_i{D}^T\right)}^T{V}_i{D}^T\right)~\text{tr}\left(\mathcal{P}{\left(V_i{\left(U_L\right[\sum 0\left]U_R\right)}^T\right)}^T{V}_i{\left(U_L\right[\sum 0\left]U_R\right)}^T\right)\\ ~\text{tr}\left(U_L\mathcal{P}{\left(V_i\right[\begin{array}{c}\sum \\ 0\end{array}\left]\right)}^T{V}_i\right[\begin{array}{c}\sum \\ 0\end{array}\left]U_L^T\right)\\ ~\text{tr}\left(\mathcal{P}{\left(V_i\right[\begin{array}{c}\sum \\ 0\end{array}\left]\right)}^T{V}_i\right[\begin{array}{c}\sum \\ 0\end{array}\left]\right)\\ ~\frac{1}{\sqrt{\mathit{dp}}}\text{tr}(\mathcal{P}{(G\sqrt{d}\sum )}^{T}G\sqrt{d}\sum ),\end{array}$$

where G is a d × d Gaussian matrix with $\mathcal{N}\left(0,\frac{1}{d}\right)$ entries.

This means that

$$A_D(V)=\frac{1}{n}{\displaystyle \sum _{i=1}^n{X}_i},$$

with X_i i.i.d. distributed as $\frac{1}{\sqrt{dp}}\text{tr}\left(\mathcal{P}{\left(G\sqrt{d}\sum \right)}^{T}G\sqrt{d}\sum \right)$.

Since ${\Vert \sqrt{d}\sum \Vert }_F^2=d$, by (21), we get

$$\mathbb{E}\text{ tr}\left(\mathcal{P}{\left(G\sqrt{d}\sum \right)}^{T}G\sqrt{d}\sum \right)\le d{\alpha }_{ℝ}^{\ast }(d).$$

This, together with Theorem 13, gives

$$\mathbb{E}{X}_i\le \sqrt{\frac{d}{p}}{\alpha }_{ℝ}(d).$$ (25)

In order to give tail bounds for $A_D(V)=\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{X}_i}$ we will show that X_i is subgaussian and use Hoeffding’s inequality (see Vershynin’s notes [Ver12]). In fact,

$$X_i~\frac{1}{\sqrt{dp}}\text{tr}\left(\mathcal{P}{\left(G\sqrt{d}\sum \right)}^{T}G\sqrt{d}\sum \right)\le \frac{1}{\sqrt{p}}{\Vert \mathcal{P}\left(G\sum \right)\Vert }_F{\Vert G\sum \Vert }_F=\sqrt{\frac{d}{p}}{\Vert GD\Vert }_F\le \sqrt{\frac{d}{p}}{\Vert G\Vert }_F.$$

Note that $\sqrt{\frac{d}{p}}{\Vert G\Vert }_F$ is a subgaussian random variable as ‖G‖_F is smaller than the entry wise ℓ₁ norm of G which is the sum of d² half-normals (more specifically, the absolute value of a $\mathcal{N}\left(0,\frac{1}{d}\right)$ random variable). Since half-normals are subgaussian and the sum of subgaussian random variables is a subgaussian random variable with subgaussian norm at most the sum of the norms (see the Rotation invariance Lemma in [Ver12]) we get that X_i is subgaussian. Furthermore, the subgaussian norm of X_i, which we define as ${\Vert X_i\Vert }_{\psi 2}={\sup }_{p\ge 1}{p}^{-1/2}{\left(\mathbb{E}|X{|}^p\right)}^{1/p}$, is bounded by ${\Vert X_i\Vert }_{\psi 2}\le C\sqrt{\frac{d^2}{p}}=C\frac{d}{\sqrt{p}}$, for some universal constant C.

Hence, we can use Hoeffding’s inequality (see [Ver12]) and get, since $\mathbb{E}{X}_i\le \sqrt{\frac{d}{p}}{\alpha }_{ℝ}(d)$,

$$\text{Prob}\left[A_D\ge \sqrt{\frac{d}{p}}{\alpha }_{ℝ}(d)+t\right]\le \text{Prob}\left[\left|A_D-\mathbb{E}{X}_i\right|\ge t\right]\le \exp \left(1-\frac{c_2{t}^{2}n}{{\Vert X_i\Vert }_{{\psi }_2}^2}\right)\le 3\exp \left(-c_1\frac{t^{2}p}{d^2}n\right),$$

where c_i are universal constants.

To find an upper bound for $A={max}_{D\in {ℝ}^{d\times pd}:{\Vert D\Vert }_F=1}{A}_D$ we use a classicl ε-net argument. There exists a set $\mathcal{N}$ of matrices D_k ∈ ℝ^d×pd satisfying ‖D_k‖_F = 1, such that for any D ∈ ℝ^d×pd with Frobenius norm 1, there exists an element $D_k\in \mathcal{N}$ such that ${\Vert D-D_k\Vert }_F\le \epsilon$. $\mathcal{N}$ is called an ε-net, and it’s known (see [Ver12]) that there exists such a set with size

$$|\mathcal{N}|\le {\left(1+\frac{2}{\epsilon }\right)}^{d^{2}p}.$$

By the union-bound, with probability at least

$$1-\left|\mathcal{N}\right|\text{Prob}\left[A_D\ge \sqrt{\frac{d}{p}}{\alpha }_{ℝ}(d)+t\right]\ge 1-\left[{\left(1+\frac{2}{\epsilon }\right)}^{d^{2}p}3\exp \left(-c_1\frac{t^{2}n}{d^3}\right)\right],$$

all the D_k’s in $\mathcal{N}$ satisfy

$$A_{D_k}\le \sqrt{\frac{d}{p}}{\alpha }_{ℝ}^{\ast }(d)+t.$$

If D is not in $\mathcal{N}$, there exists $D_k\in \mathcal{N}$ such that ‖D − D_k‖_F ≤ ε. This means that

$$\begin{array}{l}{A}_D\le \frac{1}{n}{\displaystyle \sum _{i=1}^n\text{tr}}\left(\mathcal{P}{(V_i{D}^T)}^T{V}_i{D}_{\ast }^T\right)+\frac{1}{n}{\displaystyle \sum _{i=1}^n\text{tr}}\left(\mathcal{P}{(V_i{D}^T)}^T{V}_i(D_{\ast }^T-D^T)\right)\\ \le \frac{1}{n}{\displaystyle \sum _{i=1}^n\text{tr}}\left(\mathcal{P}{(V_i{D}_{\ast }^T)}^T{V}_i{D}_{\ast }^T\right)+\frac{1}{n}{\displaystyle \sum _{i=1}^n\Vert \mathcal{P}{(V_i{D}^T)}^T{V}_i}{\Vert }_F{\Vert D_{\ast }-D\Vert }_F\\ \le \sqrt{\frac{d}{p}{\alpha }_{ℝ}^{\ast }}(d)+t+\epsilon \left(\frac{1}{n}{\displaystyle \sum _{i=1}^n{\Vert V_i\Vert }_F}\right).\end{array}$$

We can globally bound $\left(\frac{1}{n}{\sum }_{i=1}^n{\Vert V_i\Vert }_F\right)$ by Hoeffding’s inequality as well (see [Ver12]). Using the same argument as above, it is easy to see that ‖V_i‖_F has subgaussian norm bounded by $\sqrt{d}$, and an explicit computation shows its mean is $\frac{1}{\sqrt{dp}}\sqrt{2}\frac{\mathrm{\Gamma }((d^{2}p+1)/2)}{\mathrm{\Gamma }(d^{2}p/2)}\le 2\sqrt{d}$, where the inequality follows from lemma 20.

This means that by Hoeffding’s inequality (see [Ver12])

$$\begin{array}{l}\text{Prob}\left[\frac{1}{n}{\displaystyle \sum _{i=1}^n{\Vert V_i\Vert }_F}\ge 2\sqrt{d}+t\right]\le \exp \left(1-\frac{c_4{t}^{2}n}{{\Vert {\Vert V_i\Vert }_F\Vert }_{{\psi }_2}^2}\right)\\ \le 3\exp \left(-c_3\frac{t^{2}n}{d}\right),\end{array}$$

with c_i universal constants.

By union-bound on the two events above, with probability at least

$$1-3\exp \left(-c_3\frac{t^{2}n}{d}\right)-\left[{\left(1+\frac{2}{\epsilon }\right)}^{d^{2}p}3\exp \left(-c_1\frac{t^{2}n}{d^3}\right)\right],$$

we have

$$A\le \sqrt{\frac{d}{p}}{\alpha }_{ℝ}^{\ast }(d)+t+\epsilon (2d+t).$$

Choosing $t=\frac{1}{2p}$ and $\epsilon =\frac{1}{6dp}$ we get

$$A\le \sqrt{\frac{d}{p}}{\alpha }_{ℝ}^{\ast }(d)+\frac{1}{p},$$

with probability at least

$$\begin{array}{l}1-3\exp \left(-c_3\frac{n}{4p^2}\right)-\left[{(1+12dp)}^{d^{2}p}3\exp \left(-c_1\frac{n}{4p^2{d}^3}\right)\right]\\ =1-6\left[{(1+12dp)}^{d^{2}p}3\exp \left(-c_1\frac{n}{4p^2{d}^3}\right)\right]\end{array}$$

which can be made arbitrarily close to 1 by taking n large enough.

This means that

$$\underset{O_1,\dots ,O_n\in \mathcal{O}d}{max}{\Vert \frac{1}{n}{\displaystyle \sum _{i=1}^n{O}_i^T{V}_i}\Vert }_F^2\le \frac{d}{p}{\alpha }_{ℝ}{(d)}^2+\frac{1}{p},$$

with high probability, proving the lemma.      □

Regarding w_r, we know that it is at least the value of $\frac{1}{n^2}{\displaystyle {\sum }_{i,j}^n\text{tr}\left({\left(V_i{V}_j^T\right)}^T{X}_i{X}_j^T\right)}$ for $X_i=\mathcal{P}(V_i)$. Since, for p large enough, $V_i{V}_i^T\approx I_{d\times d}$ we essentially have $w_r\gtrsim \frac{1}{n^2}{\displaystyle {\sum }_{i,j}^n{\Vert V_i{V}_j^T\Vert }_F^2}$ which should approximate $\mathbb{E}{\Vert V_i{V}_j^T\Vert }_F^2\approx \frac{d}{p}$. This is made precise in the following lemma:

Lemma 16

For any d and ɛ > 0 there exists p₀ and n₀ such that, for any p > p₀ and n > n₀,

$\frac{1}{n^2}{\displaystyle \sum _{i,j}^n\text{tr}({(V_i{V}_j^T)}^T{\mathcal{P}}_{(d,dp)}(V_i){\mathcal{P}}_{(d,dp)}{(V_j)}^T)}\ge \frac{d}{p}-\epsilon ,$

with probability strictly larger than 1/2.

Proof

Recall that ${\mathcal{P}}_{(d,dp)}(V_i)$ is the d × dp matrix polar component of V_i, meaning that

$$\text{tr}({\mathcal{P}}_{(d,dp)}{(V_i)}^T{V}_i)={\displaystyle \sum _{k=1}^d{\sigma }_k(V_i)}.$$

Hence,

$$\begin{array}{l}\frac{1}{n^2}{\displaystyle \sum _{i,j}^n\text{tr}({(V_i{V}_j^T)}^T{\mathcal{P}}_{(d,dp)}(V_i){\mathcal{P}}_{(d,dp)}{(V_j)}^T)}={\Vert \frac{1}{n}{\displaystyle \sum _{i=1}^n\mathcal{P}{(V_i)}^T{V}_j}\Vert }_F^2\\ \ge \frac{1}{{\Vert I_{dp\times dp}\Vert }_F^2}{\left[\frac{1}{n}{\displaystyle \sum _{i=1}^n\text{tr}(\mathcal{P}{(V_i)}^T{V}_i{I}_{dp\times dp})}\right]}^2\\ =\frac{1}{dp}{\left[\frac{1}{n}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{k=1}^d{\sigma }_k(V_i)}}\right]}^2.\end{array}$$

We proceed by using a lower bound for the expected value of the smallest eigenvalue (see [Ver12]), and get

$$\mathbb{E}{\displaystyle \sum _{k=1}^d{\sigma }_k(V_i)}\ge d\mathbb{E}{\sigma }_{min}(V_i)=d\left(1-\frac{1}{\sqrt{p}}\right).$$

Since ${\displaystyle {\sum }_{k=1}^d{\sigma }_k(V_i)}\le \sqrt{d}{\Vert V_i\Vert }_F$, it has subgaussian norm smaller than Cd, with C an universal constant (using the same argument as in Lemma 15). Therefore, by Hoeffding’s inequality (see [Ver12]),

$$\begin{array}{l}\text{Prob}\left[\frac{1}{n}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{k=1}^d{\sigma }_k(V_i)}\le d\left(1-\frac{1}{\sqrt{p}}\right)-t}\right]\le \exp (1-\frac{c_1{t}^2}{{\Vert {\displaystyle {\sum }_{k=1}^d{\sigma }_k(V_i)}\Vert }_{{\psi }_2}^2}n)\\ \le \exp (1-c_2\frac{t^2}{d^2}n),\end{array}$$

where c_i are universal constants.

By setting $t=\frac{d}{\sqrt{p}}$, we get

$$\frac{1}{n^2}{\displaystyle \sum _{i,j}^n\text{tr}({(V_i{V}_j^T)}^T{\mathcal{P}}_{(d,dp)}(V_i){\mathcal{P}}_{(d,dp)}{(V_j)}^T)}\ge \frac{d}{p}{(1-2\frac{1}{\sqrt{p}})}^2,$$

with probability at least $1-\exp \left(1-c_2\frac{1}{p}n\right)=1-o_n(1)$ proving the Lemma.

Theorem 14 immediately follows from these two lemmas.

We note that these techniques are quite general. It is not difficult to see that these arguments, establishing integrality gaps that match the approximation ratios obtained, can be easily adapted for both the unitary case and the rank constrained case introduced in Section 5. For the sake of exposition we omit the details in these cases.

7 Open Problems and Future Work

Besides Conjecture 8, there are several extensions of this work that the authors consider to be interesting directions for future work.

A natural extension is to consider the little Grothendieck problem (3) over other groups of matrices. One interesting extension would be to consider the special orthogonal group $S{\mathcal{O}}_d$ and the special unitary group $S{\mathcal{U}}_d$, these seem more difficult since they are not described by quadratic constraints.³

In some applications, like Synchronization [BSS13, Sin11] (a similar problem to Orthogonal Procrustes) and Common Lines [SS11], the positive semidefiniteness condition is not natural. It would be useful to better understand approximation algorithms for a version of (3) where C is not assumed to be positive semidefinite. Previous work in the special case d = 1, [NRT99, CW04, AMMN05] for ${\mathcal{O}}_1$ and [SZY07] for ${\mathcal{U}}_1$, suggest that it is possible to obtain an approximation ratio for (3) depending logarithmically on the size of the problem. Moreover, for ${\mathcal{O}}_1$, the logarithmic term is known to be needed in general [AMMN05].

It would also be interesting to understand whether the techniques in [AN04] can be adapted to obtain an approximation algorithm to the bipartite Grothendieck problem over the orthogonal group; this would be closer in spirit to the non commutative Grothendieck inequality [NRV13].

Another interesting question is whether the approximation ratios obtained in this paper correspond to the hardness of approximation of the problem (perhaps conditioned on the Unique-Games conjecture [Kho10]). Our optimality conditions are restricted to the particular relaxation we consider and do not exclude the existence of an efficient algorithm, not relying on the same relaxation, that approximates (3) with a better approximation ratio. Nevertheless, Raghavendra [Rag08] results on hardness for a host of problems matching the integrality gap of natural SDP relaxations suggest that our approximation ratios might be optimal (see also the recent results in [BRS15]).

Figure 2.

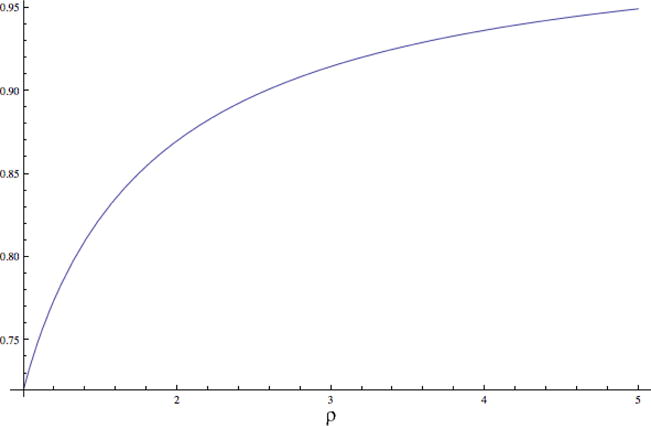
Plot of ε(ρ) = lim_{d → ∞} α_ℝ(d, ρd) for ρ ∈ [1, 5].

A Technical proofs – analysis of algorithm for the Stiefel Manifold setting

Lemma 17

Let r ≥ d. Let G be a d × r Gaussian random matrix with real valued i.i.d. $\mathcal{N}(0,\frac{1}{r})$ entries and let α_ℝ(d, r) as defined in Definition 11. Then,

$$\mathbb{E}\left({\mathcal{P}}_{d,r}\left(G\right)G^T\right)=\mathbb{E}\left(G{\mathcal{P}}_{d,r}{\left(G\right)}^T\right)={\alpha }_{ℝ}\left(d,r\right)I_{d\times d}.$$

Furthermore, if G is a d × r Gaussian random matrix with complex valued i.i.d. $\mathcal{N}(0,\frac{1}{r})$ entries and α_ℂ(d, r) the analogous constant (Definition 11), then

$$\mathbb{E}\left({\mathcal{P}}_{d,r}\left(G\right)G^H\right)=\mathbb{E}\left(G{\mathcal{P}}_{d,r}{\left(G\right)}^H\right)={\alpha }_{ℂ}\left(d,r\right)I_{d\times d}.$$

The proof of this Lemma is a simple adaptation of the proof of Lemma 6.

Proof

We restrict the presentation to the real case. As before, all the arguments are equivalent to the complex case, replacing all transposes with Hermitian adjoints and α_ℝ(d, r) with α_ℂ(d, r).

Let G = U[Σ 0]V^T be the singular value decomposition of G. Since GG^T = UΣ²U^T is a Wishart matrix, it is well known that its eigenvalues and eigenvectors are independent and U is distributed according to the Haar measure in ${\mathcal{O}}_d$ (see e.g. Lemma 2.6 in [TV04]). To resolve ambiguities, we consider Σ ordered such that Σ₁₁ ≥ Σ₂₂ ≥ … ≥ Σ_dd.

Let $Y={\mathcal{P}}_{(d,r)}(G)G^T$. Since

$${\mathcal{P}}_{(d,r)}(G)={\mathcal{P}}_{(d,r)}(U\sum V^T)=U{I}_{d\times d}{V}^T,$$

we have

$$Y={\mathcal{P}}_{(d,r)}(U\sum V^T){(U\sum V^T)}^T=U{I}_{d\times d}{V}^{T}V\sum U^T=U\sum U^T.$$

Note that $G{\mathcal{P}}_{\left(d,r\right)}{\left(G\right)}^T=U\sum U^T=Y$.

Since $Y_{\mathit{ij}}=u_i\sum u_j^T$, where u₁, …, u_d are the rows of U, and U is distributed according to the Haar measure, we have that u_j and −u_j have the same distribution conditioned on any u_i, for i ≠ j, and Σ. This implies that, if i ≠ j, $Y_{\mathit{ij}}=u_i\sum u_j^T$ is a symmetric random variable, and so $\mathbb{E}{Y}_{\mathit{ij}}=0$. Also, u_i ~ u_j implies that Y_ii ~ Y_jj. This means that $\mathbb{E}Y=c{I}_{d\times d}$ for some constant c. To obtain c,

$$c=c\frac{1}{d}\text{tr}(I_{d\times d})=\frac{1}{d}\mathbb{E}\text{ tr}(Y)=\frac{1}{d}\mathbb{E}\text{ tr}(U\sum U^T)=\frac{1}{d}\mathbb{E}{\displaystyle \sum _{k=1}^n{\sigma }_k(G)={\alpha }_{ℝ}(d,r),}$$

which shows the lemma.      □

Lemma 18

Let r ≥ d. Let M, N ∈ ℝ^d×nd such that M M^T = N N^T = I_d×d. Let R ∈ ℝ^nd×r be a Gaussian random matrix with real valued i.i.d. entries $\mathcal{N}\left(0,\frac{1}{r}\right)$. Then

$$\mathbb{E}\left[{\mathcal{P}}_{(d,r)}(MR){(NR)}^T\right]=\mathbb{E}\left[(MR){\mathcal{P}}_{(d,r)}{(NR)}^T\right]={\alpha }_{ℝ}(d,r)M{N}^T,$$

where α_ℝ(d, r) is the constant in Definition 11.

Analogously, if M, N ∈ ℂ^d×nd such that MM^H=N N^H = I_d×d, and R ∈ ℂ^nd×r is a Gaussian random matrix with complex valued i.i.d. entries $\mathcal{N}\left(0,\frac{1}{r}\right)$, then

$$\mathbb{E}\left[{\mathcal{P}}_{(d,r)}(MR){(NR)}^H\right]=\mathbb{E}\left[(MR){\mathcal{P}}_{(d,r)}{(NR)}^H\right]={\alpha }_{ℂ}(d,r)M{N}^H,$$

where α_ℂ(d, r) is the constant in Definition 11.

Similarly to above, the proof of this Lemma is a simple adaptation of the proof of Lemma 5.

Proof

We restrict the presentation of proof to the real case. Nevertheless, all the arguments trivially adapt to the complex case by, essentially, replacing all transposes with Hermitian adjoints and α_ℝ(d) and α_ℝ(d, r) with α_ℂ(d) and α_ℂ(d, r).

Let A = [M^T N^T] ∈ ℝ^dn×2d and A = QB be the QR decomposition of A with Q ∈ ℝ^nd×nd an orthogonal matrix and B ∈ ℝ^nd×2d upper triangular with non-negative diagonal entries; note that only the first 2d rows of B are nonzero. We can write

$$Q^{T}A=B=\left[\begin{array}{cc}{B}_{11}& B_{12}\\ 0_d& B_{22}\\ 0_d& 0_d\\ ⋮& ⋮\\ 0_d& 0_d\end{array}\right]\in {ℝ}^{dn\times 2d},$$

where B₁₁ ∈ ℝ^d×d and B₂₂ ∈ ℝ^d×d are upper triangular matrices with non-negative diagonal entries. Since

$${(Q^T{M}^T)}_{11}^T{(Q^T{M}^T)}_{11}={(Q^T{M}^T)}^T(Q^T{M}^T)=MQ{Q}^T{M}^T=M{I}_{nd\times nd}{M}^T=M{M}^T=I_{d\times d},$$

B₁₁ = (Q^T M^T)₁₁ is an orthogonal matrix, which together with the non-negativity of the diagonal entries (and the fact that B₁₁ is upper-triangular) forces B₁₁ to be B₁₁ = I_d×d.

Since R is a Gaussian matrix and Q is an orthogonal matrix, QR ~ R which implies

$$\mathbb{E}[{\mathcal{P}}_{(d,r)}(\mathit{MR}){(\mathit{NR})}^T]=\mathbb{E}\left[{\mathcal{P}}_{(d,r)}(\mathit{MQR}){(\mathit{NQR})}^T\right].$$

Since $MQ=\left[B_{11}^T,0_{d\times d},\dots ,0_{d\times d}\right]=\left[I_{d\times d},0_{d\times d},\dots ,0_{d\times d}\right]$ and $NQ=\left[B_{12}^T,B_{22}^T,0_{d\times d},\dots ,0_{d\times d}\right]$,

$$\mathbb{E}\left[{\mathcal{P}}_{(d,r)}(MR){(NR)}^T\right]=\mathbb{E}\left[{\mathcal{P}}_{(d,r)}(R_1){(B_{12}^T{R}_1+B_{22}^T{R}_2)}^T\right],$$

where R₁ and R₂ are the first two d × r blocks of R. Since these blocks are independent, the second term vanishes and we have

$$\mathbb{E}\left[{\mathcal{P}}_{\left(d,r\right)}\left(MR\right){\left(NR\right)}^T\right]=\mathbb{E}\left[{\mathcal{P}}_{\left(d,r\right)}\left(R_1\right)R_1^T\right]B_{12}.$$

The Lemma now follows from using Lemma 17 to obtain $\mathbb{E}\left[{\mathcal{P}}_{\left(d,r\right)}\left(R_1\right)R_1^T\right]={\alpha }_{ℝ}\left(d,r\right)I_{d\times d}$ and nothing that $B_{12}={(Q^T{M}^T)}^T(Q^T{N}^T)=M{N}^T$.

The same argument, with Q′B′ the QR decomposition of A′ = [N^TM^T] ∈ ℝ^dn×2d instead, shows

$$\mathbb{E}\left[(MR){\mathcal{P}}_{(d,r)}{(NR)}^T\right]=\mathbb{E}\left[R_1{\mathcal{P}}_{(d,r)}{(R_1)}^T\right]M{N}^T={\alpha }_{ℝ}(d,r)M{N}^T.$$

B Bounds for the average singular value

Lemma 19

Let $G_{ℂ}\in {ℂ}^{d\times d}$ be a Gaussian random matrix with i.i.d. complex valued $\mathcal{N}(0,d^{-1})$ entries and define ${\alpha }_{ℂ}(d):=\mathbb{E}\left[\frac{1}{d}{\displaystyle {\sum }_{j=1}^d{\sigma }_j(G_{ℂ})}\right]$. We have the following bound

$${\alpha }_{ℂ}(d)\ge \frac{8}{3\pi }-\frac{5.05}{d}.$$

Proof

We express ${\alpha }_{ℂ}(d)$ as sums and products of Gamma functions and then use classical bounds to obtain our result.

Recall that from equation (16),

$${\alpha }_{ℂ}(d)=d^{-3/2}{\displaystyle \sum _{n=0}^{d-1}{T}_n,}$$ (26)

where

$$T_n={\displaystyle {\int }_0^{\infty }{x}^{1/2}{e}^{-x}{L}_n{(x)}^{2}dx,}$$

and L_n(x) is the nth Laguerre polynomial,

$$L_n(x)={\displaystyle \sum _{k=0}^n\left(\begin{array}{c}n\\ k\end{array}\right)\frac{{(-1)}^k}{k!}{x}^k.}$$

This integral can be expressed as (see [GR94] section 7.414 equation 4(1))

$$T_n=\frac{\mathrm{\Gamma }(n+3/2)}{\mathrm{\Gamma }(n+1)}{\displaystyle \sum _{m=0}^n\frac{{\left(\frac{-1}{2}\right)}_m{(-n)}_m}{{(m!)}^2{\left(-n-\frac{1}{2}\right)}_m}},$$ (27)

where (x)_m is the Pochhammer symbol

$${(x)}_m=\frac{\mathrm{\Gamma }(x+m)}{\mathrm{\Gamma }(x)}.$$

The next lemma states a couple basic facts about the Gamma function that we will need in the subsequent computations.

Lemma 20

The Gamma function satisfies the following inequalities:

$$\begin{array}{l}\frac{1}{\sqrt{n}}\le \frac{\mathrm{\Gamma }(n)}{\mathrm{\Gamma }(n+1/2)}\le \frac{1}{\sqrt{n-1/2}}\\ \sqrt{n}\le \frac{\mathrm{\Gamma }(n+1)}{\mathrm{\Gamma }(n+1/2)}\le \frac{1}{\sqrt{n+1/2}}.\end{array}$$

Proof

See [AS64] page 255.

We want to bound the summation in (27), which we rewrite as

$$\begin{gathered} {\displaystyle \sum _{m=0}^n\frac{{\left(\frac{-1}{2}\right)}_m{(-n)}_m}{{(m!)}^2{\left(-n-\frac{1}{2}\right)}_m}}={\displaystyle \sum _{m=0}^{\infty }\frac{{\left(\frac{-1}{2}\right)}_m^2}{{(m!)}^2} \\ -{\displaystyle \sum _{m=n+1}^{\infty }\frac{{\left(\frac{-1}{2}\right)}_m^2}{{(m!)}^2}} \\ -{\displaystyle \sum _{m=0}^n\frac{{\left(\frac{-1}{2}\right)}_m^2}{{(m!)}^2}\left(1-\frac{{(-n)}_m}{{\left(-n-\frac{1}{2}\right)}_m}\right).}} \end{gathered}$$

For simplicity define

$$\begin{array}{c}(I):={\displaystyle \sum _{m=0}^{\infty }\frac{{\left(\frac{-1}{2}\right)}_m^2}{{(m!)}^2}}\\ (\mathit{II}):={\displaystyle \sum _{m=n+1}^{\infty }\frac{{\left(\frac{-1}{2}\right)}_m^2}{{(m!)}^2}}\\ (\mathit{III}):={\displaystyle \sum _{m=0}^n\frac{{\left(\frac{-1}{2}\right)}_m^2}{{(m!)}^2}(1-\frac{{(-n)}_m}{{(-n-\frac{1}{2})}_m}),}\end{array}$$

so that (27) becomes

$$T_n=\frac{\mathrm{\Gamma }(n+3/2)}{\mathrm{\Gamma }(n+1)}((I)+(\mathit{II})+(\mathit{III})).$$

The first term we can compute explicitly (see [GR94]) as

$$(I)=\frac{4}{\pi }.$$

For the second term we use the fact that ${\left(\frac{-1}{2}\right)}_m=\mathrm{\Gamma }(m-1/2)/\mathrm{\Gamma }(-1/2)$ to get

$$(\mathit{II})={\displaystyle \sum _{m=n+1}^{\infty }\frac{1}{\mathrm{\Gamma }{(-1/2)}^2}\frac{\mathrm{\Gamma }{(m-1/2)}^2}{\mathrm{\Gamma }{(m+1)}^2}=\frac{1}{4\pi }{\displaystyle \sum _{m=n+1}^{\infty }\frac{\mathrm{\Gamma }{(m-1/2)}^2}{\mathrm{\Gamma }{(m+1)}^2}.}}$$

Using the first inequality in Lemma 20 and the multiplication formula for the Gamma function,

$$\frac{\mathrm{\Gamma }(m-1/2)}{\mathrm{\Gamma }(m+1)}=\frac{1}{m-1/2}\frac{\mathrm{\Gamma }(m+1/2)}{\mathrm{\Gamma }(m+1)}\le \frac{1}{(m-1/2)\sqrt{m}}$$

so we have

$$(\mathit{II})\le \frac{1}{4\pi }{\displaystyle \sum _{m=n+1}^{\infty }\frac{1}{{(m-1/2)}^{2}m}\le \frac{1}{4\pi }{\displaystyle {\int }_{n-1/2}^{\infty }\frac{1}{x^3}dx=\frac{1}{2\pi {(2n-1)}^2}.}}$$

For the third term, we use the formula ${(x)}_m=\frac{\mathrm{\Gamma }(x+n)}{\mathrm{\Gamma }(x)}$ to deduce

$$\begin{array}{l}(\mathit{III})={\displaystyle \sum _{m=0}^n\frac{{\left(\frac{-1}{2}\right)}_m^2}{{(m!)}^2}\left(1-\frac{{(-n)}_m}{{(-n-\frac{1}{2})}_m}\right)}\\ =\frac{1}{4\pi }{\displaystyle \sum _{m=0}^n\frac{\mathrm{\Gamma }{(m-1/2)}^2}{\mathrm{\Gamma }{(m+1)}^2}\left(1-\frac{\mathrm{\Gamma }(n+1)\mathrm{\Gamma }(n-m+3/2)}{\mathrm{\Gamma }(n+3/2)\mathrm{\Gamma }(n-m+1)}\right)}\\ =\frac{\mathrm{\Gamma }(n+1)}{\mathrm{\Gamma }(n+3/2)}\frac{1}{4\pi }{\displaystyle \sum _{m=0}^n\frac{\mathrm{\Gamma }{(m-1/2)}^2}{\mathrm{\Gamma }{(m+1)}^2}\left(\frac{\mathrm{\Gamma }(n+3/2)}{\mathrm{\Gamma }(n+1)}-\frac{\mathrm{\Gamma }(n-m+3/2)}{\mathrm{\Gamma }(n-m+1)}\right).}\end{array}$$

Using the second bound in Lemma 20,

$$\frac{\mathrm{\Gamma }(n-m+3/2)}{\mathrm{\Gamma }(n-m+1)}\ge \sqrt{n-m+1/2},$$

and also

$$\frac{\mathrm{\Gamma }(n+3/2)}{\mathrm{\Gamma }(n+1)}\le \sqrt{n+1},$$

so that

$$(\mathit{III})\le \frac{1}{4\pi \sqrt{n+1/2}}{\displaystyle \sum _{m=0}^n{\left(\frac{1}{(m-1/2)\sqrt{m+1/2}}\right)}^2\left(\sqrt{n+1}-\sqrt{n-m+1/2}\right).}$$

If we multiply top and bottom by $\sqrt{n+1}+\sqrt{n-m+1/2}$ and use the fact that

$$\frac{m+1/2}{\sqrt{n+1}+\sqrt{n-m+1/2}}\le \frac{m+1/2}{\sqrt{n+1}},$$

then

$$\begin{array}{l}(\mathit{III})\le \frac{1}{4\pi \sqrt{n+1/2}}{\displaystyle \sum _{m=0}^n\frac{1}{{(m-1/2)}^2(m+1/2)}\frac{m+1/2}{\sqrt{n+1}}}\\ \le \frac{1}{2\pi (n+1)}{\displaystyle \sum _{m=0}^n\frac{1}{{(m-1/2)}^2}}\\ \le \frac{1}{n+1}\frac{8+{\pi }^2}{2\pi }\\ \le \frac{3}{n+1}.\end{array}$$

Combining our bounds for (I), (II) and (III),

$$\begin{array}{l}{T}_n=\frac{\mathrm{\Gamma }(n+3/2)}{\mathrm{\Gamma }(n+1)}[(I)-(\mathit{II})-(\mathit{III})]\\ \ge \frac{\mathrm{\Gamma }(n+3/2)}{\mathrm{\Gamma }(n+1)}\left(\frac{4}{\pi }-\frac{1}{2\pi {(2n-1)}^2}-\frac{3}{n+1}\right)\\ \ge \sqrt{n+1/2}\left(\frac{4}{\pi }-\frac{1}{2\pi {(2n-1)}^2}-\frac{3}{n+1}\right),\end{array}$$

and by (26),

$${\alpha }_{ℂ}(d)\ge \frac{1}{d^{3/2}}{\displaystyle \sum _{n=1}^{d-1}\sqrt{n+1/2}}\left(\frac{4}{\pi }-\frac{1}{2\pi {\left(2n-1\right)}^2}-\frac{3}{n+1}\right).$$

The term $\frac{1}{d^{3/2}}{\displaystyle {\sum }_{n=1}^{d-1}4\sqrt{n+1/2}}/\pi$ is the main term and can be bounded below by

$$\begin{array}{l}\frac{1}{d^{3/2}}{\displaystyle \sum _{n=1}^{d-1}\frac{4\sqrt{n+1/2}}{\pi }}\ge \frac{1}{d^{3/2}}\frac{8}{3\pi }({(d-1/2)}^{3/2}-{(1/2)}^{3/2})\\ \ge (1-{(2d)}^{-1})\frac{8}{3\pi }-{(2d)}^{-3/2}\\ \ge \frac{8}{3\pi }-(\frac{8}{3\pi }+\frac{1}{2})d^{-1}.\end{array}$$

The other error terms are at most

$$\begin{array}{l}{d}^{-3/2}{\displaystyle \sum _{n=1}^{d-1}\sqrt{n+1/2}}(\frac{1}{2\pi {(2n-1)}^2}+\frac{3}{n+1})\le \frac{1}{d^{3/2}}{\displaystyle \sum _{n=1}^{d-1}\frac{4}{\pi (n+1)}}\sqrt{n+1/2}\\ \le \frac{1}{d^{3/2}}{\displaystyle \sum _{n=1}^{d-1}\frac{4}{\pi {(n+1)}^{1/2}}}\\ \le \frac{4}{\pi d^{3/2}}2\sqrt{d+1}.\end{array}$$

Combining the main and error term bounds, the lemma follows.

Lemma 21

For $G_{\mathbb{K}}\in {\mathbb{K}}^{d\times d}$ a Gaussian random matrix with i.i.d. $\mathbb{K}$ valued $\mathcal{N}$ (0, d⁻¹) entries, define ${\alpha }_{\mathbb{K}}(d):=\mathbb{E}\left[\frac{1}{d}{\displaystyle {\sum }_{j=1}^d{\sigma }_j(G_{\mathbb{K}})}\right]$. The following holds

$${\alpha }_{ℂ}(d)-{\alpha }_{ℝ}(d)\le 4.02d^{-1}.$$

Proof

To find an explicit formula for α_ℝ(d), we need an expression for the spectral distribution of the wishart matrix $d{G}_{ℝ}{G}_{ℝ}^T$, which we call $p_d^{ℝ}(x)$, given by equation (16) in [LV11]:

$$p_d^{ℝ}(x)=\frac{1}{2d}\left(2R_d(x)-\frac{\mathrm{\Gamma }\left(\frac{d}{2}+\frac{1}{2}\right)}{\mathrm{\Gamma }\left(\frac{d}{2}\right)}{L}_{d-1}(x)\{{\psi }_1(x)-{\psi }_2(x)\}\right),$$

where

$$\begin{array}{c}{\psi }_1(x)=e^{-x}{\displaystyle \sum _{k=0}^{(\kappa +d-2)/2}{\delta }_k}{L}_{2k+1-\kappa }(x),\\ {\psi }_2(x)={\left(\frac{x}{2}\right)}^{-1/2}{e^{-}}^{\frac{x}{2}}[(1-\kappa )\frac{2\mathrm{\Gamma }(\frac{1}{2},\frac{x}{2})}{\mathrm{\Gamma }\left(\frac{1}{2}\right)}+2\kappa -1],\\ R_d(x)=e^{-x}{\displaystyle \sum _{m=0}^{d-1}{(L_m(x))}^2},\\ {\delta }_k=\frac{\mathrm{\Gamma }\left(k+1-\frac{\kappa }{2}\right)}{\mathrm{\Gamma }\left(k+\frac{3}{2}-\frac{\kappa }{2}\right)},\end{array}$$

κ = d mod 2 and $\mathrm{\Gamma }(a,y)={\displaystyle {\int }_y^{\infty }{t}^{a-1}{e}^{-t}dt}$ is the incomplete Gamma function.

This means that

$$\begin{array}{l}{\alpha }_{ℝ}(d)=d^{-1/2}{\displaystyle {\int }_0^{\infty }{x}^{1/2}{p}_d^{ℝ}(x)}dx\\ =\frac{1}{d^{3/2}}{\displaystyle {\int }_0^{\infty }{x}^{1/2}{R}_d(x)dx}-\frac{1}{2d^{3/2}}{\displaystyle {\int }_0^{\infty }{x}^{1/2}}\frac{\mathrm{\Gamma }(\frac{d}{2}+\frac{1}{2})}{\mathrm{\Gamma }\left(\frac{d}{2}\right)}{L}_{d-1}(x)\{{\psi }_1(x)-{\psi }_2(x)\}dx.\end{array}$$

Recall that (see section 5)

$${\alpha }_{ℂ}(d)=d^{-3/2}{\displaystyle \sum _{n=0}^{d-1}{\displaystyle {\int }_0^{\infty }{x}^{1/2}{e}^{-x}{L}_n}}{\left(x\right)}^{2}dx$$

which implies

$${\alpha }_{ℝ}(d)={\alpha }_{ℂ}(d)-\frac{1}{2d^{3/2}}{\displaystyle {\int }_0^{\infty }{x}^{1/2}}\frac{\mathrm{\Gamma }\left(\frac{d}{2}+\frac{1}{2}\right)}{\mathrm{\Gamma }\left(\frac{d}{2}\right)}{L}_{d-1}(x)\{{\psi }_1(x)-{\psi }_2(x)\}dx.$$ (28)

We are especially interested in the following terms which appear in the full expression for α_ℝ(d):

$$Q(m,k)={\displaystyle {\int }_0^{\infty }{x}^{1/2}}{e}^{-x}{L}_m(x)L_k(x)dx.$$ (29)

From [GR94] section 7.414 equation 4(1), we have

$$Q(m,k)=\frac{1}{4\pi }{\displaystyle \sum _{i=0}^{min\{m,k\}}\frac{\mathrm{\Gamma }(i+3/2)}{\mathrm{\Gamma }(i+1)}}\frac{\mathrm{\Gamma }(m-i-1/2)}{\mathrm{\Gamma }(m-i+1)}\frac{\mathrm{\Gamma }(k-i-1/2)}{\mathrm{\Gamma }(k-i+1)}.$$

The following lemma deals with bounds on sums involving Q(m, k) terms.

Lemma 22

For Q(m, k) as defined in (29) we have the following bounds

$${\displaystyle \sum _{k=0}^m\frac{\mathrm{\Gamma }(k+1/2)}{\mathrm{\Gamma }(k+1)}}Q(2m,2k)\le 2.8$$ (30)

$${\displaystyle \sum _{k=1}^m\frac{\mathrm{\Gamma }(k+3/2)}{\mathrm{\Gamma }(k+1)}}Q(2m-1,2k-1)\le 5.6$$ (31)

Proof

Note that in (30),

$$Q(2m,2k)=\frac{1}{4\pi }{\displaystyle \sum _{i=0}^{2k}\frac{\mathrm{\Gamma }(i+3/2)}{\mathrm{\Gamma }(i+1)}}\frac{\mathrm{\Gamma }(2m-i-1/2)}{\mathrm{\Gamma }(2m-i+1)}\frac{\mathrm{\Gamma }(2k-i-1/2)}{\mathrm{\Gamma }(2k-i+1)}$$

since m ≥ k.

For 0 < i < 2k − 1, the ith term in the summation of Q(2m, 2k) can be bounded above by

$$\begin{array}{l}\frac{\mathrm{\Gamma }(i+3/2)}{\mathrm{\Gamma }(i+1)}\frac{\mathrm{\Gamma }(2m-i-1/2)}{\mathrm{\Gamma }(2m-i+1)}\frac{\mathrm{\Gamma }(2k-i-1/2)}{\mathrm{\Gamma }(2k-i+1)}\le \sqrt{i+1}\frac{1}{(2k-i)\sqrt{2k-i-1}}\frac{1}{(2m-i)\sqrt{2m-i-1}}\\ \le \sqrt{i+1}\frac{1}{{(2k-i-1)}^{3/2}{(2m-i-1)}^{3/2}}.\end{array}$$

This means that

$$\begin{array}{l}Q(2m,2k)\le \frac{1}{8\sqrt{\pi }}\frac{\mathrm{\Gamma }(2m-1/2)\mathrm{\Gamma }(2k-1/2)}{\mathrm{\Gamma }(2m+1)\mathrm{\Gamma }(2k+1)}\\ +\frac{1}{4\pi }{\displaystyle \sum _{i=1}^{2k-1}\sqrt{i+1}}\frac{1}{{(2k-i-1)}^{3/2}{(2m-i+1)}^{3/2}}\\ +\frac{1}{4\pi }\sqrt{\pi }\frac{\mathrm{\Gamma }(2k+1/2)}{\mathrm{\Gamma }(2k)}\frac{\mathrm{\Gamma }(2m-2k+1/2)}{\mathrm{\Gamma }(2m-2k+2)}\\ +\frac{1}{4\pi }max(\frac{\mathrm{\Gamma }(2k+3/2)}{\mathrm{\Gamma }(2k+1)}\frac{\mathrm{\Gamma }(2m-2k-1/2)}{\mathrm{\Gamma }(2m-2k+1)}(-2\sqrt{\pi }),0).\end{array}$$

We bound the sum from i = 1 to 2k − 3 by

$$\begin{array}{l}\frac{1}{4\pi }{\displaystyle \sum _{i=1}^{2k-3}\sqrt{i+1}}\frac{1}{{(2k-i-1)}^{3/2}{(2m-i+1)}^{3/2}}\le \frac{1}{4\pi }{\displaystyle \sum _{i=0}^{2k-3}\sqrt{i+1}}\frac{1}{{(2k-i-1)}^{3/2}{(2m-2k+1)}^{3/2}}\\ \le \frac{1}{4\pi {(2m-2k+1)}^{3/2}}{\displaystyle {\int }_0^{2k-2}\frac{\sqrt{x+1}}{{(2k-x-1)}^{3/2}}dx}\\ \le \frac{1}{4\pi {(2m-2k+1)}^{3/2}}(\sqrt{8k}+\frac{\sqrt{4k}}{2k-1}),\end{array}$$

so that for k ≥ 1,

$$\begin{array}{l}Q(2m,2k)\le \frac{1}{8\sqrt{\pi }}\frac{\mathrm{\Gamma }(2m-1/2)\mathrm{\Gamma }(2k-1/2)}{\mathrm{\Gamma }(2m+1)\mathrm{\Gamma }(2k+1)}\\ +\frac{1}{4\pi {(2m-2k+1)}^{3/2}}(\sqrt{8k}+\frac{\sqrt{4k}}{2k-1})\\ +\frac{1}{4\pi }\frac{\sqrt{2k-1}}{{(2m-2k+3)}^{3/2}}\\ +\frac{1}{4\pi }\sqrt{\pi }\frac{\mathrm{\Gamma }(2k+1/2)}{\mathrm{\Gamma }(2k)}\frac{\mathrm{\Gamma }(2m-2k+1/2)}{\mathrm{\Gamma }(2m-2k+2)}\\ +\frac{1}{4\pi }max(\frac{\mathrm{\Gamma }(2k+3/2)}{\mathrm{\Gamma }(2k+1)}\frac{\mathrm{\Gamma }(2m-2k-1/2)}{\mathrm{\Gamma }(2m-2k+1)}(-2\sqrt{\pi }),0).\end{array}$$

For k = 0, Q(2m, 0) < 0 except for the term $Q(0,0)=\sqrt{\pi }/2$ which also becomes negative in the full sum, so we ignore these terms.

We now turn our attention to the full sum ${\displaystyle {\sum }_{k=0}^m\frac{\mathrm{\Gamma }(k+1/2)}{\mathrm{\Gamma }(k+1)}}Q(2m,2k)$. As before, we define for clarity

$$\begin{array}{l}(I):=\frac{1}{8\sqrt{\pi }}{\displaystyle \sum _{k=1}^m\frac{\mathrm{\Gamma }(k+1/2)}{\mathrm{\Gamma }(k+1)}\frac{\mathrm{\Gamma }(2m-1/2)\mathrm{\Gamma }(2k-1/2)}{\mathrm{\Gamma }(2m+1)\mathrm{\Gamma }(2k+1)}}\\ (\mathit{II}):=\frac{1}{4\pi }{\displaystyle \sum _{k=1}^m\frac{\mathrm{\Gamma }(k+1/2)}{\mathrm{\Gamma }(k+1)}\frac{1}{{(2m-2k+1)}^{3/2}}}(\sqrt{8k}+\frac{\sqrt{4k}}{2k-1})\\ (\mathit{III}):=\frac{1}{4\pi }{\displaystyle \sum _{k=1}^m\frac{\mathrm{\Gamma }(k+1/2)}{\mathrm{\Gamma }(k+1)}\frac{\sqrt{2k-1}}{{(2m-2k+3)}^{3/2}}}\\ (IV):=\frac{1}{4\sqrt{\pi }}{\displaystyle \sum _{k=1}^m\frac{\mathrm{\Gamma }(k+1/2)}{\mathrm{\Gamma }(k+1)}\frac{\mathrm{\Gamma }(2k+1/2)}{\mathrm{\Gamma }(2k)}}\frac{\mathrm{\Gamma }(2m-2k+1/2)}{\mathrm{\Gamma }(2m-2k+2)}\\ (V):=\frac{1}{4\pi }{\displaystyle \sum _{k=1}^m\frac{\mathrm{\Gamma }(k+1/2)}{\mathrm{\Gamma }(k+1)}}max(\frac{\mathrm{\Gamma }(2k+3/2)}{\mathrm{\Gamma }(2k+1)}\frac{\mathrm{\Gamma }(2m-2k-1/2)}{\mathrm{\Gamma }(2m-2k+1)}(-2\sqrt{\pi }),0).\end{array}$$

Using the bounds in lemma 20,

$$\begin{array}{l}(I)\le {\displaystyle \sum _{k=1}^m\frac{1}{32\sqrt{\pi }{k}^{1/2}}\frac{1}{\mathit{mk}}\frac{1}{\sqrt{2m-1}\sqrt{2k-1}}\le \frac{1}{32\sqrt{\pi }},}\\ (\mathit{II})\le \frac{1}{4\pi }{\displaystyle \sum _{k=1}^m\frac{1}{k^{1/2}{(2m-2k+1)}^{3/2}}(4\sqrt{k})}\\ \le \frac{1}{\pi }(1-\frac{1}{\sqrt{2m-1}})\le \frac{1}{\pi },\\ (\mathit{III})\le \frac{1}{4\pi }{\displaystyle \sum _{k=1}^m\frac{1}{k^{1/2}}\frac{\sqrt{2k-1}}{{(2m-2k+3)}^{3/2}}}\\ \le \frac{1}{\sqrt{24\pi }},\\ (\mathit{IV})\le \frac{1}{4\sqrt{\pi }}\left({\displaystyle \sum _{k=1}^m\frac{{(2k)}^{1/2}}{k^{1/2}}\frac{1}{(2m-2k+1)\sqrt{2m-2k}}+\sqrt{\pi }}\right)\\ \le \frac{1}{2\pi }+\frac{1}{2},\\ (V)=\frac{1}{4\pi }4\pi \frac{\mathrm{\Gamma }(2m+3/2)}{\mathrm{\Gamma }(2m+1)}\frac{\mathrm{\Gamma }(m+1/2)}{\mathrm{\Gamma }(m+1)}\\ \le \frac{\sqrt{2m+1}}{\sqrt{m}}\le \sqrt{3}.\end{array}$$

Finally,

$$\begin{array}{c}{\displaystyle \sum _{k=0}^m\frac{\mathrm{\Gamma }(k+1/2)}{\mathrm{\Gamma }(k)}Q(2m,2k)\le (I)+(\mathit{II})+(\mathit{III})+(IV)+(V)}\\ \le \mathrm{2.8.}\end{array}$$

To deduce the inequality (31), we use the previously derived bounds to show that

$$\begin{array}{l}Q(2m-1,2k-1)\le \frac{1}{4\pi }{\displaystyle \sum _{i=1}^{2k-3}\sqrt{i+1}\frac{1}{{(2k-i-2)}^{3/2}{(2m-i)}^{3/2}}}\\ +\frac{1}{4\pi }\sqrt{\pi }\frac{\mathrm{\Gamma }(2k-1/2)}{\mathrm{\Gamma }(2k-1)}\frac{\mathrm{\Gamma }(2m-2k+1/2)}{\mathrm{\Gamma }(2m-2k+2)}\\ +\frac{1}{4\pi }max\left(\frac{\mathrm{\Gamma }(2k+1/2)}{\mathrm{\Gamma }(2k)}\frac{\mathrm{\Gamma }(2m-2k+1/2)}{\mathrm{\Gamma }(2m-2k+2)}(-2\sqrt{\pi }),0\right),\end{array}$$

so that Q(2m − 1; 2k − 1) ≤ Q(2m, 2k). Now it suffices to note that in the full sum, ${\displaystyle {\sum }_{k=1}^m\frac{\mathrm{\Gamma }(k+3/2)}{\mathrm{\Gamma }(k+1)}Q(2m-1,2k-1)\le 2}{\displaystyle {\sum }_{k=1}^m\frac{\mathrm{\Gamma }(k+1/2)}{\mathrm{\Gamma }(k)}Q(2m-1,2k-1)}$ and we get

$${\displaystyle \sum _{k=1}^m\frac{\mathrm{\Gamma }(k+3/2)}{\mathrm{\Gamma }(k+1)}Q(2m-1,2k-1)\le 2{\displaystyle \sum _{k=1}^m\frac{\mathrm{\Gamma }(k+1/2)}{\mathrm{\Gamma }(k)}Q(2m,2k)\le \mathrm{5.6.}}}$$

We now return our focus to finding a bound on the expression for α_ℝ (d) given in (28). Since ψ₁, ψ₂ depend on the parity of d, we split in to two cases.

Odd d = 2m + 1

From (see [GR94] section 7.414 equation 6),

$${\displaystyle {\int }_0^{\infty }{e}^{-x/2}{L}_{2m}(x)dx=2,}$$

thus equation (28) becomes

$${\alpha }_{ℂ}(2m+1)-{\alpha }_{ℝ}(2m+1)=\frac{1}{{(2m+1)}^{3/2}}\frac{\mathrm{\Gamma }(m+1)}{\mathrm{\Gamma }(m+1/2)}\left({\displaystyle \sum _{k=0}^m\frac{\mathrm{\Gamma }(k+1/2)}{\mathrm{\Gamma }(k)}Q(2m,2k)-2^{1/2}}\right),$$

and using the first bound in Lemma 22,

$${\alpha }_{ℂ}(2m+1)-{\alpha }_{ℝ}(2m+1)\le 2.8\sqrt{m+1/2}\frac{1}{{(2m+1)}^{3/2}}\le m^{-1}.$$

Even d = 2m

For d = 2m, we have

$${\alpha }_{ℝ}(2m)={\alpha }_{ℂ}(2m)-\frac{1}{2{(2m)}^{3/2}}{\displaystyle {\int }_0^{\infty }{x}^{1/2}}\frac{\mathrm{\Gamma }(m+1/2)}{\mathrm{\Gamma }(m)}{L}_{2m-1}(x)\{{\psi }_1(x)-{\psi }_2(x)\}dx.$$

We split the integral into two parts,

$$\begin{array}{l}(I):=\frac{1}{2{(2m)}^{3/2}}{\displaystyle {\int }_0^{\infty }{x}^{1/2}\frac{\mathrm{\Gamma }(m+1/2)}{\mathrm{\Gamma }(m)}{L}_{2m-1}(x){\psi }_1(x)dx}\\ (\mathit{II}):=\frac{-1}{2{(2m)}^{3/2}}{\displaystyle {\int }_0^{\infty }{x}^{1/2}\frac{\mathrm{\Gamma }(m+1/2)}{\mathrm{\Gamma }(m)}{L}_{2m-1}(x){\psi }_2(x)dx}.\end{array}$$

Expanding from the definition of ψ₁ above, we have

$$\begin{array}{l}(I)=\frac{1}{2{(2m)}^{3/2}}{\displaystyle {\int }_0^{\infty }\frac{\mathrm{\Gamma }(m+1/2)}{\mathrm{\Gamma }(m)}{x}^{1/2}{L}_{2m-1}(x)e^{-x}{\displaystyle \sum _{k=0}^{m-1}\frac{\mathrm{\Gamma }(k)}{\mathrm{\Gamma }(k+1/2)}{L}_{2k-1}(x)dx}}\\ =\frac{1}{2{(2m)}^{3/2}}\frac{\mathrm{\Gamma }(m+1/2)}{\mathrm{\Gamma }(m)}{\displaystyle \sum _{k=1}^m\frac{\mathrm{\Gamma }(k+3/2)}{\mathrm{\Gamma }(k+1)}Q(2m-1,2k-1),}\end{array}$$

so by Lemma 22,

$$(I)\le \frac{1}{2{(2m)}^{3/2}}\frac{\mathrm{\Gamma }(m+1/2)}{\mathrm{\Gamma }(m)}5.6\le \frac{1}{m^{1/2}}.$$

The other part of the integral is

$$\begin{array}{c}(\mathit{II})=\frac{-1}{2{(2m)}^{3/2}}{\displaystyle {\int }_0^{\infty }{x}^{1/2}\frac{\mathrm{\Gamma }(m+1/2)}{\mathrm{\Gamma }(m)}{L}_{2m-1}(x){(x/2)}^{-1/2}{e}^{-x/2}\left[\frac{2\mathrm{\Gamma }(1/2,x/2)}{\mathrm{\Gamma }(1/2)}-1\right]dx}\\ =\frac{-1}{4m^{1/2}}{\displaystyle {\int }_0^{\infty }\frac{\mathrm{\Gamma }(m+1/2)}{\mathrm{\Gamma }(m)}{L}_{2m-1}(x)e^{-x/2}\frac{2\mathrm{\Gamma }(1/2,x/2)}{\mathrm{\Gamma }(1/2)}dx+\frac{1}{2m^{3/2}}\frac{\mathrm{\Gamma }(m+1/2)}{\mathrm{\Gamma }(m)},}\end{array}$$

where we use the fact that for odd 2m − 1 (see [GR94] section 7.414 equation 6),

$${\displaystyle {\int }_0^{\infty }{L}_{2m-1}(x)e^{-x/2}dx=-2.}$$

We can bound the first integral in the expression of (II) by

$$\begin{array}{l}\left|{\displaystyle {\int }_0^{\infty }{L}_{2m-1}(x)e^{-x/2}\mathrm{\Gamma }(1/2,x/2)dx}\right|\le {\left({\displaystyle {\int }_0^{\infty }{e}^{-x}{L}_{2m-1}{(x)}^{2}dx}\right)}^{1/2}{\left({\displaystyle {\int }_0^{\infty }\mathrm{\Gamma }{(1/2,x/2)}^{2}dx}\right)}^{1/2}\\ ={\left[{\displaystyle {\int }_0^{\infty }{\left({\displaystyle {\int }_x^{\infty }{t}^{-1/2}{e}^{-t}dt}\right)}^{2}dx}\right]}^{1/2}\\ ={\left[{\displaystyle {\int }_0^1{\left({\displaystyle {\int }_x^{\infty }{t}^{-1/2}{e}^{-t}dt}\right)}^{2}dx+{\displaystyle {\int }_1^{\infty }{\left({\displaystyle {\int }_x^{\infty }{t}^{-1/2}{e}^{-t}dt}\right)}^{2}dx}}\right]}^{1/2}\\ \le {\left(\mathrm{\Gamma }{(1/2)}^2+{\displaystyle {\int }_1^{\infty }{(e^{-x})}^{2}dx}\right)}^{1/2}\le {(\pi +e^{-2}/2)}^{1/2},\end{array}$$

so finally

$$\begin{array}{l}(\mathit{II})\le \frac{{(\pi +1/2e^{-2})}^{1/2}}{2\sqrt{\pi }{m}^{3/2}}\frac{\mathrm{\Gamma }(m+1/2)}{\mathrm{\Gamma }(m)}+\frac{m^{1/2}}{2m^{3/2}}\\ \le 1.01m^{-1}.\end{array}$$

Combining the above bounds we see that in the case of even d = 2m,

$${\alpha }_{ℂ}(2m)-{\alpha }_{ℝ}(2m)=(I)+(\mathit{II})\le 2.01m^{-1}.$$