Direct observation of RuvAB-catalyzed branch migration of single Holliday junctions

Abstract

Holliday junctions form during DNA repair and homologous recombination processes. These processes entail branch migration, whereby the length of two arms of a cruciform increases at the expense of the two others. Branch migration is carried out in prokaryotic cells by the RuvAB motor complex. We study RuvAB-catalyzed branch migration by following the motion of a small paramagnetic bead tethered to a surface by two opposing arms of a single cruciform. The bead, pulled under the action of magnetic tweezers, exerts tension on the cruciform, which in turn transmits the force to a single RuvAB complex bound at the crossover point. This setup provides a unique means of measuring several kinetic parameters of interest such as the translocation rate, the processivity, and the force on the substrate against which the RuvAB complex cannot effect translocation. RuvAB-catalyzed branch migration proceeds with a small, discrete number of rates, supporting the view that the monomers comprising the RuvB hexameric rings are not functionally homogeneous and that dimers or trimers constitute the active subunits. The most frequently encountered rate, 98 ± 3 bp/sec, is approximately five times faster than previously estimated. The apparent processivity of branch migration between pauses of inactivity is ≈7,000 bp. Branch migration persists against opposing forces up to 23 pN.

Evolution has given rise to elaborate mechanisms that allow organisms to cope with ubiquitous damage to their genomes. Damage may prevent the replication of the genome and thus cell division. One of the mechanisms for damage repair and bypass involves strand exchange between two homologous DNA segments, resulting in the formation of a Holliday junction (1). Recombinational repair mechanisms entail the motion of a junction in a process called branch migration. The RuvA and RuvB proteins drive branch migration of Holliday intermediates formed during recombination and DNA repair in Escherichia coli (2). Electron microscopy (3–5), footprinting and centrifugation (6), and x-ray structure determination (5) indicate that working complexes consist of two hexameric RuvB rings that bind around opposite arms of a Holliday junction, sandwiching two RuvA tetramers that bind at the crossover point. This structure suggests that during branch migration (7), the RuvB ATPases (8) increase the length of the two arms around which they assemble, at the expense of the other two arms.

Not much is known about how RuvAB induces branch migration at the microscopic level. Biochemical evidence suggests that the catalytic activity of monomers in an RuvB hexamer is nonhomogeneous (9, 10) and that RuvB monomers form functional subunits, each of which carries out a complete mechanochemical cycle. Structural studies support these conclusions (5, 11). However, it has not been determined whether these functional subunits are dimers or trimers, what the implications of functional inhomogeneity on enzyme activity are, or whether RuvB rings rotate or remain fixed relative to the RuvA octamer to which they are bound. Key parameters characterizing the enzymatic activity of the RuvAB complex, such as the rate of branch migration, its homogeneity, or its processivity, have not been determined with precision.

To shed light on some of these issues, we studied RuvAB-induced branch migration at the level of single cruciforms. In our setup, a single cruciform tethers a paramagnetic bead to a surface through two opposing arms (Fig. 1). Branch migration induced by a single RuvAB complex bound at the junction is monitored through the motion of the bead, on which an external load can be applied by using magnetic tweezers. The force on the bead induces tension on the cruciform substrate, which can either oppose RuvAB-induced branch migration or bias its motion forward. Single-molecule manipulation techniques have been crucial in the characterization of enzymatic behavior and have provided important insights into the detailed biochemical mechanism that generates the resultant motion in the case of other DNA-processing protein motors such as RNA polymerase (12, 13), DNA polymerase (14, 15), the φ 29 portal motor (16), and helicases (17–19).

Fig. 1.

Scheme for observing branch migration by a single RuvAB complex under an applied force. A junction with two very long arms formed from seven oligonucleotides (see Materials and Methods) and two ≈20-kbp segments of the λ-phage DNA tethers a paramagnetic bead to a glass surface. Regions of heterology (denoted by shaded regions in the four arms; 12 bp in the vertical arms and 40 bp in the horizontal arms) prevented spontaneous branch migration. The gray square at the crossover point and the pair of black ovals sandwiching it represent the RuvA and RuvB components of the complex, respectively. Dotted arrows represent the direction of migration for the shown orientation of the RuvAB complex after addition of ATP. The pair of magnets induces a field (gray dashed lines) that effects a force opposing branch migration (hatched arrow). When the RuvB rings assemble on the vertical arms, the direction of branch migration is reversed. The motion of the bead was followed through a microscope and recorded at video rate.

Our studies reveal the existence of a small number of different, well defined branch-migration states characterized by a discrete set of branch-migration rates. The most frequent of these rates is larger than previously estimated. This behavior provides direct evidence for independent functional subunits within the hexameric RuvB rings, each of which can generate translocation one at a time. The measured rate during a branch-migration episode depends on the number of active functional subunits. Additionally, our measurements allow us to estimate directly the processivity of the RuvAB complex and the force a single complex can exert against tension applied on the cruciform substrate. These characteristics are either not measurable or not easily accessed through experiments in which large ensembles of protein–DNA complexes are interrogated simultaneously.

Materials and Methods

Assembly of a Cruciform DNA Template with Two Long Arms. Cruciforms used in our experiments were constructed in three stages (for details see Supporting Materials and Methods, which is published as supporting information on the PNAS web site). First, small synthetic Holliday junctions were constructed from seven oligomers. Second, λ DNA (100 μg; Roche, Indianapolis) was cut with NgoMIV at the unique site, generating a 20,040-bp fragment starting from the left cos site. Third, the 20-kbp fragments were divided into two portions and ligated with appropriate oligos modified with either biotin or digoxigenin. Finally, the labeled λ arms and Holliday junctions were mixed and ligated to form the cruciforms.

Bead–DNA Constructs and Sample Cell Preparation. Bead–DNA constructs were formed by incubation of the biotin- and digoxigenin-tagged cruciforms with 2.8-μm-diameter M280 magnetic tosyl-activated beads (Dynal, Oslo). The beads were coated with digoxigenin antibodies for 30 min in PBS buffer with 0.5 M NaCl, followed by diluting 10× with GB buffer (10 mM Tris·HCl/200 mM KCl/5% DMSO/0.1 mM EDTA/0.2 mg/ml α-casein, pH 8.0). Experiments were carried out within capillary cells as described (20). The bead–Holliday junction constructs in GB buffer were flushed through the capillary and anchored to the streptavidin-coated walls by their biotin tags. The single bonds between the cruciform and the bead on one hand, and the cruciform and the surface on the other hand, ensure that no twist accumulates during the activity of the RuvAB complex. The design of the sticky ends of all DNA molecules also ensured that the only way in which a bead could be tethered stably to the surface at the appropriate contour length was by ligation of arms and properly assembled junctions. All other DNA molecules were flushed away or did not form part of a tether. Applying a sufficiently high force before the addition of proteins and ATP yielded the expected ≈13.6-μm length of the cruciform, which allowed us to discriminate against beads tethered by nonspecific binding or by more than one cruciform.

RuvA and RuvB Proteins and Branch-Migration Assays. RuvA and RuvB were purified from overexpressing E. coli as described (21). Their activity was tested by electrophoretic mobility-shift assays using radiolabeled junctions as probes. In these assays, RuvA protein alone bound junctional DNA in a stable gel-shifted complex. Junction dissociation as a result of branch migration necessitated the presence of RuvA, RuvB, and ATP in the concentrations used, as described (22).

All single-molecule experiments were carried out at 37°C, with 0.85 μM RuvA, 1.7 μM RuvB, and 1 mM ATP unless specified otherwise. The proteins were flushed through the capillary in a modified GB buffer including 100 μg/ml BSA and 5 mM MgCl₂ as well.

Force, Contour-Length Determination, and Optical Setup. Samples containing cruciform-tethered magnetic beads were observed by bright-field illumination using a home-built inverted microscope and tracked by video for subsequent computer analysis. Height–force measurements were made by using a magnetic force technique (20, 23). The temporal, height, and force resolutions of our measurements are 40 msec, ≈80 bp, and 1% of the measured force, respectively.

Data Processing and Analysis. The bead height z(t) was determined as a function of time as follows. First, a field of view in which both a bead tethered by a cruciform and a reference bead stuck to the glass surface by Van der Waals forces were found. Next, the longitudinal fluctuations of both the reference and cruciform were simultaneously tracked by a two-step procedure. First, the radial profile of each bead in a tracking movie was correlated to its corresponding library (20), obtaining a match to an accuracy of ≈400 nm. Second, a refined estimate was obtained by calculating the phase difference in the outer rings of the image between that of the tracked bead and the library's rough maximum, generating an improved match to an accuracy of <30 nm (23). Finally, z(t), the height of the bead, was obtained by subtracting the library match of the cruciform from that of the reference, the signal of which represents the fluctuations of the optical focus.

Measured changes in z(t) were translated into changes in the contour length of the cruciform arms tethering the bead L(t), assuming the fluctuating cruciform to be in equilibrium during branch migration. This assumption allowed us to describe its elastic behavior by the worm-like chain model (24), an expression for the pulling force f in which the linear extension of the tethering molecule as given by the height z appears only through the ratio z/L. Because the force on the bead is held constant during branch migration, L must be such as to keep the ratio z/L and therefore f constant. Migration rates were derived from L(t) data by fitting the latter with piecewise linear functions using the Levenberg–Marquardt algorithm. To avoid overfitting, the number n of line segments was chosen as the smallest integer for which fitting with n + 1 segments reduced the mean square deviation from the data by 3–5%, relative to the fit with n segments (25).

Results and Discussion

To observe branch migration in a synthetic cruciform (26), we assembled the construct shown in Fig. 1 (see Materials and Methods). A small DNA four-way junction (50–60 bp per arm) was assembled from seven oligonucleotides. The junction then was used to ligate together two identical 20-kbp DNA fragments in a head-to-head orientation. The long arms of the cruciform were labeled, allowing the cruciform to tether a bead to a glass surface, the motion of which was followed in real time. Small regions of heterology in the arms of the small junction prevented appreciable spontaneous branch migration, ensuring near uniformity in the initial conditions of all the nucleoprotein complexes. The side arms of the cruciform are initially just long enough to accommodate the RuvB rings (6). Therefore, branch migration can occur initially only by the extension of the side arms, driving a bead downward.

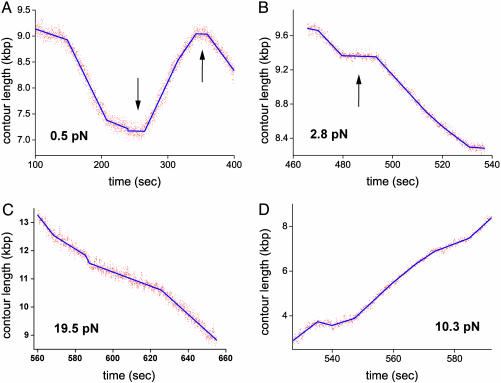
Branch-Migration Episodes Are Separated by Pauses. Results of typical branch-migration experiments obtained at different values of the applied force are depicted in Fig. 2. Each panel shows a plot of the total contour length L(t) of the arms of a single cruciform tethering a bead to a surface as a function of time. Episodes of activity typically spanning several kilobase pairs (>10 sec in duration) are interrupted by pauses typically 10–20 sec long, during which L(t) remains unchanged (as shown in A and B by arrows). After a pause, the direction of branch migration changes in ≈50% of cases. Branch migration can take place in either the forward direction, during which L(t) decreases (Fig. 2C), or reverse direction, during which L(t) increases (Fig. 2D). Note that for forward migration, the applied force acts against the RuvAB complex, whereas for reverse migration, the RuvAB complex and the applied force act in the same direction. The fact that transitions between forward and reverse directions are equally likely after pauses strongly suggests that pauses are caused by the dissociation of at least the RuvB motors from the junction and that resumption of branch migration in either direction corresponds to the two equal probabilities of assembling two new RuvB hexamers around each of the two pairs of opposing arms.

Fig. 2.

RuvAB-catalyzed migration of single Holliday junctions. The contour length of cruciform arms tethering beads to a surface is plotted as a function of time for four values of the applied force. (A and B) Episodes of branch-migration activity are interrupted by pauses (arrows). Branch migration changes direction after a pause (as illustrated in A) in ≈50% of cases. (C) Branch-migration episode illustrating forward motion, in which the height of the bead decreases, against the applied force. (D) Reverse branch-migration event in which the applied force and the RuvAB complex promote branch migration in the same direction. Changes in branch-migration rate are observed in both forward and reverse motion (as illustrated in B and C). The data were fitted with piecewise linear functions by using the Levenberg–Marquardt algorithm.

Branch Migration Exhibits Discrete Changes of Rate. Another salient feature of the traces shown in Fig. 2 is the occurrence of sharp changes in the rate of branch migration, both in the forward (Fig. 2C) and reverse (Fig. 2D) directions. Note that these changes do not necessarily occur after pauses. Furthermore, the succession of rates observed during different runs carried out under the same experimental conditions varies. No DNA sequence dependence was observed within the resolution of our experiments. To test whether the sharp changes in rate may be caused by the assembly/dissociation of additional RuvB rings around the junction arms, in tandem with the rings sandwiching the RuvA octamer, we carried out preliminary experiments at lower RuvB concentrations. For our protein preparation, enzymatic activity was observed only for RuvB concentrations that are >0.25 μM. This result does not depend on the concentration of RuvA, and it is consistent with similar observations in bulk experiments by Marrione and Cox (10) and West and coworkers (26), who also reported that a relatively high concentration of RuvB is necessary to generate enzymatic activity. It is interesting that neither group observed any significant activity for RuvB concentrations <0.25 μM either. This fact precluded protein titrations over a larger range.

A typical trace of contour length as a function of time is shown in Fig. 3A, taken at a RuvB concentration of 0.9 ± 0.2 μM. As in the traces of Fig. 2 obtained at 1.7 μM, sharp changes of rate are also observed. Moreover, the rates and the processivity (see below) are comparable with those at the higher concentration. The only significant difference in the behaviors at the two concentrations seems to be in the duration of pauses: pauses at the lower RuvB concentration are considerably longer than those observed at the higher concentration. Note that in other runs, longer pauses were observed. Thus, changes in rate seem to be a characteristic feature of an active complex, and different RuvB concentrations affect only the typical time for complex formation.

Fig. 3.

Branch migration of individual Holliday junctions. (A) Branch-migration trace obtained at 0.9 ± 0.2 μM RuvB and 0.6 pN. The contour length as a function of time exhibits sharp changes in branch-migration rates and pauses of much longer duration than traces obtained at 1.7 μM RuvB (Fig. 2). The rates are comparable in both cases. (B) Force-induced branch migration. RuvAB-induced branch migration is interrupted by fast runaway or force-induced migration episodes of the bead upward (arrows). Runaway migration episodes interrupt RuvAB-catalyzed branch migration either in the reverse or forward direction or after pauses.

For forces above ≈12 pN, bead motion may change sharply from an RuvAB-catalyzed migration state (either forward or reverse) to a runaway state in which the bead moves rapidly upward as a result of the applied force (Fig. 3B). Rates of force-induced migration fall in the range of 1,000 bp/sec (≈10 times faster than RuvAB-induced migration). As the force increases above 12 pN, RuvAB-induced migration episodes are interrupted more frequently by runaway branch migration until no RuvAB-catalyzed branch migration is observed above 25 pN.

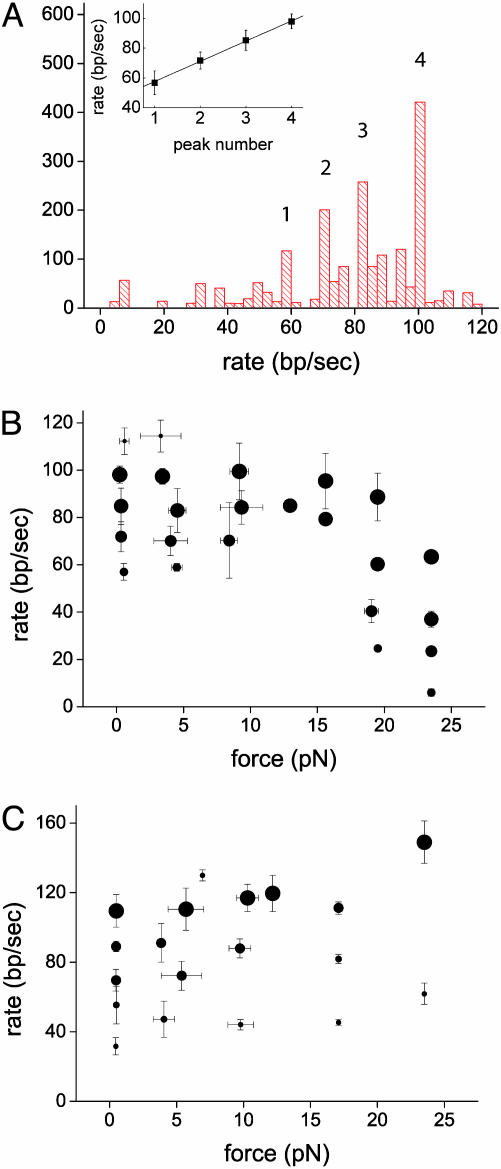
Branch-Migration Rates Cluster into Nearly Equally Spaced Values. By fitting contour-length data with piecewise continuous sets of lines (Fig. 2), we obtained the associated migration rates during each run. Fig. 4A shows a histogram of forward migration rates compiled from 15 runs carried out for forces <1 pN. Because episodes corresponding to some branch-migration rates are considerably longer and thus more frequent than others, rates have been weighted by the duration of the corresponding episodes in compiling the histogram. The histogram exhibits distinct, well defined peaks (for a statistical analysis ruling out the null hypothesis that RuvAB effects branch migration in a unimodal fashion see Supporting Materials and Methods). The peak with the most frequently occurring rate is centered at 98 ± 3 bp/sec, a value that is 2.5–10 times faster than values lying within the range of 8–40 bp/sec estimated from bulk measurements (22, 27). An average of rates weighted by the duration of the respective episodes yields 77 ± 24 bp/sec (mean ± standard error). The lower values within this interval are close to the high-end values measured in the bulk. However, the relatively large inaccuracy in the bulk-measured rates, which derives from an uncertainty in the determination of the position of Holliday junctions, precludes a more detailed comparison between bulk and single-molecule rates. The measurements presented here are fundamentally different from bulk measurements in that migration rates are measured directly, isolated from other effects such as assembly or initiation of migration. Note that the step time for spontaneous, uncatalyzed migration of Holliday junctions per base pair, measured at 37°C, is 300 msec (28, 29).

Fig. 4.

Statistics of migration rates and their dependence on force. (A) Histogram of rates of forward episodes from 15 runs carried out at forces <1 pN. The statistically significant peaks in the histogram, corresponding to the rate values 57 ± 4, 71 ± 5, 85 ± 4, and 98 ± 3 bp/sec, are numbered. (Inset) Branch-migration rates corresponding to the peaks in A as a function of the peak number. The straight line is a best fit yielding an average separation of 14 ± 3bp/sec between adjacent peaks. Migration rates as a function of force in the forward (B) and reverse (C) direction are shown. Data points correspond to the peak centers of rate histograms averaged over bins 1-pN wide and comprise five different runs on average. Symbol diameter is proportional to the height of the corresponding peak in the appropriate histogram of rates. Error bars correspond to peak widths at half-height.

A plot of the mean migration rate corresponding to each peak as a function of the peak number is shown in Fig. 4A Inset. Error bars were calculated by adding in quadrature the individual errors from rates contributing to each peak. The slope of a straight line fit to these data, 14 ± 3bp/sec, is an estimate of the mean difference in rate between adjacent peaks in the histogram. The fact that the observed rates of branch-migration cluster into a small number of peaks, i.e., four, together with the nearly equal difference in rate between adjacent peaks, provides evidence for the existence of functional subunits within RuvB hexamers (not necessarily monomers), each of which is capable of generating a translocation step of identical size, working one after the other: ATP is hydrolyzed into ADP within a given functional subunit. ADP turnover is then triggered allosterically by the binding of ATP to a different functional subunit (10), and this sequence of events is then repeated (it is unknown at which stage in the cycle translocation occurs). In this picture, the rate measured during a given branch-migration episode depends on the number of functional subunits capable of completing a full mechanochemical cycle. Inactive units induce dead time, lowering the step frequency and thus the branch-migration rate. The rate can change in discrete steps, because additional subunits become either active or inactive.

A number of investigations lend support to the picture described above. The hydrolysis of two ATPs per catalytic step of an RuvB hexamer (9, 10) and the fact that RuvA octamers bound at the crossover point bind to only two RuvB monomers in each hexameric ring (5) have strongly suggested that hexamers are not homogeneous and that dimers or trimers are the functional units involved in each mechanochemical cycle (5, 10, 11, 30). Furthermore, not all functional subunits are indispensable for branch migration to take place: experiments with RuvB hexamers consisting of both wild-type and ATPase-defective subunits in a 1:1 ratio exhibit branch migration, albeit with a reduced efficiency (30, 31).

One could also envision an alternative “truck-wheel” scenario in which changes in migration rate are caused by changes in the number of RuvB hexamers bound per arm of the cruciform, each additional hexamer generating translocation or possibly hindering the motion. In this scenario, changes of rate may therefore reflect the assembly or disassembly of hexamers from the junction complex. We cannot rule out this scenario completely. However, biochemical evidence argues against it: RuvA greatly enhances the effects of DNA on the ATPase activity of RuvB (10, 32–34). Furthermore, it induces a more intimate and continuous contact of RuvB with DNA, and thus its effects are not limited merely to localize the RuvB hexamers to the crossover point. Therefore, the RuvB hexamers bound to the RuvA octamer at the crossover point have a higher ATPase activity than any hexamers bound in tandem around the same arms farther out. Consequently, RuvA-bound RuvB hexamers will induce branch migration at a higher rate than RuvB rings not bound to RuvA.

Dependence of Branch-Migration Rates on the Applied Load. The behavior of migration of the cruciform–RuvAB complex in the reverse and forward directions is similar for loads below ≈10 pN. In both cases, a discrete set of migration rates, which coincide within experimental error, is observed. However, above 10 pN, the behavior of forward and reverse directions differs. This behavior is shown in Fig. 4 B and C, in which the position of the peak centers in the histograms is plotted as a function of the applied force f in both the forward and reverse directions. The size of symbols in these plots represents the height of the respective peaks in the histograms. In the forward case, the peak centers show little or no dependence on f below ≈15 pN. Above ≈15 pN, peak centers shift to lower values, and no RuvAB-catalyzed branch migration is observed above f ≈ 25 pN. The fact that four migration rates are still observed at f ≈ 23 pN, as opposed to a possible decrease in the number of branch-migration states with increasing load, indicates that the externally applied tension on the cruciform is transmitted and affects each functional subunit of the RuvB hexamers as it becomes active, slowing down its respective mechanochemical cycle. Thus, it is plausible to conclude that the maximal force that an RuvAB complex can exert against tension on the substrate while still generating branch migration is f ≈ 25 pN.

When both f and the RuvAB complex promote branch migration in the same direction, there is a moderate increase in rates for small values of f. As f increases more and more above 12 pN, runaway migration becomes prevalent and RuvAB-catalyzed migration events become more rare.

RuvAB Processivity Is Several Kilobase-Pairs Long. Given the multiplicity of branch-migration rates observed in these experiments, many definitions of processivity are possible. One estimate can be made by measuring the length of branch-migration episodes between pauses, assuming such pauses entail the dissociation of at least the RuvB hexamers. A histogram of episode lengths for forces <1 pN (shown in Fig. 5) is characterized by a median episode length of 7,200 ± 3,000 bp.

Fig. 5.

Processivity of single RuvAB complexes. Histogram of the length of episodes of RuvAB activity (kbp) in the forward direction. (Inset) Histogram of the duration of episodes of forward branch migration proceeding at a fixed rate. The observed rates have been compiled from experiments carried out with opposing forces <1 pN.

Whereas changes in the direction of branch migration occur after pauses, transition between states with different branch-migration rates are sharp and not mediated by pauses, which suggests an alternative measure of processivity given by the average length of tracts covered with the same rate. A histogram of duration of events for runs carried out for forces <1 pN is shown in Fig. 5 Inset independent of rate (there was no statistical difference between duration histograms for given rates). The median tract duration is 15 ± 3 sec, which translates to 1,500 bp at the most frequently occurring rate. Using both estimates, we claim that the RuvAB can maintain stability for several kilobase pairs. More precise measurements of processivity would entail both titration of RuvB and the presence of competitor.

Finally, we have studied the effects of varying ATP concentration on the rate of branch migration. The data shown in Table 1 demonstrate that all the results presented above were carried out under conditions in which ATP concentration was not rate limiting.

Table 1. Effects of varying ATP concentration on the rate of branch migration.

ATP concentration, mM	Dominant rate, bp/sec	Median rate, bp/sec	Difference between peaks, bp/sec
0.1	13 ± 3	7 ± 4	<4
0.3	35 ± 63	29 ± 5	6 ± 3
1	98 ± 3	86 ± 5	14 ± 3
2	99 ± 5	86 ± 7	16 ± 3

Conclusions

A hallmark of RuvAB-catalyzed branch migration revealed by the present experiments is the existence of a small, discrete number of states with different, nearly uniformly separated migration rates. This signature may be a direct manifestation of the functional asymmetry of monomers in the RuvB hexamers and the existence of functional subunits, dimers or trimers, each capable of completing one mechanochemical cycle. Such a scheme may make the RuvAB complex more reliable as a motor, relative to a motor in which all the subunits are indispensable. Although biochemical evidence combined with our data at lower RuvB concentrations lend further support to this model, additional experiments will be needed to obtain a more clear picture, because alternative scenarios such as the truck wheel discussed above are also possible and at this point cannot be ruled out.

At low loads, the most frequently occurring migration rate is 2–10 times larger than the values estimated from bulk assays. Inhomogeneous activity in large ensembles of complexes, as well as the existence of other rate-limiting steps in these assays (e.g., binding of RuvAB complexes at junctions and/or initiation of branch migration) may account for this difference. Branch migration persists for at least 1,500 bp on average before a change in rate is observed or for several thousand base pairs before a pause in activity occurs. Thus, the processivity of the RuvAB complex is high.

The tension on a cruciform above which no branch migration is observed, namely ≈25 pN, indicates that the RuvAB complex can exert forces that are large enough to either displace the histone-like proteins that shape local nucleoid structure, e.g., IHF or HU, or to dislodge nucleosomes (35, 36).