Abstract
Social cognitive theory (SCT) is among the most influential theories of behavior change and has been used as the conceptual basis of health behavior interventions for smoking cessation, weight management, and other health behaviors. SCT and other behavior theories were developed primarily to explain differences between individuals, but explanatory theories of within-person behavioral variability are increasingly needed as new technologies allow for intensive longitudinal measures and interventions adapted from these inputs. These within-person explanatory theoretical applications can be modeled as dynamical systems. SCT constructs, such as reciprocal determinism, are inherently dynamical in nature, but SCT has not been modeled as a dynamical system. This paper describes the development of a dynamical system model of SCT using fluid analogies and control systems principles drawn from engineering. Simulations of this model were performed to assess if the model performed as predicted based on theory and empirical studies of SCT. This initial model generates precise and testable quantitative predictions for future intensive longitudinal research. Dynamic modeling approaches provide a rigorous method for advancing health behavior theory development and refinement and for guiding the development of more potent and efficient interventions.
Keywords: Dynamical system modeling, Computational modeling, Control systems engineering, Health behavior theory, Social cognitive theory
SOCIAL COGNITIVE THEORY
Social cognitive theory (SCT) is among the most influential theories of human behavior [1] and has been used as the basis for many health behavior interventions [2–4]. SCT has served as the theoretical basis for most eHealth diet and physical activity interventions [5]. A recent review of mobile health interventions found that SCT or one of its variants served as the basis for all of the smoking cessation interventions that reported a theoretical basis, and was the predominant theoretical basis for weight management interventions [6].
SCT has a long history rooted in learning theory and the role of respondent and operant conditioning in shaping behavior. The seminal work of Bandura and Walters [7] on social learning theory expanded learning theory by incorporating observational or vicarious learning. Social learning theory, however, did not include self-beliefs or perceptions of the individual that could influence behavior, leading to the introduction of self-efficacy [8]. SCT grew from self-efficacy theory as cognitive, self-regulatory, and self-reflective processes became central to Bandura’s thinking [9]. Core to SCT is the concept of reciprocal determinism or triadic reciprocity in which behavior, personal factors, and environment interact and dynamically shape one another. Self-efficacy, the perceived capability to do what is required to perform a given behavior under varying conditions, plays a core role as a personal factor that influences behavior and that is influenced by behavior and the environment [8].
DYNAMIC COMPUTATIONAL MODELING OF HEALTH BEHAVIOR THEORIES
Conceptual and statistical models of SCT
Health behavior theories such as SCT are conceptual models of the hypothesized influences on behavior and their interrelations. These conceptual models are often tested via statistical models such as structural equation modeling (SEM) which estimate latent constructs via measured variables. For example, Anderson-Bill and colleagues [10] conducted a large, cross-sectional SEM study of a web-based weight management intervention and showed that perceived social support and self-regulatory skills were associated with physical activity and nutrition behavior. A similar cross-sectional SEM analysis of dietary intake in adolescent girls found that self-efficacy was positively associated with healthy eating but that behavioral intentions were not associated with dietary intake [11]. In a study of risky sexual behavior, Safren et al. [12] used cross-sectional SEM to assess the influence of SCT constructs on condom use and found that self-efficacy was associated with outcome expectancies and that vicarious learning was associated with condom use, but that these associations were only found in non-depressed participants.
Statistical modeling of cross-sectional data can provide information on the relative association among theoretical constructs, but longitudinal data are necessary to provide information on temporal directionality and potential causality among these constructs. Rimal [13], in one of the few longitudinal SEM studies of SCT, modeled self-reported exercise behavior, exercise knowledge, and exercise self-efficacy at baseline and years 2 and 6 post-baseline, and found a reciprocal relationship in which self-efficacy and knowledge predicted subsequent exercise behavior and vice versa. More recently, Dishman and colleagues [14] used latent growth modeling to examine the influences of self-efficacy and perceived social support at grade 6 on physical activity at grade 8. They found that self-efficacy was directly related to physical activity and that self-efficacy and perceived social support indirectly influenced the relationship between perceived barriers and physical activity.
Application of computational models to health behavior theories
In contrast to conceptual and statistical modeling approaches for representing and testing health behavior theories, dynamic computational modeling can more precisely represent dynamic feedback systems hypothesized by these theories (e.g., reciprocal determinism) and can generate more precise theoretical predictions [6]. For example, the statistical modeling research described above generally concluded that the results were supportive of SCT. These conclusions were based on some, but not all, SCT constructs having significant associations as hypothesized, and the full model accounting for modest to moderate variance (i.e., < 30 %) in self-reported behavior, often assessed at the same time (i.e., cross-sectional, not longitudinal). In contrast, a dynamic computational model of health behavior would test precise predictions of the behavior of interest at a specific future time point based on specific unit changes in the theoretical mediators. Failure to predict not only the direction but also the magnitude and timing of the behavior change would necessitate a revision of the model. Therefore, dynamic computational modeling provides a comprehensive analytic technique for testing theories of human behavior [6, 15–17]. Furthermore, this level of predictive precision facilitates the development of intensively adaptive interventions (IAIs) that adjust treatment over time based on real-time inputs [18] by identifying potential tipping points in the model and the doses of intervention required to produce the desired outcome.
Behavior has long been considered amenable to dynamical or control systems computational approaches [19–21]. Carver and Scheier [22] have argued that dynamical regulatory systems are critical to understanding behavior, and Bandura describes SCT in dynamic and self-regulatory terms [23]. Advances in technology, particularly in ecological momentary assessment [24] and passive sensor technologies [25] are beginning to provide the intensive longitudinal data necessary to model and test dynamic computational models. Recently, Navarro-Barrientos, Rivera, and Collins [16] developed a control system fluid analogy model for the theory of planned behavior (TPB), and Orr and colleagues [26] proposed a parallel constraint dynamical model of its precursor, the theory of reasoned action (TRA).
Purpose
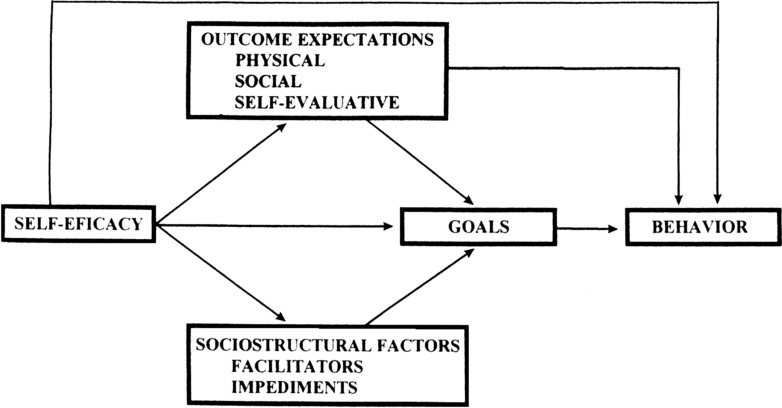
Following from this work on TRA/TPB dynamic models, we sought to develop a dynamic computational model of SCT. TRA and TPB have well-defined graphical representations of the theoretical constructs and their interdependencies [27] that, along with SEM studies based on this complete conceptual model, provided the basis for translating TRA/TBP conceptual and statistical models to a control systems computational dynamic model [16]. In contrast, SCT is a theory that has been described primarily in narrative form and has been refined, revised, and augmented over decades of writings by Bandura and others [28]. In 2004, Bandura offered a graphical schematic of SCT [29], shown in Fig. 1, that illustrates self-efficacy directly influencing behavior and also indirectly influencing behavior via its effects on outcome expectancies, goals, and sociocultural factors such as facilitators and impediments. This schematic has been used as the conceptual basis for previous SEM studies [e.g., 11], but we believe that it is a simplified and incomplete conceptual model of SCT when compared to the narrative descriptions of SCT elucidated over decades. For example, SCT specifies a number of factors such as social persuasion and observational learning that influence self-efficacy [8], but the schematic shows no influences on self-efficacy. SCT also postulates that outcome expectancy is influenced by many more factors than just self-efficacy, including the direct and observational experiences of outcomes over time [30], but these additional influences on outcome expectancy are not represented in the schematic. Perhaps most importantly, reciprocal determinism, a core aspect of SCT, postulates feedback loops between the intrapersonal constructs of SCT and the behavior and the environment [23], but the Bandura schematic represents only linear influences with none of these dynamic influences core to SCT. Therefore, in addition to the potential added precision of a computational dynamic model of SCT, we also sought to provide a more complete and comprehensive conceptual schematic of SCT that could guide future statistical modeling as well.
Fig. 1.
Conceptual schematic of SCT from Bandura (2004)
DEVELOPMENT AND DESCRIPTION OF A CONTROL SYSTEM MODEL OF SOCIAL COGNITIVE THEORY
Model development methods
To develop an initial dynamical system model of SCT, we reviewed the classic works on social cognitive theory [e.g., 9] and the literature on the statistical modeling of SCT described above. Since, to our knowledge, this is the first effort to produce a dynamic computational model of SCT, we adhered as closely as possible to Bandura’s theoretical writings, from the early work in social learning theory [31] through his more recent writings on social cognitive theory [32]. However, a lack of specificity of some associations between constructs, especially over time, required us to iterate the graphical representation of the dynamical system based on our understanding and interpretation of SCT and on the results of model simulations. For model parameters unspecified by SCT (e.g., magnitude, timing, or speed of change), iterative adjustments were made based on consistency of simulation outputs to theory as judged by the authors. The resulting graphical representation and parameters adjusted via simulations were then used as the basis for a set of differential equations that represented the influences of these SCT constructs on behavior over time.
The goal of this effort was to propose a more complete conceptual model of SCT and generate a computational model of SCT that represents SCT constructs as state variables and the relations among them as state transitions via differential equations. To aid in interpreting these equations, we graphically represent the influences among SCT constructs via the control systems fluid analogy which conceptualizes core constructs such as self-efficacy as “inventories” or “reservoirs” with levels that increase or decrease over time based on inflows and outflows [15–17]. These inventories represent the amount of a given theoretical construct that an individual or his/her environment possesses at any given time, and the inflows and outflows from these inventories represent the influences on these constructs over time. This fluid analogy model has similarities to the stock and flow models of system dynamics [33] and has been used to explicate other theories as a dynamic computational model [16]. Explicitly specifying SCT constructs and their corresponding hypothetical differential equations in a graphical control system representation has the potential not only to improve the explanatory and predictive power of the theory but also has relevant implications for how theory-based interventions are developed and optimized [34]. To examine the behavior of the proposed SCT model, simulations were performed to determine if the model performed as expected based on theoretical hypotheses and prior statistical modeling results.
The initial model derived from the narrative SCT descriptions was simulated in a number of scenarios. A comparison of the simulation results to empirical and logical constraints revealed the need to modify some influences among variables. For example, self-efficacy is generally found to be more predictive of behavior than outcome expectancies [e.g., 35] so the parameters in the model were adjusted to reflect a larger effect from self-efficacy than outcome expectancies on behavior over time. These simulations also revealed a number of inconsistent or illogical outcomes of the model under certain conditions that required additional iterations to better specify the values of parameters not previously specified by theory such as “inventory capacities” (i.e., the size of each construct “container” and the speed with which it fills) and input/output transformations. These simulations and successive iterative revisions to the model resulted in the proposed model and the fluid analogy described below. Given the number of inputs and parameters in the model, there are an exceedingly large numbers of simulations that could be performed for various parameter values across all possible combinations of inputs; therefore, we limited the simulations and iterative revisions of the model to simulations that varied one or two inputs over time. The full set of parameter specifications and additional simulations not reported in this paper are available at http://csel.asu.edu/SCT. While the fluid analogy schematic and the differential equations that underlie this schematic were developed in an interactive, incremental manner, we describe first the details of the model from the fluid analogy schematic, then the differential equations that underlie the model.
Description of the resulting SCT fluid analogy model
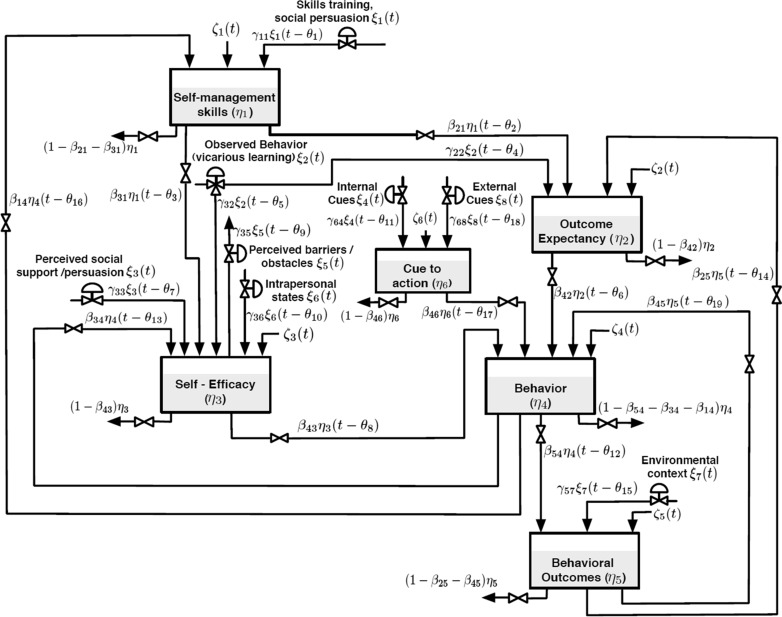
Figure 2 represents the resulting fluid analogy control system of social cognitive theory (SCT) that depicts how the various components of SCT interact with each other over time to increase or decrease behavior. Behavior (η 4) is an observable state variable depicted as a fluid inventory that represents the frequency and/or duration (i.e., amount) of the behavior as a function of time. For specific behaviors, the behavior inventory could be characterized by different metrics (e.g., frequency and duration of smoking, caloric intake). For this generic model intended for applicability across behaviors, the behavior inventory simply represents the amount of behavior. The model represents a continuous process, but could be used to test aggregated timeframes (i.e., aggregate frequency × duration of behavior within any given day).
Fig. 2.
Control system model of social cognitive theory
Self-efficacy (SE) (η 3), a state variable representing confidence in one’s ability to perform a given behavior, is a core construct of SCT [8] and is depicted as an inventory of varying levels that differs not only between individuals and specific behaviors but also fluctuates within an individual over time. SE influences the likelihood of engaging in the associated behavior and is influenced by the modeled variables that increase or decrease self-efficacy at any given time. The following are the SCT variables that are theorized to increase or decrease the SE value (i.e., the amount of SE depicted analogously as the volume of fluid in a reservoir).
Perceived barriers and obstacles (ξ 5) to engaging in any given behavior deplete self-efficacy (SE) [8]. For example, SE to engage in physical activity can be depleted due to perceived environmental barriers such as insufficient time, bad weather, and/or limited access to exercise facilities or safe walking paths. These perceived barriers are often conceptualized in SCT as slowly changing variables such as limited safe walking areas in a neighborhood; however, perception of these variables can vary substantially from day to day [36].
Perceived social support and verbal persuasion from others (ξ 3) increase the inventory of SE [8]. For instance, the availability of others who are willing to engage in physical activity with the individual or who verbally support increased physical activity of the individual increase SE to engage in physical activity. We represent perceived social support and verbal persuasion as an inflow that increases self-efficacy, but like many other inputs in the model, one could represent the opposite, the lack of social support and verbal dissuasion as an outflow instead. For model simplicity, when a construct could have positive (inflow or input) or negative (outflow or output) influences, we represented this graphically as an inflow. Representing these influences as inflows or outflows is irrelevant to the underlying differential equation since these equations treat inflows and outflows as positive or negative functions regardless of how they are graphically represented.
Observed behavior (vicarious learning) (ξ 2) of others successfully performing the behavior increases SE [8]. Observational or vicarious learning is central to Bandura’s social learning theory, a precursor to SCT, and influences not only self-efficacy for engaging in the behavior, but also outcome expectancies as the individual observes the result of others performing the behavior. There is considerable literature on the factors that influence the strength of vicarious learning [37], but for simplicity, we represent observed behavior here as a single input.
An array of physical, mental, and emotional intrapersonal states (ξ 6) either add or deplete the inventory of self-efficacy (SE) at any given time [8]. These intrapersonal factors are treated as a single input or inflow in this model, but a more complex model could represent these various intrapersonal factors as multiple inflows (positive) and outflows (negative).
Prior experience engaging in the behavior (β 34) is a gain parameter representing the critical learning feedback loop that adds or depletes SE to subsequently engage in the behavior. This is a positive feedback loop in which successfully engaging in the behavior increases self-efficacy to engage in the behavior, which subsequently increases the likelihood of engaging in the behavior [8]. Conversely, failure to successfully engage in the desired behavior depletes self-efficacy, which subsequently decreases the likelihood of engaging in the behavior in the future. It is important to note that “success” and “failure” are defined differently between individuals and within individuals over time, and the β 34 parameter adjusts the influence of behavior on self-efficacy to account for this inter- and intra-person variability.
Self-management or self-regulatory skills (η 1) contribute to self-efficacy [38]. This set of skills involves a class of activities such as self-monitoring, goal setting, self-reinforcement, and related methods by which the individual increases the potential likelihood for engaging in a given behavior. Self-management skills influence both self-efficacy and outcome expectancies. SCT is philosophically an agentic system in which the individual is the “controller,” and these self-regulatory skills are central to that perspective. Inputs into the self-management inventory include formal skill training, planned observational learning, and verbal persuasion from self or others (ξ 1), all tools commonly used in health behavior interventions to improve self-management skills. SEM studies have modeled self-efficacy as directly influencing self-management or self-regulatory skills [e.g., 10], but we have modeled this influence as occurring indirectly through the effects of self-efficacy on behavior (i.e. the effect of trial and error experience of these self-management skills on the likelihood of engaging in the behavior to subsequently influence self-management skills (β 14)). These self-management or self-regulatory inputs are potentially complex and deserve their own control system model (system within a system), but for simplicity of this model, we have restricted this complexity by representing self-management or self-regulatory skills as a single state variable.
Outcome expectancies (η 2) is another important construct in SCT that contributes to the likelihood of any given behavior [39]. Outcome expectancies are the outcomes an individual expects from engaging in the behavior based on prior experience, observational learning, and/or self-management. Behaviors are followed by positive and/or negative consequences, some proximal and some distal, or lack of consequences. For example, engaging in physical activity could result, short term, in feeling fatigued or less stressed. Social reinforcement may ensue from engaging in physical activity. Over the longer term, physical activity may lead to improved fitness and health or, conversely, to injury. These behavioral outcomes (η 5) produce a positive feedback loop to outcome expectancies (β 25). Experiencing and/or expecting positive outcomes from engaging in the behavior will lead to an increased likelihood of subsequently engaging in the behavior. Experiencing and/or expecting negative outcomes will lead to a decreased likelihood of subsequently engaging in the behavior. This positive feedback loop is consistent with operant conditioning principles, and since operant conditioning also can occur outside of conscious awareness [40], a direct feedback loop from behavioral outcomes back to behavior that has no influence on outcome expectancies is also included in the model.
Based on this feedback loop from behavioral outcomes to outcome expectancy to behavior, individuals should be expected to engage in differing rates of behavior depending on outcome valence (e.g., reinforcing, punishing) and the schedule of reinforcement or punishment (e.g., fixed, intermittent). These behavioral outcomes for any given behavior are greatly influenced by the environmental context in which the behavior occurs (ξ 7). These dynamic changes in environmental context cause the same behavior that is not reinforced or even punished in one context to be reinforced in a different context [41]. Conceptually, the input of environmental context into behavioral outcomes also represents the various factors that influence operant conditioning including the magnitude (i.e., size or amount), latency (i.e., immediate or delayed), and schedules (i.e. fixed or intermittent) of reinforcement that can vary across different environmental contexts. As with other aspects of the SCT model presented here, this “system within a system” is much more complex than the single “environmental context” input presented for simplicity.
The second input into outcome expectancies is observational or vicarious learning (ξ 2). Observing the consequences of the behavior experienced by others adds to or depletes the outcome expectancy inventory for that behavior [39]. For example, observing an individual receiving or experiencing positive attention from others for engaging in physical activity increases the outcome expectancies of the individual engaging in these behaviors. This observational input is core to Bandura’s social learning theory, a precursor to SCT.
The third component that influences outcome expectancies is self-regulatory or self-management skills (β 21) [42]. This set of skills influences the potential successful outcomes attained through engaging in the behavior (i.e., outcome expectancies). In the physical activity example, the individual may decide, based on the information within the SCT system (e.g., social information/persuasion, observation, self-efficacy, outcome expectancies) to set a goal of at least 30 min of exercise every day. The individual can set up a monitoring program to record the frequency and duration of exercise, set incremental goals, assess status at reaching these goals, and self-reward when the goals are met.
Finally, “cue to action” (η 6) directly influences behavior [31]. In SCT, self-efficacy and outcome expectancies are often conceptualized as predispositions for engaging in any given behavior that is then triggered by a cue to action. Given that there are multiple internal and external cues for action at any time-point, we have represented cue to action as an inventory with both external (e.g., friend asks you to take a walk) or internal (e.g., getting tired or stiff from sitting) inputs. These cues can occur naturally (e.g., good weather for a walk) or artificially (e.g., alarm reminder on phone to go for a walk) in the environment.
Although treated as separate inputs in this model, it is important to note that cue to action (η 6) and environmental context (ξ 7) are closely linked. Cue to action is often a discriminative stimulus that signals if a given behavior is more or less likely to be reinforced and has evocative effects on behavior [43]. Therefore, although cue to action and environmental context are treated separately in this model, cues to action are typically formed from the pairing of specific environmental contexts that predict behavioral outcomes.
To account for random variability of observations, all state variables are combined additively with random variables—referred to as disturbances (ζ i). Disturbances represent any uncontrolled factors that influence the inventories and can be thought of as unexplained variance. The inputs of SE, OE, and cues to action are postulated to substantially influence the likelihood of engaging in a behavior, but unaccounted for are factors other than these three inputs that also may directly influence the likelihood that the individual will engage in a given behavior.
It is important in understanding the fluid analogy graphic representation that engaging in the behavior does not result in a depletion of SE, OE, or cue to action. A more useful heuristic is to envision gradations of switches within the inventory that signal when these variables have met certain thresholds, each of which is associated with an increasing level of the frequency/duration of behavior.
Mathematical model of SCT
The process for building the mathematical model parallels the work previously described by Navarro-Barrientos, Rivera, and Collins [16]. Six inventories (state variables) are considered, and their levels are represented by the variables η 1,…,η 6. Seven exogenous signals (inputs) are represented by ξ 1,…,ξ 7. From each inventory, there are a number of inflow resistances represented by the coefficients γ 11,…,γ 68, and outflow resistances represented by β 21,…,β 54. These resistances can be thought of as the fraction of each inventory or input that leave the previous instance and then feeds the next inventory. In the absence of an empirical basis for these inflow and outflow resistance parameters, we refined these parameters based on numerous simulations of the model such that the simulations were consistent with theory and SEM findings.
Parameters that represent the transient time response of each inventory and flow were also specified. Time constants for each inventory τ 1,…,τ 6 represent the capacity of the inventory and allow for exponential decay (or growth) of the inventory to accommodate various learning curves. Time delays (θ 1,…,θ 19) for each flow signal are used. Unmeasured disturbances (which may reflect unmodeled dynamics) are also represented as ζ 1,…,ζ 6. As with the resistance parameters above, in the absence of direct empirical data for specifying these parameters, we set and iterated these parameters via simulations until the model functioned as per theory and empirical data regarding SCT, but all of these parameters should be considered as preliminary hypotheses that require testing and refinement.
In the process of specifying the parameters, we established mathematical relationships such that the sum of all the inflows (increases) minus all the outflows (reductions) for each inventory balance out and results in an accumulation with the rate controlled by the time constant τ times the rate of change (derivative) in the level of the inventory. The differential equations describing the dynamics of the state variables (inventories) are as follows:
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
Although this initial model is a series of first-order linear differential equations, higher-order differential equations may need to be developed to capture under-damped (i.e., oscillatory) dynamics and forms of auto-regulation in each inventory. This is further explained in Navarro-Barrientos, Rivera, and Collins [16].
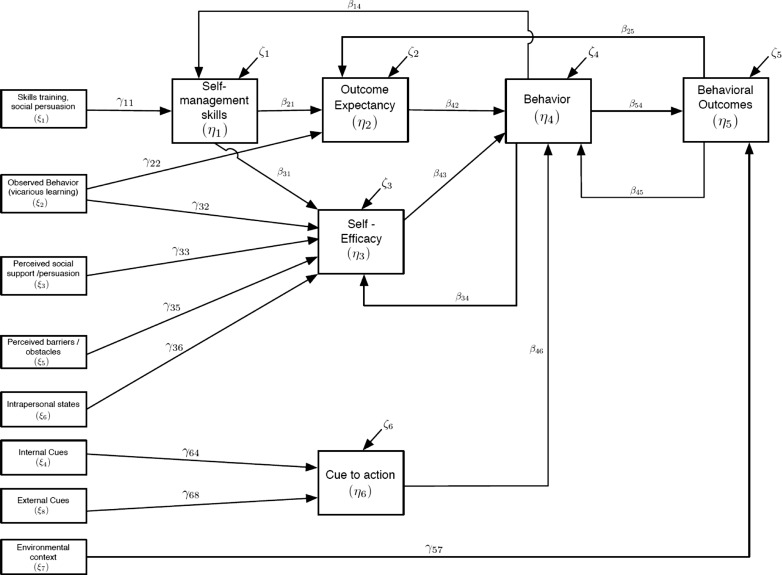
Derivation of a statistical model of SCT
In prior work, Rivera and colleagues [16] utilized path diagrams from the theory of planned behavior (TPB) to construct a dynamical system model and fluid analogy diagram. Since one of the purposes of this project was also to provide a more complete graphical schematic of SCT for statistical modeling, we worked in reverse and used the developed control systems model to generate a path diagram. Figure 3 represents the resulting system of differential equations depicted as a path diagram for those interested in statistical modeling efforts based on this more complete schematic model of SCT.
Fig. 3.
Path diagram of SCT based on fluid analogy in Fig. 1
MODEL SIMULATION OF SCT MODEL APPLIED TO PHYSICAL ACTIVITY
To illustrate the utility of the model, a few of the many scenarios considered in refining this model are depicted showing the dynamic response of the system to different input variations. For illustrative purposes, the inputs are assumed normalized with a range from 0 to 10. The variables were arbitrarily scaled to have values in the range from 0 to 100. Any change in this assumption (i.e., a different metric for expressing the results of a self-report measure) would be compensated for by the scaling parameters (γ).
For the simulations, unmeasured disturbances (ζ i) were considered Gaussian:
Gaussian distributions are commonly assumed to describe random measurement errors, incorporating the definition of finite means and standard deviations. This assumption is a common starting point for signal analysis that can be later improved or refined as required. Two inputs, intrapersonal states (ξ 6) and environmental context (ξ 7) were generated as autoregressive signals computed as:
For scenario 1: ϕ6 = 0.6, ϕ7 = 0.8, σ6 2 = σ7 2 = 100.
For scenarios 2 and 3: ϕ6 = 0.6, ϕ7 = 0.8, σ6 2 = 0.25, σ7 2 = 2.25.
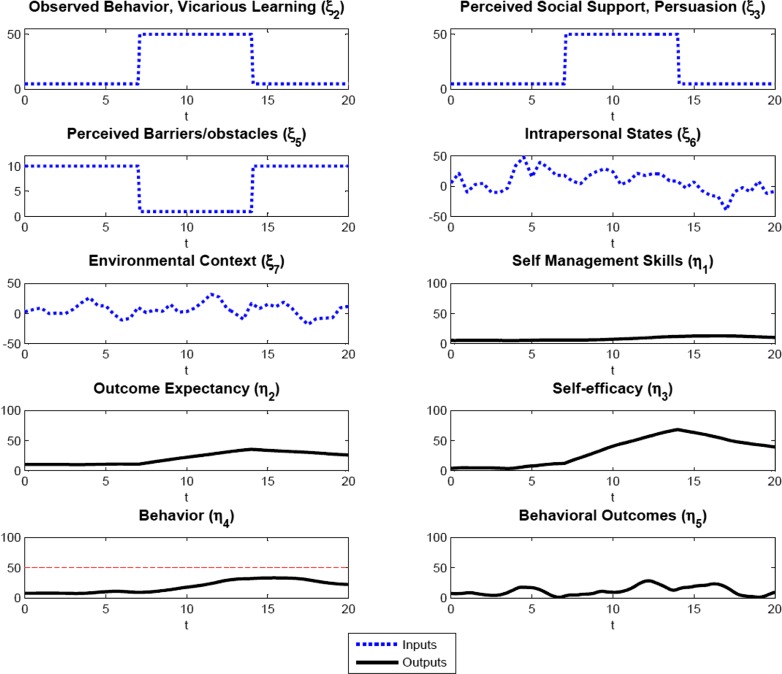
The first scenario, depicted in Fig. 4, is generated both from theory and empirical data showing that increases in self-efficacy produce increases in behavior. Given partial correlations from SEM studies, both direct and indirect, of approximately 0.5 between self-efficacy and behavior [e.g., 10], we assumed for the simulation that 25 % of the variance in behavior should be due to self-efficacy changes. The simulation shown in Fig. 4 shows how changes in social persuasion and observational learning, as one might anticipate would occur from an intervention, results in a change in self-efficacy and a subsequent lagged and attenuated change in behavior that is consistent with 25 % of the variance in behavior accounted for by changes in self-efficacy. Additionally, outcome expectancy also increases, albeit modestly, as self-efficacy increases, consistent with the modest partial correlations observed in SEM trials between self-efficacy and outcome expectancy [11]. This dynamical system model of SCT does not posit a direct relationship between self-efficacy and outcome expectancies, but instead posits that outcome expectancy is influenced indirectly by the effects of self-efficacy on behavior and subsequently on behavioral outcomes. This is in contrast to the conceptual schematic of SCT described by Bandura [29], but we believe that it is more consistent with the principle of reciprocal determinism to postulate that the influence of self-efficacy on outcome expectancies is indirect and mediated by behavioral outcomes.
Fig. 4.
Simulated scenario of changing self-efficacy inputs and effects on behavior
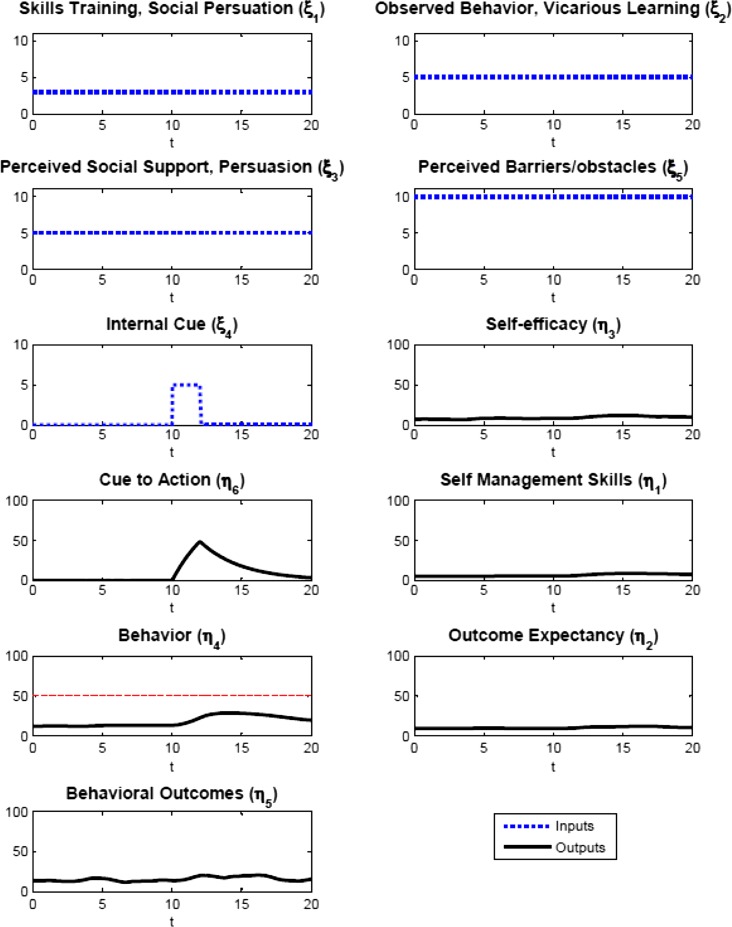
In addition to simulating how changes in self-efficacy affected changes in the other inventories in the model to compare to SEM results, we ran numerous additional simulations to ensure that the model performed as expected as various inputs were manipulated. Although describing all of these additional simulations is beyond the scope of this paper (see http://csel.asu.edu/SCT for additional simulations), we report two additional simulations below involving the effects of a change in cue to action on the model in the context of either low or high self-efficacy. To simulate low self-efficacy, we held skills training (ξ 1 = 3), observed behavior (ξ 2 = 5), and perceived social support (ξ 3 = 5) at a constant low level. Perceived barriers were maintained at a higher value (ξ 5 = 10). Within this context, the input of internal cues are simulated to occur beginning at day 10 (ξ 4 = 5) and ending at day 12 (see Fig. 5). The result of the applied signals on the inventories is a small increase of behavior that subsides when the cue to action is subsequently depleted.
Fig. 5.
Simulated scenario of cue to action under low self-efficacy condition
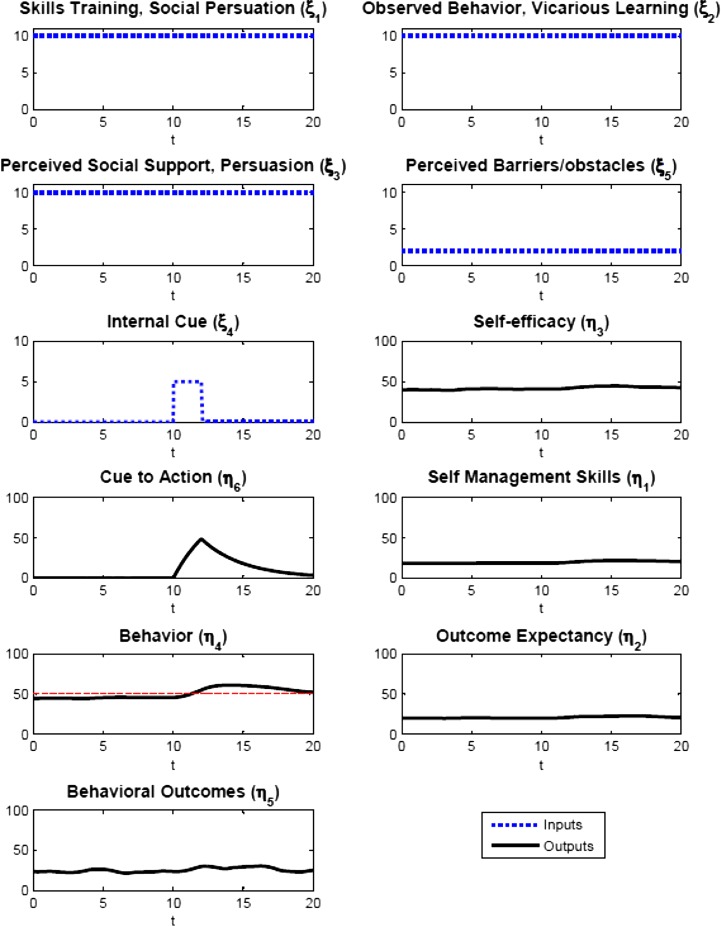
Figure 6 illustrates a similar activity for cue to action at day 10 but within the context of high self-efficacy. Skills training, observed behavior, and perceived social support are kept at high levels (ξ 1 = 10, ξ 2 = 10, ξ 3 = 10) and perceived barriers are decreased to a low level (ξ 5 = 2). The result is a considerable increase of the behavior inventory. In both scenarios, variations in the other inventories (self-management skills, outcome expectancy, and behavioral outcomes) can be observed resulting from the three feedback loops in the system. The simulations represented in Figs. 5 and 6 represent the role of self-efficacy in attenuating the impact of a cue to action on behavior. The model behaves consistent with theory with weaker effects of cues under conditions of low self-efficacy and stronger effects under conditions of high self-efficacy.
Fig. 6.
Simulation scenario of cue to action under high self-efficacy condition
DISCUSSION AND IMPLICATIONS
Although the predominantly narrative nature of SCT and the lack of specificity for some of the interrelations between constructs, especially over time, presented challenges in determining how best to represent SCT from a dynamic systems perspective, social cognitive theory (SCT) is inherently a dynamical system that is amenable to representation as a computational dynamic model. Despite its prominence as the theoretical basis for many health behavior interventions, the process of generating and simulating this model highlighted the lack of precision in the theoretical description of the relations among SCT constructs. First, while some relations are clearly articulated in current theory (e.g., self-efficacy increases the likelihood of engaging in the behavior), other relationships are less clear (e.g., do self-management skills influence self-efficacy and/or vice versa, and is this association direct or indirect via the influence of self-efficacy on behavior?). Second, while SCT describes the presence and direction of the relations between constructs, it does not specify the magnitude or nature of these relations, at least not sufficiently to guide the generation of initial differential equations for a dynamic system model without considerable extrapolation from the theory. Third, like most other health behavior theories, SCT was devised primarily to explain the differences between individuals, but not necessarily changes within individuals over time [44]; therefore, SCT provides little guidance on the time lagged effects of one construct on another or if these effects are linear (remain constant over time) or nonlinear (vary over time). Clearly, one advantage of subjecting any health behavior theory to computational dynamic modeling is that the process results in an improvement in theoretical specificity and opportunities to postulate intervention strategies that target this within-person process more explicitly.
It is important to note that the additional theoretical specificity required to create this model was based on the authors’ understanding and interpretation of SCT. While we strove to be consistent with the theory and existing data on SCT construct relationships, some of the specificity in this model was based not on explicitly stated SCT hypotheses but on what the theory, or its precursors, might lead one to hypothesize. Adhering to SEM analyses of SCT to specify the model also was challenging, especially since we believe the Bandura schematic [29] was a simplified and thus an incomplete conceptual schematic of SCT. The SEM studies reviewed measured only a subset of SCT constructs, found different associations and magnitudes of association, and were often generated from cross-sectional, not longitudinal data. For example, SEMs that included both self-efficacy and outcome expectancies typically found a small to moderate potential influence of self-efficacy on outcome expectancies [10, 11], but for system modeling of intensive longitudinal data over time, it seemed more plausible that this influence of self-efficacy on outcome expectancies was not direct or immediate but instead the result of self-efficacy resulting in increased likelihood of engaging in the behavior and more positive behavioral outcomes that subsequently influenced outcome expectancies. This example is but one of a number of ways in which this influence, and other SCT influences identified by theory and SEM studies, could be modeled as a dynamical system. The intent of this effort was not to produce the definitive dynamical system model of SCT but instead to propose an initial model that could serve as a roadmap for further testing and revision of the model.
The process of developing a fluid analogy system model for SCT and testing this model via a variety of simulations led to some key insights that require further study. First, SCT posits that self-efficacy and behavior form a positive feedback loop which suggests that, over time, self-efficacy should move toward the extremes, all other factors being equal. Consequently, self-efficacy assessed over time should be represented by a bimodal distribution, but self-efficacy scores are typically normally distributed [45]. This suggests that the other inputs into self-efficacy have a greater influence than the positive feedback loop from behavior, that the distribution within an individual over time is different from the distribution across individuals, and/or that self-efficacy is more stable and less influenced by behavior than the theory suggests.
The simulations described in this paper illustrate the potential impact of manipulating various inputs (e.g., observational learning) to target specific theoretical mechanisms (e.g., self-efficacy) to change behavior and the attenuated impacts that might be expected as these manipulations flow through the model. This illustrates an important advantage of dynamical system modeling of SCT or other behavioral theories that such a model allows interventionists to simulate the impact of an intervention that targets specific inputs, including the intensity and duration of intervention dose needed to produce the desired outcome. Similar implications, as well as practical steps utilizing computational modeling to advance health behavior theories and interventions, were described recently by the International Workshop on New Computationally-Enabled Theoretical Models to Support Health Behavior Change and Maintenance [46].
While simulations provide useful iterative feedback on how the model performs on various scenarios, testing the model with actual data is a critical next step. As noted earlier, measurement technologies are advancing rapidly and provide the intensive longitudinal data on behavior and predictors of behavior needed to test and revise these models and the theories they represent. SCT, like many health behavior models, represent a large number of constructs that need to be measured regularly over time to test the full model. Therefore, it may be prudent to test components of the model when data on all components of the model are not available. It also may be useful to start from an historical perspective of SCT and model some of the primary learning processes (e.g., stimulus control, reinforcement, extinction) that have considerable laboratory-based data that can be utilized, and then expand to model social learning processes (e.g., vicarious or observational learning) followed by an expansion to SCT cognitive constructs as needed to improve the model. Modeling these primary learning processes on which SCT is based also better integrates this work with similar modeling efforts in behavioral neuroscience [e.g., 47]. While models are intended to simplify complex systems and although we chose to represent some complex subsystems as single inputs in this model, the result of this effort to provide a complete dynamic model of SCT resulted in a rather complex model. Only by testing various components of the model with actual data will we be able to determine if this complexity is necessary or if the model can be further simplified and streamlined. We believe that this model provides a reasonable starting point for testing various aspects of SCT and that representing SCT as a control system offers a computational robustness and rigor that is critically needed for health behavior theory testing and intervention development.
Acknowledgments
DR and EH were supported by a grant from National Science Foundation (IIS-1449751). DR also was supported by a grant from the National Institute on Drug Abuse (K25DA021173). MP was supported by a grant from the National Institute of Nursing Research (P20NR015320). AK was supported by grants from National Heart, Lung, and Blood Institute (R01HL116448), National Institute of Diabetes and Digestive and Kidney Diseases (R01DK102016), and National Institute of Biomedical Imaging and Bioengineering (U54EB020405). This paper represents the views and perspectives of the authors, not the funders or the National Institutes of Health. All authors participated in this article and take responsibility for the integrity of the conceptualizations and models described.
Compliance with ethical standards
This article presents conceptual and computational models; no human subject data were collected.
Conflict of interest
The authors declare that they have no competing interests.
Footnotes
Implications
Researchers: Using this initial computational dynamic model social cognitive theory (SCT) as a guide, researchers can test interrelations of SCT constructs that go beyond covariation and specify how much and in which ways SCT constructs influence one another.
Practitioners: Based on these theory-derived SCT equations, interventionists can generate hypothetical estimates of how much of a change in various SCT constructs is necessary to produce a clinically meaningful change in behavior.
Policymakers: These theory-derived SCT equations can generate hypothetical estimates of how policies targeting specific SCT parameters might impact behavior.
References
- 1.Glanz K, Bishop DB. The role of behavioral science theory in development and implementation of public health interventions. Annu Rev Public Health. 2010;31:399–418. doi: 10.1146/annurev.publhealth.012809.103604. [DOI] [PubMed] [Google Scholar]
- 2.Cole K, Waldrop J, D'Auria J, et al. An integrative research review: effective school-based childhood overweight interventions. Journal for Specialists in Pediatric Nursing. 2006;11:166–177. doi: 10.1111/j.1744-6155.2006.00061.x. [DOI] [PubMed] [Google Scholar]
- 3.Lopez LM, Tolley EE, Grimes DA, et al. Theory-based interventions for contraception. Cochrane Database Syst Rev. 2011; CD007249. [DOI] [PubMed]
- 4.Villanti AC, McKay HS, Abrams DB, et al. Smoking-cessation interventions for U.S. young adults: a systematic review. Am J Prev Med. 2010;39:564–574. doi: 10.1016/j.amepre.2010.08.009. [DOI] [PubMed] [Google Scholar]
- 5.Norman GJ, Zabinski MF, Adams M, et al. A review of eHealth interventions for physical activity and dietary behavior change. Am J Prev Med. 2007;33:336–345. doi: 10.1016/j.amepre.2007.05.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Riley WT, Rivera DE, Atienza AA, et al. Health behavior models in the age of mobile interventions: are our theories up to the task? Translational Behavioral Medicine. 2011;1:53–71. doi: 10.1007/s13142-011-0021-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bandura AA, Walters RH. Social Learning and Personality Development. New York: Holt, Rinehart & Winston; 1963. [Google Scholar]
- 8.Bandura A. Self-efficacy: toward a unifying theory of behavior change. Psychol Rev. 1977;84:191–215. doi: 10.1037/0033-295X.84.2.191. [DOI] [PubMed] [Google Scholar]
- 9.Bandura A. Social Foundations of Thought and Action. Englewood Cliffs: Prentice Hall; 1986. [Google Scholar]
- 10.Anderson-Bill ES, Winett RA, Wojcik JR. Social cognitive determinants of nutrition and physical activity among web-health users enrolling in an online intervention: the influence of social support, self-efficacy, outcome expectations, and self-regulation. Journal of Medical Internet Research. 2011;13 doi: 10.2196/jmir.1551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lubans DR, Plotnikoff RC, Morgan PJ, et al. Explaining dietary intake in adolescent girls from disadvantaged secondary schools. A test of Social Cognitive Theory. Appetite. 2012;58:517–524. doi: 10.1016/j.appet.2011.12.012. [DOI] [PubMed] [Google Scholar]
- 12.Safren SA, Traeger L, Skeer M, et al. Testing a social-cognitive model of HIV transmission risk behaviors in HIV-infected MSM with and without depression. Health Psychol. 2010;29:215–221. doi: 10.1037/a0017859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Rimal RN. Longitudinal influences of knowledge and self-efficacy on exercise behavior: tests of a mutual reinforcement model. J Health Psychol. 2001;6:31–46. doi: 10.1177/135910530100600103. [DOI] [PubMed] [Google Scholar]
- 14.Dishman RK, Dunn AL, Sallis JF, et al. Social-cognitive correlates of physical activity in a multi-ethnic cohort of middle-school girls: two year prospective study. J Pediatr Psychol. 2010;35:188–198. doi: 10.1093/jpepsy/jsp042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Deboeck PR, Bergeman CS. The reservoir model: a differential equation model of psychological regulation. Psychol Methods. 2013;18:237–256. doi: 10.1037/a0031603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Navarro-Barrientos JE, Rivera DE, Collins LM. A dynamical model for describing behavioural interventions for weight loss and body composition change. Math Comput Model Dyn Syst. 2011;17:183–203. doi: 10.1080/13873954.2010.520409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Rivera DE, Pew MD, Collins LM. Using engineering control principles to inform the design of adaptive interventions: a conceptual introduction. Drug Alcohol Depend. 2007;88:S31–S40. doi: 10.1016/j.drugalcdep.2006.10.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Riley WT, Serrano KJ, Nilsen W, et al. Mobile and wireless technologies in health behavior and the potential for intensively adaptive interventions. Current Opinion in Psychology. 2015;5:67–71. doi: 10.1016/j.copsyc.2015.03.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hanneman RA. Computer-Assisted Theory Building: Modeling Dynamic Social Systems. Newbury Park: Sage Publications; 1988. [Google Scholar]
- 20.Powers WT. Feedback: beyond behaviorism. Science. 1973;179:351–356. doi: 10.1126/science.179.4071.351. [DOI] [PubMed] [Google Scholar]
- 21.Wiener N. Cybernetics: On Communication and Control in Animals and Machines. Cambridge: MIT Press; 1948. [Google Scholar]
- 22.Carver CS, Scheier MF. On the Self-regulation of Behavior. Cambridge: Cambridge University Press; 2001. [Google Scholar]
- 23.Bandura A. The self system in reciprocal determinism. Am Psychol. 1978;33:344–358. doi: 10.1037/0003-066X.33.4.344. [DOI] [Google Scholar]
- 24.Shiffman S, Stone AA, Hufford MR. Ecological momentary assessment. Annu Rev Clin Psychol. 2008;4:1–32. doi: 10.1146/annurev.clinpsy.3.022806.091415. [DOI] [PubMed] [Google Scholar]
- 25.Chan M, Esteve D, Fournois J-Y, et al. Smart wearable systems: current status and future challenges. Psychol Health. 2012;27:1009–1020. doi: 10.1080/08870446.2011.645213. [DOI] [PubMed] [Google Scholar]
- 26.Orr MG, Thrush R, Plaut DC. The Theory of Reasoned Action as parallel constraint satisfaction: towards a dynamic computational model of health behavior. PLoS One. 2013;8 doi: 10.1371/journal.pone.0062490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ajzen I. The theory of planned behavior. Organ Behav Hum Decis Process. 1991;50:179–211. doi: 10.1016/0749-5978(91)90020-T. [DOI] [Google Scholar]
- 28.Bandura A. The evolution of social cognitive theory. In: Smith G, Hitt MA, editors. Great Minds in Management. Oxford: Oxford University Press; 2005. pp. 9–35. [Google Scholar]
- 29.Bandura A. Health promotion by social cognitive means. Health Education and Behavior. 2004;31:143–164. doi: 10.1177/1090198104263660. [DOI] [PubMed] [Google Scholar]
- 30.Williams DM, Anderson ES, Winett RA. A review of the outcome expectancy construct in physical activity research. Ann Behav Med. 2005;29:70–79. doi: 10.1207/s15324796abm2901_10. [DOI] [PubMed] [Google Scholar]
- 31.Bandura A. Social Learning Theory. Oxford: Prentice-Hall; 1977. [Google Scholar]
- 32.Bandura A. Social cognitive theory. In: Van Lange PAM, Kruglanski AW, Higgins TE, editors. Handbook of Theories of Social Psychology (Vol 1) Thousand Oaks: Sage Publications; 2012. pp. 349–373. [Google Scholar]
- 33.Forrester J. Counterintuitive behavior of social systems. Technol Rev. 1971;73:52–68. [Google Scholar]
- 34.Savage JS, Downs DS, Dong Y, et al. Control systems engineering for optimizing a prenatal weight gain intervention to regulate infant birth weight. Am J Public Health. 2014;104:1247–1254. doi: 10.2105/AJPH.2014.301959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ayotte BJ, Margrett JA, Hicks-Patrick J. Physical activity in middle-aged and young-old adults: the roles of self-efficacy, barriers, outcome expectancies, self-regulatory behaviors and social support. J Health Psychol. 2010;15:173–185. doi: 10.1177/1359105309342283. [DOI] [PubMed] [Google Scholar]
- 36.Hekler EB, Buman MP, Ahn D, et al. Are daily fluctuations in perceived environment associated with walking? Psychol Health. 2012;27:1009–1020. doi: 10.1080/08870446.2011.645213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Gariépy JF, Watson KK, Du E, et al. Social learning in humans and other animals. Front Neurosci. 2014;8:58. doi: 10.3389/fnins.2014.00058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Bandura A. Social cognitive theory of self-regulation. Organ Behav Hum Decis Process. 1991;50:248–287. doi: 10.1016/0749-5978(91)90022-L. [DOI] [Google Scholar]
- 39.Bandura A. Self-regulation of motivation and action through goal systems. In: Hamilton V, Bower GH, Frijda NH, editors. Cognitive Perspectives on Emotion and Motivation. NATO ASI series D: Behavioural and social sciences. New York: Kluwer; 1988. pp. 37–61. [Google Scholar]
- 40.Kirsch I, Lynn SJ, Vigorito M, et al. The role of cognition in classical and operant conditioning. J Clin Psychol. 2004;60:369–392. doi: 10.1002/jclp.10251. [DOI] [PubMed] [Google Scholar]
- 41.Hovell MF, Walgren DR, Adams MA. The logical and empirical basis for the behavioral ecological model. In: DiClemente RJ, Crosby RA, Kegler MC, editors. Emerging Theories in Health Promotion Practice and Research. Strategies for Enhancing Public Health (2nd ed.) San Francisco: Jossey-Bass Publishers; 2009. pp. 415–449. [Google Scholar]
- 42.Bandura A. The primacy of self-regulation in health promotion. Applied Psychology: An International Review. 2005;54:245–254. doi: 10.1111/j.1464-0597.2005.00208.x. [DOI] [Google Scholar]
- 43.Dickinson A, de Wit S. The interaction between discriminative stimuli and outcomes during instrumental learning. The Quarterly Journal of Experimental Psychology B: Comparative and Physiological Psychology. 2003;56B:127–139. doi: 10.1080/02724990244000223. [DOI] [PubMed] [Google Scholar]
- 44.Dunton GF, Atienza AA. The need for time-intensive information in healthful eating and physical activity research: a timely topic. J Am Diet Assoc. 2009;109:30–35. doi: 10.1016/j.jada.2008.10.019. [DOI] [PubMed] [Google Scholar]
- 45.Romppel M, Hermann-Lingen C, Wachter R, et al. A short form of the General Self-Efficacy Scale (GSE-6): development, psychometric properties and validity in an intercultural non-clinical sample and a sample of patients at risk for heart failure. Psychosoc Med. 2013; 10, Doc01. [DOI] [PMC free article] [PubMed]
- 46.Spruijt-Metz D, Hekler E, Saranummi N, et al. Building new computational models to support health behavior change and maintenance: new opportunities in behavior research. Translational Behavioral Medicine. 2015;5:335–346. doi: 10.1007/s13142-015-0324-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Sheynin J, Moustafa AA, Beck KD, et al. Testing the role of reward and punishment sensitivity in avoidance behavior: a computational modeling approach. Behavior and Brain Research. 2015;283:121–138. doi: 10.1016/j.bbr.2015.01.033. [DOI] [PMC free article] [PubMed] [Google Scholar]