The duration of reaching movement is longer than predicted by minimum variance

Despite more than a century of research, it is unclear how we select the duration of arm movements. Here we show that the preferred duration is longer than the duration that minimizes end-point variability. These results show the need to modify the minimum variance theory of motor control. Instead, our data are consistent with the view that humans choose movement durations that achieve a compromise between minimum variance and minimum effort.

Abstract

Whether the central nervous system minimizes variability or effort in planning arm movements can be tested by measuring the preferred movement duration and end-point variability. Here we conducted an experiment in which subjects performed arm reaching movements without visual feedback in fast-, medium-, slow-, and preferred-duration conditions. Results show that 1) total end-point variance was smallest in the medium-duration condition and 2) subjects preferred to carry out movements that were slower than this medium-duration condition. A parsimonious explanation for the overall pattern of end-point errors across fast, medium, preferred, and slow movement durations is that movements are planned to minimize effort as well as end-point error due to both signal-dependent and constant noise.

NEW & NOTEWORTHY

Despite more than a century of research, it is unclear how we select the duration of arm movements. Here we show that the preferred duration is longer than the duration that minimizes end-point variability. These results show the need to modify the minimum variance theory of motor control. Instead, our data are consistent with the view that humans choose movement durations that achieve a compromise between minimum variance and minimum effort.

although most motor tasks can be carried out in an infinite number of ways with our redundant musculoskeletal system, arm movements exhibit striking regularities. In particular the durations of reaching movements vary systematically with the amplitudes and the directions of movements (Gordon et al. 1994). According to the optimal control theory of human motor control (e.g., Flash and Hogan 1985; Hoff 1994; Uno et al. 1989), these regularities correspond to the minimum of a cost function that the central nervous system (CNS) considers in planning motion. Despite much research on this topic, however, it is still unclear how the CNS determines the duration of movement during planning.

The stochastic optimal control model of Harris and Wolpert (1998, 2006) proposes that the CNS determines movement planning by minimizing the movement end-point variability due to signal-dependent noise. Although this model successfully predicts trajectories and durations of saccadic eye movements and planar arm reaching movements, it is not clear whether movement end-point variability or effort is minimized. Indeed, mathematically, the expression of movement end-point error due to signal-dependent noise in the motor commands and the expression of effort are equivalent (O'Sullivan et al. 2009).

Minimizing effort (or, equivalently, minimizing end-point variability due to signal-dependent noise) will slow down planar movements, because the torques necessary to move the arm decrease with an increase in movement duration.¹ For instance, movements performed by the right hand to leftward targets are slower than movements to rightward targets (Gordon et al. 1994; Park et al. 2016). This can be attributed to greater effort (or equivalently signal-dependent noise) for leftward targets because of greater inertia at the hand for these movements (Cos et al. 2011; Guigon et al. 2007; Schweighofer et al. 2015).

In addition to signal-dependent noise, motor commands are also corrupted by constant noise (van Beers 2007; van Beers et al. 2004). Although such constant noise was not considered in the models of Harris and Wolpert (1998, 2006) and of O'Sullivan et al. (2009), it can be quite substantial. For instance, by fitting the end-point distributions generated by simulated arm movements to actual data, van Beers et al. (2004) estimated that the standard deviation of constant noise is about twice that of signal-dependent noise. Minimizing variability due to constant noise shortens the movement, because variability due to this type of noise increases with movement duration [see Fig. 1 in Todorov (2005) for simulation results of the respective effects of signal-dependent and constant noise for varying durations of arm movements]. Thus minimizing variability due to both signal-dependent and constant noise would yield a minimum that could determine movement duration. Correspondingly, our first hypothesis is that the CNS chooses intermediate reaching movement durations to minimize end-point variability in the face of signal-dependent and constant noise.

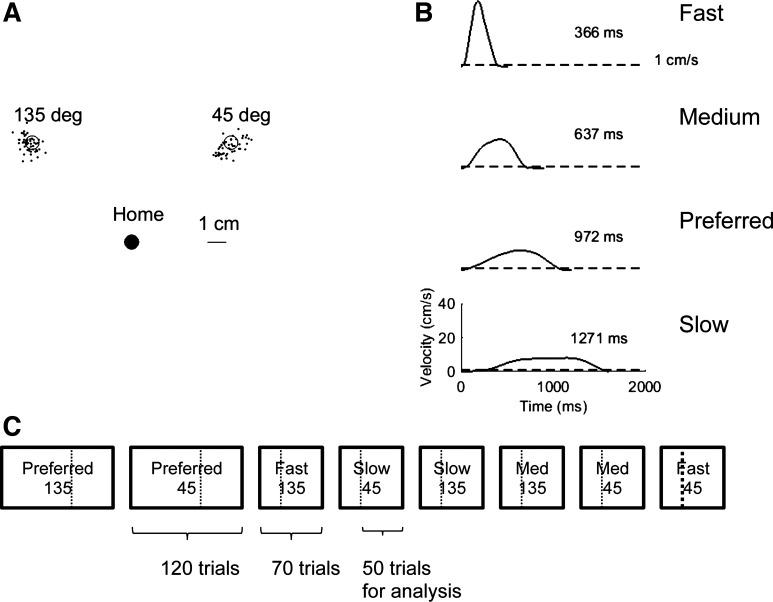
Fig. 1.

Methods overview. A: subjects performed horizontal reaching movements without online visual feedback to 45° and 135° targets in 4 duration conditions: preferred, fast, medium, and slow. The black dots around the targets show end points for 1 subject in the preferred condition. For each condition and each target, we measured end-point variability from the variance of the end-point distribution. B: example of velocity profiles in the 4 conditions: preferred, fast, medium, and slow. The movement duration was determined via a tangential velocity threshold of 1 cm/s. C: timeline of the experiment: example of the schedule for 1 subject. The 2 preferred movement blocks were always given first to avoid biasing the preferred duration by other conditions (the order of the 2 blocks were counterbalanced across subjects). The other 6 blocks (3 conditions, 2 targets) were then given, with the order counterbalanced for targets and conditions. Only the last 50 trials of each block (shown by dotted line) were analyzed, to remove possible initial drift and carryover in movement duration at the beginning of the blocks.

While minimizing end-point variability due to both signal-dependent and constant motor noise would be sufficient to determine the duration of movements, the results of Burdet et al. (2001) suggest that effort minimization contributes to movement planning in addition to noise. In that experiment, training arm reaching movements in a divergent force field led to reduced end-point variability by increasing cocontraction of antagonist muscles. If the CNS only minimized end-point variability, then it would use this energetically costly cocontraction strategy to reduce end-point error (Osu et al. 2004). The fact that habitual movements (performed without force field) yield more relaxed muscle activity than in the experiment of Burdet et al. suggests that the CNS also minimizes effort. Minimization of effort independently from minimization of end-point variability due to signal-dependent and constant noise sources would lengthen movement duration.

Our second hypothesis is therefore that the CNS chooses intermediate durations that are longer than those minimizing variability. To test these two hypotheses and examine how humans select movement durations, we conducted an arm movement experiment without visual feedback and measured end-point variability in movements of four duration conditions, fast, medium, slow, and preferred, in which subjects choose to move at their preferred speed. The results verify our hypotheses, providing evidence for the concurrent minimization of effort and variability due to signal-dependent and constant motor noise.

METHODS

Eleven young adult right-handed volunteers (between 20 and 30 yr old; 3 women, 8 men) with no declared neurological impairments gave written informed consent to participate in the experiment described below, approved by the University of Southern California Ethics Committee.

Subjects performed reaching movements with their right arms to one of two targets at 45° and 135° (relative to the rightward direction parallel to the body) without online visual feedback in four conditions: preferred, fast, medium, and slow (Fig. 1, A and C). Hand movements were recorded via a digitizing pen moving on a tablet (Wacom Tech). The tablet height was positioned such that the arm was moving approximately in a two-dimensional horizontal plane, with movements primarily involving horizontal shoulder and elbow rotations. The home position was placed such that the shoulder formed approximately a 45° angle with the coronal plane and the elbow flexed at 90°. The distance from home position to targets was 7.4 cm. Target positions (45° and 135°) were selected to maximize the difference in inertia at the hand (see Gordon et al. 1994). To minimize fatigue due to the large number of trials, the forearm was supported with a sling attached to a ∼4-m-long cable hanging from the ceiling. Because of the long cable length, the pendulum effect was small.

In the preferred condition, subjects reached for the targets as accurately as possible using their own selected movement duration (they were instructed to “reach naturally”). In the fast, medium, and slow conditions, subjects reached for the targets quickly (<350 ms), at a medium speed (400–800 ms), and slowly (>1,200 ms), respectively (Fig. 1B). When the movement duration was outside the range, a “too fast” or “too slow” message was displayed and the trial was repeated. After a “go” signal, subjects were instructed to aim at the target presented on a computer screen facing the subjects. Final cursor position was displayed for 1 s after the recording period (900 ms for fast, 1,400 ms for intermediate, 2,400 ms for preferred and slow movement conditions).

Subjects first practiced all conditions in a familiarization session with online visual feedback of the cursor position, with 25 trials in each condition. To avoid possible carryover effects, the preferred movement duration condition was performed first, with the order of the two targets counterbalanced across subjects (Fig. 1C). Subjects performed 120 trials for each target in the preferred condition and then 80 trials in the other six conditions (3 movement durations, fast, medium, slow for both targets), which were counterbalanced across subjects. The numbers of trials were determined in a pilot study, in which we noted that movement duration and final error stabilized only after a few dozen trials and that more trials were needed in the preferred condition for this stabilization to occur. This was confirmed in preliminary mixed-model analysis of the actual experiment, which showed a significant effect of a trial covariate on movement duration when all trials were considered. This effect disappeared (P > 0.05) when only the last 50 trials in each condition and target were analyzed. Thus, for each subject, 400 movements were analyzed (50-trial block for each target in the 4 duration conditions).

End-point variance was computed by the trace of the covariance matrix of the end-point distribution (Fig. 1A). Because total end-point variance was highly right-skewed, we analyzed the natural logarithm of total variance, which was approximately normal, as shown by both absolute values of skewness and kurtosis < 2. Movement duration (MD) was computed with a velocity threshold of 1 cm/s across all conditions (Fig. 1B).

We report the estimates of fixed effect parameters. MD and mean logarithm of variance were analyzed with mixed-effect models, with condition (fast, medium, preferred, and slow) and target (45° and 135°) and their interaction as fixed effects and subjects as random intercepts. Bonferroni corrections were used for multiple comparisons. We used SPSS 18 with Restricted Maximum Likelihood method for these statistical analyses.

RESULTS

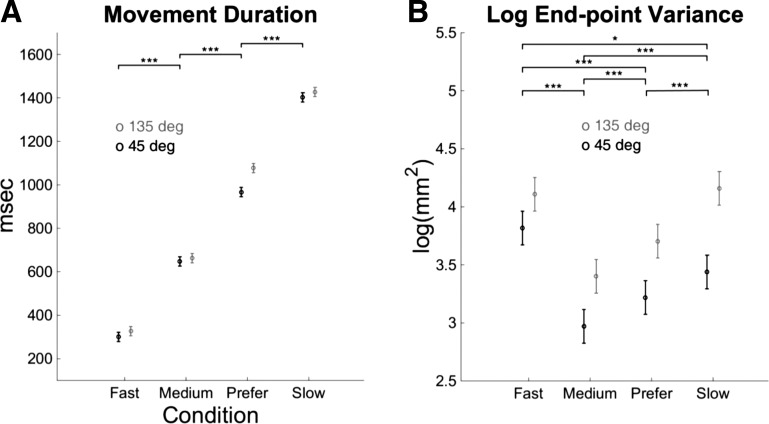
Mixed-model analysis shows significant fixed effects of condition and target on MD (both with P < 0.0001) as well as a significant condition × target interaction (P < 0.0001; Fig. 2A). Overall, the subjects' preferred MDs were longer than the medium MD and shorter than the slow MD (Fig. 2A; P < 0.0001). In addition, MD was overall smaller for targets at 45° compared with targets at 135° (Fig. 2A). Individual comparisons with Bonferroni corrections show that MD was shorter for the target at 45° compared with the target at 135° for the fast condition (P = 0.003), the slow condition (P = 0.006), and the preferred condition, for which the difference was the largest (967 ms vs. 1,077 ms, P < 0.0001). The difference between MD for the 45° and 135° targets was not significantly different for the medium condition (P = 0.097).

Fig. 2.

Movement duration and end-point movement variability in each condition for the 45° and 135° targets across subjects in experiment 1. A: movement duration in the 4 conditions for both targets. B: natural logarithm of end-point variance in the 4 conditions for both targets. Both panels show estimated fixed effect coefficients with their confidence intervals in a model using mixed models with condition and target as main effects and target × condition interactions; see text for details. Asterisks show significance of difference between conditions for both targets (Bonferroni corrected): *P < 0.05, ***P < 0.0005; see text for additional comparison results.

Mixed-model analysis shows significant fixed effects of condition and target on the (logarithm of) total end-point variance (both with P < 0.0001) as well as a significant condition × target interaction (P = 0.003). End-point variance was lowest for the medium duration (Fig. 2B). Notably, for both targets, total end-point variance in the medium movement duration condition was smaller than that in the preferred condition (P < 0.0001). Total variance in the fast condition was greater than in the three other conditions (P < 0.0001, P < 0.0001, and P = 0.029 for medium, preferred, and slow conditions, respectively). Variance in the slow condition was greater than variance in the preferred and medium conditions (P < 0.0001 for both).

For all conditions, variance was greater for the 135° target than for the 45° target (all P < 0.0001). For the 45° target, all differences between conditions were significant (P < 0.0001), except for variance between fast and slow conditions, for which P = 1. For the 135° target, all differences were significant at P < 0.001, except for the differences between preferred and medium, which was significant at P = 0.015, and between preferred and slow, which was significant at P = 0.027.

DISCUSSION

It has long been known that the duration of arm movements has an effect on end-point variability (Fitts 1954; Woodworth 1899), but the relationship had not been systematically characterized. The present study provides two valuable additions to our understanding of movement planning.

First, our results show that, in arm reaching movement without visual feedback, an intermediate movement duration minimizes end-point variability. Such minimum of end-point variability was previously found in saccadic movements (van Beers 2008) but, to our knowledge, not in arm reaching movements. Kinematic variability in human motion originates from a number of sources (Faisal et al. 2008). In particular, the noise in individual motor neurons is well approximated by signal-dependent noise (see rationale in Harris and Wolpert 1998). However, noise in the final motor command departs from signal-dependent noise because this aggregate command combines the activities of many motor neurons distributed over multiple muscles. It is in particular possible that cocontraction yields a departure from signal-dependent noise. As a result, studies aimed at identifying the properties of noise in the motor commands of saccades (van Beers 2007) and arm movements (van Beers et al. 2004) found that the noise is best characterized as a combination of signal-dependent noise and constant noise, with constant noise making a substantial contribution. With these two sources of noise, signal-dependent noise increases end-point variability for short movement durations and constant noise increases variability for long movement durations by inducing a drift in final position.

The variability in task execution caused by the inherent noisiness of the neuromuscular system can be reduced by feedback mechanisms. In our experiment, movements were performed without vision, and thus only proprioceptive feedback was available to the subjects. The effect of proprioceptive feedback on movements appears small for movements at normal speed [see, e.g., Fig. 4 in Franklin et al. (2007)]. However, for slower movements the effect of such feedback on end-point error may become more important, especially with vision. Future work will be needed to compare variability with and without vision at different and self-chosen speed.

Second, our results show that the durations of reaching movements chosen by our subjects were longer than the durations minimizing end-point variance. Thus, unlike what has been suggested for arm movements (Harris and Wolpert 1998, 2006), natural movements without vision at self-selected speed do not minimize variance. The longer preferred durations than the duration that minimizes variance may be due to effort minimization, which tends to lengthen movement duration. Our between-target results, as well as those from previous studies (e.g., Gordon et al. 1994; Park et al. 2016) showing that subjects slowed down for movements toward the 135° target, which require greatest (estimated) effort because of greater inertia at the hand (see Schweighofer et al. 2015), are consistent with this view.

We therefore propose that movement duration is determined by minimizing both variability and effort in the context of signal-dependent noise and constant noise in the motor command. In optimal control models of movements, the duration is determined to minimize antagonistic factors. In previous models, effort and signal-dependent noise were considered as factors to lengthen movement duration, and cost of time (Hoff 1994) and temporal discounting (Haith et al. 2012; Rigoux and Guigon 2012; Shadmehr et al. 2010) were considered as a factor to shorten it. However, if we consider that constant noise is responsible for greater variability in slow movements, no additional factor is needed to shorten movement time. Instead, using a combination of signal-dependent noise and constant noise, simultaneous minimization of effort and end-point variability provides a parsimonious mechanistic explanation for the overall pattern of errors across the fast, medium, preferred, and slow movement durations. In future work, estimating effort for different targets and speeds via quantification of metabolic costs (e.g., Huang et al. 2012) will be necessary to determine whether the minimization of variability and effort is sufficient to determine movement time.

GRANTS

This work was funded in part by National Institute of Child Health and Human Development Grant R01-HD-065438 and National Science Foundation Grant BCS 1031899 to N. Schweighofer. E. Burdet is funded in part by the EU-FP7 grants CONTEST (ITN-317488), BALANCE (ICT-601003), and SYMBITRON (ICT-661626) and EU-H2020 grant COGIMON (ICT-23-2014).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

C.W., Y.X., J.G., and N.S. conception and design of research; C.W. and Y.X. performed experiments; C.W., Y.X., and N.S. analyzed data; C.W., Y.X., E.B., and N.S. interpreted results of experiments; C.W. and N.S. prepared figures; C.W., E.B., J.G., and N.S. edited and revised manuscript; C.W., Y.X., E.B., J.G., and N.S. approved final version of manuscript; E.B. and N.S. drafted manuscript.